Modulational Instability and Discrete Localized Modes in Two Coupled Atomic Chains with Next-Nearest-Neighbor Interactions

Abstract

A pair of one dimensional atomic chains which are coupled via the Klein-Gordon potential is considered in this study, with each chain experiencing both nearest and next-nearest-neighbor interactions. The discrete nonlinear Schrödinger amplitude equation with next-nearest-neighbor interactions is thus derived from the out-phase equation of motion of the coupled chains. This is achieved by using the rotating wave approximations perturbation method, in which both the carrier wave and envelope are explicitly treated in the discrete regime. It is shown that the next-nearest-neighbor interactions greatly modifies the region of observation of modulational instability in the atomic chain. By exploring the discrete Hirota-Bilinear method, we obtain the discrete one-soliton solution which is localized around the origin and structurally stable because it conserves it form as time evolves. However when the atomic chain is purely subjected to a symmetric coupling potential, we observe a structurally unstable discrete excitation that changes into an up-and-down asymmetric localized modes; both in the presence and absence of next-nearest-neighbor interactions. Results of numerical simulations clearly depicts the long term evolution of these discrete nonlinear excitations, that evolve from symmetric to asymmetric localized modes in the atomic chain.

1 Introduction

Modulational instability (MI) is an ubiquitous phenomena in nonlinear dynamics that have been observed in a broad spectrum of systems ranging from dual-core nonlinear optical fiber [1], nonlinear LC self-dual circuits [2], fibers with random polarization mode dispersion [3], negative refractive index medium [4], discrete optical nonlinear arrays [5], Bose-Einstein condensates [6, 7], deoxyribonucleic acid (DNA) chains [8], plasmas [9], among other nonlinear physical systems. In fact, MI is generally observed in systems where there is a dynamic balance between nonlinearity and dispersion, and characterized by small amplitude and phase perturbations growing exponentially.

Since the discovery of solitary waves by John Scott Russell, solitons have been experimentally observed in many spatially discrete physical systems, such as granular materials, nonlinear Hamiltonian lattices [10], electrical transmission lines, and neural networks [11,12,13,14]. The recurrence phenomenon was originally observed in the Fermi-Pasta-Ulam lattice [15, 16]. The eventual formulation of the soliton concept by Zabusky and Kruskal to elucidate on the recurrence phenomenon, triggered enormous interest in scientists around the world to investigate on this fascinating soliton entity [16]. Of particular interest is in discrete regimes, where the role and consequences of MI have been extensively studied within the frame work of discrete nonlinear Schrödinger (DNLS) amplitude equations [17,18,19,20,21,22,23,24,25]. This generally leads to the observation of discrete breathers, that were first identified by Takeno and Sievers in a perfect anharmonic lattice [26, 27]. Physically, the discrete MI emanates from the interplay between nonlinearity and spatial discreteness, and a potential mechanism for the formation of nonlinear localized modes. This fully accounts for energy localization in discrete nonlinear lattices [28].

Numerous research activities in the past have so far concentrated on the properties of MI and discrete breathers in the DNLS equation, with nearest-neighbor (NN) interactions. However to effectively study the dynamics of most real physical systems, necessary measures must be taken to incorporate long-range coupling interactions, which may play an important role in explaining some important physical processes in the discrete lattice. In this light, we see that charged groups of molecules which are mediated by Coulomb interactions in DNA systems are governed by long range interactions [29,30,31,32,33]. The dipole-dipole interaction characterized by a typical long range power law dependence within molecular subunits, mimics a long-range interaction that is responsible for exciton and vibron energy transfers in biomolecules and crystals [34]. Also, in the dynamics of excitons and photons interaction in semiconductors, the polariton effects naturally leads to long range interaction radius in molecular crystals [29, 30, 35]. Furthermore an optical zigzag waveguide array [36], depicts a classical zigzag lattice model which have been successfully applied to improving the next-nearest-neighbor (NNN) coupling in some planar lattices. The NNN coupling is thus enhanced, and eventually leads to a modification of the region of linear dispersion curve. Consequently, there is an increase in the range of allowed frequencies for the effective propagation of electromagnetic waves in photonic crystal waveguide and coupled resonator optical waveguide in the form of robust soliton entity with minimal distortions [36]. The NNN interactions of peptide groups along a polypeptide chain enhances stability in the secondary structure of $\alpha -$helix and $\beta -$sheet regions of proteins [31, 34]. Finally results from studies carried out, strongly suggests that the NNN coupling accounts for interesting phenomena in discrete lattices. These include the identification of the staggering and unstaggering stationary localized breather modes [20], observation of pulse propagation in nonlinear photonic crystal wave guides [36], existence of bright and dark discrete breathers in $\phi ^4$ nonlinear lattice [37], linear increase of the input power required for soliton formation in lattices [38], and the reversal phenomenon of the propagation direction of the Brillouin zone boundary mode [39]. This study mainly captures a generic model of an atomic lattice and theoretically investigate on the effects of the NNN coupling, with potential applications in quantum-information storage [40] and DNA systems [41] serving like a driving force behind our current investigation.

In this work, we consider two atomic chains which are nonlinearly coupled via Klein-Gordon potential, and experiencing both nearest and NNN interactions. Consequently in Sect. 2, we obtain the Hamiltonian of the coupled chains and explore the Hamilton-Jacobi formalism to obtain the appropriate equations of motion. By using the rotating wave approximation scheme in which both the amplitude and phase of the wave are constraint in the discrete regime, the DNLS amplitude equation with NNN interaction is obtained. In Sect. 3 we discuss the stability of carrier plane wave solutions of the DNLS equation with NNN coupling. Regions of occurrence of MI in the parameter space are identified, with the influence of NNN interaction on this parameter space demonstrated. Analysis in Sect. 4 focuses on analytically obtaining discrete breather mode solutions of the amplitude equation, with the help of the Hirota’s binilearization method. We also utilize a numerical integration based on the standard fourth order runge-Kutta scheme, to investigate the effects of the NNN interactions on the evolution of discrete localized modes in the atomic chain. Finally we give a brief summary in Sect. 5.

2 The Model

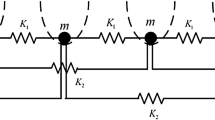
Figure 1 depicts the mechanical model of the two one-dimensional atomic chains under consideration. We assume that each atom on each chain is subjected to linear interactions with its nearest and NNN couplings on the same chain. The atoms are equally spaced along each chain in the rest position. The chains are lying parallel to each other and nonlinearly coupled by nonlinear springs represented by the hollow rectangular blocks, and the coils represent linear springs. In forming kinetic equations for the motion of such a lattice, we assume that all atoms have identical mass m, the spring constant for NN interaction is $k_1$, while that for NNN interaction is $k_2$. The energy stored in the nonlinear springs is denoted by the potential $V(x_n-\chi _n)$, where the atomic displacements of atoms in the chains are $x_n$ and $\chi _n$.

Fig. 1

A diagram showing connectivity of the two parallel lattice atomic chains under consideration. Each bullet point represents a node and boxes represent a nonlinear spring modeled by Klein–Gordon potential

Physically, the system can be characterized by the following Hamiltonian

$$\begin{aligned} H&=\sum _{n=1}^{N}\frac{1}{2}m(\dot{x_n}^2+\dot{\chi _n}^2)+\frac{1}{2}k_1(x_{n+1}-x_n)^2+\frac{1}{2}k_1(\chi _{n+1}-\chi _n)^2 +\frac{1}{2}k_2(x_{n+2}-x_n)^2+\frac{1}{2}k_2(\chi _{n+2}-\chi _n)^2 \nonumber \\&\quad +\,\,\,\,\,V(x_n-\chi _n), \end{aligned}$$

(1)

with the Klein-Gordon coupling potential given by

$$\begin{aligned} V(x_n-\chi _n) = \frac{\eta _1}{2}\left( x_{n}-\chi _{n} \right) ^{2} + \frac{\eta _2}{3}\left( x_{n}-\chi _{n} \right) ^{3} + \frac{\eta _3}{4}\left( x_{n}-\chi _{n} \right) ^{4}, \end{aligned}$$

(2)

where $\eta _1,\,\eta _2,\,\eta _3$ are constants. The Klein-Gordon potential emanates from a more general potential known as Morse-potential. It is given by $V(\xi )=D_{0}(exp(a\xi )-1)^2$, and can be approximated as

$$\begin{aligned} V(\xi ) = \frac{\gamma _1}{2}\xi ^{2} + \frac{\gamma _2}{3}\xi ^{3} + \frac{\gamma _3}{4}\xi ^{4} + \frac{\gamma _4}{5}\xi ^{5} + \frac{\gamma _5}{6}\xi ^{6} + ...\,\,\,\,\,. \end{aligned}$$

(3)

The terms in equation (3) are derived by using the Taylor series expansion, with $\gamma _{1,2,3,4,5}$ being the quadratic, cubic, quartic, ... coefficients respectively. The potential is symmetric for $\gamma _2 = \gamma _4 =0;$ hence termed $\phi ^4$ potential for $\gamma _1\ne 0,\,\gamma _3\ne 0,\,\gamma _5 =0$ as in reference [37], or a more general case of $\phi ^6$ potential for coefficients $\gamma _1\ne 0,\,\gamma _3\ne 0,\,\gamma _5 \ne 0$ [42]. However for non-varnishing values of $\gamma _2$ and $\gamma _4$, the potential wells are asymmetric as with equation (2). The dynamics of periodic base pairs opening in a finite stacking enthalpy DNA was recently investigated for non zero values of all the coefficients $\gamma _1,\,\gamma _2,\,\gamma _3,\,\gamma _4,\,\gamma _5$ [43].

For $k_2=0$, the Hamiltonian (1) of the coupled chains is physically similar to the Peyrard-Bishop model that governs the dynamics of localized large amplitude excitations in the DNA molecule [44, 45]. By using the Hamilton-Jacobi formalism, the equation of motion for $x_n$ and $\chi _n$ thus reads

$$\begin{aligned} m\ddot{x}_n&=k_1(x_{n+1}-2x_n+x_{n-1})+k_2(x_{n+2}+x_{n-2}-2x_n)-V'\left( x_{n}-\chi _{n} \right) , \end{aligned}$$

(4a)

$$\begin{aligned} m\ddot{\chi }_n&=k_1(\chi _{n+1}-2\chi _n+\chi _{n-1})+k_2(\chi _{n+2}+\chi _{n-2}-2\chi _n)+V'\left( x_{n}-\chi _{n}\right) . \end{aligned}$$

(4b)

It is convenient for us to use the in-phase motion $u_n=x_n+\chi _n,$ and out-phase motion $v_n=x_n-\chi _n$, in order to transform equation (4) into

$$\begin{aligned} \ddot{u}_n&=K_1(u_{n+1}-2u_n+u_{n-1})+K_2(u_{n+2}+u_{n-2}-2u_n), \end{aligned}$$

(5a)

$$\begin{aligned} \ddot{v}_n&=K_1(v_{n+1}-2v_n+v_{n-1})+K_2(v_{n+2}+v_{n-2}-2v_n)-(\Omega _0^2v_{n}+\alpha v_{n}^2+\beta v_{n}^3), \end{aligned}$$

(5b)

where $K_1=k_1/m,\,K_2=k_2/m,\,\Omega _0=\sqrt{2\eta _1/m},\,\alpha =2\eta _2/m,\,\beta =2\eta _3/m$. Equation (5a) is a linear differential-difference equation with the usual plane wave solutions (phonons), while (5b) is the equation that contains the nonlinear terms and can only be solved using perturbation techniques. By considering linear oscillations of the out-phase motion $v_n$, at frequency $\omega$ and wavenumber q, with the chain of lattice spacing a, we can easily obtain the dispersion relation given by

$$\begin{aligned} \omega ^2=\Omega _{0}^{2}+4K_{1}sin^{2}\left( \frac{qa}{2}\right) +4K_{2}sin^{2}\left( qa\right) . \end{aligned}$$

(6)

Figure 2 depicts the profile of the dispersion curve for different values of NNN coupling strength $K_{2}$. As clearly shown in this Fig. 2, variations in $K_{2}$ significantly modify the linear dispersion curve of wave propagation in the atomic chain. For higher values of $K_{2}$, the maximum value of wave frequency $\omega$ is no longer at the edge of the Brillouin zone $q=\pi /a$, but is now shifted to a new position with wavenumber $q_o$ given by [37]

$$\begin{aligned} q_0=\frac{\pi }{a}-\frac{1}{a}cos^{-1}\Big (\frac{K_1}{4K_2}\Big ). \end{aligned}$$

(7)

Fig. 2

Linear dispersion curve of the chain according to Eq. (6) for $\Omega _{0}^2=0.032,\,K_1=1.00,$ and the values of $K_{2}$ are varied

The system of equation (5b) for $K_{2}=0$ has been extensively studied within the framework of nonlinear Schrödinger amplitude equation, and myriad of breather and envelope-soliton solutions obtained in the low-amplitude limit [18, 19, 42]. For example, Kivshar et al. exploited the rotating-wave approximation method to derive the DNLS equation [18, 19], with solutions in the form of bright and dark-profile localized structures.

In a highly discrete regime where the nearest and NNN coupling forces between particles are weak (i.e. $\Omega _{0}>>K_{1}$ and $\Omega _{0}>>K_{2}$), the equation that governs the out-phase motion (5b) can now be re-written as

$$\begin{aligned} \ddot{v}_n=\varepsilon ^2K_1(v_{n+1}-2v_n+v_{n-1})+\varepsilon ^2K_2(v_{n+2}+v_{n-2}-2v_n)-\Omega _0^2v_{n}-\alpha v_{n}^2-\beta v_{n}^3, \end{aligned}$$

(8)

where $\varepsilon<<1$ is a small perturbation parameter. The rotating-wave approximation scheme where both the carrier wave and envelope are strictly treated in the discrete regime [26, 46, 47], seems to be the most suitable method to explore. Consequently we now analyze slow temporal variations of the wave envelope by considering solution of equation (8) in the form [18]

$$\begin{aligned} v_n(t)&=\varepsilon \Big [A_n(T)exp(-i\Omega _0t)+A_n^*(T)exp(i\Omega _0t)\Big ] \nonumber \\&\quad +\varepsilon ^2\Big [B_n(T)+C_n(T)exp(-2i\Omega _0t)+C_n^*(T)exp(2i\Omega _0 t)\Big ], \end{aligned}$$

(9)

where the discrete amplitudes $A_n,\,B_n,\,C_n$ and their complex conjugates $A_n^*,\,C_n^*,$ are functions of $T=\varepsilon ^2 t$, and we are strictly operating at the lower cut-off mode frequency $\Omega _0$. Upon substituting the ansatz (9) into equation (8) and simplifying, we now obtain the following equations in their respective harmonics:

$$\begin{aligned}&\varepsilon ^3exp(-i\Omega _0t): 2i\Omega _0\frac{dA_n}{dT}=-K_1(A_{n+1}-2A_n+A_{n-1})-K_2(A_{n+2}-2A_n+A_{n-2}) +2\alpha (B_nA_n+A_n^*C_n)+3\beta |A_n|^2A_n, \end{aligned}$$

(10)

$$\begin{aligned}&\varepsilon ^2exp(-0i\Omega _0t):\,\,B_n\approx -\frac{2\alpha }{\Omega _0^2}|A_n|^2, \end{aligned}$$

(11)

and

$$\begin{aligned} \varepsilon ^2exp(-2i\Omega _0t):\,\,C_n\approx \frac{\alpha }{3\Omega _0^2}A_n^2. \end{aligned}$$

(12)

Finally, upon substituting relations (12) and (11) into equation (10), leads us to

$$\begin{aligned} i\frac{dA_n}{dT}+P_{1}(A_{n+1}-2A_n+A_{n-1})+P_{2}(A_{n+2}-2A_n+A_{n-2})+\varrho |A_n|^2A_{n}=0, \end{aligned}$$

(13)

where

$$\begin{aligned} P_1=\frac{K_1}{2\Omega _0},\,\,\,\,\,\,\,P_2=\frac{K_2}{2\Omega _0},\,\,\,\,\,\,\varrho =\frac{1}{2\Omega _0}\Big [\frac{10\alpha ^{2}}{3\Omega _0^2}-3\beta \Big ]. \end{aligned}$$

(14)

Equation (13) is the DNLS equation with NNN interactions. For $P_2=0$, equation (13) can equally govern the propagation of laser wave packets in optical media, dynamics of matter wave solitons in Bose–Einstein condensates, nonlinear excitations in DNA molecules, among other potential applications [48,49,50]. We will investigate on the MI of the amplitude equation (13) in the next section, in order to effectively map out the appropriate regions for the observation of localized modes in the atomic chain.

3 Modulational Instability Analysis

MI generally precedes the generation of localized wave modes in discrete lattices, which has been experimentally identified in electrical transmission lines [51]. The generation of higher order-rogue wave solutions for the generalized discrete Hirota equation was equally shown to be driven by the process of MI [52]. Consequently, we now explore the stability properties of equation (13) which possesses exact plane wave solutions

$$\begin{aligned} A_{n}(T)=A_{0}\,exp(i(qan-\omega T)), \end{aligned}$$

(15)

where $A_{0}$ is the amplitude, $\omega$ is the angular frequency, and q is the wavenumber. By substituting (15) into the discrete amplitude equation (13), leads to the nonlinear dispersion relation

$$\begin{aligned} \omega =\omega _0(qa)-\varrho |A_{0}|^2, \end{aligned}$$

(16)

where $\omega _0(qa)=4P_{1}sin^{2}\left( \frac{qa}{2}\right) +4P_{2}sin^{2}\left( qa\right) .$ To examine the linear stability of the solution (15), we consider small perturbations $B_n\,(.i.e\,\,|B_n|<<A_{0})$ on the amplitude of the plane wave such that

$$\begin{aligned} A_{n}(T)=[A_{0}+\varepsilon B_n(T)]exp(i(qan-\omega T)). \end{aligned}$$

(17)

Using Equations (13), (16), and (17), we obtain the following linearized equation in $B_n(T)$ as

$$\begin{aligned} i\frac{dB_n}{dT}= & {} -P_1\Big [(B_{n + 1}-{B_n})exp(iqa) +(B_{n - 1}-{B_n})exp(-iqa)\Big ]-P_2\Big [(B_{n + 2}- \nonumber \\&B{_n})exp(2iqa) +(B_{n - 2}-{B_n})exp(-2iqa)\Big ]-\varrho \Big [A_{0}^2B_n^*+|A_{0}|^2B_n\Big ], \end{aligned}$$

(18)

where the asterisk denotes complex conjugation.

We now assume a general modulation solution to equation (18) of the form

$$\begin{aligned} B_n(T) = b_1\,exp(i(Qan - \Omega T)) + b_2^*\,exp(-i(Qan - \Omega ^* T)), \end{aligned}$$

(19)

where Q and $\Omega$ respectively represent the wave vector and the frequency of the linear modulation. From the systems (18) and (19), we can easily deduce the dispersion relation for the perturbation wave as

$$\begin{aligned} \Omega =P_{1}sin(Qa)sin(qa)+P_{2}sin(2Qa)sin(2qa)+2\sqrt{\Gamma (\Gamma -\varrho |A_0|^{2})}, \end{aligned}$$

(20)

where $\Gamma =P_{1}cos(qa)sin^{2}(Qa/2)+P_{2}cos(2qa)sin^{2}(Qa)$. The imaginary part of $\Omega$ can only be realized when $\Gamma (\Gamma -\varrho |A_0|^{2})<0$, hence leading to the exponential growth in the perturbation $B_n(T)$ which triggers the generation of localized modes in the coupled chains. Figure 3 depicts the regions in the $(qa,\,Qa)$ plane for identifying such modes, which is realized by computing the magnitude of the imaginary part of equation (20). It should be noted that for the special case $P_{2}=0$, equation (20) reduces to result obtained by Kivshar [18].

As shown in Fig. 3, the exponential growth in small perturbations $B_n(T)$ generally occurs at small amplitudes plane waves with the NNN coupling parameter $P_2$ greatly modifying their area of occurrence. This is inextricably linked to the dispersion relation (16). To comprehensively analyze this, we consider small values of Qa and simplifying $\Gamma$ in order to have

$$\begin{aligned} \Gamma (qa, Qa<<1)\approx \frac{(Qa)^2}{4}\Big [P_1cos(qa)+4P_2cos(2qa)\Big ]=\frac{(Qa)^2}{8}\omega ''_0(qa). \end{aligned}$$

(21)

It is clear that for small values of Qa and positive values of the curvature of the dispersion ($i.e.\,\omega ''_0(qa)>0$), then $\Gamma >0$. Hence MI is only possible when $\varrho>0\,(i.e.\,10\alpha ^2>9\Omega _0^2\beta )$; since $\Gamma \,\varpropto \,(Qa)^2$, a minimal amplitude $A_0$ equally triggers infinitesimal-Qa instability. On the other hand, if $\omega ''_0(qa)<0$, then minimal-Qa instability is only possible at small amplitudes provided $10\alpha ^2<9\Omega _0^2\beta$. We can now confidently say that the regions of the Brillouin zone in which $\omega ''_0(qa)>0$, are more vulnerable to MI provided $10\alpha ^2>9\Omega _0^2\beta$. For the special case in Fig. 3(a) where $P_1=1.00,\,P_2=0.00,$ and $\varrho |A_0^2|=1.00$, MI is rare to observe for any small values of Qa probably because $\omega ''_0(qa)<0$. However by progressively increasing the values of $P_2$ from 0.20 to 1.00 as in Fig. 3b–f, we increase our chances of observing MI in the chain because the yellowish area(s) also progressively stretches downward. We also note that for these small values of Qa; two major distinct regions of MI progressively emerges with boundaries around $qa=1.00$, as the values of $P_2$ is progressively increased. However, the MI phenomena for the region where $qa\,<\,1.00$, is weaker compared to their counterpart region $qa\,>\,1.00$.

We further investigate a more interesting MI phenomena at wavenumber $qa=0.00$ and varying values of Qa. At this stage, we have

$$\begin{aligned} \Gamma (qa=0, Qa)=P_1sin^2\Big (\frac{Qa}{2}\Big )+P_2sin^2(Qa)=\frac{1}{4}\omega _0(Qa)\ge 0, \end{aligned}$$

(22)

since $P_1,\,P_2$ are assumed to be positive constants. Consequently, for MI to be observed at $qa=0$, it requires that $10\alpha ^2>9\Omega _0^2\beta$, with the amplitude of plane wave constraint in the interval

$$\begin{aligned} |A_0|^{2}>\frac{\omega _0(Qa)}{4\varrho }. \end{aligned}$$

(23)

Values of Qa with smaller $\omega _0(Qa)$ become unstable for smaller plane wave amplitudes, and the first instability always emerging at the global minimum where $\omega _0(Qa)=0$ for $Qa=0.00$. There is also an additional local minimum in the dispersion curve that will induce another region of MI in the chain. This will occur at $Qa=\pi$, which corresponds to another critical plane wave amplitude given by

$$\begin{aligned} |A_0|^{2}=\frac{P_1}{4\varrho }. \end{aligned}$$

(24)

A careful examination of Fig. 3c–f, clearly indicates two regions of MI for $qa=0.00$, which is consistent with the analytical predictions.

Fig. 3

Regions of MI in the $(qa,\,Qa)$ plane indicated by the yellowish area(s). This is for parameters $P_{1}=1.00,\,\varrho |A_0|^{2}=1.00$. a $P_{2}=0.00,$ ; b $P_{2}=0.20$; c $P_{2}=0.40,$ ; d $P_{2}=0.60$; e $P_{2}=0.80,$ ; f $P_{2}=1.00$

4 Discrete Localized Modes

Enormous effort has been made to obtain analytical solutions to a number of discrete nonlinear partial differential equations. Some prominent analytical methods includes: quadrature method, ansatz method, method of separation of variables, Painlevé method, Hirota method, IST method, B$\ddot{a}$cklund transform method, Darboux transformation method among others [11, 18, 51, 53,54,55,56]. Furthermore, a more powerful analytical method like the discrete generalized $(m,\,N-m)$-fold Darboux transformation technique; have already been developed to obtain two-component localized wave solutions for a reduced semi-discrete two-component coupled system on a two-chain lattice [57]. By exploiting this latter method, breathing-soliton and singular rogue wave solutions were obtained for a discrete nonlocal coupled Ablowitz-Ladik equation of reverse-space type [58]. Some of these methods are more appropriate with some mathematical problems under specific conditions. A variety of intrinsically localized stationary solutions which are also termed discrete breathers or discrete bright solitons, can be obtained for the DNLS amplitude equation (13), by exploiting the Bilinear Hirota analytical technique as elaborated below.

4.1 Bilinear Hirota Method

Concretely, the Hirota’s bilinear method was proposed by Hirota in 1971 to solve the Korteweg-de Vries equation [53]. It does not involve any sophisticated technique, but only differentiation. This method can construct multiple-soliton solutions as well as one-soliton solutions effectively using exponentials. Hence it also helps to study discrete equations as will be demonstrated here. The principle of the Hirota bilinear method lies on the implementation of the Hirota bilinear operator, which transforms the nonlinear evolution equations into several coupled bilinear equations. This act breaks down the original complicated equation into a series of relatively simple equations. A detail study on the Hirota bilinear transformation to different nonlinear evolution equations can be found in Ref. [56]. The Hirota’s bilinear operator (or D-operator) is defined as

$$\begin{aligned} D^{s}_{T}D^{l}_{n}G_{n}(T).F_{n}(T)=\Big (\frac{\partial }{\partial T}-\frac{\partial }{\partial T'}\Big )^{s}\Big (\frac{\partial }{\partial n}-\frac{\partial }{\partial n'}\Big )^{l}G_{n}(T)F_{n'}(T)\Big \arrowvert T=T',n=n', \end{aligned}$$

(25)

where s and l are positive integers. Depending on the nature of the physical problem in question, several modifications and improvements are made on the D-operator in system (25), to obtain appropriate solutions.

We now set the amplitude $A_n$ of equation (13) as

$$\begin{aligned} A_n=\frac{G_n(T)}{F_n(T)}, \end{aligned}$$

(26)

where $G_n(T)$ is a complex function while $F_n(T)$ is a real function. By making use of the Hirota’s operator (25) and the expression (26), the discrete amplitude equation (13) can now be transformed to

$$\begin{aligned}&i\frac{D_{T}G_{n}.F_{n}}{F_{n}F_{n}}+P_{1}\Big [\frac{2(cosh\,D_n-1)G_n.F_n}{F_n F_n}-\frac{G_nF_n}{(F_n F_n)^2}2(cosh\,D_n-1)F_n.F_n \Big ] \\ +P_{2}\Big [ \nonumber \\&\frac{2(cosh\,2D_n-1)G_n.F_n}{F_n F_n}-\frac{G_nF_n}{(F_n F_n)^2}2(cosh\,2D_n -1)F_n.F_n\Big ]+\varrho \frac{G_n.G_n^*}{F_nF_n}\Big (\frac{G_n}{F_n}\Big )=0. \end{aligned}$$

(27)

Upon simplification of equation (27), yields two decoupled equations given by

$$\begin{aligned} \Big [iD_{T}&+ 2P_{1}(cosh\,D_n-1)+2P_{2}(cosh\,2D_n-1)\Big ]G_n.F_n=0, \end{aligned}$$

(28a)

$$\begin{aligned} \Big [\frac{2P_1}{\varrho }&(cosh\,D_n-1)+\frac{2P_{2}}{\varrho }(cosh\,2D_n-1)\Big ]F_n.F_n=G_n.G_n^*\,\,\,\,\,. \end{aligned}$$

(28b)

We now consider one-soliton solution of equation (13) by assuming the ansatz

$$\begin{aligned} G_n=\epsilon G_n^{(1)};\,\,F_n=1+\epsilon ^2F_n^{(2)}, \end{aligned}$$

(29)

which upon substituting into equation (28) and grouping terms in order of $\epsilon$ yields

$$\begin{aligned} \epsilon ^1:\,&\Phi _1\Big [G_n^{(1)}.1\Big ]=0, \end{aligned}$$

(30a)

$$\begin{aligned} \epsilon ^2:\,&\Phi _2\Big [1.F_n^{(2)} + F_n^{(2)}.1\Big ]=G_n^{(1)}.G_n^{(1)*}, \end{aligned}$$

(30b)

$$\begin{aligned} \epsilon ^3:\,&\Phi _1\Big [G_n^{(1)}.F_n^{(2)}\Big ]=0, \end{aligned}$$

(30c)

$$\begin{aligned} \epsilon ^4:\,&\Phi _2\Big [F_n^{(2)}.F_n^{(2)}\Big ]=0, \end{aligned}$$

(30d)

where $\Phi _1=iD_{T}+ 2P_{1}(cosh\,D_n-1)+2P_{2}(cosh\,2D_n-1)$ and $\Phi _2=\frac{2P_1}{\varrho }(cosh\,D_n-1)+\frac{2P_{2}}{\varrho }(cosh\,2D_n-1)$. We now set

$$\begin{aligned} G_n^{(1)}=exp[\kappa n +\theta T];\,\,F_n^{(2)}=F_0\,exp\Big [(\kappa +\kappa ^*)n+(\theta + \theta ^*)T\Big ], \end{aligned}$$

(31)

and use equation (30) to obtain

$$\begin{aligned} \theta&=2i(P_{1}+P_{2})\Big [cosh(\kappa )-1\Big ]+2iP_{2}\,cosh(\kappa ), \end{aligned}$$

(32a)

$$\begin{aligned} F_{0}&=\frac{\varrho }{8(P_{1}+P_{2})sinh^{2}\Big (\frac{\kappa +\kappa ^*}{2}\Big ) + 8P_{2}\,cosh(\kappa +\kappa ^*)}. \end{aligned}$$

(32b)

The one-soliton solution of equation (13) is thus given by

$$\begin{aligned} A_{n}(T)=\frac{\epsilon \Big \{8(P_1+P_2)sinh^{2}\left( \frac{k+k^*}{2}\right) +8P_2\,cosh(k+k^*)\Big \}exp\Big \{J\Big \}}{8(P_1+P_2)sinh^{2}\left( \frac{k+k^*}{2}\right) +8P_2\,cosh(k+k^*)+\epsilon ^{2}\varrho \,exp\left[ (k+k^*)n\right] }, \end{aligned}$$

(33)

where $J=kn +\Big [2i(P_1+P_2)[cosh(k)-1]+2iP_2cosh(k)\Big ]T.$ For the special case where $P_2=0.0$, solution (33) degenerates to the one obtained by C. B. Tabi in the study of formation and interaction of bright solitons with shape changing in a DNA model [59]. The various intensity profiles of these discrete bright solitons are plotted in Figs. 4 and 5 as parameter $P_2$ is varied from 0.00 to 1.00. It is observed that the amplitude $|A_n(T)|^2$ of the stationary discrete soliton increases as $P_2$ is increased, and remain constant so long as the values of $P_2$ is fixed.

Fig. 4

Stationary discrete bright solitons governed by solution (33) for parameters $P_{1}=1.00,\,k=1+0.001i,\,\varrho =1.00$ and $\epsilon =1.00$. a, b, c $P_{2}=0.00,$ d, e, f  $P_{2}=0.20,$ g, h, i $P_{2}=0.40$

Fig. 5

Stationary discrete bright solitons governed by solution (33) for parameters $P_{1}=1.00,\,k=1+0.001i,\,\varrho =1.00$ and $\epsilon =1.00$. a, b, c $P_{2}=0.60,$ d, e, f  $P_{2}=0.80,$ g, h, i $P_{2}=1.00$

The most appropriate discrete localized modes of equation (8) is now obtained by using the ansatz (9), in order to have

$$\begin{aligned} v_{n}(t)&= 2\varepsilon \Bigg \{\frac{\Big [8(P_1+P_2)sinh^{2}(a)+8P_2cosh(2a)\Big ]exp\Big [an -2\varepsilon ^2t(P_1+2P_2)sinh(a)sin(b)\Big ]}{8(P_1+P_2)sinh^{2}(a)+8P_2cosh(2a)+\varrho \,exp(2an)}\Bigg \}cos(\Phi ) \nonumber \\&+\frac{2\varepsilon ^2\alpha }{\Omega _0^2}\Bigg \{\frac{\Big [8(P_1+P_2)sinh^{2}(a)+8P_2cosh(2a)\Big ]exp\Big [an -2\varepsilon ^2t(P_1+2P_2)sinh(a)sin(b)\Big ]}{8(P_1+P_2)sinh^{2}(a)+8P_2cosh(2a)+\varrho \,exp(2an)}\Bigg \}^2 \nonumber \\&\times \Big [\frac{cos(2\Phi )}{3}-1\Big ], \end{aligned}$$

(34)

with $\Phi =bn+\Omega _0t +\varepsilon ^2\Big [2(P_1+2P_2)cosh(a)cos(b)-2(P_1+P_2)\Big ]t.$ We have set $\kappa =a+ib$ and $\epsilon =1.00$, without loss of generality. We thus obtain the profile of the solution given in Fig. 6 for the asymmetric coupling potential (i.e. for $\alpha =-1.00$), while Fig. 7 depicts the profile in the case of symmetric coupling potential (i.e. for $\alpha =0.00$). For another case of asymmetric coupling potential in which $\alpha =1.00$; we obtain the profiles in Fig. 8 that generally shows dark-like localized modes because of the constant dip. Concretely for $\alpha =-1.00$ and $b=1+0.001i$ as shown in Fig. 6, we observe a structurally stable stationary discrete bright solitary wave centered around the origin. It is a dynamic structure that mimics a localized standing wave in a breathing mode, owing to the slight variation in the wave amplitude as time evolves. In fact, the wave amplitudes in Fig. 6d–f for $P_2=1.00$ supersedes those of their counterparts in Fig. 6a–c for $P_2=0.00$; indicating that the NNN coupling enhances the amplitude of the localized modes. The nature of the coupling potential greatly influence the form of the localized mode in the atomic chain. This is reflected in Fig. 7 for $\alpha =0.00$, where the nonlinear excitation evolve into a discrete localized mode with up-and-down asymmetry [13, 60]. For $P_2=1.00$ as in Fig. 7d–f, there is a rapid transformation of the up-and-down asymmetric localized mode with minimal change in amplitude. As time increases, we observe that the amplitude of the asymmetric discrete solitary wave drastically reduces as shown in Fig. 7a–c for $P_2=0.00$. This loss may be as a result of thermal vibration in the lattice with the energy of the localized modes carried away as small amplitude linear waves in the form of radiation [18]. Lastly, the wave profile observed in Fig. 8 for $\alpha =1.00$ is just the reflection about the spatial axis of the wave pattern identified in Fig. 6. The dark-like localized modes identified in the atomic chain as in Fig. 8, may signal the absence of MI. This therefore underscores the crucial role played by the asymmetric parameter $\alpha$, in the dynamics of discrete soliton of the two coupled chains.

Fig. 6

Evolution of discrete localized modes in the chain, which is governed by solution (34). This is for the parameters: $\alpha =-1.00,\,P_{1}=a=1.00,\,b=0.001,\,\Omega _0=0.50,\,\beta =4.11$, and $\varepsilon =1.00$. a $P_{2}=0.00,\,t=0.00$; b  $P_{2}=0.00,\,t=0.50$; c $P_{2}=0.00,\,t=1.00$ ; d $P_{2}=1.00,\,t=0.00$ ; e  $P_{2}=1.00,\,t=0.50$ ; f $P_{2}=1.00,\,t=1.00$

Fig. 7

Evolution of discrete localized modes in the chain, which is governed by solution (34). This is for the parameters: $\alpha =0.00,\,P_{1}=a=1.00,\,b=0.001,\,\Omega _0=0.50,\,\beta =4.11$, and $\varepsilon =1.00$. a $P_{2}=0.00,\,t=0.00$ ;b  $P_{2}=0.00,\,t=0.50$ ; c $P_{2}=0.00,\,t=1.00$ ; d $P_{2}=1.00,\,t=0.00$ ; e  $P_{2}=1.00,\,t=0.50$ ; f $P_{2}=1.00,\,t=1.00$

Fig. 8

Evolution of discrete localized modes in the chain, which is governed by solution (34). This is for the parameters: $\alpha =1.00,\,P_{1}=a=1.00,\,b=0.001,\,\Omega _0=0.50,\,\beta =4.11$, and $\varepsilon =1.00$. a $P_{2}=0.00,\,t=0.00$; b  $P_{2}=0.00,\,t=0.50$; c $P_{2}=0.00,\,t=1.00$ ; d $P_{2}=1.00,\,t=0.00$ ; e  $P_{2}=1.00,\,t=0.50$ ; f $P_{2}=1.00,\,t=1.00$

4.2 Numerical Analysis

All the solution profiles so far obtained are approximations because of the assumptions made in the analytical calculations. We now conduct direct numerical simulations of equation (8) to determine the outcome of the long term evolution of the localized discrete solutions derived in the previous subsection. Consequently, we initially split the second order discrete equation (8) into two first order discrete ordinary differential equations. We then define the differential equations as a function that takes one vector of variables in the differential equation plus a time vector as an argument. Lastly, we return the derivative of the vector and use the built-in MATLAB solver ode45; that is based on the fourth order Runge-Kutta scheme. The initial displacement is given by

$$\begin{aligned} v_{n}(0)&= 2\varepsilon \Bigg \{\frac{\Big [8(P_1+P_2)sinh^{2}(a)+8P_2cosh(2a)\Big ]exp(an)}{8(P_1+P_2)sinh^{2}(a)+8P_2cosh(2a)+\varrho \,exp(2an)}\Bigg \}cos(bn)\,\,\,\,\,\,+ \nonumber \\&\quad \frac{2\varepsilon ^2\alpha }{\Omega _0^2}\Bigg \{\frac{\Big [8(P_1+P_2)sinh^{2}(a)+8P_2cosh(2a)\Big ]exp(an)}{8(P_1+P_2)sinh^{2}(a)+8P_2cosh(2a)+\varrho \,exp(2an)}\Bigg \}^{2}\Big [\frac{cos(2bn)}{3}-1\Big ], \end{aligned}$$

(35)

while the initial velocity is simply obtained by differentiating solution (34) with respect to time and set $t=0.0$. This leads to the long term evolution of discrete localized modes as shown in Fig. 9. At the initial stage (i.e. $t=0$), we observe a bright discrete pulse in Fig. 9 that is symmetric about the origin. As time changes, the localized discrete bright pulse becomes structurally unstable as it evolves from a symmetric to asymmetric wave profile around the origin. A close examination between Figs. 9 and 6d–f reveal the same structural features of the discrete localized wave profiles, as they share the same parameter values. In fact the amplitudes of the localized modes in both figures fluctuates around the numerical value of 80, clearly showing the consistency between the analytical curves and long term numerical profiles of the discrete localized modes.

Fig. 9

Evolution of discrete localized modes based on the numerical integration of Eqn. (8) with initial condition (35). This is for the parameters: $\alpha =-1.00,\,P_{1}=P_{2}=a=1.00,\,b=0.001,\,\Omega _0=0.50,\,\beta =4.11$, and $\varepsilon =1.00$

5 Conclusion

For integrable systems, the word “soliton" has a mathematical meaning of maintaining constant amplitude wave profile with it form unchanged even after collision. For non-integrable systems like the DNLS equation with NNN coupling earlier derived, the equation merely support but solitary waves (localized modes) which can loosely be referred to as soliton because of the localized and long-lived nonlinear energy packet. Due to non-integrability, a soliton may lose energy due to radiation [18]. It can equally acquire an internal mode as a result of a degree of freedom corresponding to shape deformation [61, 62], which is a clear indication that solitons may carry with them an internal store of energy.

We have investigated on the MI properties and discrete localized modes in two chains which are non-linearly coupled via Klein-Gordon potential. Each chain independently experiences both nearest and NNN interactions, with the model mimicking the Peyrard-Bishop DNA model. The DNLS equation with NNN interactions was derived from the out-phase equation of motion by exploring the rotating wave approximation, in which the wave amplitude and phase are constraint in the discrete regime. Within the frame work of the linear stability analysis, we calculated the growth rate of the MI, and graphically captured the areas of their existence. It was established that the introduction of the NNN coupling parameter $P_2$, significantly modified the shape of the areas of MI. We further explored the Hirota-Bilinear method to obtain discrete one-soliton of the DNLS equation with NNN interactions. Our results showed that for symmetric coupling potential (i.e. $\alpha =0.0$) and in the absence of NNN interaction parameter $P_2$, our system supports a discrete asymmetric localized mode which is structurally unstable as time unfolds. However by introducing the $P_2$ parameter, the discrete localized modes evolve into standing wave profile with up-and-down asymmetry. We equally identified structurally stable discrete localized mode in the form of a dark soliton when the asymmetric parameter $\alpha$ assumes a positive value. Results of numerical investigations mainly confirmed the long term evolution of the discrete symmetric pulse around the origin to asymmetric pulse structures.

This study provides an elegant mathematical approach that can be used to rigorously study highly localized discrete modes in a DNA molecule. The dynamics of DNA is increasingly being investigated in order to adequately comprehend the formation of genetic codes, and intrinsic processes of replication and transcription [41, 43, 63, 64]. Discrete solitons have also been shown to be very robust entities. This is the case with elastic soliton interactions investigated on a triangular-lattice ribbon, in which the dynamics of the system is governed by the discrete reduced integrable nonlinear Schrödinger coupled equations [65]. In the same light, the propagation and elastic interactions of discrete solitons have equally been investigated with higher-order coupled Ablowitz-Ladik equation [66]. Consequently, our next study will focus on using the discrete Hirota-Bilinear method to obtain multi-soliton (i.e. two, three, and four soliton solutions) for the DNLS equation with NNN interactions. This will give us the opportunity to investigate on the effects of helicoidal interactions on the propagation and elastic collision of discrete solitons in DNA structures.