Multiple Periodic Vibrations of Auxetic Honeycomb Sandwich Plate with 1:2 Internal Resonance

Abstract

In this paper, we focus on the multiple periodic vibration behaviors of an auxetic honeycomb sandwich plate subjected to in-plane and transverse excitations. Nonlinear equation of motion for the plate is derived based on the third-order shear deformation theory and von Kármán type nonlinear geometric assumptions. The Melnikov method is extended to detect the bifurcation and multiple periodic vibrations of the plate under 1:2 internal resonance. The effects of transverse excitation on nonlinear vibration behaviors are discussed in detail. Evolution laws and waveforms of multiple periodic vibrations are obtained to analyze the energy transfer process between the first two order modes. Even quite small transverse excitation can cause periodic vibration in the system, and there can be at most three periodic orbits in certain bifurcation regions. The periodic orbits are classified into two families by tracing their sources. The study provides the possibility for the classification study on generation mechanism of system complexity and energy transfers between different modes.

1 Introduction

Honeycomb sandwich structure is widely used in virtually every branch of modern industry due to its superior properties of light weight, high specific stiffness, high specific strength, good fatigue resistance and energy absorption [1]. A typical honeycomb sandwich structure consists of two (top and bottom) thin face sheets and a (middle) light-weight core layer, and usually the core is a polygonal lattice made of metal, paper or other materials. Honeycomb sandwich structure can be artificially designed to exhibit a unique range of physical and mechanical properties by selecting various materials or structures of core.

Auxetic materials, named by Evans [2], refer to materials with negative Poisson’s ratio (NPR). As one of novel excellent promising metamaterials, auxetic materials have gradually captured the attention of numerous material engineers and scientists. An amount of work had done to achieve NPR, see [3,4,5,6,7] and references therein. A review on what Poisson’s ratio means in the contemporary understanding of the mechanical characteristics of modern materials was assessed by Greaves et al. [8]. Lim [9] investigated the suitability of auxetic materials for load-bearing circular plates and showed that the optimal Poisson’s ratio for minimizing the bending stresses was strongly dependent on the final deformed shape, load distribution, and the type of edge supports. Thereafter, three models for the shear correction factor of plates as a function of Poisson’s ratio were proposed: an analytical model, a cubic fit model and a modified model [10], and the effect of auxeticity on shear deformation in thick plates was concerned. The effects of cell-wall thickness on the deformation mode of metallic auxetic reentrant honeycomb, and the effects of NPR on the crushing stress were clarified by Dong et al. [11].

In recent decades, the auxetic materials are increasingly used as the core in structural designs of honeycomb sandwich plates because of their engineering advantages over traditional materials, including increased indentation resistance [12, 13], plane strain fracture toughness [14, 15], crashworthiness [16] and high energy absorption [17,18,19]. Yang et al. [20] presented a comparative study of ballistic resistance of sandwich panels with aluminum foam and auxetic honeycomb cores. They found that the sandwich panel with auxetic core is far superior to the panel with aluminum foam core in ballistic resistance because of the material concentration at the impacted area due to the NPR effect. Imbalzano et al. [21] analyzed the equivalent sandwich panels composed of auxetic and conventional honeycomb cores with metal facets, and compared their resistance performances against impulsive loadings. Zhang et al. [22] studied nonlinear transient responses of an auxetic honeycomb sandwich plate under impact dynamic loads, and found that the honeycomb sandwich plate with NPR would be a better choice compared with the positive one.

As common structural elements, sandwich plates with auxetic honeycombs are widely used in aerospace, defense and other industries. The mechanical and dynamical properties of the plates have attracted attention of many researchers. For instance, Strek et al. [23] studied the dynamic response of a sandwich panel made of two face sheets and auxetic core, and considered the influence of filler material on the effective properties of the sandwich panel. Zhu et al. [24] investigated the frequencies and energies of free vibrations and vibrations with the damping and in-plane force of a honeycomb sandwich plate with NPR. Quyen et al. [25] investigated the nonlinear free and forced vibration of auxetic sandwich cylindrical plate on visco-Pasternak foundations in thermal environment subjected to blast load. And the effects of geometrical parameters, visco foundations, initial imperfection, temperature increment, nanotube volume fraction and blast load on the nonlinear vibration characteristics of the plate were numerical studied.

Considerable progress has been made in the study of theory and application of nonlinear dynamic response and vibrations for various plates [22,23,24,25,26]. In the future studies, more attentions should be drawn on the multiple periodic vibrations of sandwich plates with auxetic honeycombs, and the following aspects should be emphasized: (1) For the theory of auxetic sandwich plate, Lim [10] suggested that the use of classical plate theory is permitted only when the material is highly auxetic for that the auxeticity reduces shear deformation in thick plates. Ma et al. [26] believed that the accuracy of third-order shear deformation theory (TSDT) was higher than the first-order shear deformation theory (FSDT) for a moderately thick plate; (2) Internal resonance usually causes coupling of different modes, which will lead to energy transfer between different modes [27]. Due to the presence of in-plane excitation, the internal resonance can occur between two modes even though the excitation frequency is not close to any linear natural frequencies [28]; (3) A nonlinear system may have multiple solutions, the coexistence and evolution mechanism of multiple periodic solutions should be concerned, which is closely related to the second part of the well-known Hilbert’s 16th problem.

In the present work, we focus our attention on a simply supported concave hexagonal composite metamaterial sandwich plate with auxetic honeycombs subjected to in-plane and transverse excitation. The method of TSDT is used to derive the two degrees of freedom nonlinear equation of motion which can be recast into a four dimensional non-autonomous system. Melnikov method is improved by combination of curvilinear coordinates and Poincaré map to detect the bifurcation and coexistence of multiple periodic vibrations as well as the parameter conditions for the plate under 1:2 internal resonance. The occurrence and disappearance of periodic orbits are analyzed in detail. Phase portraits of nonlinear vibration characteristics and waveforms of different modes for the plate in different bifurcation regions induced by transverse excitation are also obtained.

2 Nonlinear Equation of Motion

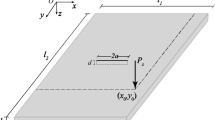
In this paper, a simply supported concave hexagonal composite metamaterial sandwich plate with length a, width b and thickness h is taken into account. The top and bottom face sheets of the plate are made of isotropic aluminum materials and the auxetic core layer has honeycomb structure using the same aluminum material. The thicknesses of the top, core and bottom layers are $h_1,\,h_2$ and $h_3$, respectively. Thus $h=h_1+h_2+h_3$. A Cartesian coordinate system Oxyz with its origin located in the middle surface of the plate is established in which the x (y) direction is along the length (width) of the plate, and the out-of-plane z direction points to the bottom face sheet. The mid-surface displacements of triangular plates in the x, y and z directions are respectively represented by the symbols u, v and w. The plate is subjected to transverse excitation of the form $F(x,\, y)\cos (\Omega _1 t)$ and in-plane excitations of the form $p_0-p_1\cos (\Omega _2 t)$. The method of TSDT [29] is applied to express the displacement components

$$\begin{aligned} u(x,\,y,\,z,\,t)&= u_0(x,\,y,\,t)+z\,\varphi _x(x,\,y,\,t)-\frac{4}{3h^2}z^3 \left( \varphi _x+ \frac{\partial w_0}{\partial x} \right) \end{aligned}$$

(1a)

$$\begin{aligned} v(x,\,y,\,z,\,t)&= v_0(x,\,y,\,t)+z\,\varphi _y(x,\,y,\,t)-\frac{4}{3h^2}z^3 \left( \varphi _y+ \frac{\partial w_0}{\partial y} \right) \end{aligned}$$

(1b)

$$\begin{aligned} w(x,\,y,\,z,\,t)&= w_0(x,\,y,\,t) \end{aligned}$$

(1c)

where $u_0$, $v_0$ and $w_0$ respectively represent the displacements of a point in the middle surface of the plate in x, y and z directions. $\varphi _x$ and $\varphi _y$ are rotations of normals to the mid-surface with respect to the x and y axes.

The von Kármán large geometric deformation theory is taken into account to obtain the strain-displacement relations

$$\begin{aligned} \varvec{\varepsilon }=\varvec{\varepsilon }^0+z\,\varvec{\varepsilon }^1+z^3 \,\varvec{\varepsilon }^3,\quad \varvec{\gamma }=\varvec{\gamma }^0+z^2\,\varvec{\gamma }^2 \end{aligned}$$

(2)

where $\varvec{\varepsilon }=(\varepsilon _{xx},\, \varepsilon _{yy}, \,\gamma _{xy})^\mathrm{T},\,\varvec{\varepsilon }^i=(\varepsilon _{xx}^i,\, \varepsilon _{yy}^i, \,\gamma _{xy}^i)^{\mathrm{T}},\, \varvec{\gamma }=(\gamma _{yz},\ \gamma _{xz})^{\mathrm{T}},\,\varvec{\gamma }^j=(\gamma _{yz}^j,\ \gamma _{xz}^j)^{\mathrm{T}}\,(i=0,\,1,\,3;\, j=0,\,2)$. $\varepsilon _{xx},\, \varepsilon _{yy}$ are normal strains; $\gamma _{xy}$ is the in-plane shear strain; $\gamma _{yz},\ \gamma _{xz}$ are the transverse shear strain deformations, and

$$\begin{aligned} \begin{aligned} \varepsilon _{ii}^0&=\frac{\partial n_{i}}{\partial i}+\frac{1}{2} \left( \frac{\partial w_0}{\partial i} \right) ^2,\quad \varepsilon _{ii}^1=\frac{\partial \varphi _i}{\partial i},\quad \varepsilon _{ii}^3=\frac{\partial \varphi _i}{\partial i}+\frac{\partial ^2 w_0}{\partial i^2} \\ \gamma _{xy}^0&=\frac{\partial u_0}{\partial y}+\frac{\partial v_0}{\partial x}+\frac{\partial w_0}{\partial x}\frac{\partial w_0}{\partial y},\quad \gamma _{xy}^1=\frac{\partial \varphi _x}{\partial y}+\frac{\partial \varphi _y}{\partial x} \\ \gamma _{xy}^3&=\frac{\partial \varphi _x}{\partial y}+\frac{\partial \varphi _y}{\partial x}+2\frac{\partial ^2 w_0}{\partial x \partial y},\quad \gamma _{iz}^0=\varphi _i+\frac{\partial w_0}{\partial i},\quad \gamma _{iz}^2=-\frac{4}{h^2}\,\gamma _{iz}^0 \end{aligned} \end{aligned}$$

(3)

where $i=x,\,y\,;\ n_i\vert _{i=x}=u_0,\,n_i\vert _{i=y}=v_0$. The expressions for stress components of the k-th ($k=1,\, 2,\, 3$) layer of the auxetic honeycomb sandwich plate are obtained by constitutive relations.

$$\begin{aligned} \begin{aligned} \varvec{\sigma }_{x,\,y}^{(k)}&=\left( \sigma _{xx}^{(k)},\,\sigma _{yy}^{(k)},\, \sigma _{xy}^{(k)} \right) ^{\mathrm{T}}=\varvec{Q}_1^{(k)} \, \varvec{\varepsilon }\\ \varvec{\sigma }_{z}^{(k)}&=\left( \sigma _{yz}^{(k)},\,\sigma _{xz}^{(k)} \right) ^{\mathrm{T}}=\varvec{Q}_2^{(k)} \, \varvec{\gamma }\end{aligned} \end{aligned}$$

(4)

where

$$\begin{aligned} \begin{aligned} \varvec{Q}_1^{(k)}&=\partial _{1,\,1}^{2,\,2} \left( \partial _{i,\,j}^{2,\,2} \left( Q_{ij}^{(k)}\right) \right) + \partial _{2,\,2}^{2,\,2}\left( Q_{66}^{(k)}\right) \\ \varvec{Q}_2^{(k)}&=\mathrm{diag}\left( Q_{44}^{(k)},\,Q_{55}^{(k)}\right) \end{aligned} \end{aligned}$$

(5)

with

$$\begin{aligned} \begin{aligned} Q_{11}^{(k)}&=\frac{E_1^{(k)}}{1-v_{12}^{(k)}v_{21}^{(k)}},\quad Q_{22}^{(k)}=\frac{E_2^{(k)}}{1-v_{12}^{(k)}v_{21}^{(k)}} \\ Q_{21}^{(k)}&=Q_{12}^{(k)}= \frac{v_{12}^{(k)}E_1^{(k)}}{1-v_{12}^{(k)}v_{21}^{(k)}} \\ Q_{44}^{(k)}&=G_{23}^{(k)},\quad Q_{55}^{(k)}=G_{13}^{(k)},\quad Q_{66}^{(k)}=G_{12}^{(k)} \end{aligned} \end{aligned}$$

(6)

In above equations, the symbol $\partial _{i,\,j}^{m,\, n}(\varvec{M})$ denotes a partitioned matrix with m row blocks and n column blocks, and the $(i,\,j)$-th block is $\varvec{M}$, a smaller matrix, all other blocks are zero matrices, and the symbol $\mathrm{diag}(\lambda _1,\,\ldots ,\, \lambda _m)$ denotes an $m\times m$ diagonal matrix with the $(i,\,i)$-th element $\lambda _i$, i.e. $\mathrm{diag}(\lambda _1,\,\ldots ,\, \lambda _m)=\sum _{i=1}^m \partial _{i,\,i}^{m,\, m}(\lambda _i)$, where $i \le m$; $j \le n$  ($i, \,j,\, m,\, n \in {\mathbf{{N}}^ + }$) (see more details in Ref. [30]). $Q_{ij}^{(k)}$ called the plane stress-reduced stiffness. $E_1^{(k)},\, E_2^{(k)};\, G_{12}^{(k)},\, G_{13}^{(k)},\, G_{23}^{(k)}$ and $v_{12}^{(k)},\, v_{21}^{(k)}$ are the Young’s modulus, shear elastic modulus, and Poisson’s ratios of the skins and the core, respectively. The superscript $k=1,\, 2,\, 3$ represent the top outer skin, core material and bottom outer skin, respectively. The material property of the core layer are calculated by the following formulas.

$$\begin{aligned} \begin{aligned} E_1^{(2)}&=\ E_0\frac{\tau ^3L_2}{(\tau ^3l_2+l_1^2L_4)\cos \theta },\, E_2^{(2)}=E_0\frac{\tau ^3l_1^2 \cos \theta }{L_2L_5} \\ G_{12}^{(2)}&=E_0 \frac{\tau ^3}{l_1l_2L_1 \cos \theta },\, G_{13}^{(2)}=\ G_0 \frac{\tau \cos \theta }{L_2},\, G_{23}^{(2)}=G_0\frac{\tau (2L_2^2+L_1L_3)}{4l_1L_1L_2 \cos \theta } \\ v_{12}^{(2)}&=-\frac{L_6}{l_1L_4+\tau ^2l_2} v_{21}^{(2)}=\ -\frac{l_1L_6\cos ^2\theta }{L_2L_5},\, \rho ^{(2)}=\rho _0\frac{\tau (l_2+2l_1)}{2l_1L_2\cos \theta } \end{aligned} \end{aligned}$$

(7)

in which

$$\begin{aligned} \begin{aligned} L_1&= l_1+2l_2,\quad L_2=l_2-l_1 \sin \theta ,\, L_3=l_2+2l_1 \sin ^2\theta \\ L_4&= \tau ^2 \sin ^2\theta +l_1^2 \cos ^2\theta ,\, L_5=l_1^2 \sin ^2\theta +\tau ^2 \cos ^2\theta ,\, L_6=(l_1^2-\tau ^2) \sin \theta \end{aligned} \end{aligned}$$

where $E_0,\, G_0$ and $\rho _0$ are Young’s modulus, shear modulus and mass density of the origin material. $l_1$ and $l_2$ represent the length of the inclined and horizontal cell rib of the unit cell of concave hexagonal honeycomb core. $\tau$ is the uniform thickness of cell rib, $\theta$ is the inclined angle. Here $0<\theta <\frac{\pi }{2}$ for that the unit cell possesses concave shape (auxetic) as shown in Fig. 1 [31].

Fig. 1

Unit cell of the core structure with inclined rib length $l_1$, horizontal rib length $l_2$, inclined angle $\theta$, and rib thickness $\tau$

The nonlinear equation of motion for the auxetic plate can be derived by Hamilton’s principle, as shown in Appendix A. For the simply supported sandwich plate with NPR, the boundary conditions are expressed as follows.

$$\begin{aligned} \begin{aligned}&w=0,\ \varphi _y=0,\ M_{xx}=N_{xy}=0,\quad \mathrm{at}\ x=0,\ a\\&w=0,\ \varphi _x=0,\ M_{yy}=N_{xy}=0,\quad \mathrm{at}\ y=0,\ b\\&{\int _{\,0}^{\,b}N_{xx}\vert _{x=0,\,a} \mathrm{d}y}={\int _{\,0}^{\,b}\big (p_0-p_1\cos (\Omega _2t)\big )\,\mathrm{d}y} \end{aligned} \end{aligned}$$

(8)

Consider the first two order modes of the plate, the displacements and transverse excitation can be written in the following forms.

$$\begin{aligned} u_0&=u_1\cos \frac{3\pi x}{a}\sin \frac{\pi y}{b}+u_2\cos \frac{\pi x}{a}\mathrm{sin}\frac{3\pi y}{b} \end{aligned}$$

(9a)

$$\begin{aligned} v_0&=v_1\sin \frac{3\pi x}{a}\cos \frac{\pi y}{b}+v_2\sin \frac{\pi x}{a}\cos \frac{3\pi y}{b} \end{aligned}$$

(9b)

$$\begin{aligned} w_0&=w_1\sin \frac{3\pi x}{a}\sin \frac{\pi y}{b}+w_2\sin \frac{\pi x}{a}\sin \frac{3\pi y}{b} \end{aligned}$$

(9c)

$$\begin{aligned} F&=F_1\sin \frac{3\pi x}{a}\sin \frac{\pi y}{b}+F_2\sin \frac{\pi x}{a}\sin \frac{3\pi y}{b} \end{aligned}$$

(9d)

where $u_i,\, v_i,\, w_i \,(i=1,\, 2)$ represent the amplitudes of the first two order modes, respectively; $F_1, \, F_2$ represent the amplitudes of the transverse excitation corresponding to the first two order modes.

Considering the transverse motion of the auxetic honeycomb sandwich plate, a two degrees of freedom dimensionless nonlinear equation of motion for the plate in the first two order modes is obtained based on the Galerkin method.

$$\begin{aligned} \ddot{\varvec{w}}+\varvec{\omega }\,{\varvec{w}}+\mu \, \varvec{\alpha }_1\dot{\varvec{w}}+ \cos (\Omega _2t)\,\varvec{\alpha }_2 \varvec{w}+\varvec{W}({\varvec{w}})=\cos (\Omega _1t)\, \varvec{f} \end{aligned}$$

(10)

where

$$\begin{aligned} \varvec{w}&=(w_1,\,w_2)^{\mathrm{T}},\quad \varvec{\omega }=\mathrm{diag}(\omega _1^2,\, \omega _2^2) \\ \varvec{\alpha }_1&=\mathrm{diag}(\alpha _{11},\, \alpha _{21}), \quad \varvec{\alpha }_2=\mathrm{diag}(\alpha _{12},\, \alpha _{22}) \\ \varvec{f}&=(f,\, f)^{\mathrm{T}}, \quad \varvec{W}=(W_1,\, W_2)^{\mathrm{T}} \\ W_i&=\sum \limits _{j=0}^{3}{\alpha _{i(j+3)} w_i^{3-j}w_{3-i}^j} \, (i=1,\,2) \end{aligned}$$

$\omega _i$ are linear natural frequencies, $\mu$ is the damping coefficient, f is the transverse excitations, $\Omega _1$ and $\Omega _2$ are the frequencies of transverse and in-plane excitation respectively, $\alpha _{ij}(\ne 0)$ are non-dimensional coefficients, $i=1,\, 2;\ j=1,\, \ldots , \,6$ .

Let $x_{i1}=\omega _i\, w_i,\, x_{i2}={\dot{w}}_i \,(i=1,\,2)$, and introducing the scale transformations $\alpha _{ij}\rightarrow \varepsilon \,\alpha _{ij},\, f\rightarrow \varepsilon \, f \ (i=1,\,2;\ j=1,\,\ldots ,\,6)$. The two degrees of freedom nonlinear equation can be recast into the following four dimensional non-autonomous equation.

$$\begin{aligned} \dot{\varvec{x}}=\varvec{Ax}+\varepsilon \,\varvec{F}(t,\, \varvec{x}) \end{aligned}$$

(11)

where $\varvec{x}=(x_{11},\, x_{12},\, x_{21},\,x_{22})^{\mathrm{T}} \in {\mathbf{{R}}^4}$, $\varvec{A}=\sum \nolimits _{i,\,j=1}^{2} \partial _{i,\,i}^{2,\,2} \left( \partial _{j,\,3-j}^{2,\, 2}\Big ((-1)^{j+1}\omega _i \Big ) \right)$. $\varvec{F}=\big (0,\, F_{12},\, 0,\,F_{22}\big )^{\mathrm{T}}$ is a vector-valued function in variables of $(x_{11},\,x_{12},\,x_{21},\,x_{22},\,t)$, and

$$\begin{aligned} F_{i2}= f\cos (\Omega _1t)-\alpha _{i1}\mu x_{i2}-\frac{\alpha _{i2}}{\omega _i}x_{i1}\cos (\Omega _2t)\nonumber \\&-\sum \limits _{j=0}^{3} {\frac{\alpha _{i(j+3)}}{\omega _i^{3-j}\omega _{3-i}^j} x_{i1}^{3-j}x_{(3-i)1}^j}\quad i=1,\,2 \end{aligned}$$

(12)

The following analysis should be focused on the bifurcation and coexistence of the multiple periodic vibrations and the effects of transverse excitation on the nonlinear vibration behaviors.

3 Multiple Periodic Vibration Analysis

In this section, Melnikov method is improved to analyze the bifurcation and coexistence of multiple periodic vibrations of system (11). When $\varepsilon =0$, system (11) degenerates to two uncoupled Hamiltonian systems with Hamilton functions

$$\begin{aligned} H_i(\varvec{x}_i)=\frac{1}{2}\omega _i\,\left( x_{i1}^2+x_{i2}^2\right) \quad i=1,\,2 \end{aligned}$$

(13)

where $\varvec{x}_i=(x_{i1},\,x_{i2})^{\mathrm{T}} \in \mathbf{R}^2$. Then there exists an open interval $\mathbf{K} \subset \mathbf{R}^2$ and ${\varvec{h}} = (h_1,\, h_2)^{\mathrm{T}} \in \mathbf{K}$ such that each system has a family of periodic orbits in ${\varvec{x}}_i$ plane, which can be expressed as ${\Gamma _i}=\Big \{\varvec{x}_i^{{h_i}}\ \vert {H_i}({\varvec{x}_i}) = {h_i} \Big \}$, and the corresponding period is $T_i(h_i)$. Assuming that there exists ${\varvec{h}}_0 = (h_{10},\, h_{20})^{\mathrm{T}} \in \mathbf{K}$ and a pair of coprime integers $r_i,\,k_i$ such that $\frac{T_i(h_{i0})}{T}= \frac{r_i}{k_i}$, then system (11)$_{\varepsilon =0}$ has a family of periodic orbits with period $r_0T$ in the invariant torus $\Gamma _{10}\times \Gamma _{20}$, $r_0$ is the least common multiple of $r_1$ and $r_2$.

When $\varepsilon \ne 0$, by defining the function $\psi : \,\mathbf{R}\rightarrow \mathbf{S}$ as $t\rightarrow t$ (mod T), we can rewrite system (11) in the form of a five dimensional autonomous system, i.e. adding $\dot{t}=1$ in system (11). Introducing the curvilinear coordinates $(s_1,\, n_1,\, s_2,\, n_2,\, t)$ in the sufficiently small neighborhood of the invariant torus $\Gamma _{10}\times \Gamma _{20}\times \mathbf{S}=\mathbf{T}^3$, where $s_i=\int _{\,0}^{\,t} {\vert \,{\varvec{J}}\,\mathrm{D}H_i({\varvec{x}}_i(\tau ))\,\vert \ \mathrm{d}\tau }$ represent the arc length of ${\Gamma _i}$, ${\varvec{J}}=\partial _{j,\,3-j}^{2,\,2}\left( (-1)^{j+1} \right) ,\,i=1,\,2$. Define a global cross section $\Sigma =\big \{s_1, \,n_1,\, s_2,\, n_2,\, t \,\vert \, t=0\big \}$ in the phase space $\mathbf{R}^2 \times \mathbf{T}^3$, and construct the ${m_0}$-th iteration of Poincaré map ${P^{{\,m_0}}}:\Sigma \rightarrow \Sigma$ as $\big (s_{10},\, n_{10},\, s_{20},\, n_{20}\big ) \rightarrow \big ({s_1}({m_0}T),\, {n_1}({m_0}T),\, {s_2}({m_0}T),\, {n_2}({m_0}T)\big )$, where $s_{i0}=s_i(0),\,n_{i0}=n_i(0)\,(i=1,\,2)$ are initial values. A fixed point of ${P^{{\,m_0}}}$ corresponds to a periodic solution of system (11). $(s_{10},\,n_{10},\,s_{20},\,n_{20})$ is a fixed point if and only if

$$\begin{aligned} P_{i1}&= s_i(m_0T)-s_{i0}=\int _{\,0}^{\,m_0T} { {\dot{s}}_i\, \mathrm{d}\,t}=0 \nonumber \\ P_{i2}&= n_i(m_0T)-n_{i0}=\int _{\,0}^{\,m_0T} {\mathrm{D}_{s_i}n_i\cdot {\dot{s}}_i\, \mathrm{d}\,t}=0 \end{aligned}$$

(14)

where $\mathrm{D}_s=\frac{\partial }{\partial s},\,i=1,\,2$.

Then the Melnikov function $\varvec{M}= \big ({M_{11},\, M_{12},\, M_{21},\, M_{22}\big )^{\mathrm{T}}}$ will be obtained as follows [32].

$$\begin{aligned} M_{i1}&= \int _{\,0}^{\,m_0T} {\frac{\omega _i^2}{2h_i}x_{i1}F_{i2} \ \mathrm{d}\,t} \nonumber \\ M_{i2}&= \int _{\,0}^{\,m_0T} {\omega _i x_{i2}F_{i2} \ \mathrm{d}\,t} \qquad i=1,\,2 \end{aligned}$$

(15)

Thus, a fixed point of $P^{\,m_0}$ is equivalent to a zero solution of the Melnikov function.

Suppose that the family of periodic obits ${\Gamma _i} (i=1,\,2)$ for system (11)$_{\varepsilon =0}$ can be expressed as

$$\begin{aligned} x_{i1}= \sqrt{\frac{2h_i}{\omega _i}} \cos \big (\omega _i(t+t_i)\big ),\quad x_{i2}= \sqrt{\frac{2h_i}{\omega _i}} \sin \big (\omega _i(t+t_i)\big ) \end{aligned}$$

(16)

The corresponding periods of the orbits are $T_1(h_1)=\frac{2\pi }{\omega _1}$ and $T_2(h_2)=\frac{2\pi }{\omega _2}$, respectively. In this paper, we focus on the case of 1:2 internal resonance, the resonance relations satisfy

$$\begin{aligned} \omega _1:\omega _2:\Omega _1:\Omega _2=1:2:2:2 \end{aligned}$$

(17)

Assuming that $\Omega _1=\Omega _2 = 2$, thus ${T_1}({h_1}) = 2{T_2}({h_2}) = 2\pi$. Taking Eqs. (12) and (16) into Eq. (15), and let $\varvec{M}$ be zero, yields

$$\begin{aligned} M_{11}&=\frac{\pi }{8}\,\Big (12\alpha _{13}h_1+\alpha _{15}h_2 +4\alpha _{12}\cos (2t_1) \Big )=0 \end{aligned}$$

(18a)

$$\begin{aligned} M_{12}&=\frac{\pi }{16}\, \Big (16\alpha _{25}h_1+3\alpha _{23}h_2 -32f\cos (2t_2)\,h_2^{-\frac{1}{2}}\Big )=0 \end{aligned}$$

(18b)

$$\begin{aligned} M_{21}&=\pi h_1 \,\Big (2\mu \alpha _{11}+\alpha _{12}\sin (2t_1) \Big )=0 \end{aligned}$$

(18c)

$$\begin{aligned} M_{22}&=2\pi \sqrt{h_2}\ \Big (\,\mu \alpha _{21}\sqrt{h_2} -f\sin (2t_2) \Big )=0 \end{aligned}$$

(18d)

For convenience, we denote $m_i=\cos (2t_i),\,n_i=\sin (2t_i), \,i=1, \,2$.

(1) If $f=0$ (that is without transverse excitation), from Eqs. (18b) and (18d), we have $h_1=h_2=0$, there is no periodic solution for system (11).

(2) If $f\ne 0$, we can solve

$$\begin{aligned} m_1&=-\frac{1}{4\alpha _{12}}(12\alpha _{13}h_1+\alpha _{15}h_2),\quad n_1=-\frac{2\mu \alpha _{11}}{\alpha _{12}} \end{aligned}$$

(19a)

$$\begin{aligned} m_2&=\frac{\sqrt{h_2}}{32f}(16\alpha _{25}h_1+3\alpha _{23}h_2),\,\quad n_2=\frac{\mu \alpha _{21}}{f}\sqrt{h_2} \end{aligned}$$

(19b)

From $m_1^2+n_1^2=1$, we can solve

$$\begin{aligned} h_1^\pm =\frac{1}{12\alpha _{13}}\left( -\alpha _{15}h_2\pm 4\sqrt{\alpha _{12}^2 -4\mu ^2\alpha _{11}^2}\ \right) \,\overset{\text {def}}{=}\, h_\pm (h_2) \end{aligned}$$

(20)

Taking Eqs. (19b) and (20) into $m_2^2+n_2^2=1$, yields

$$\begin{aligned} g_\pm (h_2)=A^2h_2^3\pm 2AB\,h_2^2+(B^2+C^2)\,h_2-D^2=0 \end{aligned}$$

(21)

where

$$A=9\alpha _{13}\alpha _{23}-4\alpha _{15}\alpha _{25},\, B=16\alpha _{25}\sqrt{\alpha _{12}^2-4\mu ^2\alpha _{11}^2},\, C=\mu \alpha _{21}a,\, D=af,\,a=96\alpha _{13}$$

.

Obviously, $CD\ne 0$. If $A=0$, then we can solve

$$\begin{aligned} h_2=\frac{D^2}{B^2+C^2} \end{aligned}$$

(22)

There can be at most one set of positive real solution for $(h_1,\,h_2)$. Else, if $A\ne 0$, according to the relations between roots and coefficients of cubic equations, we have

$$\begin{aligned} h_{21}\,h_{22}\,h_{23}=\frac{D^2}{A^2},\quad h_{21}+h_{22}+h_{23}=\mp \frac{2B}{A} \end{aligned}$$

(23)

By analyzing the sign of Eq. (23), we can only get a rough estimation on the number of periodic solutions. Once the coefficients of the system (11) are given, the existence and precise number of periodic solutions can be obtained.

In this paper, we choose the coefficients as follows.

$$\begin{aligned} PC&=\{\,\mu ,\,\alpha _{11},\,\alpha _{12},\,\alpha _{13},\,\alpha _{15},\, \alpha _{21},\,\alpha _{23},\,\alpha _{25}\,\} \nonumber \\&=\{\,0.2,\,10,\,-5,\,0.5,\,-3,\,10,\,0.5,\,-12\,\} \end{aligned}$$

(24)

The transverse excitation f is left as a control parameter. Under this condition, we can calculate $A=-141.75,\,B=-576,\,C=96,\,D=48f$.

Fig. 2

Variation of the solutions $h_1$ and $h_2$ with f under condition PC: $\pm f_1,\,\pm f_2$ are critical values

By analyzing the sign of solutions $(h_1,\,h_2)$ in equations $h_\pm$ (Eq. (20)) and $g_\pm$ (Eq. (21)), we obtain four critical values of the parameter $f=\pm f_1,\,\pm f_2$, where

$$\begin{aligned} f_1=\frac{32}{189}\sqrt{1890-231\sqrt{33}},\quad f_2=\frac{1}{8}\sqrt{1033} \end{aligned}$$

(25)

The graph of the solution $(h_1,\,h_2)$ changing with parameter $f\, (f\ne 0)$ is plotted in Fig. 2 which provides a visualization of the existence and number of periodic solutions.

Note that there is a one-to-one correspondence between the solutions $h_1$ and $h_2$, and all the solutions of $h_2$ for equation $g_\pm$ are positive. So we can analyze the solution of $h_1$ for equation $h_\pm$ only. For equation $h_+$, as can be seen in Fig. 2, there is always one positive solution of $h_1$. For equation $h_-$, there is no positive solution of $h_1$ when $0<\vert f \vert <f_1$, one positive solution when $\vert f \vert =f_1$, two positive solutions when $f_1<\vert f \vert <f_2$, one positive and one zero solution when $\vert f \vert =f_2$, and one positive solution when $\vert f \vert >f_2$.

For convenience, we classify the periodic solutions obtained from $h_+$ and $g_+$ as family $\Gamma ^+$, and classify the periodic solutions obtained from $h_-$ and $g_-$ as family $\Gamma ^-$. Thus, there will be always one periodic solution in family $\Gamma ^+$. For family $\Gamma ^-$, there is no periodic solution when $0<\vert f \vert <f_1$, one periodic solution when $\vert f \vert =f_1$, two periodic solutions when $f_1<\vert f \vert \le f_2$ and one periodic solution when $\vert f \vert >f_2$. In summary, there can be at most three periodic solutions for the system in a certain bifurcation region.

4 Numerical Simulations

There will be interactions between the first two order modes of the system, and the energy will be transferred between them. In this section, the patterns of multiple periodic vibrations and waveforms of the first two order modes are presented graphically to reveal the vibration law and energy transfer styles for the system as the parameter varies from one region to another.

Fig. 3

Phase portraits of $f=0$: (a) $(x_{11},\,x_{22})$-plane; (b) $(x_{11},\,x_{12},\,x_{22})$-space

(1) $f=0$

Recall that, when $f=0$, i.e. without transverse excitation, there is no periodic orbit under condition PC. The phase portraits are shown in Fig. 3, where Fig. 3a, b represent the two and three dimensional projections, respectively. As shown in these figures, the solution curves are densely distributed, and no closed orbit can be found in the portraits.

Fig. 4

Phase portraits of one periodic orbit when $0<\vert f \vert <f_1$: (a) $(x_{11},\,x_{12})$-plane; (b) $(x_{21},\,x_{22})$-plane; (c) $(x_{11},\,x_{12},\,x_{21})$-space; (d) $(x_{11},\,x_{21},\,x_{22})$-space

Fig. 5

Waveforms of $w_1$ and $w_2$ modes of $\Gamma _1$ when $0<\vert f \vert <f_1$

(2) $0<\vert f \vert <f_1$

There is one periodic orbit when $0<\vert f \vert <f_1$ under condition PC, denote as $\Gamma _1$ ($\in \Gamma ^+$). The phase portraits are shown in Fig. 4, where Fig. 4a, b represent the two dimensional projections, Fig. 4c, d represent the three dimensional projections. One closed orbit can be found in each portrait, and the spiral form of the orbit is clearly visible. Figure 5 shows the waveforms of $w_1$ mode and $w_2$ mode of the periodic orbit $\Gamma _1$ when $0<\vert f \vert <f_1$ under condition PC. In the first half of the period, $w_1$ and $w_2$ increase simultaneously in a certain time range, whereafter $w_1$ keeps increasing and $w_2$ will decrease and then increase again. $w_2$ nearly equals to zero when $w_1$ reaches its peak. After the peak, in the second half of the period, $w_1$ decreases gradually, $w_2$ changes in the same way as before and nearly equals to zero when $w_1$ reaches its valley.

Fig. 6

Phase portraits of periodic orbits when $\vert f \vert =f_1$: (a) $(x_{11},\,x_{12})$-plane; (b) $(x_{21},\,x_{22})$-plane; (c) $(x_{11},\,x_{12},\,x_{21})$-space; (d) $(x_{11},\,x_{21},\,x_{22})$-space

Fig. 7

Waveforms of $w_1$ and $w_2$ modes of (a) $\Gamma _1$ and (b) $\Gamma _2$ when $\vert f \vert =f_1$

Fig. 8

Phase portraits of periodic orbits when $f_1<\vert f \vert <f_2$: (a) $(x_{11},\,x_{12})$-plane; (b) $(x_{21},\,x_{22})$-plane; (c) $(x_{11},\,x_{12},\,x_{21})$-space; (d) $(x_{11},\,x_{21},\,x_{22})$-space

Fig. 9

Waveforms of $w_1$ and $w_2$ modes of (a) $\Gamma _1$, (b) $\Gamma _{21}$ and (c) $\Gamma _{22}$ when $f_1<\vert f \vert <f_2$

Fig. 10

Phase portraits of periodic orbits when $\vert f \vert =f_2$: (a) $(x_{11},\,x_{12})$-plane; (b) $(x_{21},\,x_{22})$-plane; (c) $(x_{11},\,x_{12},\,x_{21})$-space; (d) $(x_{11},\,x_{21},\,x_{22})$-space

Fig. 11

Waveforms of $w_1$ and $w_2$ modes of (a) $\Gamma _1$, (b) $\Gamma _{21}$ and (c) $\Gamma _{22}$ when $\vert f \vert =f_2$

Fig. 12

Phase portraits of periodic orbits when $\vert f \vert >f_2$: (a) $(x_{11},\,x_{12})$-plane; (b) $(x_{21},\,x_{22})$-plane; (c) $(x_{11},\,x_{12},\,x_{21})$-space; (d) $(x_{11},\,x_{21},\,x_{22})$-space

Fig. 13

Waveforms of $w_1$ and $w_2$ modes of (a) $\Gamma _1$ and (b) $\Gamma _{21}$ when $\vert f \vert >f_2$

(3) $\vert f \vert =f_1$

When $\vert f \vert$ increases gradually and reaches $\vert f \vert =f_1$, bifurcation occurs and a new periodic orbit $\Gamma _2$ ($\in \Gamma ^-$) generated. Then there exist two periodic orbits when $\vert f \vert =f_1$ under condition PC. The phase portraits of periodic vibrations are shown in Fig. 6, where Fig. 6a, b represent the two dimensional projections, Fig. 6c, d represent the three dimensional projections. Figure 7 shows the waveforms of $w_1$ mode and $w_2$ mode of periodic vibration $\Gamma _1$ (Fig. 7a) and $\Gamma _2$ (Fig. 7b). Compared with Fig. 5, the energy transfer style between $w_1$ and $w_2$ mode of $\Gamma _1$ ($\in \Gamma ^+$) when $\vert f \vert =f_1$ is similar to that of $\Gamma _1$ when $0<\vert f \vert <f_1$. However, the energy transfer style between $w_1$ and $w_2$ mode of $\Gamma _2$ ($\in \Gamma ^-$) is quite different from that of $\Gamma _1$ ($\in \Gamma ^+$). As shown in Fig. 7b, when $w_2$ reaches its peak, $w_1$ will reach the peak or valley at the same time; when $w_2$ reaches its valley, $w_1$ nearly equals to zero.

(4) $f_1<\vert f \vert <f_2$

When $\vert f \vert$ passes the critical value $f_1$, the periodic orbit $\Gamma _2$ will split into two periodic orbits immediately, denote as $\Gamma _{21}$ and $\Gamma _{22}$. Thus, there are total three periodic orbits when $f_1<\vert f \vert <f_2$ under condition PC. The phase portraits are shown in Fig. 8, where Fig. 8a, b represent the two dimensional projections, Fig. 8c, d represent the three dimensional projections. With the increase of transverse excitation, the amplitude of $\Gamma _{21}$ increases whereas the amplitude of $\Gamma _{22}$ decreases gradually. Figure 9 shows the waveforms of $w_1$ mode and $w_2$ mode of periodic vibration $\Gamma _1$ (Fig. 9a), $\Gamma _{21}$ (Fig. 9b) and $\Gamma _{22}$ (Fig. 9c). Compared with Fig. 7, the energy transfer style between $w_1$ and $w_2$ mode of $\Gamma _1$ ($\in \Gamma ^+$) when $f_1<\vert f \vert <f_2$ is similar to that of $\Gamma _1$ when $\vert f \vert =f_1$. The energy transfer styles between $w_1$ and $w_2$ mode of $\Gamma _{21}$ and $\Gamma _{22}$ ($\in \Gamma ^-$) are similar to that of $\Gamma _2$ ($\in \Gamma ^-$) when $\vert f \vert =f_1$, but quite different from that of $\Gamma _1$ ($\in \Gamma ^+$).

(5) $\vert f \vert =f_2$

When $\vert f \vert$ increases continuously and reaches $\vert f \vert =f_2$, the Hamiltonian $\varvec{h}=(h_1,\,h_2)$ of $\Gamma _{22}$ satisfies $h_1=0,\, h_2>0$. Thus, there are still three periodic orbits for the system when $\vert f \vert =f_2$ under condition PC. The phase portraits are shown in Fig. 10, where Fig. 10a, b represent the two dimensional projections, Fig. 10c, d represent the three dimensional projections. As shown in Fig. 10a, the projection of orbit $\Gamma _{22}$ on $(x_{11},\,x_{12})$-plane degenerates to a point because $h_1=0$. Figure 11 shows the waveforms of $w_1$ mode and $w_2$ mode of periodic vibration $\Gamma _1$ (Fig. 11a), $\Gamma _{21}$ (Fig. 11b) and $\Gamma _{22}$ (Fig. 11c). Compared with Fig. 9, the energy transfer style between $w_1$ and $w_2$ mode of $\Gamma _1$ ($\in \Gamma ^+$) when $\vert f \vert =f_2$ is similar to that of $\Gamma _1$ when $f_1<\vert f \vert <f_2$. The energy transfer styles between $w_1$ and $w_2$ mode of $\Gamma _{21}$ and $\Gamma _{22}$ ($\in \Gamma ^-$) are similar to that of $\Gamma _{21}$ and $\Gamma _{22}$ ($\in \Gamma ^-$) when $f_1<\vert f \vert <f_2$, but different from that of $\Gamma _1$ ($\in \Gamma ^+$).

(6) $\vert f \vert >f_2$

When $\vert f \vert$ passes the critical value $f_2$, the periodic orbit $\Gamma _{22}$ vanishes immediately. So, there are only two periodic orbits remain ($\Gamma _1$ and $\Gamma _{21}$) when $\vert f \vert >f_2$ under condition PC. The phase portraits are shown in Fig. 12, where Fig. 12a, b represent the two dimensional projections, Fig. 12c, d represent the three dimensional projections. Figure 13 shows the waveforms of $w_1$ mode and $w_2$ mode of periodic vibration $\Gamma _1$ (Fig. 13a) and $\Gamma _{21}$ (Fig. 13b). The energy transfer style between $w_1$ and $w_2$ mode of $\Gamma _1$ ($\in \Gamma ^+$) when $\vert f \vert >f_2$ is similar to that of $\Gamma _1$ when $\vert f \vert =f_2$. The energy transfer style between $w_1$ and $w_2$ mode of $\Gamma _{21}$ ($\in \Gamma ^-$) when $\vert f \vert >f_2$ is similar to that of $\Gamma _{21}$ when $\vert f \vert =f_2$, but quite different to that of $\Gamma _1$.

From the above analysis, there exists one periodic orbit ($\Gamma _1$) when $0<\vert f \vert <f_1$ for the system under 1:2 internal resonance. With the increase of excitation $\vert f \vert$, the amplitude of $\Gamma _1$ increases gradually. Another periodic orbit ($\Gamma _2$) occurs at the critical parameter value $\vert f \vert =f_1$, and then immediately splits into two periodic orbits ($\Gamma _{21}$ and $\Gamma _{22}$) once the excitation $\vert f \vert$ passes $f_1$. The amplitude of $\Gamma _{21}$ increases whereas the amplitude of $\Gamma _{22}$ decreases as the parameter value $\vert f \vert$ continues to increase, and the periodic orbit $\Gamma _{22}$ will disappear immediately when $\vert f \vert$ passes $f_2$. From then on, there remain only two periodic orbits $\Gamma _1$ and $\Gamma _{21}$, and their amplitudes will increase gradually with the increase of excitation $\vert f \vert$. The detailed evolution law of periodic orbits (including number and amplitude) changing with parameter f can be seen intuitively in the phase-parameter space (see Fig. 14). The number of periodic orbits changes as: $2 \rightarrow 3 \rightarrow 2 \rightarrow 1 \rightarrow 0 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 2$. They are classified into two families: $\Gamma ^+$ and $\Gamma ^-$. The energy transfer style between $w_1$ mode and $w_2$ mode is similar for the orbits in the same family but quite different for the orbits in different families.

Fig. 14

Bifurcation of multiple periodic orbits in the $(f,x_{11},x_{12})$ phase-parameter space under condition PC: NP represents the number of the periodic orbit, BA represents the bifurcation areas, PO represents the periodic orbits and BP represents the bifurcation parameter values

5 Conclusions

Sandwich plates in auxetic honeycombs with special properties can meet the need of modern science and technology development and have been widely used in aerospace, defense and other industries. When they are used as the horizontal retaining or vertical bearing structures, the plates have to carry complex loads in the service process which would lead to performance degradation or produce structural damages. A major concern in the design and construction stages is to predict the force and vibration behaviors.

In this paper, multiple periodic vibrations of auxetic honeycomb sandwich plates subjected to in-plane and transverse excitation are investigated. The two degrees of freedom nonlinear equation of motion for the plate is derived based on TSDT and von Kármán type nonlinear geometric assumptions. The 1:2 internal resonance is taken into account to analyze the bifurcation and coexistence of multiple periodic orbits with the extended Melnikov method. Phase portraits of geometric structures and waveforms of multiple periodic vibrations in different bifurcation regions induced by transverse excitation are obtained with numerical method. The changes of number and amplitude of the multiple periodic orbits are intuitive described in the phase-parameter bifurcation portrait. Through this investigation, some remarks can be listed as follows:

• Without transverse excitation, there will be no periodic vibrations. Even quite small transverse excitation can cause small amplitude periodic vibration. The amplitudes of some certain vibrations will increase gradually with the increase of excitation.

• Effects of transverse excitation on nonlinear vibration behaviors are discussed in detail. Five bifurcation values of the parameter f can be found under condition PC for the system: $f=0,\,\pm f_1,\,\pm f_2$.

• Numerical results show that the system displays different vibration properties as the parameter varies from one bifurcation region to another, and there can be at most three periodic orbits coexisting under certain conditions.

• The periodic vibrations are classified into two families. By comparing the waveform portraits with each other, the energy transfer style between $w_1$ mode and $w_2$ mode is similar for the orbits in the same family but quite different for the orbits in different families.

• The current method can trace the source of periodic solutions, which provides the possibility for the classification study on generation mechanism of system complexity and energy transfers.

Appendix A

The nonlinear equation of motion for the auxetic plate derived by Hamilton’s principle is as follows.

$$\begin{aligned}&\frac{\partial N_{xx}}{\partial x}+\frac{\partial N_{xy}}{\partial y}=I_0\ddot{u}_0+ \left( I_1-\frac{4}{3h^2}I_3 \right) \ddot{\varphi }_x -\frac{4}{3h^2}I_3\frac{\partial \ddot{w}_0}{\partial x} \end{aligned}$$

(A1a)

$$\begin{aligned}&\frac{\partial N_{yy}}{\partial y}+\frac{\partial N_{xy}}{\partial x}=I_0\ddot{v}_0+ \left( I_1-\frac{4}{3h^2}I_3 \right) \ddot{\varphi }_y -\frac{4}{3h^2}I_3\frac{\partial \ddot{w}_0}{\partial y} \end{aligned}$$

(A1b)

$$\begin{aligned} \\&\left( \frac{\partial N_{yy}}{\partial y}\frac{\partial w_0}{\partial y}+N_{yy}\frac{\partial ^2 w_0}{\partial y^2} \right) + \left( \frac{\partial N_{xy}}{\partial x}\frac{\partial w_0}{\partial y}+2N_{xy}\frac{\partial ^2 w_0}{\partial x \partial y}+\frac{\partial N_{xy}}{\partial y}\frac{\partial w_0}{\partial x} \right) \\&\ \qquad \qquad +\left( \frac{\partial N_{xx}}{\partial x}\frac{\partial w_0}{\partial x}+N_{xx}\frac{\partial ^2 w_0}{\partial x^2} \right) +\frac{4}{3h^2} \left( \frac{\partial ^2P_{xx}}{\partial x^2}+2\frac{\partial ^2P_{xy}}{\partial x \partial y}+\frac{\partial ^2P_{yy}}{\partial y^2} \right) \\&\ \qquad \qquad +\left( \frac{\partial Q_{x}}{\partial x}-\frac{4}{h^2}\frac{\partial R_{x}}{\partial x}\right) +\left( \frac{\partial Q_{y}}{\partial y}-\frac{4}{h^2}\frac{\partial R_{y}}{\partial y} \right) +F-\mu \dot{w}_0 \\&\ \quad \qquad =I_0 \ddot{w}_0+\frac{4}{3h^2}I_3 \left( \frac{\partial \ddot{u}_0}{\partial x}+\frac{\partial \ddot{v}_0}{\partial y}\right) -\frac{16}{9h^4}I_6\left( \frac{\partial ^2 \ddot{w}_0}{\partial x^2}+\frac{\partial ^2 \ddot{w}_0}{\partial y^2}\right) \\&\ \qquad \qquad +\frac{4}{3h^2}\left( I_4-\frac{4}{3h^2}I_6\right) \left( \frac{\partial \ddot{\varphi }_x}{\partial x}+\frac{\partial \ddot{\varphi }_y}{\partial y}\right) \end{aligned}$$

(A1c)

$$\begin{aligned}&\frac{\partial M_{xx}}{\partial x}+\frac{\partial M_{xy}}{\partial y} -\frac{4}{3h^2}\left( \frac{\partial P_{xx}}{\partial x}+\frac{\partial P_{xy}}{\partial y}\right) -\left( Q_x-\frac{4}{h^2}R_x\right) \\&\ \quad \qquad =\left( I_1-\frac{4}{3h^2}I_3\right) \ddot{u}_0 +\left( I_2-\frac{8}{3h^2}I_4+\frac{16}{9h^4}I_6 \right) \ddot{\varphi }_x \\&\ \qquad \qquad -\frac{4}{3h^2}\left( I_4-\frac{4}{3h^2}I_6\right) \frac{\partial \ddot{w}_0}{\partial x} \end{aligned}$$

(A1d)

$$\begin{aligned}&\frac{\partial M_{yy}}{\partial y}+\frac{\partial M_{xy}}{\partial x} -\frac{4}{3h^2}\left( \frac{\partial P_{yy}}{\partial y}+\frac{\partial P_{xy}}{\partial x}\right) -\left( Q_y-\frac{4}{h^2}R_y\right) \\&\ \quad \qquad =\left( I_1-\frac{4}{3h^2}I_3\right) \ddot{v}_0 +\left( I_2-\frac{8}{3h^2}I_4+\frac{16}{9h^4}I_6 \right) \ddot{\varphi }_y \\&\ \qquad \qquad -\frac{4}{3h^2}\left( I_4-\frac{4}{3h^2}I_6\right) \frac{\partial \ddot{w}_0}{\partial y} \end{aligned}$$

(A1e)

where $\mu$ is damping coefficient, and

$$\begin{aligned} \begin{aligned} I_i&=\sum \limits _{k=1}^{3}{\int _{\,z_k}^{\,z_{k+1}}\rho ^{(k)}z^i\, \mathrm{d}z},\qquad i=0,\, 1,\, 2,\, \ldots ,\, 6 \\ z_1&=-h_1-\frac{h_2}{2},\, z_2=-\frac{h_2}{2},\, z_3=\frac{h_2}{2},\, z_4=\frac{h_2}{2}+h_3 \end{aligned} \end{aligned}$$

(A2)

The internal-strain relations are expressed as

$$\begin{aligned} \begin{aligned} \varvec{N}_{x,\,y}&=\varvec{A}_1 \, \varvec{\varepsilon }^0,\quad \varvec{Q}_{x,\,y}=\varvec{A}_2 \, \varvec{\gamma }^0,\quad \varvec{M}_{x,\,y}=\varvec{D}_1 \, \varvec{\varepsilon }^1+\varvec{F}_1 \, \varvec{\varepsilon }^2 \\ \varvec{P}_{x,\,y}&=\varvec{F}_1 \, \varvec{\varepsilon }^1+\varvec{H}_1 \, \varvec{\varepsilon }^2 ,\quad \varvec{R}_{x,\,y}=\varvec{D}_2 \, \varvec{\gamma }^0 +\varvec{F}_2 \, \varvec{\gamma }^2 \end{aligned} \end{aligned}$$

(A3)

in which

$$\begin{aligned}&\varvec{X}_{x,\,y}= \big (X_{xx},\,X_{yy},\, X_{xy} \big )^{\mathrm{T}}, \quad \varvec{Y}_{x,\,y}= \big (Y_y,\,Y_x \big )^{\mathrm{T}} \\&\varvec{Z}_1=\partial _{1,\,1}^{2,\,2} \left( \partial _{i,\,j}^{2,\,2} \big (Z_{ij}\big ) \right) + \partial _{2,\,2}^{2,\,2}\big (Z_{66}\big ),\, \varvec{Z}_2=\partial _{1,\,1}^{2,\,2} \big (Z_{44}\big )+ \partial _{2,\,2}^{2,\,2}\big (Z_{55}\big ) \\&\varvec{X}=\varvec{N},\,\varvec{M},\,\varvec{P};\quad \varvec{Y}=\varvec{Q},\,\varvec{R};\quad \varvec{Z}=\varvec{A},\,\varvec{D},\,\varvec{F} \end{aligned}$$

The stiffness coefficients are defined as

$$\begin{aligned} \big (A_{ij},\, B_{ij},\, D_{ij},\, E_{ij},\, F_{ij},\, H_{ij} \big ) =\sum \limits _{k=1}^{3}{\int _{\,z_k}^{\,z_{k+1}}Q_{ij}^{(k)}\Big (1,\, z,\, z^2,\, z^3,\, z^4,\, z^6 \Big )\ \mathrm{d}z} \end{aligned}$$

(A4)