1 Introduction

Rolling bearings are extensively applied in rotary machine of aerospace, railway, construction, mining and other industries because of their convenient installation and reliable operation [1]. Generally, various types of rolling bearing failures occur due to incorrect installation, poor maintenance and surface fatigue. Through theoretical modeling and experimental analysis, the relation between system responses and kinetic parameters can be obtained so as to understand the mechanism of defects generation. Therefore, it is of great significance to establish a reasonable mathematical model of the bearing for accurately identifying defect characteristics, determining defect types and analyzing defect causes. Thus, scholars have conducted a large number of research on the modeling of rolling bearing with defects.

In 1984, McFadden and Smith [2] constructed the first vibration response model with local fault using periodic pulses with equal amplitude to simulate the impact force produced by the defect. McFadden and Smith [3] further improved their model to study the frequency components of acceleration signals with two point damages. Su et al. [4] improved the model proposed by Refs. [2, 3] to analyze the vibration frequency generated by single point and multi-point faults under different types of loads. Unlike the Refs. [2,3,4], Tandon and Choudhury [5] proposed a model using three different types of pulse shapes—rectangle, triangle and half sine. Cong et al. [6] presented an impulse-train model with defective raceways to investigate the vibration response of bearing. The impulse-train models mentioned above [2,3,4,5,6] cannot consider the fault morphology, so the influence of fault size and shape on bearing vibration and fault size estimation cannot be studied. Therefore, the nonlinear multi-body dynamic models were adopted by many researchers.

The simplest multi-body dynamic model [7] had only two degrees of freedom. That is, only the planar translational movements of the inner ring are considered. Sunnersjo [7] first proposed the concept of variable compliance vibrations explaining the vibrations of rolling bearing even under the perfect manufacture. Based on this model, a number of scholars had carried out the failure dynamic analysis of bearings [8, 9, 21, 22]. Patil et al. [8] presented a 2-DOF dynamic model using half-sinusoidal displacement excitation to simulate the raceway defects, and analyzed the influence of defect size and location on dynamic characteristics. Qin et al. [9] constructed a novel vibration model of defective bearing considering the coupling effects of loaded balls. The above models [7,8,9] only considered the defects as the displacement excitation, which is obviously not comprehensive. Shao et al. [10] considered the time-varying contact characteristics on the defective zone, more accurately describing the impact produced by the defect. Liu et al. [11] further considered the different edge topographies of raceway defects to construct the numerical model of a bearing. Liu et al. [12] investigated the effect of the raceway dent on the bearing dynamic characteristic considering the time-varying contact force caused by the dent.

The rolling elements were not contained in the above models [7,8,9,10,11,12]. Xu et al. [13] proposed an improved quasi-static model of deep groove ball bearing considering the axial force and overturning torque to analyze its ultimate load-bearing capacities. Liu et al. [14] constructed a dynamic model of rolling bearing considering the rolling elements and flexible cage. Some models [15,16,17,18] regarded the rolling element as a point mass, but ignored the size of the rolling elements, so the vibration response was not completely consistent with the reality. Patel et al. [15] presented a model with multiple raceway defects and analyzed the components of the spectrum. Harsha [16] presented a nonlinear vibration model with surface waviness on raceways considering the mass of the rollers. Sawalhi et al. [17, 18] established a defective bearing-gear composite model considering the slipping, Hertz contact and nonlinear stiffness. Ahmadi et al. [19] constructed a vibration model of rolling bearings with defective outer race considering the size of rollers on the basis of Refs. [16,17,18].

The above models were mainly focused on raceway defects. Some researchers also studied the bearing dynamic characteristics with rolling element defects. Cao [20] constructed a numerical model of the double-row ball bearing with local faults. Rafsanjani et al. [21] proposed a 2-DOF dynamic model with raceway and ball defects. Kankar et al. [22] presented a 2-DOF dynamic model with defective ball and raceway considering the unbalanced force of the rotor. Niu et al. [23] constructed a bearing dynamic model with defective roller and elaborated the multiple impulses when the roller defect passes through the raceway based on the Gupta’s dynamic model [24]. Yang et al. [25] presented a vibration model of rolling bearing-rotor-casing system and investigated the influence of localized defects on the system dynamic characteristics.

More and more researchers considered the cage, lubrication and flexibility in their models. Han et al. [26] presented a 3-D dynamic model considering the roller crown profile and analyzed the influence of load conditions on sliding behavior. Liu et al. [27] analyzed the influence of flexibility on the bearing vibration response. Shi et al. [28] constructed a planar dynamic model of the bearing considering the elastic supports of the shaft and housing, the cage-to-rollers interaction. Shi et al. [29] constructed a dynamic model of ceramic bearing-steel pedestal system including the thermal deformation. Liu et al. [30] established a friction-vibration model of faulty ACBBs considering the sliding behavior at the contact area based on the acoustic calculation methods given by Sharma [31] and Patil [32].

The lumped-parameter models usually need to make assumptions and simplifications. Unlike analytical models, finite element (FE) models can minimize the assumptions, which is in more accord with the actual situation. Therefore, a number of researchers used the finite element methods to construct the dynamic model of bearing. Laniado-jacome et al. [33] analyzed the sliding behavior of rollers using the FE method. Singh et al. [34] investigated the contact force characteristics and acceleration responses of the bearing with defective outer race using explicit dynamic FE software package LS-DYNA. Yang et al. [35] proposed a dynamic model of bearing-rotor system with transverse crack. Parametric uncertainties were considered using the Polynomial Chaos Expansion. Xu et al. [36] proposed a new method for calculating the radial time-varying stiffness of cylindrical roller bearings with localized defects using analytical-finite-element method.

The above models with rolling element defects [20,21,22] only considered the rolling elements as the point mass without considering the size of the rolling elements and faults, nor the friction inside the bearing, the inertia force and the sliding of the rolling elements. The Refs. [26, 33] only studied the sliding behavior of healthy bearing without considering the effects of defects on the roller sliding. To overcome these problems, a nonlinear dynamic model of rolling bearing with roller defects is proposed using explicit FE analysis method in this paper. In the proposed model, the flexible deformation of all the components is considered, which makes the load distribution more accurate. In addition to the contact force generated by the local deformation, the friction force, the centrifugal force, the interaction between rollers and cage are also considered. The size of the rollers is also considered so that the trajectory of the defective roller can be investigated, from which the slippage of the roller can be reflected. Then the proposed model is verified theoretically and experimentally. Based on the proposed model, the effect of roller defects on vibration response of the bearing and the cage skidding are investigated.

2 Dynamic Modeling

Explicit FE software package, ANSYS/LS-DYNA, is used to model the roller bearing with roller spalling. The components in the proposed model only have translational motions in the plane of bearing.

2.1 Discretization of the Explicit FE Model

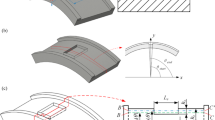
The model comprises an outer ring, an inner ring, a cage, 13 rollers and an adapter that supports the bearing. The geometrical and material parameters of components are given in Table 1. All the components within the model are meshed using two-dimensional quadrilateral shell elements because high-quality quadrilateral elements can improve the precision of the model and shorten the solution time. The element size is 0.25 mm. There are 39,196 elements and 41,361 nodes within the whole explicit FE model. The meshed 2-D explicit FE model is shown in Fig. 1. An approximate rectangular defect is modeled on one of the rollers. The dimension parameters of the roller defect are shown in Fig. 2.

Table 1 Geometrical and material parameters of the components within the FE model
Full size table
Fig. 1
figure 1

Diagrams of the 2-D FE bearing model: a schematic of all the components, and b an enlarged drawing showing the defect on one of the rollers

Full size image
Fig. 2
figure 2

Dimensions of the roller defect

Full size image

For appropriate mesh size, it is suggested to use at least 20 elements-per-wavelength (EPW) [34]. The bending wave propagation velocity can be calculated by

$$C_{{\text{b}}} = \sqrt \omega \left[ {\frac{{Eh^{2} }}{{12\left( {1 - \upsilon^{2} } \right)\rho }}} \right]^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 4}}}$$
(1)

where E is the elastic modulus, h is the thickness, υ is Poisson’s ratio, ρ is the density, and ω is the highest angular frequency of concern. The bending wave propagation velocity for the 3.5 mm outer ring of the bearing at 40 kHz is 1159.15 m/s, and the corresponding wavelength is 0.0289 m. That is, there are about 116 EPW for the element size of 0.25 mm, which is about six times of the recommended value. Therefore, the mesh size of the proposed model can ensure the accuracy requirements.

Loads and boundary conditions of the explicit FE model are as follows. (1) All the DOF of the bottom nodes of the adapter are constrained. (2) A radial load of 10 kN is applied on the inner ring. (3) The rotating speed of the inner ring rises from zero uniformly before 0.005 s and then a constant angular velocity of 1200 r/min is applied. (4) A static frictional coefficient of 0.01 and a dynamic frictional coefficient of 0.005 are defined in the proposed model. (5) A global damping of 2% is applied to the proposed model [34].

2.2 Calculation of Contact Force and Friction Force

Calculation of contact force in the proposed model uses the symmetric penalty function method. The location of each slave node is examined for penetration through the master surface every time step. If there is no penetration, no force will be exerted to the slave node. When penetration occurs, a contact force will be applied between the slave node and the master surface. Then the same process is executed again to each master node. Figure 3 shows the contact relationship between the slave node ns and the master surface. The gap function gn represents the penetration distance between the slave node ns and the contact point pc. The normal contact force Fn can be calculated by

$$F_{{\text{n}}} = - K_{{\text{n}}} g_{{\text{n}}}$$
(2)
Fig. 3
figure 3

Schematic of the contact relationship between the slave node and the master surface

Full size image

where Kn is the penalty stiffness calculated by [38]

$$K_{{\text{n}}} = \frac{{\alpha_{{\text{f}}} E_{{\text{b}}} A_{{\text{b}}} }}{{L_{{{\text{max}}}} }}$$
(3)

where αf is the scale factor, Eb is the bulk modulus, Ab is the area of the contact element, and Lmax is the maximum diagonal length of shell elements.

After obtaining the normal contact Fn of the slave node, tangential friction force is given based on the Coulomb frictional model [38]. The maximum friction force Fm of the slave node is given by

$$F_{{\text{m}}} = \mu \left| {F_{{\text{n}}} } \right|$$
(4)

where \(\mu\) is the frictional coefficient. Suppose f k is the friction force of the slave node at time tk, then the trial friction force f * at time tk+1 is calculated by

$$f^{*} = f^{k} - K_{{\text{s}}} \Delta m$$
(5)

where Ks is the interface stiffness, Δm is the increment movement of the slave node given by

$$\Delta m = r^{k + 1} (\xi^{k + 1} ,\eta^{k + 1} ) - r^{k + 1} (\xi^{k} ,\eta^{k} )$$
(6)

where r is the position vector of the slave node, ξ and η are the coordinates. Then the friction force of the slave node at time tk+1 is calculated by

$$\left\{ \begin{gathered} f^{k + 1} = f^{*} {\text{ if }}\left| {f^{*} } \right| \le F_{{\text{m}}} \hfill \\ f^{k + 1} = \frac{{F_{{\text{m}}} f^{*} }}{{\left| {f^{*} } \right|}}{\text{ if }}\left| {f^{*} } \right| > F_{{\text{m}}} \hfill \\ \end{gathered} \right.$$
(7)

According to the principle of reacting force, Fn and f are applied at the contact point in the opposite direction, then are allocated to the four master nodes on the master surface and finally assembled to the total load vector P.

2.3 Kinetic Equations of the Explicit FE Model

The kinetic equations of the explicit FE model can be written as

$${\mathbf{M\ddot{x}}} + {\mathbf{C\dot{x}}} = {\mathbf{P}} - {\mathbf{F}} + {\mathbf{H}}$$
(8)

where M is the mass matrix, C is the damping matrix, P is the external force vector, F is the internal force vector, H is the hourglass force vector. The detailed calculating process of F and H can be obtained from Ref. [38]. The step-changing explicit central difference method is used to solve the kinetic equation Eq. (8). The calculation flowchart is shown in Fig. 4.

Fig. 4
figure 4

Flowchart of explicit finite element method

Full size image

3 Verification of the Explicit FE Model

In this section, the presented explicit finite element model is verified by comparing the contact force with the analytical model and by comparing the vibration responses with the experimental results.

3.1 Contact Force Verification

An analytical model of Harris–Jones [33] is applied to obtain the roller-to-raceway contact force compared with that obtained from the explicit FE model. The Harris–Jones model consists of a set of nonlinear force balance equations.

For the inner race, the equilibrium equation can be expressed as

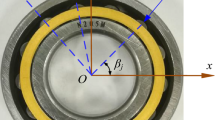
$$F_{{\text{r}}} - K_{{{\text{in}}}} \sum\limits_{j = 1}^{j = z} {\left( {\delta_{{{\text{in }}j}} } \right)^{10/9} \cos \psi_{j} } = 0$$
(9)

where Fr is the radial load applied on the inner ring, Kin is the contact stiffness between the roller and inner race calculated according to the Harris’s method [39], z is the number of rollers, δin j is the contact deformation between the jth roller and inner race, ψj is the angle between the jth roller and the negative y-axis.

For a single roller, the equilibrium equation can be expressed as

$$K_{{{\text{in}}}} \left( {\delta_{{{\text{in }}j}} } \right)^{10/9} + F_{{\text{c}}} = K_{{{\text{out}}}} \left( {\delta_{{{\text{r }}j}} - \delta_{{{\text{in }}j}} } \right)^{10/9} , \, j = 1 \ldots z$$
(10)

where Kout is the contact stiffness between the roller and outer race, δr j is the total contact deformation between the jth roller and raceways, Fc is centrifugal force of the rollers obtained by the Harris’s method [39].

Equations (9) and (10) are solved by Newton–Raphson iteration. After obtaining the contact deformation δin j between the inner race and the roller, the outer race-to-roller contact force can be obtained according to the following formula

$$F_{{{\text{out }}j}} = K_{{{\text{in}}}} \left( {\delta_{{{\text{in }}j}} } \right)^{10/9} + F_{{\text{c}}}$$
(11)

Figure 5 compares the vertical roller-to-outer race contact force calculated by the analytical model with that obtained by the explicit FE model. It can be found that good agreement is obtained between the simulated and the analytical results. Because the components of bearing are discretized into finite elements, the surface of components is not strictly smooth but polygonal, which leads to the fluctuation of contact force.

Fig. 5
figure 5

Contact force verification of explicit FE model: a schematic of roller position and b contact force comparison between the two models

Full size image

3.2 Vibration Response Verification

Experiments are conducted to verify the vibration response of the explicit FE model. The experimental system is shown in Fig. 6a. The bearing acceleration signals in the y and z directions are measured using two accelerometers (CA-YD-182) placed on the top and one side of the bearing housing, as shown in Fig. 6b. Data acquisition system (DH5956) is used to collect the acceleration signals with a sampling frequency of 20 kHz, as shown in Fig. 6c. One end of the rotating shaft is supported by SKF6205 bearing and the other end is supported by the tested bearing N205EM, as shown in Fig. 6d. A rectangular spall on the roller is manufactured by wire-electrode cutting. The geometrical dimensions of the defective bearing is the same as that of the explicit FE model. The rotation speed of the shaft is 1200 r/min.

Fig. 6
figure 6

Experimental system: a test rig, b accelerometer, c data acquisition system and d defective roller

Full size image

Figure 7 shows the bearing acceleration responses in the z direction obtained by simulation and experiment. It should be noted that due to the interference of various factors in the test, the amplitudes of the response of simulation and test are difficult to be consistent, the normalization procedure is applied to the both results. Periodic impulses produced by the roller defect can be observed in the time domain signals of the simulation and experiment (Fig. 7a, c). It can be found that the impulses due to the impact are larger when the defective roller locates in the loaded zone. From the envelope spectrum (Fig. 7b, d), it can be found that the simulated signal and the experimental signal have the same frequency components: defect frequency fb and its harmonics, sidebands spaced at the cage rotation frequency fc. The theoretical values of the cage rotation frequency fc and the roller defect frequency fb can be calculated according to Ref. [39].

Fig. 7
figure 7

Simulation and experiment results: a simulated acceleration signal in time domain, b envelope spectrum of the simulated signal, c experimental acceleration signal in time domain, d envelope spectrum of the experimental signal

Full size image

The cage rotation frequency is given by

$$f_{{\text{c}}} = \frac{{f_{{\text{s}}} }}{2}\left( {1 - \frac{d}{D}{\text{cos}}\alpha } \right)$$
(12)

where fs is the shaft rotation frequency, d is the roller diameter, D is the pitch diameter, and α is the contact angle. For the cylindrical roller bearing, α = 0.

The roller spinning frequency is given by

$$f_{{\text{r}}} = \frac{{Df_{{\text{s}}} }}{2d}\left( {1 - \frac{{d^{2} }}{{D^{2} }}\cos^{2} \alpha } \right)$$
(13)

When the roller rotates, the defect will alternately contact the inner and outer race, so the roller defect frequency is twice of its spinning frequency, i.e.

$$f_{{\text{b}}} = 2f_{{\text{r}}}$$
(14)

The calculated theoretical values fb = 115.08 Hz, fc = 8.31 Hz, approximately equal to the simulated (fb = 114.49 Hz, fc = 8.69 Hz) and experimental values (fb = 113.48 Hz, fc = 8.2 Hz), indicating the correctness of the simulation and experiment. It should be noted that the roller defect frequency of the simulated and the experimental results are slightly smaller than that of the theoretical results, which is because the theoretical formulas do not consider the skidding of the defective roller.

4 Results and Discussions

4.1 Explanation of the Sliding Behavior

Figure 8 shows the experimental and the simulated acceleration responses. The normalization procedure is applied to the both results. It can be found that there exists the time delay between the two impacts produced by the roller defect. The real running state of the defective roller during the experiment can not be observed, while it can be achieved using the proposed model.

Fig. 8
figure 8

Sliding behavior of the defective roller: a experimental time domain acceleration and b simulated time domain acceleration

Full size image

Trajectory of the node located on the edge of the defective roller during a period of time obtained from the proposed model are presented in Fig. 9. It can be clearly found that there exists the sliding of defective roller during this time. At point A (time t1), the defective roller stops rolling and starts to slip. In the process of sliding, the trajectory of the node located on the edge of the defective roller overlaps the outer race, and the defect keeps rubbing with the raceway until reaches the point B, where the defective roller resumes rolling. When the roller rotates, the defect will interact alternately with the raceways, intensifying the vibration of bearing. When the roller slips, the defect continually rubbing with the raceway without impact, alleviating the vibration of bearing. The proposed model has realized the simulation of sliding, using which the mechanical characteristics of roller sliding can be investigated. This further proves that the proposed model can well simulate the real running state of bearings.

Fig. 9
figure 9

Trajectory of the node located on the edge of the defective roller

Full size image

Figure 10a, b show the rollers-to-cage contact force at the same position relative to the loaded zone [(a) healthy roller-to-cage and (b) defective roller-to-cage]. It can be found that under the normal condition, the contact between rollers and cage is highly random and the contact force is small. When the spalls exist on the roller, the defective roller-to-cage contact force increases and the contact time also increases. Figure 10c shows the defective roller-to-inner race contact force when the defective roller is sliding. At time t1, the defective roller is in the location as shown in Fig. 9. Due to the increased clearance between the defective roller and raceways, the defective roller-to-raceways contact force decrease to zero, leading to a lack of traction of the inner race on the defective roller. The defective roller stops rotating around its axis and starts to slide along the raceway. During this time, the cage begins to play a role in promoting the movement of the defective roller, so the defective roller-to-cage contact force increases. The motion state of the defective roller is not stable because it has just gone from rolling to sliding. The trend of rolling still exists, so there are fluctuations of inner race-to-defective roller contact force. After time t2, the defective roller goes into a stable state under the combined force of the cage and the raceway, and the defective roller-cage contact force continues to maintain a large value. Until the time t3, the defective roller enters into the unstable sliding state again and gradually turns to the rolling state.

Fig. 10
figure 10

Contact force analysis during the sliding of the defective roller: a healthy roller-to-cage, b defective roller-to-cage and c defective roller-to-inner race

Full size image

Figure 11 is the stress nephogram of the defective roller when it is sliding, from which the position and stress state of the defective roller can be seen. Figure 11a shows the stress nephogram at three moments when the defective roller is in an unstable state. It can be seen that the roller alternately collides with the front and the rear ends of the cage pocket. Figure 11b shows the stress nephogram at three moments when the defective roller is in a stable state. It can be found that the defective roller contact continually with the rear end of the cage pocket.

Fig. 11
figure 11

Contact state of the defective roller during sliding: a unstable sliding state and b stable sliding state

Full size image

4.2 Effects of the Defects Parameter on the Dynamic Characteristics

4.2.1 Effects of the Defect Width

To analyze the effect of the defect width on the dynamic characteristics of the bearing, the defect depth is given as 0.59 mm and the defect width varies from 0.46 to 2.27 mm. Figures 12 and 13 show the simulated and the experimental acceleration responses of the bearing in the vertical direction in the cases of three different defect widths respectively. The shaft rotating speed of the explicit finite element model is 6000 r/min and that of the experiment is 1200 r/min. In order to better show the law, the simulated and experimental acceleration response are processed with following dimensionless method:

$$X_{i} ^{\prime} = \frac{{X_{i} }}{{Y_{{{\text{max}}}} }}{, }\quad i{ = 1,2,3,} \ldots {,}N$$
(15)
Fig. 12
figure 12

The simulated vibration responses in the vertical direction with three different defect widths: a–c acceleration signals for 0.46, 1.38, and 2.27 mm respectively, d–f envelope spectrum for 0.46, 1.38, and 2.27 mm respectively

Full size image
Fig. 13
figure 13

The experimental vibration responses in the vertical direction with three different defect widths: a–c acceleration signals for 0.46, 1.38, and 2.27 mm respectively, d–f envelope spectrum for 0.46, 1.38, and 2.27 mm respectively

Full size image

where \(X_{i} ^{\prime}\) is the processed acceleration response, \(X_{i}\) is the original acceleration response, Ymax is the maximum of the acceleration response of bearing without defect, N is the data size. The same data processing method is adopted in the following analyses.

It can be clearly found that the level of the vibration increases as the defect width is increased. Figure 14a shows the vertical defective roller-to-outer race contact force when the defective roller rolls in the loaded zone in the cases of three different defect widths. For the case of defect width wd = 0.46 mm, the defective roller-to-outer race contact force is slightly reduced due to a small increase of the clearance when the defect rolls through the raceway, so the impact produced by roller defect is slight and there is no obvious impulse in the acceleration response signal and no fault feature frequency in the envelope spectrum. For the case of defect width wd = 1.38 mm, when the roller defect rolls through the raceway, the clearance increases greatly and the defective roller-to-raceway contact force will be reduced to zero in a short time, which leads to an impulse in the acceleration signal. For the case of defect width wd = 2.27 mm, it is similar to the case of wd = 1.38 mm. The defective roller-to-raceway contact force will be reduced to zero when the roller defect rolls through the raceway. Unlike the case of wd = 1.38 mm, the defective roller does not immediately resume contact with the raceway because it will take a bit longer for the rear edge of the wider roller defect to come into contact with raceway. Before the rear edge of the defect resume contact with the raceway, the defective roller impact the raceway due to its inertia and centrifugal force, leading to the contact force impulses, so the vibration response in the case of wd = 2.27 mm is greater than that in the case of wd = 1.38 mm.

Fig. 14
figure 14

Defective roller-to-outer race contact force: a effects of the width and b effects of the depth

Full size image

Figure 15a shows the cage rotation speed in the cases of three different defect widths. It can be found that with the increment of defect width, the fluctuation of the cage rotation speed become larger. That is, the motion instability of the cage is increased.

Fig. 15
figure 15

Effects of the defect width on the cage sliding ratio and the roller-to-cage contact force: a rotation speed of the cage, b RMS value of the cage sliding ratio, c contact force in time domain and d contact force RMS value

Full size image

The sliding ratio is often used to measure the sliding of the cage, which can be depicted as

$$S = \frac{{\omega_{{\text{c}}} - \overline{\omega }_{{\text{c}}} }}{{\overline{\omega }_{{\text{c}}} }} \times 100\%$$
(16)

where ωc is the actual cage rotation speed, and \(\overline{\omega }_{{\text{c}}}\) is the theoretical cage rotation speed.

Figure 15b shows the RMS value of the cage sliding ratio in the cases of five different defect widths. It can be found that the sliding ratio of the cage increases as the defect width is increased. Figure 15c shows the defective roller-to-cage contact force in time domain with three different defect widths, and Fig. 15d shows the RMS value of the contact force with five different defect widths. It is found that the defective roller-to-cage contact force increases as the defect width is increased. By comparing Fig. 15b, d, it can be found that the motion stability and sliding ratio of the cage depend on the roller-to-cage contact force. The greater roller-to-cage contact force results in the greater motion instability and sliding ratio of the cage.

4.2.2 Effects of the Defect Depth

To analyze the effect of the defect depth on the dynamic characteristics of the bearing, the defect width is given as 1.38 mm and the defect depth varies from 0.46 to 1.18 mm. Figures 16 and 17 show the simulated and experimental vibration responses in the vertical direction in the cases of three different defect depths respectively. The shaft rotating speed of the explicit finite element model is 6000 r/min and that of the experiment is 1200 r/min. It can be found that the level of the vibration remains unchanged as the defect depth increases. Figure 14b shows the vertical defective roller-to-outer race contact force when the defective roller rolls in the loaded zone in the cases of three different defect depths. It can be found that under the condition of a certain defect width, the depth has almost no influence on the contact force. That is the bearing dynamic response is not sensitive to the defect depth.

Fig. 16
figure 16

The simulated vibration responses in the vertical direction with three different defect depths: a–c acceleration signals for 0.59, 0.885, and 1.18 mm respectively, d–f envelope spectrum for 0.59, 0.885, and 1.18 mm respectively

Full size image
Fig. 17
figure 17

The experimental vibration responses in the vertical direction with three different defect depths: a–c acceleration signals for 0.59, 0.885, and 1.18 mm respectively, d–f envelope spectrum for 0.59, 0.885, and 1.18 mm respectively

Full size image

Figure 18a shows the cage rotation speed in the cases of three different defect depths. It can be found that with the increment of defect depth, the amplitude of the fluctuation of the cage rotation speed remains unchanged. Figure 18b shows the RMS value of the cage sliding ratio in the cases of five different defect depths. It can be found that as the defect depth increases, the sliding ratio of the cage changes irregularly. Figure 18c shows the defective roller-to-cage contact force in time domain with three different defect depths, and Fig. 18d shows the RMS value of the contact force with five different defect depths. It can be found that as the defect depth increases, the defective roller-to-cage contact force changes irregularly. This was caused mainly by the numerical contact noise. When the rollers rotates, the vertex of polygonal components contact with raceways, which will create slight impact. The vibration response of bearing have a certain randomness due to the numerical contact noise, and the cage speed and contact force are not sensitive to the defect depth, so the root mean square values of cage speed and contact force changes irregularly. By comparing Fig. 18b, d, it can be found that with the increment of defect depth, the sliding ratio of the cage and the defective roller-to-cage contact force have the same changing trend, which further indicates that the motion stability and sliding ratio of the cage depend on the roller-to-cage contact force.

Fig. 18
figure 18

Effects of the defect depth on the cage sliding ratio and the defective roller-to-cage contact force: a rotation speed of the cage, b RMS value of the cage sliding ratio, c contact force in time domain and d contact force RMS value

Full size image

4.2.3 Effects of the Number of Defective Rollers

Figure 19 shows the schematic of number and location of defective rollers. Figures 20 and 21 show the simulated and the experimental vibration responses in the vertical direction with different numbers of defective rollers respectively. The shaft rotating speed of the explicit finite element model is 4000 r/min and that of the experiment is 1800 r/min. The dimensions of the defect are 1.38 mm (width) × 0.59 mm (depth). It can be seen that the number of defective rollers has no influence on the frequency components of vibration response, but only increases the level of vibration response. Figure 22 shows the defective roller-to-outer race contact force when the defective roller rolls in the loaded zone under these three working conditions. It can be found that when there is only one defective roller, the contact force of the defective roller will decrease to zero periodically. When multiple defective rollers are involved, not only the defective rollers-to-raceway contact force decreases to zero periodically, but also a substantial increase occurs periodically. The adjacent defective roller losing contact with the raceway will lead to a reduction of the number of loaded rollers, so an increase in magnitude of contact force occurs. The drastic fluctuation will result in the occurrence of surface fatigue cracks, accelerating the degradation of bearing.

Fig. 19
figure 19

Schematic of number and location of defective rollers

Full size image
Fig. 20
figure 20

The simulated vibration responses in the vertical direction with different numbers of defective rollers: a–c acceleration signals for 1, 2, and 3 respectively, d–f envelope spectrum for 1, 2, and 3 respectively

Full size image
Fig. 21
figure 21

The experimental vibration responses in the vertical direction with different numbers of defective rollers: a–c acceleration signals for 1, 2, and 3 respectively, d–f envelope spectrum for 1, 2, and 3 respectively

Full size image
Fig. 22
figure 22

Defective roller-to-outer race contact force: a one defective roller, b two defective rollers and c three defective rollers

Full size image

Figure 23a shows the cage rotation speed with different numbers of defective rollers. It can be found that as the number of defective rollers increases, the fluctuation of the cage rotation speed become larger. Figure 23b shows the RMS value of the cage sliding ratio. It can be found that the sliding ratio of the cage increases as the number of defective rollers is increased. Figure 23c shows the defective roller-to-cage contact force in time domain, and Fig. 23d shows the contact force RMS value. It is found that the defective roller-to-cage contact force increases as the defect number is increased. By comparing Fig. 23b, d, the same conclusion can be drawn as mentioned before: the motion stability and sliding ratio of the cage depend on the roller-to-cage contact force.

Fig. 23
figure 23

Effects of the defective rollers numbers on the cage sliding ratio and the defective roller-to-cage contact force: a rotation speed of the cage, b RMS value of the cage sliding ratio, c contact force in time domain and d contact force RMS value

Full size image

5 Conclusion

A two-dimensional explicit FE model of cylindrical roller bearing is established considering flexibility of all the components, the internal friction force, the relative sliding, the finite size of rollers and interactions between rollers and the cage. Effects of the roller spalling defects on the vibration response and the sliding behavior of the bearing are investigated by discussing the characteristics of the rollers-to-raceway and the rollers-to-cage contact force. The conclusions are summarized as follows:

  1. 1.

    The spalling defects on rollers will lead to a lack of traction of the inner race on the defective roller, aggravating the slippage of the defective roller and increasing the defective rollers-to-cage contact force.

  2. 2.

    The vibration amplitude of the bearing increases with the increment of defect width, while remains unchanged with the increment of defect depth. The sliding ratio of the cage increases with the increment of defect width, while changes irregularly with the increment of defect depth.

  3. 3.

    The number of defective rollers has no effect on the vibration response frequency components, but influences the vibration level of the bearing. The increment of defective rollers number results in a significant increase of the vibration response of bearing and the sliding ratio of cage.