1 Introduction

1.1 Literature Review

In recent years, the geotechnical engineering community has given geosynthetic-reinforced soil walls (\({\text{GRSW}}\)) much attention because they have numerous advantages over traditional gravity-retaining walls, which comprises a pleasant appearance, acceptable distortion, low cost, and speedy building [1,2,3]. Because of the growth of infrastructure, building tall, steep, earth-retaining buildings in hilly areas has become common [4,5,6]. Many practical applications have shown that these buildings provide a great solution. However, when wall height increases, the required tensile strength for building a single \({\text{GRSW }}\) generally shows an exponential development trend [7]. Reducing the vertical distance between \({\text{GRSW }}\) is part of the plan to lessen the tensile strength in reinforcement. Nevertheless, this method requires a much larger number of geosynthetic layers, which drives up expenses significantly. In situations where there is sufficient space available, the use of high \({\text{GRSW }}\) in a tiered configuration has increasingly become a prevalent practice for mitigating the effects of tensile loads on the reinforcement [8, 9].

The current design of a \({\text{GRSW }}\) ensures internal, external, and global stability via the deliberate selection of reinforcing location and the use of materials with high tensile strengths [10]. Researchers have proposed a range of analytical methodologies for the design of \({\text{GRSW }}\) [11]. The application of limit balance and lateral earth pressure methodologies is often seen in design specifications to determine the reinforcement parameters that mitigate the potential failures of \({\text{GRSW}}\). In contrast, the restricted balancing approach cannot accurately forecast deformations and neglects the consideration of the backfill material’s stress–strain correlation and the interplay between several components within the \({\text{GRSW }}\) system. On the contrary, it is dependent on conjectures on the nature of failure and the location of a critical slip plane [12]. Through past years, there has been a rise in the usage of numerical approaches to the stability and deformations’ analysis in \({\text{GRSW}}\). Prior numerical studies have shown that the shear strength reduction (\({\text{SSR}}\)) technique could be used to compute both the critical slip surface and the corresponding factor of safety (\({\text{FS}}\)) for a \({\text{GRSW }}\) [13]. Many researchers have done parametric researches utilizing numeric techniques to analyze the certain design factors’ impact on the lateral deformations of \({\text{GRSW }}\) [14]. The assessment of the effectiveness of \({\text{GRSW }}\) heavily relies on the determination of the largest lateral facing displacement observed during construction. This factor has major importance in evaluating the overall performance of \({\text{GRSW}}\). The aim of the work was to evaluate the impact of two distinct simulation techniques (i.e., interfaces featuring a single spring–slider system and interfaces featuring two spring–slider systems) for interactions between reinforcement and the surrounding medium on the numerical analyses' performances of \({\text{GRS}}\) structures. Pullout test numerical simulations showed that both techniques accurately anticipated the reinforcement's pullout failure mode in the surrounding medium. The interface shear failure mode between geosynthetics and surrounding media was not accurately predicted by the single spring–slider system technique [15]. Research examined the impact of completely wrapped geogrid sheets on the load–settlement response of medium–dense sandy soil under a single-strip foundation using small-scale physical model experiments. Recent study has shown how changing factors affect thick sandy soil reinforced with completely wraparound geogrid sheets. One layer of complete wraparound geogrid improves the carrying capacity by 280% and reduces settlement ratios by 50%. Compared to two inclusions of planar geogrid layers, one completely folded geogrid sheet reduces strain under the footing by 45.5% and applied pressure by 15.5% [16].

The greatest measured displacement for segmental \({\text{GRS}}\) walls within the USA was determined to be 3.5% of the wall height (H) using lateral displacement analysis [17]. According to the standards, it is recommended that the lateral facing distortion of whole walls should ideally range from 0.9%\(H\) to 4%\(H\). Existing research has documented several experimental methods for predicting the lateral displacement of a single \({\text{GRSW}}\) on a rigid base. These methods ignore the effect of rigidity and strengthening creep on the lateral deformations of the face. Thus, their capability to predict real-world lateral facing movement is uncertain [18,19,20]. Recently, \({\text{GRS}}\) walls have been utilized to support spread foundations on bridge abutments, replacing deep foundations. Several studies and numerical simulations have examined \({\text{GRSW}}\) with flexible face subjected to distributed footing loads' lateral displacements and bearing capacities [21]. Khosrojerdi et al. [19] proposed an experimental method to forecast a \({\text{GRSW}}\)’s maximal lateral deformation under spread foundation loads without considering the offset interval. Rahmaninezhad and Han [22] suggested a technique to forecast the lateral displacement of a \({\text{GRSW}}\) with flexible face based on the updated Bishop technique's greatest lateral displacement and \({\text{FS}}\).

According to the adaptive neuro-fuzzy inference system (\({\text{ANFIS}}\)) successful application reports and the aim of this study, it is worth scrutinizing the potential and applicability of this model in various fields [23,24,25,26,27]. Several studies have recently been developed employing different types of machine learning-based algorithms [28,29,30,31,32,33,34,35,36,37,38,39,40,41]. The application of the\({\text{ANFIS}}\)was reported successfully in several publications in single or hybrid forms [42]. The hybrid form of the \({\text{ANFIS}}\) is related to linking with various optimization algorithms, such as beluga whale optimizer, Henry gas solubility optimization, Harris hawks optimizer, reptile search algorithm, and so on [43,44,45,46,47]. However, there is no article on the coupling of the \({\text{ANFIS}}\) with gannet optimization algorithm. In a study, a comparison between two recognized techniques for evaluating slope stability was conducted [48]. Artificial neural networks (\({\text{ANN}}\)) and the\({\text{ANFIS}}\) are two computer simulations that have been extensively employed in several research and application areas. The purpose of the research was to predict various \({\text{FS}}\) values for a sustaining structure. According to the researchers, their \({\text{ANFIS}}\) framework is somewhat more efficient than the \({\text{ANN}}\) method across all \({\text{FS}}\) categories. In a distinct and noteworthy investigation, Ozturk [49] used an \(ANN\) methodology for forecasting purposes to develop and assess the retaining wall (\({\text{RW}}\))’s seismic displacement. Based on a prior investigation, Xu et al. [50] utilized ant colony optimization and \({\text{ANN}}\) methodologies to predict and optimize the \(RW\)’s \({\text{FS}}\) structure in dynamic situations. To optimize the estimate of the \(RW\)’s \({\text{FS}}\) in dynamic settings, Chen et al. [51] applied two hybrid \({\text{ANN}}\)-based models, with genetic algorithm (\({\text{GA}}\)) and the imperialist competitive algorithm (\({\text{ICA}}\)). It was noted that the \({\text{GA - ANN}}\) technique had more efficiency in comparison to the \({\text{ICA - ANN }}\) approach. Evaluating the machine learning-based techniques’ possible use in predicting the soil structures-reinforced deformation with geogrids was the main goal of the study. The paper presented unique methods that combine least squared support vector regression (\({\text{LSSVR}}\)) with the equilibrium optimizer (\({\text{EO}}\)) and reptile search algorithm (\({\text{RSA}}\)). Finding the ideal settings for the kernel function's width (\(g\)) and penalty factor (\(c\)) for \(LSSVR\) was the goal of using optimization methods. The findings indicate that there is a high probability that both of the generated models would accurately predict the deformation. A notable drop was seen when taking into account the \({\text{TIC}}\) index: in the train phase, it decreased from 0.0393 (\({\text{LSSVR}}_{{\text{E}}}\)) to 0.0215 (\({\text{LSSVR}}_{{\text{R}}}\)), and in the assessment stage, it decreased from 0.0222 (LSSVRE) to 0.0088 (LSSVRR). A thorough index called \({\text{OBJ}}\) indicated 1.8003 for LSSVRE and almost half at 0.9257 for LSSVRR [52]. Based on the above discourse, it seems that while the utilization of soft computing models demonstrates efficacy in addressing concerns pertaining to mechanical stabilized earth and \({\text{RW}}\) structures, further inquiry using more comprehensive and precise methodologies is essential.

1.2 Motivation for Conducting Research

In conclusion, the present work may be characterized by the following primary contributions:

  • The procedure for developing and evaluating machine learning algorithms to assess the soil structures-reinforced deformation with geogrids is conducted utilizing comprehensive data collection. It is important to mention that many prior academic inquiries have mostly relied on datasets defined by limited size.

  • Few works have specifically examined adaptive neuro-fuzzy inference systems (\({\text{ANFIS}}\)) for the estimation of deformation in \({\text{GRSW}}\), despite the existence of various suggested designs.

  • The choice of a model, namely the discovery of appropriate hyper-parameters, is crucial.

  • Introduced and validated in this work is a revolutionary approach that combines the beluga whale optimizer (\({\text{BWH}}\)), Henry gas solubility optimization (\({\text{HGSO}}\)), gannet optimization algorithm (\({\text{GOA}}\)), and Harris hawks optimizer (\({\text{HHO}}\)) with the \(ANFIS\) model.

  • The investigation of the possible use of approaches based on machine learning for the purpose of forecasting the geogrid-reinforced soil structures’ \(Dis\) was the major focus of this study. These efforts are made to reduce the time and cost of numerical modeling. This study aimed to enable computers to learn patterns and insights from data to make accurate predictions or decisions about unseen data.

1.3 Organization of the Study

The structure of the article is as follows. Firstly, the literature review of the article is provided to assess the novelty and contribution of the study. Secondly, the created dataset and its pre-processing were described. Following this, the considered optimization algorithms and prediction algorithms were described. Next, the effectiveness of the models was appraised through several evaluation metrics. The next step was related to outcomes and their related justifications, along with providing some restrictions and related suggestions for them. In this part, sensitivity analysis was used to estimate the effect of each input variable on the target. Finally, the main findings of the article are provided in the conclusion section.

2 Materials and Methods

2.1 Data Description and Pre-processing

A sensitivity analysis was performed on the numerical framework to generate the requisite datasets for estimate simulations. This work aimed to assess and investigate the effects of different influencing factors on the deformation of a geo-synthetically reinforced embankment. Following this, the results produced by the models were identified, whereas the data provided included the elements that had an impact. The variables examined in this research were the surcharge load, friction angle, geosynthetic stiffness, and vertical spacing among geogrid levels. The influence of supplementary variables, such as soil–foundation friction angles and surface modular blocks, on the performance of \({\text{GRS}}\) constructions is apparent but very minor.

Consequently, it was not introduced as one of the input variables. Furthermore, in the field of geotechnical engineering, the process of obtaining or assembling a significant dataset presents some difficulties. As a result, the augmentation of variables is not seen as advantageous; however, the removal of less consequential components is advised. A comprehensive set of 166 finite element studies were collected from the literature, and the resultant values were subsequently utilized as parameters in the simulations [53]. The dataset was divided into two distinct stages: training and evaluation. The learning stage included 75% (124 instances) of the dataset, while the assessment stage encompassed 25% (42 instances) of the dataset [54,55,56,57]. Understanding the design and building of a certain item help experts perform analysis and ensure compliance with engineering standards.

The dataset was divided into two subsets that guaranteed the incorporation of the entire data span in the learning and assessment phases while as well as adhering to the principles of a normal distribution. The independent and dependent variables' statistical data are shown in Table 1 within the training and testing collections. Inputs introduced for developing the \(ANFIS\) systems were surcharge \(\left( {q\;{ }\left( {{\text{kPa}}} \right)} \right)\), friction angle (\(\Phi \left(^\circ \right)\)), and the geogrid levels’ vertical interval (\(S_{{\text{v}}} \; \left( {\text{m}} \right)\)). Also, the reinforcement stiffness ratio (\(E/E_{0}\)) was selected as input, where \(E_{0}\) is the initial stiffness of the large-scale reinforcement, \(11.5\;\;{\text{KN/m}}\). The highest lateral deformation of the wall (\(Dis\)) in \(mm\) is taken into account as a target. The distribution of parameters charts shown in Fig. 1 aids in better understanding the distribution of data.

Table 1 The parameters’ statistical values introduced to models
Full size table
Fig. 1
figure 1

Distribution of circular figures of the variables

Full size image

2.1.1 Surcharge

Surcharge refers to the additional load or pressure applied to the surface of the soil, above the natural ground level. Surcharge can come from various sources, such as vehicular traffic, buildings, storage loads, or other structures placed on or near the soil wall. When a surcharge is applied, it increases the vertical stress on the soil behind the wall. This additional vertical load translates into higher lateral earth pressures acting on the wall. The increase in lateral earth pressure tends to push the wall outward, leading to greater lateral deformation. The geosynthetic layers are designed to carry tensile loads and provide additional stability. However, excessive surcharge can lead to overstressing these layers, potentially causing increased deformation or even failure. Moreover, depending on the stiffness and strength of the geosynthetic materials, the system may exhibit varying degrees of lateral deformation. Generally, a stiffer reinforcement will limit deformation, but excessive surcharge can exceed the design capacity.

2.1.2 Friction Angle

The friction angle of soil, measured in degrees, is a measure of the shear strength of the soil due to internal friction. It represents the angle at which soil particles begin to slide over each other. The friction angle is directly related to the soil's shear strength. A higher friction angle indicates greater shear strength. Soils with higher friction angles can better resist shear stresses, reducing the likelihood of lateral displacement. Conversely, soils with lower friction angles have lower shear strength and are more prone to deformation under lateral loads. Moreover, higher friction angles lead to lower lateral earth pressures acting on the wall, which reduces the forces pushing the wall outward. This results in less lateral deformation. Lower friction angles lead to higher lateral earth pressures and increased deformation. Also, improved interlock and interaction reduce relative movements between the soil and reinforcement, thus minimizing lateral deformation. Poor interaction in soils with low friction angles can lead to higher deformation.

2.1.3 The Vertical Interval of Geogrid Levels

The vertical interval refers to the vertical spacing between successive layers of geogrid reinforcement within the soil wall. This interval is determined during the design phase based on factors such as the wall height, soil properties, geogrid type, and loading conditions. Closer spacing (smaller \(S_{{\text{v}}}\)) results in better distribution of stresses and improved interaction between the soil and geogrid. This generally leads to reduced lateral deformation. Larger intervals can lead to less effective load distribution and increased deformation. Also, with closer geogrid spacing, the reinforced soil mass behaves more rigidly, resulting in smaller lateral deformations. Conversely, larger vertical intervals can lead to a more flexible system with greater lateral displacements. Furthermore, smaller vertical intervals mean the geogrid layers can more effectively distribute and manage tensile forces, minimizing lateral deformation. Larger intervals may allow more soil movement between layers, leading to increased deformation.

2.1.4 The Reinforcement Stiffness Ratio (\(E/E_{0}\))

The reinforcement stiffness ratio is the ratio of the stiffness (modulus of elasticity, \(E\)) of the geosynthetic reinforcement to the stiffness of the soil (\(E_{0}\)). The modulus of elasticity of the geosynthetic material is determined through laboratory tests and material specifications. The stiffness of the soil is derived from in situ tests or empirical correlations based on soil type and properties. A higher stiffness ratio (\(E/E_{0}\)) improves the load-carrying capacity of the geosynthetic layers, resulting in more efficient load transfer from the soil to the reinforcement. This leads to reduced lateral deformation. Conversely, a lower stiffness ratio means less effective load transfer, leading to increased deformation. Also, higher reinforcement stiffness (higher) enhances the rigidity of the wall system, reducing lateral deformation under load. Lower reinforcement stiffness (lower) results in a more flexible system with greater lateral deformation. Moreover, increased stiffness ratio enhances the shear strength of the reinforced soil, improving stability and reducing lateral deformation.

A non-parametric method of measuring correlation or association among a pair of parameters is the Spearman rank correlation coefficient (\({\text{SCC}}\)) calculated by Eq. (1) [58]. The assessment evaluates the magnitude and orientation of the monotonic association between two factors, irrespective of whether the association is linear. The use of \({\text{SCC}}\) is appropriate in situations where the variables under consideration are observed on either interval or ordinal scales.

$$\rho = 1 - \frac{{6\sum d_{i}^{2} }}{{n\left( {n^{2} - 1} \right)}}.$$
(1)

In this equation, \(d_{i}\) is the squared rank variances’ sum, and \(n\) stands for the amount of data. \(\rho\) varies between −1 and 1, where \(\rho = 1\) shows a great monotonic raising relationship, \(\rho = -\) 1 shows a great monotonic declining relationship, and \(\rho = 0\) is no monotonic relationship. As seen by the data presented in Fig. 2, a significant proportion of the \(\rho\) values exhibit very low magnitudes smaller than 0.439. As mentioned previously, the lower values of the relation show a slight monotonic relationship between variables. Nevertheless, the variable with the greatest \({\text{SCC}}\) is \({\text{Dis}}\), which has a strong positive \({\text{SCC}}\) of 0.655 with \(q\), indicating a consistent upward trend between the two variables. Conversely, the highest negative relationship is obtained between Dis and \(E{ }/{ }E_{0}\) at −0.439 (where not high). Remarkably, it is obvious that all of the variables show a relationship with the target, which depicts the acceptable selection of them as input variables.

Fig. 2
figure 2

The Spearman rank correlation coefficient

Full size image

2.2 Employed System and Optimizers

2.2.1 Beluga Whale Optimizer (\({\text{BWH}}\))

An optimization method called \(BWH\) imitates the hunting, swimming, and whale-falling actions of beluga whales (\({\text{BW}}\)s). The social predatory nature of beluga whales—which dwell in pods of 2–25 whales—is widely recognized. \({\text{BW}}\)s gather a significant quantity of food, such as salmon, trout, codfish, shrimp, and worms, by hunting, swimming, and information sharing. The hunting, swimming, and whale fall of the \({\text{BW}}\)s are conceived as \({\text{BWH}}\)’s exploitation and exploration stages [59] (Fig. 3). The positions of the \({\text{BW}}\)s were designated as the search agents for mathematical modeling of the \({\text{BWH}}\), and these agents may be started arbitrarily in the following way [59]:

$$X_{j}^{i} = {\text{Lb}}_{j} + \left( {{\text{Ub}}_{j} - {\text{Lb}}_{j} } \right) \times {\text{rand}}.$$
(2)
Fig. 3
figure 3

Behaviors of beluga whales: a swim, corresponding to the exploration phase; b foraging, corresponding to the exploitation phase; c and fall, for the whale fall phase [59]

Full size image

Each search agent’s matching goal function is given as follows [59]:

$$F_{X} = \left[ {\begin{array}{*{20}c} {f\left( {x_{1,1} ,x_{1,2} , \ldots ,x_{1,d} } \right)} \\ {f\left( {x_{2,1} ,x_{2,2} , \ldots ,x_{2,d} } \right)} \\ {\begin{array}{*{20}c} \vdots \\ {f\left( {x_{n,1} ,x_{n,2} , \ldots ,x_{n,d} } \right)} \\ \end{array} } \\ \end{array} } \right].$$
(3)

The \({\text{BWH}}\)’s exploration phase may be modeled as follows. It imitates the two sets of beluga whales’ swimming motions, and they swim tightly with each other at random in a mirrored or coordinated way [59].

$$X_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}c} {X_{{i,P_{j} }}^{t} + \left( {X_{{r,P_{1} }}^{t} - X_{{i,P_{j} }}^{t} } \right)\left( {1 + r_{1} } \right)\sin \left( {2\pi r_{2} } \right), j = {\text{even}}} \\ {X_{{i,P_{j} }}^{t} + \left( {X_{{r,P_{1} }}^{t} - X_{{i,P_{j} }}^{t} } \right)\left( {1 + r_{1} } \right)\cos \left( {2\pi r_{2} } \right), j = {\text{odd}}} \\ \end{array} } \right. .$$
(4)

Here, \(X_{i,j}^{t + 1}\) presents the modified position of the \(i_{th}\) whale in \(j_{th}\) dimension, and \(t\) shows the present iteration number. \(r_{1}\) and \(r_{2}\) define the accidental value between [0,1]. \(X_{{r,P_{1} }}^{t}\) describes an accidentally chosen beluga whale.

The \({\text{BWH}}\)’s exploitation stage resembles the preying and hunting actions of\({\text{BW}}\)s, whereby \({\text{BW}}\)s cooperate to obtain data and hunt in regard to the finest \({\text{BW}}\) locations. In this stage, the \({\text{BW}}\)s advance to capture the target using the Levy flight method. The following mathematical formula is used to characterize the \({\text{BWH}}\)’s exploitation stage according to Levy flight [59]:

$$X_{i}^{t + 1} = r_{3} X_{best}^{t} - r_{4} X_{i}^{t} + C_{1} \cdot L_{F} \cdot \left( {X_{r}^{t} - X_{i}^{t} } \right).$$
(5)

Here, \(X_{best}^{t}\) shows the \({\text{BW}}\)’s finest position. \(X_{i}^{t}\) shows the \(i{\text{th}}\) \(BW\)’s present position. \(r_{3}\) and \(r_{4}\) determine the accidental numbers between \(0 \le r_{3}\), \(r_{4} \le 1\). \(X_{r}^{t}\) shows an accidental \({\text{BW}}\). The adaptation factor measures levy flying strength \(C_{1}\), which may be determined as outlined below [59]:

$$C_{1} = 2r_{4} \left( {1 - t/t_{{{\text{max}}}} } \right).$$
(6)

The levy flight function, abbreviated \(L_{{\text{F}}}\), may be computed as outlined below [59]:

$$L_{{\text{F}}} = 0.05 \times \frac{u \times \sigma }{{\left| v \right|^{1/\beta } }},$$
(7)

in which [59]:

$$\sigma = \left( {\frac{{\Gamma \left( {1 + \beta } \right) \times \sin \left( {\pi \beta /2} \right)}}{{\Gamma \left( {\left( {1 + \beta } \right)/2} \right) \times \beta \times 2^{{\left( {\beta - 1} \right)/2}} }}} \right)^{1/\beta } .$$
(8)

In these equations, \(v\) and \(u\) show accidental numbers which are usually diffused, while \(\beta\) presents a constant value fixed at 1.5. An adaptive factor that may be computed as mentioned below is used to regulate the transition between the exploitation and exploration phases [59]:

$$B_{{\text{f}}} = B_{0} \left( {1 - t/2t_{{{\text{max}}}} } \right).$$
(9)

In Eq. (13), the value of \(B_{0}\) is randomly produced throughout each cycle, ranging between 0 and 1. When \(B_{{\text{f}}} > 0.5\), the \({\text{BW}}\)s’ position will be updated throughout the exploration phase, precisely when the value of \(B_{{\text{f}}} \le 0.5\). Whale fall describes how polar bears, killer whales, and people stalk or endanger \({\text{BW}}\)s throughout their hunting and migrating. At this point, the dead \(BW\)s fall into the deep seafloor. In this stage, the \({\text{BW}}\)s’ modified position is shown as outlined below [59]:

$$X_{i}^{t + 1} = r_{5} X_{i}^{t} - r_{6} X_{r}^{t} + r_{7} X_{{{\text{step}}}} {.}$$
(10)

\(r_{5}\), \(r_{6}\) and \(r_{7}\) show the accidental numbers which are \(0 \le r_{5} ,r_{6}\), \(r_{7} \le 1\). \(X_{{{\text{step}}}}\) stands for the whale fall’s step size that is able to be calculated as outlined below [59]:

$$X_{{{\text{step}}}} { = }\left( {u_{{\text{b}}} - l_{{\text{b}}} } \right){\text{exp}}\left( { - C_{2} t/t_{{{\text{max}}}} } \right),$$
(11)

where, \(l_{{\text{b}}}\) and \(u_{{\text{b}}}\) are the lowest and highest boundaries of the control parameters. The following is a representation of \(C_{2}\), a factor of time varying that relies on the population size and the whale fall possibility [59]:

$$C_{2} = 2W_{{\text{f}}} \times n,$$
(12)

in which:

$$W_{{\text{f}}} = 0.1 - 0.05t/t_{{{\text{max}}}} .$$
(13)

The pseudo-code for the \({\text{BWH}}\) method is described in Algorithm 1.

figure a

Algorithm 1. The pseudo-code of BWH [59]

2.2.2 Henry Gas Solubility Optimization (\({\text{HGSO}}\))

Various engineering issues are handled using the \(HGSO\) metaheuristic approach, which imitates the behavior governed by Henry’s rule [60]. Henry's rule is a fundamental gas law that establishes a quantitative relationship between the concentration of a specific gas dissolved in a liquid of a certain kind and volume while maintaining a constant temperature. The Henry’s rule relationship exhibits a significant reliance on temperature. In Eq. (14) [60], the relationship between the solubility (\(S_{{\text{g}}}\)) of a gas and the partial pressure (\(P_{{\text{g}}}\)) of the gas is demonstrated to be directly proportional [60].

$$S_{{\text{g}}} = H \times P_{{\text{g}}} .$$
(14)

Here, \(H\) shows Henry’s constant, and \(P_{{\text{g}}}\) shows the partial gas pressure. The equation describes the quantity and distribution of gases in the initial population [60].

$$X_{i}^{t + 1} = X_{{{\text{min}}}} + r \times \left( {X_{{{\text{max}}}} - X_{{{\text{min}}}} } \right).$$
(15)

In \(X_{i}\), the \(i{\text{th}}\) gas’s place in the population is stated. \(r\) shows a function which produces numbers in the range of 0 and 1. \(X_{{{\text{max}}}}\) and \(X_{{{\text{min}}}}\) preset the upper and lower boundaries of the issue. \(t\) shows the iteration number.

Clustering is the second step. Different groups were created based on the population. The kind of gas utilized and the number of cluster divisions are equal.

The evaluation step is the third step. Each cluster's gas is assessed within its kinds. The finest gas is one which achieves the greatest balance level. The cluster's components are then filtered to choose the best gas.

Modifying the coefficient of Henry is the fourth stage. The solubility is updated in the fifth step. The following formula is used to do this [60]:

$$S_{i,j} \left( t \right) = K \times H_{j} \left( {t + 1} \right) \times P_{i,j} \left( t \right).$$
(16)

\(P_{i,j} \left( t \right)\) and \(S_{i,j} \left( t \right)\), respectively, indicate the partial pressure and solubility of \(i{\text{th}}\) gas in group \(j\). The gas locations will be modified after this procedure. The determination of the universal finest element involves the computation of the optimum values for every individual element within the group. The fitness function eliminates elements from the group, and the process continues until it meets the stop requirement. Algorithm 2 depicts the pseudo-code of \(HGSO\).

figure b

Algorithm 2. The pseudo-code of HGSO [60]

2.2.3 Gannet Optimization Algorithm (\({\text{GOA}}\))

The \({\text{GOA}}\) is a swarm intelligence technique that was newly introduced [61]. To find the ideal location inside the search space, the \({\text{GOA}}\) uses the gannets’ special foraging manner, which is mathematically modeled. \({\text{GOA}}\) features two stages, called the exploration stage and the exploitation stage, much like other population-based intelligent optimization methods. Gannets use a \({\text{U}}\)-shaped dive (as illustrated in Eq. 17) and a \(V\)-shaped dive (as shown in Eq. 18) to look for hunting throughout the exploration stage (Fig. 4). When an individual in \(MX_{i}\) surpasses the present answer \(X_{i}\), \({\text{GOA}}\) additionally constructs a memory matrix, \({\text{MX}}\), to store alterations in the location of the gannet. Equation (19) demonstrates how \({\text{MX}}_{i}\) is modified throughout the exploration stage [61].

$$a = 2 \times \cos \left( {2 \times \pi \times r2} \right) \times \left( {1 - t/T} \right),$$
(17)
$$b = \left\{ {\begin{array}{*{20}c} {2 \times \left( { - \frac{1}{\pi } \times x + 1} \right) \times \left( {2 \times \pi \times r_{3} } \right) \times \left( {1 - \frac{t}{T}} \right), x \in \left( {0,\pi } \right)} \\ {2 \times \left( {\frac{1}{\pi } \times x - 1} \right) \times \left( {2 \times \pi \times r_{3} } \right) \times \left( {1 - \frac{t}{T} } \right), x \in \left( {\pi ,2\pi } \right)} \\ \end{array} } \right.,$$
(18)
$$MX_{i}^{t + 1} = \left\{ {\begin{array}{*{20}c} {x_{i}^{t} + u_{1} + \left( {2 \times r_{4} - 1} \right) \times a \times \left( {x_{i}^{t} - x_{r}^{t} } \right), q \ge 0.5} \\ {x_{i}^{t} + v_{1} + \left( {2 \times r_{5} - 1} \right) \times b \times \left( {x_{i}^{t} - \frac{1}{N}\mathop \sum \limits_{j = 1}^{N} x_{i}^{t} } \right), q < 0.5} \\ \end{array} } \right..$$
(19)
Fig. 4
figure 4

\({\text{U}}\)-shaped and \({\text{V}}\)-shaped behavior of gannet [61]

Full size image

Here, \(r_{2} , r_{3} ,r_{4} ,\) and \(q\) show accidental numbers among 1 and 0, and \(t\) shows the iterations’ present number, \(T\) shows the iterations’ highest number. \(u_{1}\) presents an accidental number from \({-}a\) to \(a\), and \(v_{1}\) presents an accidental number from \({-}b\) to \(b\). \(N\) denotes the population size, \(x_{r}^{t}\) is the chosen individual at random, and \(x_{i}^{t}\) shows the present population’s \(i{\text{th}}\) individual. The gannet will make two more movements throughout the exploitation stage to grab fish frantically attempting to get away. When the energy is diminished, the gannet fails to grab the fleeing fish and performs a Levy movement to re-find the subsequent target. When the gannet has a large grab capability, as stated in Eq. (20), it will abruptly turn and grab the fish (Fig. 5). Equation (21) provides the location modification equation throughout the exploitation stage [61].

$${\text{Cap}} = \frac{1}{{\frac{{m \times v^{2} }}{{0.2 + \left( {2 - 0.2} \right) \times r_{6} }} \times \left( {1 + \frac{t}{T}} \right)}},$$
(20)
$$MX_{i}^{t + 1} = \left\{ {\begin{array}{*{20}c} {t \times {\text{Cap}} \times \left| {x_{i}^{t} - x_{{{\text{best}}}}^{t} } \right| \times \left( {x_{i}^{t} - x_{{{\text{best}}}}^{t} } \right) + x_{i}^{t} ,{\text{Cap}} \ge c} \\ {x_{{{\text{best}}}}^{t} - \left( {x_{i}^{t} - x_{{{\text{best}}}}^{t} } \right) \times P \times t,{\text{Cap}} < c} \\ \end{array} } \right.,$$
(21)
$$P = {\text{Levy}}\left( {{\text{Dim}}} \right) = 0.01 \times \frac{\mu \times \sigma }{{\left| v \right|^{{\frac{1}{\beta }}} }}.$$
(22)
Fig. 5
figure 5

Sudden turning [61]

Full size image

Here, \(m = 2.5\;\;{\text{kg}}\) shows the gannet’s weight, \(v = 1.5\;\;{\text{m/s}}\) shows the gannet’s velocity, \(c = 0.2\), \(\mu\) and \(\sigma\) present an accidental number in the range of 1 and 0, and \(\beta\) is equal to 1.5. \(x_{{{\text{best}}}}^{t}\) denotes the finest performing individual in the present population. The \({\text{GOA}}\)’s pseudo-code is presented in Algorithm 3.

figure c

Algorithm 3. The pseudo-code of GOA [61]

2.2.4 Harris Hawks Optimizer (\({\text{HHO}}\))

Strong hunters, Harris hawks, use a cunning and swarm-based approach to pursue, surround, flush out, and strike a rabbit. The \({\text{HHO}}\) method has been presented as a novel metaheuristic optimization method and was inspired by the cooperative hunting strategy used by hawks to pursue their target, which is often a rabbit. The method has proven to be better than a number of other well-known optimization methods, including the genetic method, biogeography-based optimization, differential evolution, particle swarm optimization, cuckoo search, gray wolf optimizer, teaching–learning-based optimization, bat method, flower pollination method, firefly method, and moth–flame optimization method [62]. This approach, motivated by nature, uses two mechanisms—exploration and exploitation—to identify the best answer in an iterative manner, analogous to previous metaheuristic optimization methods (Fig. 6). Every hawk in \({\text{HHO}}\) symbolizes a potential answer, and the finest hawk in the population indicates the finest result thus far. The \({\text{HHO}}\) method gives the exploration stage more possibility to provide novel answers in successive iterations, while the exploitation stage gets more of a possibility in the final iteration. Hawks use two equally likely ways to modify their locations during exploration. Every hawk in the first tactic adjusts its location following the locations of the rabbit and other hawks, as described in Eq. (23). Every hawk searches the whole domain at random, according to Eq. (24), to examine entire areas and prevent becoming trapped in the local optima for the second technique [62].

$$\vec{H}\left( {t + 1} \right) = \left( {\vec{H}_{{{\text{Rabbit}}}} \left( t \right) - \vec{H}_{{\text{M}}} \left( t \right)} \right) - r_{1} \left( {\vec{L}_{{\text{B}}} + r_{2} \left( {\vec{U}_{{\text{B}}} - \vec{L}_{{\text{B}}} } \right)} \right),$$
(23)
$$\vec{H}\left( {t + 1} \right) = \vec{H}_{{{\text{Rand}}}} \left( t \right) - r_{3} \left| {\vec{H}_{{{\text{Rand}}}} \left( t \right) - 2r_{4} \vec{H}\left( t \right)} \right|.$$
(24)
Fig. 6
figure 6

Various phases of \({\text{HHO}}\) [62]

Full size image

Here, \(\vec{H}\left( {t + 1} \right)\) and \(\vec{H}\left( t \right)\) show the hawk’s locations in the \(\left( {t + 1} \right)_{{{\text{th}}}}\) and \(t_{{{\text{th}}}}\) iterations, \(\vec{H}_{{{\text{Rabbit}}}} \left( t \right), \vec{H}_{{{\text{Rand}}}} \left( t \right)\) and \(\vec{H}_{{\text{M}}} \left( t \right)\) present the rabbit’s locations (presumed the finest hawk of the population gained thus far), a hawk chosen at random from the population, and the entire hawk’s average location in the population in the \(t_{{{\text{th}}}}\) iteration. \(\vec{U}_{{\text{B}}}\) and \(\vec{L}_{{\text{B}}}\) show the maximum and minimum limit vectors of decision parameters and \(r_{1} , r_{2}\), and \(r_{3}\) show a uniform accidental number in the range of 1 and 0.

To maintain equilibrium among the exploration and exploitation stages, the rabbit's escape energy (\(E\)), specified by Eq. (25), is added. It suggests that the rabbit has high energy during the first iterations to flee from the hawks (\(\left| E \right| \ge 1\)), which denotes the exploration stage. The exploitation stage is shown by the rabbit's declining ability to escape throughout iterations (\(\left| E \right|. < 1\)) [62].

$$E = 2E_{0} \left( {1 - \frac{t}{T}} \right).$$
(25)

Here, \(E_{0}\) represents an accidental value among \(- 1\) and 1 assigned for modifying the location of every hawk independently in every iteration, and \(t\) and \(T\) stand for the iteration number and iterations’ highest number, respectively.

The \({\text{HHO}}\) method’s exploitation stage was motivated by the hawks' unique assault strategy known as seven kills. To achieve this, four tactics—preliminary soft besiege (\({\text{PSB}}\)), soft besiege with progressive rapid dives (\({\text{SBPRD}}\)), preliminary hard besiege (\({\text{PHB}}\)), and hard besiege with progressive rapid dives (\({\text{HBPRD}}\))—are handled to leverage the potential answers that are now accessible. When the rabbit has sufficient energy (\(1 > \left| E \right|. > 0.5\)), the hawks’ soft besiege is conducted to tire the rabbit and get it ready for the seven killings. Two primary \(PSB\) and \({\text{SBPRD}}\) tactics for the soft besiege might be regarded to have equal probability. The following formula is used to modify a hawk’s location in the \({\text{PSB}}\) tactic [62].

$$\vec{H}\left( {t + 1} \right) = \left( {\vec{H}_{{{\text{Rabbit}}}} \left( t \right) - \vec{H}\left( t \right)} \right) - E\left| {2\left( {1 - r_{5} } \right)\vec{H}_{{{\text{Rabbit}}}} \left( t \right) - \vec{H}\left( t \right)} \right|.$$
(26)

Here, \(r_{5}\) shows an accidental number in the range of 1 and 0. The \({\text{SBPRD}}\) technique utilizes the Levy flight (\({\text{LF}}\)) idea to mimic the rabbit’s erratic escape actions. The formula beneath may determine a hawk’s most recent location [62].

$$\vec{H}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {\vec{H}_{a} \left( {t + 1} \right),iff\left( {\vec{H}_{a} \left( {t + 1} \right).} \right) \le f\left( {\vec{H}\left( t \right).} \right)} \\ {\vec{H}_{b} \left( {t + 1} \right),iff\left( {\vec{H}_{b} \left( {t + 1} \right).} \right) \le f\left( {\vec{H}\left( t \right).} \right)} \\ \end{array} } \right.,$$
(27)
$$\vec{H}_{a} \left( {t + 1} \right) = \vec{H}_{{{\text{Rabbit}}}} \left( t \right) - E\left| {2\left( {1 - r_{6} } \right)\vec{H}_{{{\text{Rabbit}}}} \left( t \right) - \vec{H}\left( t \right)} \right|,$$
(28)
$$\vec{H}_{b} \left( {t + 1} \right) = \vec{H}_{a} \left( {t + 1} \right) + \vec{r}_{7} .\overrightarrow {LF} \left( t \right),$$
(29)
$${\text{LF}}\left( x \right) = 0.01 \times \frac{u}{{\left| v \right|^{{\frac{1}{\beta }}} }}\left( {\frac{{\Gamma \left( {1 + \beta } \right) \times \sin \left( {\frac{\pi \beta }{2}} \right)}}{{\Gamma \left( {\frac{1 + \beta }{2}} \right) \times \beta \times 2^{{\left( {\frac{\beta - 1}{2}} \right)}} }}} \right)^{{\frac{1}{\beta }}} .$$
(30)

Here, \(f\) represents the cost function of the optimization issue, \(\vec{r}_{7}\) represents an accidental vector within the range of (0,1), \(r_{6}\), \(u\), and \(v\) represent accidental values among 0 and 1, and a constant is fixed to 1.5.

The rabbit is now worn out during the harsh besiege stage, and the hawks are prepared for the seven kills (\(\left| E \right| \le 0.5\)). \({\text{PHB}}\) and \({\text{HBPRD}}\) are two processes that may be explored that have the same probability as the soft besiege stage. The following formula is used to modify a hawk's location in the \(PHB\) method [62].

$$\vec{H}\left( {t + 1} \right) = \vec{H}_{{{\text{Rabbit}}}} \left( t \right) - E\left| {\vec{H}_{{{\text{Rabbit}}}} \left( t \right) - \vec{H}\left( t \right)} \right|.$$
(31)

Identical formulas to those utilized by the \({\text{SBPRD}}\) approach are utilized in the \({\text{HBPRD}}\) process to modify the hawks’ locations. The following formula is used to modify Eq. (28); this is the sole change that speeds up the method's convergence [62].

$$\vec{H}_{a} \left( {t + 1} \right) = \vec{H}_{{{\text{Rabbit}}}} \left( t \right) - E\left| {2\left( {1 - r_{6} } \right)\vec{H}_{{{\text{Rabbit}}}} \left( t \right) - \vec{H}_{{\text{M}}} \left( t \right)} \right|$$
(32)

The \({\text{HHO}}\)’s pseudo-code is presented in Algorithm 4.

figure d

Algorithm 4. The pseudo-code of HHO [62]

2.2.5 Adaptive Neuro-Fuzzy Inference System (\({\text{ANFIS}}\))

Jang [63] created the adaptive neuro-fuzzy inference system (\({\text{ANFIS}}\)). In the fuzzy modeling process, a way of learning data about a dataset is provided by neuro-adaptive learning, which is analogous to neural networks [64, 65]. Because it integrates the \({\text{ANN}}\) and fuzzy logic principles, it offers the benefits of both in a single system. The Sugeno fuzzy inference system (\({\text{FIS}}\)) serves as the foundation for \({\text{ANFIS}}\). In comparison to the Mamdani system, the Sugeno \({\text{FIS}}\) approach offers a more mathematically effective representation. The Sugeno first-order fuzzy model and the aforementioned \({\text{ANFIS}}\) system particularly have functional similarities [66, 67].

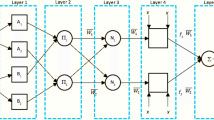
The interpretation of the input/output map may be facilitated by using a network-type structure of \({\text{ANFIS}}\), which has a resemblance to an \({\text{ANN}}\) (Fig. 7) [68]. The determination of the variables linked to the membership functions is carried out during the training stage of a neural network. ANFIS uses two learning methods \(IS\) to update the \({\text{MF}}\) variables: (1) the backpropagation technique and (2) a hybrid approach that combines least-squares analysis with the gradient reduction technique. Introduced by Sayed et al. [69] is the first-order Sugeno fuzzy model.

$${\mathbf{Rule1}}: {\varvec{if}}(x\; {\text{is}}\;A_{1} ){\text{ and }}( y\;{\text{is}}\;B_{1} )\,\, {\varvec{then}}\,\,\left( {f_{1} = p_{1} x + q_{1} y + r_{1} } \right)$$
(33)
$${\mathbf{Rule}}2: {\varvec{if}}(x\; {\text{is}}\;A_{2} ){\text{ and }}( y\;{\text{is}}\;B_{2} )\,\, {\varvec{then}}\,\,\left( {f_{2} = p_{2} x + q_{2} y + r_{2} } \right)$$
(34)
Fig. 7
figure 7

The main trend of \({\text{ANFIS}}\)

Full size image

Here, \(A_{1}\) and \(A_{2}\), and \(B_{1}\) and \(B_{2}\) show the \({\text{MF}}\) s of inputs \(x\) and \(y\), while \(p_{1}\), \(q_{1}\); \(r_{1}\) and \(p_{2}\); and \(q_{2}\), and \(r_{2}\) stand for the result function’s variables. Regarding \({\text{ANFIS}}\) concepts, a fundamental \({\text{ANFIS}}\) structure was created utilizing the initial variables. Following that, the methodologies of \({\text{GOA}}\), \({\text{BWH}}\), \({\text{HHO,}}\) and \({\text{HGSO}}\) were employed to optimize the \({\text{ANFIS}}\) framework that was built. The root mean square error (\({\text{RMSE}}\)) indicator was computed as a fitness indicator to estimate the accuracy of the optimization framework. Lastly, optimized \({\text{ANF}}_{{\text{BWH }}}\), \({\text{ANF}}_{{{\text{HG}}}}\), \({\text{ANF}}_{{{\text{GOA}}}}\), and \({\text{ANF}}_{{{\text{HH}}}} { }\) networks were defined, taking into account the number of fuzzy words and the maximum number of iterations.

2.3 Metrics to Effectiveness Appraisal

A crucial stage in the framework creation process is validating and evaluating the developed simulations [70]. After constructing the simulations, it is crucial to validate their accuracy to accomplish their intended goals effectively. The effectiveness of each of the strategies mentioned above was assessed using training and testing sets data. To evaluate the accuracy and reliability of the simulations in this study, nine statistical indicators were used (Table 2).

Table 2 \({\text{ANFIS}}\)-based systems workability criteria
Full size table

3 Outcomes and Justifications

The present work employed integrated \({\text{ANFIS}}\) systems to examine the soil structure deformation characteristics (\({\text{Dis}}\)) that are reinforced by geogrid. This study utilized four hybrid \({\text{ANFIS}}\) systems. To develop combined systems with high accuracy, four optimization algorithms were linked with the \({\text{ANFIS}}\) model, including beluga whale optimizer (\({\text{BWH}}\)), Henry gas solubility optimization (\({\text{HGSO}}\)), gannet optimization algorithm (\({\text{GOA}}\)), and Harris hawks optimizer (\({\text{HHO}}\)) shown as \({\text{ANF}}_{{\text{BWH }}}\), \({\text{ANF}}_{{{\text{HG}}}}\), \({\text{ANF}}_{{{\text{GOA}}}}\), and \({\text{ANF}}_{{{\text{HH}}}}\), respectively. The evaluation and calculation of the \({\text{Dis}}\) of \({\text{GRSW}}\) were conducted via the learning and assessment stages of the developed methodologies, as shown in Fig. 8. The inquiry included several assessment techniques, such as correlation analysis, error-based metrics, uncertainty analysis, Taylor diagram, and sensitivity analysis, to assess the efficacy of \({\text{ANF}}_{{\text{BWH }}}\), \({\text{ANF}}_{{{\text{HG}}}}\), \({\text{ANF}}_{{{\text{GOA}}}}\), and \({\text{ANF}}_{{{\text{HH}}}}\) in predicting \({\text{Dis}}\). Additionally, the previous study used the \(R^{2}\) measure to evaluate the dependability and effectiveness of the constructed models [53].

Fig. 8
figure 8

The outcomes of the fuzzy systems. a Scatter plot, b error normal distribution)

Full size image

Regarding the results of the models from Table 3, it is obvious that all coupled \(ANFIS\) models have extremely acceptable accuracy during the estimation procedure. Considering the values of \(R^{2}\), the lowest values belonged to \({\text{ANF}}_{{{\text{HG}}}}\) at 0.9584 (Train) and 0.9839 (Test), which is an acceptable and reliable prediction. Between four \({\text{ANFIS}}\) systems, the integrated one with \({\text{GOA}}\) got the largest accuracy value, accounting for 0.9841 and 0.9895 in the train and test stages, better than \({\text{ANF}}_{{{\text{BWH}}}}\), followed by \({\text{ANF}}_{{{\text{HH}}}}\). However, for the purpose of increasing the dependability of the results, various error-based metrics were calculated and evaluated, such as \({\text{RMSE}}\), \({\text{NRMSE}}\), \({\text{MAE}}\), \({\text{PI}}\), \({\text{SI}}\), and \({\text{TIC}}\), where the lower these metrics, the higher was the accuracy. Considering the values of these metrics related to the four models, for \({\text{ANF}}_{{{\text{GOA}}}}\) the smallest values in comparison to others led to favor its capability in \({\text{Dis}}\) prediction of \({\text{GRSW}}\).

Table 3 The fuzzy systems’ performance and literature comparison
Full size table

The endurance of \({\text{U}}_{{{95}}}\) has been examined by scientists, and a significant pattern of enhanced generalization power was seen as the uncertainty value declined. Based on the obtained values of \({\text{U}}_{{\text{95 - Train}}} = 9.6385\), and \({\text{U}}_{{\text{95 - Test}}} = 6.9892\), it can be shown that the \({\text{ANF}}_{{{\text{GOA}}}} { }\) scenario exhibits the least level of uncertainty in comparison to other models, hence demonstrating its greater capacity for generalization. The second, third, and fourth ranks belonged to the \({\text{ANF}}_{{{\text{BWH}}}} { }\)(\({\text{U}}_{{\text{95 - Train}}} = 9.9972\), and \({\text{U}}_{{\text{95 - Test}}} = 8.7975\)), \({\text{ANF}}_{{{\text{HH}}}} { }\)(\(U_{95 - Train} = 11.38\), and \({\text{U}}_{{\text{95 - Test}}} = 10.22\)), and \({\text{ANF}}_{{{\text{HG}}}} { }\)(\({\text{U}}_{{\text{95 - Train}}} = 13.77\), and \({\text{U}}_{{\text{95 - Test}}} = 12.69\)) models.

In addition, a complete performance assessment index called \(OBJ\) was taken into account, which concurrently assessed the values of \(R^{2}\), \({\text{RMSE}}\), and \({\text{MAE}}\) for both the train and test data (the larger the value, the more reliable was the model). Between four \({\text{ANFIS}}\) systems, \({\text{ANF}}_{{{\text{HG}}}}\) depicts the highest \({\text{OBJ}}\) value at 3.9239. The second-worth model is \({\text{ANF}}_{{{\text{HH}}}}\) with \({\text{OBJ }}\) equal to 3.1772. On the other hand, the most accurate system with the lowest \({\text{OBJ}}\) value is \({\text{ANF}}_{{{\text{GOA}}}}\) at 2.6098, followed by \({\text{ANF}}_{{{\text{BWH}}}}\) at 2.8002.

Moreover, the error distribution plots are supplied in Fig. 8b for the training and testing portions. Regarding the distributions in the training stage, although the metrics depicted that the \({\text{ANF}}_{{{\text{GOA}}}} { }\) has superior workability, it is obvious from this plot that the \({\text{ANF}}_{{{\text{HH}}}} { }\) could perform slightly better than \(ANF_{GOA}\). In contrast, this shortcoming is solved in the testing section, where \({\text{ANF}}_{{{\text{GOA}}}} { }\) showed the greatest performance compared to \(ANF_{BWH}\), followed by \({\text{ANF}}_{{{\text{HH}}}} { }\) and then \({\text{ANF}}_{{{\text{HG}}}} { }\) by indicating the sharpest distribution with limited lower and upper bounds.

To evaluate the trustworthiness of the simulations, a comprehensive evaluation was conducted via a comparison study with existing academic literature [53]. After doing a thorough examination of Table 3, it becomes apparent that the \({\text{ANF}}_{{{\text{GOA}}}}\), which was formulated in this research, exhibited superior outcomes in comparison to the prior studies discussed in the existing body of research. The estimation was conducted utilizing a standardized metric, the coefficient of determination \(R^{2}\), which was used consistently in the learning and assessment stage. Based on the learning phase, the \(R^{2}\) increases from 0.9643 to 0.9841. Similarly, in the testing phase, it increases from 0.9702 to 0.9895.

To visually show and quantitatively evaluate how well a collection of data or model simulations fits a reference dataset, Taylor diagram analysis is employed. The Taylor diagram serves as a valuable tool for academics to evaluate several critical facets of the model's efficiency, encompassing:

  • Coefficient of correlation (\(R\)): The \(R\) among the simulation and the measured data is shown in the Taylor diagram. This presents the degree to which the model accurately captures the linear connection among the factors.

  • Standard deviation ratio (\({\text{SD}}\)): The comparison is made between the standard deviation of the simulation data and that of the measured data.

  • \({\text{RMSE}}\) ratio: This statistic quantifies the mean discrepancy between the simulations and the reported data, specifically emphasizing the size of the mistakes. A smaller \({\text{RMSE}}\) ratio is indicative of the superior performance of the model.

The Taylor diagram facilitates the comparison of numerous models or simulations against a shared reference dataset or measurable data by integrating the metrics of \({\text{R, SD, }}\) and \({\text{RMSE}}\) into a unified graphical representation. The outcomes of the Taylor diagram were presented throughout the learning and assessment phases, as seen in Fig. 9. In the training section, \({\text{ANF}}_{{{\text{GOA}}}}\) showed extremely similar performance with respect to \({\text{ANF}}_{{\text{BWH }}}\) with slight superiority, located closer to the benchmark point. \({\text{ANF}}_{{{\text{HH}}}} { }\) and \({\text{ANF}}_{{{\text{HG}}}} { }\) were in the third and fourth ranking. This trend is valid in the testing part, where \({\text{ANF}}_{{{\text{GOA}}}} { }\) depicts its capability in the prediction process by surpassing others.

Fig. 9
figure 9

Taylor diagram

Full size image

3.1 Restrictions and Future Suggestions

The study is commended for its utilization of a more comprehensive dataset in comparison to other investigations. However, it is conceivable that using even bigger datasets may yield more perspectives and bolster the models’ applicability. The research outcomes might exhibit specificity to the unique soil and geogrid settings utilized within the dataset. Evaluating the models' effectiveness over a broader spectrum of soil types, geogrid designs, and environmental circumstances might provide significant insights.

There is potential for conducting research aimed at predicting and analyzing the long-term displacement behavior of soil constructions reinforced using geogrids. This may include continuously monitoring physical structures in real-world settings for prolonged durations. The simulations that have been constructed may be used for the purpose of predicting deformation in geogrid-reinforced soil structures seen in real-world scenarios. This forecasting can then be compared with field measurements to evaluate these models’ practical feasibility and usefulness. Including reliability analysis in the systems is essential for engineering applications, as it allows for the determination of confidence intervals for forecasts, enhancing their value.

3.2 Sensitivity Analysis

The current research used sensitivity analysis as a method to evaluate the influence of input parameters on effectiveness. Sensitivity analyses conducted in simulation studies supply a methodical way to understand variables’ influence on the analysis's effectiveness, intending to improve model optimization, understanding, and decision-making. The current investigation encompassed the formulation of many theories, each using distinct inputs to augment the effectiveness of the established model (\({\text{ANF}}_{{{\text{GOA}}}}\)). The research used \(R^{2}\), \(PI\), and \({\text{U}}_{{{95}}}\) metrics to evaluate the influence of different inputs, in contrast to the \({\text{ANF}}_{{{\text{GOA}}}}\) framework. The sensitivity analysis result is provided in Fig. 10 in the train and test part. As the significance of omitted elements on the result intensifies, the disparities in the metrics also escalate. The findings suggest that the exclusion of all parameters (\(q\),\(E / E_{0}\), \(S_{{\text{v}}}\), and \(\varphi\)) has a considerably worse effect on the outcome in comparison to \(ANF_{GOA}\). Significantly, with the removal of the \(q\) parameter from the input group, there is a notable increase in the values of \({\text{U}}_{{{95}}}\) and \({\text{PI}}\), coupled with a significant decrease in the value of \(R^{2}\). The \(R^{2}\) values showed a decrease from 0.9841 to 0.3559 in the learning stage and from 0.9895 to 0.3221 in the testing stage. In relation to \({\text{U}}_{{{95}}}\), a significant rise was seen from 9.6385 to 52.09 (5.5 times larger) during the training phase and from 6.9892 to 52.629 (7.5 times bigger) during the testing phase. It is important to recognize that excluding any input can reduce the comprehensiveness and dependability of the designs, since they were developed using analytical data.

Fig. 10
figure 10

The results of the sensitivity analysis

Full size image

4 Conclusion

The present work employed integrated \({\text{ANFIS}}\) systems to examine the soil structure deformation characteristics (\({\text{Dis}}\)) that are reinforced by geogrid. This study utilized four hybrid \({\text{ANFIS}}\) systems. To develop combined systems with high accuracy, four optimization algorithms were linked with the \(ANFIS\) model, including beluga whale optimizer (\({\text{BWH}}\)), Henry gas solubility optimization (\({\text{HGSO}}\)), gannet optimization algorithm (\({\text{GOA}}\)), and Harris hawks optimizer (\({\text{HHO}}\)) shown as \({\text{ANF}}_{{\text{BWH }}}\), \({\text{ANF}}_{{{\text{HG}}}}\), \({\text{ANF}}_{{{\text{GOA}}}}\), and \({\text{ANF}}_{{{\text{HH}}}}\), respectively. The investigation of the possible use of approaches based on machine learning for the purpose of predicting \({\text{Dis}}\) was the major focus of this study. These efforts are made to reduce the time and cost of numerical modeling. This study aimed to enable computers to learn patterns and insights from data to make accurate predictions or decisions about unseen data. The primary results are mentioned below:

Considering the values of \(R^{2}\), the lowest values belonged to \({\text{ANF}}_{{{\text{HG}}}}\) at 0.9584 (train) and 0.9839 (test), which is an acceptable and reliable prediction. Between the four \({\text{ANFIS}}\) systems, the integrated one with \({\text{GOA}}\) obtained the largest accuracy value, accounting for 0.9841 and 0.9895 in the train and test stages, better than \({\text{ANF}}_{{{\text{BWH}}}}\), followed by \({\text{ANF}}_{{{\text{HH}}}}\).

Considering the values of error-based metrics related to the four models, it is clear that \({\text{ANF}}_{{{\text{GOA}}}}\) showed the smallest values in comparison with others, leading to approve its capability in \({\text{Dis}}\) prediction of \({\text{GRSW}}\).

Regarding \({\text{U}}_{{{95}}}\), based on the obtained values of \({\text{U}}_{{\text{95 - Train}}} { = }9.6385\), and \({\text{U}}_{{\text{95 - Test}}} = 6.9892\), it can be shown that the \({\text{ANF}}_{{{\text{GOA}}}} { }\) scenario exhibits the least level of uncertainty in comparison to other models, hence demonstrating its greater capacity for generalization.

Between the four \({\text{ANFIS}}\) systems, the most accurate system with the lowest \(OBJ\) value is \({\text{ANF}}_{{{\text{GOA}}}}\) at 2.6098, followed by \({\text{ANF}}_{{{\text{BWH}}}}\) at 2.8002.

Turning to the Taylor diagram, in the learning and assessment sections, \({\text{ANF}}_{{{\text{GOA}}}}\) showed similar performance with respect to \({\text{ANF}}_{{\text{BWH }}}\) with small superiority, which could be located closer to the benchmark point. \({\text{ANF}}_{{{\text{HH}}}} { }\) and \({\text{ANF}}_{{{\text{HG}}}} { }\) had the third and fourth ranking.

The findings of sensitivity analysis suggested that the exclusion of entire variables (\(q\), \(E / E_{0}\), \(S_{{\text{v}}}\), and \(\varphi\)) has a considerably worse effect on the outcome in comparison to \(ANF_{GOA}\). Significantly, with the removal of the \(q\) parameter from the input group, there is a notable increase in the values of \({\text{U}}_{{{95}}}\) and \(PI\), coupled with a significant decrease in the value of \(R^{2}\). In relation to \({\text{U}}_{{{95}}}\), a significant rise was seen from 9.6385 to 52.09 (5.5 times larger) during the training phase and from 6.9892 to 52.629 (7.5 times bigger) during the testing phase.

It is conceivable that using even bigger datasets may yield more insights and bolster the applicability of the models. Evaluating the models' effectiveness over a broader spectrum of soil types, geogrid designs, and environmental circumstances might provide significant insights. This may include continuously monitoring physical structures in real-world settings for prolonged durations. This forecasting can then be compared with field measurements to evaluate these models’ practical feasibility and usefulness. Including reliability analysis in the systems is essential for engineering applications, as it allows for the determination of confidence intervals for forecasts, enhancing their value.