An Efficient Binary Hybrid Equilibrium Algorithm for Binary Optimization Problems: Analysis, Validation, and Case Studies

Abstract

Binary optimization problems belong to the NP-hard class because their solutions are hard to find in a known time. The traditional techniques could not be applied to tackle those problems because the computational cost required by them increases exponentially with increasing the dimensions of the optimization problems. Therefore, over the last few years, researchers have paid attention to the metaheuristic algorithms for tackling those problems in an acceptable time. But unfortunately, those algorithms still suffer from not being able to avert local minima, a lack of population diversity, and low convergence speed. As a result, this paper presents a new binary optimization technique based on integrating the equilibrium optimizer (EO) with a new local search operator, which effectively integrates the single crossover, uniform crossover, mutation operator, flipping operator, and swapping operator to improve its exploration and exploitation operators. In a more general sense, this local search operator is based on two folds: the first fold borrows the single-point crossover and uniform crossover to accelerate the convergence speed, in addition to avoiding falling into local minima using the mutation strategy; the second fold is based on applying two different mutation operators on the best-so-far solution in the hope of finding a better solution: the first operator is the flip mutation operator to flip a bit selected randomly from the given solution, and the second operator is the swap mutation operator to swap two unique positions selected randomly from the given solution. This variant is called a binary hybrid equilibrium optimizer (BHEO) and is applied to three common binary optimization problems: 0–1 knapsack, feature selection, and the Merkle–Hellman knapsack cryptosystem (MHKC) to investigate its effectiveness. The experimental findings of BHEO are compared with those of the classical algorithm and six other well-established evolutionary and swarm-based optimization algorithms. From those findings, it is concluded that BHEO is a strong alternative to tackle binary optimization problems. Quantatively, BHEO could reach an average fitness of 0.090737884 for the feature section problem and an average difference from the optimal profits for some used Knapsack problems of 2.482.

1 Introduction

Binary optimization is a special case of discrete optimization in which the only possible values for the decision variables are zero or one. There are a number of significant binary problems, including feature selection, bag selection, unit commitment, Knapsack, an ensemble of classifiers, unoccupied facility location [1], cryptanalysis in the Merkle–Hellman cryptosystem (MHKC) [2], and etc. [3].

Feature selection (FS) is an indispensable preprocessing technique proposed to reduce the dimensionality of problems while maintaining or increasing their quality. FS has been applied to various machine learning tasks to remove noisy, irrelevant, and redundant features to propose simpler classifiers with high performance in less time [4, 5]. FS has been employed to remove the irrelevant features that might substantially degrade the performance of the machine learning algorithms. It is employed in several applications like image classification [6], text categorization [7], cancer detection [8], genomics [9], and many others [10]. There are various types of FS methods, which are filter, wrapper, and embedding methods [11]. In filter methods, the selection of features is independent of the machine learning techniques; on the contrary, the wrapper methods employ a machine learning technique for selecting the features. Studies have shown that wrapper techniques are superior to filters in terms of performance and efficiency, but they are expensive in terms of the computational cost [12].

The 0–1 Knapsack (KP01) problem is frequently encountered in efficiently exploiting resources to maximize profit and minimize cost. KP01 decision-making problems arise in numerous fields, including investment decisions [13], available-to-promise problem [14], cryptography [15, 16], cutting stock problem [17], computer memory [18], adaptive multimedia systems [15], housing problem [19], and cutting-stock problem [20].

Any message can be encrypted with a public key and sent to a receiver, who can then use a private key to decode the message and read it as it was originally intended. This is the idea behind the public key cryptosystem (PKC). The Merkle–Hellman knapsack cryptosystem (MHKC) is a PKC that uses a two-key system (one for encrypting the message by the sender and another for decrypting this message by the receiver) to ensure the confidentiality of transmitted data [21].

Since the binary optimization problems belong to the NP-hard class, the traditional techniques could not find their near-optimal solutions in a reasonable time [4]. Hence, the need for modern techniques to overcome these problems in a reasonable time was so essential. Therefore, the researchers have recently paid attention to metaheuristic algorithms that could find acceptable solutions for several optimization problems in a reasonable time [22,23,24,25,26,27,28]; Some of these problems are traveling salesman problem [29], parameter estimation problems [30], scheduling problems [31], image segmentation problem [32], image denoising [33], and image registration [34].

Over the last few decades, several metaheuristic algorithms have been proposed to solve binary optimization problems [4, 35]. However, these algorithms have some drawbacks that prevent them from achieving high-quality outcomes, some of those drawbacks are the population diversity lack, the imbalance between exploration and exploitation operators, and the tendency to become stuck in local minima. Therefore, this paper is presented to propose a new binary technique based on integrating the equilibrium optimizer (EO)with a new local search operator to solve the binary problems with high accuracy. This local search operator is based on two folds: the first one borrows the single-point and uniform crossover to accelerate the convergence speed, and the mutation strategy to avoid falling in local minima; the second fold is based on applying two different mutation operators: the first operator is the flip mutation operator to flip a bit selected randomly from the current solution, and the second operator is the swap mutation operator to swap two unique positions selected randomly from the best-so-far solution in the hope of finding a better solution. The main contributions of this paper could be summarized as follows:

• Proposing a new local search operator based on borrowing some operators from the genetic algorithm and relating them in an effective manner;

• Combining this local search with the EO to propose BHEO, a new strong variant for dealing with binary optimization problems such as the KP01, FS, and MHKC;

• The experimental outcomes show that BHEO is a strong binary optimization technique for binary applications.

The remainder of this work is structured as follows: Sect. 2 briefly covers some of the suggested works for addressing the binary optimization problems; Sect. 3 describes the binary optimization problems; Sect. 4 explains the mathematical model of the EO; The proposed BHEO is explained and discussed in Sect. 5; Sect. 6 discusses and analyzes the results of the BHEO compared with the state-of-art-methods. Conclusions and Future directions are suggested in Sect. 7.

2 Literature Review

A considerable amount of literature has been published to propose various binary optimization algorithms able to overcome several optimization problems like FS, KP01, and cryptanalysis in MHKC. Some of the work done in the literature are reviewed in this section to show their contributions to the readers.

For applying the Emperor Penguin Optimizer (EPO) to discrete optimization problems, in [36], eight different binary EPO versions (BEPO) have been provided based on various families of transfer functions (S-shaped and V-shaped) that are employed to convert its continuous nature to a discrete one. It was tested on 12 benchmark datasets. Comparatively, BEPO performs better than other benchmarks. An efficient DoS attack detection system using the oppositional crow search algorithm (OCSA) was proposed in [37], which combines the crow search algorithm (CSA) and the opposition-based learning (OBL) technique. Both the OCSA and RNN classifier are used to identify and classify the proposed system’s characteristics. Selecting essential features using the OCSA method is followed by an RNN classifier. It has been shown through experimentation and analysis that the suggested methodology exceeds the other traditional techniques in terms of accuracy (94.12), precision (98.18%), recall (95.13%), and F-measure (93.56%).

For solving the KP01, the quantum-inspired wolf pack algorithm (QWPA) [38] has been developed. Quantum rotation and quantum collapse were the primary processes used to enhance the QWPA. The former is employed to hasten progress toward the ideal solution, while the latter is accountable for avoiding stagnation at local minima. After being tested on datasets up to 1000 dimensions, QWPA was compared to other optimization methods to show its effectiveness. In addition, for addressing KP01, butterfly optimization methods (MBO) enhanced by an OBL and Gaussian perturbation have been developed [39]. Late in the optimization process, OBL was used on half of the population to hasten the rate at which solutions converged on the ideal one. Simultaneously, weakly fit individuals are propelled forwards by Gaussian perturbation at each iteration to keep them from settling into local optima. The efficacy of this approach was tested across 15 large-scale instances.

FS was addressed in [40], using single, multi-objective, and many-objective binary variants of the artificial butterfly optimization (ABO). Aside from that, the authors offer two approaches: MO-I tries to optimize the classification accuracy of each class independently, whereas MO-II focuses on feature set reduction. Consequently, the binary single-objective ABO outperformed the other meta-heuristic approaches in terms of the number of features selected and the computing burden. Both MO-I and MO-II methods outperformed their single-objective versions when they came to multi and many-objective feature selection.

By utilizing the GWO and rough set (GWORS) approach, it is possible to determine the key aspects of the recovered mammography images as proposed in [41]. A comparison was made between the proposed GWORS and other well-known rough sets and bio-inspired feature selection approaches, such as particle swarm optimizer (PSO), genetic algorithm (GA), quick reduct (QR), and relative reduction (RR). According to empirical data, the suggested GWORS beats the prior approaches in terms of accuracy, F-measures, and receiver operating characteristic curve.

A slime mould algorithm (SMA) was presented in four binary forms for feature selection [42]. The basic SMA is combined with the best transfer function from eight V-shaped and S-shaped transfer functions. The second method, TMBSMA (two-phase mutation), merges BSMA with two-phase mutation (TM) to further explore superior options surrounding the current best-so-far solutions. A new attacking–feeding strategy (AF) is used in the third edition, abbreviated as AFBSMA, which trades off exploration and exploitation depending on each particle’s ability to save memory. The fourth variant is FMBSMA, which combined TM/AF with BSMA for producing superior solutions. Twenty-eight well-known data sets taken from UCI database were used to validate the performance of four different BSMA variations that have been proposed. Compared to several rival optimizers, the FMBSMA could provide superior results.

To tackle the feature selection problem, three binary methods based on symbiotic organisms search (SOS) were proposed in [43]. The first method was based on employing several S-shaped transfer functions for investigating their performance, while the second method used several V-shaped transfer functions based on the chaotic Tent function in a new attempt to propose a strong binary variant for tackling feature selection. The first and second method was called BSOSST and BSOSVT, respectively. In addition, the authors presented the third approach by integrating the binary SOS (BSOS) with the Gaussian mutation and the chaotic tent function to improve both exploration and exploitation operators; this approach was called EBCSOS. According to the several experiments conducted to solve 25 datasets, EBCSOS could be better than all the other rival optimizers. Wang [44] employs a new machnaism to compute the heuristic information that is used by symmetric uncertainty (SU) to reduce the number of redundant features. Afterwards, the ant colony algorithm based on the probabilistic sequence-based graphical representation is applied to find the best subset of remaining features that could maximize the classification accuracy of the support vector machine and random forest. This algorithm was abbreviated as SPACO and compared to six optimization algorithms. The experimental findings show its superiority over all the compared algorithms.

The KP01 has been proposed to be addressed by the flower pollination algorithm (FPA) [45]. Since KP01 is a binary problem, the continuous FPA could not be directly applied to solve this type of optimization problems. As a result, the sigmoid transfer function was utilized by the author to discretize the FPA output of continuous values. Furthermore, the author employed a penalty function to prevent the infeasible solutions from being chosen as the optimal option. On top of that, an improvement-repair technique was applied to such infeasible solutions to make them feasible to solve KP01. The genetic algorithm and sine cosine algorithm were combined to create a hybrid feature selection approach. Exploration and exploitation operators performed better with SCAGA [46]. It has been evaluated based on the following criteria: classification accuracy, worst fitness, mean fitness, and best fit. There was also a comparison between the sine cosine algorithm (SCA) and various other techniques. From this, it was determined that SCAGA generated the best results of all datasets taken from UCI’s dataset.

In [47], a binary optimization technique was proposed for tackling binary optimization problems, specifically KP01 problems. This technique converts the Gaining Sharing knowledge-based optimization algorithm (GSK) into a binary algorithm, namely BGSK, based on two binary gaining–sharing stages. The first stage is called binary junior, while the second stage is known as binary senior. Both of them were applied with a knowledge ratio of 1 and utilized to enable the binary GSK (BGSK) to exploit and explore the search space effectively and efficiently for finding near-optimal solutions to binary problems. In addition, BGSK is integrated with a population reduction strategy to improve its convergence speed in addition to avoiding stuck into local minima. This strategy gradually reduces the population over the course of the iteration. Comparisons with several rival optimizers over several performance metrics disclosed the superior performance of BGSK. Based on the farmland fertility algorithm (FFA), two distinct wrapper feature selection techniques, namely BFFAS and BFFAG, have been presented [48]. The sigmoid function is used in the first version to convert the continuous solutions generated by FFA into binary solutions. In the second version, binary global and local memory update (BGMU) operators, as well as a dynamic mutation (DM) operator, are employed for binarization. It also decreases three factors that are dynamically changed to preserve exploration and efficiency in the new method (BFFAG). The suggested approaches outperform competing methods, according to the results. Table 1 describes the contributions in addition to some limitations of some recently published FS algorithms.

Table 1 Contributions and limitations of some recently published FS algorithms

Metaheuristic methods for predicting the plain text for each ciphertext have recently been proposed as a means of exposing the weaknesses of MHKC systems and encouraging the development of more robust encryption techniques. We will take a look at a few of those algorithms down below. For this purpose, A mutation operation to improve the quality of the obtained solutions and a penalty function to eliminate the infeasible solution were used to adapt the whale optimization algorithm (WOA) for attacking the MHKC systems [2]. This variant of WOA was termed the modified WOA (MWOA). Several standard optimization techniques were compared to this variant, and it performed better on average. In addition, Grari et al. [49] developed an updated version of the ant-colony optimization for deciphering encrypted text.

The MHKC has been proposed to be deciphered using two binary forms of PSO (BPSO) [50]. The experimental findings illustrated that BPSO was more effective than several other rival optimizers. For the purpose of automating cryptanalysis of the reduced-Knapsack cryptosystem, three metaheuristic optimizers—genetic algorithm (GA), cuckoo search (CS), and PSO—were explored [51]. The results of the conducted experiments proved that cuckoo search is the best method for automating the cryptographic examination of a reduced cryptosystem. Kochladze [52] has presented a genetic algorithm to solve the MHKC. The experimental results demonstrated the method's superiority over the more popular Shamir algorithm. In an effort to demonstrate the weakness of these MHKC systems, a binary form of the Firefly algorithm (BFA) for guessing the plaintext from the ciphertext was suggested [53]. When compared to GA, BFA is a better choice for attacking the MHKC.

There are several other metaheuristic algorithms published recently for tackling binary optimization problems, such as the quantized SSA [65], the improved bald eagle search algorithm [66], EO integrated with simulated annealing [67], the binary chimp optimization algorithm [68], the oppositional cat swarm optimization algorithm [69], the orchard algorithm [70], the monarch butterfly optimization algorithm [71], the fast genetic algorithm [72], the artificial immune optimization algorithm [11], the Harris hawks optimization algorithm [73], the artificial jellyfish search algorithm [74], the sine cosine algorithm [75], the Aquila optimizer [76], the reptile search algorithm [77], the light spectrum optimizer [78], the golden jackel optimization algorithm [79], the marine predators algorithm [80], the binary gaining–sharing knowledge-based optimization algorithm [47, 81,82,83,84], the battle Royale optimizer [85], the simulated normal distribution optimizer [86], the sparrow search algorithm [87], the tree seed algorithm [88], and the differential evolution algorithm [89].

3 Binary Optimization Problems

3.1 Merkle–Hellman Knapsack Cryptosystem

This is a type of asymmetric public-key cryptosystem in which the sender uses a public key to encrypt the message and the recipient uses a private key to decrypt it so that only the recipient c read the original [2]. In what follows, we will go over the cryptosystem's steps for encrypting and decrypting data.

3.1.1 Encryption

Starting with a super-increasing Knapsack sequence, the following equation is used to change it into a trapdoor Knapsack sequence:

$$A = A^{\prime}_{i} \times r\% q, i = 1,2,3, \ldots \ldots , n$$

(1)

For instance, given the super increasing sequence, q, and r, as follows:

$$A^{\prime} = \left\{ {2, 3, 7, 15, 29, 65, 125, 251} \right\}$$

$$q=507$$

$$r=10$$

Then, under the aforementioned information, the trapdoor Knapsack sequence could be constructed as shown below:

$${A}_{1}=2\times 10\mathrm{\%}507=20$$

$${A}_{2}=3\times 10\mathrm{\%}507=30$$

$${A}_{3}=7\times 10\mathrm{\%}507=70$$

$${A}_{4}=15\times 10\mathrm{\%}507=150$$

$${A}_{5}=29\times 10\mathrm{\%}507=290$$

$${A}_{6}=65\times 10\mathrm{\%}507=143$$

$${A}_{7}=125\times 10\mathrm{\%}507=236$$

$${A}_{8}=251\times 10\mathrm{\%}507=482$$

Supposing that a trapdoor Knapsack sequence $A$ contains the next values: $\left\{20, 30, 70, 150, 290, 143, 236, 482\right\}$ used to encrypt the message “CAT” according to the next steps:

• An 8-bit ASCII code, as shown in Table 2, could be used to represent each character in this word. The ciphertext, or encrypted letter, is calculated by multiplying each letter’s bits by its corresponding trapdoor element. The final column of Table 2 displays the cipherText generated by adding the multiplication results for each character.

• As a final step, the ciphertexts are delivered to the recipient, who possesses the private key to decrypt them and recover the original message. In the next paragraphs, we will talk about the deciphering process.

Table 2 Ciphertexts of “CAT”

3.1.2 Decryption

In this step, we go backward from the ciphertext to the original message based on discovering the bit representation that could be used to generate the ciphertext. Methods for decrypting ciphertext using a private key are explained in detail in [2]. Is it possible to estimate the original message if the sender does not reveal their private key? Yes, it is possible by estimating the binary values that could be used to generate the cipthertext from the trapdoor sequence. In this work, we present a new binary optimization algorithm for estimating the bits which could accurately estimate the ciphertext. After findings these bits, the original message could be easily generated by converting those bits into the corresponding character in the ASCII code.

3.1.3 MHKC’s Objective Function

An objective function (or fitness function) is used by metaheuristic methods to evaluate the accuracy of each estimated ciphertext. In this study, we employ a penalty function to scale each solution’s fitness score between 0 and 1, where 0 indicates that the solution successfully estimated the ciphertext. Infeasible solutions are those whose total is bigger than the ciphertext, and this penalty function gets rid of them by assigning them higher fitness ratings. Following is the formula that describes this function mathematically [2]:

$$S=\sum_{j=1}^{n}{A}_{j}{X}_{j}$$

(3)

$${\rm M}={\text{max}}({\text{target}}, S-T)$$

(4)

$$f\left({\overrightarrow{X}}_{i}\right)=\left\{\begin{array}{c}\sqrt{\frac{\left|S\left({\overrightarrow{X}}_{i}\right)-T\right|}{T}}\quad S\le T\\ 1-\sqrt[6]{\frac{\left|S\left({\overrightarrow{X}}_{i}\right)-T\right|}{M}} \quad S>T\end{array}\right.$$

(5)

where T is the target sum, M holds the largest difference between T and the sum of the trapdoor sequence chosen by ${\overrightarrow{X}}_{i}$.

3.2 Feature Selection Problem

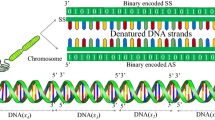
FS is an important step for machine learning techniques to prepare data before the learning process to improve classification accuracy as much as possible. Unfortunately, the traditional techniques are not suitable for tackling this problem due to their high computational cost and poor final accuracy. Therefore, the metaheuristic algorithms were the most alternative for this problem due to their ability to overcome several NP-hard problems in a reasonable time. First, the metaheuristic algorithms, before starting the optimization process, randomly distribute a number N of solutions within the search space of the optimization problem, where each solution has d features. The search space differentiates according to the nature of the problem; some problems are continuous, whose solutions store real values within the upper and lower bounds of this search space. Meanwhile, the other problems are discrete and represented by solutions including binary or integer values. In this paper, three different discrete problems, namely the FS problem, KP01, and MHKC, are solved, whose solutions include binary values to represent the selected dimensions by 0 and the unselected dimensions by 1, as represented in Fig. 1.

Fig. 1

Representation of the FS solutions

The FS belongs to the multi-objective problem because it has two conflict objectives: maximizing accuracy and minimizing the feature-length. However, most metaheuristic algorithms such as the proposed algorithm have been proposed for tackling single-objective problems and hence could not be directly applied to multi-objective problems. Several research dealt with the multi-objective FS problem in two different ways: Pareto optimality and weighting variable to convert two objectives into a single one. In our proposed work, the second way is employed to convert the multiobjective FS into a single objective by a weighting variable ${\alpha }_{1}$ which is initialized with a value between 0 and 1 according to the preference of one objective against the other. Generally, the objective function employed with the proposed algorithm to maximize classification accuracy and minimize the selected number of features is mathematically formulated by the following formula:

$$f={\alpha }_{1}\times {\gamma }_{R}\left(D\right)+\beta \times \frac{\left|S\right|}{\left|N1\right|}$$

(6)

where ${\gamma }_{R}\left(D\right)$ indicates the classification error rate feedbacked from the K-nearest neighbor algorithm. $\left|S\right|$ is the subset of features selected by an optimizer, $\left|N1\right|$ is the number of the features in the employed dataset, and $\beta$ is of $\beta =(1-{\alpha }_{1})$. The holdout method is used to divide the dataset into training and testing datasets.

3.3 0–1 Knapsack Optimization Problem (KP01)

KP01 assumes a Knapsack with a fixed capacity c and a fixed number of items n, where each item has its own profit $pr$ and weight w. To solve this problem, you must determine the items that might be added to the Knapsack without exceeding its capacity c with maximizing the total profit of those items. The formulation of the KP01 problem, which presents the objective function that has to be optimized by the proposed algorithm to solve this problem, is as follows:

$${\text{Maximize}} \sum_{z=1}^{n}{X}_{z}\times {pr}_{z}$$

(7)

$$\mathrm{Subject to} \sum_{z=1}^{n}{w}_{z}\times {X}_{z}\le c$$

$${X}_{z}=0 or 1, z=\mathrm{0,1}\dots \dots n$$

4 Equilibrium Optimizer (EO)

A novel physics-based metaheuristic algorithm, known as the EO, has been recently proposed to tackle optimization problems, especially single continuous optimization problems, and could outperform several rival algorithms [90]. Briefly, EO was proposed to simulate a generic mass balance equation for a controlled volume and seeks to find the equilibrium state, which is the balancing between the amount of mass that enters, gets out of, and is found in the system. The mathematical model of EO is explained in detail in the rest of this section.

Before starting the optimization process by EO, it creates N solutions distributed within the search space of an optimization problem that has d-dimensions/variables and evaluates each one using an objective function, which might be maximized or minimized according to the optimization problem. After that, it determines the best first solutions and assigns them to a vector, namely ${\overrightarrow{{\text{C}}}}_{{\text{eq}},{\text{pool}}}$, in addition to calculating the average of those best solutions and storing it in the same vector, as represented in (9).

$${\overrightarrow{X}}_{i}= \overrightarrow{{X}_{L}}+\left(\overrightarrow{{X}_{U}}-\overrightarrow{{X}_{L}}\right)\times \overrightarrow{r}\quad i=\mathrm{0,1},2,\dots ,N$$

(8)

$${\overrightarrow{{\text{C}}}}_{{\text{eq}},{\text{pool}}}=\left[ {\overrightarrow{{\text{X}}}}_{\mathrm{eq }\left(1\right)}, {\overrightarrow{{\text{X}}}}_{\mathrm{eq }\left(2\right)}, {\overrightarrow{{\text{X}}}}_{{\text{eq}}\left( 3\right)}, {\overrightarrow{{\text{X}}}}_{{\text{eq}}\left( 4\right)}, {\overrightarrow{{\text{X}}}}_{{\text{eq}}\left({\text{avg}}\right)}\right]$$

(9)

where $\overrightarrow{{{\text{X}}}_{{\text{L}}}}$ and $\overrightarrow{{{\text{X}}}_{{\text{U}}}}$ indicates the lower bound and upper bound values of the dimensions, and $\overrightarrow{{\text{r}}}$ is a vector generated randomly between 0 and 1.

After that, EO runs the optimization process, which starts with calculating the value of a term, namely ${t}_{1}$, using the following equation:

$${t}_{1}={\left(1-\frac{t}{T}\right)}^{\left({a}_{2}\times \left(\frac{t}{T}\right)\right)}$$

(10)

where $t$ and $T$ indicate the current and maximum function evaluations, and ${a}_{2}$ is a constant employed to manage the exploitation operator of EO. This term is related to an exponential term (F) that is designed to balance both exploration and exploitation capabilities. The mathematical model of the term F is defined as that [90]:

$$\overrightarrow{F}={a}_{1}\times {\text{sign}}(\overrightarrow{{r}_{1}}-0.5)\times {[e}^{-\overrightarrow{\lambda }\left({t}_{1}\right)}-1]$$

(11)

where $\overrightarrow{{r}_{1}}$ and $\overrightarrow{\lambda }$ are two vectors generated randomly at the range of 0 and 1, and ${a}_{1}$ is a fixed value to control the exploration capability. In addition, a new factor known as the generation rate ($\mathop{G}\limits^{\rightharpoonup}$) has been employed by EO to further improve its exploitation operator, which is mathematically described by the following equation:

$$\mathop{G}\limits^{\rightharpoonup} = \mathop{G}\limits^{\rightharpoonup} _{0} *\vec{F}$$

(12)

where $\mathop{G}\limits^{\rightharpoonup} _{0}$ could be computed according to the following mathematical equation:

$$\mathop{G}\limits^{\rightharpoonup} _{0} = \overrightarrow {GCP} *\left( {\overrightarrow {{c_{eq} }} - \vec{\lambda }*\vec{X}_{i} } \right)$$

(13)

$$\overrightarrow{{\text{GCP}}}=\left\{\begin{array}{l}0.5{r}_{2} \quad {r}_{3}\ge GP\\ \\ 0\quad otherwise\end{array}\right.$$

(14)

where ${r}_{2}$ and ${r}_{3}$ are random numbers between 0 and 1, and $\overrightarrow{GCP}$ is a vector including values of 0 and 1 determined based on a certain generation probability (GP), recommended 0.5 in the original paper. $\overrightarrow{{c}_{{\text{eq}}}}$ is a solution selected randomly from the five solutions found in ${\overrightarrow{{\text{C}}}}_{{\text{eq}},{\text{pool}}}$, and ${\overrightarrow{X}}_{i}$ indicates the current position of the ith solution. Ultimately, each solution within the optimization process will be optimized using the following equation:

$${\overrightarrow{X}}_{i}=\overrightarrow{{c}_{{\text{eq}}}}+\left({\overrightarrow{X}}_{i}- \overrightarrow{{c}_{{\text{eq}}}}\right)\times \overrightarrow{F}+\frac{\overrightarrow{G}}{\overrightarrow{\lambda }*V}\times (1-\overrightarrow{F})$$

(15)

where V is the value of velocity and recommended 1. The pseudo-code, which describes the steps of EO, is shown in Algorithm 1.

Algorithm 1

The pseudo-code of EO

5 The Proposed Work (BHEO)

In this section, the steps of the proposed algorithm will be extensively explained to clarify how it could tackle the FS problem; those steps are, briefly, initialization, transformation function, objective function, borrowed genetic operators, and the pseudocode of the proposed algorithm.

5.1 Initialization

First, the metaheuristic algorithms randomly distribute N solutions, each of which has d dimensions, within the search space of the optimization problem. The search space varies depending on the nature of the problem; some problems are continuous, and their solutions store real values between the upper and lower bounds of this search space. In contrast, the remaining problems have discrete solutions depicted by binary or integer values. In this paper, three distinct discrete problems are solved, namely the FS problem, KP01, and MHKC, whose solutions include binary values representing the selected dimensions as 0 and the unselected dimensions as 1. After randomly initializing the N solutions with binary values and evaluating each solution to determine the solution with the lowest objective value, the optimization process is started to search for better solutions. But, the updated solutions generated by the metaheuristic algorithms are not applicable for tackling the FS because they are continuous. Therefore, the hyperbolic tangent transfer function is employed to convert the continuous values generated by one of the latest metaheuristic algorithms, namely the EO, into binary values to become applicable to this problem. Next, the hyperbolic tangent transfer function is discussed in detail.

5.2 The Hyperbolic Tangent Transfer Function

Despite that there are several transfer functions that could be used to normalize the continuous solutions, but the hyperbolic tangent transfer function are used in this study due to its ability to achieve outstanding outcomes when used with several metaheuristic algorithms as shown in [19, 91]. This transfer function modeled in (16) is used to normalize the continuous solutions between 0 and 1. After that, those normalized solutions are converted into 0 and 1 using (17).

$${\overrightarrow{nX}}_{i}=F({\overrightarrow{X}}_{i})=\left|{\text{tanh}}\left({\overrightarrow{X}}_{i}\right)\right|$$

(16)

$$b{X}_{ij}=\left\{\begin{array}{l}1\quad if\quad n{X}_{ij}>0.5\\ 0 \quad otherwise\end{array}\right.$$

(17)

where ${\overrightarrow{X}}_{i}$ is a vector of d dimensions including the continuous values of $i{\text{th}}$ solution, ${\overrightarrow{nX}}_{i}$ includes the normalized values returned from the function $F({\overrightarrow{X}}_{i})$, and $b{X}_{ij}$ is the binary value of the $j{\text{th}}$ dimension in the $i{\text{th}}$ solution. Figure 2 shows the shape of this transfer function.

Fig. 2

The shape of the hyperbolic tangent transfer function

5.3 Borrowed Genetic Operators

5.3.1 One-Point Crossover Operator

This crossover is used in the genetic algorithms to generate new offspring by swapping the positions before an index selected randomly from a solution with the same positions in another solution. Figure 3 illustrates the one-point crossover.

Fig. 3

Representation of one-point crossover

5.3.2 Uniform Crossover Operator

In this operator, two solutions from the current population are selected using a selection strategy, and then two offspring are generated from those solutions based on a certain uniform probability, which determines which position from the first solution will be exchanged with the same position in the second solution. This operator is figured in Fig. 4 to be clearer to the readers. In this figure, a vector of the length of the parents, known as a mask, is randomly initialized according to the uniform probability. This vector is then used to generate two offspring as illustrated in Fig. 4

Fig. 4

Representation of uniform crossover

5.3.3 Mutation Operator

This operator is so important in genetic algorithms because it aids in disposing of the local optimum problem. This operator mutates the positions of a solution according to a certain probability known as the mutation probability (MP). Finally, the crossover operators discussed above are effectively integrated with the mutation operator to achieve two purposes: accelerating the convergence speed and avoiding getting stuck in local minima. The integration of those operators is clearly described in Algorithm 2.

Algorithm 2

Hybrid genetic operator (HGO)

5.4 Effective local search operator

In this paper, an effective local search operator has been suggested as an attempt to improve the ability of the standard EO for achieving better outcomes while solving the FS problem. This local operator is based on integrating Algorithm 2 with the flip and swap operators effectively for varying the search process during the optimization process for reaching better outcomes in fewer number iterations in addition to avoiding stuck into local optima along this process. In Algorithm 2, the one-point and uniform crossovers are integrated to improve the exploitation operator for accelerating the convergence speed, and then the obtained solution is mutated with a certain probability generated using (18) to avoid getting stuck in local optima. However, the HGO might not generate a better solution because the best solution might need slight updating in the parent, so the flip and swap operators are integrated with the GHO to propose a novel local search operator. This local search operator described in Algorithm 3 is based on a randomization process to determine the tradeoff between the HGO and flip and swap operators. Broadly speaking, Algorithm 3 takes the best-so-far solution ${\overrightarrow{bX}}_{{\text{eq}} \left(1\right)}$ and the maximum trial (maxTrial) as inputs. In Lines 1–4 within this algorithm, two random numbers, $r {\text{and}} {r}_{1}$ are generated, and if $r$ is less than ${r}_{1}$, the HGO algorithm is called to update the current position of each solution for improving both exploitation and exploration operators. However, in Lines 4–17, if $r$ is greater than ${r}_{1}$, the flip and swap operators are executed with a predefined maximum trial on the best-so-far solution as an attempt to improve the convergence speed in the right direction of the near-optimal solution.

Algorithm 3

A novel local search operator

Finally, this operator is effectively integrated with the classical EO to propose a new variant with better exploration and exploitation operator for finding the near-optimal solutions of the binary optimization problems in binary space. The pseudo-code, which describes our proposed algorithm, is listed in Algorithm 4 and figured in Fig. 5.

Algorithm 4

BHEO

Fig. 5

The steps of the proposed algorithm: BHEO

$${\text{MP}}=\alpha \times \left(\frac{T-t}{T}\right)$$

(18)

6 Experimental Findings for Binary Applications

This section is proposed to investigate the effectiveness of the proposed algorithm against several optimization algorithms when solving three binary problems, namely feature selection (FS), the KP01, and cryptanalysis in the Merkle–Hellman cryptosystem. All algorithms are implemented using the MATLAB R2019a with the same population size and maximum function evaluations of 40 and 100, respectively, to ensure a fair comparison. All experiments are herein conducted using a device with the following characteristics: 32 GB of RAM, Core i7 2.40 GHZ Intel CPU, and installed Windows 10.

6.1 Application I: Feature Selection

This section investigates the efficacy of BHEO for tackling the feature selection problem compared to two different categories of the algorithms: the first category includes three recently-published swarm-based algorithms, like the binary African vulture optimization algorithm (BAVOA) [92], the binary gravitational search algorithm (BGSA) [93], and the binary slime mould algorithm (BSMA) [42]; and the second category includes three well-established algorithms, like the genetic algorithm under tournament selection (GAT) [94], the genetic algorithm under roulette wheel selection (GA) [94], and binary simulated annealing (BSA) [95]. The controlling parameters of these algorithms are set as recommended in the cited papers; these recommendations are shown in Table 3 for each rival algorithm. Regarding GAT and GA, the crossover rate (CR) and mutation rate (MR) were set to 0.8 and 0.02, respectively, as recently recommended in [96]. Twenty-seven datasets taken from the UCI repository and described in Table 4 in terms of the number of features (N.o.F), number of classes (N.o.C), and number of samples (N.o.S) are employed in our experiments. Those datasets are used to assess the efficacy of those algorithms in terms of three performance metrics: the classification accuracy, the length of the selected feature, and the fitness value. The outcomes of those algorithms are analyzed using various statistical analyses like the best, average, worst, and standard deviation (SD) values.

Table 3 The parameters values of compared algorithms in FS

Table 4 List of the used datasets in our experiments

6.1.1 Parameter Settings

The proposed algorithm: BHEO has four controlling parameters, which need to be accurately picked to maximize its performance; those parameters are maxTrial, α, ${a}_{1}, {\text{and}} {a}_{2}$. To estimate them, extensive experiments are performed under various values for each parameter, and their outcomes within 25 independent times are averaged and shown in Fig. 6. From this figure, it is concluded that the best values for those parameters: maxTrial, α, ${a}_{1}, {\text{and}} {a}_{2}$ are of 5, 0.01, 6, and 5, respectively. Regarding the parameters K-neighbors, α₁, and $\beta$, they are set as in [64].

Fig. 6

Tuning the parameters of the proposed algorithm

6.1.2 Comparison Using Fitness Values

All algorithms are compared based on their fitness values obtained within 25 independent runs on each dataset. Those fitness values have been analyzed in terms of the best, average, worst, and SD values, as introduced in Tables 5 and 6. From observing those tables, it is clear that BHEO could be better in 20 out of 26 instances, as shown in the bold values introduced in those tables. To affirm that BHEO is better, the average of the fitness values has been calculated and exposed in Fig. 7, which shows that the proposed algorithm is the best with a value of 0.09, followed by GAT and GA, which could achieve a value of 0.10, while BSMA comes in last place with a value of 0.14.

Table 5 Statistical analysis of the fitness values obtained by different algorithms on datasets ID#1-ID#13

Table 6 Statistical analysis of the fitness values obtained by different algorithms on datasets ID#14-ID#27

Fig. 7

Comparison in term of average fitness values on all datasets

In addition, to show the stability of BHEO within the independent runs on all instances, Fig. 8 is presented to display the average of the SD obtained by each algorithm on all instances. From this figure, BHEO could rank first with a value of 0.022, while SA is a less stable one with a value of 0.035. From this analysis, it could be concluded that our proposed algorithm could overcome the rival algorithms in terms of fitness value and stability due to the local search operator, which could improve its exploration and exploitation capabilities.

Fig. 8

Comparison using average SD of fitness values on all datasets

6.1.3 Comparison Using Classification Accuracy

The analysis of the classification accuracy values obtained by each algorithm within 25 independent runs on each instance is shown in Tables 7 and 8. Inspecting those tables reveals that our proposed algorithm could be superior to rival algorithms for 20 instances, demonstrating the proposed algorithm’s ability to reach the subset of features that could maximize classification accuracy. In addition, to graphically show the superiority of our proposed algorithms in comparison to the others, the average classification accuracy values introduced in those two tables are shown in Fig. 9, which affirms its superiority with a value of 0.91 and occupies the first rank, while BSMA is the worst one.

Table 7 Statistical analysis of the classification accuracy values obtained by different algorithms on datasets ID#1–ID#13

Table 8 Statistical analysis of the classification accuracy values obtained by different algorithms on datasets ID#14–ID#27

Fig. 9

Comparison using average classification accuracy on all datasets

Moreover, Fig. 10 presents the average of the SD values presented in the same tables, which indicates that BHEO is a more stable while SA is less stable. From the previous analysis, BHEO could be the best in terms of the fitness values, which are comprised of the classification accuracy and the length of the selected features, and it could be the best in terms of the classification accuracy, which is the most important objective of machine learning techniques. However, the length of features is also important to help in minimizing the computational cost consumed during the learning and testing processes. Therefore, in the next section, the algorithms will be compared in terms of the length of the selected features.

Fig. 10

Comparison using average SD of classification accuracy on all datasets

6.1.4 Comparison Using the Selected Feature-Length

The best, worst, and average values of the feature lengths selected by each algorithm on each dataset are shown in Tables 9 and 10, which show that BEO is the best algorithm for minimizing the length of the selected features with higher classification accuracy. To show which algorithm has the lowest number of the selected features on all instances, Figs. 11 and 12 are presented to show the average of the selected features and their SD. From those figures, it is observed that BHEO could come in second place after BEO with a value of 10.09 for the selected feature length and come in fourth place after BEO, GAT, and GA in terms of the average SD.

Table 9 Statistical analysis of the selected feature-length obtained by different algorithms on datasets ID#1–ID#13

Table 10 Statistical analysis of the selected feature-length obtained by different algorithms on datasets ID#14–ID#27

Fig. 11

Comparison using the average of selected features on all datasets

Fig. 12

Comparison using the average selected features on all datasets

Despite the superiority of BEO for the length of the selected feature, our proposed algorithm is still the best one since it could outperform BEO in terms of classification accuracy, which is the most important to machine learning. Based on that, BHEO is a strong alternative to the existing feature selection techniques for finding the subset of features that could maximize the classification accuracy with a small number of features.

6.1.5 Comparison Using CPU Time

The average CPU time consumed by each algorithm on all instances is computed and presented in Fig. 13. The SA algorithm, as shown in this figure, has consumed less CPU time, while our proposed algorithm comes in second place with a value of 2.11. From this, it is concluded that BHEO consumes less CPU time compared to the classical EO, GAT, and GA, which are considered the most competitive algorithm for BHEO in terms of the classification accuracy and the length of selected features. Based on that, the proposed algorithm is a promising feature selection technique since it could overcome all the competitive algorithms for CPU time and classification accuracy and could occupy the second rank in terms of the length of selected features.

Fig. 13

Comparison among algorithms in terms of CPU time

6.1.6 Comparison Using Convergence Curve

Moreover, this section compares various algorithms using the convergence curves, which measure the superiority of each algorithm for reaching a better fitness value faster than the others. Each algorithm has been run 25 times independently, and the average of the convergence values within those runs has been calculated and presented in Fig. 14. This figure includes the convergence curve for 12 instances, which shows that BHEO is faster than the others for those instances except for ID3 and ID18. The BEO is a little superior to the proposed algorithm for ID3. In the beginning, both GA and BAVOA appear to have a faster convergence pattern for solving ID18, but in the end, the three algorithms—proposed, GA, and BAVOA—could reach the same average fitness value. Based on the analysis done here and before, the proposed algorithm is the best in terms of CPU time, convergence curve, and final accuracy.

Fig. 14

Comparison among algorithms in terms of convergence speed in some FS instances

6.1.7 Extensive Experiments Using Boxplot Between BEO and BHEO

Figure 15 extensively compares the proposed BHEO and the classical EO using the boxplot to show the effectiveness of the local search operator to improve the performance of BHEO and achieve better outcomes. The boxplot depicts a five-number summary for comparing the performance of various algorithms. This summary includes the minimum, maximum, third quartile, first quartile, and median of the outcomes obtained by each algorithm. From this figure, it is obvious that the proposed algorithm could outperform the others for most of those numbers in all investigated instances.

Fig. 15

Comparison among algorithms in terms of convergence speed in some instances

6.2 Application II: 0–1 Knapsack Problems

This section investigates the effectiveness of BHEO in tackling another binary optimization problem, namely the 0–1 Knapsack problem, to check its ability to tackle various discrete problems. To check its effectiveness, it is compared to two different categories of algorithms: the first category includes some recently-published binary algorithms, such as BEO, the binary marine predators algorithm (BMPA) [19], binary manta ray foraging optimization (BMRFO) [97], and the binary grey wolf optimizer (BGWO) [98]; and the second category includes the binary differential evolution under tangent transfer function (DE), and GAT. The comparison between those algorithms is conducted under various statistical metrics: best, average, worst, SD, and p-value returned by the Wilcoxon rank-sum test [99]. The parameter values of those algorithms used in our experiments conducted to solve KP01 are stated in Table 11. The effectiveness of BHEO over the other rival optimizers is evaluated using 50 instances for KP01, with item sizes ranging from 4 to 2000, due to its wide application in the literature [107–110]. Name of instance (IN), number of items (D), optimal solution (Opt), and Knapsack capacity (capacity) are the four criteria used to describe these instances in Table 12.

Table 11 The parameters values of compared algorithms in KP01

Table 12 Properties of the investigated KP01 instances

6.2.1 Parameter Settings

The proposed algorithm: BHEO has some controlling parameters that need to be optimized to maximize its performance when tackling a different optimization problem; those parameters are maxTrial, ${a}_{1}, {\text{and}} {a}_{2}$. Therefore, extensive experiments are conducted under various values for each parameter, and their outcomes are shown in Fig. 16. From this figure, it is concluded that the best values for those parameters: maxTrial, ${a}_{1}, {\text{and}} {a}_{2}$ are of 1, 1, and 3. Regarding the other parameters of the proposed algorithm, they are set as before.

Fig. 16

Tuning the parameters of BHEO for KP01

6.2.2 Comparison Among BHEO and Some Standard Metaheuristics Using Small-, and Medium-Scale Datasets

This section contains a detailed presentation of the experiments we ran to evaluate BHEO's performance when solving the small- and medium-scale KP01 instances. Tables 13, 14, 15 present the best, average, worst, and SD results from 25 independent runs of each method on these instances. The best, average, worst, and SD values for the proposed algorithm compared to some rival optimizers in this table are all competitive for small-scale instances. On the other hand, for the medium-scale instances solved in Table 12, BHEO has significantly superior performance for various performance metrics. In addition, to check the difference between the outcomes of BHEO and those of the other algorithms, the Wilcoxon rank sum test has been employed to compute the p value between the outcomes of BHEO and those of each algorithm. The results of this test are reported in Tables 13, 14, 15. Inspecting these tables reveals competitiveness for small-scale instances and BHEO’s superiority for medium-scale instances. In addition, the convergence curve is used to evaluate the efficacy of different methods in reaching the fittest fitness value faster. Therefore, the average convergence values during 25 separate runs of each algorithm are shown in Fig. 17. Inspecting this figure shows that the proposed could reach the highest fitness value faster than all the rival optimizers for all the depicted KP01 instances. For small- and medium-scale instances, the proposed approach has been found to be the most effective with regards to the convergence curve, and final accuracy.

Table 13 Performance evaluation using the small-scale instances (KP1 and KP10)

Table 14 Performance evaluation using the medium-scale instances (KP11 and KP20)

Table 15 Performance evaluation using the small-scale instances (KP16a and KP20e)

Fig. 17

Comparison among algorithms in terms of convergence speed for some KP01 instances

6.2.3 Comparison Using Large-Scale Datasets

This section is presented to check the superiority of the proposed algorithm for large-scale instances with various correlations between the profits and weights. Two well-performing algorithms, as well as the classical EO, are employed to check the BHEO’s effectiveness for these instances. These two algorithms, BMRFO and DE, are herein selected due to their strong performance for small- and medium-scale instances, as shown before. All algorithms are executed 25 times on these instances, and the average fitness value and the p value returned from the Wilcoxon rank-sum test are computed and reported in Fig. 18 and Table 16, respectively. According to this data, BHEO is significantly better and statistically different compared to all the rival optimizers.

Fig. 18

Comparison among algorithms for large-scale KP01 instances

Table 16 Comparison using the Wilcoxon rank-sum test on the large-scale KP01 instances

6.2.4 Comparison Among BHEO and Some Hybrid Metaheuristics Using Small-, and Medium-Scale Datasets

This section compares BHEO to five recently improved metaheuristic algorithms to further show its effectiveness when tackling the Knapsack problems. Those improved algorithms are summarized as follows:

• Binary hybrid equilibrium optimizer (BRIEO) [100]: In this study, the proposed BEO was integrated with the repair and improvement operators to repair and improve the infeasible solutions. This algorithm could achieve outstanding outcomes in comparison to several optimization techniques.

• Binary hybrid marine predators algorithm (BRIMPA) [19]: In this study, the repair and improvement operators were also used with the proposed BMPA to repair and improve the infeasible solutions. This algorithm could achieve outstanding outcomes in comparison to several optimization techniques.

• Binary modified whale optimization algorithm (BWOA) [101]: In this paper, the classical WOA was first improved by the levy flight to improve its exploitation operator. Then, it was hybridized with the repair and improvement strategy to further improve its performance for achieving better outcomes for multidimensional Knapsack problems.

• Binary improved sine cosine algorithm (BISCA) [102]: In this algorithm, the standard sine–cosine algorithm was modified and integrated with the differential evolution to improve its exploration and exploitation operators.

• Binary improved differential evolution (BIDE) [102]: In this variant, the scaling factors of the DE/current-to-rand/1 mutation rule were defined based on the objective values to improve the search ability of the presented algorithm.

Tables 17 and 18 present the best, average, worst, and SD that result from analyzing 25 independent fitness values obtained by the proposed HBEO and each hybrid method on these instances. The results of HBEO and the hybrid algorithms are competitive for small-scale instances, as shown in Table 17. Meanwhile, for the medium-scale instances, BHEO could achieve superior outcomes for the majority of those instances, as shown in Table 18.

Table 17 Comparison between BHEO and hybrid algorithms using the small-scale instances (KP1 and KP10)

Table 18 Comparison between BHEO and hybrid algorithms using the medium-scale instances (KP11 and KP20)

6.3 Application III: Merkle–Hellman Knapsack Cryptosystem (MHKC)

In this part, we examine the effectiveness of the proposed algorithm over six binary optimization methods at cracking the MHKC with a knapsack size of eight bits. To make a fair comparison, those algorithms are run 30 times independently using the same environment settings discussed before: a population size of 30 and a maximum number of iterations of 1000. Regarding the parameters of the rival algorithms, they are set as stated before. The parameters of the proposed algorithm are also set as recommended before, except for the parameter maxTrial, which needs to be estimated to maximize its performance for this problem (Fig. 19). To determine the optimal value for this parameter, a number of tests have been conducted using different values, and the results are shown in Fig. 7. According to this figure, the optimal value for this parameter is 3.

Fig. 19

Tuning of the parameter: maxTrial

6.3.1 Test Case 1: CAT Message

In this section, we compare and contrast the proposed BHEO against the rival algorithms to see which one can decipher all of the characters in the commonly used “CAT” message. This message has been encrypted and decrypted by the MHKC using the following:

$$A^{\prime} = \left\{ {2, 3, 7, 15, 29, 65, 125, 251} \right\}$$

$$q=507, r=10, {r}^{-1}=355$$

$$A=\left\{20, 30, 70, 150, \mathrm{290,143}, \mathrm{236,482}\right\}$$

Once this message has been encrypted using the preceding information, it will be transmitted to the intended recipient as the ciphertext described in Table 19. The average fitness value, average SD, and convergence speed for all characters were calculated and reported in Fig. 20 after 30 separate runs of each algorithm on the 8-bit ASCII code. From this figure, it is clear that the proposed algorithm delivers significantly higher performance for this message than any of the other methods tested. As a result, BHEO is a viable alternative to the current methods for attacking the MHKC to discover its vulnerability.

Table 19 Encryption of “Cat”

Fig. 20

Comparison on “CAT” under 8-bit ASCII code

6.3.2 Test Case 2: MACRO Message Under 8-bit

Furthermore, the proposed algorithm is further assessed using the “MACRO” message, which was widely used in the literature to evaluate the newly proposed techniques. This message is encrypted and decrypted by the MHKC using the following parameters [50]:

$$A^{\prime} = \left\{ {1,{ }3,{ }7,{ }13,{ }26,{ }65,{ }119,{ }267} \right\}$$

$$q=65423, r=21031, {r}^{-1}=5363$$

$$A=\left\{21031, 63093, 16371, 11711, 23422, 58555, 16615, 54322\right\}$$

Once this message has been encrypted using the above information, the ciphertext for each character, as indicated in Tale 20, will be delivered to the intended recipient for protection. Even if the ciphertext were intercepted, the original message would be unintelligible due to the encryption. Extensive experiments for six metaheuristic algorithms, in addition to the proposed algorithm, were done to check if anyone could guess the plaintext from the ciphertext, revealing the MHKC systems’ vulnerability in protecting this message. Figure 21 summarizes our experimental results and shows that BHEO is superior to the others in terms of average fitness value, convergence curve, and average SD.

Table 20 Encryption of “MACRO”

Fig. 21

Comparison on “MACRO” under 8-bit ASCII code

The message: “MACRO” was encrypted and decrypted in other works using alternative values for A, q, and r, as defined below:

$$A^{\prime} = \left\{ {4,{ }5,{ }13;{ }23,{ }48,{ }96,{ }193,{ }384} \right\}$$

$$q=776, r=13, {r}^{-1}=597$$

$$A=\left\{52, 65, 169, 299, 624, 472, 181, 336\right\}$$

This message will be encrypted using the above information and then transmitted to the recipient as the ciphertext for each character as indicated in Table 21. Performance metrics were calculated and reported in Fig. 22 after each method was run 30 times on each character encrypted using the preceding data, demonstrating that BHEO is superior to the others.

Table 21 Encryption of “MACRO” using MHKC

Fig. 22

Comparison on “MACRO” under 8-bit ASCII code

7 Conclusion and Future Work

This paper presents a new binary metaheuristic algorithm, namely BHEO, for solving binary optimization problems. In BHEO, the EO is integrated with a new local search operator to improve its exploration and exploitation capabilities. This local search operator is based on two folds. The first fold borrows the single-point and uniform crossover in addition to the mutation strategy to accelerate the convergence speed and avoid getting stuck in local minima. The second fold is based on employing the flip mutation operator and the swapping operator to improve the quality of the best-so-far solution. This hybrid algorithm is assessed using three binary optimization problems: 0–1 knapsack, feature selection, and MHKC datasets and compared with the classical one and six well-established optimization algorithms like GAT, BGSA, BSMA, SA, GA, and BAVOA. From the experimental findings, the proposed algorithm: BHEO, could be superior in terms of the final accuracy and convergence curve for most instances. The primary limitation of our proposed BHEO is that it requires the accurate selection of four controlling parameters prior to beginning the optimization process to maximize its performance. This restriction will be considered in the future to make our proposed algorithm self-adaptive for addressing a variety of optimization problems. Our future work involves using Pareto optimality to solve the feature selection problem for optimizing simultaneously both classification accuracy and the length of selected features.