Supplier Selection Method for Complex Product Based on Grey Group Clustering and Improved Criteria Importance

Abstract

Supplier selection is of great significance and role, which influence the quality of major product development, and economic security and life safety. However, there exists a variety of uncertain information as a result of evaluation experts’ strong subjective consciousness and complexity of decision environment in the process of supplier selection evaluation. To deal with these problems, by exploiting gray incidence analysis, cloud models and TOPSIS, we establish a multi-attribute decision-making supplier selection method for complex product based on gray group clustering and improved criteria importance through intercriteria correlation, and then a case verifies the validity and feasibility of the proposed method. The results show that (1) the proposed model can provide a better portrayal of the uncertainty of the evaluation process in terms of both the fuzziness of the semantic concept and the randomness of the affiliation degree, while taking into account the differences between the evaluated solution and the positive and negative ideal solutions. (2) The proposed model can fully voice the decision-maker’s attitude on the basis of available information, allowing the decision-making process to be better tailored to reality by taking into account the ambiguity and randomness of the evaluation process.

1 Introduction

Complex product mainly refers to the major scientific and technological product that plays an important role in supporting human scientific exploration and social and economic development. In particular, the product has an important impact on national economic security and national defense construction, plays an important supporting role in promoting the sustainable development of the national economy, and plays a positive role in economic restructuring, industrial upgrading, energy conservation and emission reduction. For example, the scientific and technological product involved in the national major scientific projects, science and technology special projects and the national major technical product independent innovation guidance catalogue. The development of major product can greatly promote the improvement of a country’s scientific and technological competitiveness and comprehensive national strength, and provide a strong guarantee for national security. In the context of the development of economic globalization, the collaborative development and production of multiple enterprises have become the current mainstream, especially in complex product field. Since the production of complex products has the characteristics of many disciplines, high technical content, long period and high investment cost [16], complex product manufacturing enterprises need more refined arrangements when cooperating with other enterprises to ensure efficient operation in the tedious production process. Then, the problems of supplier selection for complex products obviously have become an important issue for the manufacturing enterprises to produce some complex products. However, there exists a variety of uncertain information in the current complex and changeable market competition environment, and then some supplier evaluation and selection methods cannot make these decisions [28]. To reduce the distortion of results caused by subjective factors in the evaluation process and obtain a more realistic decision result, we propose a multi-attribute decision method based on gray group clustering (GGC) and improved criteria importance through intercriteria correlation (ICRITIC) targeting complex products with high demand uncertainty, response timeliness and quality requirements.

The rest of this paper is arranged as follows. Section 2 summarizes and reviews the relevant literature. Section 3 briefly introduces related works and the base model of cloud model theory. Section 4 builds an evaluation index system based on existing research and information while constructing a cloud-TOPSIS model based on a combination of GGC and ICRITIC. Section 5 uses a case to analyze the soundness of the model developed in the previous section. To conclude the paper, Sect. 6 looks at the limitations of this study and points to potential future works.

2 Literature Review

Supplier selection is critical since it influences the quality of major product development, as well as economic security and life safety. To address these supplier selection issues, many researchers focus on the aspects of the identification of influencing factors, design of the evaluation index system and the construction of the supplier selection methods.

2.1 Influence Factor Identification and Evaluation Index System

Accurately identifying influencing factors, reasonably dividing the categories of influencing factors, and establishing an effective evaluation system can effectively control and reduce the uncertainty in the evaluation process. By reviewing the relevant literature, we found that, although there are many elements that affect the supplier selection index system, and the effect factors differ depending on the environment, they mainly focus on quality risks, efficiency issues or cost issues.

With respect to the index systems, Dickson [8] identified 23 criteria influencing supplier selection using a survey sample and also concluded that quality, delivery, and historical efficiency were the three most important indexes after screening and validating them. Weber et al. [44], based on Dickson’s study, found that transport issues and on-time delivery also required significant attention when evaluating supplier selection, also he mentioned that transport and on-time delivery indexes should be included in the index. Since then, a large number of scholars had conducted extensive and in-depth research on the issue of supplier selection criteria. For example, Chang et al. [6] established supplier evaluation indexes from the whole product life cycle, including R&D, Cost, Quality, Service and Response. Fu et al. (2018) argued that in a globally competitive economy, strategic partnerships to manage supply chains could enhance competitive advantage, therefore, the literature constructed five indexes around “strategic collaboration”, including Cost, Product quality, Agility ability and among others. In the context of the current global epidemic, Sharma et al. [36] identified demand, financial, logistics and infrastructure, management and operational, policy and regulation, and biological and environmental as important concerns for the evaluation criteria through an analytical study. However, with the growth of economic globalization, early evaluation index systems were unable to meet the complex and changing environment. Some scholars have undertaken studies to develop appropriate index systems for the specificity of complex products. For example, based on the current multi-criteria index method for military supplier assessment, Li et al. (2012) coupled a complete military supplier supply performance evaluation mechanism with a whole life cycle perspective. Zhang et al. [47, 48] developed an evaluation criterion system for the selection and evaluation of product suppliers to meet the characteristics of high uncertainty in demand for military products, timeliness of response, and high-quality requirements. He et al. [15] constructed a supplier access evaluation criterion system for the product procurement supply chain from four aspects: quality, technology, service, and delivery capability. But above studies are not in the existing index system on certain optimization and selection, most of them are directly follow the existing index system or through the questionnaire, literature collation and other methods to establish their own needs of the index system.

2.2 Supplier Selection Methods

Nowadays, common supplier selection methods include hierarchical analysis [24], network analysis [17], approximating ideal points [42], VIKOR method [40], and multi-attribute utility theory [34].

As the research progressed, scholars generally agreed that uncertainty in the conversion of qualitative and quantitative information in the assessment process must be a significant component influencing the validity and accuracy of the decision outcomes [32]. Therefore, some scholars try to combine fuzzy concepts with multi-attribute decision-making methods to solve problems. Ye [46] proposed a multi-attribute group decision-making method that combined completely unknown decision-maker weights and imperfectly known attribute weights in the intuitionistic fuzzy setting and interval value intuitionistic fuzzy setting to better solve the corresponding multi-attribute group decision-making problem with unknown weights. Lin [25] used fuzzy logic reasoning to build a supplier evaluation model, and they were also trying to control costs and improve evaluation efficiency in the process of model building. Sen et al. [35] attempted to use intuitionistic fuzzy numbers set to establish a decision support system for supplier selection considering economic, environmental and social sustainability issues. While in order to minimize the bias in the decision-making process and avoid bias, Büyüközkan et al. [4] adopted the group decision-making (GDM) method, and established the intuitionistic fuzzy axiom design (IFAD) principle to establish the intuitionistic fuzzy analytic hierarchy process (IFAHP), which is used for determining the weighting of supplier evaluation criteria. Erdebilli et al. [10] proposed a fusion of the Pythagorean fuzzy analytic hierarchy process and the COPRAS mixed method. The study showed that small changes in standard weights could have a significant impact on decision-making.

However, Zhang et al. [47, 48] argued that fuzzy sets had inherent inadequacies in handling evaluative information, which would exacerbate decision-making bias. As a result, he suggested that employing hesitant fuzzy numbers to process decision-makers’ supplier assessment values was a smart option. At the same time, he employed the revised TODIM approach to assess decision-makers’ psychological preferences and rated each potential supplier, which could effectively express decision-makers’ different opinions and hesitation. Abdullah et al. [1] analyzed the internal cause and effect of the inadequacy of the intuitive fuzzy decision-making method, and believed that the “experience” criterion was the main reason for the subcontractor selection. Huang et al. [18] also realized the advantages of hesitation fuzzy numbers. It could make up for the inherent flaws from the FMEA model, like ambiguity and indecision of personal judgment and rough numbers in manipulating imprecision and subjectivity. With the development of machine learning, scholars have tried to find and uncover the semantics hidden in the depths of decision-making information. For example, matrix factorization technique provides advantages in information retrieval. Cai et al. [5] proposed Graph Regularized Nonnegative Matrix Factorization (GNMF), which could reveal the concealed semantics while also respecting the inherent geometric structure. Deng et al. [7] enhanced the GNMF algorithm by adding a $l_{1}$-norm to the low-dimensional matrix to allow for the modification of data feature values and sparsity requirements in the matrix, which increased data analysis performance. Wang et al. [37,38,39] improved non-negative matrix factorization (NMF) to better define data objects and increase clustering performance, which solved the original algorithm’s shortcomings of weak feature extraction, sluggish convergence speed, and low accuracy. Furthermore, complimentary information between views can better describe data items. Wang et al. [37,38,39] first built generalized deep learning (GDL) and then used it to learn the low-dimensional matrix and consensus moment corresponding to each view in order to increase the algorithm’s feature extraction ability, convergence speed, and accuracy. At the same time, Wang et al. [37,38,39] proposed an MCDS algorithm with higher interpretability and rapid convergence to address the problem that some techniques lacked backpropagation. The algorithm showed good clustering ability and flexible optimization of schemes.

On the other hand, scholars have begun to pay more and more attention to the quality and efficiency of the decision-making process. For example, Keskin [22] proposed an integrated model combining fuzzy theory with DEMATEL, because he believed that fuzzy theory could make up for the flaws in DEMATEL method which beneficially improved the quality of supplier selection and evaluation. Similarly, Paunović et al. [31] chose to combine fuzzy theory with the AHP method, and in order to further make the evaluation process objective and accurate, they proposed to build the model into a two-stage evaluation model from a technical point of view, which facilitates a more refined evaluation. Nevertheless, these studies only reflected the uncertainty of qualitative concepts from the perspective of fuzziness and fail to take into account the stochastic nature of affiliation. In view of this, the concept of cloud model has been proposed not only to better portray the uncertainty of concepts in natural language, but also to unify the either-or nature of fuzziness and the randomness of affiliation [41]. Most of the previous use of cloud model theory to optimize solutions had been achieved by direct comparison of three numerical features of the cloud model [9, 45]. However, the simplistic use of numerical features to measure the superiority and inferiority among cloud models had ignored the essential characteristics of cloud model ambiguity and randomness. Therefore, some scholars had proposed to evolve the three numerical features of the cloud model separately and use the relative closeness to reveal the intrinsic connection and superiority relationship of scheme decisions [14]. Gong and Yu [13] considered that decision-makers had reference-dependent and loss-averse behaviors, proposing an improved interactive multi-attribute decision solution evaluation method based on a cloud model. Liu et al. [27] combined gray correlation with cloud model theory to address the data quality problem in cluster evaluation to propose a cluster evaluation data quality improvement method, but the influence of expert weights on decision results was ignored in the research process. Wang et al. [43] developed an integrated MCDM model based on a cloud model and the QUALIFLEX method for assessing the green performance of firms under economic and environmental criteria. Liu et al. [29] combined regret theory with the QUALIFLEX method to evaluate suppliers in a two-dimensional uncertain language variable (2-DULV) environment. But they all ignored the stochastic nature of the evaluation language and the risk attitudes of decision-makers.

According to the above discussion and analysis, the existing literature primarily focuses on the establishment of a large and complex index system, but this ignores the fact that too many standard systems will increase the spatial dimensions and amount in the calculation process, while also complicating the data analysis process. As a result, optimizing the index system promotes the objectivity of decision-making outcomes. Simultaneously, most literature fails to adequately consider the randomness and ambiguity of decision-making in the decision-making process, which raises the uncertainty and incompleteness of evaluation results. Given this, and taking into account the inherent uncertainty of the evaluation criteria and the randomness of the decision-making process, as well as the characteristics of complex products, we establish a multi-attribute decision-making supplier selection method for complex products using gray incidence analysis to achieve the goal of simplifying the complexity index system.

3 Preliminaries

This subsection consists of three parts to review various preliminaries regarding cloud model theory, linguistic variables and conversion between linguistic terms and cloud model.

3.1 Cloud Model Theory

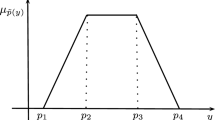
The cloud model can effectively reflect the fuzziness and randomness in human understanding or physical concepts through the expectation, entropy and super-entropy of clouds, and the fuzziness and randomness by constructing a mutual mapping relationship between qualitative and quantitative, which is shown in Fig. 1. Let $Ex,En,He$ denote the expectation, entropy, and super-entropy of the cloud, respectively.

Fig. 1

Normal cloud map

The cloud model consists of the forward generator and the inverse generator. The forward generator is the process of converting eigenvalues into cloud droplets, while the inverse generator is the process of implementing the model to convert cloud droplets into eigenvalues, which is calculated as shown below. We use python to implement the model in this paper:

$$Ex = \frac{1}{N}\sum\limits_{i = 1}^{N} {x_{i} }$$

(1)

$$En = \sqrt {\frac{\pi }{2}} \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {x_{i} - Ex} \right|}$$

(2)

$$He = \sqrt {\left| {\frac{1}{N - 1}\sum\limits_{i = 1}^{N} {\left( {x_{i} - Ex} \right)^{2} - En^{2} } } \right|}$$

(3)

Definition 1

Suppose $d(x_{i} ,x_{j} )$ represents the bias measure between $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{i} = (Ex_{i} ,En_{i} ,He_{i} )$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{j} = (Ex_{j} ,En_{j} ,He_{j} )$ in a given unified domain, where $i \ne j$. Therefore, the relevant calculation formulas are as follows.

$$d(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{i} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{j} ) = \theta_{1} d(Ex_{i} ,Ex_{j} ) + \theta_{2} d(En_{i} ,En_{j} ) + \theta_{3} d(He_{i} ,He_{j} )$$

(4)

$$d(Ex_{i} ,Ex_{j} ) = \frac{{\left| {Ex_{i} - Ex_{j} } \right|}}{{\max (Ex_{i} + 3En_{i} ,Ex_{j} + 3En_{j} ) - \min (Ex_{i} - 3En_{i} ,Ex_{j} - 3En_{j} )}}$$

(5)

$$d(En_{i} ,En_{j} ) = 1 - \frac{{\min (En_{i} ,En_{j} )}}{{\max (En_{i} ,En_{j} )}}$$

(6)

$$d(He_{i} ,He_{j} ) = 1 - \frac{{\min (He_{i} ,He_{j} )}}{{\max (He_{i} ,He_{j} )}}$$

(7)

where $\theta_{i} ,(i = 1,2,3)$ denotes the coefficients of cloud deviation in dimensions $Ex$, $En$ and $He$, respectively, and the magnitude of the coefficients represents the contribution of the corresponding dimension to the overall cloud deviation, while $\theta_{1} + \theta_{2} + \theta_{3} = 1,1 \ge \theta_{1} \ge \theta_{2} \ge \theta_{3} \ge 0$.

Definition 2

Suppose there is a synthetic cloud $a\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{i} + b\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{j}$,$i \ne j$, which represents the process of superimposing two cloud models to obtain a composite cloud model. According to the algorithm of the independent normal distribution, we get the formula shown as follows:

$$a\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{i} + b\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{j} = (aEx_{i} + bEx_{j} ,\sqrt {(aEn_{i} )^{2} + (bEn_{j} )^{2} } ,\sqrt {(aHe_{i} )^{2} + (bHe_{j} )^{2} } )$$

(8)

3.2 Linguistic Variables

The linguistic variables are used in situations that are too complex or not well defined to be reasonably represented by quantitative expressions. Suppose $L = \left\{ {l_{{n^{ - } }} , \ldots ,l_{{1^{ - } }} ,l_{0} ,l_{{1^{ + } }} \ldots l_{{n^{ + } }} } \right\}$ denotes the set of linguistic terms, where $n$ is an even integer and $l_{i}$ denotes the possible values of a linguistic variable. The linguistic term set has the characteristic: if $i > j$, we have $l_{i} > l_{j}$.

3.3 Conversion Between Linguistic Variables and Cloud Model

Assume that $Y = \left[ {y_{\min } ,y_{\max } } \right]$ represents the valid domain. Considering the accuracy of semantic information representation and the convenience of division, we adopt the golden partition method to quantify and divide the semantic information. For example, we divide the semantic information into 5 levels in this paper as follows:

$L = \left\{ {\begin{array}{*{20}l} {l_{{2^{ - } }} = Low(L)} \\ {l_{{1^{ - } }} = Relatively \, Low(RL)} \\ {l_{0} = Normal(N)} \\ {l_{{1^{ + } }} = Relatively \, High(RH)} \\ {l_{{2^{ + } }} = High(H)} \\ \end{array} } \right\}$.

Meanwhile, formulas of the language conversion are shown as follows:

$$Ex_{0} = \frac{{y_{\min } + y_{\max } }}{2}$$

(9)

$$Ex_{{2^{ - } }} = y_{\min } ,Ex_{{2^{ + } }} = y_{\max }$$

(10)

$$Ex_{{1^{ - } }} = 0.618Ex_{0}$$

(11)

$$Ex_{{1^{ + } }} = 1.382Ex_{0}$$

(12)

$$En_{{1^{ - } }} = En_{{1^{ + } }} = \frac{{0.382(y_{\max } - y_{\min } )}}{6}$$

(13)

$$En_{0} = 0.618En_{{1^{ + } }}$$

(14)

$$En_{{2^{ - } }} = En_{{2^{ + } }} = \frac{{En_{{1^{ + } }} }}{0.618}$$

(15)

$$He_{{1^{ - } }} = He_{{1^{ + } }} = \frac{{He_{0} }}{0.618}$$

(16)

$$He_{{2^{ - } }} = He_{{2^{ + } }} = \frac{{He_{{1^{ + } }} }}{0.618}$$

(17)

Notably, the effective domain $Y = \left[ {y_{\min } ,y_{\max } } \right]$ should be designated in advance. Meanwhile,$He_{0}$ also need to be pre-specified.

4 A Novel Multi-attribute Method Based on Gray Group Clustering and Improved Criteria Importance

In view of the changeable production environment of complex products and the high requirements for suppliers, we build a supplier index system adapted to the characteristics of complex products and a decision-making model considering the risk awareness of decision-makers.

4.1 Problem Description and Definitions

The essence of multi-attribute decision-making is the process that decision-makers use the existing decision information to sort and select a group of alternatives in a certain way based on multiple conflicting and contradictory attributes. Meanwhile, decision-makers, alternative scheme, decision-making objectives, decision-making situations, and decision-making consequences are key elements in the decision-making process. Therefore, it is not difficult to find that the supplier selection problem is essentially a multi-attribute group decision-making problem. The quality of the supplier is the key factor to determine the competitiveness of the supply chain. Therefore, it is very important to select the most suitable supplier. The uncertainty of the competitive environment and the increasing complexity of the business environment make decision-makers need to consider more and more uncertain factors in the decision-making process, which makes it a typical multi-attribute decision-making problem.

According to the above discussion and analysis, definitions needed for the rest of this work are given as follows.

Assume that $U_{i} (i = 1,2, \ldots ,m)$, $D^{k} (k = 1,2, \ldots ,K)$,$A_{j} (j = 1,2, \ldots ,n)$ and $w_{j} (j = 1,2, \ldots ,n)$ signify the alternative scheme, the decision-maker, the different decision index and the weight of decision index in the decision-making environment, respectively. While suppose that $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij}^{k} = (Ex_{ij} ,En_{ij} ,He_{ij} )$ represents the evaluation cloud of scheme $U_{i}$ evaluated by expert $D^{k}$ based on the decision index $A_{j}$. Meanwhile, let $F_{i}$ denote the relative closeness of scheme $U_{i}$. Since the relative closeness $F_{i}$ reflects the closeness of the solution to the positive ideal cloud, a larger value of $F_{i}$ indicates a superior solution $U_{i}$.

4.2 Index System Construction

The existing supplier evaluation index system is numerous and complex, mainly focusing on the price issue, and rarely on the innovation ability and sustainable development ability of the supplier itself, which is not suitable for the characteristics of complex products such as long cycle and investment costs. Therefore, we propose a supplier evaluation index system for complex product manufacturing enterprises based on a careful study and analysis of scholars’ research on supplier evaluation indexes, in combination with the characteristics of complex product manufacturing enterprises and the two contemporary contexts of e-commerce and environmental protection.

The index system contains technological innovation capability $A_{1}$, financial capacity $A_{2}$, reliability of product quality $A_{3}$, supplier performance $A_{4}$, production and operation management level $A_{5}$. We use Visio software to draw a fishbone diagram to get the preliminary index system, as shown in Fig. 2.

Fig. 2

Fishbone diagram for initial index system

In Fig. 2, we specify that the initial index system consists of 5 primary indexes and 20 secondary indexes. Due to the large number of indexes and the low degree of discrimination of indexes in the primary selection, it is easy to cause problems such as increasing spatial dimensions, complicating data analysis process, and adding the amount of calculation. It increases the workload and difficulty indirectly, and also affects the objectivity of the selection decision. Therefore, we use gray incidence analysis to select the indexes based on the actual situation after the construction of the initial selection index system, so that we can establish an appropriate supplier preference index system. Since the quality and reliability of the products provided by suppliers in their daily production activities potentially affects the long-term interests of the manufacturing company, we prefer a system of indexes from the point of view of product reliability.

First, let $A_{0} = (a_{0} (1),a_{0} (2), \cdots ,a_{0} (n))$ denote the sequence of overall system characteristics and $\gamma (A_{0} ,A_{i} )$ imply the gray incidence between the overall system characteristics of product reliability and the various indexes:

$$\gamma (A_{0} ,A_{i} ) = \frac{1}{n}\sum\limits_{k = 1}^{n} {\gamma (a_{0} (k),a_{i} (k))}$$

(18)

In the meantime, $\gamma (A_{0} ,A_{i} )$ strictly satisfies the following conditions:

(1) $0 < \gamma (A_{0} ,A_{i} ) \le 1$;

(2) $\gamma (A_{0} ,A_{i} ) = 1$ when and only when $A_{0} = A_{i}$;

(3) the value of $\left| {a_{0} (k) - a_{i} (k)} \right|$ is inversely proportional to $\gamma (a_{0} (k),a_{i} (k))$.

Suppose that $Y^{\prime} = \left\{ {0.2,0.4,0.6,0.8,1.0} \right\}$ represents the score group. As the values increase, the points represent average, slightly important, less important, important and extremely important in that order, respectively. A decision-making group composed of six experts grades the five first-level indexes according to the score group. Therefore, the sequence of characteristics is shown as follows:

$$\begin{array}{*{20}c} {A_{0} } \\ {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ {A_{5} } \\ \end{array} \left[ {\begin{array}{*{20}r} \hfill {0.6} & \hfill {0.6} & \hfill {0.8} & \hfill {0.6} & \hfill {0.8} & \hfill {1.0} \\ \hfill {1.0} & \hfill {1.0} & \hfill {0.8} & \hfill {0.8} & \hfill {1.0} & \hfill {0.8} \\ \hfill {0.6} & \hfill {0.2} & \hfill {0.4} & \hfill {0.2} & \hfill {0.2} & \hfill {0.2} \\ \hfill {1.0} & \hfill {0.8} & \hfill {0.8} & \hfill {0.8} & \hfill {0.8} & \hfill {0.6} \\ \hfill {0.8} & \hfill {0.6} & \hfill {1.0} & \hfill {0.8} & \hfill {0.6} & \hfill {1.0} \\ \hfill {0.4} & \hfill {0.2} & \hfill {0.2} & \hfill {0.2} & \hfill {0.2} & \hfill {0.2} \\ \end{array} } \right]$$

Consequently, the gray incidence degree for each index are calculated as $\gamma_{1} = 0.7377$,$\gamma_{2} = 0.5389$,$\gamma_{3} = 0.6724$,$\gamma_{4} = 0.7941$,$\gamma_{5} = 0.5659$. Based on the golden partition method, the three first-level indexes with higher correlation degree are selected as the preferred indexes to carry out the study, namely technological innovation capability $A_{1}$, reliability of product quality $A_{3}$ and supplier performance $A_{4}$. Finally, the system of supplier preference indexes for complex products is shown in Fig. 3.

Fig. 3

Optimal index system of complexity product supplier selection

We mainly determine the weighting of the decision-makers in making the decision. Nowadays, there are many common methods for determining the weights, including Delphi technique [30], analytic hierarchy process [20], and data envelopment analysis [19].

However, a single weight determination method cannot meet the increasingly complex decision-making environment, so we use the combined weights to avoid the subjective factors of experts interfering with the weighting of decisions and to reduce data errors. We calculate the subjective weights using the gray group clustering method, adding the coefficient of variation of the improved CRITIC method to calculate the objective weights. Finally, we use the additive combination weighting method to combine the two to produce the combined weights.

In conclusion, the following consists of three parts, namely gray group clustering to determine subjective weight, the improved CRITIC to determine objective weight and the combined weighting.

First, let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}^{k}$ represent the expert judgment matrix decided by the decision-maker $D^{k}$, which is an $n$-order judgment matrix, and the element $\varepsilon_{ij}^{k}$ represents the relative importance of the element $\varepsilon_{i}^{k}$ to $\varepsilon_{j}^{k}$, which is determined by the Saaty scale type as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}^{k} = (\varepsilon_{ij}^{k} )_{n \times n} = \left[ {\begin{array}{*{20}c} {\varepsilon_{11}^{k} } & {\varepsilon_{12}^{k} } & \cdots & {\varepsilon_{1n}^{k} } \\ {\varepsilon_{21}^{k} } & {\varepsilon_{22}^{k} } & \cdots & {\varepsilon_{2n}^{k} } \\ \vdots & \vdots & \ddots & \vdots \\ {\varepsilon_{n1}^{k} } & {\varepsilon_{n2}^{k} } & \cdots & {\varepsilon_{nn}^{k} } \\ \end{array} } \right]$$

Since testing, the compatibility of the judgment matrix can ensure the judgment results made by the decision-maker are not influenced by their own level of knowledge and subjective preferences. Therefore, we let $CI$ and $CR$ represent the consistency index and the conquest consistency ratio, respectively:

$$CI = \frac{{\lambda_{\max } - n}}{n - 1}$$

(19)

$$CR = \frac{CI}{{RI}}$$

(20)

Among them, $\lambda_{\max }$ represents the largest characteristic root of the judgment matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}^{k}$.$RI$ shows the average random consistency index. After calculation, if $CR < 0.1$, we think the consistency of the judgment matrix is acceptable; otherwise, we consider that the judgment matrix is not consistent.

Then, let $B^{k} = \left( {b_{1}^{k} ,b_{2}^{k} ,...,b_{n}^{k} } \right)^{T}$ denote a sorted vector. By normalizing the decision-making expert judgment matrix after the consistency check, we get the ranking vector of the decision-making scheme:

$$\varpi_{i}^{k} = (\mathop \Pi \limits_{j = 1}^{n} \varepsilon_{ij}^{k} )^{\frac{1}{n}}$$

(21)

$$b_{i}^{k} = \frac{{\varpi_{i}^{k} }}{{\sum\nolimits_{i = 1}^{n} {\varpi_{i}^{k} } }}$$

(22)

The decision-making expert group-sorting matrix is constructed by the sorting vector obtained after the normalization of the judgment matrix. So, let $B$ represent the decision-making expert group-sorting matrix:

$$B = \left[ {B^{1} ,B^{2} ,...,B^{k} } \right] = \left[ {\begin{array}{*{20}c} {b_{1}^{1} } & {b_{1}^{2} } & \cdots & {b_{1}^{k} } \\ {b_{2}^{1} } & {b_{2}^{2} } & \cdots & {b_{2}^{k} } \\ \vdots & \vdots & \ddots & \vdots \\ {b_{n}^{1} } & {b_{n}^{2} } & \cdots & {b_{n}^{k} } \\ \end{array} } \right]$$

Meanwhile, assume that $\upsilon_{ij}$ represents the gray incidence degree, which is used to measure the similarity between the ranking vector $B^{i}$ and the ranking vector $B^{j}$ composed of the decision results given by the decision expert $D^{i}$ and the decision expert $D^{j}$:

$$\upsilon^{ij} = \frac{{1 + \left| {\sigma^{i} } \right| + \left| {\sigma^{j} } \right|}}{{1 + \left| {\sigma^{i} } \right| + \left| {\sigma^{j} } \right| + \left| {\sigma^{i} - \sigma^{j} } \right|}}$$

(23)

$$\left| {\sigma^{i} } \right| = \left| {\sum\limits_{l = 2}^{n - 1} {b_{l}^{i} + \frac{1}{2}b_{n}^{i} } } \right|$$

(24)

$$\left| {\sigma^{i} - \sigma {}^{j}} \right| = \left| {\sum\limits_{l = 2}^{n - 1} {(b_{l}^{i} - b_{l}^{j} ) + \frac{1}{2}(b_{n}^{i} - b_{n}^{j} )} } \right|$$

(25)

Next, let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V}$ represents the gray incidence matrix of the decision-making expert group. According to the above calculation formulas, the obtained matrix is as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{V} = \left[ {\begin{array}{*{20}l} {\upsilon^{11} }{\upsilon^{12} } \cdots {\upsilon^{1k} } \\ {}{\upsilon^{22} } \cdots {\upsilon^{2k} } \\ {}{} \ddots \vdots \\ {}{}{}{\upsilon^{kk} } \\ \end{array} } \right]$$

Suppose that $\kappa (\kappa \in \left[ {0,1} \right])$ represent the clustering threshold, which is determined by the size of the decision expert group. If the value of $\kappa$ is closer to 1, we consider the classification of the decision-making expert group to be finer. Also, if there are $\upsilon^{ij} > \kappa$ and $i \ne j$, we believe that the ranking vector $B^{i}$ and the ranking vector $B^{j}$, respectively, given by the decision expert $D^{i}$ and the decision expert $D^{j}$ have similar judgment characteristics. Therefore, we can classify the decision expert $D^{i}$ and the decision expert $D^{j}$ into the same category.

Suppose there is a classification set $T = \left\{ {t_{1} ,t_{2} ,..,t_{i} } \right\}$, in which decision experts with similar opinions are divided into a category $t_{i}$, while assume that $\psi_{i} (\psi_{i} \le K)$ represents the number of the decision experts included in the class $t_{i}$. Experts in different categories have large differences in views, and there are also small differences among decision-makers with similar views in the same category. So, let $\beta_{t}$ represent the inter-class weight of the class $t_{i}$ where the decision expert $D^{k}$ is located, while $\alpha_{t}^{k}$ represents the intra-class weight of the decision expert in the class $t_{i}$:

$$\beta_{t} = \frac{{\psi_{t}^{2} }}{{\sum\nolimits_{t = 1}^{T} {\psi_{t}^{2} } }}$$

(26)

$$\alpha_{t}^{k} = \frac{1 - H(k)}{{\sum\nolimits_{k = 1}^{m} {\left[ {1 - H(k)} \right]} }}$$

(27)

where $H(k)$ stands for information entropy. According to the sorting vector, the smaller the information entropy is, the more reasonable the logic and the greater the weight:

$$H(k) = - \frac{1}{\ln n}\sum\nolimits_{j = 1}^{n} {b_{j}^{k} } \ln b_{j}^{k}$$

(28)

Finally, suppose that $w^{k} (k = 1,2, \cdots ,K)$ and $\omega_{j}^{G}$, respectively, represent the decision expert’s personal weight and the subjective weight of the index, which can be calculated by the inter-class weight, intra-class weight and sorting vector of decision experts referred above:

$$w^{k} = \beta_{t} \cdot \alpha_{t}^{k}$$

(29)

$$\omega_{j}^{G} = \sum\limits_{k = 1}^{K} {b_{i}^{k} \cdot w^{k} }$$

(30)

Briefly, the purpose of the step above is to classify experts with similar opinions into the same group, while giving more weight to decision-making experts with clear logic, reasonable evaluation and low uncertainty in the same group. We use the steps above to determine the index subjective weights for selecting suppliers, and calculate the objective weight through the improved CRITIC method. Compared to the traditional CRITIC method, the improved CRITIC method is improved in terms of data robustness and responsiveness to index correlation and differentiation. Therefore, the steps to calculate the objective weight are as follows.

First, we establish the decision matrix. Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{D}$ denote the decision matrix. Each decision expert uses any integer in the interval $\left[ {0,1} \right]$ to assign the index to establish a decision matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{D}$, where $d_{j}^{k}$ represents the initial sample data corresponding to the evaluation value of the index $A_{j}$ of the decision expert $D^{k}$:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{D} = (d_{j}^{k} )_{K \times n} = \left[ {\begin{array}{*{20}l} {d_{1}^{1} }{d_{2}^{1} } \cdots {d_{j}^{1} } \cdots {d_{n}^{1} } \\ {d_{1}^{2} }{d_{2}^{2} } \cdots {d_{j}^{2} } \cdots {d_{n}^{2} } \\ \vdots \vdots \ddots \vdots \ddots \vdots \\ {d_{1}^{K} }{d_{2}^{K} } \cdots {d_{j}^{K} } \cdots {d_{n}^{K} } \\ \end{array} } \right]$$

Second, we normalize the initial sample data in the decision matrix using discrete normalization. Suppose $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}$ represents a normalized matrix. Therefore, the decision matrix expression after standard optimization is obtained as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} = (s_{j}^{k} )_{K \times n} = \left[ {\begin{array}{*{20}l} {s_{1}^{1} }{s_{2}^{1} } \cdots {s_{j}^{1} } \cdots {s_{n}^{1} } \\ {s_{1}^{2} }{s_{2}^{2} } \cdots {s_{j}^{2} } \cdots {s_{n}^{2} } \\ \vdots \vdots \ddots \vdots \ddots \vdots \\ {s_{1}^{K} }{s_{2}^{K} } \cdots {s_{j}^{K} } \cdots {s_{n}^{K} } \\ \end{array} } \right]$$

Generally speaking, the evaluation indexes can be mainly divided into three types: benefit indexes, cost indexes and moderate indexes. While the standardization method of cost indexes is different from the standardization methods of benefit indexes and moderate indexes. So, if the type of matrix element $s_{j}^{k}$ is the cost index, then the expression of the cost index can be shown as follows:

$$s_{j}^{k} = \frac{{{\text{m}} \mathop a\limits_{k} x(d_{j}^{k} ) - d_{j}^{k} }}{{{\text{m}} \mathop a\limits_{k} x(d_{j}^{k} ) - {\text{m}} \mathop i\limits_{k} n(d_{j}^{k} )}}$$

(31)

In addition, moderate indexes are often used to evaluate goals such as delivery date. Therefore, in order to simplify the calculation, we use the same standardization methods to calculate benefit indexes and moderate indexes. So, if the type of matrix element $s_{j}^{k}$ represents the cost index or the moderate indexes, then the expression of matrix element $s_{j}^{k}$ can be shown as follows:

$$s_{j}^{k} = \frac{{d_{j}^{k} - {\text{m}} \mathop i\limits_{k} n(d_{j}^{k} )}}{{{\text{m}} \mathop a\limits_{k} x(d_{j}^{k} ) - {\text{m}} \mathop i\limits_{k} n(d_{j}^{k} )}}$$

(32)

Third, assume that $e_{j} \in \left[ {0,1} \right]$ represents the information entropy of the index $A_{j}$. Therefore, the calculation is as follows:

$$e_{j} = - \frac{1}{{\ln K}}\sum\limits_{{k = 1}}^{K} {\frac{{s_{j}^{k} }}{{\sum\nolimits_{{k = 1}}^{K} {s_{j}^{k} } }}\ln } \frac{{s_{j}^{k} }}{{\sum\nolimits_{{k = 1}}^{K} {s_{j}^{k} } }}$$

(33)

Meanwhile, suppose that $\rho_{ij}$ represents the correlation coefficient between the index $A_{i}$ and the index $A_{j}$:

$$\rho _{{ij}} = \frac{{\sum\limits_{{k = 1}}^{K} {(s_{i}^{k} - \bar{s}_{i} )(s_{j}^{k} - \bar{s}_{j} )} }}{{\sqrt {\sum\nolimits_{{k = 1}}^{K} {(s_{i}^{k} - \bar{s}_{i} )^{2} } } \cdot \sqrt {\sum\nolimits_{{k = 1}}^{K} {(s_{j}^{k} - \bar{s}_{j} )^{2} } } }}$$

(34)

Among them, $s_{i}^{k}$ represents the standardized value of the index $A_{i}$ given by the decision expert $D^{k}$, and $s_{j}^{k}$ is the same, while $\overline{s}_{i}$ and $\overline{s}_{j}$, respectively, represent the mean value of the index $A_{i}$ and the index $A_{j}$.

Then, we establish the correlation coefficient matrix according to the Pearson correlation coefficient method. So, let $P$ represent the correlation coefficient matrix, the matrix is shown as follows:

$$P = (\rho_{ij} )_{n \times n} = \left[ {\begin{array}{*{20}c} {\rho_{11} } & {\rho_{12} } & \cdots & {\rho_{1n} } \\ {\rho_{21} } & {\rho_{22} } & \cdots & {\rho_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {\rho_{n1} } & {\rho_{n2} } & \cdots & {\rho_{nn} } \\ \end{array} } \right]$$

While suppose that $C_{j}$ represents the amount of information, and $AD_{j}$ represents the average difference of the index $A_{j}$, the relevant calculation formulas are as follows:

$$C_{j} = (AD_{j} + e_{j} )\sum\nolimits_{i = 1}^{n} {(1 - \left| {\rho_{ij} } \right|)}$$

(35)

$$AD_{j} = \frac{{\sum\nolimits_{i = 1}^{n} {\left| {\rho_{ij} - \overline{{\rho_{ij} }} } \right|} }}{n}$$

(36)

Finally, let $\omega_{j}^{C}$ denote the weight of the index $A_{j}$ under objective weighting. If we introduce information entropy into the formula, then the expression for calculating the weight $\omega_{j}^{C}$ is shown as follows:

$$\omega_{j}^{C} = \frac{{C_{j} }}{{\sum\nolimits_{i = 1}^{n} {C_{j} } }} = \frac{{(AD_{j} + e_{j} )\sum\nolimits_{i = 1}^{n} {(1 - \left| {\rho_{ij} } \right|)} }}{{\sum\nolimits_{i = 1}^{n} {(AD_{j} + e_{j} )\sum\nolimits_{i = 1}^{n} {(1 - \left| {\rho_{ij} } \right|)} } }}$$

(37)

In order to ensure the decision results more rational and scientific, we often effectively integrate the subjective empirical knowledge of decision-makers with the raw information of the index data [21]. However, the simple combination of weights has the problem of “multiplicative effect”, which affects the objectivity of the data [40]. Therefore, in this paper, we use the additive combination weighting method to determine the weight of decision attributes by emphasizing the preference between subjective and objective weights:

$$w_{j} = \mu \omega_{j}^{G} + (1 - \mu )\omega_{j}^{C}$$

(38)

Among them, $\mu$ represents the weight preference coefficient. In order to make the weight preference coefficient $\mu$ closer to the actual value, we use the difference coefficient method to design the weight preference coefficient. The expression of the weight preference coefficient is shown in Formula (39):

$$\mu = \frac{k}{k - 1}\left[ {\frac{2}{k}(1q_{1} + 2q_{2} + ... + kq_{k} ) - \frac{k + 1}{k}} \right]$$

(39)

In Formula (39), $q_{1} ,q_{2} ,..,q_{k}$ represent the assignment of subjective weight values reordered from small to large.

4.3 The Multi-attribute Cloud Decision Model

In this subsection, we develop an evaluation model based on cloud model theory and the TOPSIS method for evaluating and screening suppliers of production components for complex products. We first integrate the expert weights with the raw evaluation information to obtain a comprehensive evaluation matrix; then we calculate the distance between the decision indexes of each solution and the positive and negative ideal solutions using the distance measure algorithm of the cloud, and finally rank the solutions using the similarity closeness. Therefore, the decision evaluation model of the multi-attribute group is as follows:

$$F_{i} = \frac{{d(U_{i} ,U^{ - } )}}{{d(U_{i} ,U^{ - } ) + d(U_{i} ,U^{ + } )}}$$

(40)

$$d_{i}^{ + } = d(U_{i} ,U^{ + } ) = \sum\limits_{j = 1}^{n} {d(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{ij} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{j}^{ + } )}$$

(41)

$$d_{i}^{ - } = d(U_{i} ,U^{ - } ) = \sum\limits_{j = 1}^{n} {d(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{ij} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{j}^{ - } )}$$

(42)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z}_{i} = \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{ij} } \right]^{m \times n} = \left[ {w_{j} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij} } \right]^{m \times n}$$

(43)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij} = \frac{1}{n}\sum\limits_{k = 1}^{n} {x_{ij}^{k} }$$

(44)

Among them, we use the cloud synthesis method to calculate the evaluation cloud $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij}^{k}$ given by different experts to obtain the group decision value $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij}$, and establish the cloud decision matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X}_{i} = \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij} } \right]^{m \times n}$ at the same time. Next, in order to comprehensively consider the evaluation information given by each decision-maker, we multiply the decision attribute weight $w_{j}$ by the cloud decision matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X}_{i}$ to obtain a weighted decision matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z}_{i}$, while, we set $U^{ + } = (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{1}^{ + } \cdots \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{i}^{ + } \cdots \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{m}^{ + } )$ and $U^{ - } = (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{1}^{ - } \cdots \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{i}^{ - } \cdots \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{m}^{ - } )$ denote positive ideal cloud (PIC) and negative ideal cloud (NIC), respectively:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{j}^{ + } = \left\{ {\begin{array}{*{20}l} {({\text{m}}\mathop {{\text{ }}a}\limits_{i} x\;Ex_{{ij}} ,{\text{m}}\mathop {{\text{ }}i}\limits_{i} n\;En_{{ij}} ,{\text{m}}\mathop {{\text{ }}i}\limits_{i} n\;He_{{ij}} ),j \in J^{ \otimes } } \hfill \\ {({\text{m}}\mathop {{\text{ }}i}\limits_{i} n\;Ex_{{ij}} ,{\text{m}}\mathop {{\text{ }}i}\limits_{i} n\;En_{{ij}} ,{\text{m}}\mathop {{\text{ }}i}\limits_{i} n\;He_{{ij}} ),j \in J^{ \oplus } } \hfill \\ \end{array} } \right.$$

(45)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{j}^{ - } = \left\{ {\begin{array}{*{20}l} {({\text{m}}\mathop {{\text{ }}i}\limits_{i} n \cdots Ex_{{ij}} ,{\text{m}}\mathop {{\text{ }}a}\limits_{i} x\;En_{{ij}} ,{\text{m}}\mathop {{\text{ }}a}\limits_{i} x\;He_{{ij}} ),j \in J^{ \otimes } } \hfill \\ {({\text{m}}\mathop {{\text{ }}a}\limits_{i} x\;Ex_{{ij}} ,{\text{m}}\mathop {{\text{ }}a}\limits_{i} x\;En_{{ij}} ,{\text{m}}\mathop {{\text{ }}a}\limits_{i} x\;He_{{ij}} ),j \in J^{ \oplus } } \hfill \\ \end{array} } \right.$$

(46)

where $J^{ \otimes }$ and $J^{ \oplus }$ stand for the benefit-based decision index and cost-based decision index, respectively. Then, we calculate the distance of scheme $U_{i}$ from the positive and negative ideal clouds, respectively, based on the concept of cloud deviation check in Definition 2 and Formula (8).

In order to explain the model proposed in this paper more clearly, we use pseudocode to describe it, as shown as follows.

Algorithm 1
Input：Dataset $V$; Decision weighting $w_{j}$; Linguistic term set $L$
Output：Sort results $F_{i}$
1:  Begin Algorithm
2:  While $k \le K,j \le n,i \le m$ do
3:    Initialize $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij}^{k}$ based on $L$
4:      for $i = 1$ to $m$ do
5:         Update $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X}_{i}$ by FRM. (44) & FRM. (8)
6:         Update $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z}_{i}$ by FRM. (43)
7:         Update $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{j}^{ + }$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{j}^{ - }$ by FRM. (45) & FRM. (46)
8:         Update $d_{i}^{ + }$ and $d_{i}^{ - }$ by FRM. (41) & FRM. (42)
9:         Update $F_{i}$ by FRM. (40)
10:     end for
11:  Sort $F_{i}$
12:   Obtain the sort results
13:   end while
14:  End Algorithm

4.4 Decision-Making Process

With respect to the supplier selection evaluation problems, according to the above analysis, the decision process of the proposed methods is shown in Fig. 4.

Fig. 4

The decision process of the proposed supplier selection approach

Figure 4 briefly depicts the decision-making process for selecting suppliers. The decision-making process constructed in this paper is mainly divided into three parts: establishing a supplier evaluation index system, determining the weights of each evaluation indicator, and constructing a multi-attribute decision model. In the first part, our main work is to establish an effective supplier evaluation index system, we fully consider the influencing factors while combining the characteristics of complex products, and use the gray correlation method to optimize the huge index system to obtain the optimal evaluation index system. In the second part, we combine subjective and objective empowerment to get the appropriate metric weights. In the third part, we consider the inherent uncertainty of evaluation criteria and the randomness of the decision-making process, so we construct a multi-criteria decision model to evaluate potential suppliers.

5 Case Analysis

In this subsection, we verify the feasibility of the above model through a case study and validate the validity of the model through comparative analysis.

A machine manufacturing company with machine tool manufacturing as its main business identified four alternative suppliers $U_{1} ,U_{2} ,U_{3} ,U_{4}$ through pre-qualification, short visiting and in-depth researching. We use the multi-attribute decision method proposed in the previous section to rank the alternative suppliers and finally determine the most suitable product supplier. First, we set $Y = \left[ {0,1} \right]$,$He_{0} = 1$. At this point, the transformation relationship between the semantic evaluation variables and the cloud model is shown in Table 1.

Table 1 The conversion relationship between linguistic terms and cloud models

Then, we can obtain evaluation information from 6 experts over the primary indexes. According to Formula (19)–(30), the personal weighting of the experts and the subjective weighting of the indexes at the first level are as shown as follows:

$$w^{k} = \{ 0.0833,0.2533,0.0833,0.2954,0.2014,0.0833\}$$

$$\omega_{j}^{G1} = \{ 0.2907,0.3745,0.3349\}$$

Since the steps for determining the subjective weight of the secondary indexes are the same, they will not be repeated here. Meanwhile, the objective weight values over each index are obtained through Formulas (31)–(37), and shown in Column 6 in Table 2. Then, the results of subjective and objective assignments are combined according to Formulas (38), (39) to obtain the risk index weights for the collaborative development process of complex product, as shown in Table 2.

Table 2 Weights of each index combination

Based on the transformation relationship between the semantic evaluation variables and the cloud model in Table 1, the decision-making group conducts a semantic evaluation of the advantages and disadvantages of the alternative suppliers [26] (Table 3), and finally forms the decision-making information $V$ The program evaluation information is shown below.

Table 3 Decision-making information $V$.

Then, calculate the group decision values from Formula (44). For example, the evaluation results of each decision index of alternative supplier $U_{1}$ and its group decision value after cloud quantification are shown in Table 4. The cloud decision matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X}_{1}$ is constructed from the group decision values of each alternative decision index, as shown in Table 5.

Table 4 The evaluation of the decision indexes and group decision values for $U_{1}$

Table 5 Cloud decision matrix

According to Formula (43), we obtain the cloud weighted decision matrix, and the positive and negative ideal solutions are obtained from Formulas (45), (46), and the calculation results are shown in Table 6.

Table 6 Cloud weighted decision matrix and its positive and negative ideal solutions

The distance between each alternative remanufacturing solution and the positive and negative ideal solution is calculated from Formulas (41), (42), and then the relative closeness $F_{i}$ of each remanufacturing solution is calculated by Formula (40) as shown in Table 7.

Table 7 The relative proximity of each alternative supplier

According to the calculation results in Table 7, the remanufacturing solutions are ranked as $U_{2} \, > \, U_{3} \, > \, U_{1} \, > \, U_{4}$. Alternative supplier $U_{2}$ is the most suitable option, with alternative supplier $U_{3}$ being the next most suitable.

In order to verify the ambiguity and degree of freedom of the proposed method, we used two different ranking methods, normal fuzzy TOPSIS and triangular fuzzy TOPSIS. First, we transformed the semantic evaluation information using the normal affiliation function and the triangular fuzzy number, respectively, and visualized and annotated the quantified relations using python software, as shown in Fig. 5. In figure, the gray point set represents the cloud model, the purple line represents the normal affiliation function and the black line represents the triangular fuzzy number.

Fig. 5

Comparison on three semantic evaluation variables

From Fig. 5, the cloud model quantization method is more discrete than the normal membership function and triangular fuzzy number, which fully reflects the fuzziness and randomness of the evaluation process. Since the normal affiliation function can be obtained from the cloud model under the condition of $He = 0$, the normal fuzzy TOPSIS and cloud-TOPSIS are calculated using the same method. The relative closeness of each alternative supplier was calculated using the normal fuzzy TOPSIS method and the triangular fuzzy TOPSIS method.

To further verify the effectiveness and superiority of the proposed method, we compared the proposed method with four other methods. Suppose that $F_{i}^{N}$, $F_{i}^{T}$, $F_{i}^{E}$ and $F_{i}^{A}$ represent the calculation results using the normal fuzzy TOPSIS method [42], the triangular fuzzy TOPSIS method [11], the E-TOPSIS method [33] and the FAHP-TOPSIS method [3], respectively. The results are as shown in Table 8.

Table 8 The relative proximity of each alternative supplier

From the calculation results in Table 8, it can be seen that the proposed method in this article ranks the superiority of the solutions as $U_{2} \, > \, U_{3} \, > \, U_{1} \, > \, U_{4}$, the normal fuzzy TOPSIS method ranks the superiority of the solutions as $U_{2} \, > \, U_{3} \, > \, U_{1} \, > \, U_{4}$, the triangular fuzzy TOPSIS method ranks the superiority of the solutions as $U_{2} \, > \, U_{3} \, > \, U_{4} \, > \, U_{1}$, the E-TOPSIS method ranks the superiority of the solutions as $U_{3} \, > \, U_{2} \, > \, U_{1} \, > \, U_{4}$ and the FAHP-TOPSIS method ranks the superiority of the solutions as $U_{3} \, > \, U_{2} \, > \, U_{1} \, > \, U_{4}$.

To make the ranking results of the methods more intuitive to express, we use Python software to draw a line graph, as shown in Fig. 6.

Fig. 6

Comparison of the closeness of the different methods

According to Fig. 6, through the comparison of the above calculation results, all the methods take $U_{2}$ as the optimal solution. The ranking results of the cloud-TOPSIS, the normal fuzzy TOPSIS, the E-TOPSIS and the FAHP-TOPSIS are identical, compared with the triangular fuzzy TOPSIS method, which differs in the ranking of $U_{1}$ and $U_{4}$. This is due to the fact that the cloud model and the normal affiliation function have more objective quantification results because their distributions obey the laws of normal distribution, while the cloud model also takes into account the randomness of the affiliation degree, so its calculation results are more reasonable and accurate compared to the normal affiliation function. In addition, the cloud-TOPSIS method differentiates the calculation results of the relative posting schedule of each solution more significantly, making it easier for decision-makers to make the final decision.

6 Conclusions

In this paper, we propose a multi-attribute group decision-making method based on a cloud model constructed by a complex product supplier selection index system and TOPSIS. Then, we apply the proposed method to a real case and compare it with different sorting methods to verify the effectiveness of this method. Based on the model and the case study, we get the following conclusions:

While considering the differences between the evaluation solution and the positive and negative ideal solutions, the model can fully express the attitude of decision-makers based on the available information, and better describe the uncertainty of the evaluation process from the aspects of ambiguity of semantic concepts and randomness of membership degree. This provides realistic practicality and interpretability to the model, which makes the decision-making results better applied to reality.

Unlike the real application of companies, this article solely analyzes supplier selection and does not include the option to distribute complicated product orders among several selected suppliers at the same time. Furthermore, the index system in this article is designed for a certain sort of company, and the index system should be enlarged and upgraded as needed in the firm’s actual application to better represent the actual scenario. In the future, we should undertake more in-depth research on the usage and study of diverse decision-making methods.