1 Introduction

With human society’s and cognition’s continuous development, the scale and complexity of application problems and scientific calculations are increasing daily [1]. It is challenging to solve these complex optimization problems with traditional optimization theories and methods [2]. A swarm intelligence optimization algorithm is a kind of bionics algorithm that simulates the behavior of some creatures in nature or is inspired by some physical phenomena [3, 4]. Its central idea is to balance global search and local search in a solution space to find the optimal solution [5]. Swarm intelligence optimization algorithms proposed in recent years include whale optimization algorithm (WOA) [6], salp swarm algorithm (SSA1) [7], moth–flame optimization (MFO) [8], squirrel search algorithm (SSA2) [9], spotted hyena optimizer, (SHO) [10], bald eagle search, (BES) [11], etc. These swarm intelligence optimization algorithms provide new ideas for solving large-scale complex problems and are widely used in many fields. With the in-depth study of different swarm intelligence algorithms, scholars have introduced more and more improved strategies to optimize the algorithms [12,13,14,15,16].

Seagull optimization algorithm (SOA) [17] is a new intelligent optimization algorithm proposed by Dhiman et al. in 2019. The migration and attack characteristics of seagulls inspire the algorithm. By simulating the characteristics of the seagulls’ constantly moving position and the continually changing angle and speed of attacking prey during the migration process, the process of the seagulls’ position is regarded as the optimization process of the algorithm. In the past 2 years, many scholars have applied the improved gull optimization algorithm to different fields, including the optimization operation of multi-reservoir power generation systems [18], prediction of water quality monitoring network [19], modification of radio wave propagation prediction model in tunnel environment [20], performance optimization of the photovoltaic solar system [21], wireless sensor network communication technology [22], fault extraction method of cyclostationarity blind deconvolution [23], air quality index forecast [24], optimal parameter estimation of proton exchange membrane fuel cell model [25], diagnosis of brain tumor based on image feature classification [26], classification of edible oil's authenticity and adulteration [27], etc.

SOA has the characteristics of a simple structure, few parameters, and low time complexity [28, 29]. However, the gull optimization algorithm still has many defects. First, there is the problem of poor population diversity in the initialization stage. Then, there are problems such as weak global search ability and difficulty in breaking away from the local optimum in the later stage of the algorithm, leading to low searching accuracy in multi-peak search optimization problems and easily falling into the local extremum space. It is difficult for the algorithm to obtain benefits from individual information.

Given the shortcomings of the traditional seagull optimization algorithm, many scholars put forward different improvement strategies in different stages of the basic algorithm. Ewees et al. [30] presented an improved version of the seagull optimization algorithm called the ISOA. The proposed approach combines two mechanisms: the Levy flight and mutation operators. Ma et al. [31] proposed a shared seagull optimization algorithm (SSOA) based on a shared multi-leader strategy, adaptive mutation operator, and seven new variants. Che et al. [32] proposed a novel hybrid algorithm, called whale optimization with seagull algorithm (WSOA), for solving global optimization problems. Dhiman et al. [33] extended SOA on multi-objective problems by introducing the concept of dynamic archiving, which has the characteristics of caching non-dominated Pareto optimal solutions. Yu et al. [34] proposed an improved SOA based on individual interference and attractive and repulsive strategies. Li et al. [35] proposed a multi-objective seagull optimization algorithm (MOSOA), which introduced constraint non-dominated sorting and external archiving mechanisms into SOA to realize simultaneous optimization of economic, energy, and environmental goals. Wu et al. [36] used an improved tent map instead of the initial population to improve diversity. In addition, nonlinear inertia weight and stochastic double helix formula are proposed to enhance SOA’s optimization accuracy and efficiency. Mohammadzadeh et al. [37] combined SOA and grasshopper optimization algorithm (GOA) to propose a hybrid multi-objective optimization algorithm. It uses chaos mapping to generate random numbers, balances utilization and detection well, and improves convergence speed.

The above research has somewhat improved swarm intelligence algorithms’ local and global optimization. However, some shortcomings, such as low precision and slow convergence rate, still exist. To further enhance the performance of the seagull optimization algorithm, a multi-strategy improved seagull optimization algorithm (MSISOA) is proposed in this paper. The contributions made in this paper are as follows. First, this paper mainly combines the logistic chaotic map and cubic chaotic map and then applies it in the initialization of the gull optimization algorithm to help the initial distribution of the algorithm be more uniform. At the same time, a new adaptive adjustment formula is introduced to make the algorithm change in different stages, and the relationship between global exploration and local search is balanced by this method. The introduction of this formula is of great help to the update of the algorithm. Then, the group dimension learning mechanism is introduced to improve the wide-area search ability of the algorithm, which is very suitable for improving the single iteration mechanism of the seagull algorithm. Finally, the golden sinusoidal tool of Levy flight guidance is used to avoid the embarrassment of the algorithm quickly falling into local extreme values. Then, the paper verifies the effectiveness and performance of the algorithm through simulation experiments and applies it to practical engineering problems, which shows that the improved algorithm has improved both efficiency and performance.

The main structure of this paper is as follows. The optimization process for SOA is described in Sect. 2. In Sect. 3, this paper proposes an improved L–C cascade chaotic mapping and grouping dimension learning and deduces how these two strategies can be applied to SOA algorithms. The convergence factor in the algorithm is reconstructed. The golden sine strategy guided by the Levy flight mechanism is added in the late stage of the algorithm. The improved pseudo-code and algorithm flow are described, and the time complexity of MSISOA is discussed. Section 4 uses CEC2017 and CEC2022 test suites for simulation experiments. The optimization performance of each strategy in SOA and the algorithm advantages of MSISOA compared with other improved SOA algorithms are analyzed. In Sect. 5, MSISOA is first applied to three specific engineering problems, compared with other algorithms for testing, and combined with the MSISOA algorithm into the optimization problem of the 21-bar plane truss and 72-bar space truss structure model. Through comparative analysis, it is found that MSISOA can better reduce the quality of the structure under constraints. All in all, MSISOA is much better than the standard SOA algorithms in solving different problems.

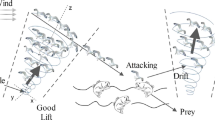
2 Seagull Optimization Algorithm

2.1 Migration (Exploration)

Avoiding the collisions: Variable \(A\) is employed to calculate the new search agent position.

$$\begin{array}{c}{\overrightarrow{C}}_{s}=A\times {\overrightarrow{P}}_{s}\left(x\right),\end{array}$$
(1)

where \({\overrightarrow{C}}_{s}\) represents the position of the search agent which does not collide with other search agents, \({\overrightarrow{P}}_{s}\) represents the current position of the search agent, \(x\) indicates the current iteration, and \(A\) represents the movement behavior of the search agent in a given search space.

$$\begin{array}{c}\begin{array}{c}A={f}_{c}-\left(x\times \left(\frac{{f}_{c}}{{\mathrm{Max}}_{\mathrm{iteration}}}\right)\right)\\ \mathrm{where}:x=\mathrm{0,1},2,\dots ,{\mathrm{Max}}_{\mathrm{iteration}}\end{array},\end{array}$$
(2)

where \({f}_{c}\) is introduced to control the frequency of employing variables \(A\) which is linearly decreased from \({f}_{c}\) to 0. In this work, the value of \({f}_{c}\) is set to 2.

The movement toward the best neighbor’s direction: after avoiding the collision between neighbors, the search agents move toward the best neighbor’s direction.

$$\begin{array}{c}{\overrightarrow{M}}_{s}=B\times \left({\overrightarrow{P}}_{bs}\left(x\right)-{\overrightarrow{P}}_{s}\left(x\right)\right),\end{array}$$
(3)

where \({\overrightarrow{M}}_{s}\) represents the positions of search agent \({\overrightarrow{P}}_{s}\) toward the best fit search agent \({\overrightarrow{P}}_{bs}\) (i.e., fittest seagull). The behavior of \(B\) is randomized and is responsible for proper balancing between exploration and exploitation. \(B\) is calculated as:

$$\begin{array}{c}B=2\times {A}^{2}\times rd,\end{array}$$
(4)

where \(rd\) is a random number that lies in the range of \([\mathrm{0,1}]\).

Remaining close to the best search agent: Lastly, the search agent can update its position with respect to the best search agent.

$$\begin{array}{c}{\overrightarrow{D}}_{s}=\left|{\overrightarrow{C}}_{s}+{\overrightarrow{M}}_{s}\right|,\end{array}$$
(5)

where \({\overrightarrow{D}}_{s}\) represents the distance between the search agent and best fit search agent (i.e., best seagull whose fitness value is less).

2.2 Attacking (Exploitation)

While attacking the prey, the spiral movement behavior occurs in the air. This behavior in \(x\), \(y\), and \(z\) planes is described as follows.

$$\begin{array}{c}{x}^{{^{\prime}}}=r\times \mathrm{cos}\left(k\right),\end{array}$$
(6)
$$\begin{array}{c}{y}^{{^{\prime}}}=r\times \mathrm{sin}\left(k\right),\end{array}$$
(7)
$$\begin{array}{c}{z}^{{^{\prime}}}=r\times k,\end{array}$$
(8)
$$\begin{array}{c}r=u\times {e}^{kv},\end{array}$$
(9)

where \(r\) is the radius of each turn of the spiral, and \(k\) is a random number in the range \(\left[0\le k\le 2\pi \right]\). \(u\) and \(v\) are constants to define the spiral shape, and \(e\) is the base of the natural logarithm. The updated position of search agent is calculated using Eqs. 5–9.

$$\begin{array}{c}{\overrightarrow{P}}_{s}\left(x\right)=\left({\overrightarrow{D}}_{s}\times {x}^{{^{\prime}}}\times {y}^{{^{\prime}}}\times {z}^{{^{\prime}}}\right)+{\overrightarrow{P}}_{bs}\left(x\right),\end{array}$$
(10)

where \({\overrightarrow{P}}_{s}\left(x\right)\) saves the best solution and updates the position of the other search agents.

SOA starts with a randomly generated population. The search agents can update their positions with respect to the best search agent during the iteration process. \(A\) is linearly decreased from \({f}_{c}\) to 0. For a smooth transition between exploration and exploitation, variable \(B\) is responsible.

3 Multi-strategy Improved Seagull Optimization Algorithm

3.1 L–C Cascade Chaotic Mapping

In the initial stage of the gull algorithm, the randomly generated population is sometimes too scattered or aggregated, which may lead to local optimization and low searching accuracy in the later stage of the algorithm. Due to chaotic ergodicity and randomness characteristics, the initial population generated by chaotic mapping has better diversity. The initial solutions are more evenly distributed in the search space, which can strengthen the local mining ability of the algorithm and effectively avoid algorithm prematurity, thus improving the convergence speed and optimization accuracy of the algorithm. This paper introduces the L–C cascade chaotic mapping in the population initialization stage of the seagull algorithm [38].

Cascading the logistic map to an improved cubic map is called L–C cascading. Logistic mapping is:

$$\begin{array}{c}{x}_{n+1}=\mu {x}_{n}\left(1-{x}_{n}\right),\end{array}$$
(11)

where \(\mu \in \left[\mathrm{0,4}\right]\), \(x\in \left[\mathrm{0,1}\right]\).

The improved cubic mapping is:

$$\begin{array}{c}{x}_{n+1}=\left|\frac{{x}_{n}^{3}}{{a}^{2}}-b{x}_{n}\right|,\end{array}$$
(12)

where \(b\in \left[\mathrm{0,3}\right]\), \(x\in \left[\mathrm{0,2}a\right]\).

In the improved cubic mapping, \(a=0.5\), \(b=3\). Constrain its value range to the same value range \(x\in [\mathrm{0,1}]\) as the logistic mapping, which is a complete mapping, and then substitute the logistic mapping into the improved cubic mapping to obtain the cascading system of the logistic iteration first and then the improved cubic iteration:

$$\begin{array}{c}{x}_{n+1}=\left|\frac{{\left[u{x}_{n}\left(1-{x}_{n}\right)\right]}^{3}}{{0.5}^{2}}-3\times u{x}_{n}\left(1-{x}_{n}\right)\right|.\end{array}$$
(13)

The bifurcation diagram of the cascade system is shown in Fig. 1c, and the parameter range of chaos is about \([\mathrm{1.55,4}]\). (There are several small periodic windows in between) The chaos parameter interval of the L–C cascade mapping is much larger than that of logistic mapping in Fig. 1a and improved cubic mapping in Fig. 1b, \(\mu \in [\mathrm{3.57,4}]\), \(b\in [\mathrm{2.41,3}]\). The full mapping range is about \([\mathrm{1.9,4}]\). Compared with the full mapping only at one parameter point, its dynamic performance is significantly improved.

Fig. 1
figure 1

Logistic, cubic, and L–C cascade chaotic mapping bifurcation diagram

Full size image

The L–C cascade chaotic mapping improves some common defects of the two alone. For example, the bifurcation parameter range of chaotic mapping is small, the whole mapping is only at one parameter point and the Lyapunov index is small. Therefore, introducing it into the population initialization stage of the SOA can better expand chaos search space and develop local extremums, which is more advantageous than chaotic mapping alone.

3.2 Nonlinear Convergence Factor

In traditional SOA algorithms, the migration process of the seagull population (global search) needs to move toward the optimal position while avoiding collision with adjacent seagulls. In the process of moving, the prey is attacked by changing the angle and speed (local search) to achieve the optimization performance of the algorithm. In this iterative mechanism, the convergence factor \(A\) is the key to coordinating global exploration and local development. According to Eq. 2, the value of \(A\) decreases linearly from 2 to 0 as the number of iterations increases. At the beginning of the iteration, the value of \(A\) is enormous and the global search ability of the seagull population is strong. However, at the later stage of the algorithm, with the constant decrease of the value of \(A\), the local optimization ability is gradually enhanced. Although the linear inertial weight can balance global exploration and local development to some extent, the actual search process is very complex and nonlinear, and the linear weight will reduce the algorithm's performance. The MSISOA algorithm proposed in this paper reconstructs the convergence factor to improve this defect. Its mathematical model is as follows:

$$\begin{array}{c}A={f}_{c}\times {\left(1-\frac{\mathrm{Iter}}{{\mathrm{Max}}_{\mathrm{Iter}}}\right)}^{\left(2\frac{\mathrm{Iter}}{{\mathrm{Max}}_{\mathrm{Iter}}}\right)}.\end{array}$$
(14)

As shown in Fig. 2, the value of \(A\) presents \(A\) nonlinear decreasing trend with the increase of iterations. It can avoid the position conflict between seagulls in each iteration and better coordinate the global search and local optimization of the population to improve the algorithm's convergence speed and optimization accuracy.

Fig. 2
figure 2

Comparison diagram of convergence factor \(A\) variation trend

Full size image

3.3 Group Dimensional Learning Strategies

In the optimization mechanism of the basic gull algorithm, some gull positions show poor fitness values because they are far from the actual optimal solution in some variable dimensions. Other dimensions are already in the solution space near the optimal global solution. Still, due to the significant difference between different dimensions, the fitness values of these seagull positions become worse.

Therefore, seagulls in poor positions need to learn attack ability from seagulls in good positions to improve themselves, and a group dimension learning strategy is integrated after the position update of the algorithm [39]. The seagull population was divided into two groups according to fitness order. The sample group was the seagulls with good fitness values in the first half, and the learning group was the seagulls with poor fitness in the second half.

3.3.1 Sample Group Dimension Crossing Strategy

An optimal individual updating mechanism based on the neighborhood dimension crossing strategy was adopted to integrate the different dimensional information of the optimal solution in the past dynasties and achieve the maximum effective retention of the optimal component [40]. The optimal solution components of the neighborhood were crossed by the dimension difference comparison of the optimal neighbor and according to the principle of maximum absolute difference crossover. If the fitness value of the optimal neighbor was better after crossover, the crossover was performed; otherwise, no crossover was performed. The mathematical expression of the update strategy is as follows:

$$\begin{array}{c}{p}_{k,h}^{i,t+1}=\left\{\begin{array}{cc}{p}_{k}^{j,t},& f\left({n}_{j,\mathrm{Cross}}^{i,t}\right)\mathrm{ is\, better \,than\, }f\left({p}^{i,t}\right)\\ {p}_{k}^{i,\mathrm{iter}},& \mathrm{otherwise}\end{array}\right.,\end{array}$$
(15)

where, \({p}_{k,h}^{i,t+1}\) is the position of seagull \(i\) after crossing dimension \(k\) for \(h\) times in \(t+1\) iteration, and \({p}_{j,\mathrm{Cross}}^{i,t}\) is the position of seagull \(i\) after crossing dimension \(k\) with seagull j. The optimal solution of the \(k\) neighbors’ generation dimension absolute difference sequence of sorting \(h\) large dimension (dimension difference formula for \({\Delta }_{k}=\left|\left|{p}_{k}^{j,t}\right|-\left|{p}_{k}^{i,t}\right|\right|\), \(h=\mathrm{1,2},\cdots \left({R}_{\mathrm{Cross}}\times d\right)\) as the seagull \(i\) performs the crossover operation frequency, where \(\left({R}_{\mathrm{Cross}}\times d\right)\) is the maximum number of crossings, and \({R}_{\mathrm{Cross}}\) is the proportion of dimension crossings.

Figure 3 shows that in the dimension crossing operation of the optimal neighbor, if the dimension difference is large and the algorithm optimization performance can be improved after crossing, the dimension will be crossed and retained; otherwise, the dimension with small difference or no significant performance improvement after crossing will be abandoned. When the cross ratio \({R}_{\mathrm{Cross}}=1\), the optimal dimensions of successive generations will be retained and contained in the offspring population. This updating strategy can effectively enhance the performance of dimension mining and local extremum escape of the algorithm.

Fig. 3
figure 3

Sample group dimensional learning diagram

Full size image

3.3.2 Learning Group Dimension Crossing Strategy

Since each dimension of the sample group has its advantages and disadvantages, the location dimension of the sample group is averaged, and each prey in the learning group learns from the average dimension of the sample group. This strategy makes a difference between each dimension of each seagull in the learning group and the average dimension value of the group. According to the principle of priority crossing with significant absolute differences, the first \(H\) corresponding dimensions with large absolute differences are crossed individually. If the fitness of the seagull after crossing is better, the corresponding dimensions are crossed; otherwise, they are not crossed. Figure 4 shows the process of dimensional cross-learning in learning groups.

Fig. 4
figure 4

Learning group dimension learning diagram

Full size image

The larger the value of \(H\), the more crossed will be the dimensions. Individuals in the learning group will gradually approach the mean of the sample group, reducing the differences between them. At this time, although the population’s average fitness decreases, the convergence speed is accelerated. Reducing individual differences will bring the risk of falling into local optimization. Even if the convergence accuracy is improved compared with the original algorithm, there is still a certain probability that the optimization accuracy of the improved algorithm will be reduced. When the value of \(H\) is smaller, the number of crossings is smaller, and the individual difference is tiny compared with that before crossing. Although individual diversity is maintained, the crossing of fewer dimensions dramatically weakens the ability of the improved algorithm to jump out of the local optimum and has the risk of falling into the local optimum. In addition, if there is too little crossover, there will be no good learning between individuals, reducing the convergence speed. Therefore, the choice of \(H\) should be considered in a compromise. After many simulation tests, the highest crossover efficiency is achieved by selecting about half of the dimensions. In this experiment, \(H\) equals half of the number of individual dimensions. In the process of dimensional learning from the average value of the sample group, the individuals of the learning group with poor quality will only span a small step size to avoid overstepping the optimal global advantage and its neighborhood. Therefore, the average dimension learning of the learning group will significantly reduce the number of iterations to the optimal value and improve the convergence speed.

3.4 Golden Sine Strategy Guided by Levy Flight Mechanism

In the optimization process of the standard SOA algorithm, seagulls find the attack position according to the fixed behavior track after the migration stage. In this process, the singleness of the action model will cause seagulls to keep flying in a fixed angle and direction when moving, thus missing the optimal position, and the high population density will significantly reduce the ability to jump out of the local extreme value. To solve this problem, the golden sine strategy guided by Levy flight mechanism was added in the later stage of the algorithm [41]. MSISOA can traverse all values of the sine function (all points on the identity element) according to the relationship between the sine function and the unit circle. In this process, the golden section number is added to narrow the search space and guide seagull individuals to approach the optimal solution. At the same time, the Levy flight mechanism was introduced for guidance. The uncertainty of the Levy flight direction and step size was used to disturb the population position, expand the unknown search range and improve the local extremum escape ability of the algorithm. The mathematical model of Levy flight is shown in (16).

$$\begin{array}{c}Levy\left(\beta \right)=0.01\times \frac{\mu }{{\left|v\right|}^{1/\beta }},\end{array}$$
(16)

where, \(\mu \) and \(v\) are typically distributed.

$$\begin{array}{c}\begin{array}{c}\mu \sim N\left(0,{\sigma }_{\mu }^{2}\right)\\ v\sim N\left(0,{\sigma }_{v}^{2}\right)\\ {\sigma }_{\mu }={\left(\frac{\Gamma \left(1+\beta \right)\times \mathrm{sin}\left(\frac{\pi \times \beta }{2}\right)}{\Gamma \left(\frac{1\times \beta }{2}\right)\times \beta \times {2}^{\left(\frac{\beta -1}{2}\right)}}\right)}^{\frac{1}{\beta }},{\sigma }_{v}^{2}=1,\end{array},\end{array}$$
(17)

where \(\Gamma \left(\beta \right)\) is Gamma function. \(\beta \) is a constant that affects the trajectory of the Levy flight step. This paper takes beta = 1.5.

The mathematical model of updating individual positions by the golden sine strategy guided by Levy flight mechanism is shown in (18).

$$\begin{array}{c}{X}_{\mathrm{new}}^{t+1}={X}_{i}^{t}\times \left|\mathrm{sin}\left({R}_{1}\right)\right|+Levy\left(\beta \right)\times {R}_{2}\times sin\left({R}_{1}\right)\times \left|{x}_{1}\times {X}_{\mathrm{best}}^{i}-{x}_{2}\times {X}_{i}^{t}\right|,\end{array}$$
(18)
$$\begin{array}{c}\begin{array}{c}{x}_{1}=-\pi +\left(1-\lambda \right)\times 2\pi \\ {x}_{2}=-\pi +\lambda \times 2\pi \\ \lambda =\left(\sqrt{5}-2\right)/2\end{array},\end{array}$$
(19)

where \({R}_{1}\) and \({R}_{2}\) are random numbers. \({R}_{1}\) determines the moving distance of each individual in the next iteration. \({R}_{1}\in \left[\mathrm{0,2}\pi \right]\). \({R}_{2}\) determines the direction of location updates for the next iteration. \({R}_{2}\in \left[0,\pi \right]\). \({x}_{1}\) and \({x}_{2}\) are the coefficients obtained by the golden ratio. \(\lambda \) is the golden section number.

Although the golden sine strategy guided by the Levy flight mechanism can improve the algorithm's optimization accuracy and help it jump out of the local optimum, it cannot directly judge whether the new individual position generated is superior to the original individual position. Therefore, after the guiding mechanism, a greedy strategy is added to compare the fitness between the old and new individuals, and according to the result, the individual position is decided whether to update. In this way, the optimal solution is obtained continuously to improve the algorithm’s optimization performance. The mathematical model of the greedy strategy is shown in (20).

$$\begin{array}{c}{X}_{\mathrm{updata}}^{t+1}=\left\{\begin{array}{c}{X}_{\mathrm{new}}^{t+1},f\left({X}_{i}^{t+1}>{X}_{\mathrm{new}}^{t+1}\right)\\ {X}_{i}^{t+1},f\left({X}_{i}^{t+1}<{X}_{\mathrm{new}}^{t+1}\right)\end{array}\right..\end{array}$$
(20)

3.5 MSISOA Algorithm Process

The execution pseudo-code of MSISOA algorithm optimization process is shown in Algorithm 1, and the algorithm flowchart is shown in Fig. 5.

Fig. 5
figure 5

Sample group dimensional learning diagram

Full size image
figure a

3.6 Time Complexity Analysis

The algorithm’s time complexity can reflect the convergence speed from the side. In SOA, set the population size to \(N\), the maximum number of iterations to \(T\), and the individual dimension to \(D\). Then the time complexity of the standard SOA is: \(O\left(N\times T\times D\right).\)

MSISOA is an improvement on standard SOA. Firstly, the initialization time complexity is calculated. The execution time of parameter initialization is \({\eta }_{0}\). The time for generating random numbers in each dimension is \({\eta }_{1}\). The time of chaotic population formation in (13) is \({\eta }_{2}\). Then the time complexity of the seagull population initialization stage is: \(O(N\times D+{\eta }_{0}+{\eta }_{1}+{\eta }_{2})=O(N\times D)\). Secondly, the time required to calculate the nonlinear convergence factor is set as \({\eta }_{3}\). The time complexity of this phase is \(O(N\times T\times D+{\eta }_{3})=O(N\times T\times D)\). Thirdly, the neighborhood dimension learning time of the sample group is \({\eta }_{4}\), and the dimension learning time of the learning group is \({\eta }_{5}\), so the time complexity of this stage is \(O(N\times D+{\eta }_{4}+{\eta }_{5})=O(N\times D)\). Finally, the time required to update individual positions in each dimension is \({\eta }_{6}\) according to (20), the time required to compare the fitness of old and new individuals by using greedy mechanisms is \({\eta }_{7}\), and the time required to retain the optimal position is \({\eta }_{8}\). The Levy flight mechanism of gold sine time needed for the strategy for \(O(N\times T\times D\times ({\eta }_{6}+{\eta }_{7})+{\eta }_{8})=O(N\times T\times D)\). In conclusion, the time complexity of MSISOA is \(O(N\times T\times D)\).

In summary, the time complexity of MSISOA is consistent with that of SOA, and the improvement strategy proposed in this paper does not increase the computing burden to address the shortcomings of standard SOA.

4 Simulation Experiment and Result Analysis

4.1 Effectiveness Analysis of Improved Strategies

To better verify the effectiveness of each improved strategy in MSISOA proposed in this paper, four more algorithms are proposed in this paper, which are SOA with L–C cascaded chaotic mapping (CSOA), SOA with the addition of nonlinear convergence factor (NSOA), SOA with the incorporation of grouped dimensional learning strategy (DSOA), and SOA with the introduction of Levy mechanism golden sine strategy (GSOA). Simulation experiments are conducted for MSISOA, SOA, CSOA, NSOA, DSOA. andGSOA by 30 functions of the CEC2017 test suite. The information on the functions is shown in Appendix 1. Other parameters are uniformly set as population quantity \(N=50\), maximum iteration times \({T}_{\mathrm{max}}=1000.\) The parameters \({f}_{c}=2\) and \(u=v=1\) in the algorithm.

Each test function was simulated 100 times, and the optimal value, average value, and standard deviation of the results were listed to analyze the optimization performance of the improved algorithm after different strategies. In addition, function graphs and convergence curves of 30 test functions are drawn to compare the convergence of each strategy. At the same time, the box plot of 100 times test data is depicted, which can more intuitively observe the average level, extreme value and outlier value of the data group and better judge the discrete distribution of data.

The specific data for the comparison of the six intelligent optimisation algorithms using the CEC2017 test functions is placed in Appendix 2. In Appendix 2, the test results of each algorithm for F1 and F2 functions are much higher than the theoretical optimum, and the optimization needs to be more satisfactory. However, the optimization results of the algorithms that incorporate the improvement strategies are all better than SOA, indicating that each improvement strategy improved the performance of the algorithms. Compared with the test results of other functions, the simulation results of the improved algorithms of each strategy are significantly improved compared with the original algorithm. The optimal values and average values obtained from the MSISOA runs are optimal among several algorithms, and the characteristics of different improvement strategies are combined to improve the algorithm performance of SOA. Except for functions F5 and F20, the standard deviation of MSISOA is the optimal value in the different dimensions of the remaining function. It shows that the MSISOA algorithm has advantages in dealing with multimodal functions and has good stability and strong adaptability in processing multi-peak test functions. It also reflects that the algorithm can mine the optimal solution. In conclusion, the simulation results show that MSISOA has better stability in the test function and has great advantages over the essential SOA. For 30 functions, MSISOA is significantly better than SOA in terms of optimal value, mean value, and standard deviation, and CSOA, NSOA, DSOA, and GSOA are also better than essential SOA. It is proved that every strategy of MSISOA adds advantages to the algorithm at different stages of the optimization process. MSISOA is superior to SOA in convergence accuracy, global search ability, and stability.

To visually compare the convergence speed of these algorithms, the convergence curves on the 30 test functions are shown in Fig. 6. The convergence curves record the average of 100 runs of each algorithm on each generation. It can be seen that the iteration curves of MSISOA on the F6–F9, F13, F15, F17, and F20 functions are similar to those of DSOA, and the iterative result of MSISOA is superior. During the iterations of other functions, the curves of SOA become flat quickly, and the speed of the optimization search iteration is slow. During the iterations of other functions, the curves of SOA become flat quickly, and the speed of the optimization search iteration is slow. The curve of MSISOA converges faster, and the average value of each generation is better. The convergence speed of CSOA, NSOA, DSOA, and GSOA algorithms is better than that of SOA in general, which proves that all four strategies improve the convergence speed of the algorithms.

Fig. 6
figure 6

Iteration diagram of the test results of different functions

Full size image

According to Fig. 7, it can be seen that the values of MSISOA run F2, F12-F13, F18–F19, and F30 functions are concentrated in line with occasional outliers. For F1, F3–F4, F11, F14, F17, F22, and F27, the values after MSISOA runs are distributed in a small range. On the remaining functions, the MSISOA runs have a slightly larger range of value dispersion. The sample distribution of MSISOA is better than that of the other algorithms overall. Meanwhile, CSOA, NSOA, DSOA, and GSOA are better than SOA in terms of dispersion and stability, and some outliers generated are acceptable.

Fig. 7
figure 7

Box plot of the test results of different standard functions

Full size image

Table 1 shows the p values of the Wilcoxon rank test for MSISOA and other algorithms in CEC2017. The symbol “+” indicates that the MSISOA algorithm outperforms the comparison algorithm in terms of optimality seeking performance, “−” indicates that it underperforms in comparison to the comparison algorithm, and “=” indicates equal performance to the comparison algorithm. MSISOA outperforms SOA, CSOA, NSOA, DSOA, and GSOA on all 30 functions, indicating that the superiority of MSISOA is statistically significant. The Friedman test results and rankings for the optimal values of each algorithm are presented in Table 2, with MSISOA ranked first.

Table 1 P values of Wilcoxon rank test (CEC2017)
Full size table
Table 2 CEC2017 test results
Full size table

Overall, CSOA, NSOA, DSOA, and GSOA have remarkable effects in solving basic test functions. This is because the L–C cascades chaotic mapping enhances the population diversity at the initial stage of the algorithm, thus improving the local development ability of the algorithm. The improved nonlinear convergence factor harmonizes the algorithm’s global exploration and local mining ability better. The grouping dimension learning strategy can effectively enhance the depth mining performance of the algorithm and improve the convergence accuracy of the algorithm. Under the guidance of the golden sine mechanism, the Levy flight mechanism reduces the optimal search area, accelerates the convergence speed of the algorithm, updates the population position disturbance, and enhances the ability of the algorithm to jump out of the local optimum.

4.2 Compare MISOA with Different Algorithms

To further verify the superiority and effectiveness of MSISOA, this paper compares MSISOA with differential evolution (DE) [42], particle swarm optimization (PSO) [43], SOA, and several other improved algorithms, namely salp swarm algorithm with random inertia weight and differential mutation operator (ISSA) [44], adaptive simulated annealing particle swarm optimization algorithm (ASAPSO) [45], adaptive T-distribution seagull optimization algorithm (ISOA1) [46], inertia seagull optimization algorithm (ISOA2) [47] and golden sine guide and sigmoid continuous seagull optimization algorithm (GSCSOA) [48]. The selected algorithms are partly new algorithms with excellent performance in recent years, and partly representative improvements to SOA, by comparing with these algorithms, it is more intuitive to find the advantages and disadvantages of the improved algorithms in this paper. The algorithms were experimented with the CEC2022 test suite. The parameter information for PSO and ASAPSO is the same as in the literature [45], and the parameter settings for the other algorithms are shown in Table 3. Population quantity \(N=50\), maximum iteration times \({T}_{\mathrm{max}}=1000\). In Sect. 4.1, each function was simulated 100 times. The optimal value, mean value, and standard deviation of the results are listed (as shown in Appendix 3). The convergence curves of 12 functions were drawn. At the same time, the box plot of 100 test data is given.

Table 3 CEC2022 test results
Full size table

In general, the optimization performance of the algorithm can be reflected by the optimal value and the mean value, and the standard deviation reflects the algorithm’s stability. As can be seen in Appendix 3, the optimal values, mean values, and standard deviation of MSISOA on CF1–CF5 and CF11 are optimal among the individual algorithms. In the experimental results of the CF6 function, the value of DE converges to the theoretical optimal value. The standard deviation of MSISOA on CF7–CF10 could be more optimal among several algorithms. For the test results of the CF10 function, the mean of ISOA1, ISOA2, and GSCSOA sample data is optimal, and MSISOA is very close to it. MSISOA has better optimal and mean values among the 11 functions, which reflects that MSISOA has higher search precision and convergence accuracy than DE, PSO, SOA, ISSA, ASAPSO, ISOA1, ISOA2, and GSCSOA, and is generally better than the other compared algorithms. MSISOA outperforms other comparative algorithms on seven functions, indicating that MSISOA also has advantages in stability.

The convergence curves of the 12 functions in Fig. 8 show that MSISOA generally converges quickly in the initial stage of the algorithm iteration. The curves represent the average of 100 experiments per generation for each algorithm in the optimization process. MSISOA has an absolute advantage in convergence speed and accuracy for CF1–CF8 and CF11. For CF9 and CF12, the convergence of MSISOA is not optimal, but the difference is slight. The convergence accuracy of MSISOA on CF10 is slightly worse.

Fig. 8
figure 8

Iteration diagram of CEC2022 test results

Full size image

According to the box plots of the different algorithms given in Fig. 9, it can be found that on CF1, CF3, CF6, CF9, and CF11, the MSISOA values are concentrated around the optimal values, with occasional outliers. For CF2, CF5, and CF12, the distribution of MSISOA is more concentrated. For CF4, CF6–CF9, MSISOA has a similar dispersion as the other algorithms but with a better median and no outliers. For CF4, CF7–CF8, and CF10, MSISOA is a little more dispersed. In conclusion, MSISOA has a more concentrated distribution of values over the 12 functions, with better medians, lower margins, and fewer outliers than several comparison algorithms.

Fig. 9
figure 9

Box plot of CEC2022 test results

Full size image

The p values of the Wilcoxon rank test for MSISOA and other algorithms on the CEC2022 test suite are shown in Table 4. MSISOA outperforms DE, PSO, SOA, ISSA, ASAPSO, and ISOA1 on 12 functions and outperforms ISOA2 and GSCSOA on 11 functions. It shows that the superiority of MSISOA is statistically significant. The Friedman test results and the ranking of the optimal values of each algorithm are shown in Table 3, where MSISOA is ranked first.

Table 4 P values of Wilcoxon rank test (CEC2022)
Full size table

MSISOA has obvious advantages in solving low- and high-dimensional problems, such as strong search ability, high optimization accuracy, and good stability, which further shows that MSISOA has significant competitive advantages in solving complex optimization problems in real life.

5 Mathematical Problems in Engineering

The mechanical optimization problem is closely related to the mathematical model. The key to constructing an optimal design mathematical model is to find design variables, objective functions, and constraints.

In this section, MSISOA is compared and analyzed with SOA, marine predators algorithm (MPA) [49], Harris hawks optimization (HHO) [50], sparrow search algorithm (SSA3) [51], butterfly optimization algorithm (BOA) [52], multi-subpopulation marine predators algorithm (MSMPA) [53], chaotic elite Harris Hawks optimization (CEHHO) [54], ISOA1, ISOA2, and GSCSOA. To ensure the fairness of the comparison experiment, the algorithm parameters were set, as shown in Table 5.The maximum number of iterations is 500, the population size is 100, and the average value is taken after each algorithm runs independently 50 times.

Table 5 Parameter settings of algorithms
Full size table

5.1 Optimization of Mechanical Design

This section uses MSISOA to optimize three mechanical design problems: tensile/compression spring design problem, welded beam design problem, and pressure vessel design problem.

5.1.1 Optimum Design Case of Tension/Compression Spring

The tension/compression spring design is optimized to minimize the weight of the spring under three decision variables and four constraints. The decision variables are wire diameter \((D)\), average coil diameter \((d)\), and effective coil number \((N)\). Constraints include minimum deviation \((G1)\), shear stress \((G2)\), impact frequency \((G3)\), and outer diameter limit \((G4)\). Its structure optimization design schematic is shown in Fig. 10.

Fig. 10
figure 10

Description of the tension/compression spring design

Full size image

The mathematical model of the tension/compression spring design is described as follows:

Set \(x=\left[{x}_{1} {x}_{2} {x}_{3}\right]=\left[d D N\right].\)

$$\begin{array}{l}Minimize\, f\left(x\right)={x}_{1}^{2}{x}_{2}\left(2+{x}_{3}\right),\end{array}$$
(21)
$$\begin{array}{l}Subject\, to\,\left\{\begin{array}{l}{g}_{1}\left(x\right)=1-\frac{{x}_{2}^{3}{x}_{3}}{71785{x}_{1}^{4}}\le 0\\ {g}_{2}\left(x\right)=\frac{4{x}_{2}^{2}-{x}_{1}{x}_{2}}{12566\left({x}_{2}{x}_{1}^{3}-{x}_{1}^{4}\right)}+\frac{1}{5108{x}_{1}^{2}}-1\le 0\\ {g}_{3}\left(x\right)=1-\frac{140.45{x}_{1}}{{x}_{2}^{2}{x}_{3}}\le 0\\ {g}_{4}\left(x\right)=\frac{{x}_{1}+{x}_{2}}{1.5}-1\le 0\end{array}\right.,\end{array}$$
(22)

where \({x}_{1}\in [0.05, 2]\), \({x}_{2}\in [0.25, 1.3]\), and \({x}_{3}\in [2, 15]\) are design variables.

It can be seen in Table 6 that the fitness value obtained by MSISOA is superior to that of other comparison algorithms. On the other hand, the quality of MSISOA optimization design is 7.41% lower than that of standard SOA. Compared with other algorithms, there are also different amplitudes of reduction. Therefore, MSISOA effectively solves tension/compression spring design problems.

Table 6 Comparison of optimization results of different algorithms in the tension/compression spring design problem
Full size table

5.1.2 Optimum Design Case of the Welding Beam

The design of the welded beam is optimized to minimize the total cost under four decision variables and seven constraints. The decision variables are weld thickness \((h)\), steel bar connection length \((L)\), steel bar height \((t)\), and steel bar thickness \((b)\), and their structural optimization design is shown in Fig. 11.

Fig. 11
figure 11

Description of the welding beam design

Full size image

The mathematical model of the welding beam design is as follows:

Set \(x=\left[{x}_{1} {x}_{2} {x}_{3} {x}_{4}\right]=\left[h \,l \,t \,b\right].\)

$$\begin{array}{l}Minimize\, f\left(x\right)={1.10471x}_{1}^{2}{x}_{2}+0.04811{x}_{3}{x}_{4}\left(14+{x}_{2}\right),\end{array}$$
(23)
$$\begin{array}{l}Subject \, to \,\left\{\begin{array}{l}{g}_{1}\left(x\right)=\tau \left(X\right)-13600\le 0\\ {g}_{2}\left(x\right)=\sigma \left(X\right)-30000\le 0\\ {g}_{3}\left(x\right)={x}_{1}-{x}_{4}\le 0\\ {g}_{4}\left(x\right)=0.10471{x}_{1}^{2}+0.04811{x}_{3}{x}_{4}\left(14+{x}_{2}\right)-5\le 0\\ {g}_{5}\left(x\right)=0.125-{x}_{1}\le 0\\ {g}_{6}\left(x\right)=\delta \left(X\right)-0.25\le 0\\ {g}_{7}\left(x\right)=6000-{P}_{c}\left(x\right)\le 0\end{array}\right.,\end{array}$$
(24)
$$\begin{array}{l}where \,\left\{\begin{array}{l}\tau \left(X\right)=\sqrt{{{(\tau }^{{^{\prime}}})}^{2}+2{\tau }^{{^{\prime}}}{\tau }^{{^{\prime}}{^{\prime}}}\frac{{x}_{2}}{2R}+{{(\tau }^{{^{\prime}}{^{\prime}}})}^{2}}\\ {\tau }^{{^{\prime}}}=\frac{6000}{\sqrt{2}{x}_{1}{x}_{2}},{\tau }^{{^{\prime}}{^{\prime}}}=\frac{MR}{J},M=6000\left(14+\frac{{x}_{2}}{2}\right)\\ R=\sqrt{\frac{{x}_{2}^{2}}{4}+{\left(\frac{{x}_{1}+{x}_{3}}{2}\right)}^{2}},J=2\left\{\sqrt{2}{x}_{1}{x}_{2}\left[\frac{{x}_{2}^{2}}{12}+{\left(\frac{{x}_{1}+{x}_{3}}{2}\right)}^{2}\right]\right\}\\ \sigma \left(X\right)=\frac{504000}{{x}_{3}^{2}{x}_{4}},\delta \left(X\right)=\frac{65856000}{\left(30\times {10}^{6}\right){x}_{3}^{3}{x}_{4}}\\ {P}_{c}\left(x\right)=\frac{4.013\left(30\times {10}^{6}\right)\sqrt{\frac{{x}_{3}^{2}{x}_{4}^{6}}{36}}}{196}\left[1-\frac{{x}_{3}\sqrt{\frac{30\times {10}^{6}}{4\left(12\times {10}^{6}\right)}}}{28}\right]\\ {0.1\le x}_{i}\le 2, {i=\mathrm{1,4};0.1\le x}_{j}\le 10,j=\mathrm{2,3}\end{array}\right.,\end{array}$$
(25)

where \(\tau \) is the shear stress, \(\sigma \) is the bending stress of the beam, \({P}_{c}\) is the buckling load, \(\delta \) is the deflection of the beam, and \(f\left(x\right)\) is the minimization of the design cost.

As shown in Table 7, the design cost of MSISOA is 1.38% lower than that of the SOA algorithm. It is very similar to the optimization results of MPA and MSMPA, only 0.07% higher than that of other improved SOAs, and the fitness value is better than that of other improved SOAs. Therefore, it shows that MSISOA is suitable for the welding beam design.

Table 7 Comparison of the optimization results of different algorithms for the welding beam design
Full size table

5.1.3 Optimum Design Case of Pressure Vessel

The design of the pressure vessel is optimized to minimize the total cost of the pressure vessel under four decision variables and four constraints. The decision variables are shell thickness \((Ts)\), head thickness \((Th)\), inner radius \((R)\), and cylinder length \((L)\). Its structure optimization design schematic is shown in Fig. 12.

Fig. 12
figure 12

Pressure vessel design description

Full size image

The mathematical model of the pressure vessel design is as follows:

Set \(x=\left[{x}_{1} {x}_{2} {x}_{3} {x}_{4}\right]=\left[Ts Th R L\right].\)

$$\begin{array}{l}Minimize\, f\left(x\right)=0.6224{x}_{1}{x}_{3}{x}_{4}+1.7781{x}_{1}{x}_{3}^{2}+3.1661{x}_{1}^{2}{x}_{4}+19.84{x}_{1}^{2}{x}_{3},\end{array}$$
(26)
$$\begin{array}{l}Subject\, to\,\left\{\begin{array}{l}{g}_{1}\left(x\right)=0.0193{x}_{3}-{x}_{1}\le 0\\ {g}_{2}\left(x\right)=0.0095{x}_{3}-{x}_{2}\le 0\\ {g}_{3}\left(x\right)=-\pi {x}_{3}^{2}{x}_{4}-\frac{4}{3}\pi {x}_{3}^{3}-1296000\le 0\\ {g}_{4}\left(x\right)={x}_{4}-240\le 0\end{array}\right.,\end{array}$$
(27)

where \({x}_{\mathrm{1,2}}\in [0.1, 99]\) and \({x}_{\mathrm{3,4}}\in [10, 200]\) are design variables.

It can be observed in Table 8 that the total cost of MSISOA optimized design is 8050.9172, which is 0.968% lower than that of basic SOA and also lower than that of other algorithms to varying degrees. It shows that MSISOA can minimize the total cost of the pressure vessel design, which has a massive advantage over other algorithms in this problem.

Table 8 Comparison of optimization results of different algorithms in the pressure vessel design problem
Full size table

5.2 Truss Structure Optimization Design

In this section, MSISOA is used to optimize the optimization design of two truss structures: the 21 bars plane truss structure model and the 72 bars spatial structure model.

5.2.1 21 Bars Plane Truss Structure Model

The defining conditions of the truss are: the maximum displacement limit of all nodes along the X-axis and Y-axis is \(6.35\mathrm{ mm}\), the maximum stress is \([-172.375,172.375]\mathrm{MPa}\), the density \(\rho =2678\mathrm{ kg}/{\mathrm{m}}^{3}\), the elastic modulus \(E=68950\mathrm{ MPa}\), the lower limit of the cross-sectional area of each rod is \(0.645{\mathrm{ cm}}^{2}\), and the upper limit is \(258 {\mathrm{cm}}^{2}\). The loading position is shown in Fig. 13, which is \(500\mathrm{ kN}\). Figure 14 shows the displacement diagram of the truss in the optimization process. Red represents the pressure rod, green represents the tie rod, and black dots represent the constrained nodes. For the consideration of local stability, a penalty function is set to make all bars at least meet Euler’s formula for the stability of the compression bar (regardless of the tension and compression bar), and assume that the cross section of the bar is circular to calculate the moment of inertia:

Fig. 13
figure 13

21 bars plane truss drawing

Full size image
Fig. 14
figure 14

Displacement diagram of 21 bars structure

Full size image
$$\begin{array}{c}{F}_{i}\le {F}_{cr}=\frac{{\pi }^{2}EI}{{\left(\mu l\right)}^{2}}.\end{array}$$
(28)

According to the design results of MSISOA and other algorithms for optimizing the quality of the 21 bars plane truss structure given in Table 9, it can be seen that the numerical value obtained by MSISOA in the comparison algorithm is optimal. Compared with the basic SOA algorithm, the optimization result of MSISOA is reduced by 28.6%, the total mass of the truss structure is significantly reduced, and the material and cost are saved. Compared with other algorithms, MSISOA has a significant competitive advantage in the design of 21 bars truss.

Table 9 Optimization results of 21 bars truss structures
Full size table

5.2.2 72 Bars Spatial Truss Structure Model

Establish the 72 bars space truss structure model as shown in Fig. 15. The rods are divided into 16 groups according to the cross-sectional area. Material density \(\rho =2678\mathrm{ kg}/{\mathrm{m}}^{3}\), elastic modulus \(E=68950\mathrm{ MPa}\), each steel bar in each direction of the maximum displacement cannot exceed \(6.35\mathrm{ mm}\), \(L=1. 524\mathrm{ m}\), and the maximum allowable stress is \([-172.375,172.375]\mathrm{ MPa}\). The grouping of rods is shown in Table 10.

Fig. 15
figure 15

72 bars spatial truss structure

Full size image
Table 10 72 bars plane truss structure grouping
Full size table

The objective function is as follows:

$$\begin{array}{l}W\left(A\right)=\sum_{i=1}^{n}\rho {A}_{i}{l}_{i},\end{array}$$
(29)

where \({A}_{i}\) is the cross-sectional area of the \(i\)th element, \({l}_{i}\) is the length of the \(i\)th rod, and \(\rho \) is the material density.

It can be observed from Table 11 that MSISOA optimizes a 15.26% reduction in total mass compared to standard SOA, resulting in a lighter total mass than the other algorithms. In the design of 72 bars space truss structure, The optimization performance of MSISOA is more prominent, and its application in practical engineering can reduce the project's total cost.

Table 11 Comparison of optimal results for the 72 bars spatial truss structure
Full size table

6 Conclusion

This paper presents an improved seagull optimization algorithm based on multi-strategy fusion. The idea is to add four optimization strategies to the standard SOA. Firstly, the L–C cascade chaotic mapping is introduced in the initial population initialization stage of the algorithm to enhance the population diversity of the algorithm. Secondly, introducing a nonlinear convergence factor balances the global search and local population development. The group dimension learning strategy is adopted to improve the algorithm’s population quality and optimization performance. Finally, the golden sine strategy of the Levy flight guidance mechanism is used to enhance the local search ability of the algorithm in the later stage. In the simulation experiments, mechanical optimization problems, and truss structure optimization problems, it is found that MSISOA has a good ability for global exploration and local development, which can promote the seagull to move to the optimal global value to effectively avoid the “premature” phenomenon. At the same time, compared with other improved algorithms, MSISOA can still give very competitive results, indicating that the algorithm has good convergence speed, precision, and robustness. In future studies, the algorithm will be applied to engineering problems, to find suitable industrial parameters.