1 Introduction

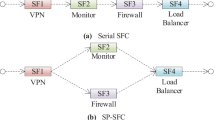
With the continuous emergence of use cases, such as augmented reality (AR), virtual reality (VR), and autonomous driving, network traffic is growing explosively. According to GlobeNewswire’s prediction, the global mobile data traffic will reach 211EB per month by 2026 [1]. However, in traditional networks, network functions are implemented on dedicated hardware devices, resulting in a series of problems, such as high cost and poor scalability. Network function virtualization (NFV) technology is an effective way to solve the above problems. It decouples network functions from hardware devices, and network traffic reaches users according to user needs through service function chain (SFC) composed of multiple virtual network functions (VNFs) in a specific order. For example, the 5G network is cut into a number of virtual end-to-end network slices to support new use cases and diversified services required by multidimensional performance [2]. Each slice provides users with specific services through SFC [3], as shown in Fig. 1. At present, Huawei [4], Cisco [5], and other equipment manufacturers also support SFC technology.

Fig. 1
figure 1

Network slicing

Full size image

VNF is the core function unit of SFC [6]. However, after a long period of continuous operation of VNF, phenomenon of software aging will occur, leading to the destruction of the availability and reliability of SFC and even causing service interruption [7]. In the past 3 decades, outage events caused by software aging have occurred frequently. For example, the Patriot missile defense system failed to intercept enemy missiles due to software aging caused by the continuous accumulation of rounding errors, resulting in significant losses [8].

Software rejuvenation technique can effectively combat software aging before service interruption, thus achieving the goal of high availability and high reliability of SFC [9]. However, the effectiveness of software rejuvenation technique in improving the availability and reliability of SFC needs to be evaluated. The quantitative analysis method based on analytical model is an effective method to evaluate the service availability and reliability in virtualization systems. In recent years, research teams have developed various models. Some studies assumed that the occurrence times of all events followed exponential distribution, and some studies ignored the trigger intervals of software rejuvenation technique. In addition, few studies comprehensively evaluated the effectiveness of software rejuvenation technique from three aspects: steady-state availability, transient availability, and reliability. Therefore, when applying analytical model-based methods to evaluate the availability and reliability of SFC, there are still many problems to be solved, as follows:

  • In a SFC, each VNF has different resource requirements, resulting in different occurrence times of their abnormal events and recovery events. Therefore, how to capture the differences of VNF behaviors is a problem to be solved.

  • The occurrence time of event does not necessarily follow the exponential distribution in the actual system. For example, since the failure rate of components increases with time in practice, the occurrence times of failure events should follow the distribution function with increasing failure rate, such as hypoexponential distribution. Therefore, how to accurately capture the occurrence time of each event in the actual system is a problem to be solved.

  • The trigger intervals of software rejuvenation technique can affect its effectiveness. In addition, triggering software rejuvenation technique at intervals corresponding to the optimal availability of SFC does not necessarily achieve the optimal reliability. Therefore, how to analyze the impact of trigger intervals of software rejuvenation technique on each metric is a problem to be solved.

  • In many key use cases, such as autonomous driving, transient analysis is more important than steady-state analysis. Therefore, how to evaluate the effectiveness of software rejuvenation technique from both transient and steady-state aspects is a problem to be solved.

To overcome the limitations of the above model, we propose a semi-Markov model, which describes the behaviors of each VNF in a SFC from suffering from software aging to recovery by software rejuvenation technique. As far as we know, it is the first time to apply a semi-Markov model to quantitatively evaluate the effectiveness of software rejuvenation technique from steady-state availability, transient availability, and reliability of SFC, taking into account trigger intervals of software rejuvenation technique. The SMP model can avoid the loss of accuracy inherent caused by the inability of non-state-space models to capture the time dependencies between abnormal and recovery behaviors. In addition, compared with the continuous-time Markov chain, it can relax the assumption that the occurrence times of all events follow exponential distribution, to capture SFC system behaviors more accurately. The main contributions of this paper are summarized as follows:

  • We propose an effective semi-Markov model to quantitatively evaluate the effectiveness of software rejuvenation technique, which describes the behaviors of the SFC system deploying software rejuvenation technique from suffering from software aging to recovery. In addition, our model can capture the time dependence between various behaviors.

  • We derive the calculation formulas of steady-state availability, transient availability and reliability of the SFC composed of any number of VNFs. These formulas can prevent the problem of state-space explosion caused by the increase of the number of VNFs in a SFC.

  • We carry out simulation experiments to verify the correctness of the method proposed in this paper. Sensitivity analysis and numerical analysis experiments are also carried out to quantitatively evaluate the impact of system parameters on various metrics. The numerical results provide a theoretical basis for operators to design and deploy SFC elastically.

The rest of this paper is arranged as follows. Section 2 introduces related work. Section 3 introduces the system description, the semi-Markov model proposed in this paper, and the process of calculating availability and reliability. Section 4 introduces the results of numerical experiments. Section 5 presents the conclusions and future work.

2 Related Work

Analytical model-based methods and simulation are two types of model-based quantitative evaluation methods, which can be cross-verified to make the evaluation results more accurate [20]. The goal of this paper is to evaluate the availability and reliability of SFC using the analytical model-based method. Therefore, this section focuses on the studies which applied the analytical model-based method to analyze the availability and reliability of service in the virtualization system.

Analytical models for evaluating availability and reliability can be divided into the following three categories: non-state-space models, such as reliability block diagrams (RBD); state-space models, such as Markov model and semi-Markov model; multi-level models, namely the combination of non-state-space model and state-space model [20].

Fan et al. [10] estimated the SFC availability utilizing a RBD model, in which primary VNFs in the SFC were protected by backup VNFs. Wang et al. [11] applied a RBD model to analyze the availability of SFC executed in parallel, in which the working SFCs used multiple backup SFCs for protection. These non-state-space models did not allow to depict the time dependence of abnormal behaviors (namely software aging and failure behaviors) and recovery behaviors.

Nguyen et al. [12] studied the availability of virtualized server system deploying virtual machine real-time migration technology and failover technology by constructing stochastic reward nets (SRNs) model. Zhu et al. [13] considered a virtualization system where both virtual machines and virtual machine monitors can fail, and analyzed the availability and reliability of the system. Machida et al. [14] proposed a semi-Markov model to study the effectiveness of different software recovery strategies in improving availability. The authors in [15,16,17] evaluated the availability and reliability of the vehicle platooning service, the SFC consisting of serial VNFs and the SFC consisting of serial and parallel VNFs based on semi-Markov models, respectively.

Mauro et al. [18] described the dependence between VNFs in a SFC by constructing a RBD model, and captured the behaviors of a single VNF by constructing SRN models. In addition, the authors in [19] used a RBD model and SRN model to evaluate the availability of IP multimedia subsystem (IMS).

The differences between our work and the existing studies are as follows:

  • The studies [10] and [11] failed to capture the interaction between abnormal behaviors and recovery behaviors of components. The studies [12] and [13] assumed that the occurrence times of all events followed exponential distribution. The studies [10,11,12,13,14,15,16,17,18,19] ignored the impact of trigger intervals of software rejuvenation technique on service reliability and availability. The models developed in studies [12,13,14] were not applicable to evaluating the availability and reliability of services composed of multiple sub-services. Different from these models, our model allows to analyze the time dependence between abnormal behaviors and recovery behaviors of each VNF, as well as the time dependence between various behaviors of VNFs in a SFC, when the occurrence times of failure events and recovery events follow any type of distribution (namely, general distribution). In addition, it can also capture the behaviors of system, considering trigger intervals of software rejuvenation technique.

  • The studies [10,11,12,13,14, 17, 18] only analyzed one or two of the three metrics of steady-state availability, transient availability, and reliability of service. Different from these studies, this paper derives formulas for calculating steady-state availability, transient availability and reliability to analyze the effectiveness of software rejuvenation technique in multiple dimensions.

  • The studies [11,12,13,14] did not carry out simulation experiments. The studies [10, 11, 13,14,15] and [17] did not carry out sensitivity analysis experiments. Different from these studies, this paper verifies the correctness of the model and formulas proposed in this paper by performing simulation experiments. In addition, by conducting sensitivity analysis experiments, we identify bottlenecks that restrict the improvement of the effectiveness of software rejuvenation technique, laying the foundation for optimizing the availability and reliability of SFC.

Table 1 shows the comparison between our work and the aforementioned studies.

Table 1 Comparison of existing models discussed in Sect. 2
Full size table

3 System Description and Model

This section first introduces the system illustrated in this paper. Then, the semi-Markov model constructed in this paper is introduced. Finally, the calculation formulas of steady-state availability, transient availability, and reliability metrics are given.

3.1 System Description

Figure 2 shows an example of the SFC system architecture studied in this paper. There are multiple hosts in the system, and each host operating system runs multiple containers. The active containers execute active VNFs in a SFC and backup containers execute backup VNFs which are used to support failover technology. We assume that the backup resources running on each host are sufficient, so there is an available backup VNF at any time. User requests are processed sequentially by VNFs in a SFC. After running for a period of time, these VNFs can suffer from software aging and failure caused by software aging. The details are as follows: if an active VNF is detected to suffer from software aging, a healthy backup VNF will be selected to support failover technology. After a certain interval, the failover technology is triggered, that is, the backup container takes over the request being processed. During failover or the trigger interval of failover technology, if other VNFs are detected to suffer from software aging, all VNFs in the system will be restarted. If a VNF is detected to fail, this component will be repaired. After it is repaired, all hosts in the system will be rebooted.

Fig. 2
figure 2

System architecture

Full size image

In addition, we assume that the occurrence times of failure events and recovery events in the system follow general distribution, and the occurrence times of software aging events follow exponential distribution.

3.2 Semi-Markov Model

Define an n-tuple index \((i_{S1} ,i_{S2} ,i_{S3} , \ldots ,i_{Sn} )\) to represent the system state, where \(i_{Sn}\) represents the state of the nth VNF. Each VNF may have five states: healthy (H), software aging (A), failure (F), failover (L), and restart (R). Each state is defined as follows:

  • Healthy (H): in this state, all VNFs can run efficiently.

  • Software aging (A): in this state, software aging occurs, and the rate of executing requests slows down.

  • Failure: in this state, VNF fails due to software aging.

  • Failover: in this state, failover technology will be triggered.

  • Restart: In this state, VNF will be restarted.

There are \(5^{n}\) system states, among which the number of meaningless states is \(5^{n} - 2n - 3\). For example, because VNFs in a SFC are connected together in a sequential order, the request processing stops when a VNF fails. Therefore, the state \((F_{S1} ,H_{S2} ,H_{S3} ,...,H_{Sn} )\) is meaningless.

Based on the aforementioned analysis, the semi-Markov model can be used to capture the behaviors of each VNF in a SFC from the occurrence of software aging to the recovery using software rejuvenation technique. The state sequence of this random process at transition occurrence time points forms an embedded discrete time Markov chain (EDTMC). The occurrence times of failure and recovery events follow general distribution. Figure 3 shows an example of the semi-Markov model, which is used to describe the behaviors of a SFC consisting of 6 VNFs. The definition of variables used in the figure is shown in Table 2. In this model, the SFC system starts with state \((H_{S1} ,...,H_{S6} )\). After a period of operation, VNFs in the system can suffer from software aging. If the 1st VNF suffers from software aging, the system will enter state \((D_{S1} ,...,H_{S6} )\). When the system stays at state \((D_{S1} ,...,H_{S6} )\), if the 1st VNF fails, the system will enter state \((F_{S1} ,...,F_{S6} )\), if one of other VNFs suffers from software aging, the system will enter state \((R_{S1} ,...,R_{S6} )\), and if failover technology is triggered after a certain interval, the system will enter state \((L_{S1} ,...,H_{S6} )\). When the system stays at state \((L_{S1} ,...,H_{S6} )\), if the 1st VNF fails, the system will enter state \((F_{S1} ,...,F_{S6} )\), if one of the other VNFs suffers from software aging, the system will enter state \((R_{S1} ,...,R_{S6} )\), and if the backup container takes over requests, the system will enter state \((H_{S1} ,...,H_{S6} )\). When the system stays at state \((R_{S1} ,...,R_{S6} )\), the system enters state \((H_{S1} ,...,H_{S6} )\) after restarting all VNFs. From state \((F_{S1} ,...,F_{S6} )\), the system returns back to state \((H_{S1} ,...,H_{S6} )\) after repairing the failed VNF and rebooting all VNFs. The subsequent state transitions after other VNFs suffer from software aging are similar to that after the 1st VNF suffers from software aging.

Fig. 3
figure 3

Semi-Markov model

Full size image
Table 2 Variable definition
Full size table

3.3 Transient Availability Analysis

The transient availability \(\pi_{{{\text{availability}}}} {(}t{)}\) of the SFC composed of n VNFs can be calculated by solving the probability that the system is unavailable at time t, which is shown in Eq. (1):

$$\begin{aligned} \pi_{{{\text{availability}}}} {(}t) & = 1 - \pi_{{S_{{{(}2n + 1{)}}} }} (t) - \pi_{{S_{{{(}2n + 2{)}}} }} (t) \\ & = 1 - \sum\limits_{i = 0}^{2n + 2} {\pi_{{S_{i} }} (0)} (V_{{S_{i} S_{(2n + 1)} }} {(}t{) + }V_{{S_{i} S_{(2n + 2)} }} {(}t{)),} \\ \end{aligned}$$
(1)

where \(\pi_{{S_{i} }} {(}0{)}\) (\(0 \le i \le 2n{ + }2\)) is the initial state probability and \(V_{{S_{i} S_{j} }} {(}t{)}\) (\(0 \le i,j \le 2n{ + }2\)) is the non-zero element in the transient solution matrix of conditional transition probability \({\mathbf{V}}_{{\text{S}}} {(}t{)}\).

The calculation process of \({\mathbf{V}}_{{\text{S}}} {(}t{)}\) is shown in Eq. (2):

$${\mathbf{V}}_{{\text{S}}}^{\sim } (s) = {\mathbf{\rm E}}_{{\text{S}}}^{\sim } (s) + {\mathbf{K}}_{{\text{S}}}^{\sim } (s){\mathbf{V}}_{{\text{S}}}^{\sim } (s),$$
(2)

where \({\mathbf{V}}_{{\text{S}}}^{\sim } (s)\),\({\mathbf{K}}_{{\text{S}}}^{\sim } (s)\) and \({\mathbf{\rm E}}_{{\text{S}}}^{\sim } (s)\) are Laplace–Stieltjes transform of \({\mathbf{V}}_{{\text{S}}} {(}t{)}\), kernel matrix \({\mathbf{K}}_{{\text{S}}} {(}t{)}\) and diagonal matrix \({\mathbf{E}}_{{\text{S}}} (t)\), respectively [20]. The non-zero element \(k_{{S_{i} S_{j} }} {(}t{)}\) (\(0 \le i,j \le 2n{ + }2\)) in the kernel matrix can be solved by Eqs. (3)–(11), and the non-zero element \(E_{{S_{i} S_{i} }} {(}t{)}\) (\(0 \le i \le 2n{ + }2\)) in the diagonal matrix can be solved by Eq. (12) [20]:

$$k_{{S_{0} S_{i} }} {(}t{)} = \int_{0}^{t} {\mathop \Pi \limits_{{r \in B_{i} }} {(}1 - F_{{{\text{d}}r}} {(}t{\text{))d}}F_{{{\text{d}}i}} {(}t{)}} ,$$
(3)
$$\begin{aligned} k_{{S_{i} S_{{{(}n{ + }i{)}}} }} {(}t{)} & = F_{{{\text{u}}i}} {(}t{)(}1 - \int_{0}^{{a_{i} }} {{(}1 - F_{{{\text{dd}}i}} {(}t{\text{))d}}F_{{{\text{fd}}i}} {(}t{)}} \\ & \quad - \int_{0}^{{a_{i} }} {{(}1 - F_{{{\text{fd}}i}} {(}t{\text{))d}}F_{{{\text{dd}}i}} {(}t{)}} {),} \\ \end{aligned}$$
(4)
$$k_{{S_{i} S_{{{(2}n{ + 1)}}} }} {(}t{)} = \int_{0}^{t} {{(}1 - F_{{{\text{u}}i}} {(}t{))(}1 - F_{{{\text{dd}}i}} {(}t{\text{))d}}F_{{{\text{fd}}i}} {(}t{)}} ,$$
(5)
$$k_{{S_{i} S_{{{(2}n{ + 2)}}} }} {(}t{)} = \int_{0}^{t} {{(}1 - F_{{{\text{u}}i}} {(}t{))(}1 - F_{{{\text{fd}}i}} {(}t{\text{))d}}F_{{{\text{dd}}i}} {(}t{)}} ,$$
(6)
$$k_{{S_{{{(}i + n{)}}} S_{0} }} {(}t{)} = \int_{0}^{t} {{(}1 - F_{{{\text{fl}}i}} {(}t{))(}1 - F_{{{\text{dd}}i}} {(}t{\text{))d}}F_{{{\text{r}}i}} {(}t{)}} ,$$
(7)
$$k_{{S_{{{(}i + n{)}}} S_{{{(2}n{ + 1)}}} }} {(}t{)} = \int_{0}^{t} {{(}1 - F_{{{\text{r}}i}} {(}t{))(}1 - F_{{{\text{dd}}i}} {(}t{\text{))d}}F_{{{\text{fl}}i}} {(}t{)}} ,$$
(8)
$$k_{{S_{{{(}i + n{)}}} S_{{{(2}n{ + 2)}}} }} {(}t{)} = \int_{0}^{t} {{(}1 - F_{{{\text{r}}i}} {(}t{))(}1 - F_{{{\text{fl}}i}} {(}t{\text{))d}}} F_{{{\text{dd}}i}} {(}t{),}$$
(9)
$$k_{{S_{{{(2}n{ + }1{)}}} S_{0} }} {(}t{)} = F_{{\text{R}}} {(}t{),}$$
(10)
$$k_{{S_{{{(2}n{ + }2{)}}} S_{0} }} {(}t{)} = F_{{{\text{RS}}}} {(}t{),}$$
(11)
$$E_{{S_{i} S_{i} }} {(}t{)} = 1 - \sum\limits_{j = 0}^{2n + 2} {k_{SiSj} {(}t{)}} .$$
(12)

Therefore, at time t, the probabilities of the system in the unavailable states can be solved by Eqs. (13)–(15):

$$\begin{aligned} {\pi _{{S_{(2n + 1)}}}}{\text{(}}t{\text{)}} & = {L^{ - 1}}( - E_{{S_{(2n + 1)}}{S_{(2n + 1)}}}^\sim {\text{(}}t)(\sum\nolimits_{i = 1}^n {{\text{(}}k_{{S_0}{S_i}}^\sim (t)} k_{{S_i}{S_{(i + n)}}}^\sim (t)k_{{S_{(i + n)}}{S_{(2n + 1)}}}^\sim (t) \\ & \quad + k_{{S_0}{S_i}}^\sim (t)k_{{S_i}{S_{(2n + 1)}}}^\sim (t){\text{))}})/A, \end{aligned}$$
(13)
$$\begin{aligned} {\pi _{{S_{(2n + 2)}}}}{\text{(}}t{\text{)}} & = {L^{ - 1}}( - E_{{S_{(2n + 2)}}{S_{(2n + 2)}}}^\sim {\text{(}}t)(\sum\nolimits_{i = 1}^n {{\text{(}}k_{{S_0}{S_i}}^\sim (t)} k_{{S_i}{S_{(i + n)}}}^\sim (t)k_{{S_{(i + n)}}{S_{(2n + 2)}}}^\sim (t) \\ & \quad + k_{{S_0}{S_i}}^\sim (t)k_{{S_i}{S_{(2n + 2)}}}^\sim (t){\text{))}})/A, \end{aligned}$$
(14)
$$\begin{aligned} A & = \sum\limits_{i = 1}^n {(k_{{S_0}{S_i}}^\sim (t)k_{{S_i}{S_{(i + n)}}}^\sim (t)k_{{S_{(i + n)}}{S_0}}^\sim (t)} + k_{{S_0}{S_i}}^\sim (t)k_{{S_i}{S_{(i + n)}}}^\sim (t) \\ & \quad k_{{S_{(i + n)}}{S_{(2n + 1)}}}^\sim (t)k_{{S_{(2n + 1)}}{S_0}}^\sim (t) + k_{{S_0}{S_i}}^\sim (t)k_{{S_i}{S_{(i + n)}}}^\sim (t)k_{{S_{(i + n)}}{S_{(2n + 2)}}}^\sim (t) \\ & \quad k_{{S_{(2n + 2)}}{S_0}}^\sim (t) + k_{{S_0}{S_i}}^\sim (t)k_{{S_i}{S_{(2n + 1)}}}^\sim (t)k_{{S_{(2n + 1)}}{S_0}}^\sim (t) + k_{{S_0}{S_i}}^\sim (t) \\ & \quad k_{{S_i}{S_{(2n + 2)}}}^\sim (t)k_{{S_{(2n + 2)}}{S_0}}^\sim (t)). \end{aligned}$$
(15)

3.4 Steady-State Availability Analysis

The steady-state availability \(\pi_{{{\text{availability}}}}\) of the SFC composed of n VNFs can be calculated by solving the steady-state probabilities of the system in the unavailable states, which is shown in Eq. (16):

$$\begin{aligned} \pi_{{{\text{availability}}}} & = 1 - \pi_{{S_{{{(}2n + 1{)}}} }} - \pi_{{S_{{{(}2n + 2{)}}} }} = 1 - (V_{{S_{(2n + 1)} }} h_{{S_{(2n + 1)} }} \\ & \quad + V_{{S_{(2n + 2)} }} h_{{S_{(2n + 2)} }} )/(\sum\limits_{i = 0}^{2n + 2} {V_{{S_{i} }} h_{{S_{i} }} )} , \\ \end{aligned}$$
(16)

where \(h_{{S_{i} }}\) is the sojourn time of the system in state \(S_{i}\) (\(0 \le i \le 2n{ + }2\)), which can be solved by Eqs. (17)–(21) [20].

$$h_{{S_{0} }} = \int_{0}^{\infty } {\mathop \Pi \limits_{r \in B} {(}1 - F_{{{\text{d}}r}} {(}t{\text{))d}}t} ,$$
(17)
$$h_{{S_{i} }} = \int_{0}^{{a_{i} }} {{(}1 - F_{{{\text{fd}}i}} {(}t{))(}1 - F_{{{\text{dd}}i}} {(}t{\text{))d}}t} ,$$
(18)
$$h_{{S_{{{(}i + n{)}}} }} = \int_{0}^{\infty } {{(}1 - F_{{{\text{fl}}i}} {(}t{))(}1 - F_{{{\text{dd}}i}} {(}t{))(}1 - F_{{{\text{r}}i}} {(}t{\text{))d}}t} ,$$
(19)
$$h_{{S_{{{(2}n{ + 1)}}} }} = \int_{0}^{\infty } {{(}1 - F_{{\text{R}}} {(}t{\text{))d}}t} ,$$
(20)
$$h_{{S_{{{(2}n{ + 2)}}} }} = \int_{0}^{\infty } {{(}1 - F_{{{\text{RS}}}} {(}t{\text{))d}}t} .$$
(21)

\(V_{{S_{i} }}\) is the steady-state probability of the EDTMC for system state \(S_{i}\) (\(0 \le i \le 2n{ + }2\)). The calculation process of \(V_{{S_{i} }}\) is shown in Eqs. (22)–(27):

$$V_{{S_{0} }} = 1/M,$$
(22)
$$V_{{S_{i} }} = p_{{S_{0} S_{i} }} {/}M,$$
(23)
$$V_{{S_{{{(}i + n{)}}} }} = p_{{S_{0} S_{i} }} p_{{S_{i} S_{{{(}i + n{)}}} }} {/}M,$$
(24)
$$V_{{S_{{{(2}n{ + 1)}}} }} = \sum\limits_{i = 1}^{n} {{(}p_{{S_{0} S_{i} }} p_{{S_{i} S_{{{(}i + n{)}}} }} p_{{S_{{{(}i + n{)}}} S_{{{(2}n{ + 1)}}} }} } + p_{{S_{0} S_{i} }} p_{{S_{i} S_{{{(2}n{ + 1)}}} }} {)/}M,$$
(25)
$$V_{{S_{{{(2}n{ + 2)}}} }} = \sum\limits_{i = 1}^{n} {{(}p_{{S_{0} S_{i} }} p_{{S_{i} S_{{{(}i + n{)}}} }} p_{{S_{{{(}i + n{)}}} S_{{{(2}n{ + 2)}}} }} } + p_{{S_{0} S_{i} }} p_{{S_{i} S_{{{(2}n{ + 2)}}} }} {)/}M,$$
(26)
$$\begin{gathered} M = 1 + \sum\limits_{i = 1}^{n} {{(}p_{{S_{0} S_{i} }} p_{{S_{i} S_{{{(}i + n{)}}} }} p_{{S_{{{(}i + n{)}}} S_{{{(2}n{ + 1)}}} }} } + p_{{S_{0} S_{i} }} p_{{S_{i} S_{{{(2}n{ + 1)}}} }} { + }p_{{S_{0} S_{i} }} \hfill \\ \qquad p_{{S_{i} S_{{{(}i + n{)}}} }} p_{{S_{{{(}i + n{)}}} S_{{{(2}n{ + 2)}}} }} + p_{{S_{0} S_{i} }} p_{{S_{i} S_{{{(2}n{ + 2)}}} }} { + }p_{{S_{0} S_{i} }} + p_{{S_{0} S_{i} }} p_{{S_{i} S_{{{(}i{ + }n{)}}} }} {),} \hfill \\ \end{gathered}$$
(27)

where \(p_{{S_{i} S_{j} }}\) (\(0 \le i,j \le 2n{ + }2\)) is the non-zero element in the one-step transition probability matrix \({\mathbf{P}}_{{\text{S}}}\), which can be obtained by solving \({\mathbf{P}}_{{\text{S}}} = {\text{lim}}_{t \to \infty } {\mathbf{K}}_{{\text{S}}} {(}t{)}\) [20].

3.5 Reliability Analysis

The mean time to failure (MTTF) is one of the metrics widely used in evaluating reliability. The MTTF of the SFC composed of n VNFs can be calculated by solving the mean time of the system from the beginning to the failure [20], which is shown in Eq. (28):

$${\text{MTTF}} = \sum\limits_{i = 0}^{2n} {V_{{S_{i*}}}^*h_{{S_{i*}}}^*} ,$$
(28)

where \(V_{{S_{i*} }}^{*}\) is the expected number of accesses to state \(S_{i*}\) (\(0 \le i* \le 2n\)) before reaching the absorption state represented by the yellow state in Fig. 3 and \(h_{{S_{i*} }}^{*}\) is the sojourn time of the system in state \(S_{i*}\) (\(0 \le i* \le 2n\)). \(V_{{S_{i*} }}^{*}\) can be obtained by solving Eqs. (29)–(32), where \(p_{{S_{i*} S_{j*} }}\) (\(0 \le i*,j* \le 2n\)) can be obtained by solving \({\mathbf{P}}_{{\text{S}}}^{*} = {\text{lim}}_{t \to \infty } {\mathbf{K}}_{{\text{S}}}^{*} {(}t{)}\) [20]. \(h_{{S_{i*} }}^{*}\) can be solved by Eqs. (29)–(32):

$$V_{{S_{0} }}^{*} = - 1/W,$$
(29)
$$V_{{S_{i*} }}^{*} = - p_{{S_{0} S_{i*} }} {/}W,$$
(30)
$$V_{{S_{{{(}i* + n{)}}} }}^{*} = - p_{{S_{0} S_{i*} }} p_{{S_{i*} S_{{{(}i* + n{)}}} }} {/}W,$$
(31)
$$W = \sum\limits_{i* = 1}^{n} {(p_{{S_{0} S_{i*} }} p_{{S_{i*} S_{(i* + n)} }} p_{{S_{(i* + n)} S_{0} }} )} - 1.$$
(32)

4 Experimental Result

In this section, we first perform simulation to prove the approximate accuracy of our proposed model and derived formulas. Then we conduct sensitivity analysis experiments and numerical experiments to analyze the effects of system parameters, the number of VNFs and trigger interval of software rejuvenation technique on availability and reliability of SFC, and the effects of time-varying parameters on transient availability on SFC.

4.1 Experimental Configuration

Tables 2 and 3 show the default values of variables and the types of cumulative distribution functions that were used in the experiment, respectively. Note that some default values are set according to literature [21,22,23], and the use of other default values and cumulative distribution function types is only an example to prove the effectiveness of the model proposed in this paper. In this section, we use Maple software [23] to perform simulation experiments and numerical analysis experiments. Note that simulation and numerical analysis software can be implemented in any programming language.

Table 3 Type of cumulative distribution function and default value used in the experiment
Full size table

4.2 Verification of Model and Formulas

Figures 4, 5, and 6 show the comparison of numerical results and simulation results of transient availability, steady-state availability and MTTF of SFC, respectively. ‘Num’ and ‘Sim’ in these figures represent numerical results and simulation results, respectively. From these figures, it can be observed that the difference between the numerical results and the related simulation results is very small, which proves the approximate accuracy of our proposed model and derived formulas.

Fig. 4
figure 4

Comparison of numerical and simulation results for transient availability

Full size image
Fig. 5
figure 5

Comparison of numerical and simulation results for steady-state availability

Full size image
Fig. 6
figure 6

Comparison of numerical results and simulation results for MTTF

Full size image

4.3 Sensitivity Analysis

Table 4 shows the results of sensitivity analysis of steady-state availability and MTTF of SFC, with respect to system parameters. We observe:

  • The steady-state availability and MTTF of SFC increase with the increase of the VNF aging time and failure time, and decrease with the increase of the failover time. The steady-state availability of SFC decreases with the increase of the system repair time and the time of restarting all VNFs. The MTTF of SFC is independent of the system repair time and the time of restarting all VNFs.

  • Compared with other parameters, system repair time and the time of restarting all VNFs have the greatest impact on steady-state availability. The VNF aging time and failure time have the greatest impact on MTTF.

Table 4 Sensitivity of availability and MTTF
Full size table

These experimental results can help service providers identify bottlenecks that affect the improvement of the availability and reliability of SFC.

4.4 Effect of Trigger Interval of Software Rejuvenation Technique on Steady-State Availability and MTTF

Figure 7 shows the numerical results of the steady-state availability of SFC under different trigger intervals of software rejuvenation technique (a1) and system repair times (TR). Figure 8 shows the numerical results of MTTF of SFC under different trigger intervals of software rejuvenation technique (a1) and VNF failure times (Tfd1). It can be observed from Figs. 7 and 8 that with the increase of the trigger interval of software rejuvenation technique, the steady-state availability of SFC first increases and then decreases, and the MTTF of SFC decreases. This is because when the trigger interval of software rejuvenation technique is less than the optimal value, the sojourn time of SFC in available states increases with the increase of trigger intervals of software rejuvenation technique. When the trigger interval of software rejuvenation technique is greater than the optimal value, the failure probability of VNF before triggering software rejuvenation technique increases with the increase of trigger interval. We can also observe the optimal trigger interval of software rejuvenation technique and the corresponding maximum steady-state availability and MTTF of SFC. For example, when TR is 0.8 h, the maximum steady-state availability is 0.999990369, that is, the downtime allowed is about 5 min and 1.4 s per year, which is achieved at a1 = 1.49065 h. In addition, as the system repair time increases, the optimal trigger interval of software rejuvenation technique corresponding to the maximum steady-state availability of SFC increases, and the corresponding maximum steady-state availability of SFC increases.

Fig. 7
figure 7

Steady-state availability under different trigger intervals of software rejuvenation technique and system repair time

Full size image
Fig. 8
figure 8

MTTF under different trigger intervals of software rejuvenation technique and VNF failure time

Full size image

4.5 Effect of the Number of VNFs on Steady-State Availability, Transient Availability, and MTTF

Table 5 shows the numerical results of the steady-state availability, transient availability, and MTTF of SFC under different numbers of VNFs (n). It can be observed from Table 5 that as the number of VNFs increases, the steady-state availability, transient availability, and MTTF of SFC decrease. This is because the increase in the number of VNFs in a SFC leads to an increase in the number of components that may fail, thus increasing the time the system stays in the unavailable states.

Table 5 Steady-state availability, transient availability and MTTF under different number of VNFs
Full size table

4.6 Effect of Time-Varying Parameters on Transient Availability

Figure 9 shows the impact of time-varying parameters on transient availability of SFC. The gray line indicates that as the number of VNFs (n) increases from 6 to 7 in the 2nd hour, the transient availability decreases and then becomes stable. The yellow line indicates that when the VNF aging time (Td1) increases from 10 to 100 h in the 2nd hour, the transient availability also increases. When the VNF aging time decreases to 50 h in the 4th hour, the transient availability decreases and then becomes stable. The blue line indicates that when the time of restarting all VNFs (TRS) decreases from 15 to 10 s in the 1st hour, the transient availability increases. When the time of restarting all VNFs increases to 20 s in the 3rd hour, the transient availability decreases. When the time of restarting all VNFs decreases to 15 s in the 5th hour, the transient availability increases but decreases compared with the transient availability in the 1st hour.

Fig. 9
figure 9

Effect of time-varying parameters on transient availability

Full size image

5 Conclusions and Future Work

This paper proposes a semi-Markov model to quantitatively analyze the effectiveness of software rejuvenation technique on the steady-state availability, transient availability, and reliability of SFC. The sensitivity analysis results reveal that the system repair time and the time of restarting all VNFs have the greatest impact on the availability of SFC. The VNF aging time and failure time have the greatest impact on the reliability of SFC. The numerical experiment reveals that with the increase of the trigger interval of software rejuvenation technique, the availability of SFC first increases and then decreases, and the reliability of SFC decreases. As the number of VNFs increases, the availability and reliability of SFC decreases.

This paper assumes that the backup VNFs are sufficient. However, in practice, due to resource and cost constraints, the number of backup VNFs is limited, resulting in no backup VNFs available when triggering failover technology. Therefore, in the future, we will study the effect of the number of backup VNFs and their abnormal behaviors on the effectiveness of software rejuvenation technique.