A Large Group Decision Making Method Considering Experts’ Non-cooperative Behavior for Investment Selection of Renewable Energy Projects

Abstract

The rapid expansion of renewable energy has attracted the attention of investors, which makes the evaluation of renewable energy projects a momentous issue. As the investment selection of renewable energy projects requires the joint discussion of experts from different professional backgrounds (such as energy, transportation, construction, economy, environment, etc.), it belongs to the category of large group decision-making (LGDM). Therefore, this paper is devoted to propose a novel LGDM method considering experts’ non-cooperative behavior for investment selection of renewable energy projects. First, considering that the complexity of renewable energy projects makes it difficult for experts to express their views in a single linguistic word, the hesitant fuzzy linguistic term set is used as the tool for expert evaluation in this paper. Second, since the assessment information provided by experts from different fields are often heterogeneous, a consensus-reaching process with a feedback mechanism is introduced which comprehensively considers three reliable sources: the experts’ trust relationship in the social trust network, the consensus contribution in the subgroup and the opinions’ similarity among experts. Further, to improve the efficiency and rationality of decision-making, an experts’ historical adjustment data-based non-cooperative behavior management method is proposed. Finally, the effectiveness and innovation of the proposed method are verified by a case of renewable energy power generation project investment selection in Qingdao, China and a series of comparative analysis.

1 Introduction

As a country with the second largest energy system in the world, China’s energy reserves are in the forefront of the world, but its energy consumption is also in the forefront of the world [41]. The emergence of problems such as relatively small per capita resources, large resource consumption, unbalanced energy supply, large environmental pollution and unstable energy structure has led to an urgent need for the development of the renewable energy industry. Therefore, the state has issued numerous policies to support the rapid development of renewable energy, which has promoted the emergence of many new technologies. Meanwhile, the changes in China’s energy composition from 2018 to 2020 (as shown in Fig. 1) show that the renewable energy industry is developing steadily. Thus, in recent years, more and more renewable energy projects have been developed in response to the call for low-carbon action, which has attracted the attention of numerous investors.

Fig. 1

Changes in China’s energy composition from 2018 to 2020

However, although renewable energy has the advantages of clean, low-carbon, safe and efficient use, it is still not the preferred energy at the ideal level because the cost of renewable energy alternatives is relatively high compared with fossil fuels [2]. Therefore, the investment selection of renewable energy projects should be treated with caution, which often requires various experts from multiple fields with different professional backgrounds to jointly discuss and analyze. Therefore, it constitutes a large group decision-making problem (LGDM). Moreover, the evaluation of the investment selection of renewable energy projects needs to be carried out according to the comprehensive impact on the environment, society and economy, with high uncertainty, and many criteria are difficult to quantify. In this case, qualitative tools can be used instead of real numbers for evaluation. Therefore, this paper aims to study the investment selection of renewable energy projects with hesitant fuzzy linguistic information, which allows experts to hesitate between multiple linguistic words in the assessment process.

In addition, in group cooperation, individuals can significantly improve their rationality through mutual restriction and influence, thus maximizing group efficiency. However, in the actual group decision-making, the decision-making members are often heterogeneous, with different knowledge backgrounds, preference habits and interest goals, and various conflicts are inevitable [10, 11, 19]. For example, the architect believes that the feasibility of a wind power project is very high because its wind turbine covers a relatively small area and can be installed not only in industrial-scale facilities but also in residential facilities. However, the assessment given by environmental analysts is that the feasibility is low, because wind turbines not only pose a threat to local birds and bats but also have high noise pollution and visual pollution. It is obvious that the decision-making results obtained in the case of conflicting opinions are meaningless and cannot provide a reliable reference for the investment selection of the projects. Therefore, to obtain a highly consensus solution, it is indispensable part to revise the conflicting opinions, which means the consensus-reaching process (CRP) should be introduced into the investment selection decision-making of renewable energy projects.

Moreover, as another major challenge of LGDM, non-cooperative behavior (NCB) is not rare in the CRP [13]. In the face of the adjustment opinions provided by the feedback mechanism according to their social relations or initial evaluation opinions, not all experts are willing to cooperate with the modification and strive to reach a consensus and obtain scientific and reasonable decision-making results. There may be experts who are unwilling to cooperate with the adjustment of their personal evaluation opinions for the sake of interests [16]. For example, when evaluating multiple energy investment projects, the analysts involved in the decision-making have an interesting relationship with one of the projects. In the face of the suggestions provided by the feedback mechanism to reduce the evaluation value of the project, they may only be willing to modify some of them, or even refuse to modify the opinions. Evidently, this will slow down the overall decision-making process, and even lead to the failure of consensus and decision-making. Further, the LGDM involves at least 20 participants [3, 7, 17], which is more likely to occur. Therefore, it is imperative to propose corresponding management methods to reduce the adverse impact of non-cooperative behaviors on the process of investment selection of renewable energy projects.

Through the above analysis, it can be found that there may be the following two problems to be solved in the investment selection of renewable energy projects:

• 1. In actual decision-making, the opinions of experts from different fields and with different professional levels are often heterogeneous. The conflicting opinions should be corrected to obtain a high consensus decision-making result.

• 2. When providing a reference for experts to modify their opinions in the process of reaching a consensus, some experts may only modify some opinions or refuse to modify their opinions for the sake of individual interests.

Therefore, this paper is devoted to propose an applicative LGDM method considering experts’ NCB for the investment selection of renewable energy projects. This method not only considers the conflict of opinions among different experts but also considers the situation in that experts show different times of NCB in the feedback process. Accordingly, in view of the above two limitations, this paper mainly makes the following contributions:

• 1. A novel interactive feedback mechanism for the investment selection of renewable energy projects is constructed to reduce the conflict of opinions of different experts. In the feedback mechanism of the CRP, the trust relationship of experts in the social trust network (STN), the consensus contribution in the subgroup, and the similarity of opinions among experts are fully utilized to provide personalized and accurate feedback for experts in the non-consensus subgroup.

• 2. In the feedback mechanism, the NCB identification and management method based on the historical adjustment data of experts is introduced to can reduce the delay and even failure of decision-making caused by personal interests in the evaluation process of renewable energy projects. This method proposes different management methods for experts who show different times of NCB. Specifically, a management method based on weight punishment is proposed to manage experts who exhibit the behavior once; A two-stage management method based on opinion punishment is proposed to manage experts who exhibit the behavior twice.

• 3. The proposed method is applied to the investment selection of four renewable energy power generation projects located in Qingdao, China. By analyzing the advantages and disadvantages of the four projects in the four criteria of energy security, energy efficiency, business continuity and policy consistency, the most suitable project investment selection is determined. Finally, by comparing with the current research methods, the effectiveness of the proposed method is verified.

The rest of this paper is organized as follows. Section 2 includes the research status of renewable energy, the consensus feedback mechanism of LGDM and NCB management methods. Section 3 is a preliminary introduction to the basic knowledge related to hesitant fuzzy linguistic term set and STN. In Sect. 4, LGDM method for investment selection of renewable energy projects is proposed, which includes a novel feedback mechanism and experts’ historical adjustment data-based non-cooperative behavior management method. In Sect. 5, the LGDM method is applied to the investment selection of four renewable energy power generation projects in Qingdao, China. Section 6 includes a comparative analysis with existing methods. Finally, the conclusion and prospect are introduced in Sect. 7.

2 Literature Review

This section is divided into three parts of the literature review related to this study: (1) renewable energy; (2) CRP; (3) NCB management method.

2.1 Renewable Energy

In the context of energy transformation, renewable energy has received attention [5, 8, 26]. In the assessment and selection of renewable energy, Li et al. [12] proposed a novel decision-making experiment and evaluation laboratory method to analyze multiple renewable energy sources suitable for cities, and ranked these energy sources by preference ranking organization method. Besides, Peng et al. [24] developed a multi-criteria decision-making (MCDM) method with probabilistic linguistic information and applied it to the selection of new energy sources. In the assessment of renewable energy technologies, Zhao et al. [40] developed a hesitant fuzzy linguistic prioritized superiority and inferiority ranking method, which model the priority relationship between standards by modifying the real weight of standards. In terms of investment risk assessment of renewable energy projects, Zhou et al. [42] proposed a new mixed MCDM model based on indecisive language terms and alpha level set. And Kul et al. [9] provided an MCDM method-based three-stage decision-making framework to evaluate the risk factors of Turkey’s renewable energy investment, which includes the Delphi method-based identification stage, the AHP-based evaluation stage and the strategy selection stage to overcome the risk factors. Furthermore, according to the different preferences of investors, Wu et al. [31] proposed an investment decision-making framework for regional energy Internet projects through interval type-2 fuzzy number, Choquet integral and fuzzy comprehensive evaluation model.

However, although renewable energy projects involve expertise in many fields, most of these studies focus on decision-making involving individuals or small groups. And few studies focus on the conflict between experts’ evaluation opinions and the management of experts’ NCBs in the investment selection of renewable energy projects.

2.2 Consensus Reaching Process (CRP)

The purpose of introducing a CRP in the investment selection of renewable energy projects is to achieve a high consensus level in the decision-making results, which means the ranking of the obtained alternatives is recognized by most participants. Through a systematic review of recent consensus decision-making studies, it is found that there are two types of consensus rules commonly used in group consensus decision-making: (1) Feedback mechanism [20, 27, 35]. Through the construction of the corresponding identification and adjustment mechanism, with the help of the consensus coordinator, the evaluation opinions are adjusted iteratively, including interactive adjustment and automatic adjustment. For example, Liu et al. [21] proposed a dynamic interactive weight updating method based on consensus contribution and constructed a consensus feedback strategy based on compromise degree. Besides, Li et al. [15] proposed a consensus-reaching method for large-scale group decision-making (LSGDM) based on bounded confidence and social networks to manage expert opinions. (2) Optimization model [19, 36], which makes the group meet the consensus requirements at one time by constructing the corresponding mathematical programming model. For example, by considering three reliable sources: consistency, similarity and centrality, Liu et al. [18] designed a method to maximize the consensus level between the subgroup and the collective matrix to generate the comprehensive weight of the subgroup. Moreover, Liu et al. [17] proposed a consensus decision framework based on STN and a consensus optimization model based on bounded confidence in the context of multi-criteria LSGDM.

To make the revised evaluation information convincing to experts, the CRP based on the feedback mechanism is introduced into the investment selection of renewable energy projects. And the proposed feedback mechanism comprehensively considers the social trust relationship of experts, the consensus contribution in the consensus process and the similarity of opinions among experts.

2.3 Non-cooperative Behavior (NCB) Management Method

To ensure the efficiency and quality of renewable energy project investment decision-making, it is imperative to analyze and manage the NCBs of participants in the consensus-building process based on the feedback mechanism.

As another major challenge of group decision making (GDM), NCB is not rare in the CRP, which has attracted the attention of many scholars. For example, Gao and Zhang [6] developed an NCB management mechanism for dynamically adjusting the trust degree of social networks to reach a consensus on the GDM problem of social networks based on personalized individual semantic. And Li et al. [13] developed a method for identifying and punishing NCBs based on individual weights and trust values in an interactive network environment like WeChat. Besides, Liao et al. [16] divided the conflicts of experts into internal conflicts and external conflicts, and introduced the weight punishment mechanism and the exit-delegation mechanism to manage the NCBs under these two different conflicts. And by defining preference risk, trust risk and comprehensive risk, Xu et al. [33] classified NCBs into ordinary and serious levels, and established preference adjustment coefficients to manage NCBs. Furthermore, Xu et al. [32] conducted in-depth research on the impact of NCB on the minimum consensus cost in group decision-making.

According to the systematic review of the above literature, it can be found that the consensus of expert evaluation and individual NCB in the consensus process are rarely considered in the current research on investment selection of renewable energy projects. However, the investment selection of renewable energy projects involves professional knowledge in many fields and requires a large number of experts to discuss. In the expert evaluation process of LGDM, it is inevitable that there will be heterogeneous evaluation information, and there may be participants who do not cooperate with the adjustment of evaluation information to reach a consensus for personal interests. Therefore, this paper adopts the CRP based on the feedback mechanism and the NCB management method based on the historical adjustment data of experts to provide specific countermeasures for the investment selection of renewable energy projects.

3 Preliminaries

This section mainly reviews the basic knowledge related to hesitant fuzzy linguistic term set (HFLTS) and social trust network (STN).

3.1 Hesitant Fuzzy Linguistic Term Sets

HFLTS developed by Rodriguez et al. [28] is an ordered subset of consecutive linguistic terms of a linguistic term set (LTS) $S = \left\{ {s_{0} ,s_{1} , \ldots ,s_{2\tau } } \right\}$, and it enables DMs to use one or more linguistic values to describe individual views. Then, to facilitate the calculation between HFLTS, some basic operation laws of the HFLTS, which will be used in this paper, are introduced.

Definition 3.1

[28] Let $S = \left\{ {s_{0} ,s_{1} , \ldots ,s_{2\tau } } \right\}$ be an LTS and $H^{S} = \left\{ {h_{i} |h_{i} \in S,i = 1,2, \ldots ,\# h} \right\}$ be an arbitrary HFLE on $S$, then the upper bound $h^{S + }$, the lower bound $h^{S - }$ and the envelope $env\left( {H^{S} } \right)$ of the HFLTS $H^{S}$ are defined as:

• (a) $h^{S + } = \max \left\{ {h_{i} |h_{i} \in H^{S} } \right\}$.

• (b) $h^{S - } = \min \left\{ {h_{i} |h_{i} \in H^{S} } \right\}$.

• (c) $env\left( {H^{S} } \right) = \left[ {h^{S - } ,h^{S + } } \right]$.

Definition 3.2

[37] Let $S = \left\{ {s_{0} ,s_{1} , \ldots ,s_{2\tau } } \right\}$ be an LTS, $H_{1}^{S}$ and $H_{2}^{S}$ be two HFLTSs, then the distance between $H_{1}^{S}$ and $H_{2}^{S}$ can be measured by the following equation:

$$d\left( {H_{1}^{S} ,H_{2}^{S} } \right) = \frac{1}{\sqrt 3 }\left| {w\left( {H_{1}^{S} } \right) - w\left( {H_{2}^{S} } \right)} \right| + \left| {c\left( {H_{1}^{S} } \right) - c\left( {H_{2}^{S} } \right)} \right|$$

(1)

where $w\left( {H^{S} } \right) = \frac{1}{2}\left( {I\left( {h^{S + } } \right) - I\left( {h^{S - } } \right)} \right)$, $c\left( {H^{S} } \right) = \frac{1}{2}\left( {I\left( {h^{S + } } \right) + I\left( {h^{S - } } \right)} \right)$ and $I$ is the function that maps linguistic variable to interval $\left[ {0,1} \right]$, $I\left( {s_{i} } \right) = \frac{i}{2\tau }$.

Besides, to facilitate the comparison of different HFLTSs, the following score function and comparison rules are proposed based on Definitions 3.1 and 3.2.

Definition 3.3

Let the three HFLTSs $H^{S}$, $H_{1}^{S}$,$H_{2}^{S}$ be as easier, then the score function of the HFLTS $H^{S}$ can be defined as $E\left( {H^{S} } \right) = \frac{{c\left( {H^{S} } \right)^{2} }}{{c\left( {H^{S} } \right) + \upsilon \left( {H^{S} } \right)}}$, where $\upsilon \left( {H^{S} } \right) = \frac{1}{\# h}\sum\limits_{i = 1}^{\# h} {\left( {I\left( {h_{i} } \right) - c\left( {H^{S} } \right)} \right)^{2} }$. And the comparison rules between $H_{1}^{S}$ and $H_{2}^{S}$ is defined as if $E\left( {H_{1}^{S} } \right) < E\left( {H_{2}^{S} } \right)$, then $H_{1}^{S} < H_{2}^{S}$; and if $E\left( {H_{1}^{S} } \right) = E\left( {H_{2}^{S} } \right)$, then $H_{1}^{S} = H_{2}^{S}$.

3.2 Social Trust Network

Social network consists of three parts: DMs, trust relationship and trust degree among DMs. Suppose that $E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{U} } \right\}$ be the set of DMs in the social network GDM (SN-GDM), the social network represents the relationship among DMs and has the following three representations.

• (a) Graph: the trust relations can be described through a directed graph $G\left( {E,L} \right)$, where $L$ is the set of directed edges connecting two DMs and indicates the DM at the beginning of the directed edge trusts the DM at the end.

• (b) Adjacency matrix: the social network is expressed by a matrix $T = \left( {t_{ij} } \right)_{U \times U}$ with $t_{ij} \in \left\{ {0,1} \right\}$, where $t_{ij} = 1$ represents the directly trust relation from DM $e_{i}$ to DM $e_{j}$.

• (c) Algebraic: this notation discriminates distinct relations and signifies the combinations of relations (Table 1).

Table 1 Three forms of social networks

Since LGDM involves at least 20 experts, it is difficult to express the trust degree of experts in each other through two precise and direct relationships of trust and mistrust, which makes the traditional trust network unable to express this fuzzy relationship. Therefore, Zhang et al. [38] proposed a fuzzy sociometric approach to meet the above challenge.

Definition 3.4

[38] A fuzzy sociometric $T = \left( {t_{ij} } \right)_{U \times U}$ on the set $E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{U} } \right\}$ of experts is a relation in $E \times E$ with membership function $T:E \times E \to \left[ {0,1} \right]$, $T\left( {e_{i} ,e_{j} } \right) = t_{ij}$, where $t_{ij}$ indicates the degree to which expert $e_{i}$ trusts expert $e_{j}$.

4 The LGDM Method for Investment Selection of Renewable Energy Projects

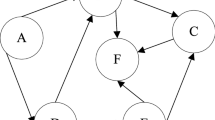
In this section, the LGDM method considering experts’ NCB for investment selection of renewable energy projects is developed. The novel LGDM method is shown in Fig. 2 and mainly includes four sub-processes: preprocessing of initial opinions, the CRP, the historical adjustment data-based NCB analysis phase, and the selection phase. The specific details are as follows.

Fig. 2

The novel LGDM method for investment selection of renewable energy projects

4.1 Preprocessing of Initial Opinions

To simplify the process of large group consensus, this part mainly includes three stages: clustering stage, weight determination stage and subgroup opinion acquisition stage.

For the investment selection of renewable energy projects, the decision-making expert group is composed of experts with professional knowledge backgrounds in multiple fields and staff with rich practical experience, which can be represented as $E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{U} } \right\}$ with $U \ge 20$. Moreover, all experts assess the multiple criteria $C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{m} } \right\}$ of existing investment alternatives $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}$ by using a 9-scale LTS $S = \left\{ {s_{0} = {\text{extremely bad}},s_{1} = {\text{very bad}},s_{2} = {\text{bad}},s_{3} = {\text{little bad}},s_{4} = {\text{medium}},s_{5} = {\text{little good}},s_{6} = } \right.$$\left. {{\text{good}},s_{7} = {\text{very good}},s_{8} = {\text{extremely good}}} \right\}$. Nevertheless, it is important to realize that experts are allowed to have hesitation during the assessment process in this paper. Therefore, the evaluation matrix of the expert $e_{u}$ based on HFLTS can be represented as $H_{u} = \left( {h_{ij,u} } \right)_{n \times m}$, where $h_{ij,u}$ represents expert’s opinion for the alternative $x_{i}$ with respect to the criterion $c_{j}$.

4.1.1 Hierarchical Clustering Stage

Clustering aims to cluster a group of multi-dimensional feature attribute data into different subgroups based on the similarity measurement between different data. In the current research of clustering methods, hierarchical clustering method is a widely used clustering algorithm owing to its superiority of few restrictions and no need to set the number of clusters in advance. The main idea of hierarchical clustering is to calculate the similarity between different types of data points, and then sort them from high to low, and gradually reconnect the nodes to create a hierarchical nested clustering tree. After the clustering is completed, a knife can be cut at any level to obtain a specified number of clusters.

Therefore, in this section, the hierarchical clustering method based on the distance measure of Eq. (1) is introduced into the investment selection of renewable energy projects. The clustering of expert subgroups is completed according to the initial evaluation information of experts. And the procedure of the hierarchical clustering algorithm for investment selection of renewable energy projects is represented in Algorithm 1.

4.1.2 Weight Determination Stage

According to Algorithm 1, the decision expert group is divided into $K$ subgroups, $G = \left\{ {G_{1} ,G_{2} , \ldots ,G_{K} } \right\}$. After obtaining the clustering of the subgroups, the subgroup weight vector $W = \left( {w_{1} ,w_{2} , \ldots ,w_{K} } \right)^{{\text{T}}}$ and the expert weight vector $W_{k} = \left( {w_{1}^{k} ,w_{2}^{k} , \ldots ,w_{{n_{k} }}^{k} } \right)^{{\text{T}}}$ of the subgroups can be obtained according to the trust relationship between experts and the similarity between expert opinions, where $\sum\nolimits_{k = 1}^{K} {w_{k} } = 1$, $\sum\nolimits_{u = 1}^{{n_{k} }} {w_{u}^{k} } = 1$, and $n_{k}$ is the number of experts in the subgroup $G_{k}$.

Weight vector is one of the tools of information fusion, which can directly affect the final decision result. Many current studies determine the weights of experts and subgroups based on the similarity of preferences, without considering the social trust relationship between individuals. However, in fact, STN plays a crucial role in determining the importance of experts in decision-making expert groups. STN can provide a superior platform for experts to initiate opinions and exchange improvements. Hence, for the renewable energy project investment selection studied in this paper, the STN is introduced to determine the weight vectors of the subgroup and the experts in the subgroup as follows.

Definition 4.1

Let $T = \left( {t_{uv} } \right)_{U \times U}$ be a fuzzy sociometric on the set $E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{U} } \right\}$ of experts, then the average trust in-degree of each expert can be denoted as $T_{u}^{in} = \frac{1}{{n_{u} }}\sum\nolimits_{v = 1}^{{n_{u} }} {t_{vu} }$ with $u = 1,2, \ldots ,U$, where $n_{u}$ represents the number of experts meeting $t_{vu} > 0$.

Besides, let $H_{u} = \left( {h_{ij,u} } \right)_{n \times m}$ be the opinion matrix of the expert $e_{u}$ with $u = 1, \ldots ,U$, then the opinion similarity between expert $e_{u}$ and other experts can be calculated as follows

$$F_{u} = 1 - \frac{1}{{nm\left( {U - 1} \right)}}\sum\limits_{v = 1,v \ne u}^{U} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u} ,h_{ij,v} } \right)} } }$$

Definition 4.2

Let $G = \left\{ {G_{1} ,G_{2} ,\ldots,G_{K} } \right\}$ be clustering results of the decision expert group $E = \left\{ {e_{1} ,e_{2} ,\ldots,e_{U} } \right\}$, $T_{u}^{in}$ with $u = 1,2,\ldots,U$ be the average trust in-degree of each expert, and $F_{u}$ with $u = 1,2,\ldots,U$ be the opinion similarity between expert $e_{u}$ and other experts, then the weights of subgroups can be denoted as

$$w_{k} = \frac{{Q_{k} }}{{\sum\nolimits_{k = 1}^{K} {Q_{k} } }}\;{\text{with}}\;k = 1,2, \ldots ,K$$

(2)

where $Q_{k} = \frac{1}{{2n_{k} }}\sum\limits_{u = 1}^{{n_{k} }} {\left( {T_{u}^{in} + F_{u} } \right)}$ represents the score of the subgroup $G_{k}$ considering the average trust in-degree of each expert in this subgroup and their opinion similarity with other experts.

And the weights of the experts in the subgroup $G_{k}$ can be denoted as.

$$w_{u}^{k} = \frac{{T_{u}^{in} + F_{u} }}{{\sum\nolimits_{v = 1}^{{n_{k} }} {\left( {T_{v}^{in} + F_{v} } \right)} }}\;{\text{with}}\;u = 1,2, \ldots ,U$$

(2)

4.1.3 Subgroups’ Opinions Acquisition Stage

At present, the research on aggregation methods in group decision-making mainly focuses on two paths: (1) aggregating opinions through aggregation operators; (2) collective opinions are obtained by minimizing the distance between individual opinions and collective opinions. Since the essence of the CRP is to obtain the decision-making results agreed by most people through gathering the opinions of expert groups, the collective opinions are expected to bring into correspondence with the individual opinions. Therefore, Zhang et al. [37] proposed an aggregation model to minimize the maximum of the distance between the individual and the collective, which is as follows:

$$\mathop {\min }\limits_{{H^{c} }} \mathop {\max }\limits_{{d^{u} \in D}} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u} ,h_{ij,c} } \right)} }$$

$${\text{s}}{\text{.t}}{.}\;\left\{ {\begin{array}{*{20}l} {2\tau \left( {I\left( {h_{ij,c}^{ + } } \right) - I\left( {h_{ij,c}^{ - } } \right)} \right) + 1 \le \beta } \hfill & {i = 1, \ldots ,n;\;j = 1, \ldots ,m} \hfill \\ {h_{ij,c} \in H^{S} } \hfill & {i = 1, \ldots ,n;\;j = 1, \ldots ,m} \hfill \\ \end{array} } \right.$$

(4)

where $H_{u} = \left( {h_{ij,u} } \right)_{n \times m}$ is the opinion matrix of $e_{u}$, $H_{c} = \left( {h_{ij,c} } \right)_{n \times m}$ is the collective opinion matrix which is also the decision variable, and $\beta$ is a constant designed to obtain a collective opinion with high accuracy.

The above aggregation model was proved to be effective and easy to calculate [37]. However, in the investment selection of renewable energy projects, there may be different trust degrees among the experts in the decision-making group, which directly leads to the different importance of each expert. Therefore, in order to adapt to the specific situation of the actual problem, the weights of experts are introduced into the above aggregation model, and the improved model is applied to obtain subgroup opinions. The specific improvements are as follows.

$$\min \sum\limits_{u = 1}^{{n_{k} }} {w_{u} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u}^{k} ,h_{ij,k} } \right)} } }$$

$$s.t.\left\{ \begin{gathered} 2\tau \left( {I\left( {h_{{ij,k}}^{ + } } \right) - I\left( {h_{{ij,k}}^{ - } } \right)} \right) + 1 \le \beta \;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, \ldots ,n;\;j = 1, \ldots ,m \hfill \\ h_{{ij,k}} \in H^{S} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, \ldots ,n;\;j = 1, \ldots ,m \hfill \\ \end{gathered} \right.$$

(5)

where $H_{u}^{k} = \left( {h_{ij,u}^{k} } \right)_{n \times m}$ and $\beta$ are as mentioned earlier, $H_{k} = \left( {h_{ij,k} } \right)_{n \times m}$ is the opinion matrix of subgroup $G_{k}$ and $h_{ij,k}$ with $i = 1,2, \ldots ,n;\;j = 1,2, \ldots ,m$ are the decision variables. And see Sect. 5.1 in [37] for details of subsequent calculation steps of the model.

4.2 Consensus Reaching Process (CRP)

As mentioned in the introduction, the investment selection of renewable energy projects requires the participation of at least 20 experts from different professional backgrounds to ensure scientific and reasonable decision-making. However, due to the different knowledge background and experience of experts, the opinions of different experts often have certain deviations, and even completely opposite evaluation opinions may exist. Therefore, it is essential to coordinate the opinions of various experts to obtain the decision-making results agreed upon by most people, which is denoted as the CRP. Furthermore, the proposed CRP for the investment selection of renewable energy projects includes two aspects: (1) consensus measurement stage; (2) feedback mechanism.

4.2.1 Consensus Measurement Stage

First, after obtaining the opinions of each subgroup, the consensus measure can be developed based on the similarity between the opinions of each subgroup. Specifically, let $H_{k} = \left( {h_{ij,k} } \right)_{n \times m}$ be the opinion matrix of subgroup $G_{k}$, then the consensus level of subgroup $G_{k}$ is calculated as follows.

$$CL_{k} = 1 - \frac{1}{{nm\left( {K - 1} \right)}}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\sum\limits_{h = 1,h \ne k}^{K} {d\left( {h_{ij,k} ,h_{ij,h} } \right)} } } \;{\text{with}}\;k = 1,2, \ldots ,K$$

(6)

Then, for checking whether the current consensus level of each subgroup has reached an acceptable level, the consensus threshold $\alpha$ is preset. In addition, to avoid the situation that the opinions of each subgroup are still greatly different after multiple adjustments, the maximum number of iterations $r_{\max }$ in the feedback adjustment process is also preset. Then, the following judgment rule (JR) is proposed to determine which stage to enter next.

JR 1: If $\min_{{G_{k} \in G}} CL_{k} \ge \alpha$, which indicates the current consensus level of each subgroup is acceptable, then the CRP ends and the selection process begins. Otherwise, if $r \le r_{\max }$, then start the feedback mechanism; if not, the decision-making process ends with consensus failure.

4.2.2 Feedback Mechanism

Next, for the circumstance without reaching a consensus, the feedback mechanism needs to be established, and the subgroups that need to be modified should be provided with some guidance and reference opinions to improve their consensus level. Thus, a novel feedback mechanism is proposed, which primarily plays a guiding role in two aspects: (1) the identification rule (DR): Identify subgroup that needs to be adjusted to achieve a higher consensus level; (2) the direction rules (IRs): Provide reference objects and directions for adjustment.

• (1) The Identification Rule

In this paper, the subgroup with the lowest consensus level is identified that further adjustments are needed to improve the consensus level. This identification rule works as:

$$G_{k} = \arg \min CL_{k}$$

(7)

When subgroup $G_{k}$ is identified as needing further modification, all members of subgroup $G_{k}$ need to modify their opinions to promote the consensus level $CL_{k}$ of subgroup $G_{k}$. Then, the following DRs are proposed to generate adjustment directions of the experts in subgroup $G_{k}$.

• (2) The Direction Rules

This part includes two steps: (1) explore the reference opinions modified by experts as guidance for determining the adjustment direction; (2) provide the exact reference range for the experts who need to modify their opinions.

Step 1 Determine the Reference Object

In the novel feedback mechanism, the reference opinions provided for the experts $e_{u}$ with $u = 1,2, \ldots ,n_{k}$ in the subgroup $G_{k}$ with $G_{k} = \arg \min_{{G_{k} \in G}} CL_{k}$ will be expanded from three dimensions: STN, consensus contribution of experts in the subgroup, and opinion similarity. First, the set of experts that do not need to be adjusted can be obtained according to the above identification rule, expressed as $E_{c} = \left\{ {e_{v} |e_{v} \notin G_{k} ,G_{k} = \arg \min_{{G_{k} \in G}} CL_{k} } \right\}$. In addition, the set of experts trusted by the expert $e_{u}$ can be obtained according to the STN, $E_{t} = \left\{ {e_{v} |t_{uv} > 0} \right\}$. And let $E_{r} = E_{c} \cap E_{t}$, then the following three circumstances for obtaining reference opinions are proposed.

• 1. If $E_{r} \ne \phi$, compared with other opinions, experts may be inclined to refer to the opinions of trusted experts for modification. Therefore, the reference opinion is based on $E_{r}$ is $\widetilde{{H_{u} }} = \sum\nolimits_{{v \in E_{r} }} {\frac{{t_{uv} }}{{\sum {t_{uv} } }} \cdot H_{v} }$.

• 2. If $E_{r} = \phi$, the opinion, which is similar to the expert’s opinions in the same subgroup but with more consensus contributions, may be more easily accepted. Thus, the consensus contribution of experts in the subgroup $G_{k}$ is defined as follows.

Definition 4.3

Let $H_{u}^{k} = \left( {h_{ij,u}^{k} } \right)_{n \times m}$ with $u = 1,2,\ldots,n_{k}$ be the opinion matrix of expert $e_{u}$ in subgroup $G_{k}$ and $H_{h} = \left( {h_{ij,h} } \right)_{n \times m}$ with $h = 1,2,\ldots,K$ and $h \ne k$ be the opinion matrix of other subgroups, then the consensus contribution $CC_{u}^{k}$ of experts in the subgroup $G_{k}$ is defined as

$$CC_{u}^{k} = 1 - \frac{1}{{nm\left( {K - 1} \right)}}\sum\limits_{h = 1,h \ne k}^{K} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = i}^{m} {d\left( {h_{ij,u}^{k} ,h_{ij,h} } \right)} } }$$

(8)

Remark 1

The main idea of the concept of consensus contribution is: Take the opinion of expert $e_{u}$ in the subgroup $G_{k}$ as the overall opinion of this subgroup, and calculate the current consensus level as the consensus contribution of the expert. It is obvious that the current consensus level is positively correlated with the consensus contribution of the expert. According to the ranking of the index value $CC_{u}^{k}$ in the subgroup $G_{k}$, the expert who most supports the group consensus in the subgroup is obtained.

Then, the reference opinions can be divided into the following two situations based on consensus contribution and opinion similarity:

• (a) If $e_{u} \ne \mathop {\arg \max }\limits_{{e_{u} \in G_{k} }} CC_{u}^{k}$, the reference opinion matrix of the expert $e_{u}$ is the expert with the highest consensus contribution in the same subgroup $G_{k}$, denoted by $\widetilde{{H_{u}^{k} }} = H_{v}$ with $e_{v} = \mathop {\arg \max }\limits_{{e_{v} \in G_{k} }} CC_{v}^{k}$.

• (b) If $e_{u} = \mathop {\arg \max }\limits_{{e_{u} \in G_{k} }} CC_{u}^{k}$, which means that the expert’s consensus contributed to the subgroup is the largest, then the opinions of experts in other subgroups, which is closest to the expert’s opinions, may be the most ablest to provide guidance to the expert $e_{u}$. Consequently, the reference opinion for expert $e_{u}$ is $\widetilde{{H_{u}^{k} }} = H_{v}$ with $e_{v} = \mathop {\arg \min }\limits_{{e_{v} \in G_{h} ,h \ne k}} d\left( {H_{u}^{k} ,H_{v}^{h} } \right)$.

According to the above IR and DRs, the experts $e_{u}$ with $u = 1,2,\ldots,n_{k}$ in subgroup $G_{k}$ all have received specific reference opinions $\widetilde{{H_{u}^{k} }} = \left( {\widetilde{{h_{ij,u}^{k} }}} \right)_{n \times m}$. Since the basic function of feedback is to provide guidance for experts, the accuracy of the elements in the reference matrix should be higher than that of the elements in the expert opinion matrix. Hence, let ${\mathop {H}\limits^{\frown}}_{u} = {\left( {\mathop {{h_{ij,u}^{k} }}\limits^{\frown}} \right)_{n \times m}}$ be the refined reference opinion matrix for expert $e_{u}$, the following model is proposed to refine the reference opinion matrix.

$$\min d\left( {\widetilde{{h_{ij,u}^{k} }}, {\mathop {{h_{ij,u}^{k} }}\limits^{\frown}}} \right)$$

$$s.t.\left\{ {\begin{array}{*{20}l} {I\left( {\mathop {{h_{ij,u}^{k+} }}\limits^{\frown}} \right) - I\left({\mathop {{h_{ij,u}^{k-} }}\limits^{\frown}} \right) \le I\left( {h_{ij,u}^{k + } } \right) - I\left( {h_{ij,u}^{k - } } \right) \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ \; \left( {\mathop {{h_{ij,u}^{k} }}\limits^{\frown}}\right) {{\text{ is a HFLTS, }}i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ \end{array} } \right.$$

(9)

The objective function aims to minimum the distance between the matrices before and after optimization, and the first constraint is to ensure that the number of linguistic words in the refined reference opinions is less than that in the initial evaluation of expert $e_{u}$, the second constraint is to ensure that the refined opinions are still HFLTSs. Apparently, the refined reference opinion matrix processed based on model (9) can provide accurate reference opinions for experts. Next, the stage to obtain the adjustment range of expert opinions is proposed below.

Remark 2

$\widetilde{{H_{u}^{k} }} = \left( {\widetilde{{h_{ij,u}^{k} }}} \right)_{n \times m}$ represents the specific reference opinions, i.e., the evaluation opinions of experts $e_{u}$ modified reference object determined through the feedback mechanism. ${\mathop {H}\limits^{\frown}}_{u} = {\left( {\mathop {{h_{ij,u}^{k} }}\limits^{\frown}} \right)_{n \times m}}$ represents the refined reference opinion matrix for experts $e_{u}$ by the model (9). It can be ensured that the hesitation degree of the refined reference opinion ${\mathop {H}\limits^{\frown}}_{u} = {\left( {\mathop {{h_{ij,u}^{k} }}\limits^{\frown}} \right)_{n \times m}}$ processed by the model (9) is less than or equal to the hesitation degree of the reference object’s evaluation opinion $\widetilde{{H_{u}^{k} }} = \left( {\widetilde{{h_{ij,u}^{k} }}} \right)_{n \times m}$.

Step 2 Determine the Modification Interval

These rules guide experts to modify the opinion matrix to improve the consensus level of subgroups. Let $H_{u}^{k} = \left( {h_{ij,u}^{k} } \right)_{n \times m}$ be the opinion matrix before modification of expert $e_{u}$ in subgroup $G_{k}$, $\widetilde{{H_{u}^{k} }} = \left( {\widetilde{{h_{ij,u}^{k} }}} \right)_{n \times m}$ be the reference opinion matrix, and $\overline{{H_{u}^{k} }} = \left( {\overline{{h_{ij,u}^{k} }} } \right)_{n \times m}$ be the modified opinion matrix.

DR. 1. If $h_{ij,u}^{k} = {\mathop {{h_{ij,u}^{k} }}\limits^{\frown}}$, then the evaluation value $h_{ij,u}^{k}$ of $e_{u}$ does not need to be changed.

DR. 2. If $h_{ij,u}^{k} \ne {\mathop {{h_{ij,u}^{k} }}\limits^{\frown}}$, then $e_{u}$ are advised to modify the evaluation value $h_{ij,u}^{k}$. Let $h^{o} = 2\tau \cdot c\left( h \right)$ be the central point of evaluation opinion $h$. The specific adjustment direction and rules for $e_{u}$ are as follows.

AR. 2.1. If $h_{ij,u}^{ko} < {\mathop {{h_{ij,u}^{ko} }}\limits^{\frown}}$, then $e_{u}$ is suggested to increase the evaluation value $h_{ij,u}^{k}$ to be as close as possible to ${\mathop {{h_{ij,u}^{k} }}\limits^{\frown}}$, i.e., $\overline{{h_{ij,u}^{k} }} = \left\{ {\overline{{h_{ij,u}^{k} }} |h_{ij,u}^{k - } \le \overline{{h_{ij,u}^{k - } }} \le {\mathop {{h_{ij,u}^{k-} }}\limits^{\frown}} ,h_{ij,u}^{k + } \le \overline{{h_{ij,u}^{k + } }} \le {\mathop {{h_{ij,u}^{k+} }}\limits^{\frown}},\overline{{hd_{ij,u}^{k} }} \le hd_{ij,u}^{k} } \right\}$.

AR. 2.2. If $e h_{ij,u}^{o} > {\mathop {{h_{ij,u}^{o} }}\limits^{\frown}}$, then $e_{u}$ is suggested to decrease the evaluation value $h_{ij,u}^{k}$ to be as close as possible to ${\mathop {{h_{ij,u} }}\limits^{\frown}}$, i.e., $\overline{{h_{ij,u}^{k} }} = \left\{ {\overline{{h_{ij,u}^{k} }} | \le {\mathop {{h_{ij,u}^{k-} }}\limits^{\frown}} \overline{{h_{ij,u}^{k - } }} \le h_{ij,u}^{k - } , {\mathop {{h_{ij,u}^{k+} }}\limits^{\frown}} \le \overline{{h_{ij,u}^{k + } }} \le h_{ij,u}^{k + } ,\overline{{hd_{ij,u}^{k} }} \le hd_{ij,u}^{k} } \right\}$.

AR. 2.3. If $h_{ij,u}^{o} = {\mathop {{h_{ij,u}^{o} }}\limits^{\frown}}$, then $e_{u}$ is suggested to reduce the hesitancy degree in the evaluation value $h_{ij,u}^{k}$ to be as close as possible to ${\mathop {{h_{ij,u} }}\limits^{\frown}}$, i.e., $\overline{{h_{ij,u}^{k} }} = \left\{ {\overline{{h_{ij,u}^{k} }} |h_{ij,u}^{k - } \le \overline{{h_{ij,u}^{k - } }} \le {\mathop {{h_{ij,u}^{k-} }}\limits^{\frown}} ,h_{ij,u}^{k + } \le \overline{{h_{ij,u}^{k + } }} \le {\mathop {{h_{ij,u}^{k+} }}\limits^{\frown}} } \right\}$.

Finally, according to the above rules, the personalized adjustment interval can be fed back to the experts who need to modify their opinion matrix and improve the consensus level of their subgroups. After the experts have revised the evaluation opinions, recalculate the subgroups’ consensus level, and judge whether the consensus level of each subgroup reaches the preset consensus threshold $\alpha$. Then, the following judgment rule is proposed.

JR 2: If $CL_{k}^{*} \ne \mathop {\min }\limits_{{G_{h} \in G}} CL_{h}$, then reidentify the subgroup with the lowest consensus level for the next round of adjustment. Otherwise, enter the stage of NCB analysis and management.

4.3 Historical Adjustment Data-Based NCB Analysis Phase

In real decision-making, not all participants are willing to cooperate with the feedback mechanism to modify the evaluation opinions. Therefore, this phase is devoted to analyzing the behavior of experts when they modify their opinions according to the feedback suggestions and proposing an experts’ historical adjustment data-based NCB management method. Different management methods are adopted for the experts who show different times of NCB: (1) When the experts show NCB for the first time, weight penalty-based management method is started to warn non collaborators; (2) When experts are considered to have exhibited NCB for the second time, opinion penalty-based management method is enabled. Details of this method are as follows.

First, to judge whether the current cooperation level is acceptable according to the modification of experts, the cooperation degree threshold $\varphi$ is set in advance. Moreover, in the $r$th iteration, according to the reference opinion matrix ${\mathop {{H_{u}^{k(r)} }}\limits^{\frown}}= {\left( {\mathop {{h_{ij,u}^{k(r)} }}\limits^{\frown}} \right)_{n \times m}}$ provided and the modified opinion matrix $\overline{{H_{u}^{k\left( r \right)} }} = \left( {\overline{{h_{ij,u}^{k\left( r \right)} }} } \right)_{n \times m}$ of expert $e_{u}$, the cooperation degree $\varphi_{u}^{\left( r \right)}$ of expert $e_{u}$ can be defined as follows:

$$\varphi_{u}^{k\left( r \right)} = 1 - \frac{{\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {\overline{{h_{ij,u}^{k\left( r \right)} }} ,} {\mathop {{h_{ij,u}^{k(r)} }}\limits^{\frown}} \right)} } }}{{\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {{\mathop {{h_{ij,u}^{k(r)} }}\limits^{\frown}} ,h_{ij,u}^{k\left( r \right)} } \right)} } }}$$

(10)

Remark 3.

The ratio of $\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {\overline{{h_{ij,u}^{k\left( r \right)} }} , {\mathop {{h_{ij,u}^{k(r)} }}\limits^{\frown}}} \right)} }$ (the distance between the modified opinion and the refined reference opinion) and $\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {{\mathop {{h_{ij,u}^{k(r)} }}\limits^{\frown}} ,h_{ij,u}^{k\left( r \right)} } \right)} }$ (the distance between the refined reference opinion and the original opinion) can indicate the degree of non-cooperation of the expert $e_{u}$. Thus, when the distance $\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( { {\mathop {{h_{ij,u}^{k(r)} }}\limits^{\frown}} ,h_{ij,u}^{k\left( r \right)} } \right)} }$ between the refined reference opinion and the original opinion is fixed, the smaller the distance $\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {\overline{{h_{ij,u}^{k\left( r \right)} }} , {\mathop {{h_{ij,u}^{k(r)} }}\limits^{\frown}}} \right)} }$ between the modified opinion and the refined reference opinion is, the lower the non-cooperation degree of the experts is, which means the higher the cooperation degree $\varphi_{u}^{\left( r \right)}$.

Furthermore, the following judgment rule on whether experts have NCBs is proposed.

JR 3: If $\varphi_{u}^{k\left( r \right)} < \varphi$, then the expert $e_{u}$ is considered to show NCB in the feedback adjustment process, which requires further management to avoid the delay of the decision-making process. Otherwise, the expert $e_{u}$ is considered to cooperate with feedback adjustment and actively promote the promotion of consensus.

Then, according to historical adjustment data of experts, two management methods are introduced for the NCB at different times.

4.3.1 Weight Penalty-Based Management Method

When the experts show NCB for the first time, no matter what purpose the experts show NCB, the proposed weight penalty-based management method can be started to warn. First, the concept of the Uninorm operator proposed by Yager [34] is introduced to punish the weights of non-cooperators.

Definition 4.4

[34] An Uninorm is a mapping: $U\left[ {0,1} \right]^{2} \to \left[ {0,1} \right]$, which properties are as follows:

• (i) Commutativity: $U\left( {x,y} \right) = U\left( {y,x} \right)$;

• (ii) Monotonicity: $U\left( {x_{1} ,y_{1} } \right) \ge U\left( {x_{2} ,y_{2} } \right){\text{ for x}}_{1} \ge x_{2} ,{\text{ y}}_{1} \ge y_{2}$;

• (iii) Associativity: $U\left( {x,U\left( {y,z} \right)} \right) = U\left( {U\left( {x,y} \right),z} \right)$;

• (iv) Identity element: $\exists g \in \left[ {0,1} \right]: \, U\left( {x,g} \right) = x,{\text{ for all }}x.$

This paper uses the special case in [1], as shown in Eq. (11).

$$U\left( {x,y} \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if }}\left( {x,y} \right) \in \left\{ {\left( {0,1} \right),\left( {1,0} \right)} \right\}} \hfill \\ {\frac{xy}{{xy + \left( {1 - x} \right)\left( {1 - y} \right)}}{,}} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$

(11)

Furthermore, according to the cooperation degree of each expert in the feedback adjustment process, the weights of experts in subgroup $G_{k}$ after the first NCB is processed can be defined as follows.

Let $G_{k1}^{\left( r \right)} = \left\{ {e_{u} |\varphi_{u}^{k\left( r \right)} \le \varphi ,e_{u} \in G_{k} } \right\}$ with $G_{k1}^{\left( r \right)} \subset G_{k}$ be the set of experts in subgroup $G_{k}$ who exhibit NCB for the first time, $w_{u}^{k\left( r \right)}$ be the weight of $e_{u}$ in the $r$-th iteration, then the weight $w_{u}^{{k\left( {r + 1} \right)}}$ of $e_{u}$ after the first NCB is processed, and can be calculated by

$$w_{u}^{{k\left( {r + 1} \right)}} = \left\{ {\begin{array}{*{20}l} {U\left( {\varphi_{u}^{k\left( r \right)} ,w_{u}^{k\left( r \right)} } \right)} \hfill & {e_{u} \in G_{k1}^{\left( r \right)} } \hfill \\ {w_{u}^{k\left( r \right)} + \frac{{\varphi_{u}^{k\left( r \right)} }}{{\sum\limits_{{e_{u} \in G_{k} \backslash G_{k1}^{\left( r \right)} }} {\varphi_{u}^{k\left( r \right)} } }}\left( {\sum\limits_{{e_{u} \in G_{k1}^{\left( r \right)} }} {\left( {w_{u}^{k\left( r \right)} - w_{u}^{{k\left( {r + 1} \right)}} } \right)} } \right)} \hfill & {e_{u} \in G_{k} \backslash G_{k1}^{\left( r \right)} } \hfill \\ \end{array} } \right.$$

(12)

where $\varphi_{u}^{k\left( r \right)}$ is the cooperation degree of experts in the $r$th iteration.

Then, the procedure of the weight penalty-based management method is shown in Algorithm 2.

4.3.2 Opinion Penalty-Based Management Method

When the experts show NCB for the second time, it is obvious that reaching a consensus becomes more difficult. Firstly, the different performances of experts in this subgroup need to be analyzed in detail to facilitate subsequent management.

If $G_{k}$ was again identified as a subgroup requiring adjustment, according to the historical data modified by experts, then the experts’ behaviors in the $r^{\prime}$th iteration with $r < r^{\prime} < r_{\max }$ can be divided into three types: (1) NCB for the first time; (2) NCB for the second time; (3) no NCB occurred.

Let $G_{k1}^{{\left( {r^{\prime}} \right)}} = \left\{ {e_{u} |\varphi_{u}^{{\left( {r^{\prime}} \right)}} \le \varphi ,e_{u} \in G_{k} \backslash G_{k1}^{\left( r \right)} } \right\}$ be the set of experts with the first type of behavior, $G_{k2}^{{\left( {r^{\prime}} \right)}} = \left\{ {e_{u} |\varphi_{u}^{{k\left( {r^{\prime}} \right)}} \le \varphi ,e_{u} \in G_{k1}^{\left( r \right)} } \right\}$ with $G_{k2}^{{\left( {r^{\prime}} \right)}} \subset G_{k1}^{\left( r \right)}$ be the set of experts with the second type of behavior, the relationship among different sets in the $r$th iteration and the $r^{\prime}$th iteration is represented as Fig. 3.

Fig. 3

The relationship between different sets in the $r$th iteration and the $r^{\prime}$th iteration

In view of this complex but common situation, how to achieve fair and just management has become a major challenge in the decision-making process. Nash bargaining game has been proved to be a very effective tool for distributing benefits, which has caused extensive discussion and research. Panda et al. [25] puts forward the approach of realizing the Nash bargaining game by maximizing the product of participants’ profits in the circumstance of cooperation. Then, Meng et al. [23] introduced this idea into the traditional CRP, and constructs a weighted Nash bargaining game-based model, which objective function is to make the adjustment quantity reduced by the participants as equal as possible. To punish the experts with twice NCB in LGDM, this paper introduces the idea of the Nash bargaining game and constructs a two-stage opinion penalty-based management method.

The main idea of this method is to make the subgroup reach the preset consensus threshold by punishing the opinions of non-cooperators in the subgroup. Specifically, the first stage aims to obtain subgroup opinions that can reach the preset consensus threshold by minimizing the distance before and after the adjustment of subgroup opinions. Moreover, in the second stage, the opinions of non-cooperators are obtained by maximizing the matching degree between the adjustment quantity and the cooperation degree of non-cooperators.

Stage 1: Let $H_{k}^{{\left( {r^{\prime}} \right)}} = \left( {h_{ij,k}^{{\left( {r^{\prime}} \right)}} } \right)_{n \times m}$ and $\overline{{H_{k}^{{\left( {r^{\prime}} \right)}} }} = \left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }} } \right)_{n \times m}$ be the initial opinion matrix and the modified opinion matrix of the subgroup $G_{k}$ in the $r^{\prime}$-th iteration respectively, and $H_{h}^{{\left( {r^{\prime}} \right)}} = \left( {h_{ij,h}^{{\left( {r^{\prime}} \right)}} } \right)_{n \times m}$ with $h = 1,2,\ldots,K\left( {h \ne k} \right)$ be the initial opinion matrices of other subgroups in the $r^{\prime}$-th iteration, then the following model can be constructed to support the first stage.

$$\min \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }} ,h_{ij,k}^{{\left( {r^{\prime}} \right)}} } \right)} }$$

$$s.t.\left\{ {\begin{array}{*{20}l} {1 - \frac{1}{{nm\left( {K - 1} \right)}}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\sum\limits_{h = 1,h \ne k}^{K} {d\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }} ,h_{ij,h}^{{\left( {r^{\prime}} \right)}} } \right)} } } \ge \alpha } \hfill \\ {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) - }} }} } \right) \le I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right) \, i = 1,2,\ldots,n;j = 1,2,\ldots,m} \hfill \\ {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }} {\text{ are HFLTSs }}i = 1,2,\ldots,n;j = 1,2,\ldots,m} \hfill \\ \end{array} } \right.$$

(13)

where $\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }}$ with $i = 1,2,\ldots,n;\;j = 1,2,\ldots,m$ are the decision variables. And the first constraint condition of model (13) enables the opinions of the adjusted subgroup $G_{k}$ to reach the preset consensus threshold $\alpha$; the second constraint makes the elements of the adjusted opinion matrix still be HFLTSs. Besides, the solution process of model (13) is described in Appendix 1.

Stage 2: This stage aims to punish the weight of experts who show NCB for the first time and the opinions of experts who show NCB for the second time. It is worth noting that in this process, the weight of the experts who show NCB for the second time remains unchanged, and the reduced weight of the experts who show NCB for the first time is allocated to the experts who have no NCB at iteration $r^{\prime}$.

Firstly, let $\overline{{H_{u}^{{k\left( {r^{\prime}} \right)}} }} = \left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right)}} }} } \right)_{n \times m}$ be the modified opinion matrix of expert $e_{u}$ with $e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}}$ at iteration $r^{\prime}$, and $H_{u}^{{k\left( {r^{\prime} + 1} \right)}} = \left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}} } \right)_{n \times m}$ be the opinion matrix after handling NCB for the second time, then the matching degree $\phi_{u}^{{k\left( {r^{\prime}} \right)}}$ between the adjustment quantity and the cooperation degree of non-cooperator is introduced:

$$\phi_{u}^{{k\left( {r^{\prime}} \right)}} = \frac{{1 - {{\sum\nolimits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}} ,\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right)}} }} } \right)} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{m} {d\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}} ,\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right)}} }} } \right)} } } {nm}}} \right. \kern-\nulldelimiterspace} {nm}}}}{{\varphi_{u}^{{k\left( {r^{\prime}} \right)}} }}$$

(14)

where $\varphi_{u}^{k\left( r \right)} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{m} {d\left( {\overline{{h_{ij,u}^{k\left( r \right)} }} , {\mathop {{h_{ij,u}^{k(r)} }}\limits^{\frown}}} \right)} } }}{{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{m} {d\left( { {\mathop {{h_{ij,u}^{k(r)} }}\limits^{\frown}} ,h_{ij,u}^{k\left( r \right)} } \right)} } }}$ is the cooperation degree and $H_{u}^{{k\left( {r^{\prime}} \right)}} = \left( {h_{ij,u}^{{k\left( {r^{\prime}} \right)}} } \right)_{n \times m}$ is the initial opinion matrix, ${\mathop {{H_{u}^{k(r^\prime)} }}\limits^{\frown}} = {\left( {\mathop {{h_{ij,u}^{k(r^\prime)} }}\limits^{\frown}} \right)_{n \times m}}$ is the reference opinion matrix of non-cooperator $e_{u}$.

Then, the first objective function is constructed to make the experts in set $G_{k2}^{{\left( {r^{\prime}} \right)}}$ receive corresponding punishment, which works as:

$$\max \lambda_{1} = \prod\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {\phi_{u}^{{k\left( {r^{\prime}} \right)}} }$$

Second, let $\overline{{H_{u}^{{k\left( {r^{\prime}} \right)}} }} = \left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right)}} }} } \right)_{n \times m}$, $H_{u}^{{k\left( {r^{\prime} + 1} \right)}} = \left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}} } \right)_{n \times m}$ and $\overline{{H_{k}^{{\left( {r^{\prime}} \right)}} }} = \left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }} } \right)_{n \times m}$ are as easier, and $H_{u}^{{k\left( {r^{\prime}} \right)}} = \left( {h_{ij,u}^{{k\left( {r^{\prime}} \right)}} } \right)_{n \times m}$ be the opinion matrix of the expert $e_{u}$ with $e_{u} \in G_{k} \backslash G_{k2}^{{\left( {r^{\prime}} \right)}}$, then the objective function of the model (5) can be written as the second objective function to minimize the distance between the opinions of experts and those of subgroup $G_{k}$, which works as:

$$\min \lambda_{2} = \sum\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}} ,\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }} } \right)} } } + \sum\limits_{{e_{u} \in G_{k} \backslash G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right)}} ,\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }} } \right)} } }$$

Finally, considering the above two objective functions, the opinion penalty-based model is proposed to deal with the situation where experts in the subgroup exhibit the NCB for the second time. Let the set $G_{k3}^{{\left( {r^{\prime}} \right)}} = G_{k2}^{{\left( {r^{\prime}} \right)}} \cup G_{k1}^{{\left( {r^{\prime}} \right)}}$ represents the collection of experts without NCB in the $r^{\prime}$-th iteration, the following model is constructed:

$$\min \sum\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}} ,\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }} } \right)} } } + \sum\limits_{{e_{u} \in G_{k} \backslash G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right)}} ,\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right)}} }} } \right)} } } - \prod\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {\phi_{u}^{{k\left( {r^{\prime}} \right)}} }$$

$${\text{s}}{\text{.t}}{.}\left\{ {\begin{array}{*{20}l} {\phi_{u}^{{k\left( {r^{\prime}} \right)}} = \frac{{1 - {{\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}} ,\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right)}} }} } \right)} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {d\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}} ,\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right)}} }} } \right)} } } {nm}}} \right. \kern-\nulldelimiterspace} {nm}}}}{{\varphi_{u}^{{k\left( {r^{\prime}} \right)}} }}} \hfill & {e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} } \hfill \\ {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} = \left\{ {\begin{array}{*{20}l} {U\left( {\varphi_{u}^{{k\left( {r^{\prime}} \right)}} ,w_{u}^{{k\left( {r^{\prime}} \right)}} } \right)} \hfill & {e_{u} \in G_{k1}^{{\left( {r^{\prime}} \right)}} } \hfill \\ {w_{u}^{{k\left( {r^{\prime}} \right)}} + \frac{{\varphi_{u}^{{k\left( {r^{\prime}} \right)}} }}{{\sum\limits_{{e_{u} \in G_{k} \backslash G_{k3}^{{\left( {r^{\prime}} \right)}} }} {\varphi_{u}^{{k\left( {r^{\prime}} \right)}} } }}\left( {\sum\limits_{{e_{u} \in G_{k1}^{{\left( {r^{\prime}} \right)}} }} {\left( {w_{u}^{{k\left( {r^{\prime}} \right)}} - w_{u}^{{k\left( {r^{\prime} + 1} \right)}} } \right)} } \right)} \hfill & {e_{u} \in G_{k} \backslash G_{k3}^{{\left( {r^{\prime}} \right)}} } \hfill \\ \end{array} } \right.} \hfill & {} \hfill \\ {I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) + }} } \right) - I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) - }} } \right) \le I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \hfill & {i = 1,2, \ldots ,n;\;j = 1,2, \ldots ,m} \hfill \\ {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}} {\text{ are HFLTSs }}} \hfill & {i = 1,2, \ldots ,n;\;j = 1,2, \ldots ,m} \hfill \\ \end{array} } \right.$$

(15)

where $h_{ij,u}^{{k\left( {r^{\prime} + 1} \right)}}$ with $i = 1,2,\ldots,n;j = 1,2,\ldots,m$ are the decision variables. And $\varphi_{u}^{{k\left( {r^{\prime}} \right)}}$ is the cooperation degree of the expert $e_{u}$ in the $r^{\prime}$th iteration, $w_{u}^{{k\left( {r^{\prime}} \right)}}$ and $w_{u}^{{k\left( {r^{\prime} + 1} \right)}}$ are the initial weight and updated weight of expert $e_{u}$ in the $r^{\prime}$th iteration respectively.

Moreover, the first constraint indicates the cooperation degree of experts in the $r^{\prime}$th iteration; The second constraint condition is to allocate the reduced weight of experts in set $G_{k1}^{{\left( {r^{\prime}} \right)}}$ to experts in set $G_{k3}^{{\left( {r^{\prime}} \right)}}$ according to the proportion of cooperation degree; The remaining constraint is to ensure that the opinions of experts in set $G_{k2}^{{\left( {r^{\prime}} \right)}}$ are still HFLTSs after being punished. Then the penalized expert opinions in the subgroup $G_{k}$ can be obtained by solving the model (15). And the solution method of model (15) is described in Appendix 2.

4.4 Selection Phase

When an acceptable level of consensus has been reached among experts, the selection phase is initiated, which works as follows.

First, the score value $E_{ij}^{k}$ of each subgroup opinion is obtained by using the score function in Definition 3.3, and the alternative score value $E_{i}^{k}$ of each subgroup can be calculated by weighted averaging the evaluation values of alternatives with different criteria, $E_{i}^{k} = \sum\limits_{j = 1}^{m} {w_{j}^{c} E_{ij}^{k} }$. Furthermore, the overall score of the alternatives is obtained, $E_{i} = \sum\limits_{k = 1}^{K} {w_{k} E_{i}^{k} }$. Then, rank and select the best alternative according to the overall score vector of the alternatives.

Finally, the steps of LGDM method for investment selection of renewable energy projects are as follows.

Step 1: Analyze the background of investment selection of renewable energy projects and determine the criteria and alternatives.

Step 2: Convene experts in the fields related to renewable energy project investment and establish a decision-making expert group $E = \left\{ {e_{1} ,e_{2} ,\ldots,e_{U} } \right\}$ with $U \ge 20$, and experts who evaluate renewable energy projects and provide trust degree to other experts.

Step 3: According to the evaluation opinions of experts, the hierarchical clustering method of Algorithm 1 is used to cluster experts.

Step 4: Construct the STN of the expert decision-making group, and calculate the weights of experts and subgroups.

Step 5: Obtain the opinions of subgroups $H_{k} = \left( {h_{ij,k} } \right)_{n \times m}$ with $k = 1,2,\ldots,K$, and calculate the consensus level of subgroups by using the similarity between the opinions of subgroups.

Step 6: If $\mathop {\min }\limits_{{G_{k} \in G}} CL_{k} \ge \alpha$, then go to Step 10. Otherwise, if $r \le r_{\max }$, then go to Step 7; if not, the decision-making process ends with consensus failure.

Step 7: The feedback mechanism in Sect. 4.2.2 is used to provide reference opinions for experts in the subgroup with the lowest consensus level, and new evaluation opinions are provided by these experts.

Step 8: If $CL_{k}^{*} \ne \mathop {\min }\limits_{{G_{h} \in G}} CL_{h}$, then go to Step 6. Otherwise, go to Step 9.

Step 9: Analyze and manage the NCBs of the experts in the subgroup $G_{k}$ by using the experts’ historical adjustment data-based NCB management method in Sect. 4.3. Then recalculate the subgroup consensus level and go to Step 6.

Step 10: Calculate the alternative score of each subgroup by weighted averaging the score values of each alternative under different criteria. Then the overall alternative score can be obtained by a weighted average of the alternative score vector of the subgroup.

Step 11: Rank and select the alternatives for investment selection of renewable energy projects.

5 Practical Case

5.1 Background and Data Collection

The shortage of fossil energy such as oil and natural gas has led to the call for low-carbon action. At present, people urgently need to develop renewable energy to replace fossil energy for human daily life and work. As renewable energy has the characteristics of high efficiency, clean, low-carbon and environmental protection, the development of renewable energy is bound to help promote the sustainable development of the ecological environment and social economy. In response to the call for low-carbon action, in recent years, Qingdao has invested in many renewable energy projects, focusing on wind power and photovoltaic power generation, supplemented by biomass energy, ocean energy and geothermal energy, to speed up the clean and low-carbon transformation, which has led to the rapid development of the local renewable energy industry.

This paper assumes that Qingdao plans to invest in new renewable energy projects, the four projects related to hydraulic energy, solar energy, wind energy and biomass energy need to be comprehensively evaluated, denoted as hydropower project ($x_{1}$), solar power project ($x_{2}$), wind power project ($x_{3}$), biomass power project ($x_{4}$). Therefore, 20 experts in the fields of energy development, construction, manufacturing, economic and environment were convened to evaluate the investment selection of the four projects. Drawing on the review of recent renewable energy literature in Sect. 2.1, the following four criteria with equally importance were selected to evaluate the performance of the four projects: business continuity ($c_{1}$), project operability ($c_{2}$), security ($c_{3}$) and productiveness ($c_{4}$).

• Business continuity $c_{1}$: It is reflected in the management requirements and regulatory processes based on the business operation rules so that an organization can respond quickly in the face of emergencies to ensure that key business functions can continue without causing business interruption or change in the nature of the business processes.

• Project operability $c_{2}$: It mainly involves the technical maturity of the project, the equipment of the project, the difficulty of construction, etc.

• Security $c_{3}$: It mainly includes whether the safety supervision system of the project is comprehensive and whether there is adverse impact on the environment and society.

• Productiveness $c_{4}$: It refers to the relationship between the expected input of the project and the expected power generation.

However, as the selection of renewable energy projects involves the impact on the local environment, society, economy and other aspects, this complexity directly makes it difficult for experts to evaluate different options with accurate figures in the assessment process. Therefore, the method proposed in this paper can be applied to the practical problem of renewable energy project investment selection.

First, let $S = \left\{ {s_{0} = {\text{exremelypoor}},s_{1} = {\text{verypoor}},s_{3} = {\text{slightlypoor}},s_{4} = {\text{fair}},s_{5} = {\text{slightlygood}},s_{6} = } \right.$$\left. {{\text{good}},s_{7} = {\text{verygood}},s_{8} = {\text{extremelygood}}} \right\}$ be the LTS for expert to evaluate the alternatives, then twenty experts assess four alternatives under the four criteria and are allowed to hesitate between multiple linguistic words. And they were invited to fill in the rating of the trust of other experts involved in the decision-making. Then, the experts’ opinion matrices $H_{u} = \left( {h_{ij,u} } \right)_{n \times m}$ with $u = 1,\ldots,20;i = 1,\ldots,4;j = 1,\ldots,4$ and trust relationships are obtained as shown in Appendix 3. Before applying the proposed LGDM method, the consensus threshold $\alpha$, the maximum number of iterations $r_{\max }$ and the cooperation degree threshold $\varphi$ are first set as $\alpha = 0.85$, $\varphi = 0.5$ and $r_{\max } = 5$. And the parameter $\beta$ in the model (5) is set to $\beta = 4$.

5.2 The LGDM Process for Investment Selection of Renewable Energy Projects

In this section, the proposed LGDM method is applied to solve the investment selection problem of the above renewable energy projects. The specific process is as follows:

Step 1: The decision expert group is divided into five subgroups according to Algorithm 1. The clustering results are shown in Table 2, and then the trust relationship between experts in different subgroups can be shown in Fig. 4, where different colors represent different subgroups.

Table 2 Subgroup clustering results

Fig. 4

Social trust network diagram

Step 2: Determine the weight of the subgroup and the weight of experts in the subgroup, $W = \left( {0.2078,0.2005,0.2056,0.2069,0.1792} \right)^{T}$,

$W^{1} = \left( {0.1666,0.1646,0.1684,0.1689,0.1639,0.1676} \right)^{T}$, $W^{2} = \left( {0.248,0.2462,0.2498,0.256} \right)^{T}$, $W^{3} = \left( {0.2002,0.2016,0.2016,0.1997,0.1969} \right)^{T}$, $W^{4} = \left( {0.3372,0.3293,0.3335} \right)^{T}$, $W^{5} = \left( {0.5047,0.4953} \right)^{T}$.

Step 3: Calculate the subgroups’ opinion matrix $H_{k} = \left( {h_{ij,k} } \right)_{4 \times 4}$ with $k = 1,\ldots,5$ by model (5).

$$H_{1} = \left( {\begin{array}{*{20}c} {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} } \right\}} \\ \end{array} } \right)\quad H_{2} = \left( {\begin{array}{*{20}c} {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right)\quad H_{3} = \left( {\begin{array}{*{20}c} {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{2} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} \\ \end{array} } \right)$$

$H_{4} = \left( {\begin{array}{*{20}c} {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} \\ {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} ,} \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} \\ \end{array} } \right)\quad H_{5} = \left( {\begin{array}{*{20}c} {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right)$ .

Step 4: Calculate the consensus level of each subgroup, $CL_{1} = 0.8383,CL_{2} = 0.8383,CL_{3} = 0.8324,CL_{4} =$ $0.8337,CL_{5} = 0.7426$.

Step 5: Consensus judgment based on JR 1. Owing to $\min CL_{k} = 0.7426 < 0.85$ and $r = 0 < 5$, the feedback mechanism in iteration 1 is activated.

Iteration 1

Step I1-1: Identify subgroups to be modified in iteration 1. Since $\mathop {\arg \min }\limits_{{G_{k} }} CL_{k} = G_{5}$, the experts in subgroup $G_{5}$ modify their opinions.

Step I1-2: According to the proposed feedback mechanism in Sect. 4.2.2, the reference object of expert $e_{13}$ and expert $e_{18}$ is both the opinion matrix of expert $e_{7}$. After model (9) processing, the modified interval is fed back to the corresponding experts. Then, expert $e_{13}$ and expert $e_{18}$ provide their modified opinion matrices.

$$\overline{{H_{13}^{5} }} = \left( {\begin{array}{*{20}c} {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right),\quad \overline{{H_{18}^{5} }} = \left( {\begin{array}{*{20}c} {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right)$$

Step I1-3: The new opinion matrix and consensus level of subgroup $G_{5}$ was calculated, $CL_{5}^{\left( 1 \right)\prime} = 0.766 < 0.85$. Then, the consensus levels of other subgroups are calculated to obtain the subgroup with the lowest consensus level, $CL_{1}^{\left( 1 \right)\prime} = 0.8442,CL_{2}^{\left( 1 \right) \prime } = 0.8481,CL_{3}^{\left( 1 \right) \prime } = 0.8383,CL_{4}^{\left( 1 \right)\prime} =$$0.8356,CL_{5}^{\left( 1 \right) \prime }= 0.766$, and $\mathop {\arg \min }\limits_{{G_{k} }} CL_{k} = G_{5}$. Thus, in iteration 1, there are experts with non-cooperative tendency in subgroup $G_{5}$.

Step I1-4: Identify non-cooperators in subgroup $G_{5}$, $\varphi_{13}^{5\left( 1 \right)} = 0.7407 > 0.5$, $\varphi_{18}^{5\left( 1 \right)} = 0.2917 < 0.5$. Then, using Algorithm 2 to update the weights of experts in subgroup $G_{5}$, $W_{5}^{\left( 1 \right)} = \left( {w_{13}^{5\left( 1 \right)} ,w_{18}^{5\left( 1 \right)} } \right)^{T} =$ $\left( {0.7044,0.2956} \right)^{T}$.

Step 6: Recalculate the consensus level of the subgroups $CL_{1}^{\left( 2 \right)} = 0.8598,CL_{2}^{\left( 2 \right)} = 0.8676,CL_{3}^{\left( 2 \right)} = 0.8461,$ $CL_{4}^{\left( 2 \right)} = 0.8513,CL_{5}^{\left( 2 \right)} = 0.8246$. Because $\min CL_{k} = 0.8246 < 0.85$ and $r = 1 < 5$, enter iteration 2.

Iteration 2

Step I2-1: Identify subgroups to be modified in iteration 2. Since $\mathop {\arg \min }\limits_{{G_{k} }} CL_{k} = G_{5}$, the experts in subgroup $G_{5}$ modify their opinions in iteration 2.

Step I2-2: Determine the reference object to be modified by the expert in the subgroup $G_{5}$. According to the direction rules in Sect. 4.2.2, the reference object of the expert $e_{13}$ is also the opinion matrix of the expert $e_{7}$ and the reference object of the expert $e_{18}$ is the opinion matrix of the expert $e_{13}$. After model (9) processing, the modified interval is fed back to the corresponding experts. Then, expert $e_{13}$ and expert $e_{18}$ provide their modified opinion matrices in iteration 2.

$$\overline{{H_{13}^{5} }} = \left( {\begin{array}{*{20}c} {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right),\quad \overline{{H_{18}^{5} }} = \left( {\begin{array}{*{20}c} {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right)$$

Step I2-3: The new opinion matrix and consensus level of subgroup $G_{5}$ was calculated, $CL_{5}^{\left( 2 \right)\prime} = 0.8481 < 0.85$. Then, the consensus levels of other subgroups are calculated to obtain the subgroup with the lowest consensus level, $CL_{1}^{\left( 2 \right) \prime } = 0.8676,CL_{2}^{\left( 2 \right) \prime } = 0.8754,CL_{3}^{\left( 2 \right) \prime } = 0.8539,CL_{4}^{\left( 2 \right) \prime } =$$0.8513,CL_{5}^{\left( 2 \right) \prime} = 0.8481$, and $\mathop {\arg \min }\limits_{{G_{k} }} CL_{k} = G_{5}$. Thus, in iteration 3, there are experts with a non-cooperative tendency in subgroup $G_{5}$.

Step I2-4: Identify non-cooperators in subgroup $G_{5}$, $\varphi_{13}^{5\left( 1 \right)} = 0.5714 > 0.5$, $\varphi_{18}^{5\left( 1 \right)} = 0.1429 < 0.5$. Then, using the two-stage opinion penalty-based management method in Sect. 4.3.2 to update the opinion of expert $e_{18}$. The new opinion matrix of expert $e_{18}$ is as follows, and $CL_{5}^{\left( 3 \right)} = 0.85$.

$$H_{18}^{5} = \left( {\begin{array}{*{20}c} {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right)$$

Step 7: Recalculate the consensus level of the subgroups $CL_{1}^{\left( 3 \right)} = 0.8637,CL_{2}^{\left( 3 \right)} = 0.8774,CL_{3}^{\left( 3 \right)} = 0.8559,$$CL_{4}^{\left( 3 \right)} = 0.8532,CL_{5}^{\left( 3 \right)} = 0.85$. All subgroups have reached the consensus threshold, then enter selection phase.

Step 8: Calculate the score vector of alternatives using definition 3.3, $E = \left( {0.4733,0.5718,0.6497,0.4402} \right)$, and obtain the ranking of alternatives, $x_{3} \succ x_{2} \succ x_{1} \succ x_{4}$.

Through expert evaluation and consultation, the final ranking of the four alternatives is: wind power project $\succ$ solar power project $\succ$ hydropower project $\succ$ biomass power project. Therefore, through the discussion of 20 experts, this wind power generation project is the project worthy of investment for the development of Qingdao, China, to continue to expand the scope of renewable energy utilization.

6 Comparison Analysis

This section is devoted to explain the innovation of the proposed method for investment selection of renewable energy projects by introducing the differences from the existing methods (as shown in Table 3), which can be classified into two aspects: feedback adjustment mechanism and management methods of NCB. In the existing methods, various consensus models considering STN and NCBs of experts are provided to improve the rationality and efficiency of decision-making.

• 1. Comparison of feedback mechanisms: Liu et al. [20] proposed a feedback mechanism to find the most reliable feedback between expert opinions and collective opinions to the experts who need to modify their opinions. However, this method does not consider the influence of the social trust relationship between experts. In fact, experts are more likely to accept the opinions of experts they trust. Wu et al. [30] determined the reference object for experts to modify through the level of social trust among experts, and determined the optimal adjustment parameters and the opinions of experts after adjustment by minimizing the adjustment cost. In this method, the adjusted opinions of experts are obtained through the optimization model, and the subjective wills of experts are not fully considered. And the above method is not applicable to the CRP in LGDM. Besides, Zhang et al. [39] proposed an SN-GDM method to provide feedback suggestions for experts based on the leadership ability and bounded confidence level of experts in social networks, without considering the differences in trust levels among experts. Li et al. [15] proposed a feedback mechanism based on the trust relationship and bounded confidence of experts. But in this feedback mechanism, the consensus level of the reference object may be lower than the consensus level of the expert to be adjusted, which may cause the expert to adjust in the opposite direction of consensus and reduce the consensus efficiency. The method proposed in this paper covers three reliable sources: the trust relationship between experts, the consensus contribution of experts in the subgroup, and the opinion similarity between experts, to provide scientific and reasonable feedback for experts .

• 2. Comparison of management methods of NCB: Liao et al. [16] divided the decision-making group into internal experts and external experts. For two different types of experts, they proposed a weight-based internal expert punishment mechanism and an exit-delegation mechanism to manage the NCB of external experts. Moreover, Gao and Zhang [6] define the non-cooperative degree according to the number of elements showing non-cooperation behavior in the expert evaluation matrix, and suggest that other experts reduce the trust value of non-cooperation experts to manage non-cooperation behavior. Furthermore, in multiple attribute GDM (MAGDM), Zhang et al. [38] defined three NCBs according to the evaluation information expressed or modified by experts: dishonesty, disobedience and disagreement. The proposed management method is to feed back the non-cooperative degree of experts to other experts, and suggest that other experts reduce their trust in non-cooperative authors. Besides, Li et al. [13] proposed a penalty mechanism to update the weights and trust values of non-cooperators at the same time. And Du et al. [4] put forward the management method of decreasing weight punishment for experts who have shown NCB for many times, which means that the punishment for experts who have shown NCB is decreasing with the number of times. It can be found that the current research methods mostly punish the weight or trust value of experts. In fact, when an expert shows NCB again despite the punishment for first showing NCB, the behavior of the expert has had a great impact on the quality and efficiency of decision-making, which requires more severe punishment to manage such behavior. Therefore, this paper proposes a management method of adjusting data based on the history of experts, and directly punishes the experts who show NCB twice to speed up the consensus process and ensure the order of decision-making.

Table 3 Comparisons with the existing GDM methods

In general, the comparative analysis of the above two points fully illustrates the innovation of the method proposed in this paper. Moreover, the methods proposed in this paper fully consider the high complexity of investment selection of renewable energy projects and the hesitation of experts in evaluation, which is the reason why many existing methods cannot be used as a solution to this problem.

7 Conclusion

The problem of low-carbon energy transformation caused by global warming has been widely concerned by all countries in the world. As a key part of this transformation, renewable energy has developed rapidly and attracted the attention of many investors. However, since renewable energy projects involve expertise in many fields such as energy, transportation, construction and economy, the investment in this area needs to be scientifically and comprehensively evaluated. Therefore, this paper proposes a large group decision-making method considering consensus and NCB to solve the following key problems.

• 1. The consensus process is introduced into the investment selection of renewable energy projects. The evaluation information of experts from different fields and with different professional levels may be quite different or even have completely opposite opinions. In addition, the high complexity of this issue also makes it a major challenge to provide appropriate reference for the experts in the decision-making expert group who need to adjust their opinions. Therefore, this paper creatively proposes a feedback mechanism by comprehensively considering three reliable factors: the social trust relationship of experts, the consensus contribution in the subgroup and the similarity of opinions with other experts.

• 2. The experts’ historical adjustment data-based NCB management method is proposed. In the process of feedback adjustment, not all experts can modify their evaluation information according to the reference opinions, and there may be experts who refuse to modify their opinions for personal interests. For this kind of NCB with a low degree of cooperation among experts, this paper proposes two NCB management methods based on the historical adjustment data of experts: the management method based on weight punishment and the management method based on opinion punishment. When an expert shows NCB for the first time, a management method based on weight punishment is implemented to warn the expert; When the experts show the second NCB, the management method based on opinion punishment is used to ensure the rationality of decision-making and improve the efficiency of decision-making.

• 3. The proposed method is applied to the investment selection of renewable energy power generation projects in Qingdao, China. Due to the shortage of fossil resources such as oil and coal, power generation with traditional energy has become a major problem in various regions. With its abundant marine resources, Qingdao still has a large space for solar energy, hydro energy, biomass energy and wind energy. This paper makes a comprehensive evaluation of four renewable energy power generation projects in Qingdao from the four criteria of business continuity, project operability, security and productiveness, which can provide a specific reference for enterprises and governments.

However, due to the variability of the environment, the method proposed in this paper still has some limitations. For example, the current massive data information leads to a dynamic change in the trust relationship between experts [14, 29]. How to provide a reliable reference for experts in this situation is a difficult point. In addition, the proposed method only considers the processing of the same type of evaluation information, and the heterogeneous evaluation information of experts in large group decision-making [22] is also an important part of the current study.

Appendices

Appendix 1

The solution method of model (13):

Firstly, by substituting the distance formula of Eq. (1) into model (13), the objective function and consensus constraints of model (13) is converted as:

$\min \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( \begin{gathered} \frac{1}{2\sqrt 3 }\left| {\left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) - }} }} } \right)} \right) - \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right| + \hfill \\ \frac{1}{2}\left| {\left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) - }} }} } \right)} \right) - \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right| \hfill \\ \end{gathered} \right)} }$,

$1 - \frac{1}{{nm\left( {K - 1} \right)}}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\sum\limits_{h = 1,h \ne k}^{K} {\left( \begin{gathered} \frac{1}{2\sqrt 3 }\left| {\left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) - }} }} } \right)} \right) - \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right| + \hfill \\ \frac{1}{2}\left| {\left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) - }} }} } \right)} \right) - \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right| \hfill \\ \end{gathered} \right)} } } \ge \alpha$.

Secondly, to simplify the calculation of model (13), let

$$\begin{gathered} a_{ij,k}^{g} = \left\{ {\begin{array}{*{20}l} {1, \, \overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} = s_{g} } \hfill \\ {0, \, \overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} \ne s_{g} } \hfill \\ \end{array} } \right.{\text{ g}} = 0,\ldots,2\tau ;i = 1,\ldots,n;\;j = 1,\ldots,m\;\; \hfill \\ b_{ij,k}^{g} = \left\{ {\begin{array}{*{20}l} {1, \, \overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) - }} }} = s_{g} } \hfill \\ {0, \, \overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) - }} }} \ne s_{g} } \hfill \\ \end{array} } \right.{\text{ g}} = 0,\ldots,2\tau ;i = 1,\ldots,n;\;j = 1,\ldots,m, \hfill \\ \end{gathered}$$

then, the model (13) can be converted to model (16):

$$\min \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( {\frac{1}{2\sqrt 3 }\left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right| + \frac{1}{2}\left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right|} \right)} }$$

$$s.t.\left\{ {\begin{array}{*{20}l} {1 - \frac{1}{{nm\left( {K - 1} \right)}}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\sum\limits_{h = 1,h \ne k}^{K} {\left( {\frac{1}{2\sqrt 3 }\left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right| + } \right.} } } } \hfill \\ {\left. {\frac{1}{2}\left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right|} \right) \ge \alpha } \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} \le I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right) \, i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {g\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} \ge 0 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {a_{ij,k}^{g} } = 1 \, i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {b_{ij,k}^{g} } = 1 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {a_{ij,k}^{g} ,b_{ij,k}^{g} \in \left\{ {0,1} \right\} \, i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ \end{array} } \right.$$

(16)

Since the objective function and consensus constraints of model (16) are nonlinear, the following parameters are introduced to simplify the calculation of model (16).

$$x_{ij}^{k} = \left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right|,\;y_{ij}^{k} = \left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right|$$

$$p_{ij}^{k} = \left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right|,\;q_{ij}^{k} = \left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right)} \right|.$$

And then the model (16) is converted into the model (17).

$$\min \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( {\frac{1}{2\sqrt 3 }x_{ij}^{k} + \frac{1}{2}y_{ij}^{k} } \right)} }$$

$$s.t.\left\{ {\begin{array}{*{20}l} {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right) - x_{ij}^{k} \le 0 \, i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ { - \sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} + \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right) - x_{ij}^{k} \le 0 \, i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right) - y_{ij}^{k} \le 0 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ { - \sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} + \left( {I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right)} \right) - y_{ij}^{k} \le 0 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {1 - \frac{1}{{nm\left( {K - 1} \right)}}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\sum\limits_{h = 1,h \ne k}^{K} {\left( {\frac{1}{2\sqrt 3 }p_{ij}^{k} + \frac{1}{2}q_{ij}^{k} } \right)} } } \ge \alpha } \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right) - p_{ij}^{k} \le 0 \, h = 1,\ldots,K,h \ne k;i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ { - \sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} + \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right) - p_{ij}^{k} \le 0 \, h = 1,\ldots,K,h \ne k;i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} - \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right) - q_{ij}^{k} \le 0 \, h = 1,\ldots,K,h \ne k;i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ { - \sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} + \left( {I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,h}^{{\left( {r^{\prime}} \right) - }} } \right)} \right) - q_{ij}^{k} \le 0 \, h = 1,\ldots,K,h \ne k;i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} \le I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,k}^{{\left( {r^{\prime}} \right) - }} } \right) \, i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {g\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} \ge 0 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {a_{ij,k}^{g} } = 1 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {b_{ij,k}^{g} } = 1 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {a_{ij,k}^{g} ,b_{ij,k}^{g} \in \left\{ {0,1} \right\} \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ \end{array} } \right.$$

(17)

The optimal solution of model (13) can be obtained by solving linear programming model (17), which can be solved by Lingo and other software packages.

Appendix 2

The solution method of model (15):

Firstly, by substituting the distance formula of Eq. (1) into model (15), the objective function of model (15) is converted as:

$$\begin{gathered} \min = \sum\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{\left( {r^{\prime} + 1} \right)}} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( \begin{gathered} \frac{1}{2\sqrt 3 }\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) + }} } \right) - I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right)} \right)} \right| + \hfill \\ \frac{1}{2}\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) + }} } \right) + I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right)} \right)} \right| \hfill \\ \end{gathered} \right)} } } + \hfill \\ \sum\limits_{{e_{u} \in G_{k} \backslash G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( \begin{gathered} \frac{1}{2\sqrt 3 }\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right)} \right)} \right| + \hfill \\ \frac{1}{2}\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right)} \right)} \right| \hfill \\ \end{gathered} \right)} } } - \hfill \\ \prod\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {\frac{1}{{\varphi_{u}^{{\left( {r^{\prime}} \right)}} }}\left( {1 - \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( \begin{gathered} \frac{1}{2\sqrt 3 }\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) + }} } \right) - I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right)} \right| + \hfill \\ \frac{1}{2}\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) + }} } \right) + I\left( {h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right)} \right| \hfill \\ \end{gathered} \right.} } } \right)} \hfill \\ \end{gathered}$$

(18)

Secondly, to simplify the calculation of model (18), let

$$\begin{gathered} a_{ij,u}^{kg} = \left\{ {\begin{array}{*{20}l} {1, \, h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) + }} = s_{g} } \hfill \\ {0, \, h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) + }} \ne s_{g} } \hfill \\ \end{array} } \right.{\text{ g}} = 0,\ldots,2\tau ;i = 1,\ldots,n;\;j = 1,\ldots,m \hfill \\ b_{ij,u}^{kg} = \left\{ {\begin{array}{*{20}l} {1, \, h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) - }} = s_{g} } \hfill \\ {0, \, h_{ij,u}^{{k\left( {r^{\prime} + 1} \right) - }} \ne s_{g} } \hfill \\ \end{array} } \right.{\text{ g}} = 0,\ldots,2\tau ;i = 1,\ldots,n;\;j = 1,\ldots,m \hfill \\ \end{gathered}$$

and $a_{ij,k}^{g}$, $b_{ij,k}^{g}$ are as easier, then the model (18) can be converted to model (19):

$$\begin{gathered} \min = \sum\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{\left( {r^{\prime} + 1} \right)}} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( {\frac{1}{2\sqrt 3 }\left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} - a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} } \right| + \frac{1}{2}\left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} + b_{ij,u}^{kg} - a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} } \right|} \right)} } } + \hfill \\ \sum\limits_{{e_{u} \in G_{k} \backslash G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( \begin{gathered} \frac{1}{2\sqrt 3 }\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right)} \right)} \right| + \hfill \\ \frac{1}{2}\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right)} \right)} \right| \hfill \\ \end{gathered} \right)} } } - \prod\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {\phi_{u}^{{k\left( {r^{\prime}} \right)}} } \hfill \\ \end{gathered}$$

$$s.t.\left\{ {\begin{array}{*{20}l} {\phi_{u}^{{k\left( {r^{\prime}} \right)}} = \frac{1}{{\varphi_{u}^{{\left( {r^{\prime}} \right)}} }}\left( {1 - \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( \begin{gathered} \frac{1}{2\sqrt 3 }\left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} } \right)} - \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right)} \right| + \hfill \\ \frac{1}{2}\left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} + b_{ij,u}^{kg} } \right)} - \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right)} \right| \hfill \\ \end{gathered} \right)} } } \right. \, e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} } \hfill \\ {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} = \left\{ {\begin{array}{*{20}l} {U\left( {\varphi_{u}^{{k\left( {r^{\prime}} \right)}} ,w_{u}^{{k\left( {r^{\prime}} \right)}} } \right) \, e_{u} \in G_{k1}^{{\left( {r^{\prime}} \right)}} } \hfill \\ {w_{u}^{{k\left( {r^{\prime}} \right)}} + \frac{{\varphi_{u}^{{k\left( {r^{\prime}} \right)}} }}{{\sum\limits_{{e_{u} \in G_{k} \backslash G_{k1}^{{\left( {r^{\prime}} \right)}} }} {\varphi_{u}^{{k\left( {r^{\prime}} \right)}} } }}\left( {\sum\limits_{{e_{u} \in G_{k1}^{{\left( {r^{\prime}} \right)}} }} {\left( {w_{u}^{{k\left( {r^{\prime}} \right)}} - w_{u}^{{k\left( {r^{\prime} + 1} \right)}} } \right)} } \right) \, e_{u} \in G_{k} \backslash G_{k1}^{{\left( {r^{\prime}} \right)}} } \hfill \\ \end{array} } \right.} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} \le I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right) \, i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {g\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} } \right)} \ge 0 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {a_{ij,u}^{kg} } = 1 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {b_{ij,u}^{kg} } = 1 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {a_{ij,u}^{kg} ,b_{ij,u}^{kg} \in \left\{ {0,1} \right\} \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ \end{array} } \right.$$

(19)

Since the absolute value function is still included in the objective function and consensus constraints of model (19), the following parameters are introduced to simplify the calculation of model (19).

$$p_{ij,u}^{k} = \left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} - a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} } \right|,\;\;q_{ij,u}^{k} = \left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} + b_{ij,u}^{kg} - a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} } \right|,$$

$$x_{ij,u}^{k} = \left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} } \right)} - \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right)} \right|,\;y_{ij,u}^{k} = \left| {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} } \right)} - \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right)} \right|.$$

$$\begin{gathered} \min \sum\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{\left( {r^{\prime} + 1} \right)}} \left( {\frac{1}{2\sqrt 3 }p_{ij,u}^{k} + \frac{1}{2}q_{ij,u}^{k} } \right)} - \prod\limits_{{e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} }} {\frac{1}{{\varphi_{u}^{{\left( {r^{\prime}} \right)}} }}\left( {1 - \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{m} {\left( {\frac{1}{2\sqrt 3 }x_{ij,u}^{k} + \frac{1}{2}y_{ij,u}^{k} } \right)} } } \right)} + \hfill \\ \sum\limits_{{e_{u} \in G_{k} \backslash G_{k2}^{{\left( {r^{\prime}} \right)}} }} {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} \left( \begin{gathered} \frac{1}{2\sqrt 3 }\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} } \right) - I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right)} \right)} \right| + \hfill \\ \frac{1}{2}\left| {\left( {I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} } \right) + I\left( {h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} } \right)} \right) - \left( {I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,k}^{{\left( {r^{\prime}} \right) + }} }} } \right)} \right)} \right| \hfill \\ \end{gathered} \right)} \hfill \\ \end{gathered}$$

$$s.t.\left\{ {\begin{array}{*{20}l} {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} - a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} - p_{ij,u}^{k} \le 0 \, e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} ;i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ { - \sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} - a_{ij,k}^{g} + b_{ij,k}^{g} } \right)} - p_{ij,u}^{k} \le 0 \, e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} ;i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} + b_{ij,u}^{kg} - a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} - q_{ij,u}^{k} \le 0 \, e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} ;i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ { - \sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} + b_{ij,u}^{kg} - a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} - q_{ij,u}^{k} \le 0 \, e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} ;i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} } \right)} - \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right) - x_{ij,u}^{k} \le 0 \, e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} ;i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ { - \sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} } \right)} + \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right) - x_{ij,u}^{k} \le 0 \, e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} ;i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} } \right)} - \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right) - y_{ij,u}^{k} \le 0 \, e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} ;i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ { - \sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} } \right)} + \left( {I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) + I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right)} \right) - y_{ij,u}^{k} \le 0 \, e_{u} \in G_{k2}^{{\left( {r^{\prime}} \right)}} ;i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {w_{u}^{{k\left( {r^{\prime} + 1} \right)}} = \left\{ {\begin{array}{*{20}l} {U\left( {\varphi_{u}^{{k\left( {r^{\prime}} \right)}} ,w_{u}^{{k\left( {r^{\prime}} \right)}} } \right) \, e_{u} \in G_{k1}^{{\left( {r^{\prime}} \right)}} } \hfill \\ {w_{u}^{{k\left( {r^{\prime}} \right)}} + \frac{{\varphi_{u}^{{k\left( {r^{\prime}} \right)}} }}{{\sum\limits_{{e_{u} \in G_{k} \backslash G_{k1}^{{\left( {r^{\prime}} \right)}} }} {\varphi_{u}^{{k\left( {r^{\prime}} \right)}} } }}\left( {\sum\limits_{{e_{u} \in G_{k1}^{{\left( {r^{\prime}} \right)}} }} {\left( {w_{u}^{{k\left( {r^{\prime}} \right)}} - w_{u}^{{k\left( {r^{\prime} + 1} \right)}} } \right)} } \right) \, e_{u} \in G_{k} \backslash G_{k1}^{{\left( {r^{\prime}} \right)}} } \hfill \\ \end{array} } \right.} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {\frac{g}{2\tau }\left( {a_{ij,k}^{g} - b_{ij,k}^{g} } \right)} \le I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) + }} }} } \right) - I\left( {\overline{{h_{ij,u}^{{k\left( {r^{\prime}} \right) - }} }} } \right) \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {g\left( {a_{ij,u}^{kg} - b_{ij,u}^{kg} } \right)} \ge 0 \, i = 1,\ldots,n;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {a_{ij,u}^{kg} } = 1 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {\sum\limits_{g = 0}^{2\tau } {b_{ij,u}^{kg} } = 1 \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ {a_{ij,u}^{kg} ,b_{ij,u}^{kg} \in \left\{ {0,1} \right\} \, i = 1,\ldots,n;\;j = 1,\ldots,m} \hfill \\ \end{array} } \right.$$

(20)

The optimal solution of model (15) can be obtained by solving the model (20) with Lingo and other software packages.

Appendix 3

The evaluation matrices given by the experts in the decision-making expert group for investment selection of renewable energy power generation projects in Sect. 5 are as follows:

$$H_{1} = \left( {\begin{array}{*{20}c} {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{6} ,s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} \\ \end{array} } \right)\quad H_{2} = \left( {\begin{array}{*{20}c} {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{5} } \right\}} \\ \end{array} } \right)$$

$$H_{3} = \left( {\begin{array}{*{20}c} {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{2} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} \\ \end{array} } \right)\quad H_{4} = \left( {\begin{array}{*{20}c} {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{4} ,s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right)$$

$$H_{5} = \left( {\begin{array}{*{20}c} {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{5} } \right\}} \\ \end{array} } \right)\quad H_{6} = \left( {\begin{array}{*{20}c} {\left\{ {s_{3} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} \\ \end{array} } \right)$$

$$H_{7} = \left( {\begin{array}{*{20}c} {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right)\quad H_{8} = \left( {\begin{array}{*{20}c} {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{2} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} ,s_{7} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ \end{array} } \right)$$

$$H_{9} = \left( {\begin{array}{*{20}c} {\left\{ {s_{2} ,s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{5} ,s_{6} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} \\ {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} & {\left\{ {s_{7} } \right\}} \\ {\left\{ {s_{2} ,s_{3} } \right\}} & {\left\{ {s_{6} ,s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} ,s_{6} } \right\}} \\ \end{array} } \right)\quad H_{10} = \left( {\begin{array}{*{20}c} {\left\{ {s_{4} ,s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} } \right\}} \\ \end{array} } \right)$$

$$H_{11} = \left( {\begin{array}{*{20}c} {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} ,s_{4} ,s_{5} } \right\}} \\ {\left\{ {s_{2} ,s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} ,s_{3} } \right\}} \\ {\left\{ {s_{2} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ \end{array} } \right)\quad H_{12} = \left( {\begin{array}{*{20}c} {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} ,s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} } \right\}} \\ \end{array} } \right)$$

$$H_{13} = \left( {\begin{array}{*{20}c} {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{7} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right)\quad H_{14} = \left( {\begin{array}{*{20}c} {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} ,s_{4} } \right\}} \\ {\left\{ {s_{4} ,s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} } \right\}} \\ \end{array} } \right)$$

$$H_{15} = \left( {\begin{array}{*{20}c} {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{2} ,s_{3} } \right\}} \\ \end{array} } \right)\quad H_{16} = \left( {\begin{array}{*{20}c} {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} & {\left\{ {s_{6} ,s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ \end{array} } \right)$$

$$H_{17} = \left( {\begin{array}{*{20}c} {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{5} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{2} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{5} } \right\}} \\ \end{array} } \right)\quad H_{18} = \left( {\begin{array}{*{20}c} {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} \\ {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{2} } \right\}} \\ {\left\{ {s_{7} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{2} } \right\}} & {\left\{ {s_{3} } \right\}} \\ \end{array} } \right)$$

$$H_{19} = \left( {\begin{array}{*{20}c} {\left\{ {s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} \\ {\left\{ {s_{2} } \right\}} & {\left\{ {s_{5} } \right\}} & {\left\{ {s_{4} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} \\ {\left\{ {s_{4} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} ,s_{7} } \right\}} & {\left\{ {s_{5} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{7} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{5} } \right\}} \\ \end{array} } \right)\quad H_{20} = \left( {\begin{array}{*{20}c} {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{6} } \right\}} & {\left\{ {s_{2} ,s_{3} } \right\}} & {\left\{ {s_{5} } \right\}} \\ {\left\{ {s_{2} } \right\}} & {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{4} } \right\}} \\ {\left\{ {s_{2} } \right\}} & {\left\{ {s_{5} ,s_{6} } \right\}} & {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} } \right\}} \\ {\left\{ {s_{3} } \right\}} & {\left\{ {s_{6} ,s_{7} } \right\}} & {\left\{ {s_{3} ,s_{4} } \right\}} & {\left\{ {s_{4} ,s_{5} } \right\}} \\ \end{array} } \right)$$

Table

Table 4 Summary of trust relation between DMs

4 shows the trust relationship and trust degree provided by the experts in the decision-making expert group for investment selection of renewable energy power generation projects in Sect. 5