Abstract
We tackle the problem of reducing non-clausal MaxSAT and MinSAT to clausal MaxSAT and MinSAT. Our motivation is twofold: (i) the clausal form transformations used in SAT are unsound for MaxSAT and MinSAT, because they do not preserve the minimum or maximum number of unsatisfied clauses, and (ii) the state-of-the-art MaxSAT and MinSAT solvers require as input a multiset of clauses. The main contribution of this paper is the definition of three different cost-preserving transformations. Two transformations extend the usual equivalence preserving transformation used in SAT to MaxSAT and MinSAT. The third one extends the well-known Tseitin transformation. Furthermore, we report on an empirical comparison of the performance of the proposed transformations when solved with a state-of-the-art MaxSAT solver.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
SAT is the problem of deciding whether there exists an assignment that satisfies a given (multi)set of propositional formulas. On the other hand, MaxSAT and MinSAT are optimization versions of SAT whose goal is to find an assignment that minimizes or maximizes the number of unsatisfied formulas, respectively. These problems have gained increasing interest, because many practical questions can be solved by first encoding them as a SAT, MaxSAT, or MinSAT problem and then finding a solution by solving the resulting encoding with a SAT, MaxSAT, or MinSAT solver. While SAT is used to solve decision problems, MaxSAT and MinSAT are used to solve optimization problems.
MaxSAT and MinSAT have been applied in real-world domains as diverse as bioinformatics [1, 2], circuit design and debugging [3], combinatorial auctions [4], combinatorial testing [5, 6], community detection in complex networks [7], diagnosis [8], planning [9], scheduling [10], and team formation [11, 12], among others.
The literature distinguishes between clausal SAT, MaxSAT, and MinSAT, and non-clausal SAT, MaxSAT, and MinSAT, respectively. In the clausal case, the input multiset only contains clauses (i.e., disjunctions of literals). In the non-clausal case, the input multiset contains propositional formulas that are not necessarily in clausal form.
Many combinatorial problems admit more natural and compact encodings when represented in non-clausal form. However, the fastest and most robust SAT/MaxSAT/MinSAT solvers require their input in clausal form. Thus, some kind of clausal form transformation is needed to solve them. In SAT, there are several algorithms that transform a multiset of arbitrary propositional formulas into a satisfiability equivalent multiset of clauses [13, 14]. Unfortunately, usual clausal form transformations used in SAT are not valid neither in MaxSAT nor MinSAT. The reason is that they are not cost-preserving, i.e., they do not preserve the minimum/maximum number of unsatisfied formulas between the input and the transformed multiset.
The main contribution of this paper is the definition of three different cost-preserving transformations. Two transformations extend the usual equivalence preserving transformation used in SAT to MaxSAT and MinSAT. The third one extends the well-known Tseitin transformation [14]. Moreover, we report on an empirical comparison of the performance of the proposed transformations when solved with a state-of-the-art MaxSAT solver.
An alternative option to solve non-clausal MaxSAT and MinSAT is to use the semantic tableaux and natural deduction calculi defined for these problems [15,16,17,18,19]. Nevertheless, no efficient implementation of such calculi is available. Furthermore, we believe that such implementations could rarely compete with the state-of-the-art clausal MaxSAT and MinSAT solvers, because they do not incorporate solving techniques such as lower bounds based on unit propagation [20] and clause learning [21].
We currently have highly optimized clausal MaxSAT solvers, due in part to the existence of a yearly MaxSAT Evaluation (MSE) since 2006 [22, 23]. There are two types of exact MaxSAT algorithms: Branch-and-Bound (BnB) and SAT-based algorithms. BnB algorithms apply restrictions of MaxSAT resolution and incorporate a bounding procedure based on detecting disjoint inconsistent cores with unit propagation [24]. Recently, they also incorporate clause learning [21, 25]. SAT-based algorithms transform MaxSAT into a sequence of SAT instances that are solved with a Conflict-Driven Clause Learning (CDCL) SAT solver [26,27,28,29]. Moreover, there exist efficient local search MaxSAT algorithms like BandMaxSAT [30] and SATLike 3.0 [31]. There has not been as much activity in MinSAT as in MaxSAT, but there exist a few clausal MinSAT solvers [4, 32,33,34].
This paper unifies the clausal forms transformations proposed in the conference papers [35, 36], provides new correctness proofs, and reports on an empirical comparison of different MaxSAT transformations. It is structured as follows: Sect. 2 introduces definitions and notations used throughout the document. Sections 3–5 define the proposed transformations and their correctness proofs. Section 6 details how the proposed transformation can be extended to weighted formulas. Section 7 reports on an empirical comparison of the transformations. Finally, Sect. 8 presents some concluding remarks.
2 Preliminaries
In this section, we briefly introduce the basic logical tools on which this work is based and present formally the problems we are going to study.
Given a set of propositional variables \({\mathcal {V}} = \{x_1, \ldots , x_n\}\), a literal \(\ell \) is a variable \(x_i\) or its negation \(\lnot x_{i}\), and a clause is a disjunction of literals. A formula, on the other hand, is any expression built from the variables in the language \(\langle \wedge /2, \vee /2, \lnot /1\rangle \), and where symbols \(\rightarrow \!\!/2, \leftrightarrow \!\!/2\) are defined from the previous ones by letting
Equivalently, a formula \(\varphi \) is any element according to the following language definition:
We will say that a formula is in conjunctive normal form if it is written as a conjunction of clauses. For convenience, we will denote by \(Fm_C\) to the set of clauses, by \(Fm_{\text {CNF}}\) to the set of formulas in conjunctive normal form, and by Fm to the set of all formulas.Footnote 1
A truth-assignment or evaluation e is a mapping from the variables into \(\{0,1\}\) that extends to all formulas in the usual classical sense (namely, where \(\wedge \) and \(\vee \) are, respectively, the minimum and maximum operations in \(\{0,1\}\), \(\lnot 0 \,{:}{=}\,1\) and \(\lnot 1 \,{:}{=}\,0\)). We will say that e satisfies a formula \(\varphi \) if \(e(\varphi ) = 1\), and that it falsifies or violates it if \(e(\varphi ) = 0\). The set of all evaluations will be denoted by Ev.Footnote 2
A weighted formula is a pair \(\langle \varphi , w\rangle \), where \(\varphi \) is a formula and w, its weight, is a positive integer or infinity. These weights, in the optimization context, are understood as penalties for violating that formula under an evaluation. Consequently, if the weight of a formula is infinity, it is called a hard formula (we will usually omit infinite weights for simplicity of the notation); otherwise, it is a soft formula.
Optimization questions in MaxSAT and MinSAT are represented using multisets instead of sets, because repeated formulas cannot be collapsed into a single formula as in SAT (e.g., if a formula appears twice in an input, the penalty for violating it will double). Considering only sets affects the preservation of the number of unsatisfied clauses and does not allow to model many problems that take into account multiplicity.
The symbols \(\cup \) and \(\bigcup \) will denote the union of sets, while \(\sqcup \) and \(\bigsqcup \) will denote the union of multisets. Similarly, the \(\in \) symbol will denote the usual set membership relation (even in multisets), and we will use the  symbol to denote multiset membership relation (taking into account the multiplicity). To clarify this with a simple example, for a multiset \(A = \{a,a\}\), we have that
symbol to denote multiset membership relation (taking into account the multiplicity). To clarify this with a simple example, for a multiset \(A = \{a,a\}\), we have that

As usual, conjunction and disjunction distribute when applied to multisets of formulas. Namely, for a multiset A and a formula \(\varphi \), we let

A weighted partial instance is a finite multiset of weighted formulas. As such, we will address it as a set of hard formulas and a multiset of soft formulas.Footnote 3 A particular case of a weighted partial instance is when all soft formulas have the same weight. In this case, we will call such a multiset a partial instance and we will usually not specify the weight. We will see that, for what concerns optimization questions, the particular weight of all the soft clauses turns out to be irrelevant in this case.
When considering an evaluation e over a multiset of weighted formulas A, we will say that the cost A under e, denoted by e(A), is the sum of the weights of the formulas in A violated by e. Formally,

The Weighted Partial MaxSAT problem, or WPMaxSAT, is defined for weighted partial instances of clauses. It consists in finding an assignment that minimizes the cost of the input instance, as long as it is below infinity (i.e., satisfying all hard clauses, since otherwise the problem has no solution). Dually, the Weighted Partial MinSAT problem, or WPMinSAT, searches for an assignment that maximizes the cost of the input weighted partial instance of clauses, also keeping this optimal cost below infinity (again, this means that only assignments satisfying the hard clauses set are deemed to be solutions of the problem).
For practical reasons (among other things, these assignments might not be unique), the outputs of the WPMaxSAT and WPMinSAT questions are usually taken to be the optimal cost (either minimal or maximal, according to the previous definition). This is the convention we will use in this work. Formally, for a weighted partial instance of clauses F,
Common subproblems of WPMaxSAT (and analogously for WPMinSAT) are: the Weighted MaxSAT (resp. WMaxSAT), which is WPMaxSAT without hard clauses; Partial MaxSAT (resp. PMaxSAT), which is WPMaxSAT when all the soft clauses have the same weight (which, for the calculations above, is considered to be 1), and MaxSAT, which is PMaxSAT without hard clauses. Observe that the above formulation is defining MaxSAT (resp. MinSAT) as the minimum (resp. maximum) number of unsatisfied clauses in the input multiset.
When WPMaxSAT (resp. WPMinSAT), as well as any of their subproblems, is studied over a weighted partial instance in general (namely, of arbitrary formulas), we refer to this problem as Non-clausal WPMaxSAT (resp. WPMinSAT). In this work, we will focus on studying the above optimization problems in full generality by means of providing faithful translations from Non-clausal WPMaxSAT (resp. WPMinSAT) into their corresponding clausal versions.
For that, recall that any propositional formula can be translated into the so-called Conjunctive Normal Form (CNF) through the recursive application of a very simple set of rules preserving logical equivalence. These are double negation elimination, De Morgan’s laws and distributivity of \(\vee \) over \(\wedge \). Further simplifications are also applied.Footnote 4 This produces a formula in CNF, namely, a conjunction of clauses. In what follows, \(CNF(\varphi )\) denotes the formula equivalent to \(\varphi \) in CNF resulting from the previous equivalences, so naturally, for any truth-assignment e, it holds that \(e(\varphi ) = e(CNF(\varphi ))\).
When inquiring about the satisfiability of a set of propositional formulas \(A = \{\varphi _1, \ldots , \varphi _n\}\), each of the \(CNF(\varphi _i)\) formulas can be split into a set of clauses (simply removing the conjunctions) to get a set of clauses that will serve as input to a SAT solver. We will refer to the union of these sets by \(T_{{\mathrm{SAT}}}(A)\). The satisfiability of \(T_{{\mathrm{SAT}}}(A)\) coincides with that of A, i.e., \({\mathrm{SAT}}(A)\) if and only if \({\mathrm{SAT}}(T_{{\mathrm{SAT}}}(A))\). As we show below, this approach does not serve to solve non-clausal MinSAT or MaxSAT.
Example 1
Let \(A=\{(\lnot x \leftrightarrow x) \wedge (\lnot y \leftrightarrow y), x \vee y\}\) be a multiset of propositional formulas. Applying the transformation defined above, we get \(T_{{\mathrm{SAT}}}(A)=\{x,\lnot x, y,\lnot y, x \vee y\}\). The evaluation \(e(x) = e(y) = 0\) violates two formulas of A and three clauses of \(T_{{\mathrm{SAT}}}(A)\), despite being an optimal MinSAT solution for both A and \(T_{{\mathrm{SAT}}}(A)\). Thus, that transformation is not cost-preserving and \({\mathrm{MinSAT}}(A) \ne {\mathrm{MinSAT}}(T_{{\mathrm{SAT}}}(A))\). Similarly, the evaluation \(e(x) = e(y) = 1\) is an optimal MaxSAT solution for both A and \(T_{{\mathrm{SAT}}}(A)\), but violates one formula of A and two clauses of \(T_{{\mathrm{SAT}}}(A)\).
Example 1 illustrates how the preservation problem arises at the step when the CNF is split into clauses. This operation can generate additional clauses that violate the preservation of the minimum or the maximum number of unsatisfied formulas. To overcome this drawback, we propose several new cost-preserving transformations for WPMaxSAT and WPMinSAT in the next three sections. For convenience, we will present the transformations for unweighted MaxSAT and MinSAT. In Sect. 6, we will see that adding weights in full generality (thus, covering also the WPMaxSAT/WPMinSAT and PMaxSAT/PMinSAT problems) can be easily done.
3 A Uniform Transformation Preserving the Variables Space: \(T_u\)
We first define a uniform transformation in the sense that it is cost-preserving for both MaxSAT and MinSAT, which we denote by \(T_u\). It does not add new variables, and so, it does not expand the search space.
Recall that \(Fm_{\text {CNF}}\) denotes the formulas in Conjunctive Normal Form (i.e., conjunctions of clauses). For convenience, let us denote by \(\overline{FM_C}\) the negations of clauses, i.e., formulas of the form \(\lnot c\) where c is a clause.
We define inductively the mapping \(^*:Fm_{\text {CNF}} \cup \overline{Fm_C} \rightarrow MS\), where MS denotes the set of all multisets of clauses, as follows:
where \(F \in Fm_{\text {CNF}}\), \(c \in Fm_{C}\) (i.e., is a clause) and \(\ell \) is a literal. Furthermore, the following very basic simplifications of the clauses in \(\varphi ^*\) are applied:
-
1.
If a trivial clause (one including a literal and its negation) appears—and it is not the only clause—in \(\varphi *\), it is removed.
-
2.
If a literal is repeated in a clause, the repetitions are removed.
-
3.
The negation of a negated literal is the corresponding variable, namely \(\lnot \lnot x\), is substituted by x, for any variable x.
Definition 1
(Transformation \(T_u\)) Let \(A = A_{NC} \sqcup A_C\) be a multiset of formulas of which \(A_{NC}\) are not clauses and \(A_C\) are clauses. \(T_u(A)\) is the multiset of clauses

Conceptually, the transformation \(T_u\) is the one providing a deeper understanding of the preservation of MaxSAT or MinSAT without using a partial instance. It preserves the kind of input (as opposed to the transformations, we will present in the next sections, which are partial instances), and preserves the variables used in the original multiset. Moreover, it is based on the idea of preserving one-to-one the number of unsatisfied elements. However, all this comes at the cost of deriving a multiset whose size can be exponential in the size of the input multiset, due to the distributivity rules.
Example 2
Let \(\varphi \) be the formula \(\lnot (\lnot x_1 \wedge \lnot x_2) \wedge (x_3 \vee x_4)\}\). We have that \(CNF(\varphi )=(x_1 \vee x_2) \wedge (x_3 \vee x_4)\). We convert it into the multiset of clauses \(T_u(\{\varphi \})\) as follows:
Example 3
Let A be the multiset of propositional formulas \(\{\lnot x_1 \vee \lnot x_2, x_1 \wedge (\lnot x_1 \vee x_2), x_1 \wedge (\lnot x_1 \vee x_2), \lnot (\lnot x_1 \wedge \lnot x_2) \wedge (x_3 \vee x_4)\}\). We translate it into the multiset of clauses \(T_u(A)\) as follows:

To prove that transformation \(T_u\) is cost-preserving for both MaxSAT and MinSAT, we first study how translation \(*\) behaves. Since it is, in an intuitive way, working from the inner most level to the outer most, let us first study the most internal level, and later, how the full translation works.
Proposition 1
For arbitrary clause c and truth-assignment e, the following holds:
-
1.
\(e(c) = 1\) if and only if all clauses in \((\lnot c)^*\) are evaluated to 1 except for one;
-
2.
\(e(c) = 0\) if and only if all clauses in \((\lnot c)^*\) are evaluated to 1.
Proof
We can easily check these properties by induction on the number k of literals appearing in clause c. For \(k = 2\), we have that \(c=\ell _1 \vee \ell _2\). By definition \((\lnot c)^* \,{:}{=}\,\{\lnot \ell _1, \ell _1 \vee \lnot \ell _2\}\).
-
1.
An evaluation e with \(e(c) = 1\) is such that either \(e(\ell _1) = 1\) (hence, the first clause in \((\lnot c)^*\) is evaluated to 0 and the second to 1), or, if \(e(\ell _1) = 0\), necessarily \(e(\ell _2) = 1\), and then, \(e(\lnot \ell _1 ) = 1\) and \(e(\ell _1 \vee \lnot \ell _2) = 0\).
-
2.
\(e(c) = 0\) if and only if \(e(\ell _1) = e(\ell _2) = 0\), and so, \(e(\lnot \ell _1) = 1\) and also \(e(\ell _1 \vee \lnot \ell _2)= 1\).
For \(k = n+1\), we can write \(c = \ell _1 \vee c_2\) (where \(c_2 = \ell _2 \vee \cdots \vee \ell _k\), and it has only n literals). Then, \((\lnot c)^* \,{:}{=}\,\{\lnot \ell _1, \ell _1 \vee d :d \in (\lnot c_2)^*\}\).
-
1.
Assume e with \(e(c) = 1\). If \(e(\ell _1) = 1\), the first clause in \((\lnot c)^*\) is trivially evaluated to 0 and all the others to 1. Otherwise, if \(e(\ell _1) = 0\), necessarily \(e(c_2) = 1\), in which case, \(e(\lnot \ell _1 ) = 1\) and, by Induction Hypothesis (I.H.), all clauses \(d_i \in (\lnot c_2)^*\) are evaluated to 1 except for one, let us call it \(d_0\). Then, \(e(\ell _1 \vee d_0) = 0\) and all other clauses \(\ell _1 \vee d\) in \((\lnot c)^*\) are evaluated to 1.
-
2.
\(e(c) = 0\) if and only if both \(e(\ell _1) = e(c_2) = 0\). The first clause in \((\lnot c)^*\) is trivially again evaluated to 1. By I.H., all clauses \(d_i\) in \((\lnot c_2)^*\) are evaluated to 1, and so, all remaining clauses \(\ell _1 \vee d_i\) in \((\lnot c)^*\) are so too. \(\square \)
Proposition 2
For any formula in CNF F and any truth-assignment e, the following holds:
-
1.
\(e(F) = 1\) if and only if all clauses in \(F^*\) are evaluated to 1;
-
2.
\(e(F) = 0\) if and only if all clauses in \(F^*\) are evaluated to 1 except for one.
Proof
Similarly to how it was done in the previous proposition, it is easily provable by induction on k, the number of clauses in F. For \(k = 2\), we have that \(F=c_1 \wedge c_2\). By definition \(F^* \,{:}{=}\,\{c_1, (\lnot c_1)^* \vee c_2^*\} = \{c_1, (\lnot c_1)^* \vee c_2\} = \{c_1, d \vee c_2:d \in (\lnot c_1)^*\}\).
-
1.
For \(e(F) = 1\), necessarily \(e(c_1) = e(c_2) = 1\), and so, both clauses in \(F^*\) are trivially evaluated to 1.
-
2.
Assume \(e(F) = 0\). If \(e(c_1) = 0\), the first clause in \(F^*\) is evaluated to 0, and by Proposition 1 (2), all clauses d in \((\lnot c_1)^*\) are evaluated to 1, proving our point. Otherwise, if \(e(c_1) = 1\), necessarily \(e(c_2) = 0\). The first clause in \(F^*\) is evaluated to 1, and by Proposition 1 (1), all \(d \in (\lnot c_1)^*\) are evaluated to 0 except for one, call it \(d_0\). Then, for all \(d \in (\lnot c_1)^*\) except for \(d_0\), we know that \(e(d \vee c_2) = 1\), and \(e(d_0 \vee c_2)\) is the only clause in \(F^*\) evaluated to 0.
For \(k = n+1\), we have that \(F=c_1 \wedge F_2\) (where \(F_2 = c_2 \wedge \cdots \wedge c_k\), and it has n clauses only). By definition \(F^* \,{:}{=}\,\{c_1, (\lnot c_1)^* \vee (F_2)^*\} = \{c_1, d \vee f:d \in (\lnot c_1)^*, f \in (F_2)^*\}\).
-
1.
For \(e(F) = 1\), necessarily \(e(c_1) = e(F_2) = 1\). Thus, the first clause in \(F^*\) is trivially evaluated to 1, and any \(d \in (F_2)^*\) is, by I.H., also evaluated to 1, proving our point.
-
2.
Assume \(e(F) = 0\). If \(e(c_1) = 0\), the first clause in \(F^*\) is evaluated to 0, and by Proposition 1 (2), all clauses d in \((\lnot c_1)^*\) are evaluated to 1, proving our point. Otherwise, if \(e(c_1) = 1\), necessarily \(e(F_2) = 0\). The first clause in \(F^*\) is evaluated to 1, and by Proposition 1 (1), all \(d \in (\lnot c_1)^*\) are evaluated to 1 except for one, call it \(d_0\). Similarly, by I.H., all \(f \in (F_2)^*\) are evaluated to 1 except for one, call it \(f_0\). Henceforth, \(e(d_0 \vee f_0) = 0\), and it is the only clause in \(F^*\) evaluated to 0. \(\square \)
Proposition 2 implies that, for any (multi) set of formulas in clausal form A, and any truth assignment e, it holds that

Observe that, since for any evaluation e and any formula F in CNF either \(e(F) = 1\) or \(e(F) = 0\), we know that for any evaluation e, either all clauses in \(F^*\) are evaluated to 1 or exactly one clause in \(F^*\) is evaluated to 0 (and the rest to 1).
Since there is no restriction on the kind of evaluation e, the fact that \(T_u\) preserves both MaxSAT and MinSAT is fairly straightforward.
Theorem 3
Let A be an arbitrary finite multiset of formulas. Then, the following holds:
-
1.
\(\mathrm{MaxSAT}(A)= \mathrm{MaxSAT}(T_u(A))\);
-
2.
\(\mathrm{MinSAT}(A)= \mathrm{MinSAT}(T_u(A))\).
Proof
Assume \(A = A_{NC} \sqcup A_C\), where \(A_C\) are clauses and \(A_{NC}\) are not, and let e be any evaluation of the variables in A. Recall that, for any formula \(\psi \) and any evaluation e, by definition \(e(\psi ) = e(CNF(\psi ))\). Then,

Henceforth, it is immediate that for any evaluation e,

Assume \({\mathrm{MaxSAT}}(A) = n\) for some number n, it means that n is the minimum number of unsatisfied formulas in A. Then
-
For any evaluation e, we have that
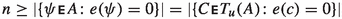 , and
, and -
There is some evaluation f for which
 . Thus,
. Thus,  .
.
Then, by definition, n is the minimum number of unsatisfied clauses in \(T_u(A)\), namely, \({\mathrm{MaxSAT}}(T_u(A)) = n\).
Similarly, if \({\mathrm{MinSAT}}(A) = n\) for some number n, then n is the maximum number of unsatisfied formulas in A. Thus
-
For any evaluation e, we have that
 , and
, and -
There is some evaluation f for which
 . Thus, \(n = \vert \{c \in T_u(A):f(c) = 0\}\vert \).
. Thus, \(n = \vert \{c \in T_u(A):f(c) = 0\}\vert \).
Again, by definition, n is the maximum number of unsatisfied clauses in \(T_u(A)\), namely, \({\mathrm{MinSAT}}(T_u(A)) = n\). \(\square \)
Example 4
Transformation \(T_u\), applied to the multiset of formulas \(A=\{\lnot (\lnot x_1 \wedge \lnot x_2) \wedge (x_3 \vee x_4)\}\) from Example 2, derived the multiset of clauses \(\Phi =\{x_1 \vee x_2, \lnot x_1 \vee x_3 \vee x_4, x_1 \vee \lnot x_2 \vee x_3 \vee x_4\}\). This multiset satisfies Theorem 3.
4 More Compact Transformations: \(T_M\) and \(T_m\)
We can propose a different kind of transformation that relies on the addition of one fresh variable for each (non-clausal) formula in the original multiset. Then, Partial MaxSAT/MinSAT can be used to encode strict knowledge that will relate the behavior of the new variable and the original formulas, and soft knowledge that will relate the optimal answers of MaxSAT and MinSAT.
Two dual transformations can be introduced, each one preserving one of the two optimization problems we are studying: \(T_M\), which will preserve MaxSAT, and \(T_m\), which will preserve MinSAT.
Definition 2
Let \(A = A_{NC} \sqcup A_C\) be a multiset of formulas of which \(A_{NC}\) are not clauses and \(A_C\) are clauses, and let \(\{y_{\varphi _i} :\varphi _i \in A_{NC}\}\) be a set of fresh variables.
-
1.
\(T_M(A)\) is the partial instance having as hard clauses the set
$$\begin{aligned} HC(T_M(A)) \,{:}{=}\,\bigcup _{\begin{array}{c} \varphi \in A_{NC}, \\ C \in T_{{\mathrm{SAT}}}(\varphi ) \end{array}} C\vee \{\lnot y_{\varphi }\} \end{aligned}$$and as soft clauses the set

-
2.
\(T_m(A)\) is the partial instance having as hard clauses the set
$$\begin{aligned} HC(T_m(A)) \,{:}{=}\,\bigcup _{\begin{array}{c} \varphi \in A_{NC},\\ C \in T_{{\mathrm{SAT}}}(\lnot \varphi ) \end{array}} C\vee \{y_{\varphi }\} \end{aligned}$$and as soft clauses the set

Transformations \(T_m\) and \(T_M\) are more compact than \(T_u\) in the sense that the number of soft restrictions in the problem is much smaller, preserving the number of elements from the original input to the set of soft restrictions. Moreover, since in partial instances, the set of hard restrictions must be fully satisfied, it is not necessary to consider it as a multiset but rather as a set of clauses. Nevertheless, as in \(T_u\), the size of the set of hard clauses can be exponential in the size of the multiset of input formulas for the same reason.
Example 5
Let A be the multiset of propositional formulas \(\{\lnot x_1 \vee \lnot x_2, x_1 \wedge (\lnot x_1 \vee x_2), x_1 \wedge (\lnot x_1 \vee x_2), \lnot (\lnot x_1 \wedge \lnot x_2) \wedge (x_3 \vee x_4)\}\). We translate it to the partial instances \(T_M(A)\) and \(T_m(A)\) as followsFootnote 5:

Proposition 4
Let e be an arbitrary evaluation. Then, the following conditions hold:
-
1.
If \(e(HC(T_M(A))) = \{1\}\), then \(e(y_{\varphi }) = 1\) implies \(e(\varphi ) = 1\), for each \(\varphi \in A_{NC}\).
-
2.
If \(e(HC(T_m(A))) = \{1\}\), then \(e(y_{\varphi }) = 0\) implies \(e(\varphi ) = 0\), for each \(\varphi \in A_{NC}\).
Proof
First claim is immediate, since the hard clauses in \(T_M(A)\) are imposing that, if \(e(y_{\varphi }) = 1\), necessarily \(e(C) = 1\) for each \(C \in T_{{\mathrm{SAT}}}(\varphi )\). By definition of \(T_{{\mathrm{SAT}}}\), it follows that \(e(\varphi )= e(\bigwedge _{C\in T_{{\mathrm{SAT}}}(\varphi )} C) = 1\).
Dually, the hard clauses in \(T_m(A)\) are imposing that, if \(e(y_{\varphi }) = 0\), necessarily \(e(C) = 1\) for each \(C \in T_{{\mathrm{SAT}}}(\lnot \varphi )\). Again, by definition of \(T_{{\mathrm{SAT}}}\), \(e(\lnot (\varphi )) = e(\bigwedge _{C\in T_{{\mathrm{SAT}}}(\lnot \varphi )} C )= 1\) and by the definition of the negation in classical logic, we get that \(e(\varphi ) = 0\). \(\square \)
Corollary 5
Let e be an arbitrary evaluation. Then, the following holds:
-
1.
If \(e(HC(T_M(A))) = \{1\}\), then

-
2.
If \(e(HC(T_m(A))) = \{1\}\), then
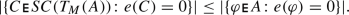
Proof
For e satisfying \(HC(T_M(A))\), from Proposition 4 (1), we know (by contraposition) that, for any \(\varphi \in A_{NC}\), if \(e(\varphi )= 0\), then \(e(y_{\varphi }) = 0\) too. Since the clauses in \(SC(T_M(A))\) preserve the multiplicity from A (in particular, the formulas in \(A_C\) are literally copied), it follows that  .
.
Similarly, if e satisfies \(e(HC(T_m(A)))\), from Proposition 4, (2) we know that, for any \(\varphi _i \in A_{NC}\), if \(e(y_{\varphi _i}) = 0\), then \(e(\varphi ) = 0\) too. As above, it is immediate that  . \(\square \)
. \(\square \)
Theorem 6
Let A be an arbitrary finite multiset of formulas. Then, the following holds:
-
1.
\({\mathrm{MaxSAT}}(A) = {\mathrm{MaxSAT}}(T_M(A))\);
-
2.
\({\mathrm{MinSAT}}(A) = {\mathrm{MinSAT}}(T_m(A))\).
Proof
Let \({\mathrm{MaxSAT}}(A) = n\), so n is the minimum number of unsatisfied formulas in A. By definition, we have that
-
For any evaluation e,
 . From Corollary 5 (1), it follows that
. From Corollary 5 (1), it follows that  too. Namely, \(n \le {\mathrm{MaxSAT}}(T_M(A))\).
too. Namely, \(n \le {\mathrm{MaxSAT}}(T_M(A))\). -
There is some evaluation f, such that \(n = \vert \{\varphi \in A:e(\varphi ) = 0\}\vert \). Consider the evaluation \(f'\) defined by letting \(f'(x) \,{:}{=}\,f(x)\) for each variable x appearing in A, and \(f'(y_{\varphi }) = f(\varphi )\) for each formula \(\varphi \in A_{NC}\). It is immediate that
 . On the other hand, any hard clause \(C \vee y_{\varphi }\) in \(HC(T_M(A))\) is satisfied: either \(f(\varphi ) = 1\), and so, \(1 = f(C) = f'(C)\) for each
. On the other hand, any hard clause \(C \vee y_{\varphi }\) in \(HC(T_M(A))\) is satisfied: either \(f(\varphi ) = 1\), and so, \(1 = f(C) = f'(C)\) for each  , or \(f(\varphi ) = 0\), and so, \(f'(\lnot y_{\varphi }) = 1\). Together with the previous point, this proves that the minimum number of unsatisfied clauses in \(T_M(A)\) is n, namely, \({\mathrm{MaxSAT}}(T_M(A)) = n\).
, or \(f(\varphi ) = 0\), and so, \(f'(\lnot y_{\varphi }) = 1\). Together with the previous point, this proves that the minimum number of unsatisfied clauses in \(T_M(A)\) is n, namely, \({\mathrm{MaxSAT}}(T_M(A)) = n\).
In a dual way, we prove the theorem for \({\mathrm{MinSAT}}\). If \({\mathrm{MinSAT}}(A) = n\), we know that n is the maximum number of unsatisfied formulas in A. This implies that
-
For any evaluation e,
 . From Corollary 5 (2), it follows that
. From Corollary 5 (2), it follows that 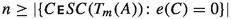 too. Namely, \(n \ge {\mathrm{MaxSAT}}(T_m(A))\).
too. Namely, \(n \ge {\mathrm{MaxSAT}}(T_m(A))\). -
There is some evaluation f, such that \(n = \vert \{\varphi \in A:e(\varphi ) = 0\}\vert \). Let \(f'\) be as above, the evaluation defined by letting \(f'(x) \,{:}{=}\,f(x)\) for each variable x appearing in A, and \(f'(y_{\varphi }) = f(\varphi )\) for each formula \(\varphi \in A_{NC}\). Again, it is immediate that
 . On the other hand, it is again easy to see that \(f'\) satisfies any clause \(C \vee y_{\varphi }\) in HC(Tm(A)): if \(f(\varphi ) = 1\), then \(f'(y_{\varphi }) = 1\), and otherwise, if \(f(\varphi ) = 0\), then \(f(\lnot \varphi ) = 1\), and so, \(1 = f(C) = f'(C)\) for each \(C \in T_{{\mathrm{SAT}}}(\lnot \varphi )\). Together with the previous point, this proves that the maximum number of unsatisfied clauses in \(T_m(A)\) is n, namely, \({\mathrm{MinSAT}}(T_m(A)) = n\). \(\square \)
. On the other hand, it is again easy to see that \(f'\) satisfies any clause \(C \vee y_{\varphi }\) in HC(Tm(A)): if \(f(\varphi ) = 1\), then \(f'(y_{\varphi }) = 1\), and otherwise, if \(f(\varphi ) = 0\), then \(f(\lnot \varphi ) = 1\), and so, \(1 = f(C) = f'(C)\) for each \(C \in T_{{\mathrm{SAT}}}(\lnot \varphi )\). Together with the previous point, this proves that the maximum number of unsatisfied clauses in \(T_m(A)\) is n, namely, \({\mathrm{MinSAT}}(T_m(A)) = n\). \(\square \)
5 Non-exponential Translation: \(T_M^t\) and \(T_m^t\)
As we already said, the transformations proposed in the previous two sections might produce multisets of clauses whose size is exponential in the size of the input multiset, due to the distributivity rules in the CNF and \(T_{{\mathrm{SAT}}}\) transformations. A simple way of overcoming this question is to use a Tseitin-style encoding of the original set of formulas [14] and encode the new problem as a partial instance. This transformation adds one fresh variable for each formula in the set of subformulas of the original input. Henceforth, the resulting hard clauses of the partial instance are at most of length 3. In contrast, the number of hard clauses will be bigger than in the previous case.
For a formula \(\varphi \), let us denote by \(SFm(\varphi )\) the set of subformulas of \(\varphi \). Then, for each \(\psi \in SFm(\varphi )\), consider a new variable \(y_\psi \), and for each formula \(\psi \), we define the set of clauses \(Def(\psi )\) byFootnote 6
Recall that all connectives different from \(\wedge , \vee , \lnot \) (i.e., \(\rightarrow \) and \(\leftrightarrow \)) are simply wrapping some expression involving the other three, so any formula \(\varphi \) is written in fact in the previous language, and so, Def is correctly defined for all formulas. It is clear that the above definitions generate clauses with at most 3 literals each. For a formula \(\varphi \), its Tseitin definition is the set of clauses
Further, the Tseitin-SAT transformation \(Ts_{{\mathrm{SAT}}}(\varphi )\) is the set of clauses
It is routine to see that, for any evaluation e and any formula \(\varphi \)
Consequently, as it is well known, \(\varphi \) is in SAT if and only if \(Ts_{{\mathrm{SAT}}}(\varphi ))\) is in SAT. Naturally, also for a set of formulas A, we have that \({\mathrm{SAT}}(A)\) if and only if \({\mathrm{SAT}}(Ts_{{\mathrm{SAT}}}(A))\), where, as usual, by \(Ts_{{\mathrm{SAT}}}(A)\), we denote the set \(\bigcup _{\varphi \in A}T(\varphi )\).
To use the previous approach preserving MaxSAT and \({\mathrm{MinSAT}}\), it is only necessary to do a slight modification to the previous transformation, to consider multisets as inputs and allow for the formulas at the outermost level to be unsatisfied, and then rely on a Partial SAT instance.
Definition 3
(Transformation \(T_{Ts}\)) Let \(A = A_{NC} \sqcup A_C\) be a multiset of formulas of which \(A_{NC}\) are not clauses and \(A_C\) are clauses. We call \(T_{Ts}(A)\) to the partial instance having as hard clauses the set
and as soft clauses the set

Example 6
Given the multiset of formulas \(A=\{x_1 \wedge x_2, x_1 \wedge x_2, x_3 \wedge x_4\}\), \(T_{Ts}(A)\) derives the following partial MinSAT instanceFootnote 7:
Theorem 7
Let \(A = A_{NC} \sqcup A_C\) be a multiset of formulas. Then, the following holds:
-
1.
\({\mathrm{MaxSAT}}(A) = {\mathrm{MaxSAT}}(T_{Ts}(A))\),
-
2.
\({\mathrm{MinSAT}}(A) = {\mathrm{MinSAT}}(T_{Ts}(A))\).
Proof
It is first immediate that, as for the usual Tseitin transformation, for any evaluation e, such that \(e(HC(T_{Ts}(A))) = \{1\}\), and for any \(\varphi \in A_{NC}\), we have that \(e(\varphi ) = e(y_{\varphi })\).
Observe that for each formula  , we have one clause (singleton) \(y_\varphi \) in \(T_{Ts}(A)\) (and this relation preserves the multiplicity of \(\varphi \) in \(A_{NC}\)). Henceforth, by definition of MaxSAT and MinSAT (and the corresponding definitions of these questions over partial instances), it follows that:
, we have one clause (singleton) \(y_\varphi \) in \(T_{Ts}(A)\) (and this relation preserves the multiplicity of \(\varphi \) in \(A_{NC}\)). Henceforth, by definition of MaxSAT and MinSAT (and the corresponding definitions of these questions over partial instances), it follows that:
On the other hand, assume that there is an evaluation f, such that  . We can easily build an evaluation \(f'\), in a similar way to how we did in Theorem 6, so
. We can easily build an evaluation \(f'\), in a similar way to how we did in Theorem 6, so  . Indeed, let \(f'(x) \,{:}{=}\,f(x)\) for all variable x appearing in the original A, and \(f'(y_{\psi }) = f(\psi )\) for each variable \(y_{\psi }\) in \(T_{Ts}(A)\) that did not appear in A. It is immediate that
. Indeed, let \(f'(x) \,{:}{=}\,f(x)\) for all variable x appearing in the original A, and \(f'(y_{\psi }) = f(\psi )\) for each variable \(y_{\psi }\) in \(T_{Ts}(A)\) that did not appear in A. It is immediate that  . On the other hand, any hard clause \(C \vee y_{\varphi }\) in \(HC(T_{Ts}(A))\) is satisfied by construction, since, as we said before, Eq. 1 holds for any evaluation, and we built \(f'\) in such a way that the left side of the equation is met. This concludes the proof of the theorem. \(\square \)
. On the other hand, any hard clause \(C \vee y_{\varphi }\) in \(HC(T_{Ts}(A))\) is satisfied by construction, since, as we said before, Eq. 1 holds for any evaluation, and we built \(f'\) in such a way that the left side of the equation is met. This concludes the proof of the theorem. \(\square \)
In the following, \(T_M^t\) (resp. \(T_m^t\)) denotes that the input to \(T_{Ts}\) is a non-clausal MaxSAT (resp. MinSAT) instance.
6 Adding Weights
It is fairly natural to incorporate weighted formulas and clauses into the transformations presented in the previous sections.
For what concerns \(T_u\), the weight of each formula \(\varphi \) in the original multiset A must simply be preserved to all clauses in the multiset of clauses \(\varphi ^*\). From Proposition 2, it follows that, if \(\varphi \) was not satisfied by some evaluation e (and so, its weight was added up to the cost computation), then exactly one of the clauses in \(CNF(\varphi )^*\) is not satisfied by e, thus adding up the same cost to the cost of e. Furthermore, since the proposition works in both directions, the cost of an evaluation e is also faithfully preserved from the translated multiset of clauses \(T_u(A)\) to the original multiset of formulas A.
Example 7
Let A be the weighted multiset of formulas \(\{\langle \lnot x_1 \vee \lnot x_2, 3\rangle , \langle x_1 \wedge (\lnot x_1 \vee x_2), 4\rangle ,\langle x_1 \wedge (\lnot x_1 \vee x_2), 7\rangle , \langle \lnot (\lnot x_1 \wedge \lnot x_2) \wedge (x_3 \vee x_4), 2\rangle \}\). We translate A to the weighted multiset of clauses \(T_u(A)\) as follows:

For transformations \(T_M, T_m\) and \(T_{Ts}\), the weight associated with each formula \(\varphi \) in the original multiset A must simply be attached to each fresh variable \(y_\varphi \) added to the set of soft clauses of the corresponding translated multiset. Indeed, since the relation between the satisfaction of the original formulas and the soft clauses in the resulting multisets is one-to-one, by doing so, the weights are faithfully preserved.
Example 8
Let A be the weighted multiset of formulas \(\{\langle \lnot x_1 \vee \lnot x_2, 3\rangle , \langle x_1 \wedge (\lnot x_1 \vee x_2), 4\rangle ,\langle x_1 \wedge (\lnot x_1 \vee x_2), 7\rangle , \langle \lnot (\lnot x_1 \wedge \lnot x_2) \wedge (x_3 \vee x_4), 2\rangle \}\).
We translate A to the weighted partial multisets of clauses \(T_M\) and \(T_m\) by preserving the hard clauses from the non-weighted example (5) and the set of weighted soft clauses is defined as follows:
7 Experimental Investigation
This section reports on an empirical comparison of the three MaxSAT transformations proposed in the paper: \(T_u\), \(T_M\), and \(T_M^t\). The experiments were run with the MaxSAT solver RC2 [27] on an Intel Core i7-5820K CPU at 3.30 GHz under a Linux system with 32 GB of memory. We did not consider MinSAT instances, because there are no robust and publicly available MinSAT solvers.
We first generated clausal SAT instances using the random generator [q]bfGen [37]. We fixed the number of literals per clause to 3 and the ratio of the number of clauses to the number of variables to 5. This ratio ensures, with a high probability, that the instances are unsatisfiable. Second, the obtained CNF instances are converted to non-clausal instances as follows: we partition the set of clauses into subsets of size k and create formulas by creating a conjunction of k clauses for each subset. The hardness of the instances is adjusted by varying the group size and the number of variables.
Example 9
Assuming \(k=2\), the CNF instance \(\{x_1 \vee x_2 \vee x_3, \lnot x_1 \vee x_2 \vee x_3, x_1 \vee \lnot x_2 \vee x_3, \lnot x_1 \vee \lnot x_2 \vee x_3, x_1 \vee x_2 \vee \lnot x_3, \lnot x_1 \vee x_2 \vee \lnot x_3, x_1 \vee \lnot x_2 \vee \lnot x_3, \lnot x_1 \vee \lnot x_2 \vee \lnot x_3\}\), which contains eight clauses, is transformed into the non-clausal instance \(\{(x_1 \vee x_2 \vee x_3) \wedge (\lnot x_1 \vee x_2 \vee x_3), (x_1 \vee \lnot x_2 \vee x_3) \wedge (\lnot x_1 \vee \lnot x_2 \vee x_3), (x_1 \vee x_2 \vee \lnot x_3) \wedge (\lnot x_1 \vee x_2 \vee \lnot x_3), (x_1 \vee \lnot x_2 \vee \lnot x_3) \wedge (\lnot x_1 \vee \lnot x_2 \vee \lnot x_3)\}\), which contains four formulas. In this case, we say that we have a non-clausal instance with a group size of 2.
Third, the resulting formulas are transformed into (partial) MaxSAT instances by applying the \(T_u\), \(T_M\) and \(T_M^t\) transformations.
In the first experiment, we compared transformations \(T_u\), \(T_M\), and \(T_M^t\). We first derived the transformations and then solved the obtained transformations with the MaxSAT solver RC2. We considered (Partial) MaxSAT instances with 60 variables whose group size ranges from 2 to 10. For each transformation and group size, we solved 50 instances. Table 1 shows the experimental results. Each cell contains the mean time, in seconds, needed to solve 50 instances with the transformation indicated in the same row and considering the group size indicated in the same column. Figure 1 graphically displays the results. We observe the behavior of the transformations as the group size increases, as well as that transformation \(T_u\) is not competitive when compared with transformations \(T_M\) and \(T_M^t\). The poor performance is due to the fact that the \(T_u\) instances have a larger number of clauses and all the clauses are soft, whereas the \(T_M\) and \(T_M^t\) instances have fewer clauses and contain both hard and soft clauses.
In the second experiment, we only compare \(T_M\) and \(T_M^t\) on harder instances. We considered Partial MaxSAT instances with 100 and 150 variables. For 100 variables, the group size ranges from 2 to 14. For 150 variables, the group size ranges from 50 to 200 in steps of 25. For each transformation and group size, we solved 50 instances. Such ranges were selected to obtain instances that could be solved in a reasonable amount of time. For instance, the mean times for \(T_M\) and \(T_M^t\) with 150 variables and a group size of 25 are 32.76 s and 40.74 s, respectively. Figure 2 graphically displays the results. We observe, as in Table 1, that \(T_M\) significantly outperforms \(T_M^t\). Hence, our results indicate that \(T_M\) should be the first option and \(T_M^t\) should be the second option.
8 Conclusions
We have defined three transformation from non-clausal MaxSAT to clausal MaxSAT (\(T_u\), \(T_M\), and \(T_M^t\)) and three transformations from non-clausal MinSAT to clausal MinSAT (\(T_u\), \(T_m\), and \(T_m^t\)). Moreover, we have performed an empirical comparison of the MaxSAT transformations \(T_u\), \(T_M\), and \(T_M^t\). The experimental results indicate that \(T_M\) is the best-performing option, followed by \(T^t_M\). In general, \(T_u\) is not so competitive, because it generates larger instances and all its clauses are soft.
The contributions of this paper are relevant, because, to our best knowledge, we have proposed the first efficient way of solving non-clausal MaxSAT and MinSAT with state-of-the-art clausal MaxSAT and MinSAT solvers. As future work, we propose to extend our results to signed CNF formulas [38] and conduct an empirical investigation.
Availability of Data and Materials
Detailed results can be obtained from the authors on demand. The same holds for all problem instances used in this work.
Notes
We omit the set of variables, since it will always be clear from the context.
The set of variables is omitted from the notation, since it will either be clear from the context or specified in each case.
Observe that hard formulas can always be considered with multiplicity one, i.e., to form a set as opposed to a multiset, since we require all of them to be satisfied.
e.g., removing clauses with a literal and its negation, or repeated clauses.
For the sake of a simple reading, we change the subindexes in the fresh variables from formulas to simple natural numbers in the obvious way, namely, \(y_1\) denotes \(y_\varphi \) for \(\varphi = x_1 \wedge (\lnot x_1 \vee x_2)\) and \(y_2\) denotes \(y_\psi \) for \(\psi = (x_3 \wedge x_2) \vee (\lnot x_3 \wedge x_2)\). Observe \(y_3\) does not exist, because in the original multiset, there are not three different clauses, but two different clauses with one of them repeated once.
To simplify the notation, we do not distinguish between propositional variables and more complex formulas. Thus, a variable p will receive a fresh variable \(y_p\) in the new language, and p will no longer appear in the translation. The definition of Def over propositional variables is also included to lighten notation later on, and observe that this approach does not affect the resulting number of clauses.
For the sake of readability, we simplify the naming of the new variables with natural indexes associated to the formulas in A, i.e., \(y_1\) denotes \(y_\varphi \) for \(\varphi = x_1 \wedge x_2\) and \(y_2\) denotes \(y_\psi \) for \(\psi = x_3 \wedge x_4\).
Abbreviations
- SAT:
-
Satisfiability
- MaxSAT:
-
Maximum satisfiability
- MinSAT:
-
Minimum satisfiability
- PMaxSAT:
-
Partial maximum satisfiability
- PMinSAT:
-
Partial minimum satisfiability
- WPMaxSAT:
-
Weighted partial maximum satisfiability
- WPMinSAT:
-
Weighted partial minimum satisfiability
- CNF:
-
Conjunctive normal form
References
Guerra, J., Lynce, I.: Reasoning over biological networks using maximum satisfiability. In: Proceedings of the 18th International Conference on Principles and Practice of Constraint Programming, CP, Québec City, QC, Canada, pp. 941–956 (2012)
Marques-Silva, J., Argelich, J., Graça, A., Lynce, I.: Boolean lexicographic optimization: algorithms and applications. Ann. Mat. Artif. Intell. 62(3–4), 317–343 (2011)
Safarpour, S., Mangassarian, H., Veneris, A.G., Liffiton, M.H., Sakallah, K.A.: Improved design debugging using maximum satisfiability. In: Proceedings of 7th International Conference on Formal Methods in Computer-Aided Design, FMCAD, Austin, Texas, USA, pp. 13–19 (2007)
Li, C.M., Zhu, Z., Manyà, F., Simon, L.: Optimizing with minimum satisfiability. Artif. Intell. 190, 32–44 (2012)
Ansótegui, C., Izquierdo, I., Manyà, F., Jiménez, J.T.: A Max-SAT-based approach to constructing optimal covering arrays. In: Proceedings of the 16th International Conference of the Catalan Association for Artificial Intelligence, CCIA 2013, Vic, Spain. IOS Press, Frontiers in Artificial Intelligence and Applications, vol. 256, pp. 51–59 (2013)
Ansótegui, C., Manyà, F., Ojeda, J., Salvia, J.M., Torres, E.: Incomplete MaxSAT approaches for combinatorial testing. J. Heurist. 107, 2411–2502 (2022)
Jabbour, S., Mhadhbi, N., Raddaoui, B., Sais, L.: A SAT-based framework for overlapping community detection in networks. In: Proceedings of the 21st Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining, Part II, PAKDD, Jeju, South Korea, pp. 786–798 (2017)
D’Almeida, D., Grégoire, É.: Model-based diagnosis with default information implemented through MAX-SAT technology. In: Proceedings of the IEEE 13th International Conference on Information Reuse and Integration, IRI, Las Vegas, NV, USA, pp. 33–36 (2012)
Zhang, L., Bacchus, F.: MAXSAT heuristics for cost optimal planning. In: Proceedings of the 26th AAAI Conference on Artificial Intelligence, Toronto, Ontario, Canada, pp. 1846–1852 (2012)
Bofill, M., Coll, J., Garcia, M., Giráldez-Cru, J., Pesant, G., Suy, J., Villaret, M.: Constraint solving approaches to the business-to-business meeting scheduling problem. J. Artif. Intell. Res. 74, 263–301 (2022)
Manyà, F., Negrete, S., Roig, C., Soler, J.R.: A MaxSAT-based approach to the team composition problem in a classroom. In: Autonomous Agents and Multiagent Systems—AAMAS 2017 Workshops, Visionary Papers, São Paulo, Brazil, Revised Selected Papers. Springer LNCS, vol. 10643, pp. 164–173 (2017)
Manyà, F., Negrete, S., Roig, C., Soler, J.R.: Solving the team composition problem in a classroom. Fundam. Inf. 174(1), 83–101 (2020)
Plaisted, D.A., Greenbaum, S.: A structure-preserving clause form translation. J. Symb. Comput. 2, 293–304 (1986)
Tseitin, G.S.: On the complexity of derivations in the propositional calculus. In: Studies in Constructive Mathematics and Mathematical Logic, Part II. Steklov Mathematical Inst., pp. 115–125 (1968)
Casas-Roma, J., Huertas, A., Manyà, F.: Solving MaxSAT with natural deduction. In: Proceedings of the 20th International Conference of the Catalan Association for Artificial Intelligence, Deltebre, Spain. IOS Press, Frontiers in Artificial Intelligence and Applications, vol. 300, pp. 186–195 (2017)
Fiorino, G.: A non-clausal tableau calculus for MinSAT. Inf. Process. Lett. 173, 106167 (2022)
Fiorino, G.: New tableau characterizations for non-clausal MaxSAT problem. Log. J. IGPL 30(3), 422–436 (2022)
Li, C.M., Manyà, F., Soler, J.R.: A tableau calculus for non-clausal maximum satisfiability. In: Proceedings of the 28th International Conference on Automated Reasoning with Analytic Tableaux and Related Methods, TABLEAUX, London, UK. Springer LNCS, vol. 11714, pp. 58–73 (2019)
Soler, J.R.: New solving techniques for maximum and minimum satisfiability. Ph.D. Thesis, Universitat Autònoma de Barcelona (UAB) (2021)
Li, C.M., Manyà, F., Mohamedou, N.O., Planes, J.: Resolution-based lower bounds in MaxSAT. Constraints 15(4), 456–484 (2010)
Li, C., Xu, Z., Coll, J., Manyà, F., Habet, D., He, K.: Combining clause learning and branch and bound for MaxSAT. In: Proceedings of the 27th International Conference on Principles and Practice of Constraint Programming, CP, Montpellier, France. LIPIcs, vol. 210, pp. 38–13818 (2021)
Argelich, J., Li, C.M., Manyà, F., Planes, J.: The first and second Max-SAT evaluations. J. Satisfiab. Bool. Model. Comput. 4(2–4), 251–278 (2008)
Bacchus, F., Berg, J., Järvisalo, M., Martins, R.: MaxSAT Evaluation 2020: Solver and Benchmark Descriptions. University of Helsinki, Department of Computer Science (2020)
Li, C.M., Manyà, F.: MaxSAT, hard and soft constraints. In: Biere, A., Heule, M., van Maaren, H., Walsh, T. (eds.) Handbook of Satisfiability, pp. 903–927. IOS Press, New York (2021)
Li, C., Xu, Z., Coll, J., Manyà, F., Habet, D., He, K.: Boosting branch-and-bound MaxSAT solvers with clause learning. AI Commun. 35(2), 13–151 (2021). https://doi.org/10.3233/AIC-210178
Bacchus, F., Järvisalo, M., Ruben, M.: Maximum satisfiability. In: Biere, A., Heule, M., van Maaren, H., Walsh, T. (eds.) Handbook of Satisfiability, pp. 929–991. IOS Press, New York (2021)
Ignatiev, A., Morgado, A., Marques-Silva, J.: RC2: an efficient MaxSAT solver. J. Satisfiab. Bool. Model. Comput. 11(1), 53–64 (2019)
Le Berre, D., Parrain, A.: The Sat4j library, release 2.2. J. Satisfiab. Bool. Model. Comput. 7(2–3), 59–64 (2010)
Ansótegui, C., Gabàs, J.: WPM3: an (in)complete algorithm for weighted partial MaxSAT. Artif. Intell. 250, 37–57 (2017)
Zheng, J., He, K., Zhou, J., Jin, Y., Li, C.M., Manyà, F., BandMaxSAT: a local search MaxSAT solver with multi-armed bandit. In: Proceedings of the 31st International Joint Conference on Artificial Intelligence, IJCAI, Vienna, Austria, pp. 1901–1907 (2022)
Cai, S., Lei, Z.: Old techniques in new ways: clause weighting, unit propagation and hybridization for maximum satisfiability. Artif. Intell. 287, 103354 (2020)
Abramé, A., Habet, D.: Local search algorithm for the partial minimum satisfiability problem. In: Proceedings of the 27th IEEE International Conference on Tools with Artificial Intelligence, ICTAI, Vietri Sul Mare, Italy, pp. 821–827 (2015)
Ansótegui, C., Li, C.M., Manyà, F., Zhu, Z.: A SAT-based approach to MinSAT. In: Proceedings of the 15th International Conference of the Catalan Association for Artificial Intelligence, CCIA-2012, Alacant, Spain, pp. 185–189 (2012)
Li, C.M., Zhu, Z., Manyà, F., Simon, L.: Minimum satisfiability and its applications. In: Proceedings of the 22nd International Joint Conference on Artificial Intelligence, IJCAI, Barcelona, Spain, pp. 605–610 (2011)
Li, C.M., Manyà, F., Soler, J.R.: Clausal form transformation in MaxSAT. In: Proceedings of the 49th IEEE International Symposium on Multiple-Valued Logic, ISMVL, Fredericton, Canada, pp. 132–137 (2019)
Li, C.M., Manyà, F., Soler, J.R., Vidal, A.: From non-clausal to clausal MinSAT. In: Proceedings of the 23rd International Conference of the Catalan Association for Artificial Intelligence, CCIA, Lleida, Spain, pp. 27–36 (2021)
Creignou, N., Egly, U., Seidl, M.: A framework for the specification of random SAT and QSAT formulas. In: Proceedings of the 6th International Conference on Tests and Proofs, TAP, Prague, Czech Republic. Springer LNCS, vol. 7305, pp. 163–168 (2012)
Beckert, B., Hähnle, R., Manyà, F.: The SAT problem of signed CNF formulas. In: Basin, D., D’Agostino, M., Gabbay, D., Matthews, S., Viganò, L. (eds.) Labelled Deduction. Kluwer, Applied Logic Series, vol. 17, pp. 61–82 (2000)
Acknowledgements
We acknowledge administrative and technical support by the Spanish National Research Council (CSIC).
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 101027914. This work has been supported by the French Agence Nationale de la Recherche, reference ANR-19-CHIA-0013-01, and Grant PID2019-111544GB-C21 funded by MCIN/AEI/10.13039/501100011033. F. Manyà was supported by mobility Grant PRX21/00488 of the Spanish Ministerio de Universidades.
Author information
Authors and Affiliations
Contributions
All authors have contributed in the development and revision of the whole work. The experimental results are mainly due to J.R. Soler, and the theoretical proofs to A. Vidal.
Corresponding author
Ethics declarations
conflict of interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, C.M., Manyà, F., Soler, J.R. et al. Clausal Forms in MaxSAT and MinSAT. Int J Comput Intell Syst 15, 97 (2022). https://doi.org/10.1007/s44196-022-00143-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s44196-022-00143-z





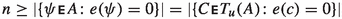 , and
, and . Thus,
. Thus,  .
. , and
, and . Thus,
. Thus, 


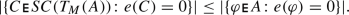
 . From Corollary
. From Corollary  too. Namely,
too. Namely,  . On the other hand, any hard clause
. On the other hand, any hard clause  , or
, or  . From Corollary
. From Corollary 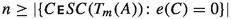 too. Namely,
too. Namely,  . On the other hand, it is again easy to see that
. On the other hand, it is again easy to see that 
