1 Introduction

Linguistic group decision-making (GDM) is a field devoted to obtaining a set of alternatives to reach consensus within a group using possible linguistic values or rich expressions. The linguistic expression is the basic unit of human decision-making, as well as the carrier of preferences. Computing with word (CW) methods are a popular tool for representing and calculating linguistic information [1,2,3]. Herrera and Martinez [4] proposed a 2-tuple linguistic model to reflect expressions of opinions and information processing. However, DMs require more flexible expressions for complex and uncertain decision problems [5, 6]. Rodriguez et al. [7] proposed a hesitant fuzzy linguistic term set (HFLTS), whereas Zhang et al. [8] proposed linguistic distribution assessments (LDAs) to assign weights to linguistic terms, further improving the HFLTS model.

As one of the most widely used decision-making tools, HFLTS has experienced significant progress in recent years. Many researchers have extended the development of HFLTS into different directions for various applications. Chen et al. [9] designed a proportional HFLTS for linguistic distribution assessments, which includes the proportional information of each generalized linguistic term, as well as basic operations with closed properties based on t-norms and t-conorms. Unlike traditional assumptions that equate the possibility of being an expert’s assessment value, Wu and Xu [10] suggested the possibility that the alternative has an assessment value provided by the expert. In addition, linguistic distributions are a common tool that enables the assignment of symbolic proportions to all terms in a linguistic term set [8]. Accordingly, Zhang et al. [11] developed a hesitant linguistic distribution wherein the sum proportion for the HFLTS was provided by an expert. A clustering and management method for large-scale HFLTS was proposed and applied to group decision consensus, including the model designed by Chen et al. [12]. Chen et al. [13] further proposed a proportional interval type-2 hesitant fuzzy TOPSIS approach for linguistic decision-making under uncertainty.

In addition to hesitant fuzzy expressions, the individual emotional factors contained in an HFLTS are crucial to promoting consensus, as they serve as a window to accurately grasp individual decision-making behavior. Researchers refer to these personalized individual semantics (PIS) as the difference between the individual preference matrix provided by the decision-maker, and its corresponding perfect consistency preference matrix. Since PIS was first introduced in linguistic GDM [28], another approach for modeling PIS with the OWA operator and HFLTS has also been developed for decision-making. Chen et al. [14] proposed a novel computation structure for HFLTS possibility distributions based on the similarity measures of linguistic terms. Chen et al. [15] also designed a new framework model to address multiple-attribute GDM with hesitant fuzzy linguistic information, and proposed a weighted average operator, as well as an ordered weighted average operator, for such information. Labella et al. [16] developed an objective metric based on the cost of modifying expert opinions to evaluate CRPs in GDM problems. García-Zamora et al. [17] summarized the main methods and fields of large-group decision-making, and proposed potential directions for future research.

In real-life GDM, DMs do not always provide an absolutely reliable judgment between alternatives owing to time pressure or expertise restrictions. Reliability of information was therefore developed to evaluate the extent of knowledge in the decision-making context [18]. Generally, a DM explicitly adds reliability information to synthesize a linguistic triplet. Liu et al. [19] introduced a reliability measurement for self-confident decision problems.

Many previous studies have carried out relevant research on confident behavior in the consensus-reaching aspect of GDM.

  1. 1.

    The detection and management of overconfidence behaviors [20]. Considering personalized semantics, Zhang et al. [21] proposed an individual semantic model in hesitant fuzzy linguistic preference relations with self-confidence.

  2. 2.

    Consensus reaching process (CRP) in GDM with self-confidence. A feedback mechanism is the most common panel for preference modification. Such a mechanism may implement identification and direction rules [22, 23], as well as minimum adjustment or cost feedback [24,25,26,27,28] to minimize the adjustments or consensus cost.

Although many models have been developed for linguistic GDM with self-confidence behavior, their practical applicability remains a challenge due to the complex and diverse nature of real-world decision problems.

  1. 1.

    Different people may understand the same word differently [29,30,31]. For example, in a speech, two judges may both evaluate the current participant’s performance as excellent, but whereas one judge gives 85 points, the other gives 90 points. Therefore, personalized individual semantics (PIS) must be investigated in various contexts.

  2. 2.

    Multiple self-confidence levels in GDM exist because of the reliability of information provided by DMs. The combination of preference relations and self-confidence levels in the context of personalized semantics is unclear.

Motivated by the aforementioned real-life requirements, we propose a fuzzy linguistic GDM model that accounts for PIS and self-confidence behavior. First, we converted linguistic representation models into unified models. We then incorporated the dual information of preference values and associated self-confidence levels into our model to learn the PIS of the linguistic term set. Subsequently, we designed a consensus mechanism that considers underconfidence behavior. Finally, we conducted a quantitative experiment to demonstrate the effectiveness of our method.

As major contributions, this paper addresses the differences in individualized semantics of confident decision-makers in the HTLTS environment, and proposes a management method for PIS in the context of CRP in linguistic GDM.

The remainder of this paper is organized as follows. Section 2 provides an overview of relevant basic information. Section 3 establishes the linguistic GDM model and presents the solution process. We 4 further describes the linguistic GDM model in the context of PIS and confidence. Section 4 presents a numerical example and verifies the proposed method’s advantages. Section 5 summarizes the results of this study.

2 Preliminaries

In this section, we introduce the preliminary knowledge used in this study, including individual preference expression relationships, PIS, self-confidence, and the general consensus process.

2.1 Linguistic Representation Models

A linguistic symbolic computational model consists of ordinal scales on a linguistic term set.

Definition 1

[4, 32] Let \(S = \left\{ {S_{0} ,S_{1} ,...,S_{g} } \right\}\) be a linguistic term set and \(g + 1\) be odd. The linguistic symbolic computational model is defined as follows:

  1. 1.

    The set is ordered: \(S_{i} \ge S_{j}\) if \(i \ge j\);

  2. 2.

    A negation operator exists: \({\text{Neg}}(S_{i} ) = S_{g - i}\).

A 2-tuple linguistic model was proposed to compute the loss degree of information [36, 37].

Definition 2

[4] Let \(S = \left\{ {S_{0} ,S_{1} ,...,S_{g} } \right\}\) be as above, and \(\beta \in \left[ {0,g} \right]\) be a value representing the result of a symbolic aggregation operation. If \(\overline{S} = S \times \left[ { - 0.5,0.5} \right)\) and \(S_{i} \in S\), then the linguistic 2-tuple expresses assessment information equivalent to \(\beta\). This relationship can be described as

$$\begin{gathered} \Delta :[0,g] \to \overline{S} \hfill \\ \beta \to (S_{i} ,\alpha ) = \left\{ {\begin{array}{*{20}c} {S_{i} ,i = round(\beta )} \\ {\alpha = \beta - i,\alpha \in \left[ { - 0.5,0.5} \right)} \\ \end{array} } \right., \hfill \\ \end{gathered}$$
(1)

where \({\text{round}}( \cdot )\) is the usual rounding operation.

Correspondingly, \(\Delta^{ - 1}\), the inverse function of \(\Delta\), aims to transform a linguistic 2-tuple into the value \(\beta\). This transform function is expressed as

$$\begin{gathered} \Delta^{ - 1} :\overline{S} \to [0,g] \hfill \\ \Delta^{ - 1} (S_{i} ,\alpha ) = i + \alpha = \beta . \hfill \\ \end{gathered}$$
(2)

To describe the situation of a hesitant decision, HFLTS is defined as follows:

Definition 3

[7] Let \(S = \left\{ {S_{0} ,S_{1} ,...,S_{g} } \right\}\) be a linguistic term set. HFLTS \(H_{s}\) is an ordered finite subset of consecutive linguistic terms of \(S\).

Definition 4

[7] The upper bound \(H_{s}^{ + }\), lower bound \(H_{s}^{ - }\), envelope of, and complement \(H_{s}^{C}\) of \(H_{s}\) are denoted as follows:

$$\begin{gathered} H_{S}^{ + } = \mathop {{\text{Max}}(S_{i} )}\limits_{{S_{i} \in H_{s} }} ,\forall i \hfill \\ H_{S}^{ - } = \mathop {{\text{Min}}(S_{i} )}\limits_{{S_{i} \in H_{s} }} ,\forall i \hfill \\ {\text{env}}(H_{S} ) = \left[ {H_{S}^{ - } ,H_{S}^{ + } } \right] \hfill \\ H_{S}^{C} = \{ S_{i} \left| {S_{i} \in S \cap S_{i} \notin H_{S} } \right.\} . \hfill \\ \end{gathered}$$
(3)

Because the aforementioned linguistic terms are equally important fuzzy sets, Zhang et al. [8] used a probabilistic model, called the LDA model, to indicate the varying importance of linguistic terms.

Definition 5

[8] Let \(S = \left\{ {S_{0} ,S_{1} ,...,S_{g} } \right\}\) be defined as previously and \(P_{D}\) be the distribution assessment of \(S\). \(P_{D} = \{ (S_{i} ,\beta_{i} )\left| {i = 1,2,...,g} \right.\}\), where \(\beta_{i} \ge 0\) is a symbolic proportion of \(S_{i}\), \(S_{i} \in S\), or \(\sum\nolimits_{i = 1}^{g} {\beta_{i} } = 1\).

Zhang et al. [8] proposed the following negation operator of \(P_{D}\): \({\text{Neg(S}}_{i} {,}\beta_{i} {\text{) = (S}}_{i} {,}\beta_{g - i} {)}\).

2.2 Heterogeneous Preference Relation with Self-confidence

While confidence influences reasonable decision-making, it often leads to bias in the judgment of alternatives. A preference relation with self-confidence allows DMs to provide their preference values with self-confidence levels, as designed by Liu et al. [19].

Definition 6

[19] Let \(X = \{ x_{1} ,x_{2} ,...,x_{m} \} (m \ge 2)\) be a finite set of alternatives, and \(S = \{ S_{0} ,S_{1} ,...,S_{g} \}\) be a linguistic term set. \(F = (f_{ij} |c_{ij} )_{m \times m}\) is defined as a preference relation with self-confidence. Its elements have two components: \(f_{ij} \in [0,1]\) denotes the preference degree of alternative \(x_{i}\) over \(x_{j}\), and \(c_{ij} \in S\) denotes the self-confidence level related to \(f_{ij}\). The following conditions are satisfied: \(f_{ij} + f_{ji} = 1\),\(f_{ii} = 0.5\), \(c_{ii} = S_{g}\), and \(c_{ji} = c_{ij}\), for \(\forall i,j \in \{ 1,...,m\}\).

In linguistic GDM, we also introduce preference relations with self-confidence.

Definition 7

Let \(X = \{ x_{1} ,x_{2} ,...,x_{m} \}\), \(S = \{ S_{0} ,S_{1} ,...,S_{g} \}\) be equivalent to the above definitions. A heterogeneous preference relation with self-confidence (HPR-SC) \(L = (l_{ij} |c_{ij} )_{m \times m}\) is composed of two parts: \(l_{ij} \in S\) represents the preference value of alternatives \((x_{i} ,x_{j} )\), and \(c_{ij} \in S\) represents the self-confidence level associated with \(l_{ij}\). An HPR-SC also satisfies \(l_{ji} = {\text{Neg}} (l_{ij} )\), \(c_{ii} = S_{g}\), and \(c_{ji} = c_{ij}\)\(\forall i,j \in \{ 1,...,m\}\).

Remark

Preference values are expressed in linguistic terms—HFLTS or LDA—and the level of self-confidence is shown by a simple single linguistic term.

Example 1

Let \(S = \left\{ {S_{0} ,S_{1} ,...,S_{6} } \right\}\) be a set of seven linguistic terms and \(X = \{ x_{1} ,x_{2} ,...,x_{4} \}\) be a set of alternatives. For the evaluated linguistic preference values, the meaning of \(S\) can be expressed as

$$\begin{aligned} S &= \{ S_{0} = {\text{nothing}};\,S_{1} = {\text{poor}};\,S_{2} = {\text{slightlypoor}}; \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} S_{4} &= {\text{fair;}}\,S_{5} = {\text{slightlygood}};\,S_{6} = {\text{perfect}}\} . \hfill \\ \end{aligned}$$

Assume that a DM expresses a preference relation with self-confidence using an HFLTS as follows:

$$L = \left( {\begin{array}{*{20}c} {(S_{3} \left| {S_{6} } \right.)} & {(\{ S_{4} ,S_{5} \} \left| {S_{6} } \right.)} & {(\{ S_{2} ,S_{3} ,S_{5} \} \left| {S_{4} } \right.)} & {(\{ S_{4} ,S_{5} \} \left| {S_{5} } \right.)} \\ - & {(S_{3} \left| {S_{6} } \right.)} & {(S_{5} \left| {S_{5} } \right.)} & {(\{ S_{2} ,S_{3} \} \left| {S_{6} } \right.)} \\ - & - & {(S_{3} \left| {S_{6} } \right.)} & {(S_{4} \left| {S_{4} } \right.)} \\ - & - & - & {(S_{3} \left| {S_{6} } \right.)} \\ \end{array} } \right).$$

In HPR-SC, \(l_{24} = \{ S_{2} ,S_{3} \}\) indicates that the preference degree of \(x_{2}\) over \(x_{4}\) is between \(S_{4}\) and \(S_{5}\) (i.e., between slightly good and good). Accordingly, \(c_{24} = S_{6}\) indicates that the DM’s self-confidence level associated with \(l_{24}\) is \(S_{6}\) (i.e., maybe absolutely confident).

2.3 PIS Model Based on Numerical Scale (NS)

Consistency measurement ensures that each judgment is logical based on a preference relation. Dong et al. [33] proposed the concept of NSs.

Definition 8

[33]. Let \(S = \{ S_{0} ,S_{1} ,...,S_{{\text{g}}} \}\) be a linguistic term set, and let \(R \in \Re\). A mapping function \({\text{NS}} :S \to R\) is a one-to-one injection, and \({\text{NS}} (S_{i} )\) is called the NS of \(S_{i} (i = 0,1,...,g)\). If \({\text{NS}} (S_{i} ) < {\text{NS}} (S_{i + 1} )\), then \({\text{NS}}\) is ordered.

On the basis of a balanced linguistic term set \(S\), the NSs satisfy \({\text{NS}} (S_{i} ) + {\text{NS}} (S_{g - i} ) = 1\).

Definition 9

[34, 35]. We assume that \(L^{*} = (l_{ij} )_{m \times m}\) is a linguistic preference relation. Based on NS, the consistency index of \(L^{*}\) is defined as

$${\text{CI}}(L^{*} ) = 1 - \frac{2}{3m(m - 1)(m - 2)}\sum\nolimits_{i,j,z = 1;i \ne j \ne z}^{m} {\left| {{\text{NS}}(l_{ij} ) + {\text{NS}}(l_{jz} ) - {\text{NS}}(l_{iz} ) - 0.5} \right|} ,$$
(4)

where \({\text{NS}}(l_{ij} ) \in [0,1],i,j = 1,2,...,n\). A larger value of \(CI(L^{*} )\) indicates better consistency of \(L^{*}\). If \({\text{CI}}(L^{*} ) = 1\), then the matrix \(L^{*}\) is completely consistent.

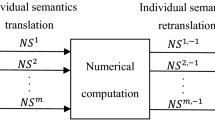
Words can have different meanings provided by different people. Accordingly, Li et al. [28] proposed a framework for handling preference information in linguistic GDM with a PIS. The individual semantic translation process converts linguistic input into corresponding personalized numerical scales (PNSs), and the individual semantic retranslation process converts the PNS output back into linguistic values.

Let \(S = \{ S_{0} ,S_{1} ,...,S_{{\text{g}}} \}\) be a linguistic term set, and \(D = \{ d_{1} ,d_{2} ,...,d_{n} \}\) be a set of DMs. \({\text{PNS}}^{k}\) represents the personalized numerical scale on \(S\) associated with DM \(d_{k}\). The function \(\Delta^{ - 1} ({\text{PNS}}^{k} )\) can transform a numerical scale into its equivalent linguistic values. This process is described in more detail in Li et al. [28].

3 Linguistic GDM Framework to Handle PIS and Self-confidence Behavior

In this section, we propose an HPR-SC model and a corresponding resolution framework.

Let \(X = \{ x_{1} ,x_{2} ,...,x_{m} \}\) be a set of alternatives, \(D = \{ d_{1} ,d_{2} ,...,d_{n} \}\) be a set of DMs, and \(S = \{ S_{0} ,S_{1} ,...,S_{g} \}\) be a linguistic term set. DM \(d_{k} (k = 1,2,...,n)\) pairwise compares alternatives \((x_{i} ,x_{j} )\) to generate an HPR-SC \(L^{k} = (l_{ij}^{k} |c_{ij}^{k} )_{m \times m}\), where \(l_{ij}^{k}\) represents the preference degree of \(x_{i}\) over \(x_{j}\), and \(c_{ij}^{k} \in S\) denotes the self-confidence level associated with preference value \(l_{ij}^{k}\). Each DM has personalized semantics for \(L^{k}\), and \(k = 1,2,...,n\).

Our model handles heterogeneous preference relations with self-confidence and reach consensus by accounting for PIS and confidence. The process comprises the following three consensus steps (Fig. 1).

Fig. 1
figure 1

Consensus framework

Full size image

3.1 Transformation Process

LDAs are used to capture the maximum amount of information provided by DMs. We converted each HPR-SC into a linguistic distribution preference relation with self-confidence (LDPR-SC). The LDPR-SC represents the degree of affirmation of a linguistic distribution preference relation made by DMs for alternatives, and it expresses linguistic preferences under different confidence levels to improve the accuracy of linguistic representation. In our model, this confidence level is represented by linguistic preference. The following definitions and examples illustrate its transformation:

A single linguistic term can be regarded as a special LDA, obtained by converting an HFLTS.

Definition 10

Let \(S = \{ S_{0} ,S_{1} ,...,S_{g} \}\) be a linguistic term. For an HFLTS based on \(S\) and \(H_{S}\), we transform \(H_{S}\) into a distribution assessment \(P_{D} = \{ (S_{i} ,\beta_{i} )|i = 0,1,...,g\}\) by solving the following model:

$$\begin{gathered} H_{S} \to P_{D} = \left\{ {\left( {S_{i} ,\beta_{i} } \right)\left| {i = p,p + 1,...,q} \right.} \right\} \hfill \\ {\text{s.t}}{.}\left\{ {\begin{array}{*{20}c} {S_{p} = \mathop {\min }\limits_{{S_{j} \in H_{S} }} (S_{j} ),S_{q} = \mathop {\max }\limits_{{S_{j} \in H_{S} }} (S_{j} )} \\ {\beta_{i} = \frac{1}{{\# H_{S} }}(i = p,p + 1,,...,q - 1)} \\ {\beta_{q} = 1 - \sum\limits_{p}^{q - 1} {\beta_{i} } } \\ {\# H_{S} \le g + 1} \\ \end{array} } \right., \hfill \\ \end{gathered}$$
(5)

where \(\# H_{S}\) denotes the number of linguistic terms in \(H_{S}\). We refer to Model (5) \(M1\).

Let \(X = \{ x_{1} ,x_{2} ,...,x_{m} \}\) be a set of alternatives, and \(D = \{ d_{1} ,d_{2} ,...,d_{n} \}\) be a set of DMs. After unification, each heterogeneous preference relation with self-confidence \(L^{{\text{k}}}\) can be transformed into an LDPR-SC

$$P^{{\text{k}}} = \left( {p_{ij}^{k} \left| {c_{ij}^{k} } \right.} \right)_{m \times m} = \left( {\begin{array}{*{20}c} {\left( {p_{11}^{k} \left| {c_{11}^{k} } \right.} \right)} & {\left( {p_{12}^{k} \left| {c_{12}^{k} } \right.} \right)} & \cdots & {\left( {p_{1m}^{k} \left| {c_{1m}^{k} } \right.} \right)} \\ {\left( {p_{21}^{k} \left| {c_{21}^{k} } \right.} \right)} & {\left( {p_{22}^{k} \left| {c_{22}^{k} } \right.} \right)} & \cdots & {\left( {p_{2m}^{k} \left| {c_{2m}^{k} } \right.} \right)} \\ \vdots & \vdots & \cdots & \vdots \\ {\left( {p_{m1}^{k} \left| {c_{m1}^{k} } \right.} \right)} & {\left( {p_{m2}^{k} \left| {c_{m2}^{k} } \right.} \right)} & \cdots & {\left( {p_{mm}^{k} \left| {c_{mm}^{k} } \right.} \right)} \\ \end{array} } \right),$$

where \(p_{ij}^{k} = \{ (S_{t} ,\beta_{ij.t}^{k} )\left| {t = 0,1,...,g} \right.\} ,c_{ij}^{k} \in S,i,j = 1,2,...,m,k = 1,2,...,n\).

For example, the following preference relation with self-confidence \(L^{1}\)

$$L^{1} = \left( {\begin{array}{*{20}c} {(S_{3} |S_{6} )} & {(\{ S_{1} ,S_{2} \} |S_{4} )} & {(\{ S_{4} ,S_{5} ,S_{6} \} |S_{5} )} & {(S_{4} |S_{6} )} \\ - & {(S_{3} |S_{6} )} & {(\{ S_{5} ,S_{6} \} |S_{6} )} & {(\{ S_{4} ,S_{5} \} |S_{3} )} \\ - & - & {(S_{3} |S_{6} )} & {(\{ S_{1} ,S_{2} \} |S_{2} )} \\ - & - & - & {(S_{3} |S_{6} )} \\ \end{array} } \right)$$

can be transformed into a corresponding LDPR-SC \(P^{1}\):

$$P^{3} = \left( {\begin{array}{*{20}c} {\left( {S_{3} \left| {S_{6} } \right.} \right)} & {\left( {\left\{ {\left( {S_{1} ,0.5} \right),\left( {S_{2} ,0.5} \right)} \right\}\left| {S_{4} } \right.} \right)} & {\left( {\left\{ \begin{gathered} \left( {S_{4} ,0.33} \right),\left( {S_{5} ,0.33} \right) \hfill \\ \left( {S_{6} ,0.34} \right) \hfill \\ \end{gathered} \right\}\left| {S_{5} } \right.} \right)} & {\left( {S_{4} \left| {S_{6} } \right.} \right)} \\ - & {\left( {S_{3} \left| {S_{6} } \right.} \right)} & {\left( {\left\{ {\left( {S_{5} ,0.5} \right),\left( {S_{6} ,0.5} \right)} \right\}\left| {S_{6} } \right.} \right)} & {\left( {\left\{ {\left( {S_{4} ,0.5} \right),\left( {S_{5} ,0.5} \right)} \right\}\left| {S_{3} } \right.} \right)} \\ - & - & {\left( {S_{3} \left| {S_{6} } \right.} \right)} & {\left( {\left\{ {\left( {S_{1} ,0.5} \right),\left( {S_{2} ,0.5} \right)} \right\}\left| {S_{2} } \right.} \right)} \\ - & - & - & {\left( {S_{3} \left| {S_{6} } \right.} \right)} \\ \end{array} } \right).$$

Remark

In the above example, \(\left( {\left\{ {\left( {S_{1} ,0.5} \right),(S_{2} ,0.5)} \right\}\left| {S_{4} } \right.} \right)\) is a distribution assessment transformed from \(\left( {\{ S_{1} ,S_{2} \} \left| {S_{4} } \right.} \right)\). The credibility of group decision-making is precisely a result of the group opinion comprising the information of all decision-makers, so conflict may be reduced. If some decision-makers do not perceive a higher degree of confidence in the given preferences, the information will be identified, and guided adjustments will be applied in the consensus-reaching process in subsection C, thus reducing the impact of uncertainty. However, this information is not directly removed.

Self-confidence is a psychological expectation that exists in the process of making decisions or comparing preferences for every individual DM. In the supply chain inventory strategy, overconfident decisions are positively affected by the DMs’ psychological expectations of market demand, as market forecasts are published through annual financial reports or decision reports. In addition, in credit management, the risk preference type can be determined by answers to a questionnaire, which is a necessary link before credit is issued.

If the confidence level cannot be provided by experts, it can be determined by the decision-makers’ area of expertise.

3.2 PIS Model

We obtained each LDPR-SC and used a consistency-driven optimization method to test the PIS. We then transformed LDPR-SC into additive preference relations with self-confidence (APRs-SC).

Consistency is a metric used to ensure that a preference relation is reasonable and not random. Li et al. [19] proposed a consistency-driven optimization method that calculates NSs corresponding to the linguistic term set of each DM to reflect the PIS.

Definition 11

Let \(X = \{ x_{1} ,x_{2} ,...,x_{m} \}\) be a set of alternatives, and \(F = (f_{ij} |c_{ij}^{a} )_{m \times m}\) be an APR-SC,\(f_{ij} ,c_{ij}^{a} \in [0,1]\). \(f_{ij} = 0.5\) implies indifference between \(x_{i}\) and \(x_{j}\). For three alternatives,\(x_{i}\), \(x_{j}\), and \(x_{z}\), if their associated preference values \(f_{ij} ,f_{jz} ,f_{iz}\) fulfill \(f_{ij} + f_{jz} - f_{iz} = 0.5\), then the preference has additive transitivity at the self-confidence level \(c_{ijz}^{a}\), where \(c_{ijz}^{a} = \min \{ c_{ij}^{a} ,c_{jz}^{a} ,c_{iz}^{a} \}\).

If all elements in \(F\) satisfy \(f_{ij} + f_{jz} - f_{iz} = 0.5\), then \(F\) is considered completely consistent at the self-confidence level \(c^{a}\), where \(c^{a} = \min \{ c_{ij}^{a} \}\), and \(i,j = 1,2,...,m\).

Let \(S = \{ S_{0} ,S_{1} ,...,S_{{\text{g}}} \}\) be a linguistic term set, \(D = \{ d_{1} ,d_{2} ,...,d_{n} \}\) be a set of DMs, \(P^{k} = (p_{ij}^{k} |c_{ij}^{k} )_{m \times m}\) be an LDPR-SC provided by DM \(d_{k}\), and \({\text{PNS}}^{k}\) be the NSs associated with \(d_{k}\). To ensure that the preference relation \(P^{k}\) given by DM \(d_{k}\) is as consistent as possible, we maximize the consistency index using the objective function

$$\begin{array}{*{20}c} {{\text{Max}}} & {CI(P^{k} )} \\ \end{array} .$$
(6)

In LDPR-SC \(P^{k} = (p_{ij}^{k} |c_{ij}^{k} )_{m \times m}\), each element \(p_{ij}^{k} = \{ (S_{t} ,\beta_{ij.t}^{k} )\left| {t = 0,1,...,g} \right.\}\) is a distribution assessment, and \(c_{ij}^{k}\) is the corresponding self-confidence level. Taking personalized semantics into account, we translate \(p_{ij}^{k}\), \(c_{ij}^{k}\) to corresponding numerical values \(f_{ij}^{k}\),\(c_{ij}^{ka}\). That is, the individual APR-SC \(F^{k} = (f_{ij}^{k} |c_{ij}^{ka} )_{m \times m}\) associated with \(P^{k}\) can be obtained as follows:

$$f_{ij}^{k} = \sum\limits_{t = 0}^{g} {{\text{PNS}}^{k} (S_{t} ) \times \beta_{ij,t}^{k} } ,$$
(7)
$$c_{ij}^{ka} = {\text{PNS}}^{k} (c_{ij}^{k} ).$$
(8)

The consistency index \(CI(P^{k} )\) is calculated as

$${\text{CI}}(L^{*} ) = 1 - \frac{2}{3m(m - 1)(m - 2)}\sum\nolimits_{i,j,z = 1;i \ne j \ne z}^{m} {{\text{PNS}}^{k} (c_{ij}^{k} )\left| {f_{ij}^{k} + f_{jz}^{k} - f_{iz}^{k} - 0.5} \right|} .$$
(9)

The range of \(PNS(S_{t} )\) for linguistic term \(S_{t}\) is

$${\text{PNS}}^{k} \left( {S_{t} } \right) = \left\{ \begin{gathered} = 0,t = 0 \hfill \\ = 0.5,t = \frac{g}{2} \hfill \\ 1,t = g \hfill \\ \in \left[ {\frac{t - 1}{g},\frac{t + 1}{g}} \right], \quad t = 1,2, \ldots ,g - 1; \quad t \ne \frac{g}{2} \hfill \\ \end{gathered} \right..$$
(10)

To make \({\rm PNS}^{k}\) ordered, a constraint value \(\sigma \in (0,1)\) is introduced

$${\text{PNS}}^{k} (S_{t + 1} ) - {\text{PNS}}^{k} (S_{t} ) \ge \sigma ,\quad {\text{for}}\quad t = 1,2,...,g - 1.$$
(11)

Based on Eqs. (6)–(11), we utilize a consistency-driven optimization method to determine the PIS as follows:

$$\begin{gathered} \max 1 - \frac{2}{{3m\left( {m - 1} \right)\left( {m - 2} \right)}}\sum\limits_{i,j,z = 1;i \ne j \ne z}^{m} {{\text{PNS}}^{k} \left( {c_{ijz}^{k} } \right)} \left| {f_{ij}^{k} + f_{jz}^{k} - f_{iz}^{k} - 0.5} \right| \hfill \\ s.t\left\{ \begin{gathered} c_{ijz}^{k} = \min \left\{ {c_{ij}^{k} ,c_{jz}^{k} ,c_{iz}^{k} } \right\},i,j,z = 1,2, \cdots ,m \hfill \\ f_{ij}^{k} = \sum\limits_{t = 0}^{g} {{\text{PNS}}^{k} \left( {S_{t} } \right)} \times \beta_{ij,t}^{k} ,i,j = 1,2, \cdots ,m \hfill \\ {\text{PNS}}^{k} \left( {S_{t} } \right) \in \left[ {\frac{t - 1}{g},\frac{t + 1}{g}} \right],t = 1,2, \cdots ,g - 1;t \ne \frac{g}{2} \hfill \\ {\text{PNS}}^{k} \left( {S_{0} = 0} \right) \hfill \\ {\text{PNS}}^{k} \left( {S_{g/2} } \right) = 0.5 \hfill \\ {\text{PNS}}^{k} \left( {S_{g} } \right) = 1 \hfill \\ {\text{PNS}}^{k} \left( {S_{t} } \right) + {\text{PNS}}^{k} \left( {S_{g - 1} } \right) = 1,t = 0,1, \cdots ,g \hfill \\ {\text{PNS}}^{k} \left( {S_{t + 1} } \right) - {\text{PNS}}^{k} \left( {S_{t} } \right) \ge \sigma ,t = 0,1, \cdots ,g - 1 \hfill \\ \end{gathered} \right.. \hfill \\ \end{gathered}$$
(12)

We call model (12) is denoted as \(M2\), and \({\text{PNS}}^{k} (S_{t} )\) refers to the decision variable. We can solve \(M2\) using traditional software such as Lingo. Subsequently, \({\text{PNS}}^{k}\) is performed.

3.3 Consensus Process

We gather member preferences to obtain group preferences, and subsequently calculate individual and group consensus levels. If the group consensus level is unacceptable, we enter the feedback-adjustment stage. Otherwise, the selection process can be entered to obtain the final decision result. In the feedback-adjustment phase, we detect underconfidence behaviors and provide preference modification advice based on identification and direction rules to improve group consensus.

We use a weighted operator to aggregate individual APR \((F^{k} )^{*} = (f_{ij}^{k} )_{m \times m}\) and obtain collective APR \(F^{c} = (f_{ij}^{c} )_{m \times m}\)

$$f_{ij}^{C} = \sum\limits_{k = 1}^{n} {f_{ij}^{k} \cdot w_{k} } ,$$
(13)

where \(w_{k} \in [0,1]\) is a weight vector of DMs, and \(\sum\nolimits_{k = 1}^{n} {w_{k} = 1}.\)

After obtaining collective opinions, we enter a consensus measurement and feedback-adjustment phase, which aims to coordinate and resolve conflicts among DMs.

Definition 12

Let \((F^{k} )^{*} = (f_{ij}^{k} )_{m \times m}\) be an individual APR, and let the collective opinion \(F^{c} = (f_{ij}^{c} )_{m \times m}\) be as defined previously. The individual consensus level of DM \(d_{k}\) is defined as follows:

$${\text{CL}}^{k} = 1 - \frac{1}{m(m - 1)}\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1;j \ne i}^{m} {\left| {f_{ij}^{k} - f_{ij}^{c} } \right|} } .$$
(14)

The collective consensus level is calculated as

$${\text{CL}} = 1 - \frac{1}{nm(m - 1)}\sum\limits_{k = 1}^{n} {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1;j \ne i}^{m} {\left| {f_{ij}^{k} - f_{ij}^{c} } \right|} } } ,$$
(15)

where \({\text{CL}} \in [0,1]\), and a larger value of \({\text{CL}}\) indicates a higher consensus level for all DMs.

If the consensus level obtained in Eq. (15) is acceptable, the priority vector of the alternatives is computed. Let \(O^{c} = (o_{1}^{c} ,o_{2}^{c} ,...,o_{m}^{c} )^{\rm T}\) be the priority vector generated to rank alternatives as follows:

$$o_{i}^{c} = \frac{1}{m - 1}\sum\limits_{j = 1;j \ne i}^{m} {f_{ij}^{c} } .$$
(16)

When the collective consensus level is higher than a certain preset threshold, we assume that the group consensus level is acceptable; otherwise, we trigger a feedback mechanism to reach a higher consensus level. However, underconfidence hinders the achievement of a group consensus. We first define such underconfidence behavior.

Definition 13

Let \(F = (f_{ij} |c_{ij}^{a} )_{m \times m}\) be an APR-SC and \(f_{ij} ,c_{ij}^{a} \in [0,1]\).\(f_{ij}\) denotes the preference degree of alternative \(x_{i}\) over \(x_{j}\), and \(c_{ij}^{a}\) represents the self-confidence level associated with \(f_{ij}\). If \(c_{ij}^{a} = 0.5\), the DM is moderately confident. We then set a threshold \(\eta (\eta \le 0.5)\) for underconfidence behavior. If \(c_{ij}^{a} < \eta\), then they have underconfidence in evaluating alternatives \((x_{i} ,x_{j} )\). In this study, we used \(\eta = 0.5\).

Next, we detect underconfidence behaviors. Let \(D_{U}\) be a set of DMs with underconfidence behaviors. For individual APR-SC \(F^{k} = (f_{ij}^{k} |c_{ij}^{ka} )_{m \times m} (k = 1,2,...,n)\)

$$D_{U} = \{ d_{l} \left| {c_{ij}^{la} < \eta ,l \in (1,n)} \right.\} ,\forall i,j \in \{ 1,2,...,m\} .$$
(17)

Some individuals may be unconfident regarding preference expressions because of their lack of access to background information or relevant professional knowledge. We can then provide additional supplementary knowledge for DMs to improve their self-confidence and consensus levels. Therefore, we propose the following feedback mechanism, which includes identification and direction rules.

Identification rule: Identify DM \(d_{z}\) which satisfies

$$\left\{ {\begin{array}{*{20}l} {{\text{CL}}^{z} = \mathop {\min }\limits_{{k \in \{ 1,2,...,n\} }} {\text{CL}}^{k} ,{\text{if}},D_{U} = \emptyset } \\ {{\text{CL}}^{z} = \mathop {\min }\limits_{{d_{k} \in D_{U} }} {\text{CL}}^{k} ,{\text{if}},D_{U} \ne \emptyset } \\ \end{array} } \right..$$
(18)

Direction rule: The DM revises their preference values in accordance with the suggested direction.

Let matrix \((F^{z} )^{*} = (f_{ij}^{z} )_{m \times m}\) be the individual APR associated with the identified DM \(d_{z}\), matrix \(F^{c} = (f_{ij}^{c} )_{m \times m}\) be the collective APR, and \(X = \{ x_{1} ,x_{2} ,...,x_{m} \}\) be a set of alternatives. The adjustment direction of DM \(d_{z}\) conforms to the following rules:

  1. 1.

    If \(f_{ij}^{z} < f_{ij}^{c}\), then DM \(d_{z}\) should increase the value of \(f_{ij}^{z}\) to be closer to \(f_{ij}^{c}\).

  2. 2.

    If \(f_{ij}^{z} > f_{ij}^{c}\), then DM \(d_{z}\) should decrease the value of \(f_{ij}^{z}\) to be closer to \(f_{ij}^{c}\).

  3. 3.

    Otherwise, \(f_{ij}^{z}\) should remain unchanged.

If the group reaches a consensus, we select the best alternatives.

3.4 Solution Algorithm

The solution and overall process are summarized in Table 1.

Table 1 Solution algorithm
Full size table

4 Numerical Example and Simulation Analysis

In this section, we present a quantitative example and simulation analysis to illustrate the effectiveness of the proposed model.

4.1 Numerical Example

We assume that in a real-life GDM issue, such as the green supplier selection in supply chain management, four alternatives need to be evaluated by six DMs. The expressions of FLPR-SC \(L^{k} = (l_{ij}^{k} |c_{ij}^{k} )_{m \times m} (k = 1,2,...,6)\) are as follows:

$$L^{1} = \left( {\begin{array}{*{20}c} {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{4} |S_{4} } \right)} & {\left( {S_{6} |S_{2} } \right)} & {\left( {S_{5} |S_{5} } \right)} \\ - & {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{4} |S_{6} } \right)} & {\left( {S_{4} |S_{5} } \right)} \\ - & - & {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{2} |S_{6} } \right)} \\ - & - & - & {\left( {S_{3} |S_{6} } \right)} \\ \end{array} } \right),$$
$$L^{2} = \left( {\begin{array}{*{20}c} {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{5} |S_{3} } \right)} & {\left( {S_{6} |S_{5} } \right)} & {\left( {S_{4} |S_{4} } \right)} \\ - & {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{5} |S_{3} } \right)} & {\left( {S_{2} |S_{2} } \right)} \\ - & - & {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{1} |S_{2} } \right)} \\ - & - & - & {\left( {S_{3} |S_{6} } \right)} \\ \end{array} } \right),$$
$$L^{3} = \left( {\begin{array}{*{20}c} {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {S_{1} ,S_{2} } \right\}|S_{4} } \right)} & {\left( {\left\{ {S_{4} ,S_{5} ,S_{6} } \right\}|S_{5} } \right)} & {\left( {S_{4} |S_{6} } \right)} \\ - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {S_{5} ,S_{6} } \right\}|S_{6} } \right)} & {\left( {\left\{ {S_{4} ,S_{5} } \right\}|S_{3} } \right)} \\ - & - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {S_{1} ,S_{2} } \right\}|S_{2} } \right)} \\ - & - & - & {\left( {S_{3} |S_{6} } \right)} \\ \end{array} } \right),$$

\(L^{4} = \left( {\begin{array}{*{20}c} {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{3} |S_{4} } \right)} & {\left( {\left\{ {S_{3} ,S_{4} } \right\}|S_{3} } \right)} & {\left( {\left\{ {S_{4} ,S_{5} ,S_{6} } \right\}|S_{6} } \right)} \\ - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {S_{4} ,S_{5} } \right\}|S_{5} } \right)} & {\left( {S_{4} |S_{4} } \right)} \\ - & - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {S_{3} ,S_{4} } \right\}|S_{6} } \right)} \\ - & - & - & {\left( {S_{3} |S_{6} } \right)} \\ \end{array} } \right),\)

$$L^{5} = \left( {\begin{array}{*{20}c} {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {\left( {S_{3} ,0.2} \right),\left( {S_{4} ,0.8} \right)} \right\}|S_{5} } \right)} & {\left( {\left\{ \begin{gathered} \left( {S_{4} ,0.3} \right),\left( {S_{5} ,0.5} \right) \hfill \\ \left( {S_{6} ,0.2} \right) \hfill \\ \end{gathered} \right\}|S_{4} } \right)} & {\left( {\left\{ {\begin{array}{*{20}l} {\left( {S_{3} ,0.2} \right),\left( {S_{4} ,0.25} \right)} \hfill \\ {\left( {S_{5} ,0.45} \right),\left( {S_{6} ,0.1} \right)} \hfill \\ \end{array} } \right\}|S_{6} } \right)} \\ - & {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{4} |S_{5} } \right)} & {\left( {\left\{ {\left( {S_{4} ,0.35} \right),\left( {S_{5} ,0.65} \right)} \right\}|S_{4} } \right)} \\ - & - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {\left( {S_{3} ,0.4} \right),\left( {S_{4} ,0.6} \right)} \right\}|S_{6} } \right)} \\ - & - & - & {\left( {S_{3} |S_{6} } \right)} \\ \end{array} } \right)$$
$$L^{6} = \left( {\begin{array}{*{20}c} {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{1} |S_{5} } \right)} & {\left( {\left\{ \begin{gathered} \left( {S_{4} ,0.1} \right),\left( {S_{5} ,0.6} \right) \hfill \\ \left( {S_{6} ,0.3} \right) \hfill \\ \end{gathered} \right\}|S_{5} } \right)} & {\left( {\left\{ {\begin{array}{*{20}l} {\left( {S_{3} ,0.1} \right),\left( {S_{4} ,0.4} \right)} \hfill \\ {\left( {S_{5} ,0.5} \right)} \hfill \\ \end{array} } \right\}|S_{6} } \right)} \\ - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ \begin{gathered} \left( {S_{4} ,0.15} \right),\left( {S_{5} ,0.45} \right) \hfill \\ \left( {S_{6} ,0.4} \right) \hfill \\ \end{gathered} \right\}|S_{5} } \right)} & {\left( {S_{5} |S_{2} } \right)} \\ - & - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ \begin{gathered} \left( {S_{3} ,0.4} \right),\left( {S_{4} ,0.5} \right) \hfill \\ \left( {S_{5} ,0.1} \right) \hfill \\ \end{gathered} \right\}|S_{6} } \right)} \\ - & - & - & {\left( {S_{3} |S_{6} } \right)} \\ \end{array} } \right).$$

Based on the model \(M1\),we transform each HPR-SC \(L^{k}\) to a corresponding LDPR-SC \(P^{k}\).

$$P^{k} = L^{k} ,k = 1,2,5,6.$$
$$P^{3} = \left( {\begin{array}{*{20}c} {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {\left( {S_{1} ,0.5} \right),\left( {S_{2} ,0.5} \right)} \right\}|S_{4} } \right)} & {\left( {\left\{ \begin{gathered} S_{4} ,0.33),\left( {S_{5} ,0.33} \right) \hfill \\ \left( {S_{6} ,0.34} \right) \hfill \\ \end{gathered} \right\}|S_{5} } \right)} & {\left( {S_{4} |S_{6} } \right)} \\ - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {\left( {S_{5} ,0.5} \right),\left( {S_{6} ,0.5} \right)} \right\}|S_{6} } \right)} & {\left( {\left\{ {\left( {S_{4} ,0.5} \right),\left( {S_{5} ,0.5} \right)} \right\}|S_{3} } \right)} \\ - & - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {\left( {S_{1} ,0.5} \right),\left( {S_{2} ,0.5} \right)} \right\}|S_{2} } \right)} \\ - & - & - & {\left( {S_{3} |S_{6} } \right)} \\ \end{array} } \right)$$
$$P^{4} = \left( {\begin{array}{*{20}c} {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{3} |S_{4} } \right)} & {\left( {\left\{ {\left( {S_{3} ,0.5} \right),\left( {S_{4} ,0.5} \right)} \right\}|S_{3} } \right)} & {\left( {\left\{ \begin{gathered} \left( {S_{4} ,0.33} \right),\left( {S_{5} ,0.33} \right) \hfill \\ \left( {S_{6} ,0.34} \right) \hfill \\ \end{gathered} \right\}|S_{6} } \right)} \\ - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {\left( {S_{4} ,0.5} \right),\left( {S_{5} ,0.5} \right)} \right\}|S_{5} } \right)} & {\left( {S_{4} |S_{4} } \right)} \\ - & - & {\left( {S_{3} |S_{6} } \right)} & {\left( {\left\{ {\left( {S_{3} ,0.5} \right),\left( {S_{4} ,0.5} \right)} \right\}|S_{6} } \right)} \\ - & - & - & {\left( {S_{3} |S_{6} } \right)} \\ \end{array} } \right).$$

We then obtain the personalized semantics of each DM on the basis of model \(M2\), as shown in Table 2.

Table 2 PNS of linguistic terms for each DM
Full size table

After PIS management, we transform LDPR-SC into APR-SC based on Eqs. (7, 8)

$$F^{1} = \left( {\begin{array}{*{20}c} {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.67\left| {0.67} \right.} \right)} & {\left( {1\left| {0.33} \right.} \right)} & {\left( {0.83\left| {0.83} \right.} \right)} \\ - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.67\left| 1 \right.} \right)} & {\left( {0.67\left| {0.83} \right.} \right)} \\ - & - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.33\left| 1 \right.} \right)} \\ - & - & - & {\left( {0.5\left| 1 \right.} \right)} \\ \end{array} } \right),$$
$$F^{2} = \left( {\begin{array}{*{20}c} {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.75\left| {0.5} \right.} \right)} & {\left( {1\left| {0.75} \right.} \right)} & {\left( {0.62\left| {0.62} \right.} \right)} \\ - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.75\left| {0.5} \right.} \right)} & {\left( {0.38\left| {0.38} \right.} \right)} \\ - & - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.25\left| {0.38} \right.} \right)} \\ - & - & - & {\left( {0.5\left| 1 \right.} \right)} \\ \end{array} } \right),$$
$$F^{3} = \left( {\begin{array}{*{20}c} {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.275\left| {0.55} \right.} \right)} & {\left( {0.817\left| {0.9} \right.} \right)} & {\left( {0.55\left| 1 \right.} \right)} \\ - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.95\left| 1 \right.} \right)} & {\left( {0.725\left| {0.5} \right.} \right)} \\ - & - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.275\left| {0.45} \right.} \right)} \\ - & - & - & {\left( {0.5\left| 1 \right.} \right)} \\ \end{array} } \right),$$
$$F^{4} = \left( {\begin{array}{*{20}c} {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.5\left| {0.62} \right.} \right)} & {\left( {0.56\left| {0.5} \right.} \right)} & {\left( {0.763\left| 1 \right.} \right)} \\ - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.645\left| {0.67} \right.} \right)} & {\left( {0.62\left| {0.62} \right.} \right)} \\ - & - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.56\left| 1 \right.} \right)} \\ - & - & - & {\left( {0.5\left| 1 \right.} \right)} \\ \end{array} } \right),$$
$$F^{5} = \left( {\begin{array}{*{20}c} {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.572\left| {0.67} \right.} \right)} & {\left( {0.712\left| {0.59} \right.} \right)} & {\left( {0.649\left| 1 \right.} \right)} \\ - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.59\left| {0.67} \right.} \right)} & {\left( {0.642\left| {0.59} \right.} \right)} \\ - & - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.554\left| 1 \right.} \right)} \\ - & - & - & {\left( {0.5\left| 1 \right.} \right)} \\ \end{array} } \right),$$
$$F^{6} = \left( {\begin{array}{*{20}c} {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.33\left| {0.67} \right.} \right)} & {\left( {0.757\left| {0.67} \right.} \right)} & {\left( {0.605\left| {0.55} \right.} \right)} \\ - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.784\left| {0.67} \right.} \right)} & {\left( {0.67\left| {0.45} \right.} \right)} \\ - & - & {\left( {0.5\left| 1 \right.} \right)} & {\left( {0.542\left| 1 \right.} \right)} \\ - & - & - & {\left( {0.5\left| 1 \right.} \right)} \\ \end{array} } \right).$$

We can then compute the collective APR \(F^{c}\) based on Eq. (13)

$$F^{c} = \left( {\begin{array}{*{20}c} {0.5} & {0.516} & {0.808} & {0.67} \\ {0.484} & {0.5} & {0.732} & {0.618} \\ {0.192} & {0.268} & {0.5} & {0.419} \\ {0.33} & {0.382} & {0.581} & {0.5} \\ \end{array} } \right).$$

Next, we set the threshold of the consensus level as \(\varepsilon = 0.9\). On the basis of Eqs. (14, 15), we obtain an unaccepted collective consensus level \({\text{CL}} = 0.8878\). The individual consensus levels are \({\text{CL}}^{1} = 0.8818\), \({\text{CL}}^{2} = 0.8498\), \({\text{CL}}^{3} = 0.8602\), \({\text{CL}}^{4} = 0.9022\), \({\text{CL}}^{5} = 0.921\), and \({\text{CL}}^{6} = 0.9118\).

We developed a feedback mechanism with confidence to provide suggestions for adjustment. In accordance with the identification and directional rules, DM \(d_{2}\) should modify their preference relationship. The updated preference relation of \(d_{2}\) is

$$\overline{{L^{2} }} = \left( {\begin{array}{*{20}c} {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{5} |S_{3} } \right)} & {\left( {S_{6} |S_{4} } \right)} & {\left( {S_{4} |S_{5} } \right)} \\ - & {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{5} |S_{3} } \right)} & {\left( {S_{4} |S_{5} } \right)} \\ - & - & {\left( {S_{3} |S_{6} } \right)} & {\left( {S_{3} |S_{4} } \right)} \\ - & - & - & {\left( {S_{3} |S_{6} } \right)} \\ \end{array} } \right).$$

Because the updated collective consensus level \({\text{CL}} = 0.9006\) is acceptable, group consensus is reached. The final collective preference relationship is obtained as follows:

$$\overline{{F^{c} }} = \left( {\begin{array}{*{20}c} {0.5} & {0.516} & {0.808} & {0.67} \\ {0.484} & {0.5} & {0.732} & {0.658} \\ {0.192} & {0.268} & {0.5} & {0.46} \\ {0.33} & {0.342} & {0.54} & {0.5} \\ \end{array} } \right).$$

We obtain the priority vector of alternative \(x_{1} \succ x_{2} \succ x_{4} \succ x_{3}\), and \(x_{1}\) is chosen as the optimal alternative.

4.2 Simulation and Comparative Analysis

Individual self-confidence levels affect the decision-making process and selection of the final result [19, 37, 38]. This section presents a comparison between our proposed method and existing methods.

In linguistic GDM, fixed NSs are used to handle linguistic preference information in a process called the FNS-based method [39]. Specifically, each DM exhibits the same semantics as a linguistic term set. For example, in the linguistic term set \(S = \{ S_{1} ,S_{2} ,...,S_{6} \}\), the NSs corresponding to \(S\) of all DMs are \(NS = [0,\;0.17,\;0.33,\;0.5,\;0.67,\;0.83,\;1]\). Fuzzy linguistic preference relations indicate that DMs are fully confident in their evaluation information; that is, \(c_{ij} = S_{g}\) for \(\forall i,j \in \{ 1,2,...,m\}\).

The consistency index, which serves as the basis of a preference relation, is a metric used to evaluate the performance of different methods. We use the numerical example data in Sect. 3 to observe the consistency indices of six DMs under different methods in Fig. 2.

  1. i.

    HPR based on FNS, the preference relation without considering personalized semantics.

  2. ii.

    HPR based on PNS, the preference relation only considers personalized semantics.

  3. iii.

    HPR-SC based on PNS: the preference relation considers personalized semantics and confidence.

Fig. 2
figure 2

Consistency indexes of DMs under different approaches

Full size image

Preference values are combined with multiple self-confidence levels to evaluate alternatives and obtain reliable evaluation information.

Figure 2 shows that the consistency index of the PNS-based method is higher than that of the FNS-based method, which indicates superior performance in the PNS-based method. Thus, the pairwise approach of preference expression (preference value and corresponding self-confidence level) can improve consistency.

A simulation experiment was conducted to illustrate the effectiveness of our model and analyze the effects of some parameters in the CRP. We randomly generated linguistic preference relations with self-confidence, and observed simulation results under different parameter settings.

In the feedback-adjustment stage, the identified DM must participate in the interaction. Thus, we replaced the adjustment direction rule in Sect. 4.3 with the following rules to automatically modify the DM’s preference values.

Simulation Experiment 1: Let \(m = 4\) and \(n \in \{ 5,6,7,8,9\}\), and then, let \(n = 6\) and \(m \in \{ 3,4,5,6,7\}\). We compared the average number of iterations in different contexts. The simulation results are shown in Fig. 3.

Fig. 3
figure 3

Average number of iterations under different settings

Full size image

Simulation Experiment 2: We set different values of m and n to compare the consensus-reaching speed and average self-confidence level. Under each set of parameters, we obtained the average value of group consensus and self-confidence level 500 times to eliminate randomness. The simulation results are shown in Figs. 4 and 5.

Fig. 4
figure 4

Average consensus level under different iterations

Full size image
Fig. 5
figure 5

Average self-confidence level under different iterations

Full size image

The results in Figs. 3, 4 and 5 show that the proposed consensus process effectively improves the group consensus level. The number of iterations required to achieve full individual confidence is obviously less than that required for a complete consensus, as the latter requires time and effort within the group (Fig. 5). Therefore, we can set acceptable consensus and self-confidence levels to facilitate decision-making in accordance with actual situations, thus exploring the range of suitable alternatives in a specific scenario (Fig. 3).

5 Conclusions

In decision-making problems, preferences are generally expressed in words. We used multiple self-confidence levels to measure the reliability of preference information. In addition, due to the subjectivity associated with the understanding of words, we employed PIS management to reflect personalized semantics.

The results show that more DMs participate in decision-making, and more iterations are required to reach an acceptable consensus level. At the same time, a higher predefined acceptable consensus level necessitates more consensus rounds for CRP. The average self-confidence level of each DM varies similarly to the group consensus level. For a certain number of DMs, the number of consensus iterations increases with the number of alternatives; however, the rate of growth in the curve gradually decreases. A quantitative analysis was performed to verify our model’s advantages.

In future studies, we can incorporate DMs into a social network to explore the influence of group interaction on decision-making and consensus processes [40,41,42]. Focusing on the application of the GDM theory to practical decision-making problems is essential [43,44,45,46,47]. Therefore, we may also consider the GDM model using a data-driven method to achieve a more accurate degree of simulation.