Abstract
Decision-makers’ subjective preferences can be well modeled using preference aggregation operators and related induced weights allocation mechanisms. However, when several different types of preferences occur in some decision environment with more complex uncertainties, repeated uses of preferences induced weights allocation sometimes become unsuitable or less reasonable. In this work, we discuss a common decision environment where several invited experts will offer their respective evaluation values for a certain object. There are three types of preferences which will significantly affect the weights allocations from experts. Instead of unsuitably performing preference induced weights allocation three times independently and then merging the results together using convex combination as some literatures recently did, in this work, we propose some organic and comprehensive rules-based screen method to first rule out some unqualified experts and then take preference induced weights allocation for the refined group of experts. A numerical example in business management and decision-making is presented to show the cognitive reasonability and practical feasibility.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Information fusion theories and methods [1,2,3,4,5,6] are powerful tools in numerous applications including management decision-making and evaluations [7,8,9, 24,25,26,27,28,29,30,31]. For a collection of n input values, which are often expressed by a vector, a commonly used aggregation operator can merge those n inputs into a single output in some strict and standard manners. Recall that a real-valued aggregation operator \(A:[0, 1]^{n} \to [0, 1]\) is a mapping satisfying two conditions: (i) \(A(0,...,0) = 0\) and \(A(1,...,1) = 1\); (ii) for any \({\varvec{x}},{\varvec{y}} \in [0,1]^{n}[0,1]\)\(^{n}\) with \({\varvec{x}} < {\varvec{y}}\), \(A({\varvec{x}}) \le A({\varvec{y}})\).
In group decision-making environment, data fusion is one particular effective and important way to diminish inconsistency among many involved evaluators or experts. To suitably apply desirable data aggregation, usually some weights should be determined and allocated to all the involved experts. When a group of experts are invited for giving their individual evaluation values for some certain object, often there may involve two types of information. The first type is their offered evaluation values, while the second type is concerned with the personal general abilities, such as reliability, fame, experience and credibility of those experts themselves. With the extents of such two types of information known, Yager’s preferences aggregation theory and related weights allocation methods [10,11,12] can be convenient to use to determine weights for those experts in a group.
However, when these two types of information, namely the evaluation values for some certain object and the reliability or credibility of experts who give those evaluation values, are with uncertainties, the direct preferences induced weights allocation [12] will become much more complex or even not feasible. In this setting, actually the two types of information with uncertainties can be expressed exactly with two basic uncertain information (BUI) [13, 14] forms. In structure, the first type of uncertainty may be also offered by the experts themselves and attached to the corresponding evaluation values they give; the second type of uncertainty is concerned with the reliability or credibility of experts and may be provided by other decision-makers who invite those experts.
BUI is a recently introduced uncertain conceptual paradigm to express and deal with different types of uncertain information. Recall that a BUI granule is with a pair form \((x,c)\) in which \(x \in [0,1]\) is a concerned evaluation value and \(c \in [0,1]\) is the certainty degree of x; and \(1 - c \in [0,1]\) is the uncertainty degree of x. Certainty degrees may represent the degrees to which decision-makers are confident, sure, certain or definite of the concerned evaluation values in flexible manners, while uncertainty degrees may show the extents to which they are unconfident, unsure, uncertain or indefinite of the concerned evaluation values. With this definition, \((x,1)\) indicates the full certainty over evaluation value x and it may be regarded as equivalent to the real value x in practice; \((x,0)\) indicates the full uncertainty over evaluation value x, implying every value between [0, 1] can be considered as a true value, and therefore there is no effective or substantial information can be taken out.
For the aforementioned group evaluation problem, we can use twice of BUI to well re-express the involved two pairs of information and associated uncertainties. First, the notational form \(((x_{i} ,c_{i} ))_{i = 1}^{n}\) can be selected to use wherein \((x_{i} )_{i = 1}^{n}\) represents the evaluation values offered by the invited group of experts while \((c_{i} )_{i = 1}^{n}\) represents respectively the certainty of \((x_{i} )_{i = 1}^{n}\) offered still by that group of experts. Second, the notational form \(((y_{i} ,d_{i} ))_{i = 1}^{n}\) can be used in which \((y_{i} )_{i = 1}^{n}\) indicates the reliability or credibility of that group of experts, and \((d_{i} )_{i = 1}^{n}\) is the certainty of the reliability or credibility, both offered by some other decision-makers like managers other from the group of experts.
Note that in such setting, we model the practical situation more realistically with considering two sources of uncertainties, and then we are precisely concerned with four different data units and thus four different types of preference. To perform the weights allocation for the group of experts, usually we should consider three types of preference (out of the four types): one is the reliability (or credibility) preference related to y (i.e., concerning whether we prefer the invited experts who are more reliable or prefer considering more experts in number regardless of their reliability), another is the certainty preference related to d (i.e., concerning the extent to which we prefer those reliability degrees (offered by decision-makers) with high certainty degrees), and still another is the certainty preference related to c (i.e., concerning the extent to which we prefer the evaluation values (offered by experts) with high certainty degrees (also offered by experts)). It should be noticed that the three preferences will play some different roles and will not be handled in absolutely equal terms, which requires us to devise some reasonable and effective weights allocation methods rather than taking the same Yager’s preference involved aggregations three times.
Indeed, some recent literatures discussed several induced weight allocations methods [15,16,17,18], but the main methods proposed in them are either first taking weighted average of inducing variables and then determining weights, or at first determining weights from different inducing variables and then taking weighted average (convex combination) of those generated weight vectors. Actually, the irregular tangle of the two elements in \((y,d)\) sometimes makes it not very reasonable to directly use of Yager’s preference induced weight allocations twice independently for y and d, which may cause some preferences of decision-makers not to be well modeled and embodied in the corresponding weights allocation process. To devise some more reasonable preferences and uncertainties induced weights allocation methods, in this work, we will apply some comprehensive and rules-based methods to address the posed issue of well embodying the three types of preferences. Further, an integrated decision model including information screen, weights allocation, BUI aggregation and decision methods will be proposed. Since there is a paucity of existing comprehensive preferences and uncertainties involved weights allocation and aggregation models, then the proposed decision model in this paper will provide some cognitively reasonable decision methods for practitioners to consider in decision-making environments where more preferences are faced and uncertainties are encountered.
As we have stated that the reliabilities of experts, the certainty degrees of such information, and the certainty degrees they offered for evaluation values play different roles in decision-making, the general way of taking a convex combination of them used in some other literatures might become actually not very reasonable in many circumstances. The advantage of the proposed weights allocation method can reasonably and flexibly take into consideration the preferences over the experts’ reliabilities, the certainty degrees of such reliabilities, and the certainty degrees the experts offer for their provided evaluation values in different ways, and combine these three types of preference in an organic and cognitively reasonable way.
The remainder of this work is organized as follows: Section 2 reviews Yager’s preference involved aggregation and related weights allocation, and proposes and illustrates the reasonability of the comprehensive rules-based preferences induced weights allocation with BUI. Section 3 systematically proposes an integrated decision model with comprehensive decision rules, preferences and uncertainties. In Sect. 4, a numerical case in business management and decision-making is given for illustrating and validating the proposed decision-making and evaluation method. Section 5 concludes and remarks this paper.
2 The Methodology for Comprehensive Rules-Based and Preferences Induced Weights Allocation with BUI
2.1 Yager’s Preference Involved Aggregation and Related Induced Weights Allocation
Ordered weighted averaging (OWA) operators [10] can flexibly and reasonably model optimism–pessimism bi-polar preference, often with subjectivity of decision-makers. Recall that an OWA operator of dimension n with a normalized weight vector \({\varvec{w}} = (w_{i} )_{i = 1}^{n}\) is an aggregation operator \(OWA_{{\mathbf{w}}} :[0,1]^{n} \to [0,1]\) such that
where \(\sigma :\{ 1,...,n\} \to \{ 1,...,n\}\) can be any appropriate permutation satisfying \(x_{\sigma (i)} \ge x_{\sigma (j)}\) whenever \(i < j\). The weight vector w used for OWA operator directly embodies a bi-polar optimism–pessimism preference which can be further quantified by orness/andness which is also introduced by Yager. Recall that the orness and andness of a vector w used in OWA operator is defined by
Yager used the (fuzzy) quantifier function to automatically generate weight vectors of any finite dimension for OWA operators [11]. A (fuzzy) quantifier \(Q:[0,1] \to [0,1]\) is a non-decreasing function with \(Q(0) = 0\) and \(Q(1) = 1\), and thus its integrability is guaranteed. For any \(n \in {\mathbb{N}}\), and any quantifier Q, the weight vector \({\varvec{w}}^{Q}\) can be generated such that
A larger quantifier can generate OWA weight vectors with larger orness degrees, and vice versa. Observe that when a quantifier Q is absolutely continuous, then there is an integrable function \(q:[0,1] \to [0, + \infty ]\) such that \(\int_{0}^{1} {q(t)dt} = 1\) and hence
With some approximate sense, the orness of a quantifier function Q can be defined by \(orness(Q) = \int_{0}^{1} {Q(t)dt}\), though in general this does not precisely equal to \({\text{orness}}({\mathbf{w}}^{Q} )\). In practice, we may choose some quantifier functions Q with \(Q(t) > t\) (\(t \in [0,1]\)) to model optimism preferences and choose some quantifier functions Q with \(Q(t) < t\) (\(t \in [0,1]\)) to model pessimism preferences. For example, \(Q(t) = t^{2}\) with \(orness(Q) = 1/3\) can be suitably used to model some pessimism attitude with moderate extent.
It is worth mentioning that orness/andness can measure not only optimism/pessimism preference but also numerous other types of bi-polar preferences such as time-related preference, which is related to given chronological order, and certainty preference as will be discussed later. In other types of preferences than optimism/pessimism, one should use induced ordered weighted averaging (IOWA) operators [12] to perform the corresponding information aggregation.
2.2 Comprehensive Rules-Based and Preferences Induced Weights Allocation with BUI
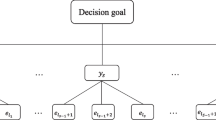
When a group of n experts \(\{ E_{i} \}_{i = 1}^{n}\) is invited, we use a vector of BUI granules \(({\varvec{y}},{\varvec{d}}) = ((y_{i} ,d_{i} ))_{i = 1}^{n}\) to denote the concerned information where \({\varvec{y}} = (y_{i} )_{i = 1}^{n} \in [0,1]^{n}\) is the reliability vector in which \(y_{i}\) represents the reliability (or credibility) degree of expert \(E_{i}\) and \({\varvec{d}} = (d_{i} )_{i = 1}^{n} \in [0,1]^{n}\) is the certainty vector in which \(d_{i}\) indicates the certainty degree to which expert \(E_{i}\) is with reliability \(y_{i}\). In general, we may prefer those BUI granules \((y_{i} ,d_{i} )\) in which both \(y_{i}\) and \(d_{i}\) are large. But this judgment for a “large” BUI pair is delicate and different from a two-dimensional real vector. Clearly, those BUI granules with low certainty degrees \(d_{i}\) will not be preferred since we are uncertain about the real reliabilities of related experts (though they may be really reliable or may not). Furthermore, those unreliable, trustless or inexperienced experts are also not favorable and unaccepted; note that for those experts to be classified under those labels (reliable or not reliable), we should have enough high certainty degrees associated to the reliabilities of them.
Moreover, note that \(((x_{i} ,c_{i} ))_{i = 1}^{n}\) is the vector of BUI granules that is offered by the group of n experts and each of which contains the evaluation value \(x_{i}\) of the certain object under evaluation with certainty degree \(c_{i}\). Since it also involves uncertainty, it is reasonable to have some preferences over the BUI granules (or the experts offer them) with higher certainty degree. In addition, in a similar way, those very uncertain evaluations (i.e., with very low certainty degrees) should not be considered and those evaluations with low (but not very low) certainty degrees should be given less weights.
Recall that rules-based decision-making [19,20,21] is often irreplaceable in a great deal of decision-making and evaluation problems. Given some preset rules, decisions can be automatically taken without further subjective intervention from decision-makers. In our weights allocation problems, given two vectors of BUI granules \(((y_{i} ,d_{i} ))_{i = 1}^{n}\) and \(((x_{i} ,c_{i} ))_{i = 1}^{n}\), we can design some reasonable rules below to screen out some experts who we are not familiar with (i.e., uncertain about), who are obviously inadequate to be invited as evaluators, and who offer evaluation values but with apparently low certainty degrees.
Screen Rule 1: If the certainty degree \(d_{i}\) for the expert \(E_{i}\) is less than a preset “enough low” threshold \(DT_{1} \in [0,1]\), then expert \(E_{i}\) should be ruled out and be regarded as “invalid” candidate for evaluating and offering his/her uncertain evaluation, i.e., a BUI granule \((x_{i} ,c_{i} )\), for a certain object under evaluation.
Screen Rule 2: If the certainty degree \(d_{i}\) for the expert \(E_{i}\) is larger than a preset “enough high” threshold \(DT_{2} \in [0,1]\) (with \(DT_{1} < DT_{2}\)) and the reliability extent \(y_{i}\) is less than a preset “enough low” threshold \(RT \in [0,1]\), then expert \(E_{i}\) should also be ruled out from further evaluating.
Screen Rule 3: If the certainty degree \(c_{i}\) offered from the expert \(E_{i}\) is less than a preset “enough low” threshold \(CT_{1} \in [0,1]\), then expert \(E_{i}\) should be ruled out and be regarded as “invalid” candidate.
Note that we have already considered the preference about certainty degrees of reliabilities, and in this work we cannot simply think that high certainty is better (due to the possibility of associating to a low reliability). Hence, the screen rules have already embodied our desired preference about certainty degrees. After singling out those unqualified experts from the above listed decision rules, the remainder of experts will still differ from each other about their reliabilities with associated certainty degrees. That is, the remaining experts is re-expressed with a refined experts set \(\{ E_{i} \}_{i = 1}^{m}\) where \(m \le n\). We may also set a minimum number \(0 < l \le n\) of experts to invite and if \(m < l\), then we should further invite more (until \(m = l\)) experts who will not be ruled out under the three screen rules. Hence, we also obtain a refined or adjusted BUI vector \(((y_{i} ,d_{i} ))_{i = 1}^{m}\) to enable us to perform our preference over reliabilities, that is, whether we prefer the invited experts who are more reliable (at the cost of reducing the number of experts invited and decreasing representativeness) or prefer considering more experts regardless of their reliability (with benefit of increasing representativeness). But note that it is not sensible for us to prefer those experts with low reliabilities to those with high reliabilities.
Another point to be noticed is that expert is a type of important resource and thus not unlimited. Therefore, when there are not enough experts available to invite (that is, we always have \(m < l\) due to the scarcity of experts), then we should correspondingly decrease \(l\) or increase funds to be enough to invite more experts.
At now, all remaining experts are valid since the certainties for their reliabilities are equal to or larger than the preset “enough low” threshold \(DT_{1} \in [0,1]\). Then, for any BUI granule \((y_{i} ,d_{i} )\), we know \(d_{i} \ge DT_{1}\). Now, if for two BUI granules \((y_{i} ,d_{i} )\) and \((y_{j} ,d_{j} )\), it further has \(d_{i} ,d_{j} \ge DT_{2}\), then we are more certain of the reliability degrees \(y_{i}\) and \(y_{j}\), and thus we can more safely compare the order of \(y_{i}\) and \(y_{j}\) (or expert \(E_{i}\) and expert \(E_{j}\)) and allocate more weight to the expert with high reliability degree; but if \(DT_{1} \le d_{i} ,d_{j} < DT_{2}\), then there is no sufficient evidence to believe that \(y_{i} > y_{j}\) (or \(y_{i} < y_{j}\)) and thus it is more reasonable for us to allocate the same weights to expert \(E_{i}\) and expert \(E_{j}\).
Therefore, for the BUI vector \(((y_{i} ,d_{i} ))_{i = 1}^{m}\), we define two sets: \(A = \{ i \in \{ 1,...,m\} :d_{i} \ge DT_{2} \}\) and \(B = \{ i \in \{ 1,...,m\} :DT_{1} \le d_{i} < DT_{2} \}\). The cardinality of finite set \(X\) is denoted by \(\# X\). In general, the total weights assigned to those BUI granules \(((y_{i} ,d_{i} ))_{i \in A}\) will sum up to \(\# A/(\# A + \# B)\) and the total weights allocated to those BUI granules \(((y_{i} ,d_{i} ))_{i \in B}\) will be \(\# B/(\# A + \# B)\). In detail, we first derive a normalized weight vector \({\varvec{w}}^{A} = (w_{i}^{A} )_{i \in A}\) for the set A using the method of quantifier function and then simply give the weight \(1/m\) to each of expert in the set B. In this case, we may select a convex quantifier function \(Q\) so that \(Q(t) \le t\) because the weight vector generated by such function is necessarily monotonic non-increasing which can well embody our various preferences with different extents over more reliable experts; that is, the weight vector generated by a smaller Q corresponds to a stronger preference over reliable experts and vice versa, and note that if we choose Q with \(Q(t) = t\) then it corresponds to that we prefer to consider as more experts as possible and we are fully regardless of their reliability as discussed previously.
With the selected quantifier function Q, the normalized weight vector \({\varvec{w}}^{A} = (w_{i} )_{i \in A}\) is derived in two steps in a similar way to the three-set method [22] such that
(From [22], it can be known that for \(Q(t) \le t\), we necessarily have \(w_{i}^{A} \le w_{j}^{A}\) whenever \(d_{i} < d_{j}\).)
Finally, a normalized weight vector with dimension m, \({\varvec{w}} = (w_{i} )_{i = 1}^{m}\), is obtained with
One can check that it is normalized by.
\(\sum\nolimits_{i = 1}^{m} {w_{i} } = \sum\limits_{k \in A} {w_{k}^{A} \cdot \frac{\# A}{{\# A + \# B}}} + \frac{1}{m} \cdot \# B = \frac{\# A}{{\# A + \# B}} + \frac{\# B}{{\# A + \# B}} = 1\).
Note that a recent work [23] has also discussed a method with some similar weight allocation mechanism with which those BUI granules whose uncertainty degrees are lower than a threshold will be equally assigned weights. However, that case considered only one threshold (not three) and had not considered other screening rules. With the eventually obtained normalized weight vector \({\varvec{w}} = (w_{i} )_{i = 1}^{m}\) assigned to each individual in the refined experts set \(\{ E_{i} \}_{i = 1}^{m}\), one can aggregate the corresponding vector of BUI granules \(((x_{i} ,c_{i} ))_{i = 1}^{m}\) in which \((x_{i} ,c_{i} )\) is offered by expert \(E_{i}\) to evaluate a certain object.
3 An Integrated Decision Model with Comprehensive Decision Rules, Preferences and Uncertainties
This section provides an integrated decision model which includes a thorough process of evaluation problem description, experts’ invitation and data preparation, weights allocation process, and final evaluation and decision-taking.
Stage 1: Evaluation problem description.
Step 1: Set a decision space \(S = \{ s_{i} \}_{i \in \Lambda }\) (with \(\Lambda\) being an index set) including different choices for deciding.
Step 2: Give an object under evaluation related to that decision problem and the evaluation result will directly affect the final decision choice to that problem.
Stage 2: Experts invitation and data preparation.
Step 1: Invite n experts who are denoted by \(\{ E_{i} \}_{i = 1}^{n}\). For each of them give a BUI granule \((y_{i} ,d_{i} )\) in which \(y_{i}\) is the reliability of expert \(E_{i}\) and \(d_{i}\) is the certainty degree of this reliability \(y_{i}\); that is, they can be also altogether denoted by a BUI vector \(((y_{i} ,d_{i} ))_{i = 1}^{n}\).
Step 2: Require each invited expert to offer a BUI granule \((x_{i} ,c_{i} )\) as uncertain evaluation value for the object in which \(x_{i}\) is the evaluation value while \(c_{i}\) is the certainty degree, both offered by expert \(E_{i}\); that is, they can be also altogether denoted by a BUI vector \(((x_{i} ,c_{i} ))_{i = 1}^{n}\).
Step 3: Preset an “enough low” threshold \(DT_{1} \in [0,1]\) and an “enough high” threshold \(DT_{2} \in [0,1]\) (with \(DT_{1} < DT_{2}\)) for certainty degrees \(d_{i}\); preset an “enough low” threshold \(RT \in [0,1]\) for reliability extents \(y_{i}\); preset an “enough low” threshold \(CT_{1} \in [0,1]\) for certainty degree \(c_{i}\).
Step 4: Use Screen Rules 1–3 as proposed in the preceding section to obtain a refined experts set \(\{ E_{i} \}_{i = 1}^{m}\) with \(m \le n\). Set a minimum number \(0 < l \le n\) of experts to invite. If \(m < l\), then further invite more (until \(m = l\)) experts who will not be ruled out under the three screen rules. Obtain the refined or adjusted m experts \(\{ E_{i} \}_{i = 1}^{m}\) with the BUI vector \(((y_{i} ,d_{i} ))_{i = 1}^{m}\) and the BUI vector \(((x_{i} ,c_{i} ))_{i = 1}^{m}\).
Stage 3: Weights allocation process.
Step 1: For the refined or adjusted BUI vector \(((y_{i} ,d_{i} ))_{i = 1}^{m}\), define two sets: \(A = \{ i \in \{ 1,...,m\} :d_{i} \ge DT_{2} \}\) and \(B = \{ i \in \{ 1,...,m\} :DT_{1} \le d_{i} < DT_{2} \}\).
Step 2: Preset a convex quantifier function \(Q\) with \(Q(t) \le t\). Smaller quantifier corresponds to the preference over more reliable experts with sacrificing representativeness while larger quantifier corresponds to the preference of considering more experts regardless of their reliability.
Step 3: Obtain the intermediate normalized weight vector \({\varvec{w}}^{A} = (w_{i} )_{i \in A}\) by (5).
Step 4: Obtain the final normalized weight vector with dimension m, \({\varvec{w}} = (w_{i} )_{i = 1}^{m}\) by (6).
Stage 4: Final evaluation and decision-taking.
Step 1: With the obtained weight vector \({\varvec{w}} = (w_{i} )_{i = 1}^{m}\) for the refined m experts and a BUI vector \(((x_{i} ,c_{i} ))_{i = 1}^{m}\) offered by them, take the weighted average of this BUI vector [13] to yield the output of a final BUI granule \((x,c)\) such that \((x,c) = (\sum\nolimits_{i = 1}^{m} {w_{i} x_{i} } ,\sum\nolimits_{i = 1}^{m} {w_{i} c_{i} } )\).
Step 2: Set some decision rules corresponding to the decision space \(S = \{ s_{i} \}_{i \in \Lambda }\); check which rule \((x,c)\) can satisfy and make the final decision accordingly from the decision space \(S = \{ s_{i} \}_{i \in \Lambda }\).
4 A Numerical Case in Business Management and Decision-Making
Suppose a company needs to decide to which scale it will manufacture a new product according to the opinions of invited several experts.
In Stage 1 (Evaluation problem description), decision-makers in that company set a decision space \(S = \{ s_{i} \}_{i = 1}^{4}\) = {1 large scale, 2 medium scale, 3 small scale, 4 no production}. The object under evaluation is the “market prospect” of the new product which is a subjective evaluation and a relatively abstract concept that is then more suitable to be measured by fuzzy information.
In Stage 2 (Experts invitation and data preparation), suppose we originally invite a panel of five experts (i.e., \(n = 5\)) \(\{ E_{i} \}_{i = 1}^{5}\) and decision-makers in that company judge that they are with different reliability degrees and the judgment for the reliability degrees are with different uncertainties. In summary, they can be concisely expressed by a BUI vector \(((y_{i} ,d_{i} ))_{i = 1}^{5} = ((0.8,0.3),(0.2,0.8),(0.5,0.6),(0.7,0.9),(1,0.9))\) in which higher value of \(y_{i}\) represents expert \(E_{i}\) is more reliable (or with more experience/higher ability) and higher \(d_{i}\) indicates the fact that “\(E_{i}\) is with reliability \(y_{i}\)” is more certain. Suppose the five originally invited experts altogether offer a BUI vector \(((x_{i} ,c_{i} ))_{i = 1}^{5} = ((0.7,0.5),(0.8,0.9),(0.3,0.3),(0.8,0.1),(0.6,0.7))\) in which \(x_{i}\) is the evaluation value for the object under evaluation and \(c_{i}\) is its certainty, both given by expert \(E_{i}\).
Next, for certainty degrees of reliabilities of experts \(d_{i}\), suppose decision-makers preset an “enough low” threshold \(DT_{1} = 0.3\) and an “enough high” threshold \(DT_{2} = 0.7\), preset an “enough low” threshold \(RT = 0.3\) for reliabilities of experts \(y_{i}\), and preset an “enough low” threshold \(CT_{1} = 0.3\) for certainty degree \(c_{i}\) offered by experts for their given evaluation values for the object under evaluation.
Subsequently, using Screen Rules 1–3 as proposed in Sect. 2 to refine the original experts set \(\{ E_{i} \}_{i = 1}^{5}\). Set a minimum number \(0 < l = 4 \le 5 = n\) of experts to invite. By simple observation, we find that for the expert \(E_{2}\), the associated BUI granule \((y_{2} ,d_{2} ) = (0.2,0.8)\) makes him/her to be excluded due to Screen Rule 2 (\(y_{2} = 0.2 < 0.3 = RT\) and \(d_{2} = 0.8 > 0.7 = DT_{2}\)); we also find that for the expert \(E_{4}\), the BUI granule \((x_{4} ,c_{4} ) = (0.8,0.1)\) offered by him/her renders him/her to be ruled out via Screen Rule 3 (\(c_{4} = 0.1 < 0.3 = CT_{1}\)). Since the number of remaining experts is \(m = 3 < 4 = l\), then we should invite one more expert who will not be ruled out by Screen Rules 1–3. For example, suppose we have successfully invited such a qualified expert and the new refined panel of experts is denoted by \(\{ E_{i} \}_{i = 1}^{4}\) (i.e., \(m = 4\)) with the refined BUI vector \(((y_{i} ,d_{i} ))_{i = 1}^{4} = ((0.8,0.3),(0.5,0.6),(1,0.9),(0.6,0.7))\) and the refined BUI vector \(((x_{i} ,c_{i} ))_{i = 1}^{4} = ((0.7,0.5),(0.3,0.3),(0.6,0.7),(0.4,0.7))\).
In Stage 3 (Weights allocation process), according to \(((y_{i} ,d_{i} ))_{i = 1}^{4} = ((0.8,0.3),(0.5,0.6),(1,0.9),(0.6,0.7))\), we first define two sets: \(A = \{ i \in \{ 1,...,4\} :d_{i} \ge DT_{2} = 0.7\} = \{ 3,4\}\) and \(B = \{ i \in \{ 1,...,4\} :DT_{1} = 0.3 \le d_{i} < 0.7 = DT_{2} \} = \{ 1,2\}\). Next, suppose the convex quantifier function \(Q\) satisfies \(Q(t) = t^{2}\), representing a moderate preference over more reliable experts. Then, by (5) we obtain \({\varvec{w}}^{A} = (w_{3} ,w_{4} ) = (0.75,0.25)\) and by (6) we further have \({\varvec{w}} = (w_{i} )_{i = 1}^{4} = (0.25,0.25,0.375,0.125)\).
In Stage 4 (Final evaluation and decision-taking), with the obtained weight vector \({\varvec{w}} = (w_{i} )_{i = 1}^{4} = (0.25,0.25,0.375,0.125)\) and the BUI vector \(((x_{i} ,c_{i} ))_{i = 1}^{4} = ((0.7,0.5),(0.3,0.3),(0.6,0.7),(0.4,0.7))\), take the weighted average of this BUI vector to yield the output of a final BUI granule \((x,c)\) such that \((x,c) = (\sum\nolimits_{i = 1}^{4} {w_{i} x_{i} } ,\sum\nolimits_{i = 1}^{4} {w_{i} c_{i} } ) = (0.525,0.55)\).
Finally, with rules-based decision-making method, decision-makers can set some decision rules corresponding to the decision space \(S = \{ s_{i} \}_{i = 1}^{4}\) = {1 large scale, 2 medium scale, 3 small scale, 4 no production}; for example, we may set some disjoint and exhaustive decision rules:
(a) if both the evaluation value x and the certainty degree c are very high (say, 0.8), then the company will manufacture the new product with “1 large scale”;
(b) if the evaluation value x is very high and the certainty degree c is relatively high (say, 0.5), or the evaluation value x is relatively high and the certainty degree c is very high, then the decision “2 large scale” will be chosen;
(c) if the evaluation value x is very low (say, 0.2) and the certainty degree c is very high, then the company will not produce any of such product and thus the decision “4 no production” will be chosen;
(d) else, the decision “3 small scale” will be chosen from the decision space.
Accordingly, we may devise a relevant decision function \(H:{\mathcal{B}} \to S\) (where \({\mathcal{B}}\) is the set of all BUI granules) such that.
\(H(x,c) = 1\) only if \((x,c) \in [0.8,1]^{2}\);
\(H(x,c) = 2\) only if \((x,c) \in [0.8,1] \times [0.5,1] \cup [0.5,1] \times [0.8,1]\);
\(H(x,c) = 4\) only if \((x,c) \in [0,0.2] \times [0.8,1]\);
\(H(x,c) = 3\) if \((x,c) \notin H^{ - 1} (\{ 1,2,4\} )\).
Since we have \((x,c) = (0.525,0.55)\), then clearly \(H(0.525,0.55) = 3\) and therefore the decision “manufacturing the new product with small scale” is suggested to managers.
5 Conclusions
A common uncertain decision environment is discussed where a panel of experts are invited and each of them required to offer his/her individual evaluation value for a certain object under evaluation. This environment involves three different types of inducing information. This first one is related to the certainty degree for his/her offered evaluation value which is also offered by him/her. The second one is about the reliability degree for each of the invited experts which is provided by decision-makers. The third one is concerned with the certainty degree for each provided reliability degree which is also provided by decision-makers.
Since the repeated uses of induced weights allocation with the three different preferences are sometimes not reasonable in human cognition, we proposed some comprehensive rules-based and preferences induced weights allocation method to be considered. In this integrated method, we first screen out some unqualified experts according to the three well designed screen rules. It is reasonable to rule out those experts who offer evaluation values but with low certainty degrees for the values. It is also sensible that if decision-makers feel quite sure that some experts are with very low reliability degrees, then those experts should be ruled out, and if decision-makers themselves cannot be sure of the experts’ reliability degrees, then those experts should also be screened out.
When a refined group of experts is decided, we then divide them into two subgroups. If the certainty degrees for the reliability degrees of experts are lower than a preset threshold, then those experts are assigned equal weights. If the certainty degrees for the reliability degrees of experts are higher than that preset threshold, then we use preference induced weights allocation method to allocate weights to them with more weights allocated to those with high reliabilities. With the weights for experts obtained and all individual evaluation values aggregated, some decision rules are explicitly made to judge which decision should be chosen from a given decision space. A numerical example in business management and decision-making is presented to show the decision method has potential in more complex preferences and uncertain environments.
The proposed method has some limitations. For example, the involved thresholds sometimes are not easy to determine, or they might not be given by real numbers but by uncertain information. In future works, we may investigate how to effectively decide such thresholds and study the decisional situations where the thresholds are given by different uncertain information instead of real numbers.
Abbreviations
- BUI:
-
Basic Uncertain Information
- OWA:
-
Ordered Weighted Averaging
- IOWA:
-
Induced Ordered Weighted Averaging
References
Grabisch, M., Marichal, J.L., Mesiar, R., Pap, E.: Aggregation Functions. Cambridge University Press, Cambridge (2009)
Boczek, M., Hovana, A., Hutník, O., Kaluszka, M.: New monotone measure-based integrals inspired by scientific impact problem. Eur. J. Oper. Res. 290, 346–357 (2021)
Boczek, M., Jin, L., Kaluszka, M.: Interval-valued seminormed fuzzy operators based on admissible orders. Inf. Sci. 574, 96–110 (2021)
Jin, L.: Some consistency properties and individual preference monotonicity for weighted aggregation operators. IEEE Trans. Fuzzy Syst. 30(6), 2113–2117 (2022)
Chen, Z.-S., et al.: K-means clustering for the aggregation of HFLTS possibility distributions: N-two-stage algorithmic paradigm. Knowl. Based. Syst 227, 107230 (2021)
Jin, L., Kolesarova, A., Mesiar, R.: Semicopula based integrals. Fuzzy. Sets. Syst. 412, 106–119 (2021)
Chen, Z.-S., et al.: Expertise-structure and risk-appetite-integrated two-tiered collective opinion generation framework for large scale group decision making. IEEE. Trans. Fuzzy Syst. (2022). https://doi.org/10.1109/TFUZZ.2022.3179594
Chen, Z.-S., et al.: Sustainable building material selection: An integrated multi-criteria large group decision making framework. Appl. Soft. Computing. 113, 107903 (2021)
Chen, Z.-S., Zhang, X., Rodríguez, R.M., Pedrycz, W., Martínez, L.: Expertise-based bid evaluation for construction-contractor selection with generalized comparative linguistic ELECTRE III. Autom. Constr. 125, 103578 (2021)
Yager, R.R.: On ordered weighted averaging aggregation operators in multicriteria decision making. IEEE Trans. Syst. Man Cybern. 18(1), 183–190 (1988)
Yager, R.R.: Quantifier guided aggregation using OWA operators. Int. J. Intell. Syst. 11, 49–73 (1996)
Yager, R.R.: Induced aggregation operators. Fuzzy Sets Syst. 137, 59–69 (2003)
Jin, L., Kalina, M., Mesiar, R., Borkotokey, S.: Certainty Aggregation and the certainty fuzzy measures. Int. J. Intell. Syst. 33(4), 759–770 (2018)
Mesiar, R., Borkotokey, S., Jin, L., Kalina, M.: Aggregation under uncertainty. IEEE Trans. Fuzzy Syst. 26(4), 2475–2478 (2018)
Zhu, C., Zhang, E., Wang, Z., Yager, R.R., Chen, Z., Jin, L., Chen, Z.-S.: An uncertain and preference evaluation model with basic uncertain information in educational management. Int. J. Computational. Intell. Syst 14(1), 168–173 (2021)
Jin, X., Yager, R.R., Mesiar, R., Borkotokey, S., Jin, L.: Comprehensive interval induced weights allocation with bi-polar preference in multi-criteria evaluation. Mathematics 9(16), 2002 (2021)
Jin, L., Mesiar, R., Yager, R.R., Kaya, S.K.: Interval basic uncertain information and related aggregations in decision making. Journal of Intelligent & Fuzzy Systems (2022). https://doi.org/10.3233/JIFS-211635
Xu, Y.-Q., Jin, L., Chen, Z.-S., Yager, R.R., Spirková, J., Kalina, M., Borkotokey, S.: Weight vector generation in multi-criteria decision making with basic uncertain information. Mathematics 10(4), 572 (2022)
Zadeh, L.A.: Outline of a new approach to analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 1, 28–44 (1973)
Takagi, T., M.: Sugeno, Fuzzy identification of systems and its application to modeling and control, IEEE Trans. on Syst. Man. Cybernetics 15, 116–132 (1985)
Pedrycz, W.: Fuzzy relational equations with generalized connectives and their applications. Fuzzy Sets Syst. 10(1–3), 185–201 (1983)
Jin, L., Mesiar, R., Yager, R.R.: Ordered weighted averaging aggregation on convex poset. IEEE Trans. Fuzzy Syst. 27(3), 612–617 (2019)
X. Jin, L. Jin, Z-S. Chen, R. Mesiar, R. R. Yager, Induced aggregation operators for interval basic uncertain information, (submitted to Journal of Intelligent & Fuzzy Systems with minor revision).
Labella, Á., et al.: A cost consensus metric for consensus reaching processes based on a comprehensive minimum cost model. Eur. J. Oper. Res. 281, 316–331 (2020)
García-Zamora, D., et al.: Large-scale group decision making: a systematic review and a critical analysis. EEE/CAA. J. Automatica Sinica 9, 949–966 (2022)
Rodríguez, R.M., et al.: A cohesion-driven consensus reaching process for large scale group decision making under a hesitant fuzzy linguistic term sets. Environ. Comput. Industrial Eng 155, 107158 (2021)
Lu, Y., Li, N., Lin, H., et al.: A Multiple and Multidimensional linguistic truth-valued reasoning method and its application in multimedia teaching evaluation. Int. J. Comput. Intell. Syst 15, 34 (2022)
Li, D., Zou, Q., Zhang, K.: Multi-experts Joint Decision with Adaptive Model Updater for Robust Visual Tracking. Int J Comput. Intell. Syst 14, 183 (2021)
Močkoř, J.: Fuzzy transforms for hesitant, soft or intuitionistic fuzzy sets. Int. J. Comput. Intell. Syst 14, 164 (2021)
Fedia, R.D., Hela, F.M.: The intuitionistic fuzzy flowsort method for multicriteria group decision making. Int. J. Fuzzy. Syst. Appl. (IJFSA) 11(1), 1–21 (2022)
Li, S., An, J., Nan, J.: The compromise ratio method with intuitionistic fuzzy distance for FMAGDM. Int. J. Fuzzy. Syst. Appl (IJFSA) 11(1), 1–17 (2022)
Acknowledgements
This paper is supported by Jiangsu Social Science Foundation with grant 18JD009. This paper is supported by grant APVV-18-0052.
Funding
This paper is supported by Jiangsu Social Science Foundation with grant 18JD009. This paper is supported by grant APVV-18–0052.
Author information
Authors and Affiliations
Contributions
GL: Idea proposing; Conceptualization; Writing; Texts checking. RRYager: Texts checking; Revising; Scrutinizing. XXZ: Conceptualization; Writing; Revising; Texts checking. RM: Model building; Revising; Theoretical support; Scrutinizing. HB: Theoretical support; Revising; Scrutinizing. LJ: Conceptualization; Writing; Model building; Revising.
Corresponding authors
Ethics declarations
Conflict of interest
There are no competing interests involved.
Data availability
All data are obtained legally.
Material availability
All materials are obtained legally.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, G., Yager, R.R., Zhang, X. et al. Comprehensive Rules-Based and Preferences Induced Weights Allocation in Group Decision-Making with BUI. Int J Comput Intell Syst 15, 54 (2022). https://doi.org/10.1007/s44196-022-00116-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s44196-022-00116-2