1 Introduction

The rural revitalization strategy is a major decision-making deployment proposed in the report of the 19th National Congress of the Communist Party of China. The strategy of implementing rural revitalization is a major historical task in the decisive fight against poverty, the decisive victory in building a moderately prosperous society in all respects, and the building of a modern socialist country in an all-around way. Regarding the implementation of the rural revitalization strategy, the talent development in rural areas must be carried out firstly, in a purposeful and planned manner. At present, the insufficiency of the rural talents has become the first shortcoming for restricting the development of agriculture and rural areas. The main theme of the younger generation of employment is to work in cities. Without the talents in the villages, it is hard neither the implementation of good policies nor the utilization of good resources. As an important part of rural talents and the main force in the construction of new countryside, the rural practical talents play a vital role in the social and economic development of rural areas, which refer to the rural laborers who have certain knowledge and skills to provide services and make contributions for the development of rural economy, science and technology, education, culture, health, and other undertakings, and play a demonstrative and leading role in the development. It is rather important and necessary to effectively strengthen the construction of the rural practical talent team and vigorously develop the rural practical talent resources, which is the urgent need for implementing the rural revitalization strategy and building a well-off society in an all-around way. A scientific and reasonable evaluation method for rural practical talents can speed up the development and utilization of rural practical talent resources, promote the construction and training of rural practical talents, and fully mobilize the enthusiasm of the vast number of rural practical talents. Therefore, it is the primary issue for the current rural revitalization work to propose a set of scientific and effective evaluation methods for well evaluating the rural practical talents.

Given different national conditions, for research on the talent aspect of rural revitalization, non-Chinese researchers mainly focus on the research of rural and agricultural development, while hardly researching the construction of the rural practical talent team. For example, Hanssen and Mathisen [8] explored the attractiveness of a Norwegian rural higher education institution using importance-performance analysis. Garcia-Casarejos and Saez-Perez [6] studied the effect of higher education student internships on the local sustainability of rural places. Vazzana and Rudi-Polloshka [22] studied the influencing factors of brain drain in American rural areas. Nieto et al. [17] studied the effects of entrepreneurial talent and site type on the business performance of rural tourism agencies in Spain. Lucie et al. [16] focused on the implementation of strategic talent management in agricultural and forestry companies, with a specific theoretical and practical orientation to talent management. Arowolo et al. [2] investigated the relevance of human capital expenditure policies in rural Nigeria and found that shortage of funds, low priority of education, and low-interest-rate were the major constraints to human capital expenditure. In contrast, Chinese researchers have been working on the evaluation of rural talent for a long time. Lu et al. [15] investigated and analyzed the current situation and the existing problems of rural practical talents in Xi’an. The results showed that the strengthening work needed to be conducted on the team structure, and the training methods and outcomes. They believed that it was imperative to have an adequate scientific talent evaluation mechanism. Based on the statistical research on the talent structure, cultural level, and categories of the rural practical talents in the Yubei District, Ren [19] believed that it was a key part of encouraging all kinds of qualified rural practical talents to actively apply for job title evaluation for establishing and improving the evaluation system of rural practical talents. Zhan et al. [30] adopted literature research methods based on fuzzy comprehensive evaluation method, systematic analysis method, and a combination of questionnaires and interviews to study the countermeasures on how to improve the innovation level of rural e-commerce application talents.

When evaluating the rural practical talents, the first problem needing to be solved is the construction of the index system and the determination of its weight. However, through literature review, it is found that few scholars have conducted specific studies on the evaluation index system of rural practical talents, and researchers mostly extract and study the indicators from the perspective of macro evaluation of rural or general talents. For example, Wang et al. [23] proposed a set of scientific index systems for evaluating rural science and technology talents, which can be used for understanding the development status and level of rural science and technology talents in various regions. Bohlouli et al. [4] in evaluating the ability of talents, divided its indicators into three primary indicators of professional ability, innovation ability, and social ability, and each primary indicator is specifically divided into four secondary indicators, and each secondary indicator is specifically divided into four tertiary indicators. Although these evaluation index systems are far from the evaluation system of rural practical talents, they can still provide some insight.

A scientific evaluation method for rural practical talents can effectively promote the development of talents, improve the quality of talents, and serve the construction of a new socialist countryside in China. Talent evaluation is a typical group decision-making problem involving multiple experts, in which everyone gathered their wisdom and worked together to multiple evaluated objects. With the progress of decision-making science, various group decision-making methods [9, 10, 13, 14, 20] have been widely proposed, which greatly promotes the effective solution of evaluation problems. In addition, talent evaluation often involves multiple evaluation indicators and can also be regarded as a multi-attribute decision-making (MADM) problem. However, there are few evaluation methods for the rural practical talents in various regions. To the best of our knowledge, Cheng [5] is the unique researcher to consider the AHP method in the research study for obtaining the weight of each indicator, based on which the final evaluation results can be sorted via the weighted summation of each indicator’s evaluation value. Although this traditional evaluation method can promote the effective development of the evaluation work, However, the existing methods are lack corresponding scientificity, which is easy to distort the information and lead to inaccurate evaluation results. As a practical method in the field of decision science, the fuzzy MADM method has been developed relatively mature. It can be used to evaluate a certain thing for different decision-making situations scientifically and reasonably, by leveraging the fuzzy information [7, 26]. MADM methods have been gradually applied to the evaluation of talents in recent years. For example, Afshari et al. [1] proposed a talent evaluation model based on fuzzy language and fuzzy integrals that can consider the dependencies between evaluation indicators. The model can calculate the fuzzy integral values of the talents, and then evaluate the talents by comparing the final fuzzy integral value of each person. Bogdanovic and Miletic [3] believed that talent evaluation was a MADM problem, which had a significant impact on the future development characteristics and the organization’s performance. They proposed an integrated method to solve the problem of talent evaluation, by combining the optimal solution ranking method and the preference ranking organization method for enrichment evaluation (PROMETHEE). Given that there were both qualitative and quantitative indicators in the talent rating indicator system, Turskis et al. [21] proposed a new fuzzy hybrid MADM method to solve the talent evaluation problem. Wang et al. [23] proposed an evaluation method of rural scientific and technological talents based on the TODIM (an acronym in Portuguese for interactive multi-criteria decision making) method with a hybrid indicator.

Through the review of the above works, we can find that the existing research on the evaluation index system of rural practical talents was mainly conducted from the perspective of macro-policy or theory. The weight of the evaluation index is usually obtained by the subjective method, which is too subjective and difficult to quantify mathematically and is easily affected by the subjective will of experts. In addition, to the best of our knowledge, there is no existing work considering the MADM method in the evaluation of the rural practical talents, especially to deal with some evaluation problems with abnormal evaluation data. The power aggregation operator proposed by Yager [29], as an important tool in fuzzy MADM methods, can be used for reducing the effect of some unreasonable evaluation data on the evaluation results by integrating the indicator values, which leverages the mutual support between expert evaluation information and the flexibly adjusted index weights. The evaluation method based on the power aggregation operator not only has a simple calculation process, but also a more scientific and reasonable evaluation mechanism, which can effectively eliminate the influence of unreasonable evaluation values given by biased experts on the evaluation results. Therefore, the MADM methods based on power aggregation operators have been widely adopted in real-world applications such as investment selection [11], assessment of express service quality [25], supplier evaluation [12, 24], and so on.

Therefore, based on the above motivation, this paper will build an evaluation indicator system and evaluation method for the rural practical talents based on hybrid indicator information. The evaluation of rural practical talents usually requires not only some objective data for quantitative evaluation, but also some qualitative subjective evaluation, so it presents hybrid diversity. Given the diversity of rural practical talents’ evaluation indicators, different indicator values need to be represented in different data forms, such as real numbers, interval numbers, linguistic variables, etc. Thus, this paper will use fuzzy information tools to conduct qualitative and quantitative research on the evaluation indicators of the rural practical talents, where we set the indicator weights via the variation coefficient method for ensuring a more objective and reasonable weight assignment strategy. In this way, we can make up for the shortcomings of subjective weight assignment introduced by the analytic hierarchy method. Then, we will conduct a comprehensive evaluation of the rural practical talents in multiple regions via the hybrid-indicator-based variation coefficient method based on the power aggregation operator. Through the analysis of the evaluation results, we aim to find out the existing problems in the process of developing, training and introducing the rural practical talents in various regions of China. Based on the research conclusions and the actual quality of the rural practical talents in various regions, we propose some relevant policy recommendations to promote the construction and development of the rural practical talents in China.

The rest of this paper is laid out as follows. In Sect. 2, we construct the evaluation index system of rural practical talents. In Sect. 3, we propose a rural practical talent evaluation method. In Sect. 4, we verify the applicability of the method through a practical case. Section 5 gives the conclusion and relevant suggestions.

2 Construction of the Evaluation Indicator System for Rural Practical Talents

In June 2018, the Party Central Committee of China issued the “Strategic Plan for Rural Revitalization (2018–2022)”, which clarified the overall requirements, basic principles, development goals, and specific content of rural revitalization. In addition, the General Office of the Central Committee of the Communist Party of China and the General Office of the State Council together issued the “Opinions on Accelerating the Promotion of Rural Talent Revitalization”, which specifically pointed out the need to accelerate the training of agricultural production and management talents and establish a sound classification and evaluation system for the rural talents. As the main force of agricultural production and rural economic development, the rural practical talents can play an important role in the development of rural areas. Therefore, it is necessary to scientifically construct the rural practical talent evaluation indicator system, for implementing the overall task of the rural revitalization strategy in China, strengthening the construction of the rural practical talent team, and improving the overall quality of rural human resources. Although the rural areas in China are quite different and different regions have different priorities and needs, a universal indicator system framework can help to differentially evaluate the rural practical talents in different regions.

A scientific and reasonable indicator system is the prerequisite and basis for effectively evaluating the rural practical talents in China. Regarding the construction of the indicator system, we must first focus on the basic characteristics of rural practical talents: they usually have certain knowledge and skills; they can be a demonstration and the lead role for rural laborers; they can promote the development of the local rural economy and society; they have the recognition of the masses, and; they have a certain degree of creativity. Then, we can construct an evaluation indicator system, by following the evaluation principles of systematicness, scientificity, feasibility, diversity, and practicality, and systematically combining the characteristics of the extensiveness, complexity, particularity, and locality of the rural practical talents.

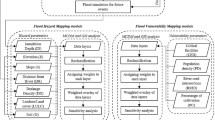
There are five types of the rural practical talents as pointed out by the “Measures for the Evaluation and Management of Rural Practical Talents in Fujian Province (for Trial Implementation)”, which are the production type, management type, skill service type, skill-driven type, and social service type, respectively. The talents in the agriculture-related industries are mainly classified into four categories: production experts, management experts, skilled craftsmen, and farmer technicians. The “Opinions on Accelerating the Rejuvenation of Rural Talents” emphasizes the need to strengthen rural vocational education and skills training, and puts forward a series of safeguards for the development of talents, including funds, systems, and the environment. Based on policy interpretation and existing literature research results, in this paper, we conducted field research by distributing questionnaires and integrating the opinions of experts in multiple regions and analyzed the quality commonality of the rural practical talents. Based on the characteristics and characteristics of the talents, we built an evaluation indicator system with three elements: basic condition, organizational guarantee, and performance. The basic condition element, based on the basic requirements and classification standards of the rural practical talents, includes four indicators, the number of talents, the number of agricultural enterprises and professional cooperative organizations, the status of skill training and research, and the education level and the skill level. For the organizational guarantee element, based on the policy guarantees of promoting the discovery of rural practical talents pointed out in various documents, the evaluation indicators can be classified into four categories: the amount of special funds, system construction and implementation, entrepreneurial environment, and the information degree of service platforms, and the implementation status of development planning. For the performance element, based on the evaluation standards and development performance of rural practical talents in various regions, the evaluation indicators are set into three categories: the total retail sales of the agricultural products in the region, the total fiscal revenue in the region, and the status of entrepreneurship and business development. For the evaluation indicators under each element, we set their values by considering both the subjective and objective, where we evaluate the subjective indicators by inviting the persons in charge of relevant departments and experts, and we evaluate the objective indicators by referring to the “China Rural Statistical Yearbook” and “China County Statistics Yearbook (Township Volume)”. The system framework is shown in Table 1.

Table 1 A comprehensive evaluation indicator system of the rural practical talents in a region
Full size table

3 The Evaluation Approach of Rural Practical Talents

3.1 The Normalization of Hybrid Indicators

In decision-making evaluation, evaluation indicators are usually categorized into two types, subjective and objective, where different types of indicators have different metrics. Even under the same type, the forms of indicator measurement are quite different. Taking objective indicators as an example, the “units” is adopted in measuring the number of talents and the number of agricultural enterprises and professional cooperative organizations, while the “100 million yuan” is preferred in measuring the total retail sales of agricultural products and the total fiscal revenue of the region. In other words, different indicators may adopt different measurement units, different dimensions, and different orders of magnitude. However, it is impossible to integrate calculations between the indicator of different metric standards, in the evaluation and ranking process of various schemes using raw index data. Therefore, we need to first normalize the original indicator data to eliminate the influence of indicator metrics, and then evaluate and rank the plans. Assume that there are evaluation schemes and evaluation indicators.

Now we assume that there are \(m\) evaluation schemes and \(n\) evaluation indicators, which \(\alpha_{ij}\) indicates the value of the \(j\)-th indicator of the \(i\)-th scheme. Then the initial evaluation matrix can be expressed as:

$$\delta {\kern 1pt} {\kern 1pt} = \left( \begin{gathered} \alpha_{11 \, } \, \alpha_{12 \, } \, \cdots \, \alpha_{1n} \hfill \\ \alpha_{21 \, } \, \alpha_{22 \, } \, \cdots \, \alpha_{2n} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \, \vdots \, \vdots \, \vdots \hfill \\ \alpha_{m1 \, } \, \alpha_{m2} \, \cdots \, \alpha_{mn} \hfill \\ \end{gathered} \right),$$

where the evaluation value \(\alpha_{ij}\) is either a real value, interval value, or a language variable.

Regarding the evaluation issue of hybrid indicators, we will then discuss the normalization methods for the benefit-type indicators and cost-type indicators, respectively. The normalized matrix is denoted as \(\vartheta = \left( {\beta_{ij} } \right)_{m \times n}\).

  1. (1)

    The normalization of real numbers [23]:

$${\text{Benefit - type indicators: }}\beta_{ij} = \frac{{\alpha_{ij} }}{{\sqrt {\sum\nolimits_{i = 1}^{m} {\alpha_{ij}^{2} } } }};\quad {\text{cost - type indicators:}}\beta_{ij} = \frac{{{1 \mathord{\left/ {\vphantom {1 {\alpha_{ij} }}} \right. \kern-\nulldelimiterspace} {\alpha_{ij} }}}}{{\sqrt {\sum\nolimits_{i = 1}^{m} {\left( {{1 \mathord{\left/ {\vphantom {1 {\alpha_{ij} }}} \right. \kern-\nulldelimiterspace} {\alpha_{ij} }}} \right)}^{2} } }}.$$
  1. (2)

    The normalization of interval number [23]:

    $${\text{Benefit - type indicators: }}\left\{ \begin{gathered} \beta_{ij}^{L} = \alpha_{ij}^{L} /\sqrt {\sum\limits_{i = 1}^{m} {(\alpha_{ij}^{L} )^{2} + (\alpha_{ij}^{U} )^{2} } } \hfill \\ \beta_{ij}^{U} = \alpha_{ij}^{U} /\sqrt {\sum\limits_{i = 1}^{m} {(\alpha_{ij}^{L} )^{2} + (\alpha_{ij}^{U} )^{2} } } \hfill \\ \end{gathered} \right.;$$
    $${\text{Cost - type indicators}}:\left\{ \begin{gathered} \beta_{ij}^{L} = \frac{1}{{\alpha_{ij}^{U} }}/\sqrt {\sum\limits_{i = 1}^{m} {\left( {\frac{1}{{\alpha_{ij}^{L} }}} \right)^{2} + \left( {\frac{1}{{\alpha_{ij}^{U} }}} \right)^{2} } } \hfill \\ \beta_{ij}^{U} = \frac{1}{{\alpha_{ij}^{L} }}/\sqrt {\sum\limits_{i = 1}^{m} {\left( {\frac{1}{{\alpha_{ij}^{L} }}} \right)^{2} + \left( {\frac{1}{{\alpha_{ij}^{U} }}} \right)^{2} } } \hfill \\ \end{gathered} \right. .$$
  1. (3)

    The normalization of the uncertain linguistic variable.

Let \(S = \left\{ {\varsigma_{\alpha } \left| {\alpha = 0,1, \cdots } \right.,g} \right\}\) be a set of finite and continuous-discrete language terms, where \(g\) is an even value (set as 4, 6, 8 by default in reality). Given \(g = 6\), the set \(S = \left\{ {\varsigma_{0} ,\varsigma_{1} ,\varsigma_{2} ,\varsigma_{3} ,\varsigma_{4} ,\varsigma_{5} ,\varsigma_{6} } \right\} =\) indicates {very bad, bad, fairly bad, fair, fairly good, good, very good}. For any language \(S\), it should meet the conditions as follows:

  1. (a)

    if \(a \ge b\), then \(\varsigma_{a} \ge \varsigma_{b}\);

  2. (b)

    \(\exists\) \({\text{neg}}\left( {\varsigma_{a} } \right) = \varsigma_{b}\), iff \(b = g - a\).

  3. (c)

    if \(s_{a} \ge s_{b}\), then \({\text{max}}\left( {\varsigma_{a} ,\varsigma_{b} } \right) = \varsigma_{a}\) and \({\text{min}}\left( {s_{a} ,s_{b} } \right) = s_{b}\).

To fully reflect the uncertainty in the information representation, Xu [27] further proposed the concept of uncertain linguistic variables, with the mathematical expression in the form of \(\tilde{\varsigma } = \left[ {\varsigma_{a} ,\varsigma_{b} } \right]\), where \(\varsigma_{a}\) and \(\varsigma_{b}\) are the lower and upper bounds of \(\tilde{\varsigma }\), respectively. However, when uncertain linguistic variables are set as subjective indicators, they cannot be directly calculated with objective indicators in the process of information integration, which requires the relevant conversion rules for normalizing the indicators namely fuzzy language (fuzzy number conversion rules) [27]. Therefore, this paper introduces the function \(y\left( {\varsigma_{\alpha } } \right):\left[ {0,g} \right] \to \left[ {0,1} \right]\) and uses the function \(y\left( {\varsigma_{\alpha } } \right) = \alpha /g\) to convert uncertain linguistic variables into interval numbers.

Thus, the normalization method of the uncertain linguistic variable \(\alpha_{ij} = \left[ {\varsigma_{a} ,\varsigma_{b} } \right]\) is

$${\text{Benefit - type indicators}}:\beta_{ij} = \left[ {\varsigma_{a} ,\varsigma_{b} } \right] = \left[ {y\left( {\varsigma_{a} } \right),y\left( {\varsigma_{b} } \right)} \right];$$
$${\text{Cost - type indicators:}} \, \beta_{ij} = \left[ {\varsigma_{y - b} ,\varsigma_{y - a} } \right] = \left[ {y\left( {\varsigma_{y - b} } \right),y\left( {\varsigma_{y - a} } \right)} \right].$$

In summary, the normalized comprehensive decision matrix is:

$$\vartheta = \left( \begin{gathered} \beta_{11 \, } \, \beta_{12 \, } \, \cdots \, \beta_{1n} \hfill \\ \beta_{21 \, } \, \beta_{22 \, } \, \cdots \, \beta_{2n} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \, \vdots \, \vdots \, \vdots \hfill \\ \beta_{m1 \, } \, \beta_{m2} \, \cdots \, \beta_{mn} \hfill \\ \end{gathered} \right).$$

3.2 The Method of Determining Indicator Weights

In the talent evaluation problem, the weight of indicators is usually obtained in a subjective way, which cannot avoid the subjective randomness of experts. However, obtaining the weight of indicators according to objective evaluation data can effectively solve this problem. When setting the indicator weights for evaluating rural practical talents, this paper will use the variation coefficient method based on objective data to determine the weights of various evaluation indicators for a more scientific and accurate result. The specific procedures are as follows [18]:

  • Step 1. Based on the normalization of the original hybrid indicators, we preprocess the \(\beta_{ij}\) to obtain normalized data. If the data is an interval number, we use \(\overline{\beta }_{ij}\) to represent its normative value, that is, \(\overline{\beta }_{ij} = (\beta_{ij}^{L} + \beta_{ij}^{U} )/2\); if the data are a real number, its normative value is itself, i.e., \(\overline{\beta }_{ij} = \beta_{ij}\).

  • Sep 2. Calculate the mean \(\overline{\beta }\) of the \(j\)-th indicator: \(\overline{\beta } = \frac{1}{m}\sum\limits_{i = 1}^{m} {\overline{\beta }_{ij} } ,\;\;j = 1,2, \cdots ,n\), where \(m\) is the number of evaluated areas, \(n\) is the number of indicators, and \(\overline{\beta }_{ij}\) is the normalized value of the \(j\)-th indicator of the \(i\)-th scheme.

  • Step 3. Calculate the mean square error of the \(j\)-th indicator: \(d_{j} = \sqrt {\frac{1}{m - 1}\sum\nolimits_{i = 1}^{m} {\left( {\overline{\beta }_{ij} - \overline{\beta }} \right)^{2} } }\).

  • Step 4. Calculate the variation coefficient, \(e_{j}\), of the \(j\)-th indicator: \(e_{j} = {{d_{j} } \mathord{\left/ {\vphantom {{d_{j} } {\overline{\beta }}}} \right. \kern-\nulldelimiterspace} {\overline{\beta }}}\).

  • Step 5. Normalize the variation coefficient of each evaluation indicator and obtain the weight of each indicator \(\omega_{j}\): \(\omega_{j} = {{e_{j} } \mathord{\left/ {\vphantom {{e_{j} } {\sum\limits_{j = 1}^{n} {e_{j} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{j = 1}^{n} {e_{j} } }}\).

3.3 The power aggregation operators

In practical evaluation problems, for some qualitative indicators, decision-makers often give some evaluation values too low or too high due to personal bias, which will produce certain operational behavior, and the power aggregation operator can reduce this adverse effect by giving a small weight to the extreme value.

Definition 1

Denote \(\beta_{ij}\) as the normalized value of the \(j\)-th indicator of the \(i\)-th scheme. The power averaging operator (PA) can be defined as [28]:

$${\text{PA}}(\beta_{i1} ,\beta_{i2} , \ldots ,\beta_{in} ) = \sum\limits_{j = 1}^{n} {\frac{{(1 + Q(\beta_{ij} ))\beta_{ij} }}{{\sum\limits_{t = 1}^{n} {(1 + Q(\beta_{it} ))} }}} ,\;\;\;i = 1,2, \ldots ,m,$$
(1)

where \(Q(\beta_{ij} ) = \sum\nolimits_{k = 1,k \ne j}^{n} {Sup(\beta_{ij} ,\beta_{ik} )} ,\;\;Sup(\beta_{ij} ,\beta_{ik} ) = 1 - d(\beta_{ij} ,\beta_{ik} )\), \(d(\beta_{ij} ,\beta_{ik} )\) indicates the distance between \(\beta_{ij}\) and \(\beta_{ik}\), \(Sup\left( {\beta_{ij} ,\beta_{ik} } \right)\) is the support degree between \(\beta_{ij}\) and \(\beta_{ik}\), and the following requirements hold:

  1. 1.

    \({\text{Sup}}\left( {\beta_{ij} ,\beta_{ik} } \right) \in \left[ {0,1} \right]\);

  2. 2.

    \({\text{Sup}}\left( {\beta_{ij} ,\beta_{ik} } \right) = {\text{Sup}}\left( {\beta_{ik} ,\beta_{ij} } \right)\);

  3. 3.

    if \(\;\left| {\beta_{ij} - \beta_{ik} } \right| \le \left| {\beta_{il} - \beta_{ir} } \right|\), then \({\text{Sup}}\left( {\beta_{ij} ,\beta_{ik} } \right) \le {\text{Sup}}\left( {\beta_{il} ,\beta_{ir} } \right)\) holds for \(1 \le j,k,l,r \le n\).

Definition 2

Given the indicator weight \(w_{j}\) obtained via the variation coefficient method and a constraint \(\sum\nolimits_{j = 1}^{n} {w_{j} } = 1\), the form of power weighted averaging (PWA) can be defined as:

$${\text{PWA}}(\beta_{i1} ,\beta_{i2} , \ldots ,\beta_{{{\text{in}}}} ) = \sum\limits_{j = 1}^{n} {\frac{{w_{j} (1 + Q(\beta_{ij} ))\beta_{ij} }}{{\sum\limits_{t = 1}^{n} {w_{j} (1 + Q(\beta_{it} ))} }}} ,\;\;\;i = 1,2, \ldots ,m.$$
(2)

Specifically, based on the normalization method discussed in Sect. 2.1, if \(\alpha_{ij}\) is a real number, we have \(\beta_{ij}\) as a normalized real number (ϵ [0, 1]); if \(\alpha_{ij}\) is an interval number, the normalized \(\beta_{ij}\) is an interval number with [0, 1]; if \(\alpha_{ij}\) is an uncertain linguistic variable, \(\beta_{ij}\) is normalized as an interval number in [0, 1]. When using the PA or PWA operators as the information integration tools, a unified information representation form is required. Therefore, when \(\beta_{ij}\) is a real number within [0, 1], we transfer it to the form of interval numbers. For example, \(\beta_{ij} = 0.5 = \left[ {0.5,0.5} \right]\).

Definition 3

Given two different indicator values \(\beta_{ij}\) and \(\beta_{ik}\), the distance between them is defined as follows:

$$d(\beta_{ij} ,\beta_{ik} ) = \frac{\sqrt 2 }{2}\sqrt {\left( {\beta_{ij}^{L} - \beta_{ik}^{L} } \right)^{2} + \left( {\beta_{ij}^{U} - \beta_{ik}^{U} } \right)^{2} } ,$$
(3)

where \(\beta_{ij}^{L}\) and \(\beta_{ij}^{U}\) are the lower and upper bounds of the interval number \(\beta_{ij}\), respectively, while \(\beta_{ik}^{L}\) and \(\beta_{ik}^{U}\) are the lower and upper bounds of the interval number \(\beta_{ik}\), respectively.

Definition 4. Let \(\alpha = \left[ {\alpha^{L} ,\alpha^{U} } \right]\) be an interval number. The score function of the \(\alpha\) is defined as:

$$S\left( \alpha \right) = \frac{{\alpha^{L} + \alpha^{U} }}{2}.$$
(4)

3.4 The Evaluation Model of Rural Practical Talents Based on Hybrid-indicator Power Aggregation Operator

To objectively and truthfully evaluate the rural practical talents of \(m\) areas \(\left\{ {A_{1} ,A_{2} ,A_{3} , \ldots ,A_{m} } \right\}\) and understand their development levels and differences, we conduct a comprehensive evaluation based on \(n\) evaluation indicators \(\left\{ {\eta_{1} ,\eta_{2} ,\eta_{3} , \ldots ,\eta_{n} } \right\}\). From Table 1, we can see that the evaluation indicator system for rural practical talents has two levels, the element level, and the indicator level. We denote the evaluation decision matrix of each indicator in each area for each element as \(\delta_{d} = \left( {\alpha_{ij}^{d} } \right)_{{m \times n_{d} }}\), where \(d(d = 1,2, \ldots ,l)\) is the number of elements, \(\alpha_{ij}^{d}\) is the evaluation value of the \(j\)-th indicator of the \(d\)-th element in the \(i\)-th area, \(\sum\limits_{d = 1}^{l} {n_{d} } = n\), and \(n_{d}\) indicates the number of indicators of the d-th element. To fully integrate the information in the evaluation matrix, this paper will adopt a hierarchical integration method, which first integrates the indicator values in each element to obtain a comprehensive evaluation value of each element, and then integrates the evaluation value of each element, and finally obtains a comprehensive evaluation value of each area. The specific decision-making steps are as follows:

  • Step 1. Obtain the original evaluation data and establish the initial decision matrix \(\delta_{d} = \left( {\alpha_{ij}^{d} } \right)_{{m \times n_{d} }}\), based on the collection of relevant yearbook data and expert evaluation scores.

  • Step 2. Establish the normalized decision-making matrix \(\vartheta_{d} = \left( {\beta_{ij}^{d} } \right)_{{m \times n_{d} }}\), via the hybrid-indicator normalization method (in Sect. 3.1).

  • Step 3. Determine the weight of each indicator, based on the method of determining indicator weights in Sect. 3.2.

  • Step 4. Calculate the support degrees \(Sup\left( {\beta_{ij}^{d} ,\beta_{ik}^{d} } \right)\) of the indicators \(\beta_{ij}^{d}\) and \(\beta_{ik}^{d}\) in each evaluation element.

  • Step 5. Calculate \(Q\left( {\beta_{ij}^{d} } \right)\).

  • Step 6. Obtain the comprehensive evaluation value of each element \(\beta_{id}\), by integrating the indicator values in each element layer via the PWA operator.

  • Step 7. Obtain the comprehensive evaluation value of each area \(\beta_{i}\), by fusing the comprehensive values of each element layer based on the PA operator.

  • Step 8. Calculate the score function \(S\left( \alpha \right)\) of the comprehensive evaluation values of each area and obtain the ranking results of all areas.

4 A Case Study on the Evaluation of Rural Practical Talents

4.1 Evaluation of the Rural Practical Talents in Four Areas

To measure the development status of rural practical talents in four regions, \(A,B,C,D\), this paper considers three elements, basic condition \(\gamma_{1}\), organizational guarantee \(\gamma_{2}\), and performance \(\gamma_{3}\), and establishes a comprehensive evaluation indicator system for rural practical talents that includes 11 indicators \(\eta_{j} (j = 1,2, \ldots ,11)\), as shown in Table 2. Specifically, we measure the basic condition element of the talents in an area from four indicators: the number of talents, the number of agricultural enterprises and professional cooperative organizations, skills training and research status, and education level and skill level; we evaluate the organizational guarantee item based on four indicators: the amount of special funds, system construction and implementation, entrepreneurial environment and service platform informatization, and development plan implementation; we evaluate the performance element (i.e., economic and social benefits brought by the talents) from three factors: the total retail sales of agricultural products in the region, the total fiscal revenue in the region, and the status of business start-ups. Tables 3, 4 and 5 illustrates the indicator evaluation matrices \(\delta_{d} = \left( {\alpha_{ij}^{d} } \right)_{{m \times n_{d} }}\)\((i = 1,2,3,4;d = 1,2,3;j = 1,2, \ldots ,11)\) of these areas in terms of the elements \(\gamma_{1}\)-\(\gamma_{3}\), respectively.

Table 2 Comprehensive evaluation indicator system of rural scientific practical talents in a region
Full size table
Table 3 Evaluation values of indicators \(\delta_{1} = \left( {\alpha_{ij}^{1} } \right)_{4 \times 3}\) under the element \(\gamma_{1}\)
Full size table
Table 4 Evaluation values of indicators \(\delta_{2} = \left( {\alpha_{ij}^{2} } \right)_{4 \times 4}\) under the element \(\gamma_{2}\)
Full size table
Table 5 Evaluation values of indicators \(\delta_{3} = \left( {\alpha_{ij}^{3} } \right)_{4 \times 3}\) under the element \(\gamma_{3}\)
Full size table

The evaluation steps of rural practical talents based on the integrated method of the hybrid-indicator power operator are shown as follows.

Step 1. Obtain evaluation data and establish an initial decision matrix \(\delta_{d} = \left( {\alpha_{ij}^{d} } \right)_{{m \times n_{d} }}\), through relevant yearbook data collection and expert evaluation scoring (with the linguistic term \(g = 6\)).

Step 3. Establish the normalized decision-making matrix \(\vartheta_{d} = \left( {\beta_{ij}^{d} } \right)_{{m \times n_{d} }}\), based on the hybrid-indicator normalization method. The results are shown in Tables 6, 7 and 8.

Step 3. Determine the indicator weights \(w_{j}\), based on the indicator weight determination method.

$$w_{j} = (0.0693,0.1528,0.0880,0.0279,0.0683,0.0546,0.0941,0.0837,0.0527,0.1725,0.1361).$$

Step 4. Calculate the support degree \(Sup\left( {\beta_{ij}^{d} ,\beta_{ik}^{d} } \right)\) between indicators \(\beta_{ij}^{d}\) and \(\beta_{ik}^{d}\) for each element. The results are shown in Tables 9(a)–9(I).

Step 5. Calculate \(Q\left( {\beta_{ij}^{d} } \right)\) based on the support degree \({\text{Sup}}\left( {\beta_{ij}^{d} ,\beta_{ik}^{d} } \right)\) between \(\beta_{ij}^{d}\) and \(\beta_{ik}^{d}\).

$$\begin{aligned} & Q\left( {\beta_{11}^{1} } \right) = 2.5572,Q\left( {\beta_{12}^{1} } \right) = 2.3026,Q\left( {\beta_{13}^{1} } \right) = 2.4870,Q\left( {\beta_{14}^{1} } \right) = 2.5024, \hfill \\ & Q\left( {\beta_{21}^{1} } \right) = 2.4784,Q\left( {\beta_{22}^{1} } \right) = 2.2308,Q\left( {\beta_{23}^{1} } \right) = 2.5865,Q\left( {\beta_{24}^{1} } \right) = 2.5563, \hfill \\ & Q\left( {\beta_{31}^{1} } \right) = 2.7962,Q\left( {\beta_{32}^{1} } \right) = 2.6917,Q\left( {\beta_{33}^{1} } \right) = 2.6747,Q\left( {\beta_{34}^{1} } \right) = 2.8540, \hfill \\ & Q\left( {\beta_{41}^{1} } \right) = 2.5107,Q\left( {\beta_{42}^{1} } \right) = 2.6871,Q\left( {\beta_{43}^{1} } \right) = 2.6235,Q\left( {\beta_{44}^{1} } \right) = 2.5599, \hfill \\ & Q\left( {\beta_{15}^{2} } \right) = 2.3704,Q\left( {\beta_{16}^{2} } \right) = 2.4449,Q\left( {\beta_{17}^{2} } \right) = 2.5403,Q\left( {\beta_{18}^{2} } \right) = 2.4922, \hfill \\ & Q\left( {\beta_{25}^{2} } \right) = 2.8677,Q\left( {\beta_{26}^{2} } \right) = 2.8128,Q\left( {\beta_{27}^{2} } \right) = 2.8021,Q\left( {\beta_{28}^{2} } \right) = 2.8494, \hfill \\ \end{aligned}$$
$$\begin{gathered} Q\left( {\beta_{35}^{2} } \right) = 2.6347,Q\left( {\beta_{36}^{2} } \right) = 2.6773,Q\left( {\beta_{37}^{2} } \right) = 2.2440,Q\left( {\beta_{38}^{2} } \right) = 2.4910, \hfill \\ Q\left( {\beta_{45}^{2} } \right) = 2.3727,Q\left( {\beta_{46}^{2} } \right) = 2.4732,Q\left( {\beta_{47}^{2} } \right) = 2.4724,Q\left( {\beta_{48}^{2} } \right) = 2.3219, \hfill \\ Q\left( {\beta_{19}^{3} } \right) = 1.3210,Q\left( {\beta_{1,10}^{3} } \right) = 1.5857,Q\left( {\beta_{1,11}^{3} } \right) = 1.4509, \hfill \\ Q\left( {\beta_{29}^{3} } \right) = 1.5942,Q\left( {\beta_{2,10}^{3} } \right) = 1.4579,Q\left( {\beta_{2,11}^{3} } \right) = 1.6681, \hfill \\ Q\left( {\beta_{39}^{3} } \right) = 1.4589,Q\left( {\beta_{3,10}^{3} } \right) = 1.6009,Q\left( {\beta_{3,11}^{3} } \right) = 1.6700, \hfill \\ Q\left( {\beta_{49}^{3} } \right) = 1.8341,Q\left( {\beta_{4,10}^{3} } \right) = 1.7596,Q\left( {\beta_{4,11}^{3} } \right) = 1.7675. \hfill \\ \end{gathered}$$

Step 6. Obtain the comprehensive evaluation value \(\beta_{id}\) of each element, by integrating the indicator values in each element based on the PWA operator.

$$\begin{aligned} & \beta_{11} = \left[ {0.2765,0.3227} \right],\beta_{21} = \left[ {0.5877,0.6427} \right],\beta_{31} = \left[ {0.3896,0.4422} \right],\beta_{41} = \left[ {0.3494,0.3961} \right]; \hfill \\ & \beta_{12} = \left[ {0.4197,0.4774} \right],\beta_{22} = \left[ {0.3377,0.4281} \right],\beta_{32} = \left[ {0.4535,0.4817} \right]\beta_{42} = \left[ {0.3946,0.4476} \right]; \hfill \\ & \beta_{13} = \left[ {0.2655,0.3066} \right],\beta_{23} = \left[ {0.2745,0.3182} \right],\beta_{33} = \left[ {0.5942,0.6371} \right],\beta_{43} = \left[ {0.5554,0.5972} \right]. \hfill \\ \end{aligned}$$

Step 7. Obtain the comprehensive evaluation value \(\beta_{i}\) of each area, based on the integration of the comprehensive evaluation values of each element based on the PA operator.

$$\beta_{1} = \left[ {0.3189,0.3671} \right],\beta_{2} = \left[ {0.3958,0.4593} \right],\beta_{3} = \left[ {0.4776,0.5187} \right],\beta_{3} = \left[ {0.4313,0.4786} \right].$$

Step 8. Calculate the function scores of all areas and obtain the areas’ ranking result.

$$S\left( {\beta_{1} } \right) = 0.3430,\;S\left( {\beta_{2} } \right) = 0.4275,\;S\left( {\beta_{3} } \right) = 0.4982,\;S\left( {\beta_{4} } \right) = 0.4549.$$

Finally, we obtain \(C \succ D \succ B \succ A\), based on which we conclude that Area C has the highest development level of the rural practical talents.

4.2 Evaluation result analysis

From the results in Sect. 4.1, we can see that the comprehensive ranking result of rural practical talents in the four regions \(A, \, B, \, C, \, D\) is \(C \succ D \succ B \succ A\). That is, the area \(C\) has the best quality of talents, followed by areas D and B (with fairly bad talent quality), while area A behaves the worst. To better evaluate the indicator values of each region, we further generate Figs. 1, 2 and 3 based on Tables 6, 7 and 8, respectively, and produce Fig. 4 based on the comprehensive evaluation value \(\beta_{id}\) of all elements. Figure 1 shows the changes of various indicators under the basic condition of each region; Fig. 2 reflects the changes of various indicators under the organizational guarantee element of each region; Fig. 3 illustrates the changes of various indicators under the performance element, and Fig. 4 demonstrates the changes of the comprehensive evaluation values of the three elements in each area (see Table 9).

Fig. 1
figure 1

Changes of the indicators under basic condition element vs. areas

Full size image
Fig. 2
figure 2

Changes of the indicators under organizational guarantee element vs. areas

Full size image
Fig. 3
figure 3

Changes of the indicators under performance element vs. areas

Full size image
Table 6 Evaluation values of indicators \(\vartheta_{1} = \left( {\beta_{ij}^{1} } \right)_{4 \times 3}\) under the element \(\gamma_{1}\)
Full size table
Table 7 Evaluation values of indicators \(\vartheta_{2} = \left( {\beta_{ij}^{2} } \right)_{4 \times 3}\) under the element \(\gamma_{2}\)
Full size table
Table 8 Evaluation values of indicators \(\vartheta_{3} = \left( {\beta_{ij}^{3} } \right)_{4 \times 3}\) under the element \(\gamma_{3}\)
Full size table
Fig. 4
figure 4

Changes of the comprehensive evaluation elements vs. areas

Full size image
Table 9 (a) \({\text{Sup}}\left( {\beta_{1j}^{1} ,\beta_{1k}^{1} } \right)\) of \(A_{1}\) w.r.t. the indicators in \(\gamma_{1}\); (b) \({\text{Sup}}\left( {\beta_{2j}^{1} ,\beta_{2k}^{1} } \right)\) of \(A_{2}\) w.r.t. the indicators in \(\gamma_{1}\); (c) \({\text{Sup}}\left( {\beta_{3j}^{1} ,\beta_{3k}^{1} } \right)\) of \(A_{3}\) w.r.t. the indicators in \(\gamma_{1}\); (d) \({\text{Sup}}\left( {\beta_{4j}^{1} ,\beta_{4k}^{1} } \right)\) of \(A_{4}\) w.r.t. the indicators in \(\gamma_{1}\); (e) \({\text{Sup}}\left( {\beta_{1j}^{2} ,\beta_{1k}^{2} } \right)\) of \(A_{1}\) w.r.t. the indicators in \(\gamma_{2}\); (f) \({\text{Sup}}\left( {\beta_{2j}^{2} ,\beta_{2k}^{2} } \right)\) of \(A_{3}\) w.r.t. the indicators in \(\gamma_{2}\); (g) \({\text{Sup}}\left( {\beta_{3j}^{2} ,\beta_{3k}^{2} } \right)\) of \(A_{2}\) w.r.t. the indicators in \(\gamma_{2}\); (h) \({\text{Sup}}\left( {\beta_{4j}^{2} ,\beta_{4k}^{2} } \right)\) of \(A_{4}\) w.r.t. the indicators in \(\gamma_{2}\); (i) \({\text{Sup}}\left( {\beta_{1j}^{3} ,\beta_{1k}^{3} } \right)\) of \(A_{1}\) w.r.t. the indicators in \(\gamma_{3}\); (j) \({\text{Sup}}\left( {\beta_{2j}^{3} ,\beta_{2k}^{3} } \right)\) of \(A_{3}\) w.r.t. the indicators in \(\gamma_{3}\); (k) \({\text{Sup}}\left( {\beta_{3j}^{3} ,\beta_{3k}^{3} } \right)\) of \(A_{2}\) w.r.t. the indicators in \(\gamma_{3}\); (l) \({\text{Sup}}\left( {\beta_{4j}^{3} ,\beta_{4k}^{3} } \right)\) of \(A_{4}\) w.r.t. the indicators in \(\gamma_{3}\)
Full size table

In the following, based on Figs. 1, 2, 3 and 4, we conduct a detailed analysis of the development level of practical talents in each area and its influence factors.

Analysis 1: From Figs. 1 and 3, area B outperforms the other three areas in terms of the number of talents, the number of agricultural enterprises and professional cooperative organizations, and the index of skills training and research in the region. However, the overall performance of the practical talents in area B is ranked as the second-worst region. The main reasons or factors behind this include inadequate construction and implementation of the regional talent system; bad entrepreneurial environment and service platform informatization; and poor implementation of development plans, which lead to the lowest region’s total fiscal revenue among the four areas. This shows that the main factors that affect the quality of rural practical talents are not the number of talents nor the number of enterprises in the region, but the extent of the region’s emphasis on rural practical talents, the level of special funding support, the construction of the talent team system, the entrepreneurial environment, the degree of informatization, etc. These non-number-related factors are the decisive factor in affecting the fiscal revenue of the region. The value of talents can be brought into full play only when the utilization rate of talents in a region is high. Otherwise, it will only be a waste of talents.

Analysis 2. From Figs. 3 and 4, there are slightly small differences in areas C and D among the three evaluation elements of the basic condition, organizational guarantee, and occupational performance indicator for the regional talents. Moreover, for the performance ranking of the talents in four areas, areas C and D are sorted as the first and second, respectively, which indicates that the quality of talents in these two regions is relatively good. From Fig. 4, we can see that the difference in the talents in areas C and D is mainly reflected in the organizational guarantee. From Figs. 2 and 4, we can see that area C beats area D in terms of the entrepreneurial environment, the degree of informatization, and the agricultural special fund support. As a result, area C obtains the maximum fiscal revenue among the four areas, by increasing investment, emphasizing the importance of both the construction of the talent work system and the construction of the entrepreneurial environment. In contrast, area C behaves the worst among the four areas in the region’s entrepreneurial environment and service platform informatization level but has an impressive performance in system implementation and planning implementation. Area D is ranked first from the perspective of the total retail sales of agricultural products. For area D, it is a traditional product production area with diligent talents and good management, which drives the total production of the entire region to a high level. However, area C does not put much attention to the development of science and technology and blindly sticks to conventional rules in technology. We believe that the development of area C will reach a new height if deserved attention is paid to the technology research and development.

Analysis 3. From Figs. 3 and 4, area A is ranked as the worst area in terms of the basic condition and professional performance of the regional talents. Based on the basic condition analysis in Fig. 1, area A has the least number of talents and the least number of enterprises, which indicates that the relevant departments in this region do not pay much attention to the introduction and training of rural practical talents, and seriously hinders the comprehensive development of the region. From the perspective of the organizational guarantee and professional performance, although area A has a strong capability in system implementation and planning, it has the lowest level in the entrepreneurship and business development of rural agricultural talents. This reflects that area A excessively emphasizes traditional economic development methods and ignores the development of the new economy and the new business format, which does not actively play the guiding role of the talents. From the above analysis, we can conclude that area A has the lowest level among the four regions in the professional performance element. Therefore, area A should pay much more attention to the introduction of rural practical talents and the guidance and support of entrepreneurship and business activities, and devote itself to the innovation and development of the region.

5 Conclusions and Suggestions

5.1 Conclusions

Rural practical talents are the main force in rural economic development and play a vital role in the implementation of the rural revitalization strategy in China. A comprehensive evaluation of the development level of rural practical talents can speed up the construction of the rural talent team in China, promote the cultivation and introduction of rural practical talents, and motivates the establishment of related incentive mechanisms. Based on a carefully designed hybrid-indicator information power operator, this paper proposes an evaluation indicator system of rural practical talents, which adopts the variation coefficient method for obtaining the indicator weights. The proposed approach can overcome the shortcomings of the original subjective weighting methods that are highly dependent on the subjective evaluation of experts and can be used for a comprehensive evaluation of the rural practical talents in multiple regions. In addition, compared with traditional evaluation methods, this method adopts the PWA operator, which can effectively solve the problem of abnormal evaluation value. The evaluation results in this paper indicate that the development level of practical talents in a certain area is not only affected by the basic condition of local talents, but also depends on whether the local place pays adequate attention to some vital factors such as the importance of talent work and the environment for talent entrepreneurship and business. We believe that the development level of talents in a region can be well evaluated only when these factors are comprehensively combined. It is worth noting that to obtain the index weight of rural practical talents evaluation more effectively, we plan to study the combination weight model combining subjective and objective in future research.

5.2 Suggestions

In this paper, we find that there are some issues in the construction of the rural practical talents in China, such as the unqualified establishment and implementation of the talent system, the poor entrepreneurial environment and the service platform, the inadequate development of science and technology, the lack of enthusiasm for villagers’ entrepreneurship, etc. To continuously strengthen the construction of the rural practical talent team and promote the development of the rural talent revitalization strategy in China, in this paper, we propose some suggestions as follows:

  1. (1)

    Strengthen the introduction of practical talents in rural areas and provide a good service conditions. We should continue to increase the introduction of agricultural graduates from colleges and universities, support them to engage in agricultural self-employment, and encourage them to go to townships and villages to establish scientific and technological promotion and cooperative entities. The government and relevant departments can issue corresponding preferential support policies, and provide good environmental protection and technical and financial support, for enabling the talents to take root in rural areas and serve rural areas.

  2. (2)

    Improve the skill level of practical talents in rural areas and devote to cultivating comprehensive practical talents. The rural practical talents are not limited to having relevant production and management capabilities, but also need to have certain scientific and technological research and development capabilities. With the development of the information industry, agriculture also needs to be modernized, which requires farmers to have relevant scientific and technological knowledge and research ability. For example, the farmers not only know the planting technique but also can improve planting; they not only know how to operate offline but also know how to operate e-commerce. Only by improving the overall quality of farmers can promote the construction of a new socialist countryside in China.

  3. (3)

    Update the concept of urban and rural residents and create a good atmosphere for farmers to get rich. Rural practical talents are the main force in promoting the development of the rural economy and the leader of farmers to get rich. They play the most direct and specific role in driving and demonstrating farmers. Therefore, we must not only pay attention to the economic benefits brought by rural talents but also pay more attention to their social benefits. It is possible to publicize and commend advanced talents who have contributed to rural economic construction and social development through radio, television, and the Internet, to raise the awareness of the whole society to respect rural talents, create a good social public opinion atmosphere, and motivate more rural practical talents to stand out and actively invest in the construction of new rural areas.

  4. (4)

    Establish and improve relevant policies and mechanisms to promote the sustainable development of rural practical talents. First, we need to establish and improve the evaluation mechanism of rural practical talents, encourage all kinds of qualified rural practical talents to apply for professional titles, and continuously improve the comprehensive quality and professional ability of talents. Moreover, we need to establish a rural practical talent database at the district (county) level and above, establish and improve various mechanisms that are conducive to the training, selection, and use of rural practical talents, and continuously optimize the level of talent structure, and fully increase the utilization rate of rural practical talents. Furthermore, we need to increase the reward mechanism for rural practical talents, and provide rewards and support to talents who have made great contributions to the rural economy and society through business assessment, ability competition, and title evaluation, to stimulate their creativity and better lead the masses. In this way, the rural practical talents will be able to continually contribute to the construction of a new socialist countryside.