1 Introduction

Two-sided matching decision-making (TSDM) is a process during which the individuals included in the two-sided matching party (e.g., the male and female, the firm and position) submit the matching demand into an intelligent computation system (e.g., Uber, 51Job and other recommendation systems), and the matching decision-maker (MDM) used some optimization computation models, which embeds into the computation system, to determine the matching alternative for each individual. The TSDM problems have been widely existed in diverse applications, such as marriage matching [1, 2], college admission matching [3, 4], roommate matching [5, 6], firm and employee matching [7, 8], and task and volunteer teams [9]. In practical TSDM problem, it is common that the individuals express the demand information via the preference ordering and linguistic evaluation [10,11,12,13,14,15,16,17,18].

At present, several studies have focused on developing the optimization model for solving the TSDM with the preference ordering. For example, Sertel and özkal-Sanver [10] aimed to two-sided matching problem with complete strict preference ordering information, considered the endowments of two-sided matching party and proposed a matching rule maximizing consumption. Alkan and Gale [17] studied the two-sided matching problem with complete strict preference ordering, in which the unrevealed preference behavior of two-sided matching party is considered. Furthermore, an extension of Gale-Shapley algorithm is developed to solve this problem. Halldorsson et al. [19] studied the stable marriage matching problem with incomplete strict preference ordering, and proposed a randomized approximation algorithm and analyzed the efficiency of the algorithm. Furthermore, they proposed an efficient algorithm to determine the optimal matching pairs. Chen et al. [20] studied the hospital/residents matching with incomplete strict and indifferent preference ordering, and proposed a unified an approach to find good stable matching pair. Knoblauch [21] aimed to the two-sided matching problem with incomplete strict and indifference preference ordering an algorithm to maximize satisfaction degree of two-sided matching party. Antler [22] studied two-sided matching with endogenous preferences, and provided a stable matching method based on the Gale–Shapley algorithm. Chen et al. [23] designed a method for effectively matching suitable knowledge service demanders and suppliers in which the expectation levels of attributes given by demanders and suppliers are considered. Erdil and Ergin [24] allowed ties in preference rankings and designed an algorithm to find the pareto efficient and stable matching. Ortega [25] investigated social integration in two-sided matching markets, and discussed the stability, integration monotonicity, and Pareto optimality. Sotomayor [26] defined the concepts of sequential stability and of perfect competitive equilibrium, and studied competition and cooperation in a two-sided matching market with replication. Liang et al. [27] designed a filling method of incomplete preference ordinal based on collaborative filtering algorithm to solve multi-attribute dynamic two-sided matching.

The existing studies have significant contributions to solving the two-sided matching decision-making with preference ordering. However, there are also some improvements needed to be noted:

  1. (i)

    Most of the existing studies assumed that each individual in one matching party can accurately provide the preference ordering (i.e., either strict preference or indifferent preference) over two individuals in another matching party. However, in practical TSDM problem, due to the limitation on the knowledge and experiences, it is difficult for all the individuals provide the preference ordering accurately. A general phenomenon is that the individuals only providing an individual in the another matching party is no worse than that another one, but these individuals cannot accurately identify whether one individual is better than another one, or one individual is indifferent from another one. We call this type of preference ordering as weak preference ordering.

  2. (ii)

    In the existing studies, it often assumed that the individuals have the same demand on the stable of alternatives. However, due to the differences on the personality and demand, different individuals have the heterogeneous demands on the stable of alternatives. For example, an individual may change her/his matching alternative when an individual in the another matching party is much better than her/his matching alternative. However, another individual may change her/his matching alternative when an individual in the another matching party is slightly better than her/his matching alternative. In practice, the most common way for expressing the fuzzy stable demand is to use the linguistic information. And the use of the linguistic information usually implies the demand of the techniques of computing with words (CW) [28,29,30,31,32,33]. In this paper, we will use the 2-tuple fuzzy linguistic representations [28] to deal with the linguistic information.

To overcome these limitations, we focus on proposing an optimization method to solving the TSDM with incomplete weak preference ordering and heterogeneous fuzzy stable demand. The contributions of this paper are summarized as follows:

  1. (i)

    We propose a method for dealing with the incomplete weak preference ordering. Specifically, we divide the incomplete weak preference ordering into multiple chains with equal probabilities. Then, we calculate the expectation ordinal values of individuals in the two-sided matching party.

  2. (ii)

    We analyze the difference on the desired matching alternatives, and divided the individuals into two categories (i.e., strong and weak perceived differences). Then, we propose a method to calculate the perceived differences and perceived values for two types of individuals in the two-sided matching party.

  3. (iii)

    We define the blocking pair under the heterogeneous fuzzy stable demand, and define the heterogeneous stable matching alternative. Then, we construct a constraint for obtaining the heterogeneous stable matching alternative. Furthermore, we develop an optimization model which maximizes the perceived values of individuals in the two-sided matching party.

The objective of this paper is proposing an optimization method to solving the TSDM with incomplete weak preference ordering and heterogeneous fuzzy stable demand. First, the description on the proposed TSDM problem is given. Then, we provide a method to transform the incomplete weak preference orderings into the expectation ordinal values. Next, the perceived values of individuals are calculated. Furthermore, based on the linguistic expressions on the heterogeneous fuzzy stable demands, an optimization model maximizing the perceived values for two-sided matching parties is developed. Finally, a numerical example is given to illustrate the feasibility of the proposed method.

The rest of this paper is organized as follows: Sect. 2 gives the description of the proposed problem and builds the framework for the proposed method. In Sect. 3, the details of TSDM-IH method are introduced. Section 4 provides an example, a comparison analysis, and a sensitivity analysis to illustrate the feasibility and effectiveness of the proposed method. Finally, Sect. 5 summarizes the main works of the proposed method.

2 Problem Description and Resolution Framework

In this section, the TSDM problem with the incomplete weak preference ordering and heterogeneous fuzzy stable demand is described. Then, we build the resolution framework for the proposed TSDM problem.

2.1 Problem Description

In the proposed TSDM problem, we assume that the two-sided matching party are as the A matching party and B matching party. Let \(A = \{ A_{1} ,A_{2} , \ldots ,A_{m} \}\) denote the set of \(m\) individuals included in the A matching party, where \(A_{i}\) denote the \(i\)th individual included in the A matching party; \(B = \{ B_{1} ,B_{2} , \ldots ,B_{n} \}\) be the set of \(n\) individuals included in the B matching parties, where \(B_{j}\) denote the \(j\) th individuals included in the B matching party.

Let \(G^{i}\)(\(G^{i} \subseteq B\)) be the set of acceptable individuals included in the B matching party for \(A_{i}\). And let \(P_{{A_{i} }}\) be the preference chain on the set \(T^{i}\) provided by \(A_{i}\). In the preference chain \(P_{{A_{i} }}\), there are three kinds of preference relations. Without loss of generality, we take two individuals \(B_{j} ,B_{h}\) included in the set \(G^{i}\) as an example to illustrate three kinds of preference relations as follows:

  1. (1)

    Strict preference (\(\succ\)): \(B_{j} \succ B_{h}\) means that \(B_{j}\) is prefer to \(B_{h}\);

  2. (2)

    Weak preference (\(\underline{ \succ }\)): \(B_{j} \underline { \succ } B_{h}\) means that \(B_{j}\) is no worse than \(B_{h}\);

  3. (3)

    Indifferent preference (\(\sim\)):\(B_{j} \sim B_{h}\) means that \(B_{j}\) is indifferent from \(B_{h}\).

Let \(U^{j}\)(\(U^{j} \subseteq A\)) be the set of acceptable individuals included in the A matching party for \(B_{j}\). And let \(P_{{B_{j} }}\) be the preference chain on the set \(U^{j}\) provided by \(B_{j}\). Similar to \(P_{{A_{i} }}\), \(P_{{B_{j} }}\) also includes three kinds of preference relations.

Let \(S = \{ s_{0} ,s_{1} ,...,s_{T} \}\) be a linguistic term set for evaluating the fuzzy stable demand on the formed matching alternatives, which satisfies: (1) the set is ordered: \(s_{\alpha } > s_{\beta }\) if and only if \(\alpha > \beta\), and (2) there is a negation operator \(Neg(s_{\alpha } ) = s_{T - \alpha }\). Each individual included in the A matching party and B matching party express the fuzzy stable demand over the linguistic term set \(S\). Let \(SD_{A}^{i}\) be the fuzzy stable demand for the individual \(A_{i}\), and \(SD_{B}^{j}\) be the fuzzy stable demand for the individual \(B_{j}\), where \(SD_{A}^{i} ,SD_{B}^{j} \in S\). The larger values for \(SD_{A}^{i}\) and \(SD_{B}^{j}\) indicate the individuals \(A_{i}\) and \(B_{j}\) are not willing to change their matching alternatives.

For example, when \(T = 6\), the linguistic term set \(S\) can be defined as \(S\) = {\(s_{0}\) = ’extremely instable’, \(s_{1}\) = ’very instable’,\(s_{2}\) = ’ instable’, \(s_{3}\) = ’medium”, \(s_{4}\) = ’stable’,\(s_{5}\) = ’very stable’, \(s_{6}\) = ’extremely stable’}. If an individual expresses the fuzzy stable demand as \(s_{5}\), then it represents that the individual provides the high standard on changing her/his current matching alternative. Only a new matching alternative is significantly better than her/his current matching alternative, and then, she/he will have the motivation to change the matching alternative.

Let \(\mu :A \cup B \to A \cup B\) be one to one two-sided matching. For \(\forall A_{i} \in A\) and \(\forall B_{i} \in B\), the matching \(\mu\) satisfies the conditions as follows:

  1. (1)

    \(\mu (A_{i} ) \in B \cup \{ A_{i} \}\). Specially, if \(\mu (A_{i} ) = A_{i}\), then \(A_{i}\) has no matching alternative;

  2. (2)

    \(\mu (B_{j} ) \in A \cup \{ B_{j} \}\). Specially, if \(\mu (B_{j} ) = B_{j}\), then \(B_{j}\) has no matching alternative;

  3. (3)

    If \(\mu (A_{i} ) = B_{j}\) and \(\mu (B_{j} ) = A_{i}\), then we call (\(A_{i}\),\(B_{j}\)) as a matching pair based on the matching \(\mu\). And we also call \(A_{i}\) is the matching alternative of \(B_{j}\), and \(B_{j}\) is the matching alternative of \(A_{i}\);

(4) If \(\mu (A_{i} ) = B_{j}\), then \(\mu (A_{i} ) \ne B_{k}\), \(B_{k} \ne B_{j}\). \(B_{k} \in B\);

The proposed TSDM problem is to find an optimal matching \(\mu\) based on the incomplete preference chains of all the individuals, and the heterogeneous fuzzy stable demand on the formed matching alternatives.

2.2 Resolution Framework

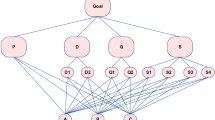
In this section, we depict a resolution framework for the TSDM in an incomplete and heterogeneous context in Fig. 1.

Fig. 1
figure 1

The framework of TSDM-IH method

Full size image

As seen from Fig. 1, the depicted framework is divided into two parts. In the left part, we show that the objective of the TSDM problem is to form several matching pairs from A matching party and B matching party. And all the formed matching pairs are composed of a set of matching alternatives.

In the right part, we show the flow of the method for determining the optimal matching alternative. First, due to the randomness of weak preference ordering, we calculate the expectation ordinal value for each individual based on her/his preference chain. Then, with the consideration of the sensitivity on the difference between the actually obtained alternative and desired matching alternative, the perceived values for each individual are calculated. Next, we analyze the linguistic expression on the fuzzy stable demand for each individual, and obtain the constraint for obtaining the stable alternatives. On this basis, we develop an optimization model which maximizes the perceived values of individuals in the A matching party and B matching party.

The details of TSDM-IH method will introduce in Sect. 3.

3 The TSDM-IH Method

In this section, the expectation ordinal values for each individual are calculated. Then, the perceived values for each individual are calculated. Next, based on the heterogeneous fuzzy stable demand by different individuals, we develop an optimization model which maximizes the perceived values of individuals in the A matching party and B matching party.

3.1 Calculate the Expectation Ordinal Value for Each Matching Party

Let \(R = (r_{ij} )_{m \times n}\) be the expectation ordinal value matrix of individuals in the A matching party, where \(r_{ij}\) is \(A_{i}\)’s expectation ordinal value on \(B_{j}\). There are two cases to be considered for dealing with the incomplete weak preference ordering of individuals in the A matching party.

Case 1. If \(B_{j} \notin G^{i}\), then \(r_{ij} = M\), where \(M\) is a large enough number.

Case 2. If \(B_{j} \in G^{i}\), then \(r_{ij}\) can be obtained as the following process.

We assume that there are \(m_{i}\) weak preference “\(\underline { \succ }\)” included in the preference chain \(P_{{A_{i} }}\). Because “\(\underline { \succ }\)” can be equivalent as “\(\succ\)” or “\(\sim\)”. Then, the preference chain \(P_{{A_{i} }}\) can be divided into \(2^{{m_{i} }}\) preference chains (i.e., \(P_{{A_{i} }}^{1} ,P_{{A_{i} }}^{2} ,...,P_{{A_{i} }}^{{2^{{m_{i} }} }}\)) with equal probability (i.e., \({1 \mathord{\left/ {\vphantom {1 {2^{{m_{i} }} }}} \right. \kern-\nulldelimiterspace} {2^{{m_{i} }} }}\))

$$\begin{gathered} \quad \;\overbrace {{\underline { \succ } , \, \underline { \succ } , \, \underline { \succ } , \ldots , \, \underline { \succ } }}^{{2^{{m_{i} }} }} \hfill \\ 2^{{m_{i} }} \left\{ \begin{gathered} \sim , \, \sim , \, \sim , \ldots , \, \sim \hfill \\ \succ , \, \sim , \, \sim , \ldots ,\sim \hfill \\ \succ , \, \succ , \, \sim , \, \ldots ,\sim \hfill \\ \succ , \, \succ , \, \succ , \, \ldots ,\sim \hfill \\ \cdots \, \cdots \, \cdots \, \cdots \hfill \\ \succ , \succ , \succ , \ldots , \succ \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

Let \(D_{ij}^{l \succ }\) be the set of individuals in the set \(B\) who are better than \(B_{j}\) based on \(A_{i}\)’s \(l\) th preference chain \(P_{{A_{i} }}^{l}\), and \(D_{ij}^{l \sim }\) be the set of individuals in the set \(B\) which is indifferent from \(B_{j}\) in \(A_{i}\)’s preference chain \(P_{{A_{i} }}^{l}\), \(l = 1,2, \cdots ,\)\(2^{{m_{i} }}\). Let \(|D_{ij}^{l \succ } |\) and \(|D_{ij}^{l \sim } |\) be the cardinalities of \(D_{ij}^{l \succ }\) and \(D_{ij}^{l \sim }\), respectively.

Suppose \(R_{il} (B_{j} )\) is the ordinal value of \(B_{j}\) in \(A_{i}\)’s \(l\) th preference chain \(P_{{A_{i} }}^{l}\). The probability vector on \(R_{il} (B_{j} )\) is represented by \(P(R_{il} (B_{j} )) = (P_{1} (R_{il} (B_{j} )), \ldots ,P_{q} (R_{il} (B_{j} )), \ldots ,P_{n} (R_{il} (B_{j} ))\), where \(P_{q} (R_{il} (B_{j} ))\) denotes the probability that \(B_{j}\) is ranked in the \(q\) th position in \(A_{i}\)’s \(l\) th preference chain \(P_{{A_{i} }}^{l}\), for \(q = 1,\)\(\ldots ,n\) and \(\sum\nolimits_{q = 1}^{n} {P_{q} (R_{il} (B_{j} )) = 1}\).

In the following, we provide the two definitions of calculating the values of \(P_{q} (R_{il} (B_{j} ))\).

Definition 1

If \(|D_{ij}^{l \sim } | > 1\), then we consider that \(R_{il} (B_{j} )\) should be ranked in position \(|D_{ij}^{l \succ } | + 1,|D_{ij}^{l \succ } |\)\(+ 2,\)\(\ldots ,\)\(|D_{ij}^{l \succ } | +\)\(|D_{ij}^{l \sim } |\) with the same probability. Motivated by this idea, \(P_{q} (R_{il} (B_{j} ))\) is calculated by:

$$P_{q} (R_{il} (B_{j} )) = \left\{ {\begin{array}{*{20}l} {{1 \mathord{\left/ {\vphantom {1 {|D_{ij}^{l\sim } |,}}} \right. \kern-\nulldelimiterspace} {|D_{ij}^{l\sim } |,}}} \hfill & {|D_{ij}^{l \succ } | + 1 \le q \le |D_{ij}^{l \succ } | + |D_{ij}^{l\sim } |} \hfill \\ {0,} \hfill & {q < |D_{ij}^{l \succ } | + 1 \, {\text{or}}\, q > |D_{ij}^{l \succ } | + |D_{ij}^{l\sim } |} \hfill \\ \end{array} } \right..$$
(1)

For example, suppose \(|D_{ij}^{l \sim } | = 3\), \(|D_{ij}^{l \succ } | = 3\), and \(n = 8\), then \(B_{j}\) is ranked as the 4th, 5th, and 6th position with the same probability (i.e., 1/3) in the preference chain \(P_{{A_{i} }}^{l}\). Thus, the probability vector on \(R_{il} (B_{j} )\) is \(P(R_{il} (B_{j} )) = (0,0,0,{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3},{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3},{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3},0,0)\).

Definition 2

If \(|D_{ij}^{l \sim } | = 1\), we consider that \(R_{il} (B_{j} )\) should be ranked in position \(|D_{ij}^{l \succ } | + 1\). Then \(P_{q} (R_{il} (B_{j} ))\) is calculated by:

$$P_{q} (R_{il} (B_{j} )) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {q = |D_{ij}^{l \succ } | + 1} \hfill \\ {0,} \hfill & {q \ne |D_{ij}^{l \succ } | + 1} \hfill \\ \end{array} } \right..$$
(2)

For example, suppose \(|D_{ij}^{l \sim } | = 1\), \(|D_{ij}^{l \succ } | = 3\), and \(n = 8\), then the probability that \(B_{j}\) is ranked as the 4th position in the preference chain \(P_{{A_{i} }}^{l}\). Thus, the probability vector on \(R_{il} (B_{j} )\) is \(P(R_{il} (B_{j} )) = (0,0,0,1,0,0,0,0)\).

Let \(E(R_{il} (B_{j} ))\) be the expectation value of \(R_{il} (B_{j} )\). Based on definitions 1–2, \(E(R_{il} (B_{j} ))\) is calculated by

$$E(R_{il} (B_{j} )) = \sum\limits_{q = 1}^{n} {qP(R_{il} (B_{j} ) = q)} .$$
(3)

Furthermore, to aggregate the expectation ordinal value on \(A_{i}\)’s total \(2^{{m_{i} }}\) preference chains, we can calculate on the expectation ordinal value of \(B_{j}\) by \(A_{i}\).

Let \(r_{ij}\) be the expectation ordinal value of \(B_{j}\) by \(A_{i}\). Because each preference chain occurs as the same probability \({1 \mathord{\left/ {\vphantom {1 {2^{{m_{i} }} }}} \right. \kern-\nulldelimiterspace} {2^{{m_{i} }} }}\), then \(r_{ij}\) is calculated by

$$r_{ij} = \sum\limits_{l = 1}^{{2^{{m_{i} }} }} {\sum\limits_{q = 1}^{n} {qP_{q} (R_{il} (B_{j} ))/2^{{m_{i} }} } } .$$
(4)

Similarly, let \(O = (o_{ij} )_{m \times n}\) be the expectation ordinal value matrix of individuals in the B matching party, where \(o_{ij}\) is \(B_{j}\)‘s expectation ordinal value on \(A_{i}\). There are also two cases to be consider for dealing with the incomplete weak preference ordering of individuals in the B matching party.

Case 1. If \(A_{i} \notin U^{j}\), then \(o_{ij} = M\), where \(M\) is a large enough number.

Case 2. If \(A_{i} \in U^{j}\), then \(o_{ij}\) can be obtained as the following process.

We assume that there are \(n_{j}\) weak preference “\(\underline { \succ }\)” included in the preference chain \(P_{{B_{j} }}\). Then, the preference chain \(P_{{B_{j} }}\) can be divided into \(2^{{n_{j} }}\) preference chains (i.e., \(P_{{B_{j} }}^{1} ,P_{{B_{j} }}^{2} ,...,P_{{B_{j} }}^{{2^{{n_{j} }} }}\)) with equal probability (i.e., \({1 \mathord{\left/ {\vphantom {1 {2^{{n_{j} }} }}} \right. \kern-\nulldelimiterspace} {2^{{n_{j} }} }}\)).

Let \(Q_{ij}^{l \succ }\) be the set of individuals in the set \(A\) who are better than \(A_{i}\) in \(B_{j}\)’s \(l\) th preference chain \(P_{{B_{j} }}^{l}\), and \(Q_{ij}^{l \sim }\) be the set of individuals in the set \(A\) who are indifferent from \(A_{i}\) in \(B_{j}\)’s \(l\) th preference chain \(P_{{B_{j} }}^{l}\), \(l = 1,2, \ldots ,2^{{n_{j} }}\). Let \(|Q_{ij}^{l \succ } |\) and \(|Q_{ij}^{l \sim } |\) be the cardinalities of \(Q_{ij}^{l \succ }\) and \(Q_{ij}^{l \sim }\), respectively. Suppose \(O_{jl} (A_{i} )\) is the preference ordinal value of \(A_{i}\) in the preference chain \(P_{{B_{j} }}^{l}\). The probability vector on \(O_{jl} (A_{i} )\) is represented by \(P(O_{jl} (A_{i} )) = (P_{1} (O_{jl} (A_{i} )), \ldots ,P_{v} (O_{jl} (A_{i} )), \ldots ,P_{m} (O_{jl} (A_{i} )))\), where \(P_{v} (O_{jl} (A_{i} ))\) denotes the probability that \(A_{i}\) is ranked in the \(v\) th position in the preference chain \(P_{{B_{j} }}^{l}\), for \(v = 1,\)\(\ldots ,m\) and \(\sum\limits_{p = 1}^{m} {P_{v} (O_{jp} (A_{i} )) = 1}\).

Because each preference chain occurs as the same probability \({1 \mathord{\left/ {\vphantom {1 {2^{{n_{j} }} }}} \right. \kern-\nulldelimiterspace} {2^{{n_{j} }} }}\), then \(o_{ij}\) is calculated by

$$o_{ij} = \sum\limits_{p = 1}^{{2^{{n_{j} }} }} {\sum\limits_{v = 1}^{n} {{{vP_{v} (O_{jp} (A_{i} ))} \mathord{\left/ {\vphantom {{vP_{v} (O_{jp} (A_{i} ))} {2^{{n_{j} }} }}} \right. \kern-\nulldelimiterspace} {2^{{n_{j} }} }}} } .$$
(5)

3.2 Calculate the Perceived Value for Each Individual

In practical TSDM, when an individual obtains a matching object, she/he often compares the matching alternative with her/his desired matching alternative. And we use the distance between the obtained alternative and desired matching alternative for measuring the perceived difference. The smaller perceived difference the matching body owns, the larger satisfaction degree the individual owns. As a result, the individual will accept her/his obtained matching alternative with a larger probability.

Let \(C = (c_{ij} )_{m \times n}\) and \(D = (d_{ij} )_{m \times n}\) be the perceived difference matrixes for A matching party and B matching party, respectively, where \(c_{ij}\) denotes \(A_{i}\)’s perceived difference on \(B_{j}\), and \(d_{ij}\) denotes \(B_{j}\)’s perceived difference on \(A_{i}\). Then, the perceived difference can be calculated by dividing into two cases as follows:

Case 1. Strong perceived difference. In this case, the individuals consider her/his most preferable matching alternative as the desired matching alternative.

Specifically, let \(A^{H}\) be the set of the individuals in the set \(A\) who have strong perceived difference, where \(A^{H} \subseteq A\). Let \(r_{i}^{*}\) be the preference ordinal values of most preferable matching alternative for \(A_{i}\), where \(r_{i}^{*} = \min \{ r_{ij} |j = 1,2, \ldots ,n\}\). Then, \(A_{i}\)’s perceived difference \(c_{ij}\) on \(B_{j}\) is calculated by

$$c_{ij} = (r_{ij} - r_{i}^{*} )^{{\beta_{i} }} \,\,\,A_{i} \in A^{H} ;\,j = 1,2, \ldots ,n,$$
(6)

where \(\beta_{i}\) represents the sensitive coefficient of \(A_{i}\) on perceived difference.

Let \(B^{H}\) be the set of the individuals in the set \(B\) who have strong perceived difference, where \(B^{H} \subseteq B\). Let \(o_{j}^{*}\) be the preference ordinal values of most preferable matching alternative for \(A_{i}\), where \(o_{j}^{*} = \min \{ o_{ij} |i = 1,2, \ldots ,m\}\). Then, \(B_{j}\)’s perceived difference \(d_{ij}\) on \(A_{i}\) is calculated by

$$d_{ij} = (o_{ij} - o_{j}^{*} )^{{\alpha_{j} }} \,\,\,i = 1,2, \ldots ,m;\,B_{j} \in B^{H} ,$$
(7)

where \(\alpha_{j}\) represents the sensitive coefficient of \(B_{j}\) on perceived difference.

Case 2. Weak perceived difference. In this case, the individuals often set a desired ordinal value on the matching alternative. When the ordinal value of obtained matching alternative is prior to this desired ordinal value, she/he will consider this matching alternative as the desired matching alternative.

Specifically, let \(A^{W}\) be the set of the individuals in the set \(A\) who have weak perceived difference, where \(A^{W} \subseteq A\) and \(A^{W} \cup A^{H} = A\). Let \(\overline{r}_{i}\) be \(A_{i}\)’s desired ordinal value on the matching alternative, where \(\overline{r}_{i} > r_{i}^{*}\) and \(\overline{r}_{i} < n\). Then, \(A_{i}\)’s perceived difference \(c_{ij}\) on \(B_{j}\) is calculated by

$$c_{ij} = \left\{ {\begin{array}{*{20}l} {(r_{ij} - \overline{r}_{i} )^{{\lambda_{i} }} ,} \hfill & {r_{ij} > \overline{r}_{i} } \hfill \\ {0,} \hfill & {r_{ij} \le \overline{r}_{i} } \hfill \\ \end{array} } \right.\,\,\,A_{i} \in A^{W} ;\,j = 1,2, \ldots ,n,$$
(8)

where \(\lambda_{i}\) represents the sensitive coefficient of \(A_{i}\).

Let \(B^{W}\) be the set of the individuals in the set \(B\) who have weak perceived difference, where \(B^{W} \subseteq B\) and \(B^{W} \cup B^{S} = B\). Let \(\overline{o}_{j}\) be \(B_{j}\)’s desired ordinal value on the matching alternative, where \(\overline{o}_{j} > o_{j}^{*}\) and \(\overline{o}_{j} < m\). Then, \(B_{j}\)’s perceived difference \(d_{ij}\) on \(A_{i}\) is calculated by

$$d_{ij} = \left\{ {\begin{array}{*{20}l} {(o_{ij} - \overline{o}_{j} )^{{\sigma_{j} }} ,} \hfill & {o_{ij} \ge \overline{o}_{j} } \hfill \\ {0,} \hfill & {o_{ij} < \overline{o}_{j} } \hfill \\ \end{array} } \right.\,\,\,i = 1,2, \ldots ,m;\,B_{j} \in B^{W} ,$$
(9)

where \(\sigma_{j}\) represents the sensitive coefficient of \(B_{j}\).

Furthermore, we utilize the determined perceived difference to calculate the perceived value for each individual. And the smaller perceived difference indicated the larger perceived values.

Specifically, let \(Y = (y_{ij} )_{m \times n}\) and \(H = (h_{ij} )_{m \times n}\) be A matching party’s and B matching party’s perceived values’ matrix, respectively, where \(y_{ij}\) denotes \(A_{i}\)’s perceived value on \(B_{j}\), and \(h_{ij}\) denotes \(B_{j}\)’s perceived value on \(A_{i}\), respectively.


We calculate the perceived value \(y_{ij}\) by dividing into the following two cases:

Case 1. \(B_{j} \notin G^{i}\). In this case, \(A_{i}\) considers \(B_{j}\) as a infeasible matching alternative, and thus, \(y_{ij} = - M\), where \(M\) is a larger enough number.

Case 2. \(B_{j} \in G^{i}\). In this case, \(A_{i}\) considers \(B_{j}\) as a feasible matching alternative. Because the smaller perceived difference \(c_{ij}\) indicates the higher larger perceived value \(y_{ij}\), then \(y_{ij}\) can be determined by

$$y_{ij} = \frac{{\overline{c}_{i} - c_{ij} }}{{\overline{c}_{i} - \tilde{c}_{i} }},\,i = 1,2, \ldots ,m\,{\text{and}}\,B_{j} \in G^{i} ,$$
(10)

where \(\overline{c}_{i} = \max \{ c_{ij} |B_{j} \in G^{i} \}\) and \(\tilde{c}_{i} = \min \{ c_{ij} |B_{j} \in G^{i} \}\).

Similarly, we also calculate the perceived value \(h_{ij}\) by dividing into the following two cases:

Case 1. \(A_{i} \notin U^{j}\). In this case, \(B_{j}\) considers \(A_{i}\) as a infeasible matching alternative, and thus, \(h_{ij} = - M\).

Case 2. \(A_{i} \in U^{j}\). In this case, \(B_{j}\) considers \(A_{i}\) as a feasible matching alternative. Because the smaller perceived difference \(d_{ij}\) indicates the larger perceived value \(h_{ij}\), then \(h_{ij}\) can be determined by

$$h_{ij} = \frac{{\overline{d}_{i} - d_{ij} }}{{\overline{d}_{i} - \tilde{d}_{i} }},\,\,i = 1,2, \ldots ,m\,{\text{and}}\,A_{i} \in U^{j} ,$$
(11)

where \(\overline{d}_{i} = \max \{ d_{ij} |A_{i} \in U^{j} \}\) and \(\tilde{d}_{i} = \min \{ d_{ij} |A_{i} \in U^{j} \}\).

3.3 Two-sided Matching model Considering Heterogeneous Fuzzy Stable Demand

Because the individuals use the linguistic terms to express the heterogeneous fuzzy stable demand, we need the techniques for CW. One of the most common techniques is the model based on 2-tuple fuzzy linguistic representations, which are introduced in Definitions 3–4.

Definition 3

[28]. Let \(\beta \in [0,T]\) be a number in the granularity interval of the linguistic term set \(S = \{ s_{0} ,s_{1} ,...,s_{T} \}\), and let \(i = {\text{round}}(\beta )\) and \(\alpha = \beta - i\) be two values, such that \(i \in [0,T]\) and \(\alpha \in [ - 0.5,0.5)\). Then, \(\alpha\) is called a symbolic translation, with round being the usual rounding operation.

The 2-tuple fuzzy linguistic representation model represents the linguistic information by means of 2-tuple (\(s_{i} ,\alpha_{i}\)), where \(s_{i} \in S\) and \(\alpha_{i} \in [ - 0.5,0.5)\).

Definition 4

[28]. Let \(S\) be a linguistic term set and \(\beta \in [0,T]\) be a value representing the result of a symbolic aggregation operation, and then, the 2-tuple that expresses the equivalent information to \(\beta\) is obtained with the following function:

$$\Delta :[0,T] \to S \times [ - 0.5,0.5)$$
$$\Delta (\beta ) = (s_{i} ,\alpha )\,{\text{with}}\,\left\{ {\begin{array}{*{20}l} {s_{i} ,i = {\text{round}}(\beta )} \hfill \\ {\alpha = \beta - i,\alpha \in [ - 0.5,0.5)} \hfill \\ \end{array} } \right..$$

Clearly, \(\Delta\) is one to one. Let \(\overline{S}\) denote the range of \(\Delta\). Then, \(\Delta\) has an inverse function with \(\Delta^{ - 1} :\overline{S} \to [0,T]\) with \(\Delta^{ - 1} ((s_{i} ,\alpha )) = i + \alpha\).

We normalize the values of \(\Delta^{ - 1} ((s_{i} ,\alpha )) = i + \alpha\) into a value in [0, 1], and then, we provide the normalized function \(NS:\overline{S} \to [0,1]\), where \(NS((s_{i} ,\alpha )) = {{(i + \alpha )} \mathord{\left/ {\vphantom {{(i + \alpha )} T}} \right. \kern-\nulldelimiterspace} T}\).

Based on the fuzzy stable demands \(SD_{A}^{i}\) and \(SD_{B}^{j}\), the heterogeneous fuzzy stable matching can be defined as follows:

Definition 5

Let \(\mu\) be one to one two-sided matching, where \(\mu (A_{i} ) = B_{j}\) and \(\mu (A_{k} ) = B_{l}\). If \(y_{il} - y_{ij} \ge NS(SD_{A}^{i} )\) and \(h_{il} - h_{kl} \ge NS(SD_{B}^{l} )\), and then, the matching pair (\(A_{i} ,B_{l}\)) is a blocking pair. And if no blocking pairs are included in the matching \(\mu\), we call \(\mu\) as heterogeneous stable matching.

Then, let \(x_{ij}\) be a 0–1 decision variable, where \(x_{ij} = 1\) denotes \(A_{i}\) and \(B_{j}\) form a matching pair, otherwise, \(x_{ij} = 0\). Based on the definition 3, the constraints for obtaining heterogeneous fuzzy stable matching can be represented as follows:

$$x_{ij} + \sum\limits_{{y_{il} - y_{ij} \ge - NS(SD_{A}^{i} )}} {x_{il} } + \sum\limits_{{h_{lj} - h_{ij} \ge - NS(SD_{B}^{j} )}} {x_{lj} } \ge 1.$$
(12)

Furthermore, we hope the optimal matching alternative can maximize the perceived values of both A matching party and B matching party in the premise of considering the heterogeneous fuzzy stable demand. Thus, the two-sided matching model is developed as follows:

$$\max \,z_{1} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {y_{ij} x_{ij} } }$$
(13a)
$$\max \,z_{2} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {h_{ij} x_{ij} } }$$
(13b)
$$s.t.\,\sum\limits_{i = 1}^{m} {x_{ij} \le 1} ,\,j = 1,2, \ldots ,n$$
(13c)
$$\sum\limits_{j = 1}^{n} {x_{ij} \le 1} ,\,i = 1,2, \ldots ,m$$
(13d)
$$x_{ij} + \sum\limits_{{y_{il} - y_{ij} \ge - NS(SD_{A}^{i} )}} {x_{il} } + \sum\limits_{{h_{lj} - h_{ij} \ge - NS(SD_{B}^{j} )}} {x_{lj} } \ge 1,$$
$$i = 1,2, \ldots ,m;\,j = 1,2, \ldots ,n$$
(13e)
$$x_{ij} = 0\,{\text{or}}\,1,\,i = 1,2, \ldots ,m;\,j = 1,2, \ldots ,n.$$
(13f)

In the model (13a–13f), Eq. (13a) represents the maximization of the overall perceived values of individuals in the A matching party; Eq. (13b) represents the maximization of the overall perceived values of individuals in the B matching party; Eq. (13c) represents that each individual in the A matching party matches an individual in the B matching party at most; Eq. (13d) represents that each individual in the B matching party matches an individual in the A matching party at most; Eq. (13e) represents the constraints for obtaining the heterogeneous stable matching alternative; Eq. (13f) represents the 0–1 variables \(x_{ij}\)(\(i = 1,2, \ldots ,m\); \(j = 1,2, \ldots ,n\)).

Theorem 1

Equation (13e) guarantees the heterogeneous stable matching alternative.

Proof

For any 0–1 variable \(x_{ij}\), we consider two cases:

Case 1. When \(x_{ij} = 1\), it implies that \(A_{i}\) and \(B_{j}\) form the matching pair. Based on definition 5, (\(A_{i}\),\(B_{j}\)) will not become the blocking pair, because the blocking pair occurs at the unmatching pair.

Case 2. When \(x_{ij} = 0\), then \(x_{ij} + \sum\limits_{{y_{il} - y_{ij} \ge - NS(SD_{A}^{i} )}} {x_{il} } + \sum\limits_{{h_{lj} - h_{ij} \ge - NS(SD_{B}^{j} )}} {x_{lj} } \ge 1\) can be equivalent as follows: \(\sum\limits_{{y_{il} - y_{ij} \ge - NS(SD_{A}^{i} )}} {x_{il} } + \sum\limits_{{h_{lj} - h_{ij} \ge - NS(SD_{B}^{j} )}} {x_{lj} } \ge 1\). Thus, we obtain that:

\(\sum\limits_{{y_{il} - y_{ij} \ge - NS(SD_{A}^{i} )}} {x_{il} } = 1\) or \(\sum\limits_{{h_{lj} - h_{ij} \ge - NS(SD_{B}^{j} )}} {x_{lj} } = 1\).

Thus, we consider two subcases:

Subcase 1. When \(\sum\limits_{{y_{il} - y_{ij} \ge - NS(SD_{A}^{i} )}} {x_{il} } = 1\), it implies that \(A_{i}\) is more willing to match with \(B_{l}\) rather than \(B_{j}\). Thus, (\(A_{i}\),\(B_{j}\)) will not become the blocking pair.

Subcase 2. When \(\sum\limits_{{h_{lj} - h_{ij} \ge - NS(SD_{B}^{j} )}} {x_{lj} } = 1\), it implies that \(B_{j}\) is more willing to match with \(A_{i}\) rather than \(A_{l}\). Thus, (\(A_{i}\),\(B_{j}\)) will not become the blocking pair.

Because any matching pairs (\(A_{i}\),\(B_{j}\)) will not become the blocking pair, thus we will obtain the heterogeneous stable matching alternative.

This completes the proof of Theorem 1.

It can be seen that model (13a–13f) is a bi-objective 0–1 linear programming model. We can transform the model (13a–13f) into a single objective 0–1 linear programming model.

Let \(w_{1}\) and \(w_{2}\) be the weights of concerning the benefit of A matching party and B matching party, where \(w_{1} +\)\(w_{2} = 1\), \(w_{1} ,w_{2} \ge 0\). We transform model (13a–13f) into the following model (14a–14e)

$$\max \,z = w_{1} \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {y_{ij} x_{ij} } } + w_{2} \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {h_{ij} x_{ij} } }$$
(14a)
$$s.t.\,\sum\limits_{i = 1}^{m} {x_{ij} \le 1} ,j = 1,2, \ldots ,n$$
(14b)
$$\sum\limits_{j = 1}^{n} {x_{ij} \le 1} ,\,i = 1,2, \ldots ,m$$
(14c)

\(x_{ij} + \sum\limits_{{y_{il} - y_{ij} \ge - NS(SD_{A}^{i} )}} {x_{il} } + \sum\limits_{{h_{lj} - h_{ij} \ge - NS(SD_{B}^{j} )}} {x_{lj} } \ge 1,\),

$$i = 1,2, \ldots ,m;j = 1,2, \ldots ,n$$
(14d)
$$x_{ij} = 0\,{\text{or}}\,1,\,i = 1,2, \ldots ,m;j = 1,2, \ldots ,n.$$
(14e)

Model (14a–14e) can be solved using the existing mathematical optimization software, such as lingo, Cplex. Specially, if the scale of the TSDM problem is large, we can solve the model using heuristic algorithm.

In the following, we summarize the main steps of TSDM-IH method as follows:

Step 1: Calculate the expectation ordinal value matrix \(R = (r_{ij} )_{m \times n}\) for the individuals in the A matching party and the expectation ordinal value matrix \(O = (o_{ij} )_{m \times n}\) for the individuals in the B matching party using Eqs. (4, 5).

Step 2: Calculate the perceived difference matrix \(C = (c_{ij} )_{m \times n}\) for the individuals in the A matching party and perceived difference matrix \(D = (d_{ij} )_{m \times n}\) of B matching party using Eqs. (6–9).

Step 3: Calculate the perceived value matrix \(Y = (y_{ij} )_{m \times n}\) for the individuals in the A matching party and perceived value matrix \(H = (h_{ij} )_{m \times n}\) for the individuals in the B matching party using Eqs. (10, 11, 12).

Step 4: Build the optimization model (13a–12f) based on matrixes \(Y = (y_{ij} )_{m \times n}\) and \(H = (h_{ij} )_{m \times n}\).

Step 5: Build the optimization model (14a–14e), and then solve this model.

Step 6: Obtain the optimal matching alternative.

4 Numerical Example and Analysis

In this section, an example on the TSDM problem with incomplete weak preference ordering and heterogeneous fuzzy stable demands is used to illustrate the use of the proposed TSDM-IH method. Then, we conduct the sensitivity analysis and comparison analysis on the proposed TSDM-IH method.

4.1 Numerical Example

Suppose an intermediary company (MDM) in China provided patents transfer for technology of mechanical products. The A matching party includes the individuals (or enterprises) who own the product patent technologies, and the B matching party includes the individuals (or enterprises) who purchase the product patent technologies.

Assume that six individuals \((A_{1} ,A_{2} ,A_{3} ,A_{4} ,A_{5} ,A_{6} )\) in the A matching party and seven individuals in the B matching party \((B_{1} ,B_{2} ,B_{3} ,B_{4} ,B_{5} ,B_{6} ,B_{7} )\) submit the transfer and purchasing information into the MDM, respectively. Each individual \(A_{i}\) in the A matching party provides the incomplete weak preference ordering on the individuals in the B matching party by considering several attributes, such as transfer cost of patent technologies, firm size and credibility, and each individual \(B_{j}\) in the B matching party provides the incomplete weak preference ordering on A matching party by considering several attributes, such as, capacity building of potent technologies, policy environment, innovation system, and trade amount of potent technologies. Table 1 shows the incomplete weak preference ordering information provided by the individuals in the A matching party and B matching party.

Table 1 Incomplete weak preference ordering information provided by the individuals in the A matching party and B matching party
Full size table

The MDM interviewed each individual in the A matching party and B matching party, determined the types of these individuals on the perceived differences, and used statistics test to determine their sensitive coefficient on the perceived differences, as shown in Table 2.

Table 2 The types and sensitive coefficient of individuals in the A matching party and B matching party
Full size table

Using Eqs. (4, 5), the expectation ordinal value matrix \(R = (r_{ij} )_{6 \times 7}\) for the individuals in the A matching party and preference ordinal value matrix \(O = (o_{ij} )_{6 \times 7}\) for the individuals in the B matching party are calculated in Tables 3 and 4.

Table 3 Expectation ordinal value matrix \(R = (r_{ij} )_{6 \times 7}\)
Full size table
Table 4 Expectation ordinal value matrix \(O = (o_{ij} )_{6 \times 7}\)
Full size table

Assume that individuals who belong to the weak perceived difference type submitted their desired ordinal value to MDM, as shown in Table 5.

Table 5 Desired ordinal value by the individuals with the weak perceived difference type
Full size table

Using Eqs. (6–9), the perceived difference matrix \(C = (c_{ij} )_{6 \times 7}\) for the individuals in the A matching party and perceived difference matrix \(D = (d_{ij} )_{6 \times 7}\) for the individuals in the B matching party are calculated in Tables 6, 7.

Table 6 Perceived difference matrix \(C = (c_{ij} )_{6 \times 7}\)
Full size table
Table 7 Perceived difference matrix \(D = (d_{ij} )_{6 \times 7}\)
Full size table

Using Eqs. (10, 11, 12), the perceived value matrix \(Y = (y_{ij} )_{6 \times 7}\) for the individuals in the A matching party and perceived value matrix \(H = (h_{ij} )_{6 \times 7}\) for the individuals in the B matching party are calculated in Tables 8, 9.

Table 8 Perceived value matrix \(Y = (y_{ij} )_{6 \times 7}\)
Full size table
Table 9 Perceived value matrix \(H = (h_{ij} )_{6 \times 7}\)
Full size table

Assume that the individuals express the linguistic expression on the fuzzy stable demand over the linguistic term set \(S\) = {\(s_{0}\) = ’extremely instable’,\(s_{1}\) = ’very instable’,\(s_{2}\) = ’instable’, \(s_{3}\) = ’medium’,\(s_{4}\) = ’stable’,\(s_{5}\) = ’very stable’, \(s_{6}\) = ’extremely stable’}. And their stable demands are expressed as follows:

Let \(M = 1000\), the two-sided matching decision-making model is developed using (13a–13f). And let \(w_{1} = w_{2} = 0.5\), then the two-sided matching decision-making model is transformed into the model (13a)-(13e). By solving the model (13a)-(13e), we obtain the optimal solution as: \(x_{11} = 1\), \(x_{24} = 1\), \(x_{32} = 1\), \(x_{45} = 1\), \(x_{56} = 1\), and \(x_{67} = 1\). Thus, the optimal matching alternatives are: \((A_{1} ,B_{1} )\), \((A_{2} ,B_{4} )\), \((A_{3} ,B_{2} )\), \((A_{4} ,B_{5} )\), \((A_{5} ,B_{6} )\), and \((A_{6} ,B_{7} )\).

4.2 Comparison Analysis and Sensitivity Analysis

In this subsection, we first conduct a comparison analysis to illustrate the advantage of the presented TSDM-IH method. Then, we provide a sensitivity analysis to investigate the properties of the presented TSDM-IH method.

  1. (1)

    Comparison analysis

In the comparison analysis, three cases are considered as follows:

Case A. The stability of the matching alternative is not considered;

Case B. The individuals have the same stable demand on the matching alternative;

Case C. The individuals have the heterogeneous stable demand on the matching alternative;

Specifically, the two-sided matching decision-making model under Case A is provided as follows:

$$\max \,z_{1} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {y_{ij} x_{ij} } }$$
(15a)
$$\max \,z_{2} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {h_{ij} x_{ij} } }$$
(15b)
$$s.t.\,\,\sum\limits_{i = 1}^{m} {x_{ij} \le 1} \,j = 1,2, \ldots ,n$$
(15c)
$$\sum\limits_{j = 1}^{n} {x_{ij} \le 1} ,\,\,i = 1,2, \ldots ,m$$
(15d)
$$x_{ij} = 0\,{\text{or}}\,1;\,j = 1,2, \ldots ,n.$$
(15e)

The two-sided matching decision-making model under Case B is provided as follows:

$$\max \,z_{1} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {y_{ij} x_{ij} } }$$
(16a)
$$\max \,z_{2} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {h_{ij} x_{ij} } }$$
(16b)
$$s.t.\,\sum\limits_{i = 1}^{m} {x_{ij} \le 1} ,\,j = 1,2, \ldots ,n$$
(16c)
$$\sum\limits_{j = 1}^{n} {x_{ij} \le 1} ,\,i = 1,2, \ldots ,m$$
(16d)
$$x_{ij} + \sum\limits_{{y_{il} \ge y_{ij} }} {x_{il} } + \sum\limits_{{h_{lj} \ge h_{ij} }} {x_{lj} } \ge 1$$
(16e)
$$x_{ij} = 0\,{\text{or}}\,1\,,i = 1,2, \ldots ,m,j = 1,2, \ldots ,n.$$
(16f)

And we use the presented model (13a–13f) in this paper to solve the two-sided matching decision-making under Case C (Table 10). Then, based on Example 4.1, we run the models under Cases A-C to obtain the matching alternatives as follows:

Table 10 The fuzzy stable demands expressed by the individuals in the A matching party and B matching party
Full size table

From Table 11, we obtain the observations as follows:

  1. (i)

    In Case A, compared with the current matching object \(B_{1}\), \(A_{3}\) is more preferred to match with \(B_{2}\). Meanwhile, compared with no matching object, \(B_{2}\) is more preferred to match with \(A_{3}\). Thus, (\(A_{3}\),\(B_{2}\)) will become a blocking pair, and then, the matching efficient will be influenced.

  2. (ii)

    In Case B, the stable matching alternative will be guaranteed. However, the heterogeneous fuzzy stable demand is not considered. For example, \(A_{1}\) is more preferred to match with \(B_{3}\) than \(B_{1}\). Since \(A_{1}\) has the strong stable demand on the matching alternative, \(A_{1}\) is not willing to change her/his matching object as \(B_{3}\) when \(A_{1}\) is matching with \(B_{1}\). Meanwhile, \(B_{1}\) will have the maximum perceived value when \(B_{1}\) is matching with \(A_{1}\), which will further promote the matching efficient.

  3. (iii)

    Because the presented TSDM-IH method yields the stable matching alternative through considering the heterogeneous fuzzy stable demand of two-sided matching parties, the presented TSDM-IH method can overcome the limitations under Cases A and B.

  4. (iv)

    Sensitivity analysis

Table 11 The obtained matching alternatives under different cases
Full size table

In the sensitivity analysis, we investigate the effect of the ratio of individuals with the strong perceived difference. Let \(\rho_{A}\) and \(\rho_{B}\) denote the ratio of individuals with the strong perceived difference in the A matching party and B matching party, respectively, where \(0 \le \rho_{A} ,\rho_{B} \le 1\). And let \(1 - \rho_{A}\) and \(1 - \rho_{B}\) denote the ratio of individuals with the weak perceived difference in the A matching party and B matching party, respectively.

Meanwhile, in the sensitivity analysis, we use the total perceived values of A matching party (\(PV^{A}\)), and the total perceived values of B matching party (\(PV^{B}\)) as the criteria, where \(PV^{A} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {y_{ij} x_{ij} } }\) and \(PV^{B} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {h_{ij} x_{ij} } }\).

Furthermore, we propose a simulation procedure to investigate the effect of the ratio of individuals with the strong perceived difference.

Simulation procedure I

Input: \(m\) and \(n\);

Output: \(PV^{A}\) and \(PV^{B}\).

Step 1. We randomly generate the incomplete weak ordering for each individual in the A matching party; specifically, for the individual \(A_{i}\), we first determine the number \(G^{i}\), where \(G^{i} \in [\frac{n}{2},n]\). Then, we randomly generate a permutation of \(G^{i}\) individuals, and the preference relations “\(\succ\)”, “\(\underline{ \succ }\)” or “\(\sim\)” occur with the same probability.

Step 2. We randomly generate the incomplete weak ordering for each individual in the B matching party; specifically, for the individual \(B_{j}\), we first determine the number \(U^{j}\), where \(U^{j} \in [\frac{m}{2},m]\). Then, we randomly generate a permutation of \(U^{j}\) individuals, and the preference relations “\(\succ\)”, “\(\underline{ \succ }\)” or “\(\sim\)” occur with the same probability.

Step 3. We randomly select \(m \times \rho_{A}\) and \(n \times \rho_{B}\) individuals as the individuals with the strong perceived differences, respectively.

Step 4. We calculate the perceived value matrix \(Y = (y_{ij} )_{m \times n}\) for the individuals in the A matching party and perceived value matrix \(H = (h_{ij} )_{m \times n}\) for the individuals in the B matching party. Then, we build the optimization model (13a–13f).

Step 5. By solving model (13a–13f), we obtain the optimal solution. Furthermore, we can calculate the perceived values \(PV^{A}\) and \(PV^{B}\).

Step 6. Output the values \(PV^{A}\) and \(PV^{B}\).

Furthermore, we run the simulation procedure I 100 times and obtain the average values of \(PV^{A}\) and \(PV^{B}\) under different values of \(m\), \(n\), \(\rho_{A}\) and \(\rho_{B}\).

From Fig. 2, we obtain the observations as follows:

  1. i.

    The average values of \(PV^{A}\) under different values of \(m\) and \(n\) decrease as the ratio \(\rho_{A}\) increases. This implies that the total perceived values of A matching party decrease as the number of individuals with the strong perceived difference in the A matching party increases.

  2. ii.

    The average values of \(PV^{B}\) under different values of \(m\) and \(n\) decrease as the ratio \(\rho_{B}\) increases. This implies that the total perceived values of B matching party decrease as the number of individuals with the strong perceived difference in the B matching party increases.

Fig. 2
figure 2

The average values of \(PV^{A}\) and \(PV^{B}\) under different values of \(m\), \(n\), \(\rho_{A}\), and \(\rho_{B}\)

Full size image

The observations (i) and (ii) can be explained as follows: As the number of individuals with the strong perceived difference in the A matching party (or B matching party) increases, the individuals will set the higher requirement on the matching objects. And the small perceived values of A matching party and B matching party will be obtained. As a result, the total perceived values of A matching party and B matching party will decrease.

5 Conclusion

In this paper, a method for the two-sided matching decision-making in an incomplete and heterogenous context is presented. The main works of this paper are summarized as follows:

First, we allow the individuals in the two-sided matching party provide the incomplete weak preference ordering, and propose a method to calculate the expectation ordinal values of individuals in the two-sided matching party.

Second, based on the difference on the desired matching alternatives, we divided the individuals into the individuals with strong and weak perceived differences. Then, we propose a method to calculate the perceived differences and perceived values for the individuals in the two-sided matching party.

Third, we analyze the linguistic expression on the fuzzy stable demand for each individual, and obtain the constraint for obtaining the stable alternatives. Then, we develop an optimization model which maximizes the perceived values of individuals in the two-sided matching party.

In terms of future research, there are two aspects needed to be further studied:

  1. (1)

    In the proposed TSDM problem, the small number of individuals in the two-sided matching party is involved. However, the practical TSDM problem based on the intelligent computation systems often includes the large number of individuals. It is necessary to extend the presented TSDM-IH method into the large-scale context.

  2. (2)

    When the intelligent computation systems recommend the obtained matching alternative to the individuals in the two-sided matching party, each individual will determine the strategy (i.e., accept or refuse) on the recommended matching alternative in an evolution context. Thus, it would be interesting to investigate the evolution of strategies for the proposed TSDM problem.