Enhancing ELECTRE I Method with Complex Spherical Fuzzy Information

Abstract

This article is concerned to delineate the strategic approach of ELiminating Et Choice Translating REality (ELECTRE) method for multi-attribute group decision-making (MAGDM) in terms of complex spherical fuzzy sets. The feasible, well-suited, and marvelous structure of complex spherical fuzzy set compliments the decision-making efficiency and ranking calibre of ELECTRE I approach to present a beneficial and supreme aptitude strategy for MAGDM. Beside the proposed methodology, a few non-fundamental properties of complex spherical fuzzy weighted averaging (CSFWA) operator inclusive of shift invariance, homogenous, linearity, and additive property are also explored. The proposed procedure validates the individual opinions into an acceptable form by the dint of CSFWA operator and the aggregated opinions are further analyzed by the proposed complex spherical fuzzy- ELECTRE I (CSF-ELECTRE I) method. Within the consideration of proposed methodology, normalized Euclidean distances of complex spherical fuzzy numbers are also contemplated. In CSF-ELECTRE I method, the score, accuracy, and refusal degrees determine the concordance and discordance sets for each pair of alternatives to calculate the concordance and discordance indices, respectively. Based on aggregated outranking matrix, a decision graph is constructed to attain the ELECTREcally outranked solutions and the best alternative. This article provides supplementary approach at the final step to profess a linear ranking order of the alternatives. The versatility and feasibility of the presented method are embellished with two case studies from the business and IT field. Moreover, to ratify the intensity and aptitude of the presented methodology, we provide a comparative study with complex spherical fuzzy-TOPSIS method.

1 Introduction

Many innovative pedagogical studies [1,2,3,4] have admired group decision-making to investigate various issues and problems. The explicit evaluation of the experts opinions about the feasible alternatives with respect to multiple conflicting attributes is interpreted as problem solving multi-attribute group decision-making (MAGDM).

1.1 Related Work

There are numerous MAGDM techniques to solve the problems from science, business, economy, and management; one of them is an ELECTRE [5] method, introduced by Benayoun in 1966. The ELECTRE outranking method is the most extensively used MAGDM method that performs pair-wise comparison of alternatives on the basis of concordance and discordance sets which yield to eliminate the less beneficial choice and identify the outranked solution. Figueria et al. [6] presented a detailed study about ELECTRE family that manage discrete parameters possessing quantifiable nature together with providing a complete ranking of the alternatives. However,the ELECTRE family encompasses the following ELECTRE methods; ELECTRE I, ELECTRE II, ELECTRE III, ELECTRE IV, and ELECTRE TRI methods. Later on, the ELECTRE method was pertained as ELECTRE I method and illustrated by many precious and useful advancements. Furthermore, the most popular ELECTRE I method is elected for comprehensive and global explorations.

In classical ELECTRE methods, the alternatives and the criteria weights cannot be measured accurately, because some decision experts used linguistic variables to enunciate their opinions [7]. Chen et al. [8, 9] proposed new decision-making methods. Since the judgments of the decision experts made under the circumstances of tight deadlines, insufficient information, and lack of refining facilities, therefore, the decision results are imprecise and doubtful. To handle imprecision and inconsistency of decision data, Zadeh [10] took initiative to propose fuzzy set (FS) theory in 1965. In FSs, a membership value from unit interval is federated to an object interpolating the satisfaction level of object related to a certain parameter. Analysts codify the decision opportunities in MAGDM problems using the mathematical intervention under fuzzy context. In fact, various surveys have been performed on extended ELECTRE methods in fuzzy perspective, such as Kabak et al. [11] introduced an MADM technique using the combination of Fuzzy-ELECTRE approach with Fuzzy TOPSIS and Fuzzy ANP for snipper selection. Vahdani et al. [12] introduced the novel ELECTRE model with the concepts of interval weights and fuzzy data. Alghamdi et al. [13] and Akram et al. [14] extended ELECTRE I method under fuzzy and bipolar neutrosophic environment, respectively. Atanassov [15] put forward the idea of intuitionistic fuzzy set (IFS) that is frequently favorable to integrate the additional feature of dissatisfaction degree $\gamma$, along with the central constitute of satisfaction degree $\alpha$ in FSs. Being an extension of FSs, IFSs have been extensively used in MAGDM fields but entirely restricted with condition $\alpha + \gamma \le 1$. Intuitionistic fuzzy-ELECTRE I method was introduced by Rouyendegh [16] and Chen et al. [17] for the selection of company site and project manager, respectively. Mishra et al. [18] presented the idea of divergence measured based on the ELECTRE method under intuitionistic fuzzy environment to analyze the performance of cellular mobile telephone service providers.

In 2013, Yager [19] introduced the notion of Pythagorean fuzzy sets $(P_{Y}FSs)$ to subdue the deficit of the IFSs by the condition $\alpha ^2+ \gamma ^2\le 1$. Later on, Akram et al. [20] proposed the $P_YF$-ELECTRE I method and utilized it for the selection of solid-waste management plant and for the selection of water desalination plant. Moreover, Akram et al. [21] extended ELECTRE II method in the context of $P_{Y}FS$ that comprises the feature of hesitation.

However, the IFSs and $P_YFSs$ were quite proficient to deal with degrees of truth and falsity, but they capitulate to attend the abstinence part of judgement. To top this flaw, a novel model of picture fuzzy set (PFS) was defined by Cuong and Kreinovich [22] that presents the inconsistent data in terms of truthness degree, falsity degree, and abstinence degree with regard to the restriction $\alpha + \beta +\gamma \le 1$. Liang et al. [23] integrated picture fuzzy EDAS-ELECTRE method and judge the cleaner production level in gold mines. Even though the theory of Cuong is more adjacent to human nature than the existing theories, but sporadically sum of their associated degrees could exceed 1.

Taking forte of circumstances, Gundogdu and Kahraman [24] proposed spherical fuzzy sets (SFSs), which have the ability to supervise three types of obscure data as well as expanded the space of associated degrees by the condition that $\alpha ^2+ \beta ^2+\gamma ^2 \le 1$. Kahraman et al. [25] exploited a MAGDM problem for the selection of hospital location by SFSs. Ashraf et al. [26] developed spherical fuzzy t-norms and t-conorms for the advancement of the aggregation operators and utilized for a food circulation center evaluation problem. A graphical representation of SFS is shown in Fig. 1. Figure 1 amply explains that the space of spherical fuzzy membership grades is above and beyond the space of Pythagorean fuzzy membership grades and intuitionistic fuzzy membership grades due to their respective constraint conditions.

Fig. 1

Graphical representation of spherical fuzzy set

All the existing fuzzy models may not be attributed for full insight information and incapable to carry out alteration during a stated period of time. Moreover, variations in periodic data arise uncertainty and vagueness in the process of data and as consequences the current ideas are insufficient to address the periodic type information in our real-life MAGDM problems. To settle this issue, complex fuzzy sets (CFSs) were initiated by Ramot et al. [27] which handle the two-dimensional insight information in the form of complex valued unit disc. The membership function in CFSs is $\alpha = \mu e^{i2\pi f}$ which consists of two parts; $\mu$ denoting amplitude term and f denoting the periodic term that is central feature of CFSs. Owing to the gradual increase in real-life complexities, researchers extended fuzzy models in the Ramot’s frame for example: Alkouri and Salleh [28] presented complex intuitionistic fuzzy sets (CIFSs), Ullah et al. [29] developed theory for complex Pythagorean fuzzy sets $(CP_{Y}FSs)$, and Akram et al. [30] commenced work on complex picture fuzzy sets (CPFSs) by integrating membership function $\alpha = \mu e^{i2\pi f}$, non-membership function $\gamma = \nu e^{i2\pi h}$, and neutral function $\beta = \rho e^{i2\pi g}$. Akram et al. [31] also put forward the extension of ELECTRE I method which is competent enough to handle $CP_{Y}F$ data.

Our consideration and interest is relevant to the latest evolution in the family of complex fuzzy models that is superior and highly accomplished than the existing theories, known as complex spherical fuzzy sets CSFSs proposed by Akram et al. [32]. Additionally, CSFSs easily manipulate the two-dimensional neutral information along with the restrictions ${\mu }^{2}+{\rho }^{2}+{\nu }^{2} \le 1$ and ${f}^{2}+{g}^{2}+ {h}^{2} \le 1$. Moreover, Akram et al. [32, 33] defined MAGDM approaches, namely, CSF-VIKOR and CSF-TOPSIS techniques to solve numerical examples from business field and for the selection of best water supply strategy for a village of Iran, respectively.

1.2 Uses/Importance of Complex Spherical Fuzzy Information

Though the existing structures of fuzzy set theory are extremely powerful to deal with hazy information, but the radical development of FSs, namely, CSFS, for two-dimensional uncertain data is more feasible and is readily prevailing on the existing models. The supreme CSFS can be converted to $CP_{Y}FS$, CIFS, CFS, and SFS by considering the relevant data and left of the supplemental information (neutral membership, non-membership, or phase terms) can be comprehended as zero.

There are numerous real-life applications of the complex spherical fuzzy information and can be illustrated through an instructive example. We can use CSF information to observe the day and night traffic conflicts on four-way road junctions. The three types of vehicle-to-vehicle traditional traffic conflicts are as follows: merging, diverging, and crossing conflicts (shown in Fig. 2). In addition, Fig. 2 provides compelling indication about the conflicting points on four-way junction and there are about 19 conflicting points in which probably six are merging conflicts, nine are crossing conflicts, and four are diverging conflicts.

Fig. 2

Conflicting points on four-way junction

To make day and night check on traffic conflicts, the complete information of possible conflicts is required that can be entirely demonstrated by CSF information. On a random four-way junction, the amplitude term of membership grade, neutral grade, and non-membership grade shows the day-time merging conflict, crossing conflict, and diverging conflict, respectively. On the other hand, the phase term of membership grade, neutral grade, and non-membership grade indicates the night-time merging conflict, crossing conflict, and diverging conflict, respectively.

If on an arbitrary four-way junction, during day-time, there are about one merging, five crossing, and two diverging conflicts, then we can allocate amplitude term 0.1, 0.7, and 0.3 to the membership grade, neutral grade, and non-membership grade, respectively. On the other hand, if the number of traffic conflicts is 12 on night-time, in which probably 3 conflicts are merging, 4 conflicts are crossing, and 5 conflicts are diverging, then we can allocate phase term $0.2\pi$, $1.2\pi$, and $1.4\pi$ to the membership grade, neutral grade, and non-membership grade, respectively. These figures can completely rendered as a $CSFN\ (0.1e^{i0.2\pi }, 0.7e^{i0.2\pi }, 0.3e^{i1.4\pi })$ which delineates the information regarding the traffic conflicts on a four-way junction.

Moreover, the CSF information also contributes to analyze the traffic conflicts on any type of road intersections as well as assists to describe the flow of traffic in a required period of time.

However, if we formally employ SFS to depict information about traffic conflicts, then it will only contain data about day-time traffic conflicts. It turns out that, the SFS does not catch up any information regarding conflicts during night as it is incompetent to detain two-dimensional information. If we expend $CP_{Y}FS$ to manage data about conflicts on a four-way junction, it can successfully represent the two-dimensional data and can capture the information about the merging conflicts and diverging conflicts. However, it does not comprise any detail about day and night crossing conflicts on four-way junction. These facts raise the standards of CSFS within the existing model as it endows information about day and night traffic conflicts along with merging, crossing, and diverging conflicts.

1.3 Motivation and Objective of Presented Work

In this research paper, we provided CSF-ELECTRE I method to solve realistic MAGDM problems. The perspicacity and complex spherical fuzzy data in decision-making ameliorated by the presented technique.

Mainly, the motivations of this manuscript are as follows:

• The complex spherical fuzzy sets possess a high calibre structure to represent obscure human opinions thoroughly in the terms of positive response, negative response, and neutrality with the another prevalent and tremendous characteristic of capturing the two-dimensional information. These dominant features of the CSFS convince us to admit the influence and supermacy of prevalent model over the other existing models of fuzzy set theory including CPFS, $CP_YFS$, CIFS, SFS, PFS, etc.

• The main incentive of this study is to benefit from the competency, efficiency, and broader space of the CSFSs under decision-making scenarios to cope with two-dimensional data. Moreover, the decision-making skill and influencing theory of the family of outranking strategies, namely, ELECTRE methods, shifted our attention to boost the decision-making calibre of an outranking approach by merging it with the beneficial and adequate environment of CSFS.

• The current decision-making methodologies that are encompassing the fuzzy-ELECTRE, IF-ELECTRE, $P_YF$-ELECTRE, and $CP_{Y}F$-ELECTRE methodologies are confined to compile vague data. However, there are few realistic applications involving two-dimensional abstinence information and the sum of associated degrees is several times greater than one. These inadequacies of the existing methods instigate us to commingle the ELECTRE I method with proficient CSFSs, namely, CSF-ELECTRE I model for the critique of MAGDM problems.

• Although, there occurs many outranking procedures in the literature of fuzzy set theory, but these versions of ELECTRE method can deal with the one-dimensional data. On the other hand, the $CP_YF$-ELECTRE I method competently proceeds to compile the two-dimensional obscure information for decision-making purpose. The expertise of the ascendant $CP_{Y}F$-ELECTRE I method is insufficient to contend with abstinence knowledge of periodic nature as the theory of $CP_{Y}FSs$ seems incompatible and inadequate to manage neutral part of the information.

• Another motivation of this study include deficiency of the existing model to represent the abstinence part of the imprecise information. The worth of the proposed technique is uprisen due to the real-valued membership functions of supreme SFSs that are inept to handle two-dimensional information of hazy human judgements.

• To confront the MAGDM problems for the frequent model, a mathematical technique of CSF-ELECTRE I is developed by synthesizing the theoretical background of ELECTRE method with the persuadable configuration of CSFS.

For the aforementioned reasons, we initiate an outranking approach, namely, CSF-ELECTRE I method, for solving MAGDM problems provided with CSF information.

1.4 Contribution of Presented Work

The endowment and major contributions of the proposed method are:

• The foremost aim of this study is set forth a ground-breaking outranking strategy to manipulate the complex spherical fuzzy information adroitly, concretely, and expertly with high accuracy for the sake of MAGDM.

• The proposed CSF-ELECTRE I method focuses on the prominent notions of concordance and discordance sets which are novelly defined by virtue of score, accuracy, and refusal degrees of complex spherical fuzzy numbers. The strategy works to indicate the best alternative by employing the outranking relation as well as outranking graphs.

• Furthermore, a comprehensive view of the proposed procedure is portrayed by the means of a flowchart diagram that delineates the stepwise procedure thoroughly.

• The practical application of the proposed CSF-ELECTRE I method is unfolded by the means of two case studies from the fields of business and IT to highlight the significance and rationality of the presented technique.

• Finally, comprehensive comparisons of the developed theory with CSF-TOPSIS method are imparted to demonstrate the capacity and accuracy of the CSF-ELECTRE I method. Moreover, the bar graphs are employed to visualize the comparison results of two MAGDM techniques.

The rest of the paper is arranged as follows: Sect. 2 describes some definitions and some useful tools like score function, accuracy function, averaging operator, and normalized Euclidean distance related to CSFSs. Section 3 describes some important and non-fundamental properties of complex spherical fuzzy averaging operator. In Sect. 4, theory of CSF-ELECTRE I method is developed. In Sect. 5, two MAGDM problems are addressed and resolved by the proposed technique. Section 6 comprises the numerical and theoretical comparisons of the presented approach with some existing methods. In Sect. 7, we conclude the paper with some limitations and future directions.

2 Preliminaries

Definition 1

[32] Let $\mathcal {Z}$ be a universal set. A complex spherical fuzzy set $(CSFS)\ \varphi$ on $\mathcal {Z}$ is of the form

$$\begin{aligned} \varphi= \,& {\langle (z, \alpha _{\varphi }(z),\beta _{\varphi }(z), \gamma _{\varphi }(z)) | z\in \mathcal {Z}\rangle },\\= \,& {\langle (z, \mu _{\varphi }(z)e^{i2\pi f_{\varphi }(z)},\rho _{\varphi }(z)e^{i2\pi g_{\varphi }(z)}, \nu _{\varphi }(z)e^{i2\pi h_{\varphi }(z)}) | z\in \mathcal {Z}\rangle }, \end{aligned}$$

where $i=\sqrt{-1}$, $\mu _{\varphi }(z), \rho _{\varphi }(z)$, $\nu _{\varphi }(z)$, denoting the amplitude terms, and $f_{\varphi }(z), g_{\varphi }(z)$, $h_{\varphi }(z)$ , denoting the periodic terms, are restricted to closed unit interval with the restriction that for every $z\in \mathcal {Z}$, ${\mu _{\varphi }(z)}^{2}+{\rho _{\varphi }(z)}^{2}+{\nu _{\varphi }(z)}^{2} \le 1$ and ${f_{\varphi }(z)}^{2}+{g_{\varphi }(z)}^{2}+ {h_{\varphi }(z)}^{2} \le 1$. The degree of refusal of z in $\mathcal {Z}$ is defined as

$$\begin{aligned} \varPsi _{\varphi }(z)= \,& \sqrt{1-({\mu _{\varphi }(z)}^2 + {\rho _{\varphi }(z)}^2 + {\nu _{\varphi }(z)}^2)}e^{i2\pi \sqrt{1-({f_{\varphi }(z)}^2 + {g_{\varphi }(z)}^2 + {h_{\varphi }(z)}^2)}}. \end{aligned}$$

For ease, the triplet $(\alpha _{\varphi }, \beta _{\varphi },\gamma _{\varphi })= (\mu _{\varphi }e^{i2\pi h_{\varphi }},\rho _{\varphi }e^{i2\pi g_{\varphi }},\nu _{\varphi }e^{i2\pi h_{\varphi }})$ is defined as complex spherical fuzzy number (CSFN).

Definition 2

[32] Let $\varphi = (\mu _{\varphi }e^{i2\pi f_{\varphi }},\rho _{\varphi }e^{i2\pi g_{\varphi }}, \nu _{\varphi }e^{i2\pi h_{\varphi }})$ be CSFN. The score function $Sc( \varphi )$ is

$$\begin{aligned} Sc({ \varphi }) = {\mu _{\varphi }(z)}^2 - {\rho _{\varphi }(z)}^2 - {\nu _{\varphi }(z)}^2 + {f_{\varphi }(z)}^2 - {g_{\varphi }(z)}^2 - {h_{\varphi }(z)}^2 , \end{aligned}$$

(1)

where $Sc( \varphi ) \in [-2,2]$. The accuracy function $Ac({ \varphi })$ is defined as

$$\begin{aligned} Ac({ \varphi }) = [{\mu _{\varphi }(z)}^2 + {\rho _{\varphi }(z)}^2 + {\nu _{\varphi }(z)}^2] + {f_{\varphi }(z)}^2 + {g_{\varphi }(z)}^2 + {h_{\varphi }(z)}^2, \end{aligned}$$

(2)

where $Ac( \varphi ) \in [0,2]$.

Definition 3

[32] Let $\varphi _{1} = ( \mu _{1}e^{i2\pi f_{1}},\rho _{1}e^{i2\pi g_{1}}, \nu _{1}e^{i2\pi h_{1}})$ and $\varphi _{2} = ( \mu _{2}e^{i2\pi f_{2}},\rho _{2}e^{i2\pi g_{2}}, \nu _{2}e^{i2\pi h_{2}})$ be two CSFNs

• 1. If $Sc({ \varphi _{1}})< Sc({\varphi _{2}})$, then $\varphi _{1} \prec \varphi _{2}$ ($\varphi _{1}$ is inferior to $\varphi _{2})$.

• 2. If $Sc({ \varphi _{1}})>Sc({\varphi _{2}})$, then $\varphi _{1} \succ \varphi _{2}$ ($\varphi _{1}$ is superior to $\varphi _{2})$.

• 3. If $Sc({ \varphi _{1}}) = Sc({\varphi _{2}})$, then

  • (i) $Ac({\varphi _{1}})<Ac({\varphi _{2}})$, then $\varphi _{1} \prec \varphi _{2}$ ($\varphi _{1}$ is inferior to $\varphi _{2});$

  • (ii) $Ac({\varphi _{1}})>Ac({\varphi _{2}})$, then $\varphi _{1} \succ \varphi _{2}$ ($\varphi _{1}$ is superior to $\varphi _{2});$

  • (iii) $Ac({\varphi _{1}})=Ac({\varphi _{2}})$, then $\varphi _{1} \sim \varphi _{2}$ ($\varphi _{1}$ is equivalent to $\varphi _{2})$.

Definition 4

[32] Let $\varphi _{1} = ( \mu _{1}e^{i2\pi f_{1}},\rho _{1}e^{i2\pi g_{1}}, \nu _{1}e^{i2\pi h_{1}})$ and $\varphi _{2} = ( \mu _{2}e^{i2\pi f_{2}},\rho _{2}e^{i2\pi g_{2}}, \nu _{2}e^{i2\pi h_{2}})$ be two CSFNs and $\hbar > 0.$ The related operations associated with CSFNs are

$$\begin{aligned} \varphi _{1}\bigoplus \varphi _{2}= \,& \Bigg ( \sqrt{\mu ^{2}_{1}+\mu ^{2}_{2}-\mu ^{2}_{1}\mu ^{2}_{2}}e^{i2\pi \sqrt{{f^{2}_{1}+f^{2}_{2}-f^{2}_{1}f^{2}_{2}}^{2}}}, \rho _{1}\rho _{2}e^{i2\pi g_{1}g_{2}}, \nu _{1}\nu _{2}e^{i2\pi h_{1}h_{2}} \Bigg ),\\ \varphi _{1}\bigotimes \varphi _{2}= \,& \Bigg ( \mu _{1}\mu _{2}e^{i2\pi f_{1}f_{2}},\sqrt{\rho ^{2}_{1}+\rho ^{2}_{2}-\rho ^{2}_{1}\rho ^{2}_{2}}e^{i2\pi \sqrt{g^{2}_{1}+g^{2}_{2}-g^{2}_{1}g^{2}_{2}}} ,\sqrt{\nu ^{2}_{1}+\nu ^{2}_{2}-\nu ^{2}_{1}\nu ^{2}_{2}} e^{i2\pi \sqrt{h^{2}_{1}+h^{2}_{2}-h^{2}_{1}h^{2}_{2}}}\Bigg ),\\ \hbar \varphi _{1}= \,& \Bigg (\sqrt{1-(1-\mu ^{2}_{1})^\hbar }e^{i2\pi \sqrt{1-(1-{f_{1}}^{2})^\hbar }}, \rho _{1}^\hbar e^{i2\pi {g_{1}}^\hbar }, \nu _{1}^\hbar e^{i2\pi {h_{1}}^\hbar } \Bigg ),\\ \varphi ^\hbar _{1}= \,& \Bigg (\mu ^\hbar _{1}e^{i2\pi {f_{1}^\hbar }}, \sqrt{1-(1-\rho ^{2}_{1})^\hbar }e^{i2\pi \sqrt{1-(1-g_{1}^{2})^{\hbar }}}, \sqrt{1-(1-\nu ^{2}_{1})^\hbar }e^{i2\pi \sqrt{1-(1-{h_{1}}^{2})^\hbar }}\Bigg ). \end{aligned}$$

Definition 5

[32] The normalized Euclidean distance between two $CSFNs\ \varphi _{1}= ( \mu _{1}e^{i2\pi f_{1}},\rho _{1}e^{i2\pi g_{1}}, \nu _{1}e^{i2\pi h_{1}})$ and $\varphi _{2}= ( \mu _{2}e^{i2\pi f_{2}},\rho _{2}e^{i2\pi g_{2}},\nu _{2}e^{i2\pi h_{2}})$ is calculated as follows:

$$\begin{aligned} d(\varphi _{1}, \varphi _{2})= \,& \sqrt{\frac{({{\mu }^{2}_{1}} -{\mu }^{2}_{2})^2 + ({\rho }^2_{1} -{\rho }^2_{2})^2 + ({\nu }^2_{1} -{\nu }^2_{2})^2 + ({f}^2_{1} -{f}^2_{2})^2 + ({g}^2_{1} -{g}^2_{2})^2 + ({h}^2_{1} -{h}^2_{2})^2}{3}}. \end{aligned}$$

Definition 6

[32] Let $\varphi _{j}= ( \mu _{j}e^{i2\pi f_{j}},\rho _{j}e^{i2\pi g_{j}},\nu _{j}e^{i2\pi h_{j}})\ (j=1,2,3,\ldots , l)$ be a collection of CSFNs and $\vartheta = (\vartheta _{1},\vartheta _{2}, \ldots \vartheta _{l} )^{T}$ be the weight vector of $\varphi _{j}$ with $\vartheta > 0$ and $\sum \nolimits _{j=1}^{l} \vartheta _{l} = 1.$ The complex spherical fuzzy weighted average (CSFWA) operator is defined as

$$\begin{aligned}&CSFWA (\varphi _{1}, \varphi _{2}, \ldots , \varphi _{l}) = \vartheta _{1}\varphi _{1} \oplus \vartheta _{2}\varphi _{2} \oplus \ldots \oplus \vartheta _{l}\varphi _{l} \nonumber \\&\quad =\Bigg (\sqrt{1- \displaystyle \prod _{j=1}^{l}(1-\mu _{j})^{\vartheta _{j}}}e^{i2\pi \sqrt{1- \displaystyle \prod _{j=1}^{l}(1-f_{j})^{\vartheta _{j}}}}, (\displaystyle \prod _{j=1}^{l}(\rho _{j})^{\vartheta _{j}})e^{i2\pi (\displaystyle \prod _{j=1}^{l}(g_{j})^{\vartheta _{j}})}, (\displaystyle \prod _{j=1}^{l}(\nu _{j})^{\vartheta _{j}})e^{i2\pi (\displaystyle \prod _{j=1}^{l}(h_{j})^{\vartheta _{j}})}\Bigg ). \end{aligned}$$

(3)

3 Some Properties of CSFWA Operator

Here, we described some mathematical properties of CSFWA operator other than the fundamental properties (idempotency, boundedness, and monotonicity) that are already discussed by Akram et al. [32].

Theorem 1

(Shift invariant) Let $\varphi _{j}= ( \mu _{j}e^{i2\pi f_{j}},\rho _{j}e^{i2\pi g_{j}},\nu _{j}e^{i2\pi h_{j}})\ (j=1,2,3,\ldots , l)$ be a collection of CSFNs and $\vartheta = (\vartheta _{1},\vartheta _{2}, \ldots \vartheta _{l} )^{T}$ be the normalized weight vector of $\varphi _{j}$, and then, $\forall \hbar \in (0, 1)$, $\forall j$

$$\begin{aligned} CSFWA (\varphi _{1}+\hbar , \varphi _{2}+\hbar , \ldots , \varphi _{l}+\hbar ) = CSFWA (\varphi _{1}, \varphi _{2}, \ldots , \varphi _{l}) +\hbar . \end{aligned}$$

Proof

Let $\varphi _{j}= ( \mu _{j}e^{i2\pi f_{j}},\rho _{j}e^{i2\pi g_{j}},\nu _{j}e^{i2\pi h_{j}})\ (j=1,2,3,\ldots , l)$ be a collection of CSFNs and $\vartheta = (\vartheta _{1},\vartheta _{2}, \ldots \vartheta _{l} )^{T}$ be the normalized weight vector of $\varphi _{j}$ along with $\hbar \in (0, 1)$, and then

$$\begin{aligned}&CSFWA (\varphi _{1}+\hbar , \varphi _{2}+\hbar , \ldots , \varphi _{l}+\hbar ) = \vartheta _{1}(\varphi _{1}+\hbar ) \oplus \vartheta _{2}(\varphi _{2}+\hbar ) \oplus \ldots \oplus \vartheta _{l}(\varphi _{l}+\hbar ) \quad {~~~(\text {using~Eq. ~3})}\\&\quad =(\vartheta _{1}\varphi _{1} \oplus \vartheta _{2}\varphi _{2} \oplus \ldots \oplus \vartheta _{l}\varphi _{l})+(\vartheta _{1}\hbar + \vartheta _{2}\hbar + \ldots + \vartheta _{l}\hbar )\\&\quad = (\vartheta _{1}\varphi _{1} \oplus \vartheta _{2}\varphi _{2} \oplus \ldots \oplus \vartheta _{l}\varphi _{l})+ \hbar \quad ~~~~~~~~~~~~~~~~~~~~(\because \displaystyle \sum _{j=1}^{l} \vartheta _{l} = 1 )\\&\quad = CSFWA (\varphi _{1}, \varphi _{2}, \ldots , \varphi _{l}) + \hbar . \end{aligned}$$

$\square$

Theorem 2

(Homogenous) Let $\varphi _{j}= ( \mu _{j}e^{i2\pi f_{j}},\rho _{j}e^{i2\pi g_{j}},\nu _{j}e^{i2\pi h_{j}})\ (j=1,2,3,\ldots , l)$ be a collection of CSFNs and $\vartheta = (\vartheta _{1},\vartheta _{2}, \ldots \vartheta _{l} )^{T}$ be the normalized weight vector of $\varphi _{j}$, and then, $\forall \hbar \in (0, 1)$, $\forall j$

$$\begin{aligned} CSFWA (\hbar \varphi _{1}, \hbar \varphi _{2}, \ldots , \hbar \varphi _{l}) = \hbar \left( CSFWA (\varphi _{1}, \varphi _{2}, \ldots , \varphi _{l})\right) . \end{aligned}$$

Proof

Let $\varphi _{j}= ( \mu _{j}e^{i2\pi f_{j}},\rho _{j}e^{i2\pi g_{j}},\nu _{j}e^{i2\pi h_{j}})\ (j=1,2,3,\ldots , l)$ be a collection of CSFNs and $\vartheta = (\vartheta _{1},\vartheta _{2}, \ldots \vartheta _{l} )^{T}$ be the normalized weight vector of $\varphi _{j}$ along with $\hbar \in (0, 1)$, and then

$$\begin{aligned}&CSFWA (\hbar \varphi _{1}, \hbar \varphi _{2}, \ldots , \hbar \varphi _{l}) = \vartheta _{1}(\hbar \varphi _{1}) \oplus \vartheta _{2}(\hbar \varphi _{2}) \oplus \ldots \oplus \vartheta _{l}(\hbar \varphi _{l}) \quad {~~~(using~Eq.~3)}\\&\quad =\hbar (\vartheta _{1}\varphi _{1} \oplus \vartheta _{2}\varphi _{2} \oplus \ldots \oplus \vartheta _{l}\varphi _{l})\\&\quad =\hbar \left( CSFWA (\varphi _{1}, \varphi _{2}, \ldots , \varphi _{l})\right) . \end{aligned}$$

$\square$

Theorem 3

(Linearity) Let $\varphi _{j}= ( \mu _{j}e^{i2\pi f_{j}},\rho _{j}e^{i2\pi g_{j}},\nu _{j}e^{i2\pi h_{j}})\ (j=1,2,3,\ldots , l)$ be a collection of CSFNs and $\vartheta = (\vartheta _{1},\vartheta _{2}, \ldots \vartheta _{l} )^{T}$ be the normalized weight vector of $\varphi _{j}$, and then, $\forall \hbar , b \in (0, 1)$, $\forall j$

$$\begin{aligned} CSFWA (\hbar \varphi _{1}+\flat , \hbar \varphi _{2}+\flat , \ldots , \hbar \varphi _{l}+\flat ) = \hbar \left( CSFWA (\varphi _{1}, \varphi _{2}, \ldots , \varphi _{l})\right) + b. \end{aligned}$$

Proof

Let $\varphi _{j}= ( \mu _{j}e^{i2\pi f_{j}},\rho _{j}e^{i2\pi g_{j}},\nu _{j}e^{i2\pi h_{j}})\ (j=1,2,3,\ldots , l)$ be a collection of CSFNs and $\vartheta = (\vartheta _{1},\vartheta _{2}, \ldots \vartheta _{l} )^{T}$ be the normalized weight vector of $\varphi _{j}$ along with $\hbar , b \in (0, 1)$, and then

$$\begin{aligned}&CSFWA (\hbar \varphi _{1}+b, \hbar \varphi _{2}+b, \ldots , \hbar \varphi _{l}+b) = \vartheta _{1}(\hbar \varphi _{1}+b ) \oplus \vartheta _{2}(\hbar \varphi _{2}+b ) \oplus \ldots \oplus \vartheta _{l}(\hbar \varphi _{l}+b ) \quad {~~~(\text {using~Eq. ~3)}}\\&\quad =(\vartheta _{1}\hbar \varphi _{1} \oplus \vartheta _{2}\hbar \varphi _{2} \oplus \ldots \oplus \vartheta _{l}\hbar \varphi _{l})+(\vartheta _{1}b + \vartheta _{2}b + \ldots + \vartheta _{l}b)\\&\quad = \hbar (\vartheta _{1}\varphi _{1} \oplus \vartheta _{2}\varphi _{2} \oplus \ldots \oplus \vartheta _{l}\varphi _{l})+b \quad ~~~~~~~~~~~~~~~~~~~~(\because \displaystyle \sum _{j=1}^{l} \vartheta _{l} = 1 )\\&\quad = \hbar \left( CSFWA (\varphi _{1}, \varphi _{2}, \ldots , \varphi _{l})\right) + b. \end{aligned}$$

$\square$

Remark 1

We can say that: the CSFWA operator is linear if and only if CSFWA operator is

• i shift invariant and

• ii homogenous.

Theorem 4

(Additive property) Let $\varphi _{j}$ and $\aleph _{j}\ (j=1,2,3,\ldots , l)$ be two families of CSFNs and $\vartheta = (\vartheta _{1},\vartheta _{2}, \ldots \vartheta _{l} )^{T}$ be the normalized weight vector of both $\varphi _{j}$ and $\aleph _{j}$, and then $\forall j$

$$\begin{aligned} CSFWA (\varphi _{1}\oplus \aleph _{1} , \varphi _{2}\oplus \aleph _{2}, \ldots , \varphi _{l}\oplus \aleph _{l}) = CSFWA (\varphi _{1} , \varphi _{2}, \ldots , \varphi _{l})\oplus CSFWA (\aleph _{1} ,\aleph _{2}, \ldots , \aleph _{l}). \end{aligned}$$

Proof

Let $\varphi _{j}= ( \mu _{j}e^{i2\pi f_{j}},\rho _{j}e^{i2\pi g_{j}},\nu _{j}e^{i2\pi h_{j}})\ (j=1,2,3,\ldots , l)$ be a collection of CSFNs and $\vartheta = (\vartheta _{1},\vartheta _{2}, \ldots \vartheta _{l} )^{T}$ be the normalized weight vector of $\varphi _{j}$ along with $\hbar \in (0, 1)$, and then

$$\begin{aligned}&CSFWA (\varphi _{1}\oplus \aleph _{1} , \varphi _{2}\oplus \aleph _{2}, \ldots , \varphi _{l}\oplus \aleph _{l}) = \vartheta _{1}(\varphi _{1}\oplus \aleph _{1}) \oplus \vartheta _{2}(\varphi _{2}\oplus \aleph _{2}) \oplus \ldots \oplus \vartheta _{l}(\varphi _{l}\oplus \aleph _{l}) \quad {~~~(\text {using~Eq. ~3)}}\\&\quad =(\vartheta _{1}\varphi _{1} \oplus \vartheta _{2}\varphi _{2} \oplus \ldots \oplus \vartheta _{l}\varphi _{l})\oplus (\vartheta _{1}\aleph _{1} \oplus \vartheta _{2}\aleph _{2} \oplus \ldots \oplus \vartheta _{l}\aleph _{l})\\&\quad = CSFWA (\varphi _{1} , \varphi _{2}, \ldots , \varphi _{l})\oplus CSFWA (\aleph _{1} ,\aleph _{2}, \ldots , \aleph _{l}). \end{aligned}$$

$\square$

4 Complex Spherical Fuzzy-ELECTRE I Method

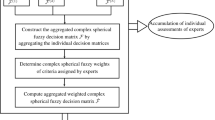
In this section, the CSFS is merged with ELECTRE I method for the extension of a novel approach in the favor of multi-attribute group decision-making (MAGDM), named as complex spherical fuzzy-ELECTRE I (CSF-ELECTRE I) method where both the allocations of the alternatives with respect to criteria and the weights of the criteria are in the mould of CSFNs. The exegesis for CSF-ELECTRE I method in MAGDM scenario pursue in the following manner:

Step 01::

Construct the complex spherical fuzzy performance matrix.

Let $\mathcal {Z}_{1}$, $\mathcal {Z}_{2}$, $\mathcal {Z}_{3}$, $\ldots$, $\mathcal {Z}_{b}$ be the alternatives and $\mathcal {P}_{1}$, $\mathcal {P}_{2}$, $\mathcal {P}_{3}$, $\ldots$, $\mathcal {P}_{d}$ be the decision attributes according to which the consultants $\mathcal {K}_{1}$, $\mathcal {K}_{2}$, $\mathcal {K}_{3}$, $\ldots$, $\mathcal {K}_{a}$ allocate CSFNs representing linguistic terms provided by the MAGDM deputation. Then, the complex spherical fuzzy performance matrix (CSFPM) $R^{(w)}$ with the entities $R^{(w)}_{uv} = (\alpha ^{(w)}_{uv}, \beta ^{(w)}_{uv}, \gamma ^{(w)}_{uv})= ( \mu ^{(w)}_{uv}e^{i2\pi f^{(w)}_{uv}}, \rho ^{(w)}_{uv}e^{i2\pi g^{(w)}_{uv}}, \nu ^{(w)}_{uv}e^{i2\pi h^{(w)}_{uv}})$ are in accordance with each expert $\mathcal {K}_{w}$. The MAGDM concerns can be delineated by the following decision-matrix:

$$\begin{aligned} R^{(w)} = \left( \begin{array}{cccc} ( \alpha ^{(w)}_{11} , \beta ^{(w)}_{11} , \gamma ^{(w)}_{11}) &{} ( \alpha ^{(w)}_{12} , \beta ^{(w)}_{12} , \gamma ^{(w)}_{12}) &{} \ldots &{} ( \alpha ^{(w)}_{1d} , \beta ^{(w)}_{1d} , \gamma ^{(w)}_{1d}) \\ ( \alpha ^{(w)}_{21} , \beta ^{(w)}_{21} , \gamma ^{(w)}_{21})&{} (\alpha ^{(w)}_{22} , \beta ^{(w)}_{22} , \gamma ^{(w)}_{22}) &{} \ldots &{} ( \alpha ^{(w)}_{2d} , \beta ^{(w)}_{2d} , \gamma ^{(w)}_{2d}) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ ( \alpha ^{(w)}_{b1} , \beta ^{(w)}_{b1} , \gamma ^{(w)}_{b1})&{} ( \alpha ^{(w)}_{b2} , \beta ^{(w)}_{b2}, \gamma ^{(w)}_{b2}) &{} \ldots &{} (\alpha ^{(w)}_{bd} , \beta ^{(w)}_{bd} , \gamma ^{(w)}_{bd}) \end{array} \right) , \end{aligned}$$

where, $u\in \{1,2,\ldots ,b\}$, $v\in \{1,2,\ldots ,d\}$ and $w\in \{1,2,\ldots ,a\}$.

Step 02::

Formulate the aggregated complex spherical fuzzy performance matrix.

In the MAGDM context, each consultant $\mathcal {K}_{w}$ has self-endorsement; therefore, the MAGDM deputation assigned linear and normalized weight vector $\mathrm {k}=(\mathrm {k}_1,\mathrm {k}_2,\ldots \mathrm {k}_a)^{T}$ to the panel of a consultants; so that the opinions of the consultants are assembled using CSFWA operator in the following manner:

$$\begin{aligned} \mathcal {R}_{uv}= \,& {CSFWA}_{\mathrm {k}}(R^{(1)}_{uv}, R^{(2)}_{uv}, \ldots , R^{(a)}_{uv})\\= \,& \mathrm {k}_{1}R^{(1)}_{uv}\oplus \mathrm {k}_{2}R^{(2)}_{uv}\oplus \ldots \oplus \mathrm {k}_{a}R^{(a)}_{uv} \\= \,& \Bigg ( \sqrt{1-\displaystyle \prod ^{a}_{w=1}(1-(\mu ^{(w)}_{uv})^2)^{\mathrm {k}_{w}}} e^{i2\pi \sqrt{1-\displaystyle \prod ^{a}_{w=1}(1-(f^{(w)}_{uv})^2)^{\mathrm {k}_{w}}}}\\&,\displaystyle \prod ^{a}_{w=1}[\rho ^{(w)}_{uv}]^{\mathrm {k}_{w}}e^{i2\pi \displaystyle \prod ^{a}_{w=1}[g^{(w)}_{uv}]^{\mathrm {k}_{w}}}, \displaystyle \prod ^{a}_{w=1}[\nu ^{(w)}_{uv}]^{\mathrm {k}_{w}}e^{i2\pi \displaystyle \prod ^{a}_{w=1}[h^{(w)}_{uv}]^{\mathrm {k}_{w}}} \Bigg )\\= \,& ( \mu _{uv}e^{i2\pi f_{uv}} , \rho _{uv}e^{i2\pi g_{uv}}, \nu _{uv}e^{i2\pi h_{uv}}). \end{aligned}$$

The aggregated complex spherical fuzzy performance matrix (ACSFPM) is constructed as follows:

$$\begin{aligned} \mathcal {R} = \left( \begin{array}{cccc} ( \alpha _{11} , \beta _{11} , \gamma _{11}) &{} ( \alpha _{12} , \beta _{12} , \gamma _{12}) &{} \ldots &{} ( \alpha _{1d} , \beta _{1d} , \gamma _{1d}) \\ ( \alpha _{21} , \beta _{21} , \gamma _{21})&{} ( \alpha _{22} , \beta _{22} , \gamma _{22}) &{} \ldots &{} (\alpha _{2d} , \beta _{2d} , \gamma _{2d}) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ ( \alpha _{b1} , \beta _{b1} , \gamma _{b1})&{} ( \alpha _{b2} , \beta _{b2} , \gamma _{b2}) &{} \ldots &{} ( \alpha _{bd} , \beta _{bd} , \gamma _{bd}) \end{array} \right) . \end{aligned}$$

Step 03::

Figure out the weights for the attributes.

The significance of the attributes are acknowledged according to their linguistic weights that are further rated by the consultants and assigned CSFNs. For the formulation of the CSF-weights of the attributes, the CSFWA operator cumulates the decisions of the consultants $\mathrm {p}^{(w)}_{v}=(\mu ^{(w)}_{v}e^{i2\pi f^{(w)}_{v}}, \rho ^{(w)}_{v}e^{i2\pi g^{(w)}_{v}}, \nu ^{(w)}_{v}e^{i2\pi h^{(w)}_{v}})$ as follows:

$$\begin{aligned} \mathrm {p}_v= \,& CSFWA_{\mathrm {k}}(\mathrm {p}^{(1)}_{v}, \mathrm {p}^{(2)}_{v}, \ldots ,\mathrm {p}^{(a)}_{v} )\\= \,& \mathrm {k}_{1}\mathrm {p}^{1}_{v}\oplus \mathrm {k}_{2}\mathrm {p}^{2}_{v}\oplus \ldots \oplus \mathrm {k}_{a}\mathrm {p}^{a}_{v} \\= \,& \Bigg ( \sqrt{1-\displaystyle \prod ^{a}_{w=1}(1-(\mu ^{(w)}_{v})^2)^{\mathrm {k}_{w}}} e^{i2\pi \sqrt{1-\displaystyle \prod ^{a}_{w=1}(1-(f^{(w)}_{v})^2)^{\mathrm {k}_w}}}\\&\displaystyle \prod ^{a}_{w=1}[\rho ^{(w)}_{v}]^{\mathrm {k}_{w}} e^{i2\pi \displaystyle \prod ^{a}_{w=1}[g^{(w)}_{v}]^{\mathrm {k}_{w}}}, \displaystyle \prod ^{a}_{w=1}[\nu ^{(w)}_{v}]^{\mathrm {k}_{w}} e^{i2\pi \displaystyle \prod ^{a}_{w=1}[h^{(w)}_{v}]^{\mathrm {k}_{w}}} \Bigg ) \\= \,& ( \mu _{v}e^{i2\pi f_{v}} , \rho _{v}e^{i2\pi g_{v}}, \nu _{v}e^{i2\pi h_{v}}). \end{aligned}$$

Step 04::

Instigate the aggregated weighted complex spherical fuzzy performance matrix.

The entities of aggregated weighted complex spherical fuzzy performance matrix (AWCSFPM) $\overline{\mathcal {R}}= (\overline{\mathcal {R}}_{uv})_{b \times d} = (\overline{m}^{j}_{k}, \overline{\mu }_{uv}e^{i2\pi \overline{f}_{uv}} , \overline{\rho }_{uv}e^{i2\pi \overline{g}_{uv}}, \overline{\nu }_{uv}e^{i2\pi \overline{h}_{uv}})$ are evaluated by employing the ACSFPM and weightage of attributes $\mathrm {p}_v$ as follows:

$$\begin{aligned} \overline{\mathcal {R}}_{uv}= \,& \mathcal {R}_{uv} \otimes \mathrm {p}_{v} \nonumber \\= \,& \Bigg (\mu _{uv}\mu _{v}e^{i2\pi f_{uv}f_{v}}, \sqrt{\rho ^{2}_{uv} +\rho ^{2}_{v} -\rho ^{2}_{uv}\rho ^{2}_{v}}e^{i2\pi \sqrt{g^{2}_{uv} +g^{2}_{v} -g^{2}_{uv}g^{2}_{v}}} \nonumber \\&, \sqrt{\nu ^{2}_{uv} +\nu ^{2}_{v} -\nu ^{2}_{uv}\nu ^{2}_{v}}e^{i2\pi \sqrt{h^{2}_{uv} +h^{2}_{v} -h^{2}_{uv}h^{2}_{v}}}\Bigg ), \end{aligned}$$

(4)

$$\begin{aligned}= \,& ( \overline{\mu }_{uv}e^{i2\pi \overline{f}_{uv}} , \overline{\rho }_{uv}e^{i2\pi \overline{g}_{uv}}, \overline{\nu }_{uv}e^{i2\pi \overline{h}_{uv}})\nonumber \\= \,& (\overline{ \alpha }_{uv} ,\overline{ \beta }_{uv} , \overline{\gamma }_{uv}). \end{aligned}$$

(5)

Then, the matrix can be formed as follows:

$$\begin{aligned} \overline{\mathcal {R} } = \left( \begin{array}{cccc} (\overline{ \alpha }_{11} ,\overline{ \beta }_{11} , \overline{\gamma }_{11}) &{} (\overline{ \alpha }_{12} ,\overline{ \beta }_{12} , \overline{\gamma }_{12}) &{} \ldots &{} (\overline{ \alpha }_{1d} ,\overline{ \beta }_{1d} , \overline{\gamma }_{1d}) \\ (\overline{ \alpha }_{21} ,\overline{ \beta }_{21} , \overline{\gamma }_{21}) &{}(\overline{ \alpha }_{22} ,\overline{ \beta }_{22} , \overline{\gamma }_{22}) &{}\ldots &{} (\overline{ \alpha }_{2d} ,\overline{ \beta }_{2d} , \overline{\gamma }_{2d}) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ (\overline{ \alpha }_{b1} ,\overline{ \beta }_{b1} , \overline{\gamma }_{b1})&{} (\overline{ \alpha }_{b2} ,\overline{ \beta }_{b2} , \overline{\gamma }_{b2}) &{} \ldots &{} (\overline{ \alpha }_{bd} ,\overline{ \beta }_{bd} , \overline{\gamma }_{bd}) \end{array} \right) . \end{aligned}$$

Step 05::

Inaugurate the complex spherical fuzzy concordance and discordance sets.

Basically, the working principle of CSF-ELECTRE I method includes the pair-wise comparison of alternatives related to some adequate attributes. To compare two CSFNs, the score values, accuracy values, and degree of refusal of CSFNs are used in CSF-ELECTRE I method. An alternative with higher score value, higher accuracy value but least refusal value is a preferable option as compared to other feasible choices. The CSF concordance and discordance sets are described as strong, mid-range, and weak concordance and discordance sets, respectively, that rely on the score degree, accuracy degree, and refusal degree of CSFN. The CSF concordance set contains indices of all the attributes whereby the alternative $\mathcal {Z}_{\kappa }$ is better than the $\mathcal {Z}_{\tau }$.

• (i) The complex spherical fuzzy strong concordance set $\mathcal {C}_{\kappa \tau }$ can be determined as follows:

  $$\begin{aligned} \mathcal {C}_{\kappa \tau } = \{v: Sc(\overline{\mathcal {R}}_{\kappa v})\ge Sc(\overline{\mathcal {R}}_{\tau v}), Ac(\overline{\mathcal {R}}_{\kappa v})\ge Ac(\overline{\mathcal {R}}_{\tau v}); \varPsi (\overline{\mathcal {R}}_{\kappa v}) < \varPsi (\overline{\mathcal {R}}_{\tau v}) \}. \end{aligned}$$

  (6)

• (ii) The complex spherical fuzzy mid-range concordance set $\mathcal {C}^{'}_{\kappa \tau }$ can be determined as follows:

  $$\begin{aligned} \mathcal {C}^{'}_{\kappa \tau } = \{v: Sc(\overline{\mathcal {R}}_{\kappa v})\ge Sc(\overline{\mathcal {R}}_{\tau v}), Ac(\overline{\mathcal {R}}_{\kappa v})\ge Ac(\overline{\mathcal {R}}_{\tau v}); \varPsi (\overline{\mathcal {R}}_{\kappa v}) \ge \varPsi (\overline{\mathcal {R}}_{\tau v}) \}. \end{aligned}$$

  (7)

  The mid-range concordance set is less concordant than the strong concordance set because of the greater refusal value of $\kappa$-th alternative from $\tau$-th alternative regarding to vth criteria in mid-range concordance set.

• (iii) The complex spherical fuzzy weak concordance set $\mathcal {C}^{''}_{\kappa \tau }$ can be determined as follows:

  $$\begin{aligned} \mathcal {C}^{''}_{\kappa \tau } = \{v: Sc(\overline{\mathcal {R}}_{\kappa v})\ge Sc(\overline{\mathcal {R}}_{\tau v}), Ac(\overline{\mathcal {R}}_{\kappa v})< Ac(\overline{\mathcal {R}}_{\tau v}); \varPsi (\overline{\mathcal {R}}_{\kappa v}) \ge \varPsi (\overline{\mathcal {R}}_{\tau v}) \}. \end{aligned}$$

  (8)

  Similarly, $\mathcal {C}^{'}_{\kappa \tau }$ is more concordant than the $\mathcal {C}^{''}_{\kappa \tau }$ due to lesser accuracy value of the alternative $\mathcal {Z}_{\kappa }$ in weak concordance set as compared to mid-range concordance set.

The CSF discordance sets are complementary subsets of the concordance sets, which contain the indices of all the attributes whereby the alternative $\mathcal {Z}_{\kappa }$ is not better than the $\mathcal {Z}_{\tau }$.

• (i) The complex spherical fuzzy strong discordance set $\mathcal {D}_{\kappa \tau }$ can be determined as follows:

  $$\begin{aligned} \mathcal {D}_{\kappa \tau } = \{v: Sc(\overline{\mathcal {R}}_{\kappa v})< Sc(\overline{\mathcal {R}}_{\tau v}), Ac(\overline{\mathcal {R}}_{\kappa v})< Ac(\overline{\mathcal {R}}_{\tau v}); \varPsi (\overline{\mathcal {R}}_{\kappa v}) \ge \varPsi (\overline{\mathcal {R}}_{\tau v}) \}. \end{aligned}$$

  (9)

• (ii) The complex spherical fuzzy mid-range discordance set $\mathcal {D}^{'}_{\kappa \tau }$ can be determined as follows:

  $$\begin{aligned} \mathcal {D}^{'}_{\kappa \tau } = \{v: Sc(\overline{\mathcal {R}}_{\kappa v})< Sc(\overline{\mathcal {R}}_{\tau v}), Ac(\overline{\mathcal {R}}_{\kappa v})< Ac(\overline{\mathcal {R}}_{\tau v}); \varPsi (\overline{\mathcal {R}}_{\kappa v}) < \varPsi (\overline{\mathcal {R}}_{\tau v}) \}. \end{aligned}$$

  (10)

• (iii) The complex spherical fuzzy weak discordance set $\mathcal {D}^{''}_{\kappa \tau }$ can be determined as follows:

  $$\begin{aligned} \mathcal {D}^{''}_{\kappa \tau } = \{v: Sc(\overline{\mathcal {R}}_{\kappa v})< Sc(\overline{\mathcal {R}}_{\tau v}), Ac(\overline{\mathcal {R}}_{\kappa v})\ge Ac(\overline{\mathcal {R}}_{\tau v}); \varPsi (\overline{\mathcal {R}}_{\kappa v}) < \varPsi (\overline{\mathcal {R}}_{\tau v}) \}. \end{aligned}$$

  (11)

$\mathcal {D}_{\kappa \tau }$ is the most discordant than $\mathcal {D}^{'}_{\kappa \tau }$ and $\mathcal {D}^{''}_{\kappa \tau }$, where, ($\kappa , \tau = 1,2,3, \ldots , b$, $\kappa \ne \tau$) and $v =1,2,3, \ldots , d$.

Step 06::

Determine the complex spherical fuzzy concordance index and matrix.

The probable CSF concordance indices $\mathfrak {I}_{\kappa \tau }$ ($\kappa , \tau = 1,2,3, \ldots , b$, $\kappa \ne \tau$) are evaluated by equipping the weights ${\mathfrak {w}}_{\mathcal {C}_{\kappa \tau }}$, ${\mathfrak {w}}_{\mathcal {C}^{'}_{\kappa \tau }}$, and ${\mathfrak {w}}_{\mathcal {C}^{''}_{\kappa \tau }}$ to the CSF strong, mid-range, and weak concordance sets, respectively. In CSF-ELECTRE I method, the concordance index $\mathfrak {I}_{\kappa \tau }= ({m^{(v)}_{\mathfrak {I}_{\kappa \tau }}}, \alpha ^{(v)}_{\mathfrak {I}_{\kappa \tau }}, \beta ^{(v)}_{\mathfrak {I}_{\kappa \tau }}, \gamma ^{(v)}_{\mathfrak {I}_{\kappa \tau }})= ({m_{\mathfrak {I}_{\kappa \tau }}}^{(v)}, \mu ^{(v)}_{\mathfrak {I}_{\kappa \tau }}e^{i2\pi f^{(v)}_{\mathfrak {I}_{\kappa \tau }}}, \rho ^{(v)}_{\mathfrak {I}_{\kappa \tau }}e^{i2\pi g^{(v)}_{\mathfrak {I}_{\kappa \tau }}}, \nu ^{(v)}_{\mathfrak {I}_{\kappa \tau }}e^{i2\pi h^{(v)}_{\mathfrak {I}_{\kappa \tau }}})$, signifying the supremacy of the alternative $\mathcal {Z}_{\kappa }$ from alternative $\mathcal {Z}_{\tau }$, is defined as follows:

$$\begin{aligned} \mathfrak {I}_{\kappa \tau }= \Bigg ({\mathfrak {w}}_{\mathcal {C}_{\kappa \tau }} \otimes \displaystyle \sum _{v\in {\mathcal {C}_{\kappa \tau }}} {\mathrm {p}_{v}}\Bigg ) \oplus \Bigg ({\mathfrak {w}}_{\mathcal {C}^{'}_{\kappa \tau }} \otimes \displaystyle \sum _{v\in {\mathcal {C}^{'}_{\kappa \tau }}} {\mathrm {p}_{v}}\Bigg ) \oplus \Bigg ({\mathfrak {w}}_{\mathcal {C}^{''}_{\kappa \tau }} \otimes \displaystyle \sum _{v\in {\mathcal {C}^{''}_{\kappa \tau }}} {\mathrm {p}_{v}}\Bigg ), \end{aligned}$$

(12)

where, $\mathrm {p}_{v} = ( \mu _{v}e^{i2\pi f_{v}} , \rho _{v}e^{i2\pi g_{v}}, \nu _{v}e^{i2\pi h_{v}}) = (\mu _{v}e^{i2\pi f_{v}}, \rho _{v}e^{i2\pi g_{v}}, \nu _{v}e^{i2\pi h_{v}})$ represents the CSF-weightage of the vth attribute. Moreover, the CSF concordance matrix $\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}$ is constructed as follows:

$$\begin{aligned} \mathfrak {M}_{\mathfrak {I}_{\kappa \tau }} = \left( \begin{array}{ccccc} - &{} (\alpha ^{(v)}_{\mathfrak {I}_{12}}, \beta ^{(v)}_{\mathfrak {I}_{12}}, \gamma ^{(v)}_{\mathfrak {I}_{12}}) &{} \ldots &{} ( \alpha ^{(v)}_{\mathfrak {I}_{1(d-1)}}, \beta ^{(v)}_{\mathfrak {I}_{1(d-1)}}, \gamma ^{(v)}_{\mathfrak {I}_{1(d-1)}}) &{} ( \alpha ^{(v)}_{\mathfrak {I}_{1d}}, \beta ^{(v)}_{\mathfrak {I}_{1d}}, \gamma ^{(v)}_{\mathfrak {I}_{1d}}) \\ (\alpha ^{(v)}_{\mathfrak {I}_{21}}, \beta ^{(v)}_{\mathfrak {I}_{21}}, \gamma ^{(v)}_{\mathfrak {I}_{21}}) &{} - &{} \ldots &{} ( \alpha ^{(v)}_{\mathfrak {I}_{2(d-1)}}, \beta ^{(v)}_{\mathfrak {I}_{2(d-1)}}, \gamma ^{(v)}_{\mathfrak {I}_{2(d-1)}}) &{} ( \alpha ^{(v)}_{\mathfrak {I}_{2d}}, \beta ^{(v)}_{\mathfrak {I}_{2d}}, \gamma ^{(v)}_{\mathfrak {I}_{2d}}) \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ ( \alpha ^{(v)}_{\mathfrak {I}_{b1}}, \beta ^{(v)}_{\mathfrak {I}_{b1}}, \gamma ^{(v)}_{\mathfrak {I}_{b1}}) &{} ( \alpha ^{(v)}_{\mathfrak {I}_{b2}}, \beta ^{(v)}_{\mathfrak {I}_{b2}}, \gamma ^{(v)}_{\mathfrak {I}_{b2}}) &{} \ldots &{} ( \alpha ^{(v)}_{\mathfrak {I}_{b(d-1)}}, \beta ^{(v)}_{\mathfrak {I}_{b(d-1)}}, \gamma ^{(v)}_{\mathfrak {I}_{b(d-1)}}) &{} - \end{array}\right) . \end{aligned}$$

Step 07::

Determine the complex spherical fuzzy discordance index and matrix.

The feasible CSF discordance indices $\mathcal {J}_{\kappa \tau }$ ($\kappa , \tau = 1,2,3, \ldots , b$, $\kappa \ne \tau$) are evaluated by employing the weights ${\mathfrak {w}}_{\mathcal {D}_{\kappa \tau }}$, ${\mathfrak {w}}_{\mathcal {D}^{'}_{\kappa \tau }}$, and ${\mathfrak {w}}_{\mathcal {D}^{''}_{\kappa \tau }}$ of the CSF strong, mid-range, and weak discordance sets, respectively. In CSF-ELECTRE I method, the discordance index $\mathcal {J}_{\kappa \tau }= ({m^{(v)}_{\mathcal {J}_{\kappa \tau }}}, \alpha ^{(v)}_{\mathcal {J}_{\kappa \tau }}, \beta ^{(v)}_{\mathcal {J}_{\kappa \tau }}, \gamma ^{(v)}_{\mathcal {J}_{\kappa \tau }})= ({m_{\mathcal {J}_{\kappa \tau }}}^{(v)}, \mu ^{(v)}_{\mathcal {J}_{\kappa \tau }}e^{i2\pi f^{(v)}_{\mathcal {J}_{\kappa \tau }}}, \rho ^{(v)}_{\mathcal {J}_{\kappa \tau }}e^{i2\pi g^{(v)}_{\mathcal {J}_{\kappa \tau }}}, \nu ^{(v)}_{\mathcal {J}_{\kappa \tau }}e^{i2\pi h^{(v)}_{\mathcal {J}_{\kappa \tau }}})$, indicating the degree to which the alternative $\mathcal {Z}_{\kappa }$ is not preferable to alternative $\mathcal {Z}_{\tau }$, is defined as follows:

$$\begin{aligned} \mathcal {J}_{\kappa \tau }= \frac{\displaystyle \max _{v\in ({\mathcal {D}_{\kappa \tau }} \cup {\mathcal {D}^{'}_{\kappa \tau }} \cup {\mathcal {D}^{''}_{\kappa \tau }})} \Bigg \{{\mathfrak {w}}_{\mathcal {D}_{\kappa \tau }} \otimes d(\overline{\mathcal {R}}_{\kappa v}, \overline{\mathcal {R}}_{\tau v}), {\mathfrak {w}}_{\mathcal {D}^{'}_{\kappa \tau }} \otimes d(\overline{\mathcal {R}}_{\kappa v}, \overline{\mathcal {R}}_{\tau v}), {\mathfrak {w}}_{\mathcal {D}^{''}_{\kappa \tau }} \otimes d(\overline{\mathcal {R}}_{\kappa v}, \overline{\mathcal {R}}_{\tau v})\Bigg \}}{\displaystyle \max _{v} d(\overline{\mathcal {R}_{\kappa v}}, \overline{\mathcal {R}_{\tau v}})}, \end{aligned}$$

(13)

where the normalized Euclidean distance $d(\overline{\mathcal {R}}_{\kappa v}, \overline{\mathcal {R}}_{\tau v})$ between two entities $\overline{\mathcal {R}}_{\kappa v}$ and $\overline{\mathcal {R}}_{\tau v}$ of AWCSFPM can be calculated as follows:

$$\begin{aligned} d(\overline{\mathcal {R}}_{\kappa v}, \overline{\mathcal {R}}_{\tau v})= \,& \sqrt{\frac{( \overline{\mu }^2_{\kappa v} -\overline{\mu }^{2}_{\tau v})^2 + (\overline{\rho }^{2}_{\kappa v} -\overline{\rho }^2_{\tau v})^2 + (\overline{\nu }^{2}_{\kappa v} -\overline{\nu }^2_{tau v})^2 + (\overline{f}^{2}_{\kappa v} -\overline{f}^2_{\tau v})^2 + (\overline{g}^{2}_{\kappa v} -\overline{g}^2_{\tau v})^2 + (\overline{h}^2_{\kappa v} -\overline{h}^2_{\tau v})^2 }{3}}. \end{aligned}$$

The CSF discordance matrix $\mathfrak {M}_{\mathcal {J}_{\kappa \tau }}$ is constructed as follows:

$$\begin{aligned} \mathfrak {M}_{\mathfrak {D}_{\kappa \tau }} = \left( \begin{array}{ccccc} - &{}\mathcal {J}_{12} &{} \ldots &{} \mathcal {J}_{1(d-1)} &{} \mathcal {J}_{1d}\\ \mathcal {J}_{21} &{} - &{} \ldots &{} \mathcal {J}_{2(d-1)} &{} \mathcal {J}_{2d} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ \mathcal {J}_{b1} &{} \mathcal {J}_{b2} &{} \ldots &{} \mathcal {J}_{b(d-1)} &{} -\end{array} \right) . \end{aligned}$$

Step 08::

Formulate the complex spherical fuzzy effective concordance matrix.

A threshold value, known as concordance level $\xi$, is defined for the purpose of achieving the dominant one from the possible set of alternatives, as follows:

$$\begin{aligned} \xi = \frac{1}{b(b-1)}\displaystyle \max _{\kappa \tau } \Big [Sc(\mathfrak {I}_{\kappa \tau })\Big ], \end{aligned}$$

(14)

$(\kappa , \tau = 1,2,3, \ldots , b$, $\kappa \ne \tau ).$

The score function is employed for the comparison of CSF concordant indices that are arranged in CSF concordant matrix $\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}$. In addition to this, two possibilities are originated that either the score value of the concordant index exceed or perceed the threshold value $\xi$. Thus, greater the value of CSF concordant index ${\mathfrak {I}_{\kappa \tau }}$ than $\xi$, more the chances of preference of alternative $\mathcal {Z}_{\kappa }$ over the $\mathcal {Z}_{\tau }$. On the other hand, the chances of preference of alternative $\mathcal {Z}_{\kappa }$ over the $\mathcal {Z}_{\tau }$ will be decreased if the CSF concordant index ${\mathfrak {I}_{\kappa \tau }}$ has less value than the $\xi$. The concordance Boolean matrix $\varrho \ = (\varrho _{\kappa \tau })_{b\times b}$ can be compiled as follows:

$$\begin{aligned} \varrho = \left( \begin{array}{ccccc} - &{}\varrho _{12} &{} \ldots &{} \varrho _{1(d-1)} &{} \varrho _{1d}\\ \varrho _{21} &{} - &{} \ldots &{} \varrho _{2(d-1)} &{} \varrho _{2d} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ \varrho _{b1} &{} \varrho _{b2} &{} \ldots &{} \varrho _{b(d-1)} &{} - \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} \varrho _{\kappa \tau } = \left\{ \begin{array}{ll} 1 , &{} \hbox {if}\,Sc({\mathfrak {I}_{\kappa \tau }}) \ge \xi ,\\ 0 &{} \hbox {if}\, Sc({\mathfrak {I}_{\kappa \tau }}) < \xi . \end{array}\right. \end{aligned}$$

Step 09::

Formulate the complex spherical fuzzy effective discordance matrix.

For the purpose of evaluating the dominant alternative from all possible choices, the discordant level $\wp$ assisted and compared with the items of the CSF concordant matrix containing the concordant indices ${\mathcal {J}_{\kappa \tau }}$ that represents the degree of inferiority of the alternative $\mathcal {Z}_{\kappa }$ over the $\mathcal {Z}_{\tau }$. The discordant level $\wp$ is formalized as follows:

$$\begin{aligned} \wp = \frac{1}{b(b-1)}\displaystyle \sum _{\kappa , \kappa \ne \tau }\sum _{\tau , \tau \ne \kappa } \mathcal {J}_{\kappa \tau }, \end{aligned}$$

(15)

when the value of $\mathcal {J}_{\kappa \tau }$ exceeds the value of discordant level $\wp$ then it enhances the premises that $\mathcal {Z}_{\kappa }$ is dispensable than $\mathcal {Z}_{\tau }$. The effective discordance matrix $\beth \ = (\beth _{\kappa \tau })_{b\times b}$ can be compiled as follows:

$$\begin{aligned} \beth = \left( \begin{array}{ccccc} - &{}\beth _{12} &{} \ldots &{} \beth _{1(d-1)} &{} \beth _{1d}\\ \beth _{21} &{} - &{} \ldots &{} \beth _{2(d-1)} &{} \beth _{2d} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ \beth _{b1} &{} \beth _{b2} &{} \ldots &{} \beth _{b(d-1)} &{} - \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} \beth _{\kappa \tau } = \left\{ \begin{array}{ll} 1 , &{} \hbox {if}\, \mathcal {J}_{\kappa \tau } \le \wp ,\\ 0 &{} \hbox {if}\, \mathcal {J}_{\kappa \tau } > \wp . \end{array} \right. \end{aligned}$$

Step 10::

Construct the aggregated outranking Boolean matrix.

The aggregated outranking Boolean matrix contributes to strengthen the facts about the ordinate relations of the feasible alternatives subject to the contentious attributes that legitimize the dominant alternative. The CSF effective concordance and discordance matrices are integrated to accomplish the aggregated outranking Boolean matrix as follows:

$$\begin{aligned} \mathfrak {R}= \left( \begin{array}{ccccc} - &{}\mathfrak {R}_{12} &{} \ldots &{} \mathfrak {R}_{1(d-1)} &{} \mathfrak {R}_{1d}\\ \mathfrak {R}_{21} &{} - &{} \ldots &{} \mathfrak {R}_{2(d-1)} &{} \mathfrak {R}_{2d} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ \mathfrak {R}_{b1} &{} \mathfrak {R}_{b2} &{} \ldots &{} \mathfrak {R}_{b(d-1)} &{} - \end{array} \right) , \end{aligned}$$

where, $\mathfrak {R}_{\kappa \tau } = \varrho _{\kappa \tau } \times \beth _{\kappa \tau }.$

The alternative $\mathcal {Z}_{\kappa }$ is better choice than the $\mathcal {Z}_{\tau }$, if $\mathfrak {R}_{\kappa \tau }= 1$, i.e., $\mathcal {Z}_{\kappa }$ is outperforming $\mathcal {Z}_{\tau }$.

Step 11::

Draw the outranking graph.

A graph is a very effective visual tool as it presents the data at a peek, provides comparison, and can display relations within the set of information; therefore, in the concluding stage of CSF-ELECTRE I method, a directed graph is used to seize the finest alternative among of the all. Let $\mathbb {G}= (\mathbb {V},\mathbb {E})$ be a directed graph, where $\mathbb {V}$(vertex set) denotes the set of alternatives and $\mathbb {E}$(edge set) denotes the relationship between the alternatives. The directed graph is constructed on the basis of the following cases:

• 1. If $\mathfrak {R}_{\kappa \tau }=1$, an arc is drawn from vertex $\mathcal {Z}_{\kappa }$ directed toward $\mathcal {Z}_{\tau }$ which delineates that $\mathcal {Z}_{\kappa }$ is outperforming $\mathcal {Z}_{\tau }$, i.e.,($\mathcal {Z}_{\kappa } \succ \mathcal {Z}_{\tau }$).

• 2. If $\mathfrak {R}_{\kappa \tau }=1$ and $\mathfrak {R}_{\tau \kappa }=1$, a bidirectional arc is drawn which explicate the equivalent association among the vertices $\mathcal {Z}_{\kappa }$ and $\mathcal {Z}_{\tau }$, i.e.,($\mathcal {Z}_{\kappa } \approx \mathcal {Z}_{\tau }$).

• 3. If $\mathfrak {R}_{\kappa \tau }=0$, no arc will be drawn in between the vertices which interprets that $\mathcal {Z}_{\kappa }$ and $\mathcal {Z}_{\tau }$ are incomparable, i.e.,($\mathcal {Z}_{\kappa }? \mathcal {Z}_{\tau }$).

Figure 3 amply portrays the above-mentioned points by means of preference, indifference, and incomparable states, respectively.

Step 12::

Evaluate the linear ranking order.

Decision graph provides partial-precedence ordering of the alternatives and helps to eradicate the less beneficial alternatives but impotent to discriminate the preference orders of feasible alternatives through the proposed CSF-ELECTRE I methodology. The linear ranking order of the alternatives eliminates the partial-precedence dilemma that can be evaluated using the net outranking indices to strengthen the proposed ELECTRE I method. Let $\overbrace{Q_u}$ be concordance outranking relation, calculated by using the concordance matrix $\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}$ and the Eq. 16, is given as follows:

$$\begin{aligned} \overbrace{Q_u} = \displaystyle \sum ^{b}_{\kappa = 1, \kappa \ne u }Sc(\mathfrak {M}_{\mathfrak {I}_{u \kappa }})-\displaystyle \sum ^{b}_{\tau = 1, \tau \ne u }Sc(\mathfrak {M}_{\mathfrak {I}_{u \tau }}). \end{aligned}$$

(16)

Let $\underbrace{Q_u}$ be discordance outranking relation, computed by employing the discordance matrix $\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}$ and Eq. 17, is defined as follows:

$$\begin{aligned} \underbrace{Q_u} = \displaystyle \sum ^{b}_{\kappa = 1, \kappa \ne u } \mathfrak {M}_{\mathcal {J}_{u \kappa }}-\displaystyle \sum ^{b}_{\tau = 1, \tau \ne u } \mathfrak {M}_{\mathcal {J}_{u \tau }}. \end{aligned}$$

(17)

It can be asserted that the elite alternative ought to have the maximum $\overbrace{Q_u}$ and the minimum $\underbrace{Q_u}$, simultaneously. Despite that, the alternative with maximum $\overbrace{Q_u}$ is not assured the minimum value of $\underbrace{Q_u}$. Consequently, to get the final linear ranking order, the net outranking index is defined as follows:

$$\begin{aligned} \yen _u = \overbrace{Q_u} - \underbrace{Q_u}. \end{aligned}$$

(18)

The alternatives are ranked in descending order regarding to the values of net outranking index. The alternative with maximum net outranking index specified as the most suitable choice of the MAGDM problem.

Figure 4 illustrates the pictorial representation of the proposed CSF-ELECTRE I method against the background of MAGDM problems.

Fig. 3

Graphical representation of outranking decision graph

Fig. 4

Flowchart of CSF-ELECTRE I method

5 Application

In this section, we discuss two case studies from business and IT management related to the “Selection of site for new branch of a company” and “Selection of network monitoring software for military purpose”, respectively, that illustrate the applicability of proposed CSF-ELECTRE I method.

5.1 Case Study: Selection of Location for New Branch of a Company

5.1.1 Problem Description

A company should have clear envision of what they have and what they want to have in future before they start looking for business site for new growth opportunities. The location should be inviting and elegant in the view of the fact that it creates positive alliance for clients and stakeholders, so that they immensely think for the company interest. The selection of location for a company is the most tedious and complex process, though many bad decisions in business can be amended later, but a unpleasant and inappropriate location is sometimes impossible to ameliorate. There is more to discover about the appropriate location than just buying an accessible structure for the company to reside as it defines the management and organization of any company. For the selection of right location, company engage group of ten consultants that are

$\mathcal {K}_{1}:$:

Two member from company administration,

$\mathcal {K}_{2}:$:

Two property dealers,

$\mathcal {K}_{3}:$:

Three PHD researchers from business field,

$\mathcal {K}_{4}:$:

Three Stakeholders.

Five locations $\mathcal {Z}_{1}$, $\mathcal {Z}_{2}$, $\mathcal {Z}_{3}$, $\mathcal {Z}_{4}$ and $\mathcal {Z}_{5}$ are elected by the four groups of consultants $\mathcal {K}_{1}$, $\mathcal {K}_{2}$, $\mathcal {K}_{3}$, and $\mathcal {K}_{4}$, after investigating the procurable features of many listed locations.

5.1.2 Attribute Selection

Searching the best location for business site demands to consider the following factors: understanding local laws, intriguing competitors sites, and asserting a keen awareness on available attributes like demographics, distance from marketplace, atmosphere, investment cost, community interest, optimizing revenue prospective, manpower, and proximity to suppliers and resources, etc. The decision-makers highlighted four crucial features that are adopted by Rouyendegh [16] for the location selection problem, the four attributes are as follows:

$\mathcal {P}_{1}:$ Distance from marketplaces::

Distance from mart or emporium affects the business, because the cost of items and transportation increases as the distance increases. The site with shortest distance from marketplace is evaluated by higher linguistic term by the MAGDM deputations.

$\mathcal {P}_{2}:$ Investment cost::

This attribute involves the general cost consumes on the location from the process of buying the site to the establishment. The minimum cost is rendered with high linguistic term.

$\mathcal {P}_{3}:$ Community interest::

People intensity and consideration about the company and trade is also an important feature to examine. The location with greater community interest is highly preferable.

$\mathcal {P}_{4}:$ Maximum revenue possibility::

The obvious and necessary point is the maximum revenue which generates profit margins that contributed in business development and also captivated many investors toward the company.

The linguistic terms are enclosed in Table 1 that are used by the experts to interpret the comparative significance of the alternatives and corresponding attributes. Decision-makers employed three numbers to express a linguistic term: first number indicates their degree of agreement, second number indicates the degree of neutrality, and third number indicates the degree of disagreement provided with relevant conditions. However, the data are collected by the director of each group.

5.1.3 Evaluation Process

The gradual approach toward the selection of best location by CSF-ELECTRE I method contains subsequent steps:

• Step 1: The linguistic terms and corresponding CSFNs are enclosed in Table 1 that are used by the experts to elucidate the comparative significance of credible alternatives and pertinent attributes. Experts examine the five attainable locations pertaining to the attributes under contemplation and accede their decision, shown in Table 2. The CSFPMs related to consultants are comprised in Tables 3, 4, 5, and 6, respectively.

• Step 2: The CSFAW operator and consultant weight vector $\mathrm {k} = [0.342,0.247,0.192,0.192]^{T}$ are put to use for the formation of ACSFPM $\mathcal {R} = (\mathcal {R}_{uv})_{b\times d}$, given in Table 7.

• Step 3: The CSF-weight vector of attributes is calculated using the stance of the decision-makers, arranged in Table 8 and 9, accumulated by CSFAW operator. The weight vector of set of attributes is given as follows:

  $$\begin{aligned} \chi = \left( \begin{array}{c} (0.861e^{i2\pi (0.768)} , 0.322e^{i2\pi (0.300)} , 0.299e^{i2\pi (0.262)}) \\ (0.597e^{i2\pi (0.573)} , 0.504e^{i2\pi (0.480)} , 0.511e^{i2\pi (0.448)}) \\ (0.502e^{i2\pi (0.511)} , 0.523e^{i2\pi (0.497)} , 0.577e^{i2\pi (0.522)}) \\ (0.475e^{i2\pi (0.466)} , 0.488e^{i2\pi (0.454)} , 0.634e^{i2\pi (0.572)}) \\ \end{array} \right) . \end{aligned}$$

• Step 4: The $AWCSFPM\ \overline{\mathcal {R}}= (\overline{\mathcal {R}}_{uv})_{b \times d}$, cumulated by Eq. 4, is manifested in Table 10.

Table 1 Linguistic terms for rating the alternatives and attributes

Table 2 Linguistic evaluation of alternatives by decision-makers

Table 3 CSFPM of decision-maker $\mathcal {K}_{1}$

Table 4 CSFPM of decision-maker $\mathcal {K}_{2}$

Table 5 CSFPM of decision-maker $\mathcal {K}_{3}$

Table 6 CSFPM of decision-maker $\mathcal {K}_{4}$

Table 7 Aggregated complex spherical fuzzy N-soft performance matrix

Table 8 Importance of attributes in the form of linguistic variables

Table 9 CSF-weights of attributes

Table 10 Aggregated weighted complex spherical fuzzy N-soft performance matrix

Table 11 Score, accuracy, and refusal degrees of AWCSFPM

• Step 5: The CSF concordance sets $\mathcal {C}_{\kappa \tau }$, $\mathcal {C}^{'}_{\kappa \tau }$, and $\mathcal {C}^{''}_{\kappa \tau }$, are figured out by utilizing the Eqs. 6–8, where the score value, accuracy value, and refusal value of the entities $\overline{\mathcal {R}}_{uv}$ of AWCSFPM comprised in Table 11. The CSF-strong concordance set $\mathcal {C}_{\kappa \tau }$, CSF-mid-range concordance set $\mathcal {C}^{'}_{\kappa \tau }$, and CSF-weak concordance set $\mathcal {C}^{''}_{\kappa \tau }$ are accorded as follows:

  $$\begin{aligned} \mathcal {C}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{ \}&{} \{ \}&{} \{ \}&{} \{ \} \\ \{ \} &{} - &{} \{ \} &{} \{ \} &{} \{ \} \\ \{ \} &{}\{ \} &{} - &{} \{ \} &{}\{ \} \\ \{ \} &{}\{ \} &{} \{ \} &{} - &{} \{3\} \\ \{1\} &{} \{1\} &{} \{1\} &{} \{1\} &{}- \\ \end{array}\right) ,\\ \mathcal {C}^{'}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{ \}&{} \{ \}&{} \{ \}&{} \{ \} \\ \{ \} &{} - &{} \{ \} &{} \{ \} &{} \{ \} \\ \{ \} &{}\{ \} &{} -&{} \{ \} &{}\{ \} \\ \{ \} &{}\{ \} &{} \{ \} &{} - &{} \{ \} \\ \{ \} &{} \{ \} &{} \{ \} &{} \{ \} &{} - \\ \end{array}\right) ,\\ \mathcal {C}^{''}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{1,3,4\}&{} \{1\}&{} \{1\}&{} \{ \} \\ \{2\} &{} - &{} \{ \} &{} \{ \} &{} \{ \} \\ \{2,3,4\} &{}\{1,2,3,4\} &{} - &{} \{1,2\} &{}\{ \} \\ \{2,3,4\} &{}\ 1,2,3,4\} &{} \{3,4\} &{}- &{} \{ \} \\ \{2,3,4\} &{} \{2,3,4\} &{} \{2,3,4\} &{} \{2,4\} &{} - \\ \end{array}\right) . \end{aligned}$$

  The CSF discordance sets $\mathcal {D}_{\kappa \tau }$, $\mathcal {D}^{'}_{\kappa \tau }$ and $\mathcal {D}^{''}_{\kappa \tau }$, are evaluated using Eqs. 9–11. The CSF-strong discordance set $\mathcal {D}_{\kappa \tau }$, CSF-mid-range discordance set $\mathcal {D}^{'}_{\kappa \tau }$, and CSF-weak discordance set $\mathcal {D}^{''}_{\kappa \tau }$ are given as follows:

  $$\begin{aligned} \mathcal {D}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{ \}&{} \{ \}&{} \{ \}&{} \{1\} \\ \{ \} &{} - &{} \{ \} &{} \{ \} &{} \{1\} \\ \{ \} &{}\{ \} &{} -&{} \{ \} &{}\{1\} \\ \{ \} &{}\{ \} &{} \{ \} &{} - &{} \{1\} \\ \{ \} &{} \{ \} &{} \{ \} &{} \{3\} &{}- \\ \end{array}\right) ,\\ \mathcal {D}^{'}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{ \}&{} \{ \}&{} \{ \}&{} \{ \} \\ \{ \} &{} - &{} \{ \} &{} \{ \} &{} \{ \} \\ \{ \} &{}\{ \} &{} - &{} \{ \} &{}\{ \} \\ \{ \} &{}\{ \} &{} \{ \} &{} - &{} \{ \} \\ \{ \} &{} \{ \} &{} \{ \} &{} \{ \} &{} - \\ \end{array}\right) ,\\ \mathcal {D}^{''}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{2\}&{} \{2,3,4\}&{} \{2,3,4\}&{} \{2,3,4\} \\ \{1,3,4\} &{}- &{} \{1,2,3,4\} &{} \{1,2,3,4\} &{} \{2,3,4\} \\ \{1\} &{}\{ \} &{} -&{} \{3,4\} &{}\{2,3,4\} \\ \{1\} &{}\{ \} &{} \{2\} &{}- &{} \{2,4\} \\ \{ \} &{} \{ \} &{} \{ \} &{} \{ \} &{} - \\ \end{array}\right) . \end{aligned}$$

• Step 6: The CSF strong, mid-range, and weak concordance sets are audited and their rationed weights. assigned by the consultants, are given in Eq. 19

  $$\begin{aligned} (\mathfrak {w}_{\mathcal {C}_{\kappa \tau }},\mathfrak {w}_{\mathcal {C}^{'}_{\kappa \tau }}, \mathfrak {w}_{\mathcal {C}^{''}_{\kappa \tau }} )= \left( 1,\frac{2}{3},\frac{1}{3}\right) . \end{aligned}$$

  (19)

  The CSF concordance indices $\mathfrak {I}_{\kappa \tau }$ are evaluated with the help of Eq. 12, which are further used to assemble concordance matrix $\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}$. In particular, a complex spherical fuzzy concordance index $\mathfrak {I}_{51}$ can be computed as follows:

  $$\begin{aligned} \mathfrak {I}_{51}= \,& [\mathfrak {w}_{\mathcal {C}_{\kappa \tau }}\otimes \mathrm {p}_{1}] \oplus [\mathfrak {w}_{\mathcal {C}^{'}_{\kappa \tau }}\otimes 0] \oplus [\mathfrak {w}_{\mathcal {C}^{''}_{\kappa \tau }}\otimes (\mathrm {p}_{2}\oplus \mathrm {p}_{3}\oplus \mathrm {p}_{4})]\\= \,& [1\otimes \mathrm {p}_{1}] \oplus [\frac{1}{3}\otimes (\mathrm {p}_{2}\oplus \mathrm {p}_{3}\oplus \mathrm {p}_{4})]\\= \,& (0.741e^{i2\pi (0.497)},0.163e^{i2\pi (0.143)},0.171e^{i2\pi (0.134)}). \end{aligned}$$

  The CSF concordance matrix $\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}$ is organized in Table 12 and their score values are given by

  $$\begin{aligned} Sc(\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}) = \left( \begin{array}{ccccccccc} -&{} &{}0.082&{}&{}-1.15&{} &{}-1.15&{} &{} 0 \\ -2.21&{}&{}- &{}&{} 0&{}&{} 0 &{}&{} 0 \\ -0.521&{}&{} 0.524&{}&{} - &{} &{} -0.299&{} &{} 0 \\ -0.521&{} &{} 0.524 &{} &{} 0.082&{} &{} -&{} &{} -0.614 \\ 1.155&{} &{}1.155&{} &{} 1.155&{} &{} 1.321&{} &{} - \\ \end{array}\right) . \end{aligned}$$

  (20)

• Step 7: The weights are granted to CSF strong, mid-range, and weak discordance sets according to viewpoint of the experts, given in Eq. 21. The CSF discordance indices $\mathcal {J}_{\kappa \tau }$ are computed using Eq. 13 for the formation of discordance matrix $\mathfrak {M}_{\mathcal {J}_{\kappa \tau }}$, where the normalized Euclidean distances $d(\overline{\mathcal {R}}_{\kappa v}, \overline{\mathcal {R}}_{\tau v})$ are arranged in Table 13

  $$\begin{aligned} (\mathfrak {w}_{\mathcal {D}_{\kappa \tau }}, \mathfrak {w}_{\mathcal {D}^{'}_{\kappa \tau }},\mathfrak {w}_{\mathcal {D}^{''}_{\kappa \tau }} )= \left( 1,\frac{2}{3},\frac{1}{3}\right) . \end{aligned}$$

  (21)

  In particular, a complex spherical fuzzy discordance index $\mathcal {I}_{53}$ can be computed as follows:

  $$\begin{aligned} \mathfrak {I}_{35}= \,& \mathcal {J}_{\kappa \tau }= \frac{\displaystyle \max _{v\in ({\mathcal {D}_{35}} \cup {\mathcal {D}^{'}_{35}} \cup {\mathcal {D}^{''}_{35}})} \{{\mathfrak {w}}_{\mathcal {D}_{\kappa \tau }} \otimes d(\overline{\mathcal {R}}_{3 v}, \overline{\mathcal {R}}_{5 v}), {\mathfrak {w}}_{\mathcal {D}^{'}_{\kappa \tau }} \otimes d(\overline{\mathcal {R}}_{3 v}, \overline{\mathcal {R}_{5 v}}), {\mathfrak {w}}_{\mathcal {D}^{''}_{\kappa \tau }} \otimes d(\overline{\mathcal {R}}_{3 v}, \overline{\mathcal {R}}_{5 v})\}}{\displaystyle \max _{v} d(\overline{\mathcal {R}}_{3 v}, \overline{\mathcal {R}}_{5 v})} \\= \,& \frac{\max \Big [1 \otimes d(\overline{\mathcal {R}}_{3 1}, \overline{\mathcal {R}}_{5 1}), \frac{2}{3} \otimes 0, \frac{1}{3} \otimes d(\overline{\mathcal {R}_{3 2}}, \overline{\mathcal {R}_{5 2}}), \frac{1}{3} \otimes d(\overline{\mathcal {R}_{3 3}}, \overline{\mathcal {R}_{53}}), \frac{1}{3} \otimes d(\overline{\mathcal {R}}_{3 4}, \overline{\mathcal {R}}_{5 4})\Big ]}{\max \Big [ d(\overline{\mathcal {R}}_{31}, \overline{\mathcal {R}}_{51}),d(\overline{\mathcal {R}}_{3 2}, \overline{\mathcal {R}}_{5 2}), d(\overline{\mathcal {R}}_{3 3}, \overline{\mathcal {R}}_{5 3}), d(\overline{\mathcal {R}}_{3 4}, \overline{\mathcal {R}}_{5 4})\Big ] }\\= \,& 0.333. \end{aligned}$$

  The CSF discordance matrix $\mathfrak {M}_{\mathcal {J}_{\kappa \tau }}$ is represented as follows:

  $$\begin{aligned} \mathfrak {M}_{\mathcal {J}_{\kappa \tau }} = \left( \begin{array}{ccccccccc} -&{} &{}0.022&{} &{}0.333&{} &{}0.333&{} &{} 0.333 \\ 0.333&{} &{} - &{} &{} 0.333&{} &{} 0.333 &{} &{} 0.333 \\ 0.194&{} &{} 0&{} &{} -&{} &{} 0.333&{} &{} 0.333 \\ 0.050&{} &{} 0 &{} &{} 0.045&{} &{} -&{} &{} 0.037 \\ 0&{} &{} 0 &{} &{} 0&{} &{} 0&{} &{} - \\ \end{array}\right) . \end{aligned}$$

Table 12 CSF concordance matrix

Table 13 Normalized Euclidean distances $d(\overline{\mathcal {R}}_{\kappa v},\overline{\mathcal {R}}_{\tau v} )$

• Step 8: The concordance level $\xi$, interpolated by Eq. 14, is 0.066 and the score values of the CSF concordance entities are pinned up in Matrix 20 that endorse for the construction of the CSF effective concordance matrix, given as follows:

  $$\begin{aligned} \varrho = \left( \begin{array}{ccccccccc} -&{} &{}1&{} &{}0&{} &{}0&{} &{} 0 \\ 0&{} &{} - &{} &{} 0&{} &{} 0 &{} &{} 0 \\ 0&{} &{} 1&{} &{} -&{} &{} 0&{} &{} 0 \\ 0&{} &{} 1 &{} &{} 1&{} &{} -&{} &{} 0 \\ 1&{} &{} 1 &{} &{} 1&{} &{} 1&{} &{} - \\ \end{array}\right) . \end{aligned}$$

• Step 9: The entities of the CSF discordance matrix are compared with the discordance threshold value $\wp =0.167$ (computed by Eq. 15) for the composition of CSF effective discordance matrix $\beth$, given as follows:

  $$\begin{aligned} \beth = \left( \begin{array}{ccccccccc} -&{} &{}1&{} &{}0&{} &{}0&{} &{} 0 \\ 0&{} &{} - &{} &{} 0&{} &{} 0&{} &{} 0 \\ 1&{} &{} 1&{} &{} -&{} &{} 0&{} &{} 0 \\ 1&{} &{} 1 &{} &{} 1&{} &{} -&{} &{} 1 \\ 1&{} &{} 1 &{} &{} 1&{} &{} 1&{} &{} - \\ \end{array} \right) . \end{aligned}$$

• Step 10: The aggregated outranking Boolean matrix is constructed by unifying the entities of CSF Boolean concordance and discordance matrices. The aggregated outranking boolean matrix $\mathfrak {R}$ is given by

  $$\begin{aligned} \mathfrak {R}= \left( \begin{array}{ccccccccc} -&{} &{}1&{} &{}0&{} &{}0&{} &{} 0 \\ 0&{} &{} - &{} &{} 0&{} &{} 0 &{} &{} 0 \\ 0&{} &{} 1&{} &{} -&{} &{} 0&{} &{} 0 \\ 0&{} &{} 1 &{} &{} 1&{} &{} -&{} &{} 0 \\ 1&{} &{} 1 &{} &{} 1&{} &{} 1&{} &{} - \\ \end{array}\right) . \end{aligned}$$

• Step 11: The outranking graph of the MAGDM problem, shown in Fig. 5, delineates that the alternative $\mathcal {Z}_{5}$ outranks all the other alternatives and the partial preferences of the alternatives are pinned up in Table 14. It is noteworthy from Fig. 5 that the location $\mathcal {Z}_{5}$ is outranking all of the other site locations $\mathcal {Z}_{1}$, $\mathcal {Z}_{2}$, $\mathcal {Z}_{3}$ and $\mathcal {Z}_{4}$ together with there is no arc in between $\mathcal {Z}_{1}$ and $\mathcal {Z}_{3}$ locations. Hence, the alternative $\mathcal {Z}_{5}$ is best site for the company and the eliminated alternatives are $\mathcal {Z}_{1}$ and $\mathcal {Z}_{3}$ as they both are incomparable.

• Step 12: The concordance outranking coefficient $\overbrace{Q_{u}}$, discordance outranking coefficient $\underbrace{Q_{u}}$, and net outranking index $\yen _{u}$ are organized in Table 15. Table 15 indicates that $\mathcal {Z}_5$ is best choice as site of a company as well as the linear ranking of the alternatives that is given as: $\mathcal {Z}_5\succ \mathcal {Z}_4\succ \mathcal {Z}_3\succ \mathcal {Z}_1\succ \mathcal {Z}_2$.

Fig. 5

Outranking decision graph

Table 14 Exploration of decision graph

Table 15 Outranking indices of the alternatives

5.1.4 Results and Discussion

The final results of the case study demonstrate that the location $\mathcal {Z}_5$ is the best choice from all of the selected alternatives.

5.2 Case Study: Selection of Best Network Monitoring Software for Military Purpose

5.2.1 Problem Description

This case study is instigated to illustrate the sustainability and strength of the proposed method. This study involves the selection of network monitoring software which successfully address and analyze the massive data of the military as well as protects sensitive and confidential information from any type of threat. A state with strong army enjoys a great proportion of security and reliability than a weak army state. Across the centuries, countries with advanced technologies emerged and strengthened the military capabilities in clashes against their enemies.

It is difficult to manage and analyze the computer systems and growing number of dependency upon them by soldiers, weapons, and advanced technologies used by the military, available resources, and internal affairs of the country. Due to the fifth generation war, increasing reliance put the networks at high risk. Therefore, to save and manage the networks with confidential information on a high level, networking monitoring software is available and used by several countries for different tasks. The network monitoring softwares are able to attain the valuable goal of situational awareness, leverage their core resources, and effectively protect their network.

In this case study, we consider data-based websites with potential participation of four highly proficient network monitoring softwares, namely, SolarWinds-Network Performance Monitor(NPM), Data Dog (DD), Paessler Router Traffic Grapher (PRTG), and Progress Whats Up Gold (PWUG). We investigate these softwares on the basis of their features and evaluate a network monitoring software that is most suitable and has the lowest risk of failure. The critical features of network monitoring software contributed to its status and rank as well as help to select the software that is most resilient.

5.2.2 Attribute Selection

The four network monitoring softwares possess different infrastructure, protocols, and cost policy, and possess individual network mapping and owing distinct type of alerts that clearly justify the necessity of MAGDM approach. To determine the relative influence of each attribute, a team of experts $\mathcal {K}_1$, $\mathcal {K}_2$ and $\mathcal {K}_3$ is assembled, where the experts’ group $\mathcal {K}_1$ consists of three members from the military administration, $\mathcal {K}_2$ consists of five IT researchers and group $\mathcal {K}_3$ contains two members from the financial ministry.

The decision-makers choose three well-known and worthwhile websites www.trustradius.com, www.g2.com, and www.pcwdld.com that judged the network monitoring softwares on the grounds of many attributes from which the following resilience attributes are adopted:

$\mathcal {P}_1:$:

    Cost policy,

$\mathcal {P}_2:$:

    Usability,

$\mathcal {P}_3:$:

   Renewability,

$\mathcal {P}_4:$:

   Scaleability,

$\mathcal {P}_5:$:

   Availability,

$\mathcal {P}_6:$:

   Implementation,

$\mathcal {P}_7:$:

   Infrastructure,

$\mathcal {P}_8:$:

    Alerts,

$\mathcal {P}_9:$:

   Network mapping.

Note that the attribute cost policy $(\mathcal {P}_1)$ is the only cost type attribute; therefore, the software with minimum price is the most favorable one.

The linguistic terms are enclosed in Table 1 that are used by the experts to interpret the comparative significance of alternatives and corresponding attributes. Decision-makers employed numerical values to express a linguistic term: first number indicated their degree of agreement, second number indicated the degree of neutrality, and third number indicated the degree of disagreement provided with relevant conditions.

5.2.3 Evaluation Process

The gradual approach toward the selection of best software by CSF-ELECTRE I method contains subsequent steps:

• Step 1: The linguistic terms and corresponding CSFNs are pinned up in Table 1 and experts evaluated the four attainable choices pertaining to the attributes, as shown in Table 16. The CSFPMs related to the decision experts $\mathcal {K}_1$, $\mathcal {K}_2$ and $\mathcal {K}_3$ are arranged in Tables 17, 18 and 19, respectively.

• Step 2: The CSFWA operator and consultant weight vector $\mathrm {k} = [0.4165,0.3422,0.2413]^{T}$ are operated for the formation of ACSFPM $\mathcal {R} = (\mathcal {R}_{uv})_{b\times d}$, given in Table 20.

• Step 3: The CSF-weight vector of attributes is calculated by summarizing the opinions of the decision-makers arranged in Tables 21 and 22. The weight vector of set of attributes is given as follows:

  $$\begin{aligned} \chi = \left( \begin{array}{c} (0.6900e^{i2\pi (0.6200)} , 0.4400e^{i2\pi (0.4100)} , 0.4700e^{i2\pi (0.3900)}) \\ (0.8648e^{i2\pi (0.8016)} , 0.3030e^{i2\pi (0.2955)} , 0.2686e^{i2\pi (0.2225)}) \\ (0.8907e^{i2\pi (0.8320)} , 0.2733e^{i2\pi (0.2680)} , 0.2280e^{i2\pi (0.1903)}) \\ (0.8044e^{i2\pi (0.7417)} , 0.3537e^{i2\pi (0.3152)} , 0.3086e^{i2\pi (0.2783)}) \\ (0.6900e^{i2\pi (0.6200)} , 0.4400e^{i2\pi (0.4100)} , 0.4700e^{i2\pi (0.3900)}) \\ (0.8819e^{i2\pi (0.8225)} , 0.2827e^{i2\pi (0.2718)} , 0.2350e^{i2\pi (0.1998)}) \\ (0.8044e^{i2\pi (0.7417)} , 0.3537e^{i2\pi (0.3152)} , 0.3086e^{i2\pi (0.2783)}) \\ (0.8300e^{i2\pi (0.7700)} , 0.3300e^{i2\pi (0.2900)} , 0.2700e^{i2\pi (0.2500)}) \\ (0.9149e^{i2\pi (0.8592)} , 0.2451e^{i2\pi (0.2560)} , 0.2067e^{i2\pi (0.1626)}) \\ \end{array}\right) . \end{aligned}$$

• Step 4: The $AWCSFPM\ \overline{\mathcal {R}}= (\overline{\mathcal {R}}_{uv})_{b \times d}$ is comprised in Table 23.

Table 16 Linguistic evaluation of alternatives by decision-makers

Table 17 CSFPM of decision-maker $\mathcal {K}_{1}$

Table 18 CSFPM of decision-maker $\mathcal {K}_{2}$

Table 19 CSFPM of decision-maker $\mathcal {K}_{3}$

Table 20 Aggregated complex spherical fuzzy N-soft performance matrix

Table 21 Importance of attributes in the form of linguistic variables

Table 22 CSF-weights of attributes

Table 23 Aggregated weighted complex spherical fuzzy N-soft performance matrix

Table 24 Score, accuracy, and refusal degrees of AWCSFPM

Table 25 CSF concordance matrix

• Step 5: The CSF concordance sets $\mathcal {C}_{\kappa \tau }$, $\mathcal {C}^{'}_{\kappa \tau }$, and $\mathcal {C}^{''}_{\kappa \tau }$, are figured out by utilizing the Eqs. 6–8, where the score value, accuracy value, and refusal value of the entities $\overline{\mathcal {R}}_{uv}$ of AWCSFPM are comprised in Table 24. The CSF-strong concordance set $\mathcal {C}_{\kappa \tau }$, CSF-mid-range concordance set $\mathcal {C}^{'}_{\kappa \tau }$, and CSF-weak concordance set $\mathcal {C}^{''}_{\kappa \tau }$ are represented as follows:

  $$\begin{aligned} \mathcal {C}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{3,9\}&{} \{2,3,6,8,9\}&{} \{6,9\} \\ \{ \} &{} - &{} \{2,4\} &{} \{6,8\} \\ \{ \} &{}\{3,9\} &{} - &{} \{9\} \\ \{ \} &{}\{ \} &{} \{ \} &{} - \\ \end{array}\right) ,\\ \mathcal {C}^{'}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{ \}&{} \{ \}&{} \{ \}\\ \{ \} &{} - &{} \{ \} &{} \{ \} \\ \{ \} &{}\{ \} &{} - &{} \{ \} \\ \{ \} &{}\{ \} &{} \{ \} &{} - \\ \end{array}\right) ,\\ \mathcal {C}^{''}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{2,4,5,6,7,8\}&{} \{4,5,7\}&{} \{2,3,5,7,8\} \\ \{ 1\} &{} - &{} \{1\} &{} \{2,3,4,7,9\} \\ \{1\} &{}\{5,6,7,8\} &{} - &{} \{2,3,4,5,6,7,8\} \\ = \{1\} &{}\{1,5\} &{} \{1\} &{} - \\ \end{array}\right) . \end{aligned}$$

  The CSF discordance sets $\mathcal {D}_{\kappa \tau }$, $\mathcal {D}^{'}_{\kappa \tau }$ and $\mathcal {D}^{''}_{\kappa \tau }$ are evaluated using Eqs. 9–11. The CSF-strong discordance set $\mathcal {D}_{\kappa \tau }$, CSF-mid-range discordance set $\mathcal {D}^{'}_{\kappa \tau }$, and CSF-weak discordance set $\mathcal {D}^{''}_{\kappa \tau }$ are given by

  $$\begin{aligned} \mathcal {D}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{ \}&{} \{ \}&{} \{ \}\\ \{3,9\} &{} - &{} \{3,9\} &{} \{ \} \\ \{2,3,6,8,9\} &{}\{2,4\} &{} - &{} \{ \} \\ \{6,9\} &{}\{6,8\} &{} \{9\} &{} - \\ \end{array}\right) ,\\ \mathcal {D}^{'}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{ \}&{} \{ \}&{} \{ \}\\ \{ \} &{} - &{} \{ \} &{} \{ \} \\ \{ \} &{}\{ \} &{} - &{} \{ \} \\ \{ \} &{}\{ \} &{} \{ \} &{} - \\ \end{array}\right) ,\\ \mathcal {D}^{''}_{\kappa \tau }= \,& \left( \begin{array}{ccccc} -&{} \{1\}&{} \{1\}&{} \{1\}\\ \{2,4,5,6,7,8\} &{} - &{} \{5,6,7,8\} &{} \{1,5\} \\ \{4,5,7\} &{}\{1\} &{} - &{} \{1 \} \\ \{ 2,3,4,5,7,8\} &{}\{2,3,4,7,9\} &{} \{2,3,4,5,6,7,8\} &{} -\\ \end{array}\right) . \end{aligned}$$

• Step 6: The CSF strong, mid-range, and weak concordance sets are audited and then rationed weights by the consultants with respect to their importance in the MAGDM problem, given in Eq. 22. The CSF concordance indices $\mathfrak {I}_{\kappa \tau }$ are evaluated with the help of Eq. 12, which are further used to assemble concordance matrix $\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}$

  $$\begin{aligned} (\mathfrak {w}_{\mathcal {C}_{\kappa \tau }},\mathfrak {w}_{\mathcal {C}^{'}_{\kappa \tau }},\mathfrak {w}_{\mathcal {C}^{''}_{\kappa \tau }} )= (1,\frac{2}{3},\frac{1}{3}). \end{aligned}$$

  (22)

  The CSF concordance matrix $\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}$ is organized in Table 25 and their score values are given by

  $$\begin{aligned} Sc(\mathfrak {M}_{\mathfrak {I}_{\kappa \tau }}) = \left( \begin{array}{ccccccccc} - &{}&{} 1.9818 &{}&{}1.9978 &{} &{}1.9811\\ -1.9255&{}&{} - &{}&{} 1.7739 &{}&{} 1.9689 \\ -1.9255&{}&{} 1.9648 &{}&{} - &{} &{} 1.9573\\ -1.9255&{}&{}-0.6631 &{}&{} -1.9255&{} &{} - \\ \end{array}\right) . \end{aligned}$$

  (23)

• Step 7: The weights are granted to CSF strong, mid-range, and weak discordance sets according to viewpoint of the experts, given in Eq. 24. The CSF discordance indices $\mathcal {J}_{\kappa \tau }$ are computed using Eq. 13 for the formation of discordance matrix $\mathfrak {M}_{\mathcal {J}_{\kappa \tau }}$, where the normalized Euclidean distances $d(\overline{\mathcal {R}}_{\kappa v}, \overline{\mathcal {R}}_{\tau v})$ are arranged in Table 26

  $$\begin{aligned} (\mathfrak {w}_{\mathcal {D}_{\kappa \tau }},\mathfrak {w}_{\mathcal {D}^{'}_{\kappa \tau }},\mathfrak {w}_{\mathcal {D}^{''}_{\kappa \tau }} )= (1,\frac{2}{3},\frac{1}{3}). \end{aligned}$$

  (24)

  The CSF discordance matrix $\mathfrak {M}_{\mathcal {J}_{\kappa \tau }}$ is represented as:

  $$\begin{aligned} \mathfrak {M}_{\mathcal {J}_{\kappa \tau }} = \left( \begin{array}{ccccccc} -&{} &{}0.1180&{} &{}0.1474&{} &{}0.1027 \\ 0.6204&{} &{} - &{} &{} 0.7802&{} &{} 0.0500\\ 0.7480&{} &{}0.4672&{} &{} -&{} &{} 0.0596 \\ 0.050&{} &{} 0.3333 &{} &{} 0.4612&{} &{} - \\ \end{array}\right) . \end{aligned}$$

• Step 8: The concordance level $\xi$, interpolated by Eq. 14, is 0.1664 and the score values of the CSF concordance entities are given in Matrix 23 that endorse for the construction of the CSF effective concordance matrix, given as follows:

  $$\begin{aligned} \varrho = \left( \begin{array}{ccccccccc} -&{} &{}1&{} &{}1&{} &{}1&{} \\ 0&{} &{} -&{} &{} 0&{} &{} 1 \\ 0&{} &{} 0&{} &{} -&{} &{} 1 \\ 0&{} &{} 1 &{} &{} 0&{} &{} -&{} \\ \end{array}\right) . \end{aligned}$$

• Step 9: The entities of the CSF discordance matrix are compared with the discordance threshold value $\wp =0.3685$ (computed by Eq. 15) for the composition of CSF effective discordance matrix $\beth$, given as follows:

  $$\begin{aligned} \beth = \left( \begin{array}{ccccccccc} -&{} &{}1&{} &{}1&{} &{}1&{} \\ 0&{} &{} - &{} &{} 1&{} &{} 1&{} \\ 0&{} &{} 1&{} &{} -&{} &{} 1&{} \\ 0&{} &{} 0 &{} &{} 0&{} &{} -&{} \\ \end{array}\right) . \end{aligned}$$

• Step 10: The aggregated outranking Boolean matrix by unifying the entities of CSF boolean concordance and discordance matrices. The aggregated outranking boolean matrix $\mathfrak {R}$ is given by

  $$\begin{aligned} \mathfrak {R}= \left( \begin{array}{ccccccccc} -&{} &{}1&{} &{}1&{} &{}1&{} \\ 0&{} &{} - &{} &{} 1&{} &{} 1\\ 0&{} &{} 0&{} &{} -&{} &{} 1&{} \\ 0&{} &{} 0 &{} &{} 0&{} &{} -&{} \\ \end{array}\right) . \end{aligned}$$

• Step 11: The outranking graph of this MAGDM problem in IT sector is shown by Fig. 6. It can be narrated that the network monitoring software $\mathcal {Z}_{1}$ is outranking all the other network monitoring softwares ( $\mathcal {Z}_{2}$, $\mathcal {Z}_{3}$ and $\mathcal {Z}_{4}$ ) and the partial preferences of the alternatives are also pinned up in Table 27. Thus, the alternative $\mathcal {Z}_{1}$ is regarded as best network monitoring software for the management of military data; furthermore, it can be noted from Fig. 6 that $\mathcal {Z}_{2}$ and $\mathcal {Z}_{3}$ are incomparable softwares.

• Step 12: The concordance outranking coefficient $\overbrace{Q_{u}}$, discordance outranking coefficient $\underbrace{Q_{u}}$, and net outranking index $\yen _{u}$ are arranged in Table 28 which indicates that $\mathcal {Z}_1$ is the most favorable choice as well as the linear ranking of the choices is: $\mathcal {Z}_1\succ \mathcal {Z}_3\succ \mathcal {Z}_2\succ \mathcal {Z}_4$.

Table 26 Normalized Euclidean distances $d(\overline{\mathcal {R}}_{\kappa v},\overline{\mathcal {R}}_{\tau v} )$

Fig. 6

Outranking decision graph

Table 27 Exploration of decision graph

Table 28 Outranking indices of the alternatives

5.2.4 Results and Discussion

The final results of the case study demonstrate that the SolarWind-NPM $(\mathcal {Z}_1)$ network monitoring software is the preferable choice from all the selected alternatives.

6 Comparison

In this section, we compare our proposed CSF-ELECTRE I method with existing CSF-TOPSIS method, introduced by Akram et al. [33], to evince the authenticity and credibility of the proposed technique. To achieve this goal, we solve MAGDM problems “Selection of best location for new branch of company” and “Selection of network monitoring software for military purpose” by CSF-TOPSIS method.

6.1 Comparison with Decision Alternatives in Business Sector

In CSF-TOPSIS method, step 1–step 4 are identical to CSF-ELECTRE I method.

• Step 5: To evaluate the complex spherical fuzzy positive ideal solution (CSF-PIS) and complex spherical fuzzy negative ideal solution (CSF-NIS), we first identify the benefit-type attributes and cost-type attributes from the given set of attributes. Apparently, “Distance from marketplaces and general investment cost” are cost-type attributes, but in CSF-ELECTRE I method, the shortest distance between marketplaces and site assessed by higher linguistic term, and similarly, a location with minimum investment cost is assigned highly ranked CSFN; therefore, all attributes under consideration are treated as benefit-type attributes. The CSF-PIS and CSF-NIS, determined by Eqs. 25 and 26, respectively, are arranged in Table 29

  $$\begin{aligned} \digamma ^{PIS}_{v} = \left\{ \begin{array}{ll} \displaystyle \max ^{b}_{u=1}\overline{\mathcal {R}}_{uv}, &{} \hbox {if}\, P_{v}\,\hbox { is Benefit-type criteria,} \\ \displaystyle \min ^{b}_{v=1}\overline{\mathcal {R}}_{uv}, &{} \hbox {if}\, P_{v}\, \hbox {is Cost-type criteria.} \end{array}\right. \end{aligned}$$

  (25)
  $$\begin{aligned} \digamma ^{NIS}_{v}= \left\{ \begin{array}{ll} \displaystyle \min ^{b}_{u=1}\overline{\mathcal {R}}_{uv}, &{} \hbox {if}\, P_{v}\, \hbox {is Benefit-type criteria,} \\ \displaystyle \max ^{b}_{u=1}\overline{\mathcal {R}}_{uv}, &{} \hbox {if}\,P_{v}\, \hbox {is Cost-type criteria.} \end{array} \right. \end{aligned}$$

  (26)

• Step 6: The distance of each alternative from CSF-PIS and CSF-NIS is calculated by the following equations:

  $$\begin{aligned}&d(\mathcal {Z}_{u}, \digamma ^{PIS}) = \Big [\frac{1}{3k}\displaystyle \sum ^{d}_{v =1}[({{\mu ^{*}}_{v}}^2 -\overline{\mu }^2_{uv})^2 + ({{\rho ^{*}}_{v}}^2 -\overline{\rho }^2_{uv})^2 + ({{\nu ^{*}}_{v}}^2 -\overline{\nu }^2_{uv})^2 \\&\quad + ({{f^{*}}_{v}}^2 - \overline{f}^2_{uv})^2 + ({{\mu ^{*}}_{g}}^2 - \overline{g}^2_{uv})^2 + ({{h^{*}}_{v}}^2 -\overline{h}^2_{uv})^2 ]\Big ]^{\frac{1}{2}},\\&d(\mathcal {Z}_{u}, \digamma ^{NIS}) = \Big [\frac{1}{3k}\displaystyle \sum ^{d}_{v =1}[({{\mu ^{'}}_{v}}^2 -\overline{\mu }^2_{uv})^2 + ({{\rho ^{'}}_{v}}^2 -\overline{\rho }^2_{uv})^2 + ({{\nu ^{'}}_{v}}^2 -\overline{\nu }^2_{uv})^2 \\&\quad + ({{f^{'}}_{v}}^2 -\overline{f}^2_{uv})^2 + ({{\mu ^{'}}_{g}}^2 -\overline{g}^2_{uv})^2 + ({{h^{'}}_{v}}^2 -\overline{h}^2_{uv})^2 ]\Big ]^{\frac{1}{2}}, \end{aligned}$$

  where, $\digamma ^{PIS}_{v}=(\mu ^{*}_{v}e^{i2\pi f^{*}},\rho ^{*}_{v}e^{i2\pi g^{*}},\nu ^{*}_{v}e^{i2\pi h^{*}})$ and $\digamma ^{NIS}_{v}=(\mu ^{'}_{v}e^{i2\pi f^{'}},\rho ^{'}_{v}e^{i2\pi g^{'}},\nu ^{'}_{v}e^{i2\pi h^{'}})$. The distances are tabulated in Table 30.

• Step 7: The revised closeness index, given in Table 31, for orderly ranking of the feasible alternatives is determined as

  $$\begin{aligned} \varpi (\mathcal {Z}_{u}) = \frac{d(\digamma ^{PIS}_{v},\mathcal {Z}_{u} )}{\displaystyle \min _{u}d(\digamma ^{PIS}_{v}, \mathcal {Z}_{u} )} - \frac{d(\digamma ^{NIS}_{v}, \mathcal {Z}_{u} )}{\displaystyle \max _{u}d(\digamma ^{NIS}_{v}, \mathcal {Z}_{u} )}. \end{aligned}$$

• Step 8: Since, the alternative with minimum index value is $\mathcal {Z}_5;$ therefore, $\mathcal {Z}_5$ is best location for new branch of company. The ranking of alternatives according to revised closeness index is arranged in Table 32.

Table 29 CSF-PIS and CSF-NIS

Table 30 Normalized Euclidean distances from ideal solution

Table 31 Revised closeness index

Table 32 Ranking of alternatives

6.2 Comparison with Decision Alternatives in IT sector

In CSF-TOPSIS method, step 1–step 4 are identical to CSF-ELECTRE I method.

• Step 5: It seems that the “Cost policy” $(\mathcal {P}_1)$ is cost-type attribute, but in CSF-ELECTRE I method, the network monitoring software with minimum price is assessed by higher linguistic term; therefore, all attributes under consideration are treated as benefit-type attributes. The CSF-PIS and CSF-NIS are arranged in Table 33.

• Step 6: The distance of each alternative from CSF-PIS and CSF-NIS is given in Table 34.

• Step 7: The revised closeness indices are given in Table 35. Ranking of alternatives are given in Table 36

Table 33 CSF-PIS and CSF-NIS

Table 34 Normalized Euclidean distances from ideal solution

Table 35 Revised closeness index

6.3 Discussion

The results of the comparative analysis can be compiled as follows:

• Table 37 describes summary of solution results for the problems of site selection by the proposed CSF-ELECTRE I method and CSF-TOPSIS method [33].

• Table 38 describes summary of solution results for the problems of software selection by the proposed CSF-ELECTRE I method and CSF-TOPSIS method [33].

• Though the MAGDM problem is scrutinized through two different methodologies, but the same results persuade the plausibility and practicality of the presented CSF-ELECTRE I technique. Thus, the same results from both techniques ensure the credibility of the alternatives $\mathcal {Z}_{5}$ as the most suitable location for a new branch of company and accuracy of the alternative SolarWinds-NPM as the best network monitoring software for military use. Moreover, consequences in the ranking of the remaining alternatives, also rendered by bar graph Figs. 7 and 8, reassure the cogency and realism of the proposed CSF-ELECTRE I method. However, Fig. 7 illustrates the comparison with the CSF-TOPSIS method in the case of business sector. Similarly, for the case of IT sector, Fig. 8 describes the ranking of the alternatives through the proposed CSF-ELECTRE I method which are being compared with the ranking of the alternatives via the CSF-TOPSIS method.

• The basic methodologies of the proposed technique and CSF-TOPSIS method [33] are different as the proposed technique is based on concordance and discordance sets that are stipulated by score degree, accuracy degree, and refusal degree where the final ranking is appraised by the outranking decision graph. On the other hand, the CSF-TOPSIS method [33] supported by positive ideal solution and negative ideal solution precisely evaluated by score degree and revised closeness index used for ultimate outcomes.

• In CSF-TOPSIS method, the linguistic terms are assigned according to nature of the attributes, i.e., benefit type or cost type; however, in CSF-ELECTRE I method, the alternatives are rated on the consequences that how the alternative is suitable pursuant to that attribute. Additionally, in CSF-ELECTRE I method, alternatives can be compared pair-wise through the decision graph; however, in CSF-TOPSIS method limited evaluation (linear ranking with best alternative) is obtained.

Table 36 Ranking of alternatives

Table 37 Comparison with CSF-TOPSIS method [33]

The comparison results emphasize the authenticity and veracity of the proposed tactic to point out the perfect decision. The results of the comparative study are visually represented by the bar graph, as shown in Fig. 7.

Fig. 7

Comparison with CSF-TOPSIS method in case of business field

Table 38 Comparison with CSF-TOPSIS method [33]

Both of the compared methodologies prefer the same alternative as best. This authenticates the competency of the presented technique under sundry decision-making scenarios. The results of the comparative study are visually represented by the bar graph, as shown in Fig. 7.

Fig. 8

Comparison with CSF-TOPSIS method in case of IT

6.4 Comparison with Existing Techniques

The existing ELECTRE I technique is successfully established and executed on MAGDM problems compromising fuzzy-related information. There are several actual facts of life in which the probable alternatives or attributes are assessed on the basis of degree of satisfaction, neutrality, and dissatisfaction, and can be manifested more powerfully by two-dimensional environment. These situations cannot be simulated or formed through fuzzy, Pythagorean fuzzy, or complex Pythagorean fuzzy version of the ELECTRE I model. The basic supremacy of the proposed approach is demonstrated as follows:

• 1. The CSF-ELECTRE I method adequately comprehend the two dimensional neutrality degree and many inconsistencies appearing in complex decision-making by competently and closely following the theory of outranking procedures.

• 2. The CSF-ELECTRE I method generates pair-wise comparison of all prospective alternatives from most convenient to inappropriate, by considering score values, accuracy values, and refusal values to establish sets of concordance and discordance which furthermore assist for outranking matrix and graph.

• 3. The thorough study of outranking graph and attributes association with the precedence of decision experts in the proposed group decision-making technique lead to the most suitable solution that are effective, profitable, and compatible.

• 4. The decision-making skills and other prevalent benefits of presented strategy is not only restricted to two-dimensional scenarios. In fact, the flexibility of CSF-ELECTRE I method enables it to confront one-dimensional MAGDM problems adroitly under the spherical fuzzy environment by placing the periodic term equal to zero in the proposed procedure.

• 5. The CSF-ELECTRE I method can be auspiciously utilized for generalized complex Pythagorean fuzzy model by placing the neutral degree equal to zero. Therefore, the proposed method serves as an efficient and eminent tactic packed with marvelous theory of ELECTRE method as well as the broader space of CSFSs to organize the independent two-dimensional inconsistent data for the sake of beneficial decisions.

7 Conclusion and Future Research

7.1 Conclusion

In MAGDM problems the obscure data can be delineated by CSF influential environment, which permits the satisfaction, neutrality, and dissatisfaction degrees in a persuasive two-dimensional frame. Furthermore, the prevalent theory and inspiring aptitude of of ELECTRE methods proved to be a major incentive for the construction modified version of the ELECTRE I technique for CSFSs that encapsulates the favorable and convenient structure of CSFSs as well as the theoretical foundations of ELECTRE I approach. The proposed methodology is perfectly applicable for MAGDM problems as it remarkably confronts the vague data of periodic nature which gives rise to appropriate and congruent decisions in the two dimensional environments. We have provided the execution of CSF-ELECTRE I approach through detailed exposition and also by a flowchart. Another advantageous feature is that the presented technique has an edge over the existing methodologies available for the traditional environments by addressing neutral membership degree along with the perspective of satisfaction and dissatisfaction degrees that broaden the decision-making space for the ratings of alternatives according to their conflicting attributes.

The presented technique has an edge over the existing methodologies available for the traditional environments by addressing neutral membership degree along with the perspective of satisfaction and dissatisfaction degrees that broaden the decision-making space for the ratings of alternatives according to their conflicting attributes. Within the procedure of proposed technique, group consensus of CSF opinions and the CSF-weights of attributes have been fused to a group opinion matrix by employing the CSFWA operator. Thereafter, the ELECTRE-based outranking method has been developed to analyze the group opinion matrix known as, AWCSFPM. The score degree, accuracy degree, and refusal degree of CSFNs in AWCSFPM have been exerted to formulate the CSF concordance and discordance indices corresponding to each couple of alternatives. Consequently, the decision graph with respect to the aggregated outranking matrix has been used for final ELECTRE-solutions.

Two numerical precedents have been performed using the proposed MAGDM approach. The outcomes generated by the proposed method are similar with the results of comparative analysis conducted by CSF-TOPSIS method. Beside the numerical comparison, a detailed argument has been presented to spotlight the dominance and merits of proposed strategy over the existing approaches.

7.2 Limitations and Future Work

• 1. The CSF-ELECTRE I method is inadequate to deal situation in which the square sum of truth membership, neutral membership, and falsity membership of amplitude terms (or phase terms) surpasses 1.

• 2. Complexity and convolution appear while evaluating three types of concordance and discordance sets against large amount of alternatives (or attributes) in the developed technique.

• 3. As future work, we are concerned to apply the presented approach for the supplier selection, selection of water desalination plant, decisions in E-commerce, and many other fields of science and management.

• 4. We are further interested to extend the other variants of ELECTRE method including ELECTRE II, ELECTRE III ,and ELECTRE IV under the adequate environment of CSFSs.