1 Introduction

The fuzzy network approach has been introduced by Gegov [1] to infuse transparency in decision making. A structure of fuzzy system without considering the intermediate variables will affect the level of trust and certainty of the alternatives. This is proven as the precision of single rule base and multiple rule base in the fuzzy system serves a moderate level of transparency and accuracy in countering multiplex procedures of problem solving [2]. Fuzzy network considers the benefit and cost subsystems of the demonstrating network. Because it analyses benefit and cost factors individually, a fuzzy network is more transparent than a single rule based and multiple rules based fuzzy system for decision making. By expressing each set of criteria as a node and the interactions between them as links, this network accounts for the internal structure of the represented process. Fuzzy network has the capacity of being straightforward and exact, which is extremely crucial to settle on better choices [1].

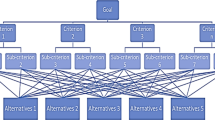
Interpretable Artificial Intelligence (AI) as a part of explainable AI model, can be discovered from the transparency delivered by fuzzy network. As claimed by Loyola-Gonzalez [3], interpretable model capable of providing information to decision makers independently. Fuzzy network also capable of serving the final decisions well as it carries the importance of criteria and decision makers expertise throughout the formulation. This statement can best demonstrate as white-box models in a fuzzy network where rule-based approach is used in order to describe the collection of intermediate variables in the process of decision making as illustrate in Fig. 1. In this situation, because of unequivocal and sufficient information of the inner structure of the modelling process present, the white-box interpretation further enhances the description of transparency in the model [2].

Fig. 1
figure 1

Black box and white box illustration

Full size image

The extension of fuzzy sets introduced by Vicenc Torra [4] can be utilized in deciding the allocation or standards of alternatives engaged with the decision-making issues confronted [5]. As proposed by [6], hesitant fuzzy sets permits several possible membership degrees to be included in a component of a set within a range [0,1] [7]. As it manages vulnerability, hesitant fuzzy sets have been demonstrated in previous studies to show proficiency in decision making. The authors in [8] incorporate hesitant fuzzy set in Technique for Order Preferences by Similarity to Ideal Solution (TOPSIS) in order to select the most appropriate energy policy with the incorporation of maximizing deviation method. On the other hand, Xu et al. [9] provided and overview of a decision support process for incomplete hesitant fuzzy preference relations (HFPRs).

Human encounters issues in settling for right choices depending on the inadequate, loss or questionable data. Thus, Zadeh introduced Z-number as a fuzzy set that can capture the reliability of decisions made through the confidence level of decision makers [10]. Z-numbers prove to be useful in putting forward questionable data as it is an idea worked together in fuzzy theory which portrays the information on individual through the unwavering reliability of decision making. As Z-number holds two elements in an ordered pair fuzzy number, the first element represents the ratings and the second element represents the confidence level of decision makers on the ratings. This new concept is broadly applied in the process involves uncertain information, as the knowledge of human beings is more closely described [11]. Based on the Fuzzy Expectation of the fuzzy set, Z-numbers can be implied as classical fuzzy sets as demonstrated by Kang et al. [10]. Other than the application of Z-number in TOPSIS as carried by Yaakob and Gegov in the enhanced fuzzy rule-based approach in MCDM using Z-number on TOPSIS [12], Aliev and Memmedova [13] applied Z-numbers in modeling the effect of Pilates exercises on psychological of human beings. To conclude, Z-numbers are flexible to be implied in several possible approaches as reliability is assigned to the ratings.

It is crucial for decision makers are aware on the performance of criteria in multicriteria in decision making. However, established TOPSIS methods disclose the performance of benefit and cost criteria due to low transparency inherited [2]. In real situation, experts encounter hesitancy in making decision, for instance, when they have hesitancy to decide whether the alternative is good or very good. Thus, if less information is adapted in the decision making, the end result could be misleading without considering different opinions. Even though there are increasing number of research on the reliability of decision information, but it still in need of better incorporation into modelling complex decision-making processes. For example, how sure the decision makers are in their opinions about their alternatives. The drawbacks mentioned above bring the motivation of this study.

This paper describes the transparency through fuzzy network approach in the formulation proposed. The incorporation of Z-numbers in fuzzy network contributes to reliability in the transparency of decision making and hesitant fuzzy set overcomes the vagueness of decisions inherit in the process. Z-numbers are evaluated by the decision makers as they decide the confidence level towards the ratings made, thus making a more reliable decision. In addition, hesitant fuzzy set is subsumed in fuzzy network to allow decision makers incorporate several possible evaluations out of doubts. When compared with the established research on fuzzy decision making, the proposed Z-HFN has the following interesting advantages and characteristics:

  1. 1.

    This proposed method allows decision makers to give several possible opinions in their evaluations on alternatives.

  2. 2.

    This proposed method allows decision makers to access the performance of alternatives in terms of benefit and cost criteria, thus, increase the level of transparency in the process of decision making.

  3. 3.

    This proposed method also considers the reliability of information which represent the confidence level of decisions.

The proposed method is verified through the comparison of the proposed method to established fuzzy methods under the Spearman’s rho correlation method. This paper presents the theoretical preliminaries in Sect. 2, method formulation in Sect. 3 and case study that testify this method through stocks ranking in Sect. 4. The analysis of results are presented in Sect. 5 with the conclusion of this paper in Sect. 6.

2 Theoretical Preliminaries

2.1 Fuzzy Numbers

A fuzzy number is defined as a fuzzy set that forms a normal convex graph with a single point on a single line [14]. A fuzzy set must represent a normal and convex graph. A fuzzy set is normal if there is only one element, \(x\) in which the membership degree is one through the universe as shown in Fig. 2. A convex fuzzy set is represented by a membership function whose membership values are increasing linearly, or whose membership values are decreasing linearly, or whose membership values are increasing linearly, then decreasing rigidly linear with increasing values for elements in the universe. Convex fuzzy set can be derived mathematically when there exists a relation between element a, b and c in fuzzy set \(\mathop D\limits_{\sim }\) as

$${\mu }_{\underset{\sim }{D}}(x)\ge \mathit{min}\left[{\mu }_{\underset{\sim }{D}}(x),{\mu }_{\underset{\sim }{D}}(z)\right]$$
(1)

when \(a<b<c\).

Fig. 2
figure 2

Membership function of fuzzy number

Full size image

2.2 Hesitant Fuzzy Numbers

In 2009, Vicenc Torra [4] originated the concept of Hesitant Fuzzy Set (HFS) where every possible evaluation made by decision makers are permitted as the membership degree values of HFS which is defined as:

Definition 1

Hesitant fuzzy set (HFS) returns a subset of [0, 1] when fixed set, X receives HFS as a function [15].

$$HFS=\left\{\langle x,{h}_{Z}\left(x\right)\rangle \left|x\in X\right.\right\}$$
(2)

\(h_{Z} \left( x \right)\) is the possible membership degree of the element \(x \in X\) as it stands as a set of values ranging from [0, 1] to the \(HFS\).

2.3 Z-numbers

Z-numbers are a concept that incorporates rating and reliability in computations as shown in Figs. 3 and 4. It is represented in the form of type-1 fuzzy number. \(\tilde{D}\) represents the evaluations in real-valued fuzzy numbers. \(\tilde{E }\) signifies the confidence of decision makers towards the rating of \(\tilde{D }\).

Fig. 3
figure 3

Membership function of ratings in Z-numbers

Full size image
Fig. 4
figure 4

Membership function of reliability in Z-numbers

Full size image
$$Z=\left(\tilde{D },\tilde{E }\right)$$
(3)

2.4 Fuzzy Network

This paper is incorporated with if-then rules and Boolean matrices that are infused through fuzzy rules in the fuzzy network, FN. The choice is demonstrated by the ability of such structured models to operate with any number of nodes in FNs. With these links, these structures can depict nodes in an FN and are used as a bridge between fuzzy systems and FNs. A fuzzy system of fuzzy network is formed through if-then rules before converting it to Boolean matrices. The established Boolean matrix is then formed through nodes that are created from the if-then rules earlier. A Boolean matrix contains information that are derived from the outputs and inputs assigned through rules that are established from if-then rules. Binary values of 1 are applied in the Boolean matrix to show the presence of rules between inputs and outputs and 0 indicates no rules presence [16].

Horizontal merging is an operation in fuzzy network that carries binary values into serial nodes in the same level of the fuzzy network. Referring to Gegov et al. [17], this method can be implied as the output from the first operand nodes and the second operand nodes are merged as the final nodes in the Boolean matrix while the intermediate nodes do not arise in the final product. In comparison to horizontal merging, vertical merging carries a pair of parallel nodes in the operation that carries the binary values. Gegov [1] presents vertical merging as a method that carries the output from the second operand nodes and input from the first operand nodes to be merged in the final product.

3 Method Formulation

A proposed method is presented in this section in the systematic manner, where evaluations made by decision makers are collected independently due to different backgrounds in the field, which contributes to a different level of expertise. The criteria assigned in the evaluation are classified as benefit and cost criteria as output generated from each subsystem will be depicted as Benefit Level (BL) and Cost Level (CL). The proposed method of Z-Hesitant Fuzzy Network (Z-HFN) can be interpreted where inputs are classified firstly into each benefit and cost subsystem before implying as output to the alternative system. The outer frame of the model represents the vertical merging carried out under rule bases and the inner frame which consists of benefit and cost subsystems represents the horizontal merging of rule bases carried in the fuzzy network.

Step 1:

Construct decision matrices where decisions, \({x}_{vy,z}\) and \({w}_{ty,z}\), made by decision makers, \(z\), are converted to Hesitant Fuzzy Sets (HFS). The decisions made by decision makers are represented by the linguistic terms in the rating in Figs. 5 and 6. As \(z = 1, 2, 3,\dots , Z\), these matrices are then categorized according to the criteria determined in the Benefit System and Cost System, which are the Benefit Criteria and Cost Criteria.

$${D}_{z}^{B}=\begin{array}{c}{B}_{1}\\ {B}_{2}\\ \vdots \\ {B}_{v}\end{array}\left[\begin{array}{cccc}{x}_{\mathrm{11,1}}& {x}_{12,z}& \cdots & {x}_{1y,z}\\ {x}_{21,z}& {x}_{22,z}& \cdots & {x}_{2y,z}\\ \vdots & \vdots & \ddots & \vdots \\ {x}_{v1,z}& {x}_{v2,z}& \cdots & {x}_{vy,z}\end{array}\right]$$
(4)
$${D}_{z}^{C}=\begin{array}{c}{C}_{1}\\ {C}_{2}\\ \vdots \\ {C}_{t}\end{array}\left[\begin{array}{cccc}{w}_{11,z}& {w}_{12,z}& \cdots & {w}_{1y,z}\\ {w}_{21,z}& {w}_{22,z}& \cdots & {w}_{2y,z}\\ \vdots & \vdots & \ddots & \vdots \\ {w}_{t1,z}& {w}_{t2,z}& \cdots & {w}_{ty,z}\end{array}\right]$$
(5)

for \(z=\mathrm{ 1,2},\dots ,Z\)

Fig. 5
figure 5

Linguistic terms for the ratings of alternatives

Full size image
Fig. 6
figure 6

Linguistic terms for the importance weight of each criterion

Full size image

The matrices \({D}_{z}^{B}\) represents the decision matrix of the benefits and \({D}_{z}^{C}\) represents the decision matrix of the costs. \({x}_{vy,z}\) represents the alternative’s rating with respect to the benefit criteria, \({B}_{v}(v=\mathrm{1,2},\dots ,V)\) and \({w}_{ty,z}\) is denoted as the rating of alternatives to the cost criteria, \({C}_{t}(t=\mathrm{1,2},\dots ,T)\)

Step 2:

The reliability of decisions, \(\tilde{E }\), in Z-numbers as shown in Eq. (6), is represented by linguistic terms in Fig. 7. Then, merge both elements in Z-numbers into Type-1 fuzzy number.

Fig. 7
figure 7

Linguistic terms for the reliability of experts

Full size image
$$Z=\left(\tilde{D },\tilde{E }\right)$$
(6)

As Z number holds the rating, \(\tilde{D }\) as \(\left\{\tilde{D }=\left(x, {\varphi }_{\tilde{D }}\right)\left|x\in \left[\mathrm{0,1}\right]\right.\right\}\) and the reliability, \(\tilde{E }\) as \(\left\{\tilde{E }=\left(x, {\varphi }_{\tilde{E }}\right)\left|x\in \left[\mathrm{0,1}\right]\right.\right\}\) where the \({\varphi }_{\tilde{D }}\) and \({\varphi }_{\tilde{E }}\) are the membership functions. The method to convert Z-number into Type-1 fuzzy number has been adopted from [10]:

  1. (a)

    Conversion of the second element (reliability) using Eq. 7

    $$\Phi =\frac{\int x{\varphi }_{\tilde{E }}\left(x\right)dx}{\int {\varphi }_{\tilde{E }}\left(x\right)dx}$$
    (7)
  2. (b)

    Multiply the reliability into the rating in \(\tilde{D }\) thus representing a weighted Z-number. Referring to [10], we can signify weighted Z-number as

    $${Z}^{\Phi }=\left\{\langle x, {\varphi }_{{\tilde{D }}^{\Phi }}(x)\rangle \left|{\varphi }_{{\tilde{D }}^{\Phi }}\left(x\right)=\Phi {\varphi }_{{\tilde{D }}^{\Phi }}\left(x\right),x\in \left[\mathrm{0,1}\right]\right.\right\}$$
    (8)

Theorem 1

\({F}_{{\tilde{D }}^{\Phi }}\left(x\right)=\Phi {F}_{\tilde{D }}\left(x\right), x\in X\)

$$s.t. \, {\varphi }_{{\tilde{D }}^{\Phi }}\left(x\right)=\Phi {\varphi }_{\tilde{D }}\left(x\right), x\in X$$
(9)

Proof

$${F}_{{\tilde{D }}^{\Phi }}\left(x\right)=\underset{x}{\overset{}{\int }}x{\varphi }_{{\tilde{D }}^{\Phi }}\left(x\right)dx=\underset{x}{\overset{}{\int }}\Phi x{\varphi }_{\tilde{D }}\left(x\right)dx=\Phi \underset{x}{\overset{}{\int }}x{\varphi }_{\tilde{D }}\left(x\right)dx=\Phi {F}_{\tilde{D }}\left(x\right)$$
(10)
  1. (c)

    Convert the weighted Z-fuzzy number into Type 1 fuzzy number as referred to the Fuzzy Expectation theory [10]. Type-1 fuzzy number can be depicted as

    $${\tilde{Z }}^{{{\prime}}}=\left\{\langle x, {\varphi }_{{\tilde{Z }}^{{^{\prime}}}}(x)\rangle \left|{\varphi }_{{\tilde{Z }}^{{^{\prime}}}}\left(x\right)={\varphi }_{\tilde{D }}\left(\frac{x}{\sqrt{\Phi }}\right),x\in \left[{0,1}\right]\right.\right\}$$
    (11)

Theorem 2

\({F}_{{\tilde{Z }}^{{^{\prime}}}}\left(x\right)=\Phi {F}_{\tilde{D }}\left(x\right), x\in \sqrt{\Phi }X\)

$$s.t. {\varphi }_{{\tilde{Z }}^{{^{\prime}}}}\left(x\right)={\varphi }_{\tilde{D }}\left(\frac{x}{\sqrt{\Phi }}\right), x\in \sqrt{\Phi }X$$
(12)

Proof

$${F}_{{\tilde{Z }}^{{^{\prime}}}}\left(x\right)=\underset{\sqrt{\Phi }x}{\overset{}{\int }}x{\varphi }_{{\tilde{Z }}^{^{\prime}}}\left(x\right)dx=\underset{\sqrt{\Phi }x}{\overset{}{\int }}x{\varphi }_{\tilde{D }}\left(\frac{x}{\sqrt{\Phi }}\right)dx=\sqrt{\Phi }q\underset{x}{\overset{}{\int }}\left(\sqrt{\Phi }q\right){\varphi }_{\tilde{D }}\left(t\right)d\left(\sqrt{\Phi }q\right)=\Phi \underset{t}{\overset{}{\int }}t{\varphi }_{\tilde{D }}\left(t\right)dt=\Phi {F}_{\tilde{D }}\left(x\right)$$
(13)

Theorem 3

$${F}_{{\tilde{Z }}^{{^{\prime}}}}\left(x\right)={F}_{{\tilde{D }}^{\Phi }}\left(x\right)$$
(14)

Proof

$${F}_{{\tilde{D }}^{\Phi }}\left(x\right)=\Phi {F}_{\tilde{D }}\left(x\right)$$
$${F}_{{\tilde{Z }}^{{^{\prime}}}}\left(x\right)=\Phi {F}_{\tilde{D }}\left(x\right)$$
$${F}_{{\tilde{Z }}^{{^{\prime}}}}\left(x\right)={F}_{{\tilde{D }}^{\Phi }}\left(x\right)$$
(15)

This method concludes that under fuzzy expectation, \({\tilde{Z }}^{{^{\prime}}}\) is equal to \({\tilde{D }}^{\Phi }\).

Step 3:

The hesitant fuzzy positive initial solution (PIS) A+ and hesitant fuzzy negative fuzzy initial solution (NIS) A are derived as follows:

A+  = \(\left\{{{x}}_{v},{ max} \langle {x}_{vy}^{\sigma (\lambda )}\rangle ,{ v }={ 1,2},\dots .{v}\right\}\)

$$=\left\{\begin{array}{l}\langle {x}_{1},\left({\left({x}_{1}^{1}\right)}^{+},{\left({x}_{1}^{2}\right)}^{+},\dots ,{\left({x}_{1}^{y}\right)}^{+}\right)\rangle \\ \times \langle {x}_{2},\left({\left({x}_{2}^{1}\right)}^{+},{\left({x}_{2}^{2}\right)}^{+},\dots ,{\left({x}_{2}^{y}\right)}^{+}\right)\rangle \\ \times \dots \langle {x}_{v},\left({\left({x}_{v}^{1}\right)}^{+},{\left({x}_{v}^{2}\right)}^{+},\dots ,{\left({x}_{v}^{y}\right)}^{+}\right)\rangle \end{array}\right\}$$
(16)

A− = \(\left\{{{x}}_{v},\mathrm{ max} \langle {x}_{vy}^{\sigma (\lambda )}\rangle ,{ v }={ 1,2},\dots .{v}\right\}\)

$$=\left\{\begin{array}{l}\langle {x}_{1},\left({\left({x}_{1}^{1}\right)}^{-},{\left({x}_{1}^{2}\right)}^{-},\dots ,{\left({x}_{1}^{y}\right)}^{-}\right)\rangle \\ \times \langle {x}_{2},\left({\left({x}_{2}^{1}\right)}^{-},{\left({x}_{2}^{2}\right)}^{-},\dots ,{\left({x}_{2}^{y}\right)}^{-}\right)\rangle \\ \times \dots \langle {x}_{v},\left({\left({x}_{v}^{1}\right)}^{-},{\left({x}_{v}^{2}\right)}^{-},\dots ,{\left({x}_{v}^{y}\right)}^{-}\right)\rangle \end{array}\right\}$$
(17)

Step 4:

Determine the distance of alternatives, \({\delta }_{i}^{+}\) and \({\delta }_{i}^{-}\) from the hesitant fuzzy PIS \({A}^{+}\) and NIS \({A}^{-}\) by incorporating the hesitant fuzzy Euclidean distance presented by Xu and Xia [18].

$${\delta }_{i}^{+}=\sum_{j=1}^{n}\delta \left({x}_{ij }, {x}_{j}^{+}\right){w}_{j}= \sum_{i=1}^{n}{w}_{j }\sqrt{\frac{1}{l}{\sum }_{\lambda =1}^{l}{\left|{x}_{ij}^{\sigma (\lambda )}- {\left({x}_{j}^{\sigma (\lambda )}\right)}^{+}\right|}^{2}}$$
(18)
$$i={1,2},\dots n$$
$${\delta }_{i}^{-}=\sum_{j=1}^{n}\delta \left({x}_{ij }, {x}_{j}^{-}\right){x}_{j}= \sum_{i=1}^{n}{w}_{j }\sqrt{\frac{1}{l}{\sum }_{\lambda =1}^{l}{\left|{x}_{ij}^{\sigma (\lambda )}- {\left({x}_{j}^{\sigma (\lambda )}\right)}^{-}\right|}^{2}}$$
(19)
$$i={1,2},\dots n$$

Step 5:

Calculate the relative closeness coefficient, \({C}_{i}\) of alternatives with respect to hesitant fuzzy PIS A+ separately, according to the level of criteria, benefit, and cost criteria, using Eq. (20).

$${\Phi }_{i}= \frac{{\delta }_{i}^{-}}{{\delta }_{i}^{+}+{\delta }_{i}^{-}}$$
(20)

Step 6:

Referring to Yaakob [2], find the Influence Closeness Coefficient (ICC) by adopting the influence degree of decision makers to each of the stock measured. This method is then continued by normalizing the ICC (NICC) by assigning the maximum value of ICC to be divided to each ICC according to the stocks.

$${\sigma }_{k}= \frac{{\theta }_{k}}{\sum_{i=1}^{k}{\theta }_{k}}, {\rm For}\, k=1, 2, \dots , K$$
(21)

\(\theta\) is denoted as the influence degree of decision maker k where the value is between 0 i.e. verified as not influential to 10 i.e. signified as most influential [2]. \(\sigma\) resembles the normalized influence degree of kth decision makers. This method is carried on by assigning the normalized influence degree to each correlation coefficient of stocks accordingly. According to j = 1, 2, … m and k = 1, 2, …, K,

$${ICC}_{j,k}^{B}= {\sigma }_{k}\times {CC}_{j.k}^{B}$$
(22)
$${ICC}_{j,k}^{C}= {\sigma }_{k}\times {CC}_{j.k}^{C}$$
(23)

\({ICC}_{j,k}^{B}\) and \({ICC}_{j,k}^{C}\) are then normalized in the equations shown below to obtain values between 0 to 1.

$${\tau }_{j.k}^{B}= {ICC}_{j,k}^{B}/{\mathrm{max}}_{j}{ICC}_{j,k}^{B}$$
(24)
$${\tau }_{j.k}^{C}= {ICC}_{j,k}^{C}/{\mathrm{max}}_{j}{ICC}_{j,k}^{C}$$
(25)

as j = 1, 2, … m and k = 1, 2, …, K.

The normalized influenced closeness coefficient is then converted into linguistic terms that are determined from Fig. 8 to evaluate the level of alternative performances.

Fig. 8
figure 8

Linguistic terms for the level of alternatives

Full size image

Step 7:

By referring to the NICC values calculated previously and evaluations made earlier by decision makers, build the antecedent and consequent matrices that depict the system of benefit and cost. Build the antecedent matrices of BS and CS with respect to groups, \(k\):

$${x}_{k}= \begin{array}{l}{B}_{1}\\ {B}_{2}\\ \begin{array}{l}\vdots \\ {B}_{m,k}\end{array}\end{array}\left[\begin{array}{lll}\begin{array}{ll}{x}_{11,k}& {x}_{12,k}\\ {x}_{21,k}& {x}_{22,k}\end{array}& \begin{array}{l}\cdots \\ \cdots \end{array}& \begin{array}{l}{x}_{1m,k}\\ {x}_{2m,k}\end{array}\\ \begin{array}{ll}\vdots & \vdots \end{array}& \ddots & \vdots \\ \begin{array}{ll}{x}_{e1,k}& {x}_{e2,k}\end{array}& \cdots & {x}_{em,k}\end{array}\right]$$
(26)
$${y}_{k}=\begin{array}{l}{C}_{1}\\ {C}_{2}\\ \begin{array}{l}\vdots \\ {C}_{l,k}\end{array}\end{array}\left[\begin{array}{lll}\begin{array}{ll}{y}_{11,k}& {y}_{12,k}\\ {y}_{21,k}& {y}_{22,k}\end{array}& \begin{array}{l}\cdots \\ \cdots \end{array}& \begin{array}{l}{y}_{1l,k}\\ {y}_{2l,k}\end{array}\\ \begin{array}{ll}\vdots & \vdots \end{array}& \ddots & \vdots \\ \begin{array}{ll}{y}_{e1,k}& {y}_{e2,k}\end{array}& \cdots & {y}_{el,k}\end{array}\right]$$
(27)

for \(k=\mathrm{1,2}, \dots , K\)\({x}_{em,k}\) and \({y}_{el,k}\) are linguistic terms that reflect the views of decision makers. Consequent matrices are built complementary to the previous antecedent matrices. \({\lambda }_{m,k}\) and \({\psi }_{m,k}\) represent the coefficients in consequent matrices for the benefit system, BS and cost system, CS, respectively.

$${\Lambda }_{k}={\left[\begin{array}{cccc}{\lambda }_{1,k}& {\lambda }_{2,k}& \cdots & {\lambda }_{m,k}\end{array}\right]}$$
(28)
$${\Psi }_{k}={\left[\begin{array}{cccc}{\psi }_{1,k}& {\psi }_{2,k}& \cdots & {\psi }_{m,k}\end{array}\right]}$$
(29)

as \(k=\mathrm{1,2},\dots , K\). where \({\Lambda }_{k}\) and \({\Psi }_{k}\) are linguistic terms representing the output of the BS and CS systems, reflecting the values of \({NICC}_{j.k}^{B}\) and \({NICC}_{j.k}^{C}\).

The benefit system consists of K matrix decision rules presented in Eq. (30).

$${If x}_{k}= \left[\begin{array}{ccc}\begin{array}{cc}{x}_{11,k}& {x}_{12,k}\\ {x}_{21,k}& {x}_{22,k}\end{array}& \begin{array}{c}\cdots \\ \cdots \end{array}& \begin{array}{c}{x}_{1m,k}\\ {x}_{2m,k}\end{array}\\ \begin{array}{cc}\vdots & \vdots \end{array}& \ddots & \vdots \\ \begin{array}{cc}{x}_{e1,k}& {x}_{e2,k}\end{array}& \cdots & {x}_{em,k}\end{array}\right], \,{\rm then}\,{\Lambda }_{k}={\left[\begin{array}{cccc}{\lambda }_{1,k}& {\lambda }_{2,k}& \cdots & {\lambda }_{m,k}\end{array}\right]}$$
(30)

The previous matrices can best be interpreted in rule bases as

$${\rm Rule\,1}: If {B}_{1}\,\,is\,\, {x}_{11,k} \,{\rm and}\,\cdots \,{\rm and}\, {B}_{e}\,\, is\,\, {x}_{e1,k} \,{\rm then}\, BL is {\lambda }_{1,k}$$
$$\begin{array}{ccc}\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}& & & \vdots \end{array}& & & \end{array}& \vdots & & \end{array}& & \vdots & \end{array}& & \end{array}$$
$${\rm Rule\, m}: If\,\, {B}_{1}\,\,is\,\, {x}_{1m,k}\,{\rm and}\,\cdots \,{\rm and}\, {B}_{e}\,\, is\,\, {x}_{em,k} \,{\rm then}\, BL\,\, is\,\, {\lambda }_{m,k}$$
(31)

where \(BL\) is the benefit level of alternatives, for \(j=1,\dots ,m\) and for \(k=1,\dots ,K\). The same formulation is implied on the cost system of K matrix decision rules where:

$${If Y}_{k}= \left[\begin{array}{ccc}\begin{array}{cc}{y}_{11,k}& {y}_{12,k}\\ {y}_{21,k}& {y}_{22,k}\end{array}& \begin{array}{c}\cdots \\ \cdots \end{array}& \begin{array}{c}{y}_{1m,k}\\ {y}_{2m,k}\end{array}\\ \begin{array}{cc}\vdots & \vdots \end{array}& \ddots & \vdots \\ \begin{array}{cc}{y}_{e1,k}& {y}_{e2,k}\end{array}& \cdots & {y}_{em,k}\end{array}\right], \,{\rm then}\, {\Psi }_{k}={\left[\begin{array}{cccc}{\psi }_{1,k}& {\psi }_{2,k}& \cdots & {\psi }_{m,k}\end{array}\right]}$$
(32)

as matrices k = 1, 2, …, K.

The previous matrices can best be interpreted in rule bases as

$${\rm Rule}\, 1: If\,\, {C}_{1}\,\, is\,\, {x}_{11,k} \,{\rm and}\, \cdots \,{\rm and}\, {C}_{f}\,\, is\,\, {x}_{f1,k} \,{\rm then}\, C{L}_{1}\,\, is\,\, {\psi }_{1,k}$$
$$\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}& & & \vdots \end{array}& & & \end{array}& \vdots & & \end{array}& & \vdots & \end{array}& & & \vdots \end{array}$$
$${\rm Rule}\, m: If\,\, {C}_{1} \,\,is\,\, {x}_{1m,k} \,{\rm and}\, \cdots \,{\rm and}\, {C}_{f} \,\,is \,\,{x}_{fm,k} \,{\rm then}\, C{L}_{m}\,\, is\,\, {\psi }_{m,k}$$
(33)

With the cost level of alternatives represented by \(CL\), for \(j=1,\dots ,m\) and, for \(k=1,\dots ,K\)

Step 8:

Define the alternative system (AS), \({M}_{k}\). AS can be constructed based on the antecedent and consequent matrices built. As k = 1,2,…..K,

$$M_{k} = \begin{array}{*{20}c} {BL} \\ {CL} \\ \end{array} \left[ {\begin{array}{*{20}c} {\lambda_{1,k} \cdots \lambda_{1,k} \cdots \lambda_{m,k} \cdots \lambda_{m,k} } \\ {\psi_{1,k} \cdots \psi_{m,k} \cdots \psi_{1k} \cdots \psi_{m,k} } \\ \end{array} } \right]$$
(34)

The measured levels of the same alternative \(j\) is represented by each row of inputs for this case. Hence, the AS antecedent matrices, \({M}_{k}\), are developed as the size of \(m\times 2\) as in Eq. (35).

$${M}_{k}=\begin{array}{c}BL\\ CL\end{array}\left[\begin{array}{c}{\lambda }_{1,k}, {\lambda }_{2,k}, {\lambda }_{3,k}\cdots {\lambda }_{m,k}\\ {\psi }_{1,k}, {\psi }_{2,k}, {\psi }_{3,k}\cdots {\psi }_{m,k}\end{array}\right]$$
(35)

To complement the antecedent matrices of AS, the AS consequent matrices are retrieved accordingly:

  1. (i)

    Calculate the aggregation, \({\xi }_{j,k}\) of the weighted \({NICC}_{j.k}^{B}\) and \({NICC}_{j.k}^{C}\) as in Eq. (36).

    $${\xi }_{j,k}=\frac{ {NICC}_{j.k}^{B}\times \left(\frac{e}{e+f}\right)+{NICC}_{j.k}^{C}\times \left(\frac{f}{e+f}\right)}{2}$$
    (36)

    According to \(j = 1, 2, \dots m\) and \(k = 1, 2, \dots , K\).

  2. (ii)

    Normalizing the values of \({\xi }_{j,k}\) to confirm their values lie in between [0,1].

    $${N\xi }_{j,k}= {\xi }_{j,k}/{\mathrm{max}}_{j}{\xi }_{j,k}$$
    (37)

    as \(j = 1, 2, \dots m\) and \(k = 1, 2, \dots , K\).

  3. (iii)

    The normalized value of \({\xi }_{j,k}\) is then translated into linguistic terms as listed in Fig. 8 which represent the alternative levels. Then, the K for AS consequent matrices, in this case of size \(1\times m\) rather than \(1 \times m\cdot m\), are described in Eq. (38).

    $${N}_{k}=AL\left[{N\xi }_{1,k}, {N\xi }_{2,k}\cdots {N\xi }_{m,k}\right] \,{\rm for}\, k=1,\dots ,K$$
    (38)

Alternative levels are categorised as AL. Thus, decision rules in \(K\) matrices, represents the system of alternatives:

If \({M}_{k}= \begin{array}{c}BL\\ CL\end{array}\left[\begin{array}{ccc}{\lambda }_{1,k}& ,& \begin{array}{ccc}{\lambda }_{2,k}& ,& \begin{array}{ccc}{\lambda }_{3,k}& \cdots & {\lambda }_{m,k}\end{array}\end{array}\\ {\psi }_{1,k}& ,& \begin{array}{ccc}{\psi }_{2,k}& ,& \begin{array}{ccc}{\psi }_{3,k}& \cdots & {\psi }_{m,k}\end{array}\end{array}\end{array}\right]\),

$${{\rm then}\,N}_{k}=AL\left[{N\xi }_{1,k}, {N\xi }_{2,k}\cdots {N\xi }_{m,k}\right]$$
(39)

for \(k=1,\dots ,K\)and can best be interpreted in rule bases

$${\rm Rule}\, 1: If \,\,B{L}_{1} \,\,is\,\, {\lambda }_{1,k}\,{\rm and}\, \cdots \,{\rm and}\, C{L}_{1}\,\, is\,\, {\psi }_{1,k} \,{\rm then}\, A{L}_{1}\,\, is\,\, N{\xi }_{1,k}$$
$$\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}& & & \vdots \end{array}& & & \end{array}& \vdots & & \end{array}& & \vdots & \end{array}& & & \vdots \end{array}$$
$${\rm Rule}\, m: If\,\, B{L}_{m}\,\, is\,\, {\lambda }_{m,k}\,{\rm and}\, \cdots \,{\rm and}\, C{L}_{m}\,\, is\,\, {\psi }_{m,k} \,{\rm then}\, A{L}_{m} \,\,is\,\, N{\xi }_{m,k}$$
(40)

as \(k=1,\dots ,K\).

Step 9:

Derived rules are interpreted into generalised Boolean matrix. Generalised Boolean matrix depict the overall system represented by \(BS\), \(CS\) and \(AS\) systems. Referring to the evaluations of decision makers,

$$\begin{array}{cccc}& {\lambda }_{j,1}& \cdots & {\lambda }_{j,K}\\ {x}_{1j,1}\cdots {x}_{ej,1}& 1& \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ {x}_{1j,k}\cdots {x}_{ej,K}& 0& \cdots & 1\end{array}, \,{\rm for}\, j = 1, 2, \dots m.$$
(41)

The possible transposition of the benefit system rule base is depicted by the rows and columns of the previous Boolean matrix. The transposition implements linguistic terms from Figs. 5 and 6 to represent the input and the linguistic terms in Fig. 8 to represent the end result.

$$\begin{array}{cccc}& {\psi }_{j,1}& \cdots & {\psi }_{j,k}\\ {y}_{1j,1}\cdots {y}_{ej,1}& 1& \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ {y}_{1j,K}\cdots {y}_{ej,K}& 0& \cdots & 1\end{array}$$
(42)

as \(j=\mathrm{1,2}, \dots , m\).

The same method is applied on CS where similar linguistic terms are also implied as BS. To form a generalized Boolean matrix that includes BS generalized Boolean matrices and CS generalized Boolean matrices, vertical merging is applied in the form of Eq. (43).

$$\begin{array}{cccc}& \begin{array}{c}{\lambda }_{j,i}\\ {\psi }_{j,1}\end{array}& \begin{array}{c}\cdots \\ \cdots \end{array}& \begin{array}{c}{\lambda }_{j,K}\\ {\psi }_{j,K}\end{array}\\ \begin{array}{c}{x}_{1j,1}\cdots {x}_{ej,1}\\ {y}_{1j,1}\cdots {y}_{ej,1}\end{array}& 1& \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ \begin{array}{c}{x}_{1j,K}\cdots {x}_{ej,K}\\ {y}_{1j,K}\cdots {y}_{ej,K}\end{array}& 0& \cdots & 1\end{array}$$
(43)

for \(j = 1, 2, \dots , m\)

AS generalized Boolean matrix are constructed based on \(j\) alternatives accordingly as in Eq. (44)

$$\begin{array}{*{20}c} {} & {N\xi_{j,1} } & \cdots & {N\xi_{j,K} } \\ {\lambda_{j,1} \cdots \psi_{j,1} } & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ {\lambda_{j,K} \cdots \psi_{j,K} } & 0 & \cdots & 1 \\ \end{array}$$
(44)

The resultant generalized Boolean matrix is then formed as in Eq. (45).

$$\begin{array}{*{20}c} {} & {N\xi_{j,1} } & \cdots & {N\xi_{j,k} } \\ \begin{gathered} x_{1j,1} \cdots x_{ej,1} \hfill \\ y_{1j,1} \cdots y_{fj,1} \hfill \\ \end{gathered} & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ \begin{gathered} x_{1j,K} \cdots x_{ej,K} \hfill \\ y_{1j,K} \cdots y_{ej,K} \hfill \\ \end{gathered} & 0 & \cdots & 1 \\ \end{array}$$
(45)

Step 10:

Generalized Boolean matrix from Eq. (45) is constructed to form the rules of alternatives as referred below for \(j = 1 , 2, ... m\)

$${\rm Rule}\, 1: if {B}_{1} is {x}_{1j1} \,{\rm and}\, \cdots \,{\rm and}\, {B}_{e} is {x}_{e,j,1} \,{\rm and}\, {C}_{1} is {y}_{1j1} \,{\rm and}\, \cdots \,{\rm and}\, {C}_{f} is {y}_{fj1} \,{\rm then}\, AL is N{\xi }_{j,1}$$
$$\begin{array}{ccc}\begin{array}{cccc}\begin{array}{cccc}\vdots & & & \end{array}& \vdots & & \end{array}& & \vdots \end{array}$$
$${\text{Rule }}n_{j} :{\text{if }}\,\,B_{1}\,\, {\text{is }}\,\, x_{1jk}\,\, {\text{ and}} \cdots {\text{and }}\,\,B_{e} \,\,{\text{ is }}\,\,x_{e,j,k} \,\,{\text{ and }}\,\,C_{1}\,\, {\text{ is }}\,\,y_{1jK}\,\, {\text{ and}}\,\, \cdots {\text{and }}\,\,C_{f} {\text{ is }}\,\,y_{fj,K} \,{\rm then}\,AL\,\,{\text{is }}\,\,N\xi_{j,K}$$
(46)

Step 11:

Derive a final score for each alternative. The final score for each alternative, \({\Omega }_{j}\) can be derived by multiplying the aggregate membership value of the consequent part of the \({n}_{j}\) rules,\({N\xi }_{j,k}\), to the summation of benefit and cost NICC, \({NICC}_{j,k}^{B}\) and \({NICC}_{j,k}^{C}\). Then, averaging in accordance to the number of rules and decision makers are performed. Thus, every alternative is ranked accordingly based on the final score attained. To evaluate its performance, we consider implementing this method in stock evaluation using 30 stocks.

$$\Omega_{j} = \frac{{\sum\nolimits_{Rule1}^{n} {\sum\nolimits_{k = 1}^{K} {N\xi_{j,K} } \times } \left( {NICC_{j,k}^{B} + NICC_{j,k}^{C} } \right)}}{n \cdot K}$$
(47)

as \(j=1, 2, \dots , m\).

4 Case Study: Stock Evaluation

This case study involves 30 stocks as alternatives to be evaluated by decision makers from 3 groups. The decisions from decision makers were merged according to groups into HFEs. Six criteria were categorised into four benefit system and two cost system. The process of ranking these stocks followed the proposed methods presented in Sect. 3.

Step 1:

The rating from 3 groups of experts were applied in the form of Z-HFS after converted to fuzzy number based on Figs. 5, 6 and 7. Here, the reliability of experts is taken into consideration during the decision-making process. The experts are advised to use the linguistic terms in Fig. 7 to evaluate the confidence in their decision. Decision makers are not supposed to use negative weight to represent their opinion. Otherwise, this would imply the use of unreliable information which is undesirable. Decision matrices were constructed afterwards according to the benefit and cost systems as Eqs. (4) (5).

Step 2:

Equations (6) and (7) were utilized in determining the hesitant fuzzy PIS (A+) and NIS (A−) according to decision makers separately:

A+  = {〈 0.745, 0.927, 0.927, 1, 〈 0.343, 0.519, 0.519, 0.716, 〈 0.025, 0.142, 0.142, 0.319, 〈 0.32, 0.522, 0.522, 0.702,〈 0.588, 0.777, 0.777, 0.928, 〈 0.089, 0.17, 0.17, 0.273}.

A- = {〈 0, 0.078, 0.078, 0.251, 〈 0, 0.016, 0.016, 0.106, 〈 0.72, 0.896, 0.896, 0.96, 〈 0, 0.016, 0.016, 0.097,〈 0, 0.026, 0.026, 0.141,〈 0.263, 0.361, 0.361, 0.43}

Step 3:

The distance, \({\delta }^{+}\) and \({\delta }^{-}\) were calculated according to each cost and benefit criteria. Alternatives, \({A}_{i}\) from the \({A}^{+}\) and A− using the Eqs. (8) and (9) as shown in Table 1.

Table 1 Separation measures of stocks from A+ and A−
Full size table

Step 4:

The relative closeness coefficient \(Ci\) of each alternative Ai to the hesitant fuzzy PIS, A+ were calculated in Table 2.

Table 2 Closeness coefficient,\(\Phi\), of stocks
Full size table

Step 5:

The Influence Closeness Coefficient (ICC) and Normalized Influence Closeness Coefficient (NICC) were calculated by referring to Eq. (11) to Eq. (15). To exemplify, influence degree of G1 is \({\theta }_{1}=5\). Influence degree is determined by the groups themselves via linguistic terms in Fig. 2 which was then interpreted into a numerical value according to the level of linguistic terms in Fig. 2. The influence degree of G1 is calculated as Table 3.

Table 3 Level of expertise
Full size table
$${\sigma }_{k}= \frac{5}{\sum_{i=1}^{3}{\theta }_{3}}=0.5$$

To generate ICC, the influence degree of each group to the closeness coefficient of alternatives were calculated accordingly as in Eqs. (12) and (13). Then in accordance to Eqs. (14) and (15), the NICC of each alternative with respect to the criteria divided were determined.

Step 6:

The rule base for the benefit System (BS) and Cost System (CS) were constructed based on the NICC calculated.

The NICC obtained was converted into linguistic terms referring to Fig. 2 in order to form the antecedent and consequent matrices of both BS and CS as performed in Eq. (16–23).

$$NIC{C}_{\mathrm{1,1}}^{B}=0.5629=R$$
$$NIC{C}_{\mathrm{1,1}}^{C}=0.8342=VG$$
$${M}_{1}= \begin{array}{c}BL\\ CL\end{array}\left[\begin{array}{ccc}{\lambda }_{\mathrm{1,1}}& ,& \begin{array}{ccc}{\lambda }_{\mathrm{2,1}}& ,& \begin{array}{ccc}{\lambda }_{\mathrm{3,1}}& \cdots & {\lambda }_{\mathrm{30,1}}\end{array}\end{array}\\ {\psi }_{\mathrm{1,1}}& ,& \begin{array}{ccc}{\psi }_{\mathrm{2,1}}& ,& \begin{array}{ccc}{\psi }_{\mathrm{3,1}}& \cdots & {\psi }_{\mathrm{30,1}}\end{array}\end{array}\end{array}\right]= \begin{array}{c}BL\\ CL\end{array}\left[\begin{array}{ccc}R& ,& \begin{array}{ccc}G& ,& \begin{array}{ccc}R& \cdots & VG\end{array}\end{array}\\ G& ,& \begin{array}{ccc}G& ,& \begin{array}{ccc}G& \cdots & G\end{array}\end{array}\end{array}\right]$$
$${\rm Rule}\, 1: If \,\, B{L}_{1}\,\, is\,\, R \,{\rm and}\, \cdots \,{\rm and}\, C{L}_{1}\,\, is\,\, G \,{\rm then}\,\,\, A{L}_{1} \,\,is \,\,N{\xi }_{1,k}$$
$$\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}\begin{array}{cccc}& & & \vdots \end{array}& & & \end{array}& \vdots & & \end{array}& & \vdots & \end{array}& & & \vdots \end{array}$$
$${\rm Rule}\, m: If \,\,B{L}_{m}\,\, is \,\,{\lambda }_{m,k} \,{\rm and}\, \cdots \,{\rm and}\, C{L}_{m}\,\, is \,\,{\psi }_{m,k} \,{\rm then}\,\,\, A{L}_{m} \,\,is \,\,N{\xi }_{m,k}$$

Step 7:

The antecedent matrices, \({M}_{k}\), of the Alternatives System (AS) of each DM \(k\) are constructed based on the Benefit Level (BL) and Cost Level (CL), which are the outputs of the benefit system BS and cost system CS, respectively. Based on the opinion of G1,

$${M}_{1}= \begin{array}{c}BL\\ CL\end{array}\left[\begin{array}{ccc}{\lambda }_{1,1}& ,& \begin{array}{ccc}{\lambda }_{2,1}& ,& \begin{array}{ccc}{\lambda }_{3,1}& \cdots & {\lambda }_{30,1}\end{array}\end{array}\\ {\psi }_{1,1}& ,& \begin{array}{ccc}{\psi }_{2,1}& ,& \begin{array}{ccc}{\psi }_{3,1}& \cdots & {\psi }_{30,1}\end{array}\end{array}\end{array}\right]= \begin{array}{c}BL\\ CL\end{array}\left[\begin{array}{ccc}R& ,& \begin{array}{ccc}G& ,\cdots ,& G\end{array}\\ G& ,& \begin{array}{ccc}B& ,\cdots , & R\end{array}\end{array}\right]$$

The AS consequent matrices are derived as follows:

  1. i.

    Calculation of the aggregation \({\xi }_{j,1}\) of weighted \({NICC}_{j.1}^{B}\) and \({NICC}_{j.1}^{C}\)

    $${\xi }_{1,1}=\frac{ {NICC}_{\mathrm{1,1}}^{B}\times \left(\frac{e}{e+f}\right)+{NICC}_{\mathrm{1,1}}^{C}\times \left(\frac{f}{e+f}\right)}{2}$$
    $$= \frac{0.484789\times \left(\frac{4}{2+4}\right)+0.631889\times \left(\frac{2}{2+4}\right)}{2}$$
    $$=0.291428$$
  2. ii.

    Normalization of the values of \({\xi }_{j,k}\) to confirm their values lie in between [0,1].

    $${N\xi }_{1,1}= {\xi }_{1,1}/{\mathrm{max}}_{j}{\xi }_{j,1}.=0.291428 /0.5=0.582856= R$$
  3. iii.

    The value of \({N\xi }_{1,1}\) were converted to linguistic terms as listed in Fig. 8.

The AS consequent matrix \({N}_{1}\) for DM1 is constructed based on the values of \({N\xi }_{j,1}\) or each alternative,\(j\).

$${N}_{1}=AL\left[{N\xi }_{1,1} , {N\xi }_{2,1}\cdots {N\xi }_{30,1}\right]=AL\left[R, B\cdots R\right]$$

The alternatives system of G1 is presented as:

If \({M}_{1}= \begin{array}{c}BL\\ CL\end{array}\left[\begin{array}{ccc}R& ,& \begin{array}{ccc}G& ,\cdots ,& G\end{array}\\ G& ,& \begin{array}{ccc}B& ,\cdots , & R\end{array}\end{array}\right]\), then \({N}_{1}=AL\left[R, B\cdots R\right]\)

can best be interpreted in rule bases as follows.

$${\rm Rule}\, 1 :if \,\,BL\,\, is \,\,R, \,{\rm and}\,\,\, CL\,\, is\,\, G, \,{\rm then}\,\,\, AL\,\, is\,\, R$$
$${\rm Rule}\, 2 :if\,\, BL \,\,is \,\,G, \,{\rm and}\, CL\,\, is\,\, B,\,\, \,{\rm then}\,\,\, AL\,\, is \,\,B$$
$$\vdots$$
$${\rm Rule}\, 30 :if BL is G, \,{\rm and}\, CL is R, \,{\rm then}\, AL is R$$

Step 8:

BS, CS and AS derived rules are presented in Boolean matrix form. The Boolean benefit system matrix for S1 is generated as shown below.

 

1

2

3

4

5

1111

0

0

0

0

0

:

:

:

:

:

:

2222

0

0

0

0

0

:

:

:

:

:

:

3333

0

0

0

0

0

:

:

:

:

:

:

4444

0

0

0

0

0

:

:

:

:

:

:

5 1 1 2

0

0

1

0

0

5 1 1 3

0

0

0

1

0

5555

0

0

0

0

0

:

:

:

:

:

:

6666

0

0

0

0

0

7 2 2 4

0

0

1

0

0

The Boolean cost system matrix for S1 is generated as shown below.

 

1

2

3

4

5

11

0

0

0

0

0

:

:

:

:

:

:

22

0

0

0

0

0

:

:

:

:

:

:

33

0

0

0

0

0

3 5

0

1

0

0

0

3 6

0

1

0

0

0

:

:

:

:

:

:

44

0

0

0

0

0

4 7

0

0

0

1

1

:

:

:

:

:

:

55

0

0

0

0

0

In order to form a generalized Boolean matrix that includes BS generalized Boolean matrices and CS generalized Boolean matrices, vertical merging was implied.

 

11

 

22

23

24

25

33

34

35

42

 

44

4444/44

0

0

0

0

0

0

0

0

0

0

0

0

:

:

:

:

:

:

:

:

:

:

:

:

:

5555/55

:

:

:

:

:

:

0

0

:

0

:

0

5 1 1 2/35

:

:

:

1

:

:

0

0

:

0

:

0

5 1 1 2/36

:

:

:

1

:

:

0

0

:

0

:

0

5 1 1 2/47

:

:

:

:

:

1

0

0

:

0

:

0

5 1 1 3/35

:

:

:

:

:

:

1

0

:

0

:

0

5 1 1 3/36

:

:

:

:

:

:

1

0

:

:

:

0

5 1 1 3/47

:

:

:

:

:

:

0

0

1

0

:

0

7 2 2 4/35

:

:

:

:

:

:

1

0

:

0

:

0

7 2 2 4/35

:

:

:

:

:

:

1

0

:

0

:

0

7 2 2 4/47

:

:

:

:

:

:

0

:

1

0

:

0

The AS Boolean matrix for S1 is evaluated as follows:

 

1

2

3

4

5

11

0

0

0

0

0

:

:

:

:

:

:

23

:

0

1

:

:

24

:

0

0

:

:

32

:

0

0

:

:

33

:

0

1

:

:

34

:

0

0

:

:

3 5

:

0

0

1

:

:

:

:

:

:

:

42

:

0

:

:

:

44

:

0

:

:

:

The resulting Boolean matrix generated to represent the overall system is as shown below.

 

1

2

3

4

5

1111/11

0

0

0

0

0

5555/55

0

0

0

0

0

5 1 1 2/35

:

0

1

:

:

5 1 1 2/36

:

0

1

:

:

5 1 1 2/47/NA

:

0

:

:

:

5 1 1 3/35

:

0

1

:

:

5113/36

:

0

1

:

:

:

:

0

:

0

:

5 1 1 3/47

:

0

:

1

:

7224/35/3

:

:

1

0

:

7224/36/3

:

:

1

0

:

7224/47

:

:

0

1

:

7777/77/5

:

:

0

:

:

From the Boolean matrix generated previously, the rule basis for stock S1 was derived as follows:

Rule 1:

5 1 1 2/35/3

5112

35

3

R

Rule 2:

5 1 1 2/36/3

5112

36

3

R

Rule 3:

5 1 1 3/35/3

5113

35

3

R

Rule 4:

5 1 1 3/36/3

5113

36

3

R

Rule 5:

5 1 1 3/47/4

5113

47

4

G

Five rules were obtained that can be interpreted according to the linguistic terms on the level of rating as:

Rule 1: If \({B}_{1}\) is VG and \({B}_{2}\) is VP and \({B}_{3}\) is VP and \({B}_{4}\) is P and \({C}_{1}\) is MP and \({C}_{2}\) is MG then \({S}_{1}\) is R.

Rule 2: If \({B}_{1}\) is VG and \({B}_{2}\) is VP and \({B}_{3}\) is VP and \({B}_{4}\) is P and \({C}_{1}\) is MP and \({C}_{2}\) is G then \({S}_{1}\) is R.

Rule 3: If \({B}_{1}\) is VG and \({B}_{2}\) is VP and \({B}_{3}\) is VP and \({B}_{4}\) is MP and \({C}_{1}\) is MP and \({C}_{2}\) is MG then \({S}_{1}\) is R.

Rule 4: If \({B}_{1}\) is MG and \({B}_{2}\) is VP and \({B}_{3}\) is VP and \({B}_{4}\) is MP and \({C}_{1}\) is MP and \({C}_{2}\) is G then \({S}_{1}\) is R.

Rule 5: If \({B}_{1}\) is VG and \({B}_{2}\) is VP and \({B}_{3}\) is VP and \({B}_{4}\) is F and \({C}_{1}\) is MG and \({C}_{2}\) is VG then \({S}_{1}\) is G.

Step 9:

For each alternative, the final score was derived from Eq. (47). There were 5 active rules formulated for S1 as the end result and the final score for S1 was obtained by implementing the equation. Then, the calculation proceeded to find the average aggregate membership value in order to be infused to the influence multiplier.

$$\frac{0.5+0.5+0.5+0.5+0.5+0.7+0.5+0.5+0.7}{8} \bullet 0.5445= 0.2995$$

A better ranking position is defined by the highest final score attained. Thus, Stock 14 was ranked the highest as compared to other stocks due to its highest final score. As proposed earlier, the Spearman’rho correlation was adapted in order to evaluate the performance of the proposed method to compare to its actual rank.

$$\rho =1-\frac{\left(6\times 1296\right)}{\left(30\times (3{0}^{2}-1)\right)}=0.71168$$

5 Analysis of Result

For the purpose of validation for the proposed method, the comparison to established Fuzzy TOPSIS methods is considered in Table 4. It is shown that Z-numbers could assist in determining better result with the merging in reliability of decisions to the ratings.

Table 4 Comparison between the proposed method and the established methods
Full size table

Table 5 presents the comparison between the proposed method and three established methods based on transparency, reliability and hesitancy. Utilizing the Spearman’s rho correlation coefficient, the rankings of stocks obtained by the methods considered are compared, where the strength of relationship between variables are measured [21]. Owing to anomalies, this statistical significance is instinctively comprehensible and less bias. It is observed that the proposed method performed as well as [22] and [20]. The proposed method offers hesitancy in comparison to Yaakob et al. [12], which scored 0.712 and 0.697 in Spearman’s rho, respectively. Thus, the proposed method proves that hesitant fuzzy set helps in solving vulnerability in decision making. In addition, both the proposed method and Wang & Mao [19] incorporated Z-numbers, but the proposed method promotes fuzzy network which contributes to improve the transparency of decisions, thus resulting in a higher score of Spearman’s rho as compared to Wang & Mao.

Table 5 Spearman’s Rho correlation coefficient of proposed method and established methods
Full size table

Chen & Lee scored the highest Spearman’s rho which was 0.715. In comparison to the proposed method, they implied a type-2 fuzzy number which offers the minimization of uncertainties effects in a rule-based fuzzy system. As highlighted in [23], type-2 fuzzy sets serve an additional degree of freedom due to its three-dimensional membership function. Thus, type-2 fuzzy set offers a membership degree with higher accuracy and precision in fuzziness. As shown in Fig. 9, it is observed that stocks ranked using Z-HFN are almost similar to the ranking of actual stocks and the rankings in the established methods. This paper proposed a novel method of Z-Hesitant Fuzzy Network TOPSIS (Z-HFN TOPSIS), in which the fuzzy network has improvised the transparency of decision making by thoroughly evaluate all subsystems and dynamical communication between them. The method is then enhanced by incorporating the Z-numbers in cooperating reliability which can depict the confidence level of ratings made by decision makers.

Fig. 9
figure 9

Ranking of stocks

Full size image

Considering the six criteria used in the case study of stock selection described in Sect. 4, the proposed model Z-HFN TOPSIS perform as well as the other established TOPSIS methods, as shown in the last row of Table 5.

6 Conclusion

This paper proposed novel decision making method using fuzzy network approach that incorporates Z- numbers with hesitant fuzzy sets. The advantages of the proposed method not only contribute to solving hesitancy in decision making, but also incorporates the expertise level of decision makers. Another contribution of proposed method is the incorporation of fuzzy network that increase the level of transparency in the process of decision making by allowing decision makers to access the performance of alternatives in terms of benefit and cost criteria. The limitation of proposed method is the attention given to the subject is only in small scale of group decision making. Hence, for the future, this research can be conducted for large scale group decision making. Moreover, it is also interesting to check relation of this research with R-sets.