1 Introduction

In the era of the connected world, our social and digital lives are confronted with the networks (or simply graphs) on a daily basis [1]. Graph-based representation of real-world problem has been proved to be very beneficial due to their improving simplicity and professional use in finding solutions to the problems [2, 3]. Graphs are generated from almost every field of today’s life. Internet browsing means traversing a big network of web pages that is interlinked via clickable (or sometimes hyper) links [4]. Online social networks such as Facebook are based on massive networks, in which different people are connected through so-called friendship links (a graph of friends) [5, 6]. Further, using mobile accessing one webpage generates a few dozen wired or wireless connections among devices in a matter of microseconds [7]. An example of a real-world graph network is given in Fig. 1.

Fig. 1
figure 1

Facebook friends relationship [8]

Full size image

Keeping in view the significance of graph structure, graph mining is estimated to start since the beginning of 1994 [8]. Since then graph mining has attracted the research community and brought a revolutionary benefit to various fields including computational biology [9, 10], social network analysis [5, 7, 11], chemical data analysis [12, 13], drug discovery [14, 15], and communication networking [16, 17]. Figure 2 shows a typical graph mining process.

Fig. 2
figure 2

A typical graph mining procedure

Full size image

Frequent Subgraph Mining (FSM) is a well-studied problem in the graph mining field and boosts several real-world applications such as chemical compound analysis and classification [18, 19], text sentiment analysis, document image clustering [20], bug isolation in software [21, 22], relationship prediction [23], web content mining [24,25,26], social network mining [8, 27,28,29], fraud detection [30], email mining [31,32,33], and anomaly detection [34, 35]. FSM has been a focused theme in graph mining for last two decades; therefore, sufficient literature was dedicated to the field, making tremendous development [35,36,37,38]. FSM is classified into two broad classes: (1) transaction-based FSM and (2) single large graph-based.

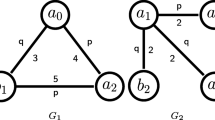
In most of the studies [39,40,41,42,43,44,45,46,47,48], the FSM techniques are decomposed into two major categories: A priori-based and pattern growth-based FSM approaches. In the last few decades, substantial literature was added to both of these FSM categories. These are included, gSpan [38], FSP [49], FFSM [50], FSG [51], Gaston [54], CloseGraph [52], SPIN [53], SUBDUE [55], TSP [56], FS3 [57], and so forth. For example, the following figure gives an example of FSM. In Fig. 3, a sample graph dataset is given.

Fig. 3
figure 3

A sample graph database

Full size image

If we assumed the support threshold value as 3, then the possible frequent subgraph can be discovered from Fig. 3 as shown in Fig. 4:

Fig. 4
figure 4

Sample-mined frequent subgraph patterns

Full size image

The major contributions of this study are fivefold:

  1. (i)

    First, the proposal of a new unifying framework A RAnked Frequent pattern-growth Framework (A-RAFF) from transaction graph datasets.

  2. (ii)

    Second, the proposal of new graph ranking measure, FSP-Rank, for addressing the ranking problem of FSPs.

  3. (iii)

    Third, comprehensive performance evaluation of the proposed FSM framework, A-RAFF, using different graph datasets.

  4. (iv)

    Fourth, computing the interestingness of the discovered FSPs.

  5. (v)

    Fifth, comparison of the FSP-Rank with the GraphRank.

The rest of the paper is organized as follows: First, we discussed the related work on FSPs’ discovery approaches in Sect. 2. Then, we present our novel FSPs ranking framework, A-RAFF, in Sect. 4, where the fundamental principle of the approach is presented. In Sect. 4, we report the experimental results obtained from the simulations of the proposed approach on various graph networks. Finally, in Sect. 5, we draw conclusions with final thoughts for future work.

2 Related Work

In this section, the literature is reviewed, which is directly related to FSM in transaction-based graph datasets. Different representative techniques from the two categories, a priori-based and pattern growth-based FSM approaches, are surveyed, emphasizing on their technique, their contributions to the FSM domain, and limitations. Research findings are also given at the end of this section.

SPIN (SPanning tree-based maximal graph mINing) was the first approach to mix two distinctive techniques: discovery FSPs in graph dataset and discovery of frequent tree structures in forests (i.e., a collection of trees) for the designing of efficient subgraph mining techniques. SPIN discovers only the maximal frequent subgraphs (MFS) (an MFS is one which is not included in any other FSPs available in the database) of a set of big-size graphs. Huan et al. discussed that extracting the only MFS offered the following advantages in processing big graph datasets [53]: (1) it significantly minimizes the total number of discovered subgraph patterns; (2) various “pruning” schemes can be efficiently combined into the discovery process, which dramatically decrease the time required to mine graph datasets; (3) the non-MFS can be reconstructed from the MFS. SPIN algorithm performance was shown using different experiments, which presented the effectiveness of SPIN in that it exponentially minimizes the number of FSPs discovered. In massive graph datasets, discovered FSPs can become too bigger to allow an entire enumeration by realistic computational resources.

HSIGRAM is another a prior-based algorithm proposed for mining frequent subgraph called HSIGRAM. Adjacency matrix was used to represent the graphs and use iterative merging for the generation of the subgraph. There are two important mechanisms introduced by the HSIGRAM algorithm, the way adopted to enumerate the candidates and the technique used to calculate the frequency of the candidate subgraphs, which considerably influence HSIGRAM overall computational complexity. The further details can be found in [59].

MARGIN is another a priori-based FSG approach to mine the maximal FSPs. The set of maximal frequent subgraphs (MFSs) is significantly smaller than the set of FSPs [53]; therefore, we provided the scope for sufficient pruning of the exponentially massive search space. MARGIN algorithm recursively discovers the candidates by using core procedure, ExpandCut, and the set of maximal FSPs was then extracted by the operation of post-processing. Although the MARGIN was found computationally faster when compared with gSpan technique using benchmark graph datasets, its efficiency totally relied on the initial chosen cut and is the flaw found in the analysis of MARGIN [60].

To handle the drawbacks in the existing complete or heuristic frequent subgraph discovery approaches, GREW was proposed [59]. GREW is specially designed and developed to execute on a large graph dataset and to discover patterns corresponding to connect subgraphs that have a large number of nodes–disjoint embeddings. There are two versions of GREW: GREW-single-edge collapsing (GREW-SE) and GREW-multi-edge collapsing (GREW-ME). It can generally operate effectively on very large graphs. The graph is represented using a sparse graph. Four different data sets were used for performance evaluation of GREW. Dynamic GREW extended FSM algorithms for time series of graphs, particularly dynamic GREW focused on the subgraph patterns which are topologically frequent within a big graph. Different experiments were performed to check the practical feasibility of the dynamic GREW; results on different real-world data validated the proposed technique for the dynamic graph scenarios. The limitation of this technique is an extra overhead in identifying dynamic patterns.

In SeuS (Structure Extraction using Summaries), the authors explored the challenge of frequent structure discovery in the semi-structured data (represented using labeled directed graphs) [61]. It is a three-step procedure: in the first step (summarization), SEuS pre-processes the given graph dataset in order to output a crisp summary. The computed summary is similar to data guides and other approximate typing mechanisms for semi-structured data [62,63,64]. Candidate generation is the second phase of SEuS. SEuS involved an expert to iteratively look for frequently occurring structures and improve the threshold value. Although the results obtained are approximate in this phase, they are accurate enough to allow tedious structures to be filtered out. When the expert filtered potential structures based on the approximate results of the search phase, an accurate count of the number of occurrences of each possible structure is generated by the third phase, which is the counting phase. SEuS can be used with large connected graph dataset as well as graph transnational datasets.

The gSpan (graph-based Substructure pattern) gSpan uses DFS searching strategy and is the fastest FSM approach [38]. DFS code is used for canonical representation of the graph dataset, while the vertex of the graph is traversed using DFS. gSpan restricts the refinement generation in two different schemes. First, fragments can only be expanded at graph nodes, which lie on the rightmost path of the DFS tree. Secondly, fragment generation is allowed by the occurrence in the appearance lists. gSpan avoids duplicate candidate generation by using a canonical code (DFS code) and rightmost path extensions. Although gSpan showed its performance using different real-world graph datasets, gSpan generated a large number of FSPs which become difficult to analyze [40, 48, 55].

Earlier FSM approaches worked to discover all the possible FSPs, which resulted in a large number of FSPs. Such huge number of FSPs were difficult to explore further and were resource intensive as well. Therefore, the concept of CloseGraph was introduced [52]. A close graph is defined by “A given input graph, g, is said to be a closed graph in a given graph database such that there exists no proper super graph of this input graph g with the same support in the database as that of graph g”. CloseGraph is an enhancement of gSpan approach [52]. Two major concepts involved in CloseGraph approach are: first is the rightmost extensions and DFS lexicographic order of the FSP generated, and the other concept is an equivalent occurrence and early termination for those graphs which are not closed graphs, so that such patterns can be pruned [40]. In different experiments, CloseGraph showed very good results. It avoided the generation of undesired subgraph patterns during the subgraph generation phase. Also, we reduced the set of FSPs but later studies showed that the CloseGraph missed some of the FSPs, which were not closed but were useful [40, 47].

The aspire of FFSM (Fast Frequent Subgraph Mining) was to mine all the connected FSPs from the graph dataset [50]. FFSM follows the DFS scheme from [20, 38] and incorporated new techniques to improve the frequent subgraph discovery efficiency. In FFSM, two efficient candidate enumeration schemes were introduced. These are FFSM-Join and FFSM-Extension. In FFSM, graphs are represented using the triangular matrices. In triangular matrices, diagonals are used to store the graph vertex labels, edge labels elsewhere. Thus, the matrix code is the combination of all matrix values, from left side to right side and row by row [47]. Using the lexicographic ordering, isomorphic graph structures have the identical canonical code. In FFSM, two matrices of graph fragments are joined to result refinements, which at most present two new structures. A restricted extension operation was also required in FFSM, in which a new edge–vertex pair may only be added to the last vertex of a canonical adjacency matrix (CAM). Once the refinement is generated, FFSM permutes lines of the matrix to examine whether a resulting matrix is in canonical form or not? If the matrix is not in canonical form, it can be ignored. In experiments, results reported that FFSM outperforms gSpan. As an central deficiency of the, FFSM needs to scan the occurrence of an additional collection of subgraph which are not canonical [50].

FSP (Frequent Substructure Pattern Mining) is a recently presented FSM appraoch, which suggested an important enhancement in the PG-based FSM category[49]. Following are the potential benefits, which were introduced to PG by FSP: (1) improving the graph canonical representation and defining an association between sub-DFS trees, whose root node shares the identical parent node in the candidate subgraph structure; (2) exploring the similarities of the structure in the DFS search space and showing two one-to-one reflection between the child subgraph patterns and latter sibling subgraph patterns; (3) two different techniques were applied to mine subgraph problem in order to minimize the total number of subgraph patterns as well as graph isomorphism tests efficiently.

The GASTON (GrAph/Sequence/Tree extractiON) is a tool, which stores all the embedding to generate just refinements to achieve efficient subgraph isomorphism tests [54]. The core idea of Gaston was to separate many types of structures such as path, tree, and graphIn Gaston working; initially, only those fragments are considered which are paths or trees and finally cyclic general graphs structures are considered. Thereby, this outsized portion of the mining work is done efficiently. In Gaston, only the last phase is critical as it faces the issue of NP-completeness of the subgraph isomorphism examination. Experiments on real datasets, Gaston performance, were very good. Since Gaston focuses on maximal FSGs, there are chances that interesting subgraphs missed from the final resultant FSPs [55].

RING is an integrated approach, which was proposed to mine the frequent representatives subgraph patterns [65]. RING is based on the distance between two graph structure for discovery of the FSPs, involving an invariant vectors’ methodology is adopted during mining of subgraph pattern. Furthermore, an invariant distance (i.e., the Euclidean distance) is used between the graphs as an alternative of the edit distance or other variation of the graph distance measures. There are two important phases of RING approach: firstly, it discovers a set of random set of FSPs before adding them in different cluster of subgraphs. Then, it picks the center of the clusters (groups) as representative subgraph patterns, which are original. Secondly, it used the depth-first searching technique. RING used the special structure of indexing, which is called R-Trees. However, RING lacks the comparative analysis with the state-of-the-art FSM approaches.

İn a recent study on FSM, GraphSig is proposed to discover the discriminative subgraph patterns with low frequencies, and GraphSig was proposed in [64,65,66]. GraphSig is a scalable approach, which extracts statistically significant patterns from a large collection of graphs. In GraphSig, using a random walk first of all graphs is converted into feature vectors. Domain knowledge was involved in selecting the important feature set from the entire set of graph features. Results reported in GraphSig showed that GraphSig is able to discover the discriminating patterns in a big graph database and still with small values of the frequencies. There is a need to decide how to decide the statistical significance rather than assuming manually, and significant graph feature selection needs to be improved further.

GraphRank is another important work in FSM field, which used the feature vector to represent a graph structure [67]. The GraphRank FSM approach is proposed to estimate the statistical significance of FSPs in a given graph dataset. GraphRank defined the statistical significance as the probability that a given graph g occurs in the graph dataset of random graphs with the value of support \(\mu \ge {\mu }_{0}\), which is termed as p value of the graph g. GraphRank converts a subgraph into a feature vector and calculates the importance of each subgraph taking into account the usefulness of the presence of the equivalent vector. Furthermore, in order to acquire a probability distribution based on the support of the feature vector, GraphRank used the probability of the feature vector in a random vector dataset based on the a priori probability of the basic items. Furthermore, the computed p value is used for the ranking of FSPs. Based on this feature vector mining, significant closed FSPs were also extracted. Their experimental outputs depicted that the GraphRank is an efficient approach and helpful for ranking of the frequent subgraphs by their statistical significance.

In addition to the above-discussed FSM extensive literature, some recent works on FSM included [57, 68, 69]. FS3 is a sampling-based FM algorithm proposed by [57] to handle the scalability issue, which arises when input graph datasets are of massive size. In [68], authors proposed LC-mine framework. The LC-mine framework is a generic and an efficient framework for FSGs’ discovery maintaining the local consistency techniques The “bias in the graph projection operator” is the core idea introduced in LC-mine.

FSM-H [70] is recently proposed distributed FSM algorithm method over a MapReduce-based framework. This framework can deal with real-world graph structured data, which may be growing in its size as well as in quantity. It works in three different phases: partitioning of data, the preparation, and the mining. In the first phase of FSM-H, input graph dataset is partitioned into k-disjoint parts, such that there are equal number of graphs in each of these partitions. Further, in parallel all the edges are removed from the graph being processed, which did not satisfy the support threshold value. In FSM-H, mining is done in the second preparation phase and the mining. FSM-H comparison with the [52] on different benchmark graph datasets showed the better performance of the FSM-H. FSM-H is evaluated with the graph datasets from real-world and few big synthetic data sets are also used. These experiments showed the efficiency of this new FSM-H FSM technique for discovering of the FSGs from massive size graphs [70].

3 A RAnked Frequent Subgraph Discovery Framework (A-RAFF)

A-RAFF is decomposed into three interlinked layers: the preprocessing layer; graph pattern mining layer; and an analytical layer, which are shown in Fig. 5. Each of the three layers focuses on different functionalities, and together they structure the conceptual framework.

Fig. 5
figure 5

A-RAFF—a proposed layered framework

Full size image

A-RAFF framework works with the transaction graph datasets, with small- to medium-size graph structures. Each graph is represented using the labels of the node and set of vertices along the labels on the edges. In the subsequent section, each of the three layers describes one by one.

The fundamental function of the preprocessing layer is to prepare the graph dataset for the graph pattern mining layer. In the preprocessing layer, graph dataset is cleanup, i.e., the graphs with isolated or disconnected nodes are detected and are removed from each of the graph structure. Moreover, if the dataset contains any graph which has single or two nodes with single edges are also removed from the graph dataset. In addition to this, two major tasks of the preprocessing layer are: graph dataset feature selection and partitioning of the graph dataset.

A graph dataset may exhibit different features, but all of the features are not important [58, 61]. The feature may include node labels, edge labels, weights to the individual nodes or weights on the edges between the nodes, the direction of the edge, and so forth [84, 85]. The second major function of the preprocessing layer is to partition the graphs into smaller chunks. In the graph dataset, larger/massive graph structures are distinguished, and then, such structures are partitioned. In the literature, various graph partitioning techniques and tools are available [71,72,73,74,75,76,77]. In the proposed framework A-RAFF, the graph partitioning is performed using a well-known graph partitioning tool KaHIP [71]. The KaHIP tool implemented a multilevel graph partitioning algorithm, called KaFFPa (Karlsruhe Fast Flow Partitioning). The KaFFPa algorithm exploits a novel local improvement technique, which is based on max-flow and min-cut computations. Furthermore, KaFFPa used more localized FM searches in addition to involving of a sophisticated global search strategy transferred from multi-grid linear solvers’ problem [72]. Finally, the graph partitions are forwarded to the pattern mining layer.

figure a

The second layer in the A-RAFF framework is the mining layer. This layer is responsible for the discovery and ranking of the FSPs. This layer retrieves the preprocessed graph structures from the graph preprocessing layer as an input and discovers the frequent subgraph. Next, the discovered FSPs are ranked using the proposed frequent subgraph ranking scheme. For ranking of the FSPs, different features of the mined FSPs and the individual FSP are used. Once the FSPs are ranked, then these are passed to the next layer of the conceptual framework for exploration of the trends in the discovered FSPs.

FSP-Rank: Ranking is considered as a significant task in the graph theory. In a graph structure, vertices correspond to objects and an edge between objects depicts the similarities [78]. Very limited research work is available in ranking on graph structure data such as in search engine [75, 77]. In graph mining domain, mainly research community is interested in the relative importance of the graph nodes with the top ranked node. In [79], centrality measure was used to compute the rank of the graph node. Ranking is also playing very significant role in FSM techniques. Some work has been done in ranking the discovered FSPs [67], in which the challenge of ranking is addressed by computing the statistical significance of the frequent subgraphs. However, there is still need of applying the ranking to the FSPs for better and effective patterns in the final set, which will be used for further analysis.

figure b

In the proposed A-RAFF framework, once the FSPs are discovered, the next step is to rank the extracted patterns. For FSPs ranking, the FSP-Rank algorithm is proposed. The FSP-Rank measure involves different characteristics of the FSPs and computes the rank value for each of the FSPs. Using the ranked values, \(f\left({R}_{k}\right)\) as computed from Eq. (1), of the FSPs, different duplicate pattern structures were identified. Such duplicate structures were removed from the final result set of the FSPs discovered by the proposed A-RAFF framework. Therefore, total number of FSPs are reduced in the final result set.

$$f\left( {R_{k} } \right) = (1 - \lambda ) *\sum\limits_{{i = 1}}^{n} {\left( {W_{i} + \lambda *\left( {\frac{{D_{i} }}{{n_{i} }}} \right)} \right)}$$
(1)

where \(\lambda\) is a normalized factor and is calculated from Eq. (2). \(W\) represents the total of the weight of all the nodes in the ith frequent subgraph. This parameter, \(W\), is used when the discovered FSPs are weighted. \({D}_{i}\) denotes the degree of FSPs. The value of \({D}_{i}\) is the total of in-degree and out-degree of ith FSP, and \(n\) represents the total number of nodes in the ith FSP. The value of \(f\left({R}_{k}\right)\) will always lie in the range \(( 0\le f\left({R}_{k}\right) \le 1)\).

$$\lambda = \left( \frac{{\sum\limits}_{i=1}^{n}{(\mathrm{FSG}}_{i}) }{{\sum }_{i=1}^{n}{T(V}_{i})}\right)$$
(2)

where \({(\mathrm{FSG}}_{i})\) denotes the number of discovered FSPs and \({T(V}_{i})\) represents the total number of vertices found in all of the \(n\) FSPs discovered so far. Therefore, the discovered FSPs are finally ranked based on the value computed from Eq. (1). Furthermore, an example is discussed here, to have in-depth understanding of the working on the concepts of the FSPs ranking described by Eqs. (1) and (2).

figure c

Example

To describe the process of computing the rank values, a simple example is given. Consider, there are following sample five FSPs mined from the graph dataset.

In Fig. 6, all the FSPs extracted from an undirected graph dataset are listed. The computation of the normalization factor \(\uplambda\) is shown in Table 1. Firstly, the degree for each FSP is computed. Using the number of nodes in each FSP and degree score, the normalization factor is computed. The value of normalization factor is computed using Eq. (2) and is shown in column 4 of Table 1.

$$\lambda = \left( { \frac{{\mathop \sum \nolimits_{i = 1}^{n} ({\text{FSP}}) }}{{\mathop \sum \nolimits_{i = 1}^{n} T(V_{i} ) }}} \right) = \, \left( {{\text{Total}}\,{\text{FSPs}}/\,\# \,{\text{of}}\,{\text{vertices}}\,{\text{in}}\,{\text{all}}\,{\text{the}}\,{\text{FSPs}}} \right) = 5/16 = 0.3125$$
Fig. 6
figure 6

Sample-extracted FSPs

Full size image
Table 1 Computation of \({\varvec{\lambda}}\) using FSP characteristics
Full size table

In Table 2, the rank value for each of the FSPs is computed. Using the computed value of the term \(\lambda \boldsymbol{*}\left( \frac{{D}_{i}}{{n}_{i}}\right)\), from the last column of Table 2, the ranking score for each of the FSPs is presented in Table 2. In this example, the value of the factor \(W\) is used as 0, as the FSPs are discovered from the unweighted graph dataset.

Table 2 Computation of the final rank score
Full size table

After computing the rank score for each of the FSPs, the FSPs are rearranged according to their ranked score. For example, in Table 3, the FSPs are ranked according to their computed rank values using the proposed FSP-Rank measure, therefore giving the ranked FSPs.

Table 3 Rank of the discovered frequent subgraphs based on FSP-rank value
Full size table

The ranked values for the FSPs are further used to identify the duplicate FSPs. All the frequent graph patterns having the same ranked score were analyzed for possible duplicate structures. After analyzing those structures which have the same ranking score were removed from the final result set of the FSPs. These FSPs were also cross-validated (manually) to ensure that these FSPs are actually the duplicate and repetitive patterns.

Moreover, since FSPs are generated solely based on frequency, not every frequent pattern is equally significant and interesting as well [80,81,82,83]. Foregoing any difficulties in defining a measure which correctly identifies what we discover interesting, the second key dilemma is the exponentially outsized search space. That is, there are exponentially many potentially interesting patterns. Naively evaluating these patterns one by one and only reporting those that meet the criteria is hence infeasible for all but the most trivial of pattern languages [84]. As such, in addition to correctly identifying what is interesting, ideally an interestingness measure also defines a structured, easily traversable search space to find these patterns [84,85,86,87]. In the next section, we have used three different measures of intrestingness including \({I}_{\mathrm{RAE}}\), \({I}_{\mathrm{CON}}\), and \({I}_{\mathrm{Variance}}\) to validate the discovered intrestingness of the FSPs discovered by the proposed FSM framework, A-RAFF. In our opinion, such measures were not incorporated in the FSM domain untill now.

The third layer of A-RAFF is the analytical layer. The goal of the analytical layer is to effectively utilize the discovered ranked FSPs. The analytical layer is therefore focusing on the notions of expediency and meaningfulness of the ranked FSPs in the domain of the graph structure dataset. Consequently, the analysis performed in this layer can be further extended for the benefits of the business and organizations. For example, analysis of the ranked FSPS can be useful to evaluate the trends (such as extraction of the most influential person/friends in the circle of an individual or a community) found in the social sites such as Facebook, Twitter, MySpace, and Orkut.

The three layers of the conceptual framework are mutually functioning on each other. It is anticipated that the results from the preprocessing layer will provide processed graph datasets and provide the basis for the next graph pattern mining and analytical layers. The graph pattern mining layer is the methodical pursuit of activities in the framework. At the meantime, the graph pattern mining layer is acting as a bridge between preprocessing and the analytical layers.

4 Results and Analysis

To evaluate the proposed framework, A-RAFF, a series of experiments is performed. This section presents the detailed analysis and discussion of the experiments. Furthermore, the performance of the A-RAFF framework is also compared with some well-known FSM approaches. The performance analysis of the A-RAFF framework with the chosen FSM approaches is performed based on the time required to discover all the FSPs and also the number of FSPs discovered by each of the FSM approach.

4.1 Evaluation Metrics

The input parameter, support threshold parameter \(({\varvec{\upsigma}}\)), is used in all the FSM techniques for extraction of FSPs. The value of the \({\varvec{\upsigma}}\) is kept same for all the FSM approaches in each experiment. For each graph dataset, the proposed A-RAFF framework is compared with the chosen FSM techniques at \({\varvec{\upsigma}}\) = 10%, 20%, 30%, 40%, and 50%. At each of the selected threshold value, we have discovered the interesting FSPs based on the ranking value. In the subsequent section, the results on each of the graph datasets and their analysis are presented.

4.2 Experimental Setup

All the experiments are executed on a 32-bit machine running the Linux operating system with 6 GB memory and 3.0 GHz Intel processor. A-RAFF is implemented using Java programming language with JDK 1.8 and NetBeans as development IDE. The proposed A-RAFF framework is compared to a number of different existing FSM approaches, such as FFSM [50], FSP[49], CloseGraph [52], gSpan [38], FSG [48], SPIN [53], and Gaston [54]. The FSM approaches, FSG, FFSM, SPIN, FSP, and CloseGraph, considered for comparison are implemented using Java language. The executables of two comparative FSM approaches are acquired from their respective authors [38, 53].

4.3 Datasets’ Description

Five different graph datasets are used for assessment purposes: three real-world graph datasets and two synthetic graph datasets. Real graph datasets are included: chemical compound, AIDS antiviral screen compound, and DTP human tumor cell line screen (CANSO3SD). These graph datasets are benchmark and are extensively used by the FSM techniques for their performance evaluations [52,53,54,55, 88].

The synthetic graph generator was provided by [51]. The synthetic graph generator allows to specify the graphs number \((D)\), average size of graph \((T)\), the number and average size of the seed graphs (S and I, respectively), and the number of distinctive labels. Two different synthetic graph datasets were generated from experiments. In the first synthetic graph dataset, synthetic graph dataset-1, there were total 10,000 graphs, with an average of 40 vertices (ranging from 1 to 90), and 10 different uniformly distributed labels of the nodes and edge; the second dataset, synthetic graph dataset-2, contained 30,000 graphs. In synthetic graph dataset-2, there were total 30,000 graph structure considered, with an average of 75 nodes (ranging from 1 to 125) and 14 uniformly distributed labels for the graph nodes and edge. The graph datasets considered were divided into two subsets. Eighty percentage of each graph dataset was used for training, and 20% of each graph dataset was reserved for testing of the proposed A-RAFF.

4.4 Experimental Results

An extensive series of the experiment was performed to empirically assess the A-RAFF framework performance in comparison with the other existing FSM approaches. Furthermore, A-RAFF was also compared with the FSM approaches with respect to the number of FSPs discovered. In all of the above experiments, the proposed FSMapproach A-RAFF framework outperforms the other FSM approaches under consideration. We have summarized the performance evaluation in the following tables, from Tables 4, 5, 6, 7, and 8, which is giving a clearer picture of the proposed A-RAFF performance with the existing FSM techniques .

Table 4 A summary of A-RAFF performance comparison with existing FSM approaches (Ex-FSM) on various benchmark graph datasets at support threshold value of 10%
Full size table
Table 5 A summary of A-RAFF performance comparison with existing FSM approaches (Ex-FSM) on various benchmark graph datasets at support threshold value of 20%
Full size table
Table 6 A summary of A-RAFF performance comparison with existing FSM approaches (Ex-FSM) on various benchmark graph datasets at support threshold value of 30%
Full size table
Table 7 A summary of A-RAFF performance comparison with existing FSM approaches (Ex-FSM) on various benchmark graph datasets at support threshold value of 40%
Full size table
Table 8 A summary of A-RAFF performance comparison with existing FSM approaches (Ex-FSM) on various benchmark graph datasets at support threshold value of 50%
Full size table

In tabular results from Tables 4, 5, 6, 7, and 8, we have shown how much time was improved by the proposed A-RAFF framework against each existing FSM approach on the entire graph datasets used. Moreover, the best performance of the proposed A-RAFF on each graph dataset at the defined threshold value was shown in bold. The running time consumed by each existing FSM approach to extract the FSPs from the given graph dataset is provided in seconds. From the tabular results shown in Tables 4, 5, 6, 7, and 8, we can see that on most of the graph datasets (both real and synthetic datasets), the performance of the A-RAFF was very promising. Moreover, the highest performance of the A-RAFF was observed against FSG approach. In Table 4, at the threshold value of 10%, the best performance achieved by the A-RAFF was 38.04% against the FSG FSM approach. Similarly, at the threshold value of 20%, A-RAFF best performance was observed against FSG approach, and it was 75.33% on the synthetic graph dataset-1, see the results in Table 5. In some cases, the performance of gSpan, Gaston tool, and FFSM was observed better than the A-RAFF framework. For example, in Table 5, on Chemical Compound and CANSO3SD gSpan and Gaston tools perform well than the A-RAFF. A-RAFF took 11 and 12 s more than the gSpan and Gaston, respectively, to discover the FSPs the threshold value of 30%. Such trends are shown with negative values enclosed in brackets.

In addition to the computational time, we also experimented the proposed A-RAFF based on the number of FSPs reduced. The results clearly show that A-RAFF performed better in terms of discovery and reducing the final set of the FSPs. Moreover, we have observed that at low values of the support threshold parameter, A-RAFF reduced less number of FSPs.


Comparing FSP-Rank with Existing Ranking Measure GraphRank: In FSM domain, to the best of our knowledge, there exists very limited work on ranking. The performance of the proposed FSP-Rank was also experimented with an existing ranking measure called GraphRank [67]. GraphRank was used for computing the statistical significance of the FSPs. GraphRank defined the statistical significance as the probability that a graph g occurs in the graph dataset of random graphs with the value of support \({\varvec{\mu}}\ge \boldsymbol{ }{{\varvec{\mu}}}_{0}\), which is termed as p-value of the graph g [67].

We have compared the proposed FSP-Rank with GraphRank measure and investigated the effectiveness of the FSP-Rank measure over the GraphRank. Using the FSP-Rank measure, the FSPs with high score of rank are considered more significant as that with low values of rank score. In contrast, GraphRank computes the rank score using the statistical significance of the FSPs [67]. Furthermore, in GraphRank, a FSP is considered more significant if it has value less than p-value as compared to the other FSPs. GraphRank applied its ranking scheme to the Close-FSPs; therefore, we have simulated our results based on the closed FSPs discovered and ranked by the A-RAFF. The FSPs were ranked using the significance value of 0.6 (i.e., p-value = 0.6). Table 11 shows the detailed results.

In Table 11, we have shown the time required by FSP-Rank and the GraphRank to rank the discovered FSPs. In most of the cases, FSP-Rank took less time to rank the discovered FSPs as compared to the GraphRank approach. For example, at \(\sigma =10\), GraphRank consumed more than 80 s to rank the discovered FSPs. Only at \(\sigma =30\), GraphRank performed better than the proposed FSP-Rank.


Measuring the Interestingness of the Discovered FSPs: Furthermore, we have evaluated the interestingness of the FSPs discovered using A-RAFF. Interestingness measures play an important role in KDD, regardless of the kind of patterns being mined [82]. All the patterns mined are not interesting or whatever the pattern mined by data mining tools is not interesting [87]. To analyze the interestingness of a rule set, various interestingness measures are proposed and analyzed by the researchers. Interestingness measures are generally divided into two main categories of objective and subjective measures of interest [82]. An objective measure uses the raw data, and no knowledge about the user or application is needed. More objective measures are based on theories in statistics, probability, or information theory. Coverage, support, accuracy, generality, peculiarity, reliability, diversity, and conciseness depend simply on the data and patterns and consequently can be considered objective [83]. The objective measures were based on the statistical strengths or properties of the discovered patterns to measure their degree of interestingness. A subjective measure takes into account both the data and the user of these data. To define a subjective measure, access to the user’s domain or background knowledge about the data is required [82, 86]. This access can be obtained by interacting with the user during the data mining process or by explicitly signifying the user’s expectations or knowledge. The measures usually determine whether a pattern is “actionable” and/or “unexpected”. An unexpectedness, actionable, novel is the criteria under subjective nature.

To compute the interestingness of the discovered FSPs, we used three different objective interestingness measure, called the \({I}_{RAE}\) measure, the measure is \({I}_{\mathrm{CON}}\) and \({I}_{\mathrm{Variance}}\) measure [82]. The \({I}_{RAE}\), \({I}_{\mathrm{CON}}\), and \({I}_{\mathrm{Variance}}\) interestingness measures are computed using Eqs. (3), (4) and (5), respectively,

$${I}_{RAE}= \frac{{\sum }_{i=1}^{m}{n}_{i}\left({n}_{i}-1\right)}{N \left(N-1\right)}$$
(3)
$${I}_{\mathrm{CON}}=\sqrt{\frac{\left({\sum }_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{p}}_{\mathrm{i}}^{2}\right)- \overline{\mathrm{q}} }{1-\overline{\mathrm{q}}} }$$
(4)
$${I}_{\mathrm{Variance}}=\frac{{\sum }_{\mathrm{i}=1}^{\mathrm{m}}{(\mathrm{p}}_{\mathrm{i}}-\overline{\mathrm{q} }{)}^{2}}{\mathrm{m}-1}$$
(5)

where \({n}_{i}\) shows the number of FSPs discovered by the A-RAFF; \(m\) corresponds to the total number of tests/experiments (i.e., a total number of different threshold settings, on which we have performed the experiments. In our problem setting, there are five different threshold settings; we have extracted the FSPs at 10%, 20%, 30%, 40%, and 50% threshold value); \(N\) shows an aggregate of total FSPs at all the threshold values; \({p}_{i}\) shows the actual probability of a specific test \(i\); and \(\overline{q }= \frac{1}{m}\) and represents the uniform probability for test \(i\) for all (\(i=1, 2, 3,\dots ,m\)).

We have applied the \({I}_{RAE}\), \({I}_{\mathrm{CON}}\), and \({I}_{\mathrm{Variance}}\) interestingness measures on the FSPs to measure the discovered patterns diversity criteria. To compute the diversity criteria, we used the extracted FSPs using A-RAFF and it is given in Tables 9 and 10. The \({I}_{\mathrm{RAE}}\), \({I}_{\mathrm{CON}}\), and \({I}_{\mathrm{Variance}}\) Interestingness measure values computed from these tabular FSP results are given in Table 12.

Table 9 A summary of number of FSPs discovered by A-RAFF with existing FSM approaches (Ex-FSM) on various benchmark graph datasets at various support threshold value of (10% to 50%)
Full size table
Table 10 A summary of number of FSPs discovered by A-RAFF with existing FSM approaches (Ex-FSM) on various benchmark synthetic graph datasets at various support threshold value of (10% to 50%)
Full size table
Table 11 Comparison of proposed FSP-rank with GraphRank on chemical compound (time is given in seconds)
Full size table
Table 12 Various interestingness measures values for FSPs discovered by the A-RAFF
Full size table

Table 12 shows the different interestingness measure values against each graph dataset where we have mined the FSPs. These values represent the interestingness of the FSPs discovered from each of the graph datasets at different threshold parameter settings. For example, on chemical compound graph dataset the interestingness value computed by \({I}_{\mathrm{RAE}}\) is 0.84, and a high value of \({I}_{\mathrm{RAE}}\) represents the more interestingness of the patterns. Similarly, the maximum interestingness value for the FSPs on the chemical compound graph dataset computed by the \({I}_{\mathrm{CON}}\) was 1. Overall interestingness of the discovered FSPs was shown very well by the \({I}_{\mathrm{CON}}\) interestingness on all the considered graph datasets. The results described in Table 12 give the indication the FSPs generated from the proposed FSM framework A-RAFF is very diverse.

5 Conclusion

In this paper, we study the problem of ranking the frequent subgraph patterns. We highlight the importance of the problem and show that current solutions are inapplicable. Therefore, a novel solution is proposed, A-RAFF, to rank the FSPs from transaction graph databases. It is based on utilizing the preprocessing of the graph dataset to identify the which nodes of the input graphs to postpone and which subgraph nodes can give quicker and effective ranked frequent subgraph patterns. This operation on the graph dataset is executed to enhance the performance of the next phase, the graph pattern mining. Furthermore, we proposed the definition of the ranking measure, FSP-Rank, to rank the mined FSPs. Also, we have used different interestingness measures to show the importance of the discovered FSPs. Our experimental results are significantly better than those with existing approaches with regard to both the runtime and reducing the discovered FSPs. Thus, we believe that the proposed methodology can be an efficient tool for ranking of the discovered frequent subgraph patterns. Although this research study reached to its objectives, few unavoidable weaknesses are observed, which are given as follows. First, the findings of this study are restricted on the discovery of the FSPs from medium-size graph datasets. However, this would be better if frequent subgraph discovery was performed on big graphs, as there is ever-increasing demand of handling the big graph structures. Second, as the proposed technique for frequent subgraph discovery works with transaction graph datasets, we have to convert the big social graphs into smaller one for exploration of trends. Third, although the proposed ranking scheme produced good results, however, to further improve the results, new similarity measures are needed.