1 Introduction

In recent decades, the global navigation satellite system (GNSS) radio occultation (RO) has become a powerful technique for observing Earth’s atmosphere (Anthes 2011; Ho et al. 2020). With a GNSS receiver aboard a Low-Earth Orbit (LEO) satellite, the phases and amplitudes of the GNSS signals measured during the RO events, together with the precise orbits and clock errors of GNSS and LEO satellites, are used to retrieve the bending angle profiles, from which the refractivity profiles of the neutral atmosphere are derived (Kursinski et al. 1997). Pressure, temperature, and water vapor profiles are further inverted from the refractivity profiles with the variational retrieval methods by taking auxiliary background information from numerical weather prediction (NWP) models (Zou et al. 1995, 1999; Poli and Paul 2002).

Since the concept of GNSS RO technology was first successfully demonstrated by the GPS/MET experiment in 1995 (Ware et al. 1996), a series of GNSS RO missions have been launched, including the German-U.S Challenging Minisatellite Payload (CHAMP), the European Gravity Recovery and Climate Experiment (GRACE), the U.S.-Taiwan FORMOsa SATellite mission-3/Constellation Observing System for the Meteorology, Ionosphere, and Climate (FORMOSAT-3/COSMIC), the European METeorological Operational satellites (MetOp-A, B and C), the U.S. Roadrunner, the German TerraSAR-X1, the Chinese Feng-Yun 3C (FY-3C), etc. (Rocken et al. 1997; Wickert et al. 2001; Beyerle et al. 2005; Anthes et al. 2008; Engeln et al. 2009; Liao et al. 2016; Schreiner et al. 2020). The evaluations of the products provided by different missions have revealed that RO data has the advantages of global coverage, high vertical resolution, long-term stability and all-weather capability, and the data have proven useful in improving numerical weather forecasts, space weather monitoring, and climate system studies (Healy et al. 2005; Cucurull et al. 2008; Xu et al. 2009; Healy and Thépaut 2006; Yue et al. 2011). It is worth noting that the COSMIC-2, the successor mission to FORMOSAT-3/COSMIC, can only provide RO observations within the middle and low latitudes. This is due to the low inclinations of the six LEO satellites used in this mission.

The Chinese FY-3C satellite, a sun-synchronous meteorological satellite launched in September of 2013, is equipped with a global navigation satellite occultation sounder (GNOS) being able to track both the Global Positioning System (GPS) and the BeiDou Satellite Navigation System (BDS) RO signals (Bai et al. 2014). Confined by the orbit characteristics of the satellite and the performance of the GNOS, the spatiotemporal distribution of the FY-3C RO observations is not uniform (Bai et al. 2014; Xu et al. 2022). The FY-3C RO atmospheric products have been provided by the National Satellite Meteorological Centre (NSMC) of China since 2014. The GNOS instrument onboard the FY-3C satellite can provide approximately 500 GPS atmospheric profiles and 500 electron concentration profiles per day. While the instrument's compatibility with BDS signal should in theory increase the number of atmospheric profiles to around 1000, the BDS RO products of the FY-3C satellite have not yet been released.

The error characteristics of FY-3C RO data set have been investigated in some previous studies. Bi et al. (2012) firstly investigated the possible accuracy of the refractivity profiles derived from the RO measurements obtained by the GNOS aboard FY-3C by simulation. A mountain-based experiment was carried out to validate the performance of GNOS before the launch of FY-3C satellite, and it indicated that the refractivity profiles obtained by GNOS are consistent with those from the radiosondes (Bai et al. 2014). After the launch of the satellite, Liao et al. (2016) evaluated the refractivity profiles derived from its RO observations and their results showed that GNOS/FY-3C meets the design requirements in terms of accuracy and precision of the sounder. Sun et al. (2018) verified and evaluated the bending angle and refractivity profiles of GNOS/FY-3C, and their conclusions were consistent with Liao et al. (2016). Wei et al. (2020) further compared FY-3C RO atmospheric profiles during 2015 to 2018 with ERA-Interim reanalysis data, and found that the global mean refractivity systematic differences are within ± 0.2% from 5 to 30 km altitude range, while the temperature differences vary within ± 0.2 K from 10 to 20 km, and the specific humidity differences are within ± 0.2 g/kg from 2 to 20 km. Shao and Zou (2002) and Chen et al. (2011) estimated and analyzed the observation error variance using apparent error (i.e., the difference between observation and background, O-B) variances minus the forecast error variances. In these previous works about the evaluations of FY-3C RO data, radiosonde observations or model data are generally used as references, and the mean biases of RO products relative to the reference data and the corresponding standard deviations are used to depict the error characteristics of the RO data. The errors of RO data derived this way are actually the “apparent errors” other than the observation errors due to that the errors of the reference data and the error covariances between the RO observations and the reference data are not taken into consideration in the evaluation process (Kuo et al. 2004). In assimilating RO observations in numerical weather predictions, an accurate estimation of the RO observation errors is important because observations are weighted proportionally to the inverse of their error variances (ErrVars) in the assimilation process (Kuo et al. 2001). In recent years, the three-cornered hat (3CH) method, which was originally brought forward for the estimation of atomic clock errors, has been applied to estimate the actual observation errors of RO data.

With three data sets as a minimum, the ErrVars of each data set can be estimated with the 3CH method assuming that the errors of different data sets are uncorrelated. The application of the 3CH method to estimate the ErrVars and standard deviations of multiple atmospheric data sets has come a long way since the first published results of Anthes and Rieckh (2018). Using multiple data sets including COSMIC RO, radiosondes, ERA-Interim, and Global Forecast System (GFS) model data at four radiosonde locations, Anthes and Rieckh (2018) estimated the ErrVars of each system by neglecting the error covariances among the different data sets, and found that different combinations of the four data sets yield similar relative ErrVar profiles of refractivity, temperature and specific humidity at the four stations, which indicate that the correlations of the errors among all data sets are small and the 3CH method yields realistic ErrVar profiles. Rieckh and Anthes (2018) further analyzed the sensitivity of the estimated ErrVars to the degree of error collocations among the data sets as well as the sample size, and found that the 3CH method is less sensitive to these factors compared with the two-cornered hat (2CH) method. The bias terms between different datasets are ignored in both the 2CH and the 3CH methods, and they also found that the 2CH method is more sensitive to the bias terms. Xu and Zou (2020) used the 3CH method to estimate the fractional error standard deviations (ErrSDs) of the MetOp-A/B RO refractivity and bending angle profiles near 48 radiosonde stations in China, and found that the RO fractional ErrSDs have significant latitudinal dependence. Schreiner et al. (2020) estimated the ErrSDs of the COSMIC-2 refractivity observations using four other data sets, and found that the effect of any correlations of errors on the results is small. Anthes et al. (2021) further used the 3CH method to evaluate the error STD of COSMIC-2 specific humidity in a hurricane environment. Sjoberg et al. (2021) present a complete discussion of the history of the 3CH method, the sensitivity of the method to factors which affect its accuracy, the effect of representativeness errors (differences) between the datasets used in the comparison, and the effect of filtering. By taking into consideration the bias terms between different datasets, Xu and Zou (2021) used the 3CH method to evaluate the ErrVars of the temperature and humidity observations of 521 globally-distributed radiosonde stations and the ErrVars of the collocated GPS RO refractivities and bending angles. They presented the latitude-height distributions of the squared bias terms for the refractivity data, and found that the bias terms have limited effect on the estimation of the ErrVars. Although the observation errors of RO data set provided by COSMIC, COSMIC-2 and MetOp-A/B has been studied with the 3CH method, till now, there is still no study about the estimation of the observation errors of FY-3C RO data set with this method. An important assumption made in estimating the FY-3C RO observation errors is the neglect of error covariance between different data sets. We need to examine how this assumption affects the accuracy of the result error estimates. Furthermore, we should investigate the characteristics of the global distribution of FY-3C RO observation errors in more detail.

In the present work, the ErrVars of the FY-3C RO refractivity, temperature and specific humidity data are estimated with the 3CH method, taking into consideration the bias terms between different datasets. On one hand, the ErrVars of FY-3C RO data at 18 selected radiosonde stations are estimated by using four collocated datasets, i.e. the RO data, the radiosonde data, the ERA-Interim and the NCEP reanalysis data sets. On the other hand, considering that radiosonde data are sparse over sea areas and polar regions, the gridded ErrVars of FY-3C RO data with the resolution of 5° × 5° are estimated by only using the RO data and the two model datasets. The gridded ErrVar estimations are then compared with the ErrVars estimated at the 18 radiosonde stations. The global distributions of the fractional ErrSDs of FY-3C RO data sets at different representative pressure levels, which are derived from the gridded ErrVars, are further analyzed, and the ErrSDs are compared statistically over different latitudes and over land and sea areas. Data and methods are introduced in Sect. 2. The results and discussions are presented in Sect. 3, and the conclusions are drawn in Sect. 4.

2 Data and methods

2.1 Data sets

To estimate the observation errors of FY-3C RO data set, the RO data from January 1, 2015 to April 30, 2019, along with three other data sets of the same time period, including radiosonde observations, ERA-Interim reanalysis, and NCEP reanalysis, are used in the present study, which are summarized briefly here.

2.1.1 FY-3C RO data

The National Satellite Meteorological Center (NSMC) of China has released FY-3C RO products since June 2014 (http://satellite.nsmc.org.cn/PortalSite/Data/DataView.aspx). The neutral atmospheric products, including refractivity, density, temperature and specific humidity profiles, are stored in three types of data files, i.e., the atmospheric refraction profile (ARP) files, the atmospheric temperature profile (ATP) files and the atmospheric moisture profile (AMP) files. Note that ATP and AMP products are derived from one-dimensional variational assimilation using the T639L60 model provided by the National Meteorological Center as the background field. The profiles inverted from GPS RO observations cover the height range of approximately 0–60 km. The vertical sampling resolution of the profiles decreases with increasing altitude. Near the surface, the vertical sampling resolution is within 10 m, and in the upper troposphere, it may extend to approximately 3 km. In this study, the FY-3C RO refractivity data from ARP files, temperature data from ATP files, and moisture data from AMP files were utilized. The analysis period spans from January 1, 2015, to April 30, 2019.

2.1.2 ERA-Interim reanalysis data

The ERA-Interim (hereafter ERA) reanalysis is a global atmospheric reanalysis produced by the European Centre for Medium-Range Weather Forecasts (ECMWF) (Dee et al. 2011). The 4-times daily dataset, which includes gridded data of temperature, pressure and specific humidity at the 37 pressure levels from 1000 to 1 hPa, with the time resolution of 6 h, are available online at https://www.ecmwf.int/en/research/climate-reanalysis/reanalysis-datasets/era-interim. In this study, the observation errors of the RO data were estimated by matching the ERA data set with the RO data first in terms of space and time. Specifically, the ERA pressure, temperature, and specific humidity were bilinearly interpolated from the gridded ERA data set with a horizontal resolution of 0.75° × 0.75° within the time window of ± 3 h for a specific RO observation (Liao et al. 2016).

The water vapor pressure is derived from the specific humidity by Eq. (1).

$$e = \frac{Pq}{{\varepsilon + \left( {1 - \varepsilon } \right) \cdot q}}$$
(1)

where \(q\) is the specific humidity in \(g/kg\), and \(P\) is the atmospheric pressure in \(hPa\). \(\epsilon\) is a constant with the value of 0.622, and \(e\) is the derived water vapor partial pressure in \(hPa.\) The refractivity, \(N\), is obtained by Eq. (2) accordingly (Smith and Weintraub 1953).

$$N = 77.6 \cdot \frac{P}{T} + 3.73 \times 10^{5} \cdot \frac{e}{{T^{2} }}$$
(2)

where \(T\) is the air temperature in \(K\).

2.1.3 NCEP reanalysis data

The 4-times daily reanalysis data set from the National Centers for Environmental Prediction (NCEP), which is available online at https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html, provides global atmospheric parameters, including temperature, pressure, water vapor pressure and specific humidity, at 17 pressure levels from 1000 to 10 hPa on 2.5° × 2.5° latitude by longitude grids, with the same time resolution as the ERA data set. In the present study, the NCEP data are matched with FY-3C RO profiles in space and time using the same collocation rules and interpolation method as applied for the ERA data set, and the matched NCEP refractivity profiles are derived accordingly using Eq. (2).

2.1.4 Radiosonde observations

This study employed the integrated global radiosonde archive 2 (IGRA2) dataset, a high-quality collection of radiosonde data that encompasses profiles of atmospheric parameters, including pressure, refractivity, water vapor partial pressure, and dew point temperature. The IGRA2 dataset was obtained from the National Centers for Environmental Information website at https://www.ncei.noaa.gov/products/weather-balloon/integrated-global-radiosonde-archive.

Due to the limited height reached by the radiosonde balloons, there are few IGRA2 observations above 30 km, so this dataset is mainly used to evaluate the errors of FY-3C RO atmospheric profiles at the height range of 1000 hPa to 200 hPa. The vertical resolutions of the radiosonde observations vary distinctly at different stations, ranging from a few meters to several hundred meters. Consequently, three cubic spline interpolation is applied to the IGRA-2 sounding data to match the pressure levels of ERA reanalysis data, ensuring consistency in subsequent data processing steps. For the collocation of radiosonde and RO profiles, the time window is set as ± 3 h and the space window is set as 300 km (Kuo et al. 2005; Ho et al. 2010; Panagiotis et al. 2014). For a radiosonde measurement, the specific humidity is derived from pressure and water vapor partial pressure using Eq. (3).

$$q = \frac{\varepsilon \cdot e}{{P - \left( {1 - \varepsilon } \right) \cdot e}}$$
(3)

where the parameters \(q, e,P \, and \, \epsilon\) have the same meanings as those in Eq. (1).

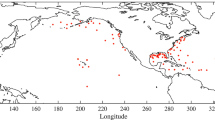
In the current investigation, 18 radiosonde stations, strategically chosen from a pool of 949 globally distributed stations, were employed to derive ErrVars for FY-3C RO data. This derivation was performed using four co-located datasets collected at these selected stations. When selecting radiosonde stations for the study, several criteria were considered. First, the stations needed to be distributed in different latitude zones to accurately reflect the impact of water vapor on the inversion of RO data. Second, the selected stations should provide continuous radiosonde measurements between January 2015 and April 2019. Finally, only Meisei (4 stations) or Vaisala (14 stations) radiosonde types were chosen. These types were previously proven to be of high quality by other studies (Ho et al. 2010; Sun et al. 2013). Figure 1 presents the geographic distribution of the 18 selected radiosonde stations.

Fig. 1
figure 1

Geographic distributions of the 18 selected radiosonde stations, include 4 Meisei type stations (black triangle) and 14 Vaisala type stations (red circle)

Full size image

2.2 Methodology

2.2.1 Data normalization

Collocated profiles of atmospheric parameters from four data sets are used for estimating the errors of FY-3C RO data set. Considering that the variations in the magnitudes of the atmospheric parameter including refractivity, temperature and specific humidity are significant from the lower to the upper troposphere, before the error estimation, the four data sets are normalized with reference to the ERA data set to highlight the similarities and differences of different data sets (Anthes and Rieckh 2018). Data normalization is achieved by subtracting the collocated ERA data set from the data set to be normalized, and then dividing the difference by the three-dimensional time average of the ERA data set, as shown by Eq. (4):

$$D_{{i,{ }normalized}} = \frac{{D_{i} - D_{ERA} }}{{\overline{D}_{ERA} }}$$
(4)

where \({D}_{ERA}\) represents the ERA data set; \({D}_{i}\) represents the data set to be normalized; \({\overline{D}}_{ERA}\) is the three-dimensional time average of the ERA data set; \({D}_{i, normalized}\) represents the data set \({D}_{i}\) after being normalized.

2.2.2 Quality control of RO and radiosonde data

Considering that erroneous observations might exist in the RO and radiosonde data sets, quality controls (QCs) are performed on the normalized data sets prior to estimating the RO data errors. The QCs process, following Zou and Zeng (2006), involves a range check and a bi-weight check on both the RO and radiosonde observations. Profiles with top pressures greater than 50 hPa or bottom pressures less than 800 hPa are eliminated during the range check. In the bi-weight examination, the median and the median absolute deviation of the data were used to estimate their weights, which are then used to calculate the bi-weight mean (BM) and bi-weight standard deviation (BSD) of the data. The BM and BSD ultimately define the Z-score of the data. When Z-score is greater than 2.5, the corresponding data will be eliminated. Figure 2a shows the statistics of the data volume before and after the QCs at different pressure layers for the radiosonde station BELEM. The blue solid line represents that 148 profiles are initial observed, and the green solid line shows that 129 profiles are kept after the QCs processing. Figure 2b shows the statistics of the numbers of profiles before and after QCs at the 18 selected stations. The station numbers marked below the horizontal axis correspond to those designated in Fig. 1. For the 18 selected stations, a total of 5081 radiosonde profiles are considered initially, among which 4452 profiles pass the quality check and are used for further analysis. It can be seen from Fig. 2b that for most stations, about 100 to 500 profiles are kept after the QCs. Among the 18 stations, the maximum and the minimum data utilization rates are 93.125% and 80.78%, which are obtained at the station RESOLUTE (No. 2) and CHICHIJIMA (No. 8), respectively.

Fig. 2
figure 2

a The number of profiles before and after QCs for the station BELEM. b Profiles data counts of 18 selected radiosonde stations before and after QCs

Full size image

2.2.3 The three-cornered hat method

With the normalized collocated data sets which pass through the quality control, the observation errors of FY-3C RO data are estimated using the 3CH method. The principle for the error estimations using the 3CH method, which was introduced for atmospheric data sets by Anthes and Rieckh (2018) and was further explained by Sjoberg et al. (2021), is summarized here. What needs to be mentioned is that when applying the 3CH method in the present work, the sample mean of the difference between different datasets, which is called the bias terms in general, is taken into consideration. When the bias terms are considered, if three collocated data sets, i.e. FY-3C RO, ERA-Interim, and NCEP reanalysis, are available, the ErrVar of FY-3C RO can be solved by Eq. (5).

$$\sigma_{RO,1}^{2} = \frac{1}{2}\left( {\sigma_{RO - ERA}^{2} + \sigma_{RO - NCEP}^{2} - \sigma_{NCEP - ERA}^{2} } \right) - \frac{1}{2}\left( {B_{RO - ERA}^{2} + B_{RO - NCEP}^{2} - B_{NCEP - ERA}^{2} } \right)$$
(5)

where \({\sigma }_{RO,1}^{2}\) is the estimated ErrVar of RO observations. \({\sigma }_{RO-ERA}^{2}\), \({\sigma }_{RO-NCEP}^{2}\), and \({\sigma }_{NCEP-ERA}^{2}\) are the mean squared difference between datasets of RO and ERA, of RO and NCEP, and of NCEP and ERA, respectively, which are also called the apparent error variances. \({B}_{RO-ERA}^{2}\), \({B}_{RO-NCEP}^{2}\) and \({B}_{NCEP-ERA}^{2}\) are the squared values of the bias terms, which are derived as the sample means of the differences between the datasets of RO and ERA, RO and NCEP, and NCEP and ERA, respectively. And the effects of the biases among the 3 datasets are considered in (5). The square root of the estimated ErrVar gives the fractional error SD of the RO data. Similarly, if another collocated data set, such as radiosonde data, is available, then the ErrVar of FY-3C RO can also be resolved with NCEP reanalysis and radiosonde data as reference ensembles, or with ERA-Interim and collocated radiosonde data as reference ensembles, using Eqs. (6) and (7), respectively.

$$\sigma_{RO,2}^{2} \, = \, \frac{1}{2}\left( {\sigma_{RO - IGRA}^{2} + \sigma_{RO - NCEP}^{2} - \sigma_{NCEP - IGRA}^{2} } \right) - \frac{1}{2}\left( {B_{RO - IGRA}^{2} + B_{RO - NCEP}^{2} - B_{NCEP - IGRA}^{2} } \right)$$
(6)
$$\sigma_{RO,3}^{2}\,=\,\frac{1}{2}\left( {\sigma_{RO - ERA}^{2} + \sigma_{RO - IGRA}^{2} - \sigma_{IGRA - ERA}^{2} } \right) - \frac{1}{2}\left( {B_{RO - ERA}^{2} + B_{RO - IGRA}^{2} - B_{IGRA - ERA}^{2} } \right)$$
(7)

In Eq. (6) and (7), \({\sigma }_{RO-IGRA}^{2}\), \({\sigma }_{NCEP-IGRA}^{2}\), and \({\sigma }_{IGRA-ERA}^{2}\) represent the apparent error variance of RO data with respect to radiosonde data, that of NCEP data with respect to radiosonde data, and that of radiosonde data with respect to ERA data, respectively. \({B}_{RO-IGRA}^{2}\), \({B}_{NCEP-IGRA}^{2}\), and \({B}_{IGRA-ERA}^{2}\) are the squared bias terms between the datasets of RO and radiosonde, NECP and radiosonde, and radiosonde and ERA, respectively. What needs to be mentioned is that to reduce the errors introduced by the spatiotemporal differences in collocated RO and radiosonde observations, the differences between collocated RO and radiosonde observations are corrected using the double-difference method (Haimberger et al. 2012; Wong et al. 2015; Tradowsky et al. 2017; Gilpin et al. 2018), and the values of \({\sigma }_{RO-IGRA}^{2}\) and \({B}_{RO-IGRA}^{2}\) are therefore corrected correspondingly. The double-difference corrected differences (\({X}_{sc}\)) for the co-location pairs are computed as follows for the comparison variables (refractivity, temperature, and specific humidity):

$$X_{sc} = \left( {X_{RO} - X_{{ERA\left( {RO} \right)}} } \right) - \left( {X_{RS} - X_{{ERA\left( {RS} \right)}} } \right)$$
(8)

where \({X}_{ERA\left(RO\right)}\)) is the ERA-Interim model value interpolated in time and space to the RO location, \({X}_{ERA\left(RS\right)}\) is the ERA-Interim model grid point value closest to the RS at the RS launch time.

Based on the three estimates obtained using Eqs. (5)–(7), the FY-3C RO observation error variance can be further described by the mean of these three estimates. It is worth noting that all the error covariance terms are ignored in the three Eqs. (5)–(7). Ideally, for large data groups with zero error correlations between different data sets, the RO ErrVars derived by the three equations should be the same. However, as shown by Rieckh and Anthes (2018), differences exist in the three estimates due to the finite length of the data sets and the non-zero error correlations among them. In the present work, the one-dimensional variational assimilation background field model used for deriving the FY-3C RO AMP products is T639L60 provided by the National Meteorological Center, and FY-3C RO data have not been assimilated into the ERA-Interim and the NCEP reanalysis models (Liao et al. 2016). So the covariance between the RO data and any one of the two reanalysis datasets can be ignored. Although both ERA and NCEP data assimilate the radiosonde data, other types of observations which are assimilated into the ERA and NCEP models are of much larger data volume, and so the correlations of model errors with radiosonde data errors are likely to be small (Rieckh and Anthes 2018).

As mentioned in Sect. 1, at the 18 selected stations where radiosonde observations are available, the ErrVars of FY-3C RO data can be estimated using the mean of the three estimates as \({\sigma }_{RO,mean}^{2}\). While considering that radiosonde stations are sparse over sea areas and polar regions, to derive a global distribution of \({\sigma }_{RO,mean}^{2}\) is impractical. Therefore, the 5° × 5° gridded error variance (ErrVar) values of FY-3C RO data were derived by exclusively utilizing the ERA and NCEP datasets as reference ensembles, i.e., the gridded ErrVar values are estimated using Eq. (5) as \({\sigma }_{RO,1}^{2}\). The consistency between these two estimates (\({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,1}^{2}\)) at the 18 selected stations are evaluated at first.

3 Results and discussions

To derive the global distributions of the ErrVars of RO data, the whole world is divided into \(5^\circ \times 5^\circ\) latitude \(\times\) longitude grids, and in each grid, profiles of collocated FY-3C RO data, ERA and NCEP model data are obtained and are used to estimate the ErrVars of FY-3C RO data of this grid by Eq. (5), which are denoted as \({\sigma }_{RO,grid}^{2}\) in the following part of the present work. The consistency between \({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,grid}^{2}\) are investigated at the 18 selected representative radiosonde stations. Specifically, for a radiosonde station, the values of \({\sigma }_{RO,grid}^{2}\) corresponding to the \(5^\circ \times 5^\circ\) grid in which the station is located are compared with the values of \({\sigma }_{RO,mean}^{2}\) estimated for this station.

3.1 The distributions of the squared bias terms

At the 18 stations where the radiosonde observations are available, the six squared bias terms in the Eqs. (5)–(7) are estimated at different pressure levels for each of the three atmospheric parameters, i.e., the refractivity, temperature and the specific humidity. It should be noted that all datasets have been normalized as introduced in Sect. 2.2.1, and so the units for the estimated squared values are all %2. Figure 3 presents these estimates in the pressure layer range of 1000 to 200 hPa. Figure 3a demonstrates that at this pressure level range, the squared values of the six bias terms for refractivity are all less than 5%2, gradually increasing with the increase of the pressure and reaching a maximum value at around 900 hPa. Moreover, both \({B}_{RO-RS}^{2}\) and \({B}_{ERA-NCEP}^{2}\) for refractivity are less than 1%2 in this pressure level range. Figure 3b shows that the squared values of the six bias terms for temperature are all below 0.02%2 at the pressure levels between 900 and 400 hPa. From Fig. 3c, it can be seen that above the pressure level of 900 hPa, all the squared bias terms for specific humidity are lower than 50%2. And at most pressure levels between 1000 to 200 hPa, the value of \({B}_{RO-RS}^{2}\) for specific humidity is generally the smallest one and \({B}_{RO-NCEP}^{2}\) and \({B}_{NCEP-RS}^{2}\) are the two largest ones.

Fig. 3
figure 3

Squared values of the six bias terms for a Refractivity, b temperature and c specific humidity

Full size image

For deriving the gridded ErrVars of FY-3C RO data using Eq. (5), the gridded values of \({B}_{RO-ERA}^{2}\), \({B}_{RO-NCEP}^{2}\), \({B}_{NCEP-ERA}^{2}\) are estimated. Figure 4 presents the height-latitude distributions of the estimates of the three squared bias terms, i.e., the parameters \({B}_{RO-ERA}^{2}\), \({B}_{RO-NCEP}^{2}\), \({B}_{NCEP-ERA}^{2}\) used in Eq. (5), for refractivity, temperature, and specific humidity. It can be seen from Fig. 4a–c that among the three squared bias terms for refractivity, \({B}_{RO-NCEP}^{2}\) is slightly larger than \({B}_{RO-ERA}^{2}\) and \({B}_{NCEP-ERA}^{2}\) at 600 hPa to 900 hPa, while the overall height-latitude distribution patterns of the three squared bias terms are similar. The bias has a larger value above the 850 hPa level in the equatorial region. It is worth noting that this finding is consistent with the results presented by Liao et al. (2016), who evaluated the FY-3C atmospheric products with traditional methods and found that the products show large deviations at a height of 2 km (~ 850 hPa). In Figs. 4d–f, the three squared bias terms for temperature are generally lower than 0.05. Figures 4g–i show that of the three squared bias terms for specific humidity, \({B}_{RO-ERA}^{2}\) is smaller than the other two, and the distribution patterns of \({B}_{RO-NCEP}^{2}\) and \({B}_{NCEP-ERA}^{2}\) are consistent, indicating a systematic difference with NCEP reanalysis data.

Fig. 4
figure 4

Height-latitude distributions of the squared bias terms for the refractivity (upper row), temperature (middle row), and specific humidity (lower row) between (a, d, g) RO and NCEP (\({B}_{RO-NCEP}^{2}\)), (b, e, h) RO and ERA (\({B}_{RO-ERA}^{2}\)), (c, f, i) NCEP and ERA (\({B}_{NCEP-ERA}^{2}\)) datasets (Unit: %2)

Full size image

Figure 4 presents that for the refractivity, temperature, and specific humidity datasets, the magnitudes of the three bias terms are generally very small, which indicates that their impacts on the estimation of the ErrVars are limited.

3.1.1 The comparison between \({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,grid}^{2}\)

Figure 5 shows the bar chart of the number of the profiles at each of the radiosonde station (RS number for short), which are used for calculating \({\sigma }_{RO,mean}^{2}\), and the number of the profiles in the corresponding \(5^\circ \times 5^\circ\) grid (grid number for short), which are used for calculating \({\sigma }_{RO,grid}^{2}\). The ratio of the grid number to the RS number at each station is also shown in the figure. It can be seen that for the 18 selected stations, the ratio of the grid number to RS number variates between 0.22 to 2.60. Specifically, the number of the RS profiles at the station No. 1 is much larger than that in the corresponding grid, and the quantity ratio is only 0.22. The ratio of the grid number to RS number is the highest at the station No.15, which is 2.60. At the stations No. 9 to 12, the profiles in the corresponding grids are all around 100, and the quantity ratios vary between 0.89 and 1.84. Over all, the variation of the grid numbers is smaller than that of the RS numbers at different stations, which indicates that the data source for deriving \({\sigma }_{RO,grid}^{2}\) are more stable than that for deriving \({\sigma }_{RO,mean}^{2}\). Using a stable number of grids is advantageous in evaluating global data quality and capturing the characteristics of refractivity, temperature and specific humidity across various regions. This compensates for the instability of the number of profiles collected by RS stations, particularly in marine areas where RS may not be able to cover adequately.

Fig. 5
figure 5

Number of profiles at each radiosonde station and in the corresponding \(5^\circ \times 5^\circ\) grid (bar chart), and the ratio of grid profile number to radiosonde profile number (red triangle referring to the right vertical axis)

Full size image

Figure 6 presents the comparisons between the values of \({\sigma }_{RO,mean}^{2}\) and those of \({\sigma }_{RO,grid}^{2}\) at the 18 selected radiosonde stations. To enhance clarity in demonstrating the relationship, the data has been transformed using the natural logarithm. In each of the scatter plots, the data pairs of \({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,grid}^{2}\) for a certain atmospheric parameter in different pressure layer ranges are denoted with dots of different colors. The correlation coefficients between \({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,grid}^{2}\), which are derived for different atmospheric parameters in different pressure layer ranges, are further presented in Table 1.

Fig. 6
figure 6

The correlations between the error variances of FY-3C RO a refractivity, b temperature and c specific humidity at the 18 selected radiosonde stations estimated with three reference data sets and the gridded values of the RO error variances estimated with two model data sets as reference

Full size image
Table 1 Correlation coefficients between \({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,grid}^{2}\) for different atmospheric parameters in different pressure layer ranges
Full size table

It can be seen from Fig. 6a that for FY-3C RO refractivity data, the correlation coefficients between \({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,grid}^{2}\) at different height ranges above 600 hPa are all higher than 0.764, and reaches 0.915 between 600 and 1000 hPa, indicating strong correlations in the lower troposphere. Figure 6b presents that for FY-3C RO temperatures, the correlation coefficients between \({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,grid}^{2}\) at different height ranges are generally higher than 0.751, reaching 0.864 above 300 hPa. Figure 6c shows that for FY-3C RO specific humidity data, the correlation coefficients between \({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,grid}^{2}\) are higher than 0.620. Moreover, the 18 chosen radiosonde stations are located near the marine regions, where significant changes in water vapor are observed. Specifically, the specific humidity, temperature, and refractivity show great variability, particularly in the deep tropical areas. The temperature and specific humidity ErrSDs of FY3C RO data are generally higher than those of COSMIC data obtained by Anthes and Rieckh (2018). Among the four collocated datasets used for deriving \({\sigma }_{RO,mean}^{2}\), the radiosonde data has been assimilated into the ERA and NCEP model data, and so these three datasets are in fact error correlated. Riech and Anthes (2018) showed that neglecting the error covariance between two of the datasets would lead to the underestimation of the error in the two relevant datasets and the overestimation of the error in the third dataset. Accordingly, using Eq. (5), the errors of the two model datasets will be underestimated, while the error of the third data sets (in this case FY-3C RO) will be overestimated. And the values of \({\sigma }_{RO,2}^{2}\) and \({\sigma }_{RO,3}^{2}\), which are obtained using Eq. (6) and Eq. (7), respectively, would also be overestimated. So at the location of a specific radiosonde station, the error correlations among the radiosonde observations and the two model datasets would all contribute to the final overestimate of \({\sigma }_{RO,mean}^{2}\) at this station. In comparison, when deriving the value of \({\sigma }_{RO,grid}^{2}\) corresponding to this station using Eq. (5), although the error correlations between the two model datasets in the specific grid would also contribute to the overestimate of RO errors, the correlations of the model datasets in the grid should be smaller than those at the radiosonde location due to that both models assimilate the same radiosonde data. Therefore, the gridded RO errors estimated using Eq. (5) should be smaller than the average of the three error estimates obtained.

In general, for all the three FY-3C RO atmospheric parameters, i.e., refractivity, temperature and specific humidity, good correlations exist between \({\sigma }_{RO,mean}^{2}\) and \({\sigma }_{RO,grid}^{2}\) at different height ranges, and the values of \({\sigma }_{RO,grid}^{2}\) are generally smaller than \({\sigma }_{RO,mean}^{2}\) between 300 and 1000 hPa, where the data ratio proportion \({\sigma }_{RO,grid}^{2}\) of being all smaller than 0.3. In the following subsection, the global distributions of the errors of FY-3C RO products will be analyzed based on the values of \({\sigma }_{RO,grid}^{2}\).

3.2 Distributions of the error standard deviations over different pressure levels

Figure 7 shows the 5° × 5° latitude–longitude contour plots of the sample size used for deriving \({\sigma }_{RO,grid}^{2}\) at the 600 hPa pressure level. The distribution of the sample size exhibits significant latitude band distribution characteristics and is generally symmetrical between the two hemispheres. Particularly, in the equatorial region, the \(5^\circ \times 5^\circ\) sample size is around 120 and increases with increasing latitude. The maximum value of the \(5^\circ \times 5^\circ\) sample size is around 300 at approximately 50° N. From 50° N to 90° N, the sample size gradually decreases, which is related to the orbital characteristics of the FY-3C satellite.

Fig. 7
figure 7

The \(5^\circ \times 5^\circ\) latitude–longitude contour map of the sample size at the pressure level of 600 hPa

Full size image

With the 3CH method, the gridded ErrVars of FY-3C RO data are estimated with the data sets of ERA and NCEP as references, and the corresponding gridded fractional ErrSDs, i.e. the square root of the ErrVars, are derived accordingly. To comprehensively illustrate the vertical variation patterns in refractivity and temperature parameters across various atmospheric layers, the error characteristics were further examined at four pressure levels: 1000 hPa, 200 hPa, 50 hPa, and 10 hPa. The 1000 hPa pressure level corresponds to the surface pressure level or the mean sea level within the atmosphere. The other three levels correspond to approximate altitudes of 12 km, 20 km, and 30 km, respectively. These four pressure levels cover a range of heights from the surface to the upper atmosphere and provide detailed information on the characteristics of refractivity and temperature errors. Figure 8 displays the global distributions of the fractional ErrSDs for FY-3C RO refractivities at the aforementioned four pressure levels.

Fig. 8
figure 8

The global distributions of the fractional error standard deviations of FY-3C RO refractivity data at the pressure levels of a 1000 hPa, b 200 hPa, c 50 hPa, d 10 hPa

Full size image

The comparisons of the four subfigures of Fig. 8 demonstrate that the magnitudes of the ErrSDs of RO refractivities vary greatly at different pressure levels. Figure 8a shows that at the pressure layer 1000 hPa, variations in the fractional ErrSDs of FY-3C RO refractivities are significant over the globe. In the Tibetan Plateau, the parts of the Antarctic region and the Cordillera Mountains in America, the ErrSDs of the RO refractivities are greater than 5%. In the Antarctic region and Tibetan Plateau the ErrSDs are greater than 10%, which is partly due to the large sampling errors in this region (Pirscher et al. 2007; Ho et al. 2009; Scherllin-Pirscher et al. 2011). At the 1000 hPa pressure level outside of the Antarctic region, there is a clear latitude-dependent distribution of refractivity ErrSDs globally, decreasing with increasing latitude. The ErrSDs of RO refractivities at 1000 hPa vary greatly over land and sea areas, while being generally less than 5% in ocean areas. The differences in the ErrSDs of FY-3C RO data over land and sea areas will be further discussed in Sect. 4. Figure 8b and c present that at the pressure levels of 200 hPa and 50 hPa, the fractional ErrSDs of FY-3C RO refractivities are mostly less than 3% except for two latitudinal bands near 30°N and 30°S, where the refractivity ErrSDs are significantly larger than those over other latitudes. Figure 8d presents that at 10 hPa, the FY-3C RO refractivity ErrSDs are generally less than 3% over the globe except for the Qinghai-Tibet Plateau and the Antarctica region. The maximum ErrSDs of RO refractivities are observed at approximately 1000 hPa, as depicted in Fig. 8. Large ErrSDs of fractional refractivity are observed near latitude bands above 200 hPa, specifically located at 30N and 10S, which become more pronounced at 50 hPa altitude. Due to the large variability of water vapor over tropical oceans, combined with seasonal ocean currents, the he ErrSDs of RO refractivities near the equator varies significantly in magnitude, with the SD of fractional refractivities ErrSDs not being a simple function of latitude but having geographical dependence. In our forthcoming research endeavors, the analysis will extend to utilizing COSMIC-2 data for a more in-depth investigation of ErrSDs within the tropical region, where an extensive dataset of RO observations is available spanning the latitudinal range of 45° S to 45° N.

Figure 9 presents the global distributions of the estimated fractional ErrSDs of FY-3C RO temperatures at the four pressure layers of 1000 hPa, 200 hPa, 50 hPa, and 10 hPa. It can be seen that the spatial distribution patterns of the ErrSDs of RO temperatures vary significantly at different pressure levels. Figure 9a shows that at the pressure level of 1000 hPa, the RO temperature ErrSDs reach about 0.9% at the latitude bands of 60° S to 90° S, while are less than 0.75% at higher latitudes over the northern hemisphere (NH). And similar to the distributions of the RO refractivity ErrSDs, the RO temperature ErrSDs at this pressure level are generally smaller over oceans than over land areas.

Fig. 9
figure 9

The global distributions of the fractional error standard deviations of FY-3C RO temperatures at the pressure levels of a 1000 hPa, b 200 hPa, c 50 hPa, d 10 hPa

Full size image

The comparison of Fig. 9b and c reveals that the distribution patterns of the FY-3C RO temperature ErrSDs at the pressure levels of 200 hPa and 50 hPa are opposite to each other. Due to the active atmospheric convection in the tropical region, refractivity changes significantly, resulting in a significant magnitude change of the ErrSDs near the equator. Consequently, ErrSDs of fractional refractivities are not a simple function of latitude. Moreover, after the one-dimensional refractivity variational assimilation, temperature parameters lead to increased temperature errors in the 50 hPa pressure layer. Specifically, the FY-3C RO temperature ErrSDs over 25° N to 25° S are generally significantly smaller/larger than those over middle and high latitudes at 200 hPa/50 hPa. Figure 9d shows that at 10 hPa, the RO temperature ErrSDs in middle and low latitudes are generally smaller than those in high latitude regions, and there are data missing in the Antarctic region and some sea areas, which is due to the data quality control.

Figure 10 presents the global distributions of the estimated fractional ErrSDs of FY-3C RO specific humidity at four representative pressure levels. Because moisture mainly concentrates below 200 hPa, here the four pressure levels selected are 1000 hPa, 850 hPa, 600 hPa and 200 hPa. From Fig. 10, it can be seen that for the four selected pressure levels, the ErrSDs of RO specific humidity generally increase with the decrease of the pressures.

Fig. 10
figure 10

The global distributions of the fractional error standard deviations of FY-3C RO specific humidity at the pressure levels of a 1000 hPa, b 850 hPa, c 600 hPa, d 200 hPa

Full size image

In Figs. 10a and b, it is shown that at the pressure levels of 1000 hPa and 850 hPa, the error standard deviations for the specific humidity derived from the FY-3C RO observations are generally less than 25% over the globe, except for the Antarctic region, which agrees with Rieckh and Anthes (2018). Figure 10c shows that at the pressure level of 600 hPa, the ErrSDs of RO specific humidity are less than 25% in most areas between 30°S and 30°N, while getting about 40% over the South Pacific, Indian Ocean and South Atlantic regions, and even reach about 60% in the Antarctic region, due to significant annual water vapor changes and seasonal variations. The increased uncertainty along the coastal areas of continents might be associated with known ducting features (Sokolovskiy 2003; Zhou et al. 2021). Figure 10d shows that at the pressure level of 200 hPa, the ErrSDs of FY-3C RO specific humidity are generally less than 25% between 30° S and 30° N, while increase significantly in the north and south polar regions. At around 1000 hPa, the standard deviation of error (ErrSD) for specific humidity derived from FY-3C RO is relatively small but it increases gradually with altitude. This trend could be attributed to the fact that the specific humidity values have a small order of magnitude and decrease rapidly with increasing altitude. The fluctuations in ErrSDs become larger as a result, which agrees with the findings of Rieckh and Anthes (2018).

3.3 Comparisons of error standard deviations over different latitudes

The global distributions of the fractional ErrSDs presented in Sect. 3.2 demonstrate that the differences in the observation errors of FY-3C RO data over different latitudes are distinct, which are further investigated in this subsection. The fractional ErrSDs of FY-3C RO data over five latitude zones, i.e., 45° N–75° N, 15° N–45° N, 15° S–15° N, 15° S–45° S, and 45° S–75° S, are compared statistically and are presented in Fig. 11a–c. The corresponding percentage of the numbers of collocated data groups after quality control are shown in Fig. 11d–f, and the maximum numbers of profiles of the corresponding data are denoted.

Fig. 11
figure 11

The fractional error standard deviations of FY-3C RO data over different latitude zones and the corresponding percentage of the number of collocated data groups for a, d refractivity, b, e temperature, and c, f specific humidity. In each subfigure, the statistical results over different latitude zones are presented with lines of different colors. In the upper right corners of subfigures (d–f), the maximum numbers of profiles at different latitude bands are given

Full size image

This paragraph discusses the spatial distribution of the fractional error standard deviations of refractivity obtained through the FY-3C RO dataset at different mean sea levels (MSL) heights, illustrated in Fig. 11. In each subfigure, the left y-axis (in black) represents mean sea level altitudes, and the right y-axis (in red) denotes the corresponding pressure levels.The statistic results presented in Fig. 11 demonstrate that the fractional ErrSDs generally decrease with decreasing height in each of the five latitude zones. The highest values of fractional ErrSD are found in the 15° N–45° N zone, and the lowest ones are in the 45° N–75° N and 45° S–75° S zones. Compared with the refractivity ErrSDs of COSMIC-2 RO data obtained by Schreiner et al. (2020), FY-3C RO data generally exhibit higher fractional ErrSDs, yet the height distribution patterns of the ErrSDs in both missions are consistent. According to Fig. 11d, the proportion of data from the same latitude bands in the two hemispheres is similar. The refractivity profiles obtained at 15° S to 15° N account for around 10% of all profiles, while the profiles obtained at 45° S to 75° S account for approximately 22.5%.

Figure 11b shows that the fractional ErrSDs of FY-3C RO temperature data are generally less than 0.6% over all the five latitude zones. Below the height of 10 km (~ 200 hPa), the temperature ErrSDs generally increase with the decrease of the height. Rieckh and Anthes (2018) estimated that the ErrVar of the COSMIC RO temperature data at the radiosonde station Mina (25.6° N, 131.5° E) is 0.3%2 below 10 km, here the maximum error SD of FY-3C RO temperature is about 0.6% (ErrVar of 0.36%2), which is comparable with Rieckh and Anthes (2018).

From Fig. 11c, it can be seen that in the height range of 0 km to 10 km, the ErrVars of FY-3C RO humidity data are generally higher in the middle and high latitudes than in the low latitudes, and the fractional ErrSDs of FY-3C RO specific humidities are the largest over the latitude zone of 45° S to 75° S and the smallest over 15° S to 15° N. Figure 11f shows that the latitude distribution of the numbers of specific humidity profiles is basically consistent with that of the refractivity profiles, and in the high latitudes, the number of humidity profiles are lower than that of the refractivity profiles. Our results show that the maximum ErrSDs of FY-3C RO specific humidity in the low latitudes of the two hemispheres are about 22% (ErrVar of 484%2). In comparison, Rieckh and Anthes (2018) revealed that at the low- latitude radiosonde station Mina, the COSMIC RO specific humidity has an ErrVar of less than 500%2 below 10 km.

3.4 Comparisons of error standard deviations over land and sea areas

The analyses in Sect. 3.3 also indicate that land-sea differences exist in the observation errors of FY-3C RO data, which is further studied in this subsection. For each \(5^\circ \times 5^\circ\) grid, the fractional ErrSDs of FY-3C RO products are calculated over land areas and over sea areas, respectively, based on which the means and the corresponding standard deviations of the fractional ErrSDs over land and sea areas of all \(5^\circ \times 5^\circ\) grids are obtained and are presented in Fig. 12. In each subfigure, the standard deviation about the mean is indicated by the shaded areas, and the left and the right vertical axes (in red) respectively denote the mean sea level height and the pressure level.

Fig. 12
figure 12

Means and the corresponding standard deviations of the fractional error SDs of FY-3C RO a refractivity, b temperature, and c specific humidity over land and sea areas

Full size image

From Fig. 12a, it is evident that, for all altitude levels, the means and standard deviations of the fractional ErrSDs of FY-3C RO refractivity data exhibit greater values over land regions compared to maritime regions. This difference is particularly pronounced at the MSL heights below 5 km. At the MSL height of about 1 km, the mean fractional ErrSD of FY-3C RO refractivity data over land areas and sea areas is around 8% and 4%, respectively. Figure 12b shows that the means and the standard deviations of the fractional ErrSDs of FY-3C RO temperatures are generally smaller than 0.7% over both land and sea areas at the height range of 6 km to 30 km, and are larger over lands than over sea areas at the height range of 0 km to 6 km. The means and the standard deviations of the fractional ErrSDs of FY-3C RO humidity data are generally smaller over sea areas than over land areas at the height below 10 km, as shown by Fig. 12c. The land-sea differences in the errors of FY-3C RO products, which is discernable in the refractivity and specific humidity products of lower troposphere, should be partly attributed to the complex environment conditions.

4 Conclusions

The aim of the present work is to investigate the global distributions of the observation errors of FY-3C RO data. The 3CH method is for the first time applied to estimate the ErrVars of FY-3C RO refractivity, temperature and specific humidity data, by using the RO data set during January 1, 2015 to April 30, 2019, along with radiosonde observations, the NCEP and the ERA reanalysis data sets, and bias terms between different datasets are taken into consideration when applying the 3CH method. Due to that radiosonde observations are very sparse over sea areas and polar regions, to derive the global distributions of the observation errors of RO data, the ErrVars can only be estimated with Eq. (5), using three of the four data sets, i.e., the RO data, the ERA and NCEP reanalysis data. Here, by using the observations of 18 globally distributed radiosonde stations, the relationships between two types of ErrVars, i.e., the ErrVars estimated with the average of the three error estimates obtained using all the four data sets, and the corresponding \(5^\circ \times 5^\circ\) gridded ErrVars estimated with Eq. (5) using three of the four data sets, are analyzed. It is found that at different height ranges, the two types of estimates are of high correlations, while the gridded estimates are generally smaller than the estimates derived using the four datasets, which should be attributed to the neglection of the error correlations among the radiosonde and the model datasets when applying the 3CH method.

Based on the gridded values of ErrVars, the global distributions of the fractional ErrSDs of FY-3C RO data at different pressure levels, and the latitudinal differences and land-sea difference of the ErrSDs are analyzed and discussed. It is found that the fractional ErrSDs of RO data generally vary greatly at different pressure layers and at different latitudes, and for different types of RO data, the characteristics in the spatial distribution patterns of the ErrSDs are different. Specifically, land-sea differences exist in the fractional ErrSDs of RO refractivity data at 1000 hPa, and at the pressure levels of 200 hPa and 50 hPa, the refractivity ErrSDs are distinctly larger over the two latitudinal bands near 30°N and 30°S than over other latitudes. The latitude–longitude distribution patterns of the FY-3C RO temperature ErrSDs at the pressure levels of 200 hPa and 50 hPa are opposite to each other, and the ErrSDs of RO specific humidity data generally increase with the decrease of the pressure levels.

Further statistics over different latitude zones show that the fractional ErrSDs of RO refractivity data are generally the smallest over 45° N–75° N and 45° S–75° S, while between the MSL height of 0 km to 10 km, the ErrSDs of RO temperature and specific humidity data are generally the largest over 45° S to 75° S. Furthermore, statistical data from both land and marine regions indicate the presence of land-sea disparities in the fractional ErrSDs for all three types of RO data. These disparities are more pronounced in the ErrSDs of refractivity and specific humidity data compared to temperature data. Specifically, for FY-3C RO refractivity data, both the means fand the standard deviations of the fractional ErrSDs are larger over lands than over sea areas at the height of about 1 km, and the mean fractional ErrSDs of RO refractivity data at 1 km over lands and sea areas are around 8% and 4%, respectively. The complex environment conditions should contribute to the land-sea differences in the errors of RO data, which are discernable in the lower troposphere.

The current investigation focuses on the assessment of FY3C RO data quality. In forthcoming research, the three-cornered hat method will be employed to conduct a more extensive evaluation of RO atmospheric products derived from other missions, including COSMIC-2, FY-3D, and FY-3E. Particular emphasis will be placed on assessing these products within low-latitude regions characterized by significant water vapor fluctuations.