1 Introduction

A rupture taking place along several fault segments and/or structures can cause an earthquake with a large magnitude (e.g., Yen and Ma 2011) and often leads to disaster. The 1935 ML7.1 Hsinchu-Taichung, Taiwan, earthquake is an example. This event is attributed to a rupture on the Shihtan and Tunzijiao faults and resulted in more than 3000 fatalities and the destruction of more than 60,000 buildings. According to the fault parameters determined by Shyu et al. (2020), either the Shihtan or Tunzijiao fault could cause an earthquake with a maximum magnitude of only 6.6 (Wang et al. 2016a). This case raises the importance of multiple-structure ruptures on seismic hazard assessment.

Thus, the Taiwan Earthquake Model (TEM) has considered the possibility of several multiple-structure ruptures for a probabilistic seismic hazard assessment for Taiwan (Chan et al. 2020) according to the finding of Shyu et al. (2020). In their procedure, however, the case that one structure could be associated with multiple pairs was determined based on geomorphological and geological evidence without detailed descriptions and possibility of the multiple-structure rupture was not discussed.

Some previous studies have quantified recurrence intervals for multiple-structure rupture. For example, Chan et al. (2020) proposed a procedure for partitioning the slip rate of each individual structure to multiple structures. The outcomes of the recurrence interval for each rupture pair have been implemented for subsequent probabilistic seismic hazard assessment (PSHA). In the study of Chan et al. (2020), however, the uncertainties contributed from different factors have not been incorporated and the case of single structure contributes to several multiple-structure ruptures is not considered. Besides, the Seismic Hazard and Earthquake Rate In Fault Systems (also known as ‘SHERIFS’, Chartier et al. 2017) considers multiple-fault (fault-to-fault) ruptures to evaluate seismicity rates for different magnitude (also known as ‘magnitude-frequency distribution, MFD’). In the SHERIFS, fault rupture could be in the forms of not only earthquakes on a fault segment, along multiple faults, but also background seismicity taking place in the vicinity of faults. The SHERIFS provide comprehensive procedure to calculate seismicity rate on a multiple-structure system, while users need to identify cases of multiple-structure rupture by themselves before applying this system.

To identify possible pairs of multiple-structure rupture, the UCERF3 (Uniform California Earthquake Rupture Forecast, Version 3; Field et al. 2014) defines two faults that could rupture simultaneously if rupture of one fault could result in increase of Coulomb stress and the distance between the two is less than 5 km. However, the impact of thresholds of Coulomb stress change and fault distance on multiple-structure rupture pair identification hasn’t been well-discussed.

Thus, this study aims to identify structures that could rupture simultaneously and propose a set of formulas to evaluate their recurrence intervals based on physics- and statistics-based models. The possibility of a multiple-structure rupture is determined based on the Coulomb stress change imparted by each structure and the distance from one to the other. Quantifying the recurrence interval relies on a scaling law and the Gutenberg-Richter law (Gutenberg and Richter 1944). We quantify uncertainties of multiple-structure rupture pair identifications and recurrence intervals considering different triggering criteria and epistemic uncertainties. In addition, the impact of multiple-structure rupture on subsequent probabilistic seismic hazard assessment is also discussed. Our approach is transparent and can be applied to reexamining the composite ruptures of the seismogenic structure system in Taiwan and other regions, which is beneficial to subsequent probabilistic seismic hazard assessments.

2 Distinguishing possible seismogenic structure pairs according to Coulomb stress change

Previous studies (e.g., Catalli and Chan 2012) have concluded that changes in the Coulomb stress resulting from previous earthquakes could trigger the occurrence of subsequent events in adjacent areas. Such an approach would be especially applicable to determining the interaction between two structures if their rupture mechanisms are known so that source rupture and receiver plane for Coulomb stress calculation can be determined. We introduce the Coulomb failure criterion to discuss interaction between structure systems, then distinguish seismogenic structure pairs that could rupture together in a coseismic period, considering different criteria. The procedure of our approach is illustrated by a flow chart (Fig. 1) and detailed in the following.

Fig. 1
figure 1

A flow chart that illustrate the procedure to identify cases of multiple-structure rupture implemented in this study

Full size image

2.1 Introduction of Coulomb stress

The Coulomb failure criterion describes mainly the characteristics of material failure (King et al. 1994; Toda et al. 2011). The criterion illustrates a plane encountering stress change, which could be decomposed into two vectors, shear stress change, ∆\(\tau\), and normal stress, ∆\(\sigma\)n:

$$\Delta CFS = \Delta \tau - \mu \prime \Delta \sigma_{n} ,$$
(1)

where ∆\(CFS\) is the Coulomb stress change, and μ′ is the effective friction coefficient that varies for different tectonic regimes. We first assume an intermediate value of μ′ = 0.4 then discuss its impact on the analysis. This study used the COULOMB 3.4 software (Toda et al. 2011) for calculation of Coulomb stress change. Based on the Coulomb stress change, we could quantify the possibility of a coseismic rupture for two faults. To explore the interactions between seismogenic structures in Taiwan, detailed structural parameters should be considered. Note that since we implemented a static Coulomb stress change to evaluate possibility of multiple-structure rupture, it is difficult to quantify the temporal evolution of rupture probability. Thus, the possibility of a multiple-structure rupture in a coseismic period might be overestimated, that is, a structure could be triggered in a postseismic or interseismic period.

2.2 Possible coseismic multiple-structure rupture defined by the Coulomb stress transfer

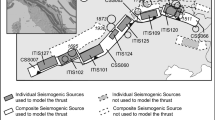
To understand stress interaction between seismogenic structures in Taiwan, we accessed the TEM database, which incorporates 45 seismogenic structures (Shyu et al. 2016, 2020, structure alignment shown in Fig. 2) and corresponding parameters (shown in Table 1). According to the surface trace and dipping angles, the three-dimensional geometry of each structure is illustrated by pieces of sub-faults.

Fig. 2
figure 2

Distribution of the 45 seismogenic structures in Taiwan. Corresponding structure parameters are listed in Table 1

Full size image
Table 1 The structure parameters of the 45 seismogenic structures in Taiwan
Full size table

Since these structures could initiate earthquakes and trigger neighboring structures, we investigated their potential interaction through Coulomb stress change. We followed the assumption of the TEM model and considered a characteristic earthquake with corresponding slip (shown in Table 1) on each structure and evaluated the Coulomb stress change solved on each sub-fault of the other structures. Previous studies concluded that stress increases greater than a threshold could trigger subsequent earthquakes. For example, Ma et al. (2005) suggested that stress increases greater than 0.1 bar could trigger seismicity activity. Thus we assumed that a structure could be triggered if more than a half of the structure’s sub-faults was enhanced with a stress increase greater than the threshold of 0.1 bar. Close distance between two structures is another key factor of rupture triggering. The UCERF3 (Field et al. 2014) defines two faults that could rupture simultaneously if the distance between the two is less than 5 km. Such criterion has also been confirmed in the case of Greece defined by Chartier et al. (2017). Following the distant criteria mentioned above, we could identify seismogenic structure pairs that could rupture in a coseismic period.

We have identified seismogenic structure pairs that could rupture in a coseismic period based on the assumptions mentioned above. Initially, we set stress and distance thresholds of ∆CFS ≥ 0.1 and 5 km, respectively, to identify potential rupture pairs. Our results showed that either the Meishan fault (ID 20) or the Chiayi frontal structure (ID 21) could trigger more than 50% of the other structure’s plane. For example, if the rupture initiates on the Chiayi frontal structure, the stress on the Meishan fault plane would be significantly disturbed, and 64% of the fault plane could be enhanced by more than 0.1 bar of the Coulomb stress. Conversely, a rupture on the Meishan fault could result in 76% of the Chiayi frontal structure’s plane experiencing a stress increase of more than 0.1 bar.

To investigate the influence of sub-fault size on Coulomb stress analysis, we reconfigured the sub-fault geometries. Initially, we divided each sub-fault into two sections and calculated the Coulomb stress. The results showed that 64% of the Meishan fault could be triggered by the rupture on the Chiayi frontal structure, while 76% of the Chiayi frontal structure could be triggered by the Meishan fault. These findings were similar to the original analysis. Subsequently, we merged two sub-faults into one and obtained trigger probabilities of 56% and 77% for the respective cases. The subtle differences could be attributed to variations in fault geometries, which emphasize the importance of precise mechanisms for calculating Coulomb stress.

Moreover, based on the three-dimensional geometries of the two seismogenic structures, their closest distance is 1.87 km, meeting our proximity criterion (< 5 km). Therefore, we conclude that the Meishan fault and the Chiayi frontal structure can mutually induce a coseismic rupture.

Based on the procedure mentioned above, we reported the ratio by which each structure plane is triggered by other structures (Additional file 1: Table S1) and the distance between each pair of structures (Additional file 2: Table S2), we defined 17 pairs of seismogenic structures that could potentially rupture in a coseismic period (Table 2).

Table 2 Potential pairs of multiple-structure ruptures, their parameters, and recurrence intervals of earthquakes
Full size table

2.3 Uncertainties of coseismic multiple-structure rupture defined from the Coulomb stress transfer and structure distance

In addition to implementing fixed thresholds for identifying multiple-structure pairs, we further discussed the impact of different thresholds of stress changes and structure distances. Considering ∆CFS of 0.01 bar as a lower bound of stress triggering (e.g., Chan and Stein 2009; Stein 2004), we proposed four sets of stress increase thresholds (0.01, 0.05, 0.1, and 0.2 bars), as well as two threshold sets for the distance between structures (2.5 and 5.0 km). Based on the criteria, multiple-structure pairs were identified (Table 3). More structure pairs were expected if a lower ∆CFS threshold and/or a longer maximum distance were assumed and vice versa. The number of identified pairs is between 6 (∆CFS ≥ 0.2 bar, distance ≤ 2.5 km) and 34 (∆CFS ≥ 0.01 bar, distance ≤ 5.0 km). It should be noted that both UCERF3 (Field et al. 2014) and Chartier et al. (2019) suggested that a distance of 5 km between structures could rupture simultaneously.

Table 3 Multiple-structure rupture pairs considering different thresholds in structure distance and Coulomb stress change
Full size table

We have identified potential structures that might rupture in a coseismic period. To understand the activities of these multiple-structure rupture cases, we will next propose a procedure to evaluate their recurrence intervals.

3 Recurrence interval of the multiple-structure rupture

The recurrence interval is a critical parameter in probabilistic seismic hazard analysis. Here, we are going to calculate the recurrence interval of multiple-structure ruptures and discuss their impact on seismic hazard assessment.

3.1 Recurrence interval of multiple-structure ruptures

According to the TEM seismogenic structure database (Shyu et al. 2020) and the TEM PSHA2020 (Chan et al. 2020), the rupture recurrence interval of a single seismogenic structure (\(L\)), \({R}_{L}\), can be evaluated as the ratio of slip of a characteristic earthquake to slip rate (denoted as \({D}_{L}\) and \(\dot{\mathrm{D}}\)L, respectively):

$${R}_{L}=\frac{{D}_{L}}{{\dot{D}}_{L}}.$$
(2)

To evaluate the seismic rate of a multiple-structure rupture on two seismogenic structures (\(L1\) and \(L2\)), we implemented the Gutenberg-Richter law (G-R law) to describe the relationship between earthquake frequency \(N\) and magnitude \(M\):

$$log\left({\varvec{N}}\right)=a-bM.$$
(3)

Considering the different moment magnitudes between single-structure and multiple-structure ruptures, the ratio of earthquake frequency to slip-rate partitioning could be evaluated by the G-R law. Here we present \({C}_{1}\) and \({C}_{2}\) as the partitioned rates from the first and second structures, \(L1\) and \(L2\), respectively, to the case of multiple-structure rupture as:

$${C}_{1}=\frac{{10}^{b({M}_{L1}-{M}_{L1+L2})}\times {D}_{L1+L2}}{{D}_{L1}}$$
(4)

and

$${C}_{2}=\frac{{10}^{b({M}_{L2}-{M}_{L1+L2})}\times {D}_{L1+L2}}{{D}_{L2}}, \mathrm{respectively}$$
(5)

where \({M}_{L1}\) and \({M}_{L2}\) represent the magnitudes of \(L1\) and \(L2\), respectively; \({D}_{L1}\) and \({D}_{L2}\) represent the displacements of \(L1\) and \(L2\), respectively; \({M}_{L1+L2}\) represents the magnitude of the multiple-structure rupture; and \({D}_{L1+L2}\) represents the displacement of the multiple-structure rupture.

The moment magnitude (\({M}_{w}\)) of the multiple-structure rupture could be evaluated according to the rupture area (denoted as \(A\)) and fault types of the two seismogenic structures. In the TEM structure database, determination of rupture magnitude (Table 1) is based on the scaling law proposed by Wells and Coppersmith (1994), represented as:

$${M}_{w} = 4.33 + 0.90 \times log \left(A\right)\dots \mathrm{for \,\,reverse \,\,faulting};$$
(6)
$${M}_{w} =3.98 + 1.02 \times log \left(A\right)\dots \mathrm{for \,\,strike}-\mathrm{slip \,\,faulting};$$
(7)
$${M}_{w} = 3.93 + 1.02 \times log \left(A\right)\dots \mathrm{for \,\,normal \,\,faulting}.$$
(8)

We first follow the procedure of the TEM model to implement these scaling relations and then evaluate uncertainty of this procedure considering different scaling relations.

Based on the Mw–M0 scale (Kanamori 1977) and the definition of seismic moment, average displacement of a seismogenic structure (\(D\), in meters) could be evaluated according to \({M}_{w}\) and \(A\) (in km2):

$$D=\frac{{10}^{{\frac{2}{3}M}_{w}}\times {10}^{-15.85}}{3A}.$$
(9)

The potential of multiple-structure ruptures could be attributed to the moment accumulation from the first and second structures, \(L1\) and \(L2\). We assumed their original slip rates, \({\dot{D}}_{L1}\) and \({\dot{D}}_{L2}\), could be partitioned into two cases, the rupture on the original structure and the rupture on multiple structures. The slip rate partitioned to individual structure ruptures (\(L1\) and \(L2\), respectively) can be represented as:

$${\dot{D}}_{L1}^{^{\prime}}=\frac{{\dot{D}}_{L1}}{\left(\frac{{A}_{L1+L2}}{{A}_{L1}}\times {C}_{1}+1\right)} \,\mathrm{and}$$
(10)
$${\dot{D}}_{L2}^{^{\prime}}=\frac{{\dot{D}}_{L2}}{\left(\frac{{A}_{L1+L2}}{{A}_{L2}}\times {C}_{2}+1\right)}\,\mathrm{respectively},$$
(11)

where \({A}_{L1}\) and \({A}_{L2}\) represent the rupture areas of \(L1\) and \(L2\), respectively; \({A}_{L1+L2}\) represents the area of the multiple-structure rupture. By integrating the obtained partitioned rates (Eqs. 10 and 11) and the slip rate partitioned to individual structure ruptures (Eqs. 4 and 5), the slip rate partitioned to the multiple-structure rupture from the original \(\mathrm{L}1\) and \(\mathrm{L}2\) can be obtained:

$${\dot{\mathrm{D}}}_{\mathrm{L}1+\mathrm{L}2}^{\mathrm{L}1}={\mathrm{C}}_{1}\times {\dot{\mathrm{D}}}_{\mathrm{L}1}^{\mathrm{^{\prime}}}\,\mathrm{ and}$$
(12)
$${\dot{\mathrm{D}}}_{\mathrm{L}1+\mathrm{L}2}^{\mathrm{L}2}={\mathrm{C}}_{2}\times {\dot{\mathrm{D}}}_{\mathrm{L}2}^{\mathrm{^{\prime}}},\mathrm{respectively}.$$
(13)

Then the sum of the slip rates for the multiple-structure rupture is calculated using the partitioned rates of the two structures, represented as:

$${\dot{D}}_{L1+L2}={\dot{D}}_{L1+L2}^{L1}+{\dot{D}}_{L1+L2}^{L2}.$$
(14)

Following the assumption presented in Eq. 2, considering the displacement and slip rate, recurrence intervals for individual structures (\({R}_{L1}\) and \({R}_{L2}\)) and the multiple-structure rupture (\({R}_{L1+L2}\)) can be represented as:

$${R}_{L1}=\frac{{D}_{L1}}{{\dot{\mathrm{D}}}_{\mathrm{L}1}^{\mathrm{^{\prime}}}},$$
(15)
$${R}_{L2}=\frac{{D}_{L2}}{{\dot{\mathrm{D}}}_{\mathrm{L}2}^{\mathrm{^{\prime}}}}, \mathrm{and}$$
(16)
$${R}_{L1+L2}=\frac{{D}_{L1+L2}}{{\dot{D}}_{L1+L2}}, \mathrm{respectively}.$$
(17)

3.2 Single structure contributes to several multiple-structure ruptures

A single seismogenic structure could be involved in multiple cases of multiple-structure rupture. For such cases, however, evaluation of the corresponding recurrence intervals has seldom been discussed. Here, we propose a procedure for quantifying the return period of this case, shown below.

When a single structure (L1) is involved in multiple cases of multiple-structure rupture (L1 + L2, …, L1 + Ln), the slip rate partitioned to the original structure can be obtained based on the revision of Eq. 10, represented as:

$${\dot{D}}_{L1}^{\prime}=\frac{{A}_{L1}\times {\dot{D}}_{L1}\times {D}_{L1}}{\left({A}_{L1}\times {D}_{L1}\right)+\sum_{i=2}^{n}\left({A}_{L1+Li}\times {D}_{L1+Li}\times {10}^{b\left({{M}_{L1}-M}_{L1+Li}\right)}\right)+\sum_{i=2}^{n-1}\sum_{j=3}^{n}\left({A}_{L1+Li+Lj}\times {D}_{L1+Li+Lj}\times {10}^{b\left({{M}_{L1}-M}_{L1+Li+Lj}\right)}\right)+\sum_{i=2}^{n-2}\sum_{j=3}^{n-1}\sum_{k=4}^{n}\ldots }, \quad 1< \mathrm{i}< \mathrm{j}<\mathrm{k}.$$
(18)

where \({D}_{L1+L2}\), ….,\({D}_{L1+Ln}\) represent the displacements of the multiple-structure rupture cases L1 + L2, …, L1 + Ln, respectively.

The slip rate partitioned to the multiple-structure rupture cases L1 + L2, …, L1 + Ln can be represented as:

$${\dot{D}}_{Lx}^{L1}=\frac{{A}_{L1}\times {\dot{D}}_{L1}\times {D}_{L1+Lx}\times {10}^{b({{M}_{L1}-M}_{Lx})}}{({A}_{L1}\times {D}_{L1})+\sum_{i=2}^{n}({A}_{L1+Li}\times {D}_{L1+Li}\times {10}^{b({{M}_{L1}-M}_{L1+Li})})+\sum_{i=2}^{n-1}\sum_{j=3}^{n}({A}_{L1+Li+Lj}\times {D}_{L1+Li+Lj}\times {10}^{b({{M}_{L1}-M}_{L1+Li+Lj})})+\sum_{i=2}^{n-2}\sum_{j=3}^{n-1}\sum_{k=4}^{n}\ldots}, \quad Lx=L1+Li+Lj+Lk+\ldots$$
(19)

respectively. In this case, evaluation of the recurrence interval for each multiple-structure rupture requires the slip rates contributed from two structures as well, similar to what is shown in Eq. 14. The total slip rate for each case of multiple-structure rupture can be represented as:

$${\dot{D}}_{Lx}={\dot{D}}_{Lx}^{L1}+\sum_{i=2}^{n}{\dot{D}}_{Lx}^{Li}.$$
(20)

The recurrence intervals for each multiple-structure rupture case can be represented as:

$${R}_{Lx}=\frac{{D}_{Lx}}{{\dot{D}}_{Lx}},$$
(21)

while the recurrence intervals for the original structure is represented in Eq. 15.

A single earthquake could be attributed to multiple (more than three) structures, for example, the 2010 El Mayor-Cucapah, US, earthquake (Wei et al. 2011); the 2016 Mw7.8 Kaikōura, New Zealand, earthquake (Hamling et al. 2017). In such special cases, the recurrence interval can be also evaluated through the procedure mentioned above. Thus, rupture probability of multiple structures could be quantified, which could constrain subsequent probabilistic seismic hazard assessment.

3.3 Multiple-structure rupture recurrence intervals and uncertainties

According to the structure parameters, the recurrence intervals of each pair of potential multiple-structure ruptures can be evaluated. Considering the 17 pairs with ∆CFS ≥ 0.1 bar and distance ≤ 5.0 km (listed in Table 2), we evaluated their potential magnitudes (Fig. 3) and recurrence intervals (Fig. 4). In addition to the mean value of each parameter, we quantified epistemic uncertainties from deviations of slip rate and rupture area. The largest magnitude is expected if the maximum rupture areas of the two structures are assumed (based on Eqs. 6–8). Also, the shortest recurrence interval is expected if the minimum rupture area and maximum slip rate are assumed (based on Eqs. 4–17).

Fig. 3
figure 3

Magnitudes for the seismogenic structures (a) by the TEM database and (b) considering multiple structure rupture pairs with ∆CFS ≥ 0.1 bar and distance ≤ 5.0 km. Corresponding parameters for the structures and multiple-structure ruptures are listed in Tables 1 and 2

Full size image
Fig. 4
figure 4

Recurrence interval for the seismogenic structures (a) by the TEM database and (b) considering multiple structure rupture pairs with ∆CFS ≥ 0.1 bar and distance ≤ 5.0 km. Corresponding parameters for the structures and multiple-structure ruptures are listed in Tables 1 and 2

Full size image

In comparison with the original recurrence intervals of the structures without considering a multiple-structure rupture (Table 4), longer recurrence intervals are expected for multiple-structure ruptures and individual structures due to slip partitioning.

Table 4 Original and revised recurrence intervals of the seismogenic structures that involve the cases of multiple-structure rupture
Full size table

Additionally, our results show that a single seismogenic structure sometimes pairs with several cases of multiple-structure ruptures. For example, the Hukou fault (ID 4) potentially ruptures with the Shuanglianpo structure (ID 2), the Fengshan river strike-slip structure (ID 5), and the Hsinchu fault (ID 6), while the Hsinchu fault (ID 6) could also result in multiple-segment ruptures with the Hsinchu frontal structure (ID 8) and the Touhuanping structure (ID 9). Besides these two cases associated with three rupture pairs, several structures could be associated with two multiple-structure pairs (Table 2), raising the importance of implementing slip partitioning from a single structure to several multiple-structure ruptures. Based on our analysis, it might be difficult for the structures that pair with several cases of multiple-structure ruptures might to rupture solely. That is, based on Eqs. 18–22, the slip rate of these structures could be partitioned to several cases of multiple-structure ruptures, resulting in longer recurrence intervals. For example, the Hukou fault (ID 4) and the Hsinchu fault (ID 6) involved four and three pairs of multiple-structure ruptures, respectively (Table 2), and their recurrence intervals became 4.4 and 5.3 times, respectively, longer than the cases without considering multiple-structure ruptures (Table 4).

Our calculations of recurrence interval for the multiple-structure ruptures are based on the scaling relations proposed by Wells and Coppersmith (1994). These relationships were obtained based on the global data summarized decades ago. To validate the sensitivity of our procedure to scaling, here we implement alternative scaling law proposed by Yen and Ma (2011), who investigated the rupture parameters of the earthquakes mainly from the Taiwan orogenic belt. This relation illustrates average displacement of a seismogenic structure (D, in meters) as a constant:

$$Log\left(D\right)=-0.32.$$
(22)

Based on this relation, recurrence intervals for each multiple-structure rupture pairs were evaluated (Table 5). Comparing these to those obtained by Wells and Coppersmith’s relations, shorter recurrence intervals were obtained (Fig. 4 and Table 2), especially for those with larger magnitude (Fig. 3 and Table 2). These results can be attributed to a smaller average displacement obtained for a large event that led to a shorter recurrence interval for the multiple-structure rupture (based on Eq. 17).

Table 5 Potential pairs of multiple-structure ruptures, their parameters, recurrence intervals of earthquakes evaluated by the scaling laws of Wells and Coppersmith (1994) and Yen and Ma (2011), respectively, and their differences
Full size table

4 Discussion and conclusion

4.1 Interaction between structures and possible coseismic ruptures

In this study, we explored possible coseismic multiple-structure ruptures and quantified their recurrence intervals by implementing the Coulomb stress change and the Gutenberg-Richter law, respectively. The analyzing procedure we proposed is based on physics- and statistics-based models, and the outcomes are reproducible.

We compared our results with Shyu et al.’s (2020) conclusion that some seismogenic structure pairs—such as the Hsinchu fault (ID 6) and the Hsinchu frontal structure (ID 8), the Touhuanping fault (ID 9) and the Miaoli frontal structure (ID 10), the Meishan fault (ID 20) and the Chiayi frontal structure (ID 21), and the Chiayi frontal structure (ID 21) and the Tainan frontal structure (ID 41)—could rupture simultaneously. Their findings were consistent with our results based on the Coulomb stress triggering, as long as they defined seismogenic structure pairs according to geological and geomorphological evidence instead.

Additionally, Shyu et al. (2020) suggested some other structure pairs for multiple-structure ruptures, such as the Shihtan fault (ID 13) and Tuntzuchiao fault (ID 15), the Houchiali fault (ID 25) and the Tainan frontal structure (ID 41), and the Chaochou fault (ID 29) and the Hengchun fault (ID 30). These pairs, however, do not fit our hypothesis. Take the Shihtan and Tuntzuchiao faults, for example. The rupture of the Tuntzuchiao fault could result in a Coulomb stress increase of more than 0.1 bar in 79% of the sub-faults of the Shihtan fault, whereas only 2% of the sub-fault in the Tuntzuchiao fault would be triggered when the Shihtan fault dislocates (Additional file 1: Table S1). Note that the 1935 Hsinchu-Taichung earthquake is attributed to a coseismic rupture on the two faults. Previous studies (Yen et al. 2016; Su 2019) indicated that this earthquake did not initiate on either the Shihtan or the Tuntzuchiao fault, but on a blind fault linking the two. Since the database we accessed (Shyu et al. 2020) did not include this blind structure, our analysis could be further improved through better understanding seismogenic structures. In addition, we discussed the interaction between structures through a kinematic model; it is desired to further incorporate dynamic models (e.g., Brodsky and van der Elst 2014; Jiao et al. 2022; Lin 2021; Ulrich et al. 2016) to constrain the behaviors of multiple-structure ruptures.

In 1906, an earthquake with magnitude 7.1 occurred due to the rupture of the Meishan fault (ID 20). Considering its fault geometry, the characteristic magnitude of this fault is only 6.6 (Table 1); therefore, this event with a larger magnitude could be associated with a multiple-structure rupture. In addition, the focal mechanism of this earthquake suggests that this event cannot be attributed solely to the rupture on the Meishan fault. The first motions of P- and S-waves recorded by the seismograph suggest oblique thrust faulting oriented in the northeast-southwest direction, with a small right-lateral component (Liao et al. 2018). Besides, large ground shaking with liquefaction took place to the west of the Meishan fault during the coseismic period (Omori 1906). According to the evidence mentioned above, the Chiayi frontal structure might rupture simultaneously. Considering parameters of the Meishan fault and the Chiayi frontal thrust (structure geometry, characteristic slip), when the Meishan fault is dislocated, the Coulomb stress on 64% of the Chiayi frontal structure plane may rise by more than 0.1 bar, and when the Chiayi frontal structure is dislocated, 72% of the Meishan fault could be closer to failure (Additional file 1: Table S1). In addition, the distance between the two faults is 1.87 km (Additional file 2: Table S2). Therefore, we concluded that these two structures could have mutually ruptured in a coseismic period and resulted in an event with magnitude 7.1 in 1906.

4.2 Uncertainty of multiple-structure rupture pair identification

In this study, we identified potential rupture pairs by considering Coulomb stress change along the shear and normal components and the effective friction coefficient (Eq. 1). We simplified this model without implementing a poroelastic assumption (Beeler et al. 2000), since previous studies (e.g., Chan and Stain 2009) concluded that the differences in their results were trivial for assuming reasonable values of Skempton’s coefficients (between 0.5 and 0.9) and dry friction (0.75). The effective friction coefficient (µ′) could alter the impact of normal stress change on the Coulomb stress change (∆CFS). Since effective friction coefficients vary for different tectonic regimes, to quantify the deviation on determining multiple-rupture pairs, we further considered µ′ = 0.2 and 0.5. Considering the stress threshold of ∆CFS ≥ 0.1 bar and distance threshold of 5 km, the potential paired structures were identified (Table 6). The results suggest slight differences in the reasonable effective friction coefficient in between 0.2 and 0.5.

Table 6 Multiple-structure rupture pairs considering different effective friction coefficients (µ′)
Full size table

In this study, we identified potential rupture pairs by considering thresholds of stress change and structure distance. We implemented four threshold sets of Coulomb stress change (+ 0.01, + 0.05, + 0.1, and + 0.2 bars) and two for distance between structures (2.5 and 5.0 km) to identify plausible pairs for multiple-structure rupture (Table 3). Also, the uncertainty of the structure rake angle could result in deviation. Our standard procedure assumed a fixed rake angle of each structure according to its rupture type (Table 1), while in reality its rupture orientation could alter slightly in small patches of the structure plane.

We expected a long distance between two structures could make it difficult for the two structures to rupture simultaneously. Thus, we followed the criterion by the UCERF3 (Field et al. 2014) and SHERIFS (Chartier et al. 2017) and assumed a distance threshold of 5 km. We are aware that an earthquake with a large coseismic slip dislocation could result in significant stress change in far field and then search the pairs with longer distances and significant stress increase. Two additional distance thresholds of 10 and 20 km were considered (Table 7), and 6 and 9 additional pairs that might rupture in a coseismic period were identified, respectively. Generally, potential magnitudes of these structures are relatively large, which could result in larger stress perturbation. For example, the Chiayi frontal structure could cause an event with magnitude 7.21, resulting in a Coulomb stress increase of more than 0.1 bar in 91% of the sub-faults of the Chungchou structures, when 80% of the sub-fault in the Chiayi frontal structure would be triggered when the Chungchou structures dislocates with an M6.89 event (Additional file 1: Table S1).

Table 7 Multiple-structure rupture pairs considering different thresholds in structure distance
Full size table

To evaluate the impact of rake angle orientation, we evaluated the Coulomb stress change on the receiving structure with different rotated rake angles (i.e., ± 10° and ± 20°). The results showed that the larger the rotated rake angles implemented for the receiver structures, the fewer structure pairs were identified (Table 8). Note that 11 pairs were identified even when the rakes rotated for ± 20°, suggesting their robustness for coseismic multiple-structure rupture.

Table 8 Potential paired structures considering various rake angle rotations. In these cases, the stress threshold of ∆CFS ≥ 0.1 bar and distance threshold of 5 km were considered to identify potential rupture pairs. The total number of paired structures without rake rotation is 17 (Table 2)
Full size table

4.3 Uncertainty of recurrence interval

Besides the uncertainty of structure pair identification, uncertainties in the rupture parameters of the multiple structures could be evaluated. Considering the range of the structures’ rupture areas (Table 1), magnitude intervals of multiple-structure ruptures could be estimated (Fig. 4 and Table 2). That is that the largest magnitude for multiple-structure rupture (Fig. 3) can be obtained when we consider the maximum rupture areas of the two structures (based on Eqs. 6–8). By further implementing structure slip rates, recurrence intervals can be quantified: the minimum rupture area and maximum slip rate obtains the shortest recurrence interval (based on Eqs. 4–17).

Rupture recurrence intervals could also be influenced by the implemented scaling relations. We proposed two relations, that is, in addition to the well-known relations by Wells and Coppersmith (1994), we also used the relations proposed by Yen and Ma (2011) that were obtained from the observations mainly from Taiwan. Since the local relationships (Yen and Ma 2011) infer a smaller displacement, shorter recurrence intervals were obtained (Table 5). Besides, although the scaling relations proposed by Wells and Coppersmith (1994) have been questioned by many modern models, especially for large megathrusts (e.g., Stirling et al. 2013), Wang et al. (2016b) concluded a similar maximal magnitude of each seismogenic structure estimated from the relations of Wells and Coppersmith (1994) and Yen and Ma (2011).

For recurrence interval, the magnitude-frequency distribution on a single-structure plays an important role. Evaluating the rupture recurrence interval on a single structure could be based on various models, for example, the Gutenberg-Richter law (Gutenberg and Richter 1944), the characteristic earthquake model (Youngs and Coppersmith 1985; Hecker et al. 2013; Stirling and Zungia 2017) in addition to others (e.g., Geist and Parsons 2019; Page et al. 2021). In this study, we evaluated the rupture recurrence interval as the ratio of slip of a characteristic earthquake (with maximum magnitude of the structure) and slip rate, shown as Eq. 2, based on the assumption proposed by the TEM seismogenic structure database (Shyu et al. 2020) and the TEM PSHA2020 (Chan et al. 2020). This factor could be replaced by other magnitude-frequency distributions since the recurrence interval of the multiple-structure rupture in our procedure is based on slip rate partitioned from individual structure ruptures (shown as Eqs. 10, 11, 14, 18, and 20).

Based on our analyses mentioned above, deviations of multiple-structure rupture pairs were indicated, and epistemic uncertainties of corresponding parameters were quantified, providing a better understanding of multiple-structure rupture behaviors, beneficial to subsequent research, such as PSHA, mentioned below.

4.4 Application of multiple-structure rupture to probabilistic seismic hazard analysis

Conducting a PSHA requires understanding potential magnitude (Fig. 3) and the recurrence interval (Fig. 4) of each seismogenic source, and implementing a hazard model with multiple-structure rupture could improve the assessment. Take the TEM PSHA2020 (Chan et al. 2020) as an example—considering the cases of multiple-structure ruptures, the hazard levels in the regions close to the Chaochou fault (ID 29) and the Tainan frontal structure (ID 41) increased significantly for a long return period (recurrence interval of 2475 years, see Fig. 3 of Chan et al. 2020). Chan et al.’s study (2020) indicated that the seismic hazard level would be misestimated if the probability of multiple-structure rupture is not implemented.

Seismic hazard analysis plays an essential role in constructing infrastructures, such as nuclear power plants, that require assuming a long return period. Thus, a seismogenic source with a long recurrence interval could be crucial for the analysis, raising the importance of multiple-fault rupture with a larger magnitude (larger than the characteristic earthquake of each structure). Our approach obtained longer recurrence intervals for multiple-structure ruptures in comparison with the original recurrence interval of each structure (Table 4). For example, the recurrence interval of the Chiayi frontal structure (ID 21) has been extended from 510 to 1724 years. Based on these results, the seismic hazard level for a short return period (e.g., 475 years, corresponding to a 10% probability exceedance in 50 years) would be lower, while a higher hazard is expected for a long return period (e.g., 2475 years, corresponding to a 2% probability exceedance in 50 years).

The possibility of multiple-structure rupture used to be determined based on geological and geomorphological evidence with subjective judgments (e.g., Shyu et al. 2020). Our study implemented a Coulomb stress change combined with statistical approaches to indicate multiple-structure rupture pairs, which is transparent and reproducible.

In addition, our approach indicated various rupture pairs and quantified uncertainties. These outcomes could be incorporated into a PSHA through a logic tree. For example, larger weightings (possibilities) could be assumed for the pairs that fulfill more thresholds in the distance, Coulomb stress change (Table 3) and rotated rake angles (Table 8). That includes, for instance, the Shuanglianpo fault (ID 2) and the Hukou fault (ID 4); the Hukou fault (ID 4) and the Fengshan River strike-slip structure (ID 5); the Hsinchu fault (ID 6) and the Hsinchu frontal structure (ID 8); the Miaoli frontal structure (ID 10) and Tuntzuchiao fault (ID 15); the Muchiliao-Liuchia fault (ID 22) and the Chungchou structure (ID 23); and the Chishan fault (ID 26) and the Fengshan structure (ID 45).

4.5 Multiple structure rupture (with more than three structures)

The 2016 Mw7.8 Kaikōura, New Zealand, earthquake is an event resulting from ruptures on multiple structures. Hamling et al. (2017) indicated that this earthquake included ruptures along four major faults and up to twelve minor faults. From this case, we are aware that multiple-structure rupture is not limited to the combination of two seismogenic structures.

Based on the multiple-structure rupture database proposed in this study (Table 2), several structures are associated with several possible rupture pairs. For instance, the Shuanglianpo fault (ID 2) may cause coseismic rupture with the Yangmei structure (ID 3) and the Hukou fault (ID 4), and the Hukou fault (ID 4) may link with the Fengshan River strike-slip structure (ID 5) and the Hsinchu fault (ID 6). Since our approach is based on a static Coulomb stress change, it is difficult to evaluate the temporal evolution of rupture probability. The possibility of a multiple-structure rupture in a coseismic period might be overestimated, that is, a structure could not only be triggered spontaneously in a coseismic period, but also be enhanced in a postseismic or interseismic period.

One potential solution is to implement a dynamic model (e.g., a discrete element model; Cundall and Strack 1979) that simulates temporal distribution of displacement and stress fields and could be helpful in identifying plausible structures that perhaps rupture within a coseismic period.