1 Introduction

The Tatun Volcano Group (TVG) formed as a result of episodic volcanism in northern Taiwan and originated from the active plate convergence between the Philippine Sea plate and the Eurasian plate (Fig. 1). The most recent phreatic eruption of the TVG is inferred by the 14C dating of the younger volcanic rocks, with dates ranging from 23 Kyr to as young as 6 Kyr (Belousov et al. 2010; Chen et al. 2010). Since the TVG is located in a metropolitan area adjacent to two nuclear power plants in northern Taiwan, its eruption will threaten the lives of citizens and create significant economic and social crises in the region (e.g., Konstantinou 2015). Recent seismic and geodetic observations have shown that the TVG is a potentially active volcano (e.g., Lin et al. 2005, 2020; Lin 2016; Konstantinou et al. 2007; Murase et al. 2014; Pu et al. 2014). The local seismic network over the TVG detected repeated occurrences of seismic swarms associated with fluid migrations and has located its magma chambers. The hydrothermal reservoirs are possibly located in the eastern limb of the TVG, as identified by multiple studies, such as the analysis of volcano-earthquake seismic waveforms (Lin et al. 2005), precise leveling surveys (Murase et al. 2014), and audio-magnetotellurics (Komori et al. 2014). Furthermore, using absolute gravity measurements collected from 2004 to 2007 around the TVG, Mouyen et al. (2016) suggested the existence of a tube-like structure that allows for large-scale hydrothermal fluid circulation below the TVG. The vigorous fumarolic eruptions in the TVG area contain large variations in gas composition, which also indicates a highly active hydrothermal system in the region (Lee et al. 2008).

Fig. 1
figure 1

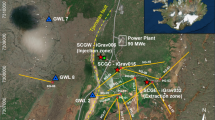
(left panel) Locations of gravity monitoring sites, groundwater wells, and rainfall stations in the TVG used in this study. Note that YMSG is a hybrid site for SG, AG, and RG gravity observations, located in Chintiengang. The water levels are for April 2012. The bold line from A to B indicates the location of the profile shown in Fig. 11. The right panel shows the summit (Chishinshan) and two fumaroles of the TVG and the geodynamic plate model and the location of the TVG in Taiwan (red square) (right lower panel)

Full size image

Gravity observations have been used to assess the states of volcanoes around the world. For example, Rymer and Brown (1989) used time-lapse gravity changes as a ground-based precursor to show that ascending magma could lead to the redistribution of underground mass before an eruption. Using gravimetric and geodetic measurements, Battaglia et al. (2006) showed that fluid migration in the Campi Flegrei caldera hydrothermal system was the cause of ground deformation and geological unrest. Kazama et al. (2015) showed that gravity changes could originate from magma and non-magma sources. The works of Hinderer et al. (2016), Carbone et al. (2017), and Van Camp et al. (2017) have also presented the idea that gravity changes can be caused by various types of volcanism in detail.

Recently, there has been no significant magmatic unrest related to the TVG. Gravity variations over the TVG are attributed to hydraulic perturbations corresponding to local groundwater settings. However, validating groundwater flow systems over volcanic regions is challenging. Hydraulic conductivity in a volcanic regime varies widely: lava flows and cinder beds exhibit high hydraulic conductivity, while ash beds, intrusive dykes, and sills correspond to relatively low hydraulic conductivity (Fetter 2001). The basement of the TVG is composed of Tertiary (Miocene and Pliocene) sedimentary rocks that consist mainly of thick beds of well consolidated sandstone intercalated with siltstone and shale. The Tatun volcanic rocks unconformably overlie the basement lithology and consist of lava flows, pyroclastic breccias, tuffs, and reworked volcaniclastic rocks (Fig. 1). The most common rock type in the TVG area is andesite lava. These andesite lavas are generally characterized as poor reservoir rocks (Chen 1970).

A gravity-based study of the TVG area began with installing an absolute gravimeter (AG) collocated with a continuously recording GPS station (station code: YMSG) at the central lava platform in 2004 (Kao et al. 2017). In 2012, a systematic gravity investigation employing one AG and two relative gravimeters (RGs) was initiated along five hiking trails over the TVG covering an area of approximately 100 km2 (Fig. 1). In addition, a superconducting gravimeter (SG, GWR T049) was installed at the YMSG station in April 2012 (the SG time series is presented in the Additional file 1: Fig. S1). Together with the seismic and geochemical monitoring in the TVG (Lee et al. 2008, https://tvo.earth.sinica.edu.tw/), gravimetric observations have been used to assess the risk of TVG eruption.

In this study, we used high quality gravity data acquired from gravity survey campaigns in 2012 to discuss the hydrological gravity effects in the TVG area. Two hydrological models with three dimensional hydraulic parameterization have been implemented to assess spatiotemporal groundwater storage variations in the TVG. The gravity effects converted from the hydrological models are then compared with the observed gravity to infer the hydrogeology over the TVG. Using gravity observations at sites sensitive and insensitive to gravity changes, we advance the understanding of the TVG aquifers that vary over time and space.

2 Gravity and hydrological data

2.1 Stability and resolution of gravimetric measurement

The wet season in northern Taiwan is caused by the northeast monsoon that prevails from late autumn to early spring, while summer rainfall is related to seasonal typhoons. In this study, time-lapse gravity measurements were collected by one FG5 AG (serial number 231) and two CG5 RGs (serial numbers 050800136 and 050800137) in April, June, September, and November 2012 to monitor the TVG hydrological changes in the wet and dry seasons (Table 1). The gravity variations are compiled from the RG measurements taken along five hiking trails. In practice, the RG measurements acquired along the trails were collected via a double-run (back and forth) survey to eliminate drifts in the RGs and enhance the point gravity accuracies. The objectives of the AG employment were twofold: (1) to measure gravity changes associated with groundwater level changes and (2) to constrain the RG measurements with the relative gravity adjustments (see below). To satisfy these objectives, four RGs were therefore stationed near the AG (Station: YAG1, 2, 3 and YMSG) (Fig. 1).

Table 1 Standard errors of the RG gravity measurements (in μGal) from all 15 readings and from the 8 selected readings
Full size table

The gravity monitoring sites are located between 25.13°N–25.19°N and 121.525°E–121.65°E, in an area of approximately 100 km2. In total, 31 gravity sites formed a measurement network over the peak of the TVG (YAG2-3, Y16-23; Chishinshan, at an elevation of approximately 1140 m), the central lava platform (Y05-15; Chintiengang), and two trails on the southeast (Y01-04) and southwest (YAG01, Y25-27) verges (Fig. 1). A few sites are located in the active fumarolic areas of Dayoukeng (Y07-08) and Xiayoukeng (YAG3, Y16). To achieve high precision and stable gravimetric readings, the sampling frequency of the RG was set to 6 Hz, and each gravity reading averaged the records over a period of 90 s (Debeglia and Dupont 2002; Scintrex Limited 2010; Mouyen et al. 2013). In total, 15 gravity and in situ temperature readings were acquired at each occupied site. Among the 15 gravity readings, 8 were selected according to the following criteria: (1) the first two readings were discarded, (2) continuous readings in which the gravity changes of the last three readings were less than 5 μGal, and the trend of the continuous readings was less than 5 μGal/reading were selected, (3) readings were selected when the temperature variations within the CG5 sensor chambers were within ± 7 mK, and when the temperature changes between two successive readings were less than 0.1 mK, and (4) readings were selected when the ranges of the tilt variations in the X and Y directions were within ± 20″. Criterion (3) is only applied to the readings when the chamber temperature stabilized to avoid causing slight variations in the readings (Fores et al. 2017). All these criteria were applied while considering the relevant statistics and stability of the experiment. More details about the RG observations and processing can be found in Lam (2013).

For each of the four gravity surveys, the RG and AG measurements were least-squares adjusted using the weighted constraint method of Hwang et al. (2002) by fixing the gravity values at the four AG gravity sites. The outliers in the RG measurements were detected prior to the adjustments. The histograms of the residuals of the RG measurements survey follow a normal distribution, suggesting that there were no systematic errors in the adjusted gravity values.

Two separate adjustments to the RG measurements were made to determine our RG data quality. One adjustment used RG measurements that were based on all 15 readings at one survey site and the other adjustment was based on the 8 selected readings. The adjustment results are presented in Table 1, which shows that the standard deviations (STDs) of the 8 selected gravity readings are less than those from all 15 readings. The accuracy improvements due to the use of the 8 selected readings for the four surveys are 11.1%, 53.8%, 10.0%, and 20.0%, respectively. The standard error of the point gravity is approximately 8 μGal on average (Table 1). The reductions in standard errors suggest that our data selection strategy, based on the four criteria, is effective.

Figure 2 shows the observed gravity changes after all the corrections at the gravity sites in April, July, September, and December 2012 were applied (see the details regarding the corrections in the following sections). At each site, gravity changes are represented as deviations from the mean of the four surveys. We shall discuss the observed gravity changes in the context of the hydrological models below.

Fig. 2
figure 2

The observed gravity changes in April, July, September, and November 2012. The stations Y20 (Chishinshan), YMSG (Chintiengang), Y08 (Dayoukeng), and Y03, at the different geological backgrounds, are denoted

Full size image

2.2 Correcting for tides and atmospheric effects within gravity observations

The temporal variability of the gravity effects related to tidal forces were removed from all gravity measurements using values from the ETGAB model (Wenzel 2002; Dehant et al. 1999). The Newtonian and the loading effects of ocean tides (called OTL correction) were removed using the FES2004 tide model (Letellier et al. 2004) and the SGOTL software (Hwang and Huang 2012), which takes the elevation of the gravity site into account. The OTL correction preformed using SGOTL improved the point gravity accuracies in the adjustments by 1.4% to 6.2% compared to the cases where OTL correction was not applied. The improved accuracies are most pronounced at the sites with elevations > 1000 m, suggesting that the altitude of a gravity site should be considered when computing the OTL effect. This conclusion is consistent with those from Hwang and Huang (2012).

We also removed the effects of barometric pressure and polar motions using an SG-based gravity-atmosphere admittance coefficient and the Earth’s rotation parameters retrieved from the International Earth Rotation Service and Reference Systems. Here, we assume that the air pressure variations at the SG are the same as those at all the survey sites. A minor contributor to the overall improved RG point gravity accuracy is the SG-based admittance coefficient for atmospheric pressure corrections. We experimented with two gravity-atmosphere admittance coefficients: one is the standard value of − 0.30 μGal/hPa (Torge 1989), and the other is − 0.35 μGal/hPa, which was derived from the analysis of the SG gravity and barometric records. Table 2 shows the averaged standard errors of the adjusted point gravity values. In the second survey, the difference between the use of the two coefficients (− 0.30 and − 0.35) is 1 μGal. Because the gravity pressure admittance coefficient can differ due to a considerable atmospheric pressure perturbation (Hwang et al. 2009), the air pressures changes around Taiwan driven by Typhoon Doksuri on June 28 and 29, 2012, influenced the second survey. In this case, using an admittance coefficient of − 0.35 μGal/hPa improves the point gravity accuracy in the second survey. Although the SG-based gravity pressure admittance coefficients improved the gravity accuracy only in the second survey, we believe such coefficients can improve atmospheric pressure corrections in future gravity data collected in the TVG.

Table 2 Standard errors of point gravity values (in μGal) based on two gravity-atmospheric admittance coefficients.
Full size table

2.3 Groundwater level, precipitation, and soil moisture

After removing the effects of tides and the atmosphere, the remaining sources for gravity changes are local seasonal hydrological changes and transitional fluid migrations (Mouyen et al. 2016). Except for the overwhelming flooding events, gravity changes of hydrological origins (called the hydrological gravity effect) are the sum of the effects over the unsaturated zone and the saturated zone below the site. A soil moisture sensor was installed at YMSG and measured soil moisture at depths of 10, 30, 50, 70, and 100 cm every 15 min. For a spatially limited area with a similar precipitation pattern over the rain gauge stations (the precipitation records in the TVG area in 2012 are provided in the Additional file 1), we assume that the gravity effect caused by the temporal evolution of soil moisture was the same for the entire TVG area. Based on the soil moisture measurements at YMSG, we employed the finite difference method to determine the soil moisture diffusion from the ground surface to a depth of 10 m. The gravity effects of the soil moisture were estimated by volumetric integration assuming that the soil moisture diffuses with depth (Lien et al. 2014). The magnitude of the gravity effects of the soil moisture content for the TVG area was less than \(\pm\) 5 μGal in 2012 (see the estimated values in Additional file 1: Fig. S1).

After excluding the gravity effects of soil moisture, the remaining hydrological effects should be attributed to the surface runoff and underground aquifer systems, which are the hydrological parameters considered in our modeling. The water table depths at the 23 wells in the TVG area were manually recorded every month throughout 2012. In addition, the precipitation records at 14 rain gauge stations installed by the Central Weather Bureau in the TVG area were also used in this study (Additional file 1: Fig. S2). Figure 3 demonstrates the gravity changes at sites Y01, Y02, and Y03 and the rainfall at two nearby weather stations, WZS and SD. We determined that the groundwater recharge at WZS and SD (red and blue lines) corresponded to rainfall (red and blue bars, Fig. 3) by using the infiltration coefficient method (Patil et al. 2019; Tarka et al. 2017). This method involves (1) multiplying daily rainfall with the infiltration coefficients to obtain daily groundwater recharge and (2) determining the 5 day moving average of groundwater recharge. Figure 3 shows that the trend of the observed gravity changes is approximately consistent with the derived groundwater recharge, except for a relatively low gravity measurement in September. Gravity changes and groundwater recharges here were based on the observations at each station in April. It is worth noting that although Typhoon Saola brought rainfall to the TVG area from late July to early August, groundwater discharges in the TVG were larger than the dry season rainfall recharge.

Fig. 3
figure 3

Gravity changes and rainfall. Red and blue bars show rainfalls recorded at stations WZS and SD and the resulting groundwater recharge. Red, cyan, and black squares show gravity changes at Y01, Y02, and Y03. The station locations are indicated in Fig. 1. Typhoon Saola traversed northern Taiwan from July 31 to August 3, bringing heavy rainfall to the TVG

Full size image

3 Methods for modeling groundwater levels and gravity conversion

We employed two hydrological models, hereafter named Models A and B, to model the redistribution of the underground water masses associated with the different hydrogeological settings. The differences between the actual and synthetic gravity changes can be used to discuss the hydrological anomaly over the gravity measurement sites. The water table data used to constrain the modeling are presented in Fig. 1. In mountainous areas, such as the TVG, the variations in groundwater levels and hydraulic head gradients may be relatively large compared to those of alluvial fans in western Taiwan. However, only a few borehole wells in the TVG provide the necessary hydrogeological parameters for the simulations. Therefore, we assumed a single layer aquifer for the two models, which consisted of the zone from the ground surface to sea level. The minimum curvature method (Wessel et al. 2013) was used to interpolate the groundwater and river levels onto a grid with a resolution of 40 m in the X (east)- and Y (north)-directions.

The hydrogeological parameters from the geological data bank of the Central Geological Survey of Taiwan (http://www.moeacgs.gov.tw/) were used in Model B (Additional file 1: Table S1). Table 3 summarizes the different aspects and parameterizations for Models A and B. The details of the two models are given below.

Table 3 A summary and comparison of Models A and B
Full size table

3.1 Model A: a continuous flow model

In Model A, the recharge and discharge are constrained by the groundwater levels at the 23 monitoring wells and the rivers (Fig. 1). At the junction of the land and the river, the groundwater levels are equal to, and in a steady-state with, the river levels. In this modeling experiment, we assumed that the strata of the TVG were highly porous and susceptible to pore-water migration and that the groundwater was transported within a homogeneous stratum over time. The specific yield for each vertical column was constant in Model A (Table 3). The Newtonian attractions exerted by the change in mass associated with the groundwater level variations were computed for the whole study area. Figure 4a demonstrates the Model A groundwater levels for the survey period in April 2012.

Fig. 4
figure 4

The modeled groundwater levels in April 2012 from Models A (a) and B (b). The locations of the groundwater wells are indicated by open stars

Full size image

The hydrological gravity effect was converted from the variation in groundwater levels by the volumetric integration method described in Lien et al. (2014). The integration domain of this model was calculated for the water column between the local groundwater levels to the lowest water level of the model within the study area.

3.2 Model B: a dynamic hydrological model

Model B uses the modular three dimensional groundwater flow model (MODFLOW) to simulate groundwater flows. MODFLOW is a widely used software developed by the United States Geological Survey (USGS; Harbaugh et al. 2000; Harbaugh 2005). MODFLOW solves for hydraulic heads using the following governing equation:

$$\frac{\partial }{\partial x}\left({K}_{xx}\frac{\partial h}{\partial x}\right)+\frac{\partial }{\partial y}\left({K}_{yy}\frac{\partial h}{\partial y}\right)+\frac{\partial }{\partial z}\left({K}_{zz}\frac{\partial h}{\partial z}\right)+W={S}_{y}\frac{\partial h}{\partial t},$$
(1)

where \(h\) is the hydraulic head (groundwater level for an unconfined aquifer such as the one in this study) at location \((x,y,z)\) and time \(t\). \({K}_{xx}, {K}_{yy},{K}_{zz}\) are the hydraulic conductivities in the east, north, and vertical directions, indicating the ease of groundwater movement. \(W\) is the volumetric flux per unit volume from the recharge of water discharge. \({S}_{y}\) is the specific yield of the porous materials, which is proportional to the water storage capacity of a rock formation. MODFLOW determines multiple groundwater levels by the numerical, block-centered finite-difference method, enabling us to model groundwater levels in mountains with a complex hydrogeological setting, such as the TVG. A sample application of MODFLOW used for groundwater level modeling near the Tseng-Wen Reservoir in southern Taiwan is given by Yang et al. (2009), who achieved a high degree of correlation between the modeled and observed groundwater levels in the mountainous region around this reservoir.

Compared to the laterally homogeneous flow in Model A, the flow in Model B is heterogeneous and is determined by Eq. (1) using the hydraulic observations as the boundary conditions. In Model B, we used river level data together with the groundwater table as constraints to determine the optimized solution by least-square fitting between modeled and observed water levels. The river elevations are assumed to be the same as the river water levels, which are fixed values that do not change with time. In addition, the local rainfall and lithology of the TVG were used in Model B. The rainfalls were the water recharges in Model B, which were acquired from 14 local rain-gauge stations (Additional file 1: Figs. S2, S3). The top layer of the TVG lithology is mainly composed of volcanic and reworked volcaniclastic rocks, such as andesites, tuffs, and pyroclastic breccias. The outcrops of the sedimentary formations are in the southeast and southwest portions of the TVG and consist of moderate to coarse gravels, sandstones, and sandstones interbedded with thin carbonaceous shales. The hydrogeological parameters were adopted from the data bank of the Central Geological Survey of Taiwan and include six lithologic zones (Additional file 1: Fig. S3; Table S1). The lowest bound of the aquifer in Model B was the sea level. Below the sea level, we assume the presence of a zone of extremely low permeability. In addition, the Shanchiao and Kanchiao Faults, located in the western and eastern TVG, respectively, were barriers to the aquifer. The optimal hydrogeological parameters corresponding to the six major lithologies are given in the Additional file 1 (Table S1; Fig. S3).

We adjusted the hydrogeological parameters by comparing the modeled and observed groundwater levels at the wells. The tuning process began with the initial hydraulic conductivities (Kxx, Kyy, Kzz) and was iterated until the differences between simulations and observations were less than 0.5 m for all wells (the optimally simulated water tables with the observations are presented in Additional file 1: Fig. S4). The corresponding gravity uncertainties are within ± 4.5 μGal, which is considerably smaller than the precision of gravity reading (Table 1). Figure 4b shows a map view of the April water level simulated by Model B. Further discussion on the differences between the two hydrological models is presented in the following sections. The integration domain of Model B used for determining hydrological gravity changes was the aquifer bounded by the ground surface and the sea level.

4 Results of simulated groundwater level changes and gravity changes

As expected, the resulting groundwater levels of Model A reflect the spatial distribution of the monitoring wells and the variations in river levels. On the other hand, the influence of fault barriers and hydrogeological conditions predominate in Model B. However, the groundwater levels between the two faults are similar for both models, except that the groundwater levels of Model B are generally higher than those of Model A. In Fig. 4 (which shows the modeled groundwater levels during April 2012), the groundwater levels of Model B are approximately 100 m higher than those of Model A for the area southwest of Y20. This is due to the dynamic flow with local hydraulic conductivity and the rainfall recharge used in Model B. According to the Central Weather Bureau precipitation data for 2012, the summer monsoon resulted in heavy rainfall from April to June (Additional file 1: Fig. S2); furthermore, Typhoon Saola brought transient flooding to the TVG region in early August. In contrast, the region was relatively dry from September through November. The groundwater levels are relatively high on the windward side of the TVG. The wind direction over the TVG is from the southwester from August to September and from the northeaster in December. Cheng and Yu (2014) showed that the topography of the TVG affects precipitation patterns on the TVG’s windward and leeward sides. The hydrological condition of the TVG is therefore a combination of meteorological and geological effects.

Figures 5 and 6 show the changes in the groundwater level of each model. Here, the changes are relative to the mean level of each model. The groundwater level change of Model B is larger than that of Model A, at approximately ± 2 m (see Model-B derived groundwater tables in Additional file 1: Fig. S4). Using this variation to scale the color range of Figs. 5 and 6, Model A exhibits a spatially smooth pattern, except for some local high and low values that vary over time. Figure 6 shows that the groundwater levels derived by Model B are evidently influenced by two fault barriers. The pattern of the groundwater levels between the two faults exhibits zonal variation over time in Model B.

Fig. 5
figure 5

Groundwater level variations of Model A. The variations are relative to the mean levels of modeled values over April–December 2012. The locations of the groundwater wells are indicated by open stars in the August map

Full size image
Fig. 6
figure 6

Same as Fig. 5 but from Model B

Full size image

To compare with the observed gravity values, we converted the water level variations to gravity changes as mentioned above. Note that the gravity contribution of the unsaturated zone is minor and has been removed from the gravity observations using the method described in Sect. 2.3. Figures 7 and 8 show the gravity changes at the survey sites converted from the two hydrological models during the four gravimetric surveys. The gravity variations derived from Models A and B both present the seasonal pattern corresponding to the modeled groundwater variations. Figure 7 shows that, along the southeast trail, the gravity changes derived from Model A were small throughout the four seasons in 2012. For instance, the Model A simulated gravity changes at Y08 and Y03 are within \(\pm\) 5 μGal. This is inconsistent with the observed gravity changes, which vary by approximately \(\pm\) 20 μGal (Fig. 2). In fact, there were few groundwater wells in the eastern TVG (Figs. 1, 4); the water level condition was hence not well constrained for the southeast trail in the modeling. Figure 8 shows the gravity changes derived from Model B, which exhibit distinctly seasonal patterns of gravity changes over all the study sites. The variation in the simulated gravity changes is approximately on the same order of magnitude as the observations (Figs. 2, 8). Furthermore, it is interesting to see a considerable variation in gravity for the sites along the southeast trail in Fig. 8. It is obvious that dynamic hydraulic modeling can provide more detailed information by considering the local lithology and geological conditions. We hence conclude that Model B performs better in modeling the hydrological changes in the TVG area.

Fig. 7
figure 7

Simulated gravity changes from the groundwater levels from Model A for the survey periods in April, July, September and November 2012

Full size image
Fig. 8
figure 8

Same as Fig. 7 but from Model B

Full size image

5 Discussion

5.1 Consistencies and inconsistences between the modelled and observed gravity changes

Figure 9 illustrates the difference between the observed and simulated gravity changes but the southeast trail is excluded from the discussion. The predominant feature is that both models deviate from the observations significantly at Chishinshan (for instance, Station Y20). The gravity difference between the simulations and observations of Chishinshan can vary seasonally up to values between + 40 and − 60 μGal. Furthermore, four gravity sites at Dayoukeng (Y06, Y07, Y08, and Y09) detected a positive gravity change (~ + 30 μGal) in the dry season (September) but a negative gravity change (~ − 20 μGal) in the wet season (April). These do not appear in the two models that were directly affected by the modelled surface recharge and discharge during the dry and wet seasons. On the other hand, the gravity differences around Chintiengang (YMSG, Y13, and Y14), which is located between Chishinshan and Dayoukeng, were minor. In particular, the gravity changes derived from Model B were almost consistent with the observations for the sites around Chintiengang (gravity differences were less than \(\pm\) 10 μGal, as shown in Fig. 9).

Fig. 9
figure 9

Differences between the observed and simulated gravity changes. The left column is for Model A, and the right column is for Model B. Positive and negative differences are shown in red and blue circles, respectively. Yellow circles correspond to the sites where the gravity differences are small. Model B results in a better fit with the gravity observations than Model A over the TVG area

Full size image

Models A and B simulate groundwater levels in continuous media. They do not consider the effect of discontinuous structures inside the TVG region. Therefore, the hydrogeological properties of the strata beneath the Chintiengang area likely involve interconnected porous media or permeable formations, as parameterized in Models A and B. However, if the actual strata contain discrete cracks or volcanic conduits, the observed groundwater levels would tend to accumulate locally. A large difference between the observed and modeled gravity change implies that the materials below the site may contain volcanic conduits or local cracks. Figure 9 shows that at most of the gravity sites over Chishinshan, the differences (red circles) between the observed and simulated gravity changes are positive during the first (April), second (July), and fourth (November) gravity surveys. This implies that the hydrological properties of the two models cannot be fully responsible for the gravity changes over Chishinshan.

Based on the discrepancies between the modeled and observed gravity changes shown in Fig. 9, we conclude that additional sources influencing the temporal gravity observations should be considered. A similar observation has been described in Murase et al. (2014), Komori et al. (2014), Wen et al. (2016), and Mouyen et al. (2016). Furthermore, the considerable gravity discrepancies at Chishinshan may imply that local subsurface hydrothermal fluids should be abundant and significantly influence the hydrological gravity effect.

5.2 Antiphased gravity change for the east and west TVG

Both the observed and modeled gravity changes exhibit weather perturbations in the TVG area. However, the gravity changes did not vary synchronously at all sites. We applied empirical orthogonal function (EOF) analysis to study the leading variabilities in gravity changes over space and time. EOFs are a form of principal component analysis (e.g., Preisendorfer 1988; Emery and Thompson 2001), and the resulting spatial patterns can be thought of as basic functions in terms of variance. The associated temporal projections are the principal components (PCs) and temporal coefficients of the EOF patterns. We decomposed the time series over the gravity sites into various orthogonal components, which would represent the different spatiotemporal patterns (EOFs/PCs) within the gravity changes. The observed and simulated gravity time series are shown in Figure S5 in the supplementary information.

The first three EOF modes can fully explain the variabilities in the gravity changes. The corresponding singular values of the first three modes sum to 100% (i.e., the singular values of the higher modes are all zeros). Figure 10 shows the time variations (left column) of the first three modes decomposed from the observed and simulated gravity changes and the corresponding spatial patterns of the first mode variabilities (right column). In fact, the first mode explained up to 65% or more of the total variabilities in both the observed and modeled gravity changes. This means that a single mode of variability dominates the gravity changes in both the observed and modeled results. In addition to the discrepancy in the first mode of gravity decomposition, the second and third modes show consistent characteristics between the observed and modeled gravities (Additional file 1: Fig. S6). Variability in the observed gravity changes in the second mode explain approximately 20% of the total variability, followed by the variability in the third mode. Given the overall performance and the contributions to the overall data variability by the second and third modes, the modeled gravity changes from Model B agree better with the observed gravity changes than the modeled gravity changes from Model A.

Fig. 10
figure 10

Three principal modes of variances (or variabilities) from the EOF analyses of the observed gravity changes (top) and the simulated gravity changes from Model A (middle) and Model B (bottom). The right column shows the variabilities of the first modes. The variances are unitless because of normalization. A negative variability indicates a negative correlation

Full size image

Because the gravity changes determined from Models A and B reflect the local drainage system, the significant recharge brought by Typhoon Saola (early August) significantly influenced our two hydrological models and caused the decomposed PC curves for the two models to rise in September. The main difference between the two models is the method of drainage. Model A reflects the horizontal flow radially moving out of the TVG area, whereas the fault barriers in Model B may help groundwater accumulate in the local low-lying area (around YMSG), which caused a gravity high due to the accumulated water mass. However, the first mode of gravity changes derived from Model B does not show such a pattern. Instead, a significant water level low was identified in the YMSG area in Model B during September (the actual variation can be derived from the spatial pattern multiplied by the temporal variation in Fig. 10). In fact, this pattern is also shown in the observed gravity data. We infer that the effect of the fault barriers is minor in terms of the groundwater migration within the central TVG.

The gravity changes derived from Model B show locally spatiotemporal variations, similar to the observed gravity changes. The observed gravity changes at Chishinshan (Y20) and Dayoukeng (Y8) vary in the opposite sense, which was also shown by the gravity changes derived from Model B (Figs. 9, 10). However, this pattern of the observed gravity changes (first EOF mode) is nearly antiphased with the Model B gravity. In the preceding section, the inconsistency between the observed and simulated gravity changes led to the conclusion that one layer hydrological models that consider surface recharge and discharge cannot explain the hydrological structure of the TVG area, and the fluids at depth are presumed to be the source of the unexpected mass.

Considering the opposite variability for the east and west TGV, we propose a possible hydrogeological scheme for the TVG gravity observation shown along Profile A-B (see location in Fig. 1) in Fig. 11. The aquifuge in Fig. 11 is based on Komori et al. (2014), and it prevents deep hydrothermal fluids from reaching the Chintiengang area. We hypothesize that the fluids may be raised from the same hydrothermal source to the shallow strata, alternately replenishing aquifers to the east and west of the TVG, where there are the major fumaroles (Xiayoukeng and Dayoukeng, Fig. 1). Because the activity of hydrothermal fluids may be an indicator of magma stability, long-term continuous gravity observations can be a tool for monitoring the threats of volcanic eruptions in the TVG. The same idea for monitoring volcanic activity has also been raised in recent works, such as Jasim et al. (2018) and Hsieh and Ingebritsen (2019).

Fig. 11
figure 11

Possible hydrogeological structure along profile A-B (see the location in Fig. 1). The porous media form an aquifer below the central TVG. Fluids from the deep hydrothermal reservoir migrate to the east and west of the TVG, where the major fumaroles are located (Xiayoukeng and Dayoukeng, Fig. 1) bypassing Chintiengang

Full size image

6 Conclusion

This study uses the time-varying gravity measurements made in 2012 to delineate the TVG aquifer by modeling the hydrological gravity effect. The gravity changes from the RG measurements in the four surveys were carefully processed to achieve a minimum standard point gravity error of approximately 8 μGal (Table 2), which is precise enough to discern the seasonal hydrological signal that varies with the aquifer. Compared to Model A, Model B displays a distinctly seasonal pattern over all gravity sites, mimicking the observed changes. We find that Model B, constructed with hydrogeological parameters, performs better in describing the TVG hydrological system.

Our two hydrological models show interconnected porous media above a layer of low permeability (aquifuge) in the central lava platform (Chintiengang). However, the gravity changes for the west (Chishinshan) and east (Dayoukeng) TVG are different from the hydrological models that consider surface recharge and discharge. From previous studies and our results, we conclude that the discrepancy in gravity changes may originate from hydrothermal reservoirs at depth. The upward-migrating fluids may bypass the central TVG and alternately replenish aquifers to the east and west of the TVG, where there are the major fumaroles Xiayoukeng and Dayoukeng. Furthermore, the large discrepancy of gravity changes at Chishinshan may imply where the subsurface hydrothermal fluids should be abundant and significantly influence the hydrological gravity effect. This poses a potential risk to the TVG: the abundant fluids at depth could cause the Chishinshan volcano to be overpressured, and any external forces, such as earthquakes, could cause eruptions. Based on our study, long term gravity observations at the TVG could capture signs of deep hydrothermal activity and provide early warnings for eruptive hazards.