1 Introduction

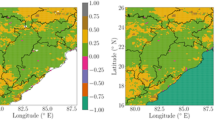
Nitrogen dioxide (NO2) and carbon monoxide (CO) are air pollutants which contribute to human mortality by exacerbating conditions like lung cancer, stroke, acute lower respiratory disease, chronic obstructive pulmonary disease, and ischemic heart disease (World Health Organization 2018). NO2 and CO are also indirect short-lived climate forcers which influence the radiation budget through the formation of nitrate aerosols (only NO2), methane and tropospheric ozone (Szopa et al. 2021). In East Africa and its surrounding regions, these gases mainly come from seasonal biomass burning in the savanna woodlands (Opio et al. 2021). Therefore, it is important to study the spatial and temporal distribution of these species over this region. Figure 1 shows the fire counts in different seasons. During December to February (DJF) the fire events are concentrated in northern Uganda and South Sudan while during July to August (JJA) and September to November (SON) the fire events are concentrated in Tanzania, eastern Democratic Republic of Congo (DRC), and the northern parts of Zambia, Malawi and Mozambique. The March to May (MAM) season generally has fewer fire events because it is an intense rainfall season, and rain creates dump conditions which do not favor the ignition of biomass (Nelson et al. 2012).

Fig. 1
figure 1

Spatial distribution of fire counts from MODIS observations during the December to January (DJF), March to May (MAM), June to August (JJA) and September to November (SON) seasons of the year 2012. Only observations with 95% confidence level were considered. This is also the WRF-chem model domain used for this study

Full size image

In comparison to the developed world, East Africa’s atmospheric chemistry is understudied. The main cause for this is the lack of sufficient data. The few available monitoring stations have a sparse coverage and the measurements made often lack continuity (DeSouza et al. 2017; Dewitt et al. 2019; Singh et al. 2020). The other cause is the weak institutional and regulatory framework for matters concerning atmospheric chemistry and air quality (DeSouza et al. 2017). These conditions make it difficult to study these chemical species over this region.

Now, however, the existence of remotely sensed satellite observations offers an alternative data source that can enable the study of the spatial and temporal distribution of these species. The available NO2 column retrievals can be obtained from instruments such as the Scanning Imaging Absorption Spectrometer for Atmospheric Chartography (SCIAMACHY) (Bovensmann et al. 1999), the Ozone Monitoring Instrument (OMI) (Levelt et al. 2006, 2018), the Global Ozone Monitoring Experiment-2 (GOME-2) (Callies et al. 2000) and the TROPOspheric Monitoring Instrument (TROPOMI) (Veefkind et al. 2012). Similarly, the available CO column retrievals can be obtained from instruments such as SCIAMACHY, TROPOMI and Measurement of Pollution in the Troposphere (MOPITT) (Deeter et al. 2003). For this study, OMI observations were used for NO2 while MOPITT observations were used for CO.

In addition to satellite observations, chemical transport models (CTMs) are used as complementary tools for studying atmospheric chemistry in data sparse regions (Barten et al. 2020; Kumar et al. 2012). However, such models need to be evaluated to understand their errors and biases before they are considered for future modeling applications. Over East Africa and its surrounding regions, CTM evaluations have been done for aerosols (Mazzeo et al., 2022), but no evaluation has so far been done for gaseous species. This study is the first evaluation of a CTM over the region for NO2 and CO from biomass burning. The CTM chosen for this study is the Weather Research and Forecasting model coupled with chemistry (WRF-chem) (Grell et al. 2005). Its base meteorological model, that is, WRF has been extensively evaluated over the region and has shown reliable performance (Kerandi et al. 2017; Nooni et al. 2022; Pohl et al. 2011). Therefore, the meteorological fields simulated by this model can be considered as adequate to be used for modeling the gaseous chemical species within WRF-chem.

In addition to evaluating WRF-chem, this study also used two bias correction methods to reduce the bias generated by this model. The first method used was linear scaling. This is a traditional method which is popularly used for correcting regional climate models (Fang et al. 2015; Jakob Themeßl et al. 2011; Lafon et al. 2013; Teng et al. 2015). The WRF-chem simulations corrected using this method are referred to as WRF-LS. The second method was the use of a deep convolutional autoencoder. This is a deep learning algorithm based on a convolutional neural network (Albawi et al. 2018). Autoencoders are specially adapted to learn the representation of singular data streams such that when given similar data but with noise in it, the algorithm can automatically separate the noise from the actual data of interest (Abirami and Chitra 2020). For a bias reduction problem, the bias is considered to be the noise in the data and the algorithm is trained to remove this noise. Using convolutional autoencoders is a more recent bias correction method that is preferred for use with gridded data (Han et al. 2021; Le et al. 2020; Tao et al. 2016). The WRF-chem simulations corrected using this method are referred to as WRF-DCA.

The other sections of this paper are ordered as follows; a description of the data and methods used, including the set-ups of WRF-chem and the convolutional autoencoder have been given in Sect. 2. The study results are presented in Sect. 3, the discussion of the results is done in Sect. 4 and the conclusions are made in Sect. 5.

2 Data and methods

2.1 Observations of chemical species

NO2 observations were obtained from the Ozone Monitoring Instrument (OMI), a spectrometer aboard NASA’s Aura satellite. It makes observations of trace gases such as ozone (O3), nitrogen dioxide (NO2) and sulfur dioxide (SO2) at a spatial resolution of 13 × 24 km2 at nadir (Levelt et al. 2006, 2018). Data for the tropospheric NO2 vertical column density (VCD) used here were downloaded from the Goddard Earth Sciences Data and Information Services Center (GES DISC). Only data with < 30% cloud fraction were used. CO observations were obtained from the Measurement of Pollution in the Troposphere (MOPITT), a gas correlation radiometer aboard NASA’s Terra satellite. It uses thermal infrared radiation to monitor tropospheric concentrations of carbon monoxide (CO) and methane (CH4) at a spatial resolution of 22 × 22 km2 at nadir (Deeter et al. 2003). The data for CO VCD that were used in this study were MOPITT version 8 observed with both near and thermal infrared radiances (Deeter et al. 2019).

2.2 WRF-Chem model inputs and set-up

Several inputs were required to run WRF-chem. The meteorological initial and boundary conditions were obtained from the National Centers for Environmental Prediction (NCEP) Final (FNL) Operational Global Analysis data (NCEP 2000) at a spatial resolution of 1o × 1° (~ 110 km) and a 6-hourly temporal resolution. The chemistry initial and boundary conditions were obtained from the Community Atmosphere Model with chemistry (CAM-chem) at a spatial resolution of 0.9° × 1.25° (Buchholz et al. 2019). Biogenic emissions were calculated online using the Model of Emissions of Gases and Aerosols from Nature (MEGAN) (Guenther et al. 2012). Anthropogenic emissions were obtained from version 2.2 of the Emissions Database for Global Atmospheric Research compiled by the taskforce on Hemispherical Transport of Air Pollution (EDGAR_HTAP_v2.2). The data were at a spatial resolution of 0.1o × 0.1° (Janssens-Maenhout et al. 2015). Data for the year 2010 was used, and offsets were applied for the years after 2010. Finally, fire emissions of the savanna wildfires were obtained from version 1.5 of the Fire Inventory from National Centre of Atmospheric Research (FINN_v1.5). The data were at a spatial resolution of 1 × 1 km2 (Wiedinmyer et al. 2011). The rest of the WRF-chem model setup is summarized in Table 1, including the domain and parameterization settings used.

Table 1 WRF-chem model setup
Full size table

2.3 Treatment of data before comparison

For a satisfactory comparison of WRF-chem output to satellite observed vertical column densities (VCDs), the satellite retrieval sensitivity needs to be accounted for in order to minimize the model—observation mismatch. This required some additional data processing as described here. For NO2, both the WRF-chem and OMI data were processed following the procedure described by Souri et al. (2016). In the first step, the model NO2 VCD in each layer \(i\) of the atmosphere was calculated using Eq. 1, for layers from the surface to the tropopause. In Eq. 1, \(MR\) is the mixing ratio of the gas in ppmv, \(ZF\) and \(ZH\) are the full and half heights of the model layer in meters, \(P\) is pressure at the model layer in pascals and \(T\) is the temperature at that model layer in Kelvins. In the second step, the air mass factor (AMF) of the model was calculated using Eq. 2. This step required the scattering weights (SW) at each layer, and these are provided as a variable in the OMI NO2 data files. In the third step, the OMI NO2 observations were modified following Eq. 3. The air mass factor of the observations \({(AMF}_{obs})\) is also provided as variable in the OMI NO2 data files. These modified observations \({(VCD}_{obs}^{*})\) were then compared with the WRF-chem output.

$${VCD}_{i} = \, {MR}_{i} \times \, \frac{2 \times ({ZF}_{i} - \, {ZH}_{i}) \times \, {P}_{i}}{{T}_{i}} \times 7.243 \times {10}^{12}$$
(1)
$${AMF}_{model} = \sum_{i=surface}^{tropopause}\left({VCD}_{i} \times {SW}_{i}\right) / \sum_{i=surface}^{tropopause}{VCD}_{i}$$
(2)
$${VCD}_{obs}^{*} = \left({VCD}_{obs}\times {AMF}_{obs}\right) / {AMF}_{model}$$
(3)

For CO, the WRF-chem model output was modified using the procedure described by Sicard et al. (2021) and Kumar et al. (2012). After the VCDs at each model layer were calculated following Eq. 1 and summed up \({(WRFChem}_{co})\), the linear transformation in Eq. 4 was then applied to obtain the modified WRF-chem output \(({WRFChem}_{CO}^{*})\). The apriori profile and averaging kernels (AK) are provided in the MOPITT data files.

$${WRFChem}_{CO}^{*}= Apriori+ {AK}_{MOPITT} \left({WRFChem}_{co}-Apriori\right)$$
(4)

Finally, bilinear interpolation was used to co-locate pixels between WRF-chem and the observations. This method is essentially linear interpolation that is performed in two dimensions, one after the other. This makes it suitable for interpolating image data (Kirkland 2010). Since the grid dimensions for both NO2 and CO were coarser than the model, they were regridded to the WRF-chem domain. The interest was to retain the higher resolution option as this provides more data points for the autoencoder to work with.

2.4 Set-up of the deep convolutional autoencoder

The network architectures used in this study have the same basic framework. The algorithms had two parts, the encoder and the decoder (Fig. 2). The encoding part had paired layers made up of a 3 × 3 convolution with a rectified linear unit (ReLU) (Nair and Hinton 2010), followed by a 2 × 2 max pooling operation while the decoding part had layers that transpose (reverse) the convolution operations made by the encoder. These layers also used the ReLU activation and a stride of 2. The only exception is the last layer that used the sigmoid activation function instead of ReLU. All layers were padded.

Fig. 2
figure 2

Structure of the deep convolutional autoencoder used for this study. The asterisk (*) sign marks the deconvolution layers

Full size image

Figure 2 and Table 2 show the structure of the algorithms used for both NO2 and CO. The first convolutional layer (Conv1) had 32 filters and these increased by 2 up to the fourth convolutional layer (Conv4) that used 256 filters. This was purposely done to enable the algorithms to compress the image to the smallest possible size and extract even the smallest detail. The intermediate representation of encoded data was the best compression achieved. Thereafter, the deconvolution layers (marked with *) reversed the data compression until the image was restored to its original dimension. The NO2 and CO data from both WRF-chem and the observations were images of size 96 × 80 pixels. Two algorithms were used, one for each variable and the images were fed into the algorithms as monthly averages. A total of 72 images were used and they were split into 3 categories. For each variable, 48 images were used for training, 12 images for validation and 12 images for testing. This choice was informed by the study period explained in Sect. 3.1 of this paper.

Table 2 Architecture of the deep convolutional autoencoder
Full size table

Neural networks have an interplay between the number of epochs (training iterations) used, the batch size, the spatial resolution of the output, computational time, and the overall model accuracy. In the experimentation done for this study, the best compromise after several rounds of experiments was to use a batch size of 1 and 250 training epochs. This was used for training both variables. The models were compiled using the Adam optimizer (Kingma and Ba 2014) with a learning rate of 0.001 and the mean squared error as the loss function. The code was built in Python 3.9 using TensorFlow 2 and the Keras deep learning library (Chollet 2015). The code has been deposited on GitHub.Footnote 1

2.5 Linear scaling (LS)

The LS method was chosen because it is fairly easy to apply due to its low data requirements and it can be adapted to handle spatial data. In some literature this method is referred to as the linear correction method (Lafon et al. 2013) and sometimes as the anomaly numerical correction with observations (Han et al. 2021; Peng et al. 2013). The LS method uses a correction factor which is derived from long term records of model and observation data. In this study, the long-term model and observation means, \(\overline{{M }_{i,j}}\) and \(\overline{{O }_{i,j}}\) for each grid cell \(\left(i,j\right)\) were first calculated as shown in Eqs. 5 and 6, using the same historical data that was used to train the autoencoder algorithm. These were 48 images, therefore, \(n\) = 48. These means were then applied to the raw model output, \({M}_{i,j}\) for the test period, to generate the bias corrected output \({M}_{i,j}^{*}\). All variables were corrected using an addition factor as shown in Eq. 7.

$$\overline{{M }_{i,j}}=\frac{1}{n}\sum {M}_{i,j}$$
(5)
$$\overline{{O }_{i,j}}=\frac{1}{n}\sum {O}_{i,j}$$
(6)
$${M}_{i,j}^{*}={M}_{i,j}+\left(\overline{{O }_{i,j}}-\overline{{M }_{i,j}}\right)$$
(7)

2.6 Evaluation metrics

Three test metrics were used to evaluate the performance of WRF-chem, WRF-LS and WRF-DCA. These metrics are the root mean squared error (RMSE), the normalized mean bias (NMB) and Pearson’s correlation coefficient (R). They are adequately described by Ivatt and Evans (2020). Scatter plots were additionally used to compare the degree of agreement that WRF-Chem, WRF-LS and WRF-DCA had with observations.

3 Results

3.1 Analysis of NO2 and CO atmospheric abundances and selection of the simulation period

Figure 3 shows the deseasonalized VCDs of NO2 and CO from 2005 to 2020. Majority of this period had NO2 below 6.5 × 1014 molecules/cm2. There were three peaks during which NO2 was above this amount. These were; March to December 2010, January to December 2012 and March to December 2015. The 2012 peak had the highest NO2 amount. The minimum and maximum NO2 amounts during that year were 6.73 × 1014 molecules/cm2 and 6.82 × 1014 molecules/cm2 respectively. Similarly, for CO, majority of the analyzed period had CO below 1.85 × 1018 molecules/cm2. The outstanding period was June 2015 to May 2016 which had the highest amounts of CO. Majority of this period had CO of more than 1.9 × 1018 molecules/cm2.

Fig. 3
figure 3

De-seasonalized timeseries of NO2 and CO observed over East Africa and its surrounding regions for the period 2005 to 2020. The red vertical lines demarcate the most outstanding peaks

Full size image

During the 12-month peak periods of both NO2 and CO, the population around these areas could potentially have had the highest exposures to these dangerous air pollutants. From an air quality perspective, these periods could be considered the most risky to their health compared to any other period between 2005 and 2020. Therefore, these peak periods have been chosen for simulation using WRF-chem. It is important to evaluate the model’s ability to simulate such high-risk events.

Importantly, to have data for training the convolutional autoencoder algorithms, additional data that does not overlap with the target study periods were also used. For NO2, whose study period was 2012, data for 2010, 2011, 2013 and 2014 were used for model training while data for 2015 was used for validation. The validated model was then tested on data for the year 2012. Similarly, for CO whose target study period was June 2015 to May 2016, data for June 2010 to May 2014 were used for training while data for June 2014 to May 2015 were used for validation. The validated model was thereafter tested on data for the period June 2015 to May 2016.

3.2 Simulation of nitrogen dioxide (NO2)

The NO2 observations for the year 2012 (Fig. 4) show that NO2 was most prevalent during the DJF and JJA seasons and least prevalent during the MAM season. This is directly related to the savanna fire regime shown in Fig. 1. When WRF-chem was applied at 23 km resolution, it overestimated NO2 in areas where NO2 was not observed. For example, in the DJF season, WRF-chem simulated an abundance of NO2 on the western side of Uganda and eastern DRC. In the MAM season, which barely had NO2 pollution, the model also overestimated NO2 throughout the entire region by up-to a maximum of ~ 2 × 1015 molecules/cm2.

Fig. 4
figure 4

Spatial patterns and differences between observed and modeled NO2 VCD over East Africa and its surrounding regions. They have been organized by seasons; DJF is December to February, MAM is March to May, JJA is June to August and SON is September to November

Full size image

In comparison, for regions in which NO2 was observed, WRF-chem exhibited variable performance. During the DJF season in the northwestern part of the domain, the model gave a close estimate of NO2 between 1 × 1015 and ~ 2.4 × 1015 molecules/cm2 but underestimated NO2 amounts above 2.5 × 1015 molecules/cm2. The NO2 maximum was misplaced in the model simulation, instead of being in northern Uganda and South Sudan, WRF-chem simulated it to be in western Uganda and eastern DRC. A similar misplacement was also seen during the SON season in the southern part of the domain. The model simulated the NO2 maximum to be over Malawi instead of northern Zambia. This was however not the case during the JJA season, the NO2 maximum was correctly positioned by the model to be in western Tanzania, eastern DRC and northern Zambia, but was severely overestimated by more than 3 × 1015 molecules/cm2.

When the bias correction models, WRF-LS and WRF-DCA were applied, they both reduced the majority of the overestimation bias that was below 2 × 1015 molecules/cm2, which was exhibited by WRF-chem in areas where NO2 pollution was not observed. Both reductions brought the bias to below 1 × 1015 molecules/cm2, although the WRF-DCA reduction was much closer to zero (0). More specifically, both WRF-LS and WRF-DCA changed the estimation bias for areas that had NO2 pollution. During the DJF season in the northwestern part of the domain, WRF-LS reduced the spatial extent of the severe overestimation in eastern DRC and western Uganda. The NO2 bias at the periphery close to Uganda was reduced from over 2 × 1015 molecules/cm2 to less than 1 × 1015 molecules/cm2, but the larger bias over eastern DRC remained unchanged. Over the same area, WRF-DCA reduced the bias from over 3 × 1015 molecules/cm2 to less than 1 × 1015 molecules/cm2.

In tandem, however, both WRF-LS and WRF-DCA increased the underestimation bias in northern Uganda and South Sudan by about 1 × 1015 molecules/cm2 and its spatial extent was larger in the WRF-LS estimate. During the JJA season, in the western parts of the domain, WRF-LS reduced the overestimation bias in many parts of that area from over 3 × 1015 molecules/cm2 to about 2 × 1015 molecules/cm2. By contrast, WRF-DCA reduced that bias much more, from over 3 × 1015 molecules/cm2 to less than 1 × 1015 molecules/cm2. During the MAM and SON seasons, WRF-LS generated small bias of about 1 × 1015 molecules/cm2 in the western parts of the domain while WRF-DCA generated almost zero (0) bias in those areas.

Overall, the bias reduction worked well for areas in which the bias was in one direction, for example, during the MAM, JJA, and SON seasons that only had the overestimation bias. WRF-LS and WRF-DCA however found it challenging in areas which had bias in two directions such as during the DJF season in eastern DRC, South Sudan and northern Uganda where NO2 pollution was concentrated. As they reduced the overestimation bias, they also inevitably increased the underestimation bias. However, in a general view, WRF-DCA performed better than WRF-LS.

Figure 5 shows the monthly comparisons based on spatial averages done over the entire domain. WRF-chem had the largest NMB of 5.4 in March and the lowest NMB of 2.08 in December. It also had its highest RMSE of 7.16 × 1015 molecules/cm2 in January and its lowest RMSE of 0.99 × 1015 molecules/cm2 in November. Overall, for the entire test period, WRF-chem generated an average NMB of 3.51 and an average RMSE of 2 × 1015 molecules/cm2. Figure 5 also shows that, for all the months of the year, both WRF-LS and WRF-DCA generated better estimates of the NO2 VCD compared to WRF-Chem. WRF-LS reduced the NMB by an average of 2.7 (76.5%), the RMSE by 0.6 × 1015 molecules/cm2 (30.2%) and the standard deviation by 0.009 (0.6%). By contrast, WRF-DCA reduced the NMB by an average of 3.2 (90.2%), the RMSE by 1.6 × 1015 molecules/cm2 (77.9%) and the standard deviation by 0.95 × 1015 molecules/cm2 (67.3%).

Fig. 5
figure 5

Monthly comparisons between modeled and observed NO2 VCD. a is the mean NO2 VCD. The vertical bars are the standard deviations from the mean. b is the root mean square error (RMSE) and c is the normalized mean bias (NMB)

Full size image

The scatter plots in Fig. 6 show that WRF-chem estimates had a low correlation to the observations during DJF (R = 0.15) and MAM (R = 0.07), but they had moderate correlation during JJA (R = 0.64) and SON (R = 0.53). It further affirms that there were several grid points where NO2 was not observed (OMI NO2 = 0 molecules/cm2) and yet WRF-chem simulated NO2 at those points. Figure 6 also shows that WRF-LS barely improved the data agreement and correlation. By contrast, WRF-DCA significantly improved the data agreement with the observations during all the four seasons. This was especially clear in the JJA and SON seasons, where the data were better aligned along the 1:1 line for both low and high NO2 amounts. Even the WRF-Chem NO2 estimates at grid points where NO2 was not observed were corrected. The correlations were improved by 0.6 (400%), 0.52 (742.8%), 0.27 (42.2%), and 0.38 (71.7%) for the DJF, MAM, JJA and SON seasons respectively.

Fig. 6
figure 6

Scatter plots with kernel density estimation and correlations for the NO2 VCD (× 1015 molecules/cm2) of WRF-chem, WRF-LS and WRF-DCA against OMI observations. The dashed red line is the 1:1 line

Full size image

3.3 Simulation carbon monoxide (CO)

The MOPITT observations (Fig. 7) show that CO was most prevalent during the SON and DJF seasons. The CO maximum was observed over eastern DRC during JJA, over northern Zambia and southern Tanzania during SON, over northeastern DRC, southern South Sudan and northern Uganda during DJF and finally over southern South Sudan during MAM. These CO spatial patterns were also directly related to the savanna fire regimes in Fig. 1. WRF-chem closely simulated the position of the CO maximum during JJA and DJF. During SON and MAM, WRF-chem positioned the CO maximum over western Kenya and eastern Uganda. This was contrary to the MOPITT observations. Overall, WRF-chem made a close estimate of CO VCD below 1.8 × 1018 molecules/cm2. The best example was during the DJF season in Tanzania and southern Kenya, the WRF-chem estimates show a difference of less than 0.5 × 1018 molecules/cm2 against observations. However, for CO amounts above 1.8 × 1018 molecules/cm2, the model underestimated them by as much as 1.5 × 1018 molecules/cm2.

Fig. 7
figure 7

Spatial patterns and differences between observed and modeled CO VCD over East Africa and its surrounding regions. Note that the scales of the WRF-chem estimates are different because of the small range in the data

Full size image

WRF-LS made minimal reduction in the bias. Its estimates were similar to those generated by WRF-chem but with a small difference of below 0.5 × 1018 molecules/cm2. Overall, the underestimation bias shown by WRF-chem persisted in the WRF-LS estimates. In comparison, WRF-DCA increased the underestimation bias by ~ 0.5 × 1018 molecules/cm2 in all the seasons. This was most prevalent in the SON and DJF seasons. Consequently, WRF-DCA worsened the estimates made by WRF-chem. For example, during the DJF season, WRF-chem made a close to zero (0) estimate in Tanzania and southern Kenya, but WRF-DCA changed this into an underestimation bias.

Figure 8 shows that WRF-chem underestimated the CO VCD for 8 months and overestimated it for only 4 months. Some of its closest estimates were in June, August, April and May which correspond to the JJA and MAM seasons that had relatively low CO column amounts. Overall, it generated an average NMB of − 0.063 and an average RMSE of 0.65 × 1018 molecules/cm2. By contrast, WRF-LS generated an average NMB of − 0.15 and an average RMSE of 0.37 × 1018 molecules/cm2 while WRF-DCA generated an average NMB of − 0.23 and an average RMSE of 0.51 × 1018 molecules/cm2. Further, the scatter plots in Fig. 9 show that WRF-chem estimates had a low correlation to the observations. The average correlation was 0.048. Figure 9 also shows that WRF-LS and WRF-DCA barely made any improvements to the correlation. In summary, the changes made by WRF-LS and WRF-DCA had no positive impact.

Fig. 8
figure 8

Monthly comparisons between modeled and observed CO VCD. a is the mean CO VCD. The vertical bars are the standard deviations from the mean. b is the root mean square error (RMSE) and c is the normalized mean bias (NMB)

Full size image
Fig. 9
figure 9

Scatter plots with kernel density estimation for the CO VCD (× 1018 molecules/cm2) of WRF-chem, WRF-LS and WRF-DCA against MOPITT observations. The dashed red line is the 1:1 line

Full size image

4 Discussion

WRF-chem generally made below adequate estimates of both NO2 and CO atmospheric abundances over East Africa and its surrounding regions. The overestimation of NO2 could indicate an overestimation of nitrogen oxide (NOx = NO + NO2) fire emissions in FINN emission inventory. Similarly, the underestimation of CO could indicate an underestimation of CO emission in the FINN data. Wiedinmyer et al. (2011) explained that uncertainties in the approximated burned area, biomass consumption, emission factors, land cover maps, and fire hotspots tend to increase the amount of error in the FINN data. Specifically for CO, the severe underestimation could also be due to the lack of the plume rise function in the chemistry parameterization used in the WRF-chem set up of this study. Kumar et al. (2012) has explained that inclusion of parameterization with this function can increase CO column abundances by about 10–50%. Furthermore, the performance of WRF-chem during the MAM season gives insight to how the model is likely to perform when tested in simulations of low gas abundances. For NO2, the model is likely to have a systematic overestimation bias while for CO, it will likely have a systematic underestimation bias.

Concerning the performance of the bias correction techniques, both WRF-DCA and WRF-LS successfully reduced the bias of the WRF-chem NO2 estimates but they were unsuccessful with the CO estimates. This can be explained by the variations of the training and validation data. Figure 2 shows that for NO2, the years 2010 and 2015 which were used for this process had NO2 amounts of comparable magnitude to the test period 2012. This implied that WRF-DCA and WRF-LS had fitting examples to learn from. By contrast, for CO, the target study period was the only CO peak of such magnitude in the entire observation record used. Therefore, WRF-DCA and WRF-LS did not have any comparable example to learn from. Even if the training and validation process had used the entire data record that did not overlap with the test period, there would still not be any improvement in the performance. Further, even though WRF-DCA is based on a deep learning algorithm and is expected to be able to generalize data, it was not able to generalize beyond the scope of the data it was trained and validated on.

Despite the bias reductions achieved using WRF-DCA and WRF-LS, the results of NO2 have shown that they find difficulty in adjusting the bias in areas which have both underestimation and overestimation bias. As they reduced one side, they also increased the other side. Such locations were not many but they were outstanding. It is highly likely that this problem could be due to the small data quantity that was used to train WRF-DCA and to generate the correction parameters for WRF-LS. Only 48 months of data were used in this study. By contrast, other studies such as Han et al. (2021) and Le et al. (2020) who used many more data samples did not experience such a problem. Therefore, even though it’s not demonstrated in this study, increasing the quantity of training data could have improved the performance of these models.

WRF-LS showed the weakest bias correction because linear scaling is only suited to correct the mean values but does not cater for higher order moments in the data series (Lafon et al. 2013; Teng et al. 2015). With this, WRF-LS was only able to remove the systematic bias. By contrast, WRF-DCA is based on non-linear functions which are able to correct even the higher order moments such as the variance and standard deviation of the data and therefore can achieve more bias reduction. In addition, WRF-DCA showed superior spatial estimation because convolutional neural networks use filters which overlap on grid cells as they move over the image. This functionality enables the algorithm to relate the spatial features occurring in neighboring grid cells (Albawi et al. 2018). On the other hand, linear scaling operates with total independence between neighboring grid cells. Based on this, it’s likely that even when both WRF-LS and WRF-DCA are provided with more data to scale-up their learning, WRF-DCA will learn more and its performance will improve by a larger magnitude than WRF-LS.

5 Conclusions

This study has used the Weather Research and Forecasting model coupled with chemistry (WRF-chem) to simulate the spatial and temporal distribution of NO2 and CO from biomass burning over East Africa and its surrounding regions. It is the first time that a chemical transport model (CTM) has been applied to study these gas abundances over this region. The model was used to simulate the atmospheric abundance of NO2 for the year 2012 and CO for the period June 2015 to May 2016 and its performance was evaluated against satellite observations from OMI and MOPITT respectively.

The evaluation highlighted a major overestimation of NO2 and an underestimation of CO over the region, and this was firstly associated with the uncertainties in the FINN fire emission inventory. In terms of atmospheric chemistry observations, East Africa is still quite remote and would benefit from data collection campaigns to help develop realistic emission inventories for the region for both biomass burning and anthropogenic emissions. The latter inventory is also considered critical since at present, the EDGAR-HTAP inventory does not have an actual inventory to use over Africa, but has filled that data gap with EDGAR version 4.3 estimates (Janssens-Maenhout et al. 2015). Secondly, the underestimation of CO was also associated with the lack of the plume rise function in the RADM2 chemistry parameterization used for this study. For future applications, it might be useful to consider the MOZART (Model for Ozone and Related Chemical Tracers) chemistry option which can be linked with the plume rise module (Emmons et al. 2010).

Further, a deep convolutional autoencoder algorithm and linear scaling were applied to reduce the bias shown by WRF-chem against the observations. Both methods successfully reduced the bias in the NO2 estimates primarily because the data used for their training and validation had NO2 amounts of comparable magnitude to the test period. For CO, the training data had much lower amounts compared to the test data, and this caused both methods to fail in their correction. Even though both methods demonstrated a high sensitivity to the type of training data, their performance could be improved by providing them with training data that has a sufficient number of examples that compare reasonably well with the intended test data. Finally, based on the NO2 results, the autoencoder algorithm made a larger bias reduction than the linear scaling method. It is thus fit to consider it as the stronger correction method.