1 Introduction

The International Service for the Geoid (ISG) is an official service of the International Association of Geodesy (IAG), performing activities under the coordination of the International Gravity Field Service (IGFS). These activities are mainly devoted to maintaining a worldwide local and regional geoid model repository and to supporting agencies or scientists in computing local and regional geoid models, especially in developing countries, by organizing special training courses and international schools on geoid determination. ISG is based in Italy, with its main centre at Politecnico di Milano, and the services are managed and provided by its internal staff with the support of individual scientists at the international level.

As for the geoid repository, ISG collects models worldwide, validates them when possible, and disseminates them to users mainly through its official website. Since the summer of 2020, a Digital Object Identifier (DOI) service is offered as well, making it possible to assign a DOI to the models of the geoid repository. This service has been established in collaboration with GFZ (GeoForschungsZentrum) Data Services and allows geoid models to be cited in publications, e.g., Barzaghi et al. (2020).

More in detail, ISG manages and preserves an openly accessible repository of continental, regional, and national geoid models at a worldwide scale. The geoid repository aims at storing and redistributing geoid models in the original data format together with a standardized ASCII format developed for purposes, also including useful metadata for gravity related analysis and allowing data interoperability. Most models in the repository can be freely downloaded, some of them require the author’s permission to be accessible, and few are private and cannot be distributed. Consequently, the current 242 geoid models of the repository are classified as public (181), on-demand (22), or private (39), respectively. Moreover, 168 of them are based on gravity data only (i.e., the so-called gravimetric models), 8 are based on GPS/levelling data only (i.e., the so-called geometric models), and 66 based on gravity data and fitted to GPS/levelling data (i.e., the so-called hybrid models). About 500 users per month visit the repository that has almost worldwide coverage, with resolution grids up to 0.5 arcminutes. As for the Asia–Pacific region, there are 58 geoid models, among which 47 are classified as public, 2 as on-demand, and 9 as private. These statistics reflect the status of the repository at the date of May 31, 2021. Each model of the repository has a dedicated web page on the website, containing all the available information, like, e.g., names of the authors, publication year, key references, and a brief description of the input data, the adopted computational method, and kind of output, in addition to the data file (when the model is classified as public) both in the original and standardized ASCII format. Furthermore, when a DOI is assigned to a model, the latter is made available also through the catalogue of GFZ Data Services, where a dedicated landing page is present, cross-referencing the data and the ISG webpage. More details about the structure of the service can be found in Reguzzoni et al. (2021).

This work aims at performing some analyses and comparisons on the geoid models that cover the Asia–Pacific area and are available in the ISG repository, thus providing a picture of the geoid knowledge over this area.

1.1 Comparative analysis

The large number of geoid models stored in the ISG repository offers the possibility of assessing them through relative comparisons. For instance, possible mismatches between geoid models referring to the same area can be revealed by analysing their residuals. Inconsistencies and/or disagreements can be detected between models computed at different epochs, with different techniques or published by different authors.

An overview of the Asia–Pacific models that are currently available at the ISG repository clearly shows that two classical methods are prevailingly used for the geoid computation, namely Stoke’s integration (Stokes 1849) and Least Squares Collocation (Moritz 1980; Tscherning 2013). The former is typically implemented by Fast Fourier Transform (Sideris 2013) after proper modifying Stoke’s kernel (e.g., Wong and Gore 1969). Both methods are generally applied in the framework of the so-called remove-restore approach (Denker 2013), where the long-wavelength gravity signal is modeled by a global gravity model given as a truncated series of spherical harmonic coefficients (Pavlis 2013) and the short-wavelength contribution is taken from a digital terrain model by computing the so-called residual terrain correction (Forsberg 1984). Even if they are not used for the geoid models under consideration for this work, it is worth recalling that there are many other methods and approaches for local geoid computations and some comparative studies have been performed on test areas to assess them, for example the Auvergne test (Duquenne 2006) or the more recent Colorado experiment (Wang et al. 2021). Results from these tests are published and freely available at the ISG website (www.isgeoid.polimi.it/Projects/Auvergne_test.html, www.isgeoid.polimi.it/Projects/colorado_experiment.html) and the readers can refer to the cited literature for detailed descriptions of the geoid computation methods.

Since the Asia–Pacific models we are going to analyse cover a time span of almost 30 years (from 1993 to 2020), besides the differences in the processing methods one cannot disregard the technological advancements and the increasing data availability during the years, leading to an improved quality of the input observations as well as more updated and accurate global gravity models as the reference for the long-wavelength components of the gravity signal. In this respect, the older Asia–Pacific models are mainly referred to EGM96 (Lemoine et al. 1998) and EGM2008 (Pavlis et al. 2012), while the most recent ones also exploits the information coming from the GOCE gravity mission (Drinkwater et al. 2003; Pail et al. 2011). For these reasons, cross-checking regional geoid models like those stored at ISG repository is meaningful for taking trace of the evolution of gravity models at different scales, from local to regional and even up to global scales.

In this study, three kinds of analyses are provided: (a) the assessment of the evolution in time of a geoid series referring to the same country, (b) the comparison of local and regional geoid models on overlapped areas, (c) the agreement between local and global models computed over the same area.

The computation of the residuals between geoid undulations from different models of the repository requires some preliminary processing. In particular, geographical coverage, spatial resolution, reference frames, and height datums must be consistent. Therefore, the models to be compared are firstly masked only over overlapping areas. Then, the grid of the model with the lower resolution is taken as reference, and the other models are interpolated (or downsampled, when possible) over this reference grid. The interpolation of geoid undulations on the coarser grid makes this approach conservative, avoiding the possibility of adding gross artefacts related to the interpolation method, and allowing to neglect possible small inconsistencies. Obviously, this step is skipped in the case of coincident grids. In the case of comparison with respect to global models, this problem does not exist because the latter are modelled through a truncated spherical harmonic expansion, and the geoid undulation can be directly synthesized on the same grid of the local geoid under assessment. Finally, regarding possible misalignments due to different reference frames and/or datums, they can be assumed to be negligible after removing the best fitting plane on the computed residuals. Considering some test cases, the results of these comparative analyses are presented and discussed in detail in the next section. The same analyses have also been carried out for all the geoid models currently stored in the ISG repository and covering the Asia–Pacific area. For the sake of brevity, the overall results are presented in the form of tables only, summarizing the information that can be inferred from the ISG repository.

2 Results and discussion

This section presents and comments the numerical results on the relative assessments introduced in the previous sections.

2.1 Local geoid series comparison

Geoid model series referring to Philippines and surrounding seas (PGM series) has been chosen as an example of the assessment regarding the evolution in time of local geoid models. The models of this series included in the ISG repository are PGM2014 (Forsberg et al. 2014), PGM2016 (Gatchalian et al. 2016), and PGM2018 (see http://www.namria.gov.ph/projects.aspx). These models were computed by the National Mapping and Resource Information Authority (NAMRIA) of the Republic of the Philippines with the technical assistance of the National Space Institute of the Denmark Technical University (DTU-Space). Table 1 summarizes their main characteristics and statistics.

Table 1 Characteristics and statistics of the PGM gravimetric geoid series, considered as an example of the assessment of the evolution of local geoid models in time
Full size table

As one can see, spatial coverage and resolution are identical for the PGM gravimetric geoid series. Therefore, the preprocessing step for harmonizing the grids is not required. Statistics reveal a bias of about 80 cm between the first PGM2014 and the subsequent PGM models (see Mean, Min and Max rows in Table 1) while maintaining the same overall variability, being the standard deviations almost identical to the millimeter level (see STD row in Table 1). This bias is consistent with the shift of 80 cm applied to PGM2014 by the authors to approximately fit the Manila tide gauge datum (see Forsberg et al. 2014).

From this preliminary analysis on the PGM gravimetric model series, it is very hard to detect localized differences and refinements applied in the latest edition of the PGM model (PGM2018) that has a declared accuracy of 1.2 cm against 30 cm of the first PGM2014. A cross-comparison among them is then required to this aim. In Table 2 the statistics of the residuals between subsequent PGM models, reduced for the fitting plane as described in the previous section, are reported.

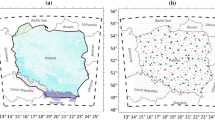
Table 2 Statistics on the residuals of the comparisons among the models of the PGM gravimetric geoid series
Full size table

From these statistics, PGM2014 and PGM2016 show a very good agreement, with a sub-centimetric standard deviation, and main differences localized in the area of Surigao del Norte (10°N, 125°E) and the southern peaks like Mount Apo (7°N, 125°E), as shown in Fig. 1. These small differences on land are due to the performed re-computation after adding new land gravity data, as reported also in Gatchalian et al. (2016). The latest PGM2018 shows higher residuals with respect to the previous geoid models, up to almost 3 cm of standard deviation. The map of residuals highlights a significantly high frequency difference related to the topography and bathymetry signal. This is probably thanks to new satellite gravity and altimetry data and densified land gravity data that were used to update the model. For instance, Philippine and Sulu trenches are well identifiable (along the eastern Philippines and in the Sulu Sea between Borneo and Philippines), as well as the undersea structures around Scarborough Shoal in the South China Sea.

Fig. 1
figure 1

Residuals of the comparisons among the models of the PGM gravimetric geoid series. The colour bars are saturated in the range between − 0.1 m and 0.1 m

Full size image

The ISG geoid repository currently stores many other geoids referring to the same country and being subsequent editions they can be analysed with the procedure just described for the Philippines. For the sake of brevity, in the following Table 3, other geoid series comparisons are reported in terms of residuals statistics among subsequent geoid models. The residuals have been computed for geoid series comprising at least three gravimetric or hybrid models, neglecting possible mismatches between geoids and quasi-geoids.

Table 3 Statistics on the residuals of national geoid series comparisons, for all the series stored in the ISG geoid repository
Full size table

As one can see, the standard deviation of the residuals decreases gradually with updating the model, thus indicating a progressive refinement of the model in that area. Only the geoid series referring to the Hawaiian Islands shows particularly low residuals between the 1999 and 2003 editions. The reason is that these two gravimetric models are the same for the Hawaiian Islands but for the reference frame (Roman et al. 2004). However, the effect of this frame transformation is substantially cancelled when removing the fitting plane from the residuals.

2.2 Local and regional geoid comparison

The regional South East Asia (SEA) geoid model (Kadir et al. 1999) have been compared with the overlapping local geoids of Brunei (Lyszkowicz et al. 2014) and the previously analysed PGM2018. SEA is the only regional/continental model that is available in the ISG repository for the Asian area, and Brunei and PGM series models are the only ones included in the SEA extensions. Due to the different native spatial resolutions and coverage, two grids with the same coarser resolution of SEA, and smaller coverages of Brunei and PGM2018 have been considered. Over these grids, SEA has been simply clipped while the two local geoids have been downsampled to a resolution of 30’ (being their native grids overlapped to that of SEA), making the geoid models consistent among them before being compared. Table 4 summarizes the characteristics of these geoids.

Table 4 Characteristics of the SEA, PGM2018, and Brunei geoid models, used as input for the local and regional geoid comparison example
Full size table

The following Table 5 reports the statistics of the residuals of the two local geoids with respect to the regional one, after reducing for the fitting planes too.

Table 5 Statistics on the residuals of the comparison of SEA regional geoid model with respect to PGM2018 and Brunei local geoid models
Full size table

Referring to the comparison between SEA and PGM2018, the residuals show a standard deviation of about 1.19 m, with values ranging between about − 6.59 m and 3.96 m. As one can see in Fig. 2, the main differences are localized in Philippines, Sulu trenches, and Borneo area (showing SEA under-estimated values) and Philippines mainland (showing SEA over-estimated values). In Brunei, the standard deviation of residuals is about 0.5 m. These residuals are quite higher if compared to the expected accuracy (declared by authors) of PGM2018 and Brunei geoids, namely 0.012 m and 0.3 m, respectively. This would suggest, for instance, that for regional investigations in this area, it would be preferable to patch together the available local geoids using SEA just as a common reference or, still better, considering recent global models (SEA is dated back to 1999). For this purpose, Fig. 3 also shows the residuals of PGM2018 and Brunei models with respect to EGM2008 (Pavlis et al. 2012). As one can see, the agreement with EGM2008 is considerably higher for both PGM2018 (STD 0.184 m) and Brunei (STD 0.103 m). In the subsequent sections, comparisons with global models will be further detailed.

Fig. 2
figure 2

Residuals of the comparison of SEA regional geoid model with respect to PGM2018 and Brunei local geoid models. The colour bars of the comparisons with SEA are saturated in the range − 4 m and 4 m. For visualization purposes the spatial resolution of the figures was increased

Full size image
Fig. 3
figure 3

Residuals of the comparison of EGM2008 global geoid model with respect to PGM2018 and Brunei local geoid models. For visualization purposes, colour bars and spatial resolution of the figures were made consistent with Fig. 2

Full size image

2.3 Local and global geoid comparison

To validate a local solution when regional or continental models are not available or they are obsolete, like in the example of the previous section, the comparison with a global model may be useful. In this respect, the Taiwanese geoid model TWGEOID2018 (Hwang et al. 2020), in its gravimetric and hybrid versions, has been evaluated with respect to EGM2008 and EIGEN6C4 (Förste et al. 2014) global models. The geoid undulations from EGM2008 and EIGEN6C4 were computed at their full resolution on the same grid points of TWGEOID2018, by exploiting the online computational tools of the International Centre for Global Earth Models (ICGEM) (Ince et al. 2019). Table 6 summarizes the main characteristics (spatial resolution and spatial coverage) and statistics of TWGEOID2018, and the geoid undulations computed from global models.

Table 6 Characteristics and statistics of the TWGEOID2018 geoid model (gravimetric and hybrid versions) and the EGM2008 and EIGEN6C4 global models (over the Taiwan area), considered in the local and global geoid comparison example
Full size table

As for the mean value, the statistics of Table 6 are quite contradictory, in the sense that the TWGEOID2018g gravimetric geoid is fully consistent with EIGEN6C4, even if it was computed by using EGM2008 for the modelling of the long-wavelength behaviour (Hwang et al. 2020). On the other hand, the mean of the TWGEOID2018h hybrid geoid is closer to the EGM2008 value rather than the one of EIGEN6C4. As for the variability, the hybrid solution has a standard deviation more similar to the reference global models (about 0.01 m and 0.03 m lower with respect to EGM2008 and EIGEN6C4, respectively), while the gravimetric solution looks a slightly smoother model.

When analysing the residuals, whose statistics are reported in Table 7, slightly better matching between TWGEOID2018 and EGM2008 is revealed, accordingly to the input data used for its computation. In particular, the residuals with respect to EGM2008 of both the gravimetric and hybrid local geoid models of Taiwan show a standard deviation of about 0.16 m, 0.02 m less than in comparison with EIGEN6C4. This also reflects on the minimum values of the residuals, but not on the maximum ones, being all practically equivalent.

Table 7 Statistics on the residuals of the comparison of the TWGEOID2018 geoid model (gravimetric and hybrid versions) with respect to EGM2008 and EIGEN6C4 global models (over the Taiwan area)
Full size table

Figure 4 presents the spatial distribution of the aforementioned residuals in the case of the Taiwanese gravimetric model (TWGEOID2018g), since the hybrid one shows a practically identical behaviour. The main differences are located on Chinese mainland on the West side and on Japanese Yaeyama Islands on the East side, where the local Taiwanese geoid model seems to provide more detailed information than the global models. Residuals against EIGEN6C4 show also that the negative maximum differences are mainly located in the sea in front of the Quanzhou area (25°N, 120°E). This is probably related to the gravity data used for computing the TWGEOID2018 models, which cover only the Taiwan Island, with gaps in the region with higher residuals (see Hwang et al. 2020).

Fig. 4
figure 4

Residuals of the comparison of the TWGEOID2018 geoid model (gravimetric version) with respect to EGM2008 and EIGEN6C4 global models (over the Taiwan area). The results of the same comparison computed with the hybrid version of the TWGEOID2018 geoid model are not reported, because they show an almost identical behaviour

Full size image

As previously stated, this kind of relative assessment between local and global geoid models can reveal useful information for conducting more refined analyses. For the sake of brevity, just the case of the Taiwanese TWGEOID2018 geoid model has been described in detail, while Table 8 summarizes the statistics of the residuals computed by applying the same procedure to all the local geoid models stored in the ISG repository, covering the Asia–Pacific area.

Table 8 Statistics on the residuals of the comparison between the Asia–Pacific geoid models available in the ISG repository with respect to EGM2008 and EIGEN6C4 global models
Full size table

As one can see, the agreement between local and global geoid models is different depending on the considered area.

For example, in the case of the Australian geoid series, residuals with respect to EGM2008 and EIGEN6C4 show very similar standard deviations, while in Guam and Northern Mariana Islands, these global models performed differently.

In the Xinjiang and Tibet area, the local geoid model is much more adherent to EGM2008 than EIGEN6C4, with statistics about 3 times better. This result matches what can be found in Shen and Han (2013), where the procedure of the Xinjiang and Tibet geoid model computation is described, highlighting the contribution of the use of EGM2008, and therefore justifying the agreement with this global model. On the other hand, Kostelecky et al. (2015) states that the main difference between EGM2008 and EIGEN6C4 is the inclusion of GOCE mission data in the EIGEN6C4 model. In their evaluation, they see long wavelength differences between the two models in remote areas of the Earth (as mountainous Tibet areas could be considered), where a scarce or bad terrestrial data coverage is present, and, for these regions, they assume a positive effect of introducing the GOCE data. This would lead thinking that, despite worse statistics, in most challenging areas, EIGEN6C4 might be a better reference for local model assessment.

Regarding the Russian quasi-geoid model RGG2003 (Medvedev and Nepoklonov 2003), statistics reveal anomalous values. Minimum and maximum values are of the order of tenths of meters, although the standard deviation is comparable to those of the other geoid models. This leads assuming the presence of outliers in the dataset. A possible strategy to find out them can be the inspection of the histogram of the residuals. Tails are expected to tend toward zero, without significant peaks or isolated values that could be considered anomalous. Once detected, the corresponding values could be removed and, eventually, interpolated if needed. With such a simple procedure, correcting just 4 points out of 651,689, the range of residuals significantly decreases, leaving the standard deviation almost unchanged, as shown in Table 8.

For the sake of completeness, the mean values of both local and global geoid models are reported in Table 9. These values clearly show how the adopted height datums are different and represent an important input towards the realization of a unified vertical reference system.

Table 9 Mean values of the Asia–Pacific geoid models available in the ISG repository, as well as those of EGM2008 and EIGEN6C4 global models computed on the same grids
Full size table

3 Conclusions

This work analysed the state-of-the-art geoid modelling in the Asia–Pacific region by considering the models that are stored in the repository of ISG, which represents the reference geoid archive for the geodetic community in the framework of IAG. It comes out that a significant portion of the region is covered by at least a model, or even more when considering series of solutions computed by the same institution in the years or by different authors exploiting different techniques. Altogether, 58 models covering more than 60% of Asia–Pacific area are available. Starting from this collection of models, some comparative statistical analyses were performed, basically showing that:

  • in all geoid series, there is a time trend with smaller and smaller corrections, suggesting that recent solutions include improvements with a sort of convergence to an “optimal” one;

  • at the regional/continental level, only a model for South-East Asia is currently included in the ISG repository, but this model is quite out-of-date, and the performances of more recent global models look better;

  • in general, local/national solutions agree quite well with global ones (EGM2008 and EIGEN6C4 were considered in this analysis), with discrepancies ranging from a few to some tens of centimetres in terms of standard deviation.

As for the future perspectives, some effort will be dedicated to enlarging the ISG repository in the Asia–Pacific region, especially covering China, Mongolia, Korean Peninsula, Indonesia, India, and the South-West Asia. Exploiting this enlarged archive and, maybe, updating some old solutions, national geoid models might also be used to address the problem of the height datum unification in the framework of IAG activities for the definition and realization of an International Height Reference System (IHRS).