1 Introduction

Rapid fluctuations of amplitude radio waves, called scintillations, were first recorded by Hay, Parsons, and Phillips in 1946 (Yeh and Liu 1982). The amplitude variations from radio star Cygnus (64 MHz) showed that the scintillations are not caused by the radio sources, but are associated with plasma irregularities in the ionosphere (Hewish 1952). According to the previous research (Aarons et al. 1982), these are usually induced by the F-layer irregularities, usually found between 225 and 400 km altitudes. Meanwhile, these signals present random temporal fluctuations include amplitude and phase (Aol et al. 2020; Kintner et al. 2007) when received at an antenna. The scintillations may either involve weak or strong scattering. The Strongest scintillation is often observed in the equatorial and aurora regions while mid-latitude regions usually exhibit weaker ones (Basu et al. 2002). The distinction of weak and strong scintillations also affects the applicability of the propagation models like the WBMOD (Wideband ionospheric scintillation model) (Fremouw et al. 1984; Rino 1979, 1980; Secan et al. 1995). Therefore, it is necessary to update such models to include the scintillation effects. SCINTMOD (High-latitude upgrade to the wideband ionospheric scintillation model), for example, combines the worldwide climatology of the ionospheric plasma-density irregularities that cause scintillation (environment model) and a model for the effects of these irregularities on a trans-ionospheric radio signal (propagation model) (Secan et al. 1997). Scintillations, especially the weak mid-latitude scintillation, are usually attributed to diffractive and refractive scattering (Crain et al. 1979). Refractive scattering is believed to be caused by plasma “holes” or “bubbles” in the ionospheric structure that is perpendicular to the line of sight especially in the equatorial region. The occurrence of these equatorial plasma bubbles varies considerably with the location near the equatorial region. Moreover, refractive scattering usually involves irregularities that are larger than the Fresnel scale, while the diffractive scattering is typically associated with irregularities near the Fresnel scale. Many comprehensive studies have been done regarding the scintillation theory and its observations (Aarons et al. 1982; Basu et al. 1985; Basu et al. 2002; Bhattacharyya et al. 1992). A detailed review of the physics of ionospheric irregularities has been discussed by Kelley (1989) and other studies (Heppner et al. 1993; Keskinen et al. 1983; Kintner et al. 1985; Tsunoda 1988). Usually, the structure and spatial features of such irregularities can be studied extensively using incoherent scatter radars. However, kinds of observations are done on a very irregular basis since they then to be very costly. For the observations of ground-based networks, nowadays (Aol et al. 2020; Kintner et al. 2007), ionospheric irregularities are observed using the signals coming from global navigation satellite systems (GNSS) and beacon receivers and it usually assumes that the ionospheric height is about 350 km where the peak of the F2 layer is usually found. But determining the actual height of these regions is not a straightforward process with these kinds of systems. This is especially when the source of scintillation event is attributed to irregularities in the E layer or F layer.

In order to receive not only FORMOSAT-3/COSMIC Tri-band Beacon signals (150, 400, 1066.7 MHz) but FORMOSAT-7/COSMIC II Tri-band Beacon signals (400, 965, and 2200 MHz), we improve the open-source beacon receiver successfully. In this paper, we present the initial result of FORMOSAT-7/COSMIC-2 beacon data for the beacon signals of 400 MHz and 965 MHz. Meanwhile, we proposed a project method to estimate the position of F layer irregularities using a network of radio beacon receivers over Taiwan. To demonstrate the method’s applicability, we present a scintillation case near midnight and the height of ionospheric penetration point for irregularities which the source of scintillation would be confirmed about at 250 km.

2 The description of Beacon Satellite receiving system

The data of open-source digital beacon receiver named GNU Radio Beacon Receiver (GRBR) (Yamamoto 2008) was used in this study. However, the GRBR received dual frequencies (150 MHz, 400 MHz) for FORMOSAT-3/COSMIC beacon signals only. Hence, Yamamoto and authors cooperate to modify the beacon receiver for FORMOSAT-7/COSMIC-2 tri-beacon signals (400 MHz, 965 MHz, 2200 MHz). The Fig. 1 shows the block diagram of the beacon receiving system. The beacon receiving system deploy the antenna, Pre-amp, down-converter board, three Universal Software Radio Peripheral boards (USRP B210 http://www.ettus.com/)), and a personal computer. The beacon signals are gained from amplifiers and then filter by band-pass filters (BPFs) to avoid the antialiasing. In order to receive the signals of FORMOSAT-7/COSMIC-2 and FORMOSAT-3/COSMIC both, the 400-MHz beacon signal of FORMOSAT-7/COSMIC-2 is down converted to 150-MHz signal, and 965-MHz of FORMOSAT-7/COSMIC-2 is down converted to 400-MHz from the down converter board. After that, the signals are used as input to a software-defined radio platform (USRP B210) using GNU Radio, a free software development framework that gives signal processing function. Finally, the data is stored as discrete series of complex data files through a USB 3.0 interface from USRP B210 to PC. The off-line data analysis program will start when the procedure of data collection is done while the satellite pass is finished. The estimation of TEC (total electron content), relative power(dB), S4 index (scintillation index) will be calculated and stored as 50 Hz sampling data rate by using off-line data analysis program and send back the data to our server via the internet. Meanwhile, the complex raw data files are huge, we delete them after the off-line data analysis usually. The detail of digital signal processing of off-line data analysis has been discussed by Yamamoto (2008).

Fig. 1
figure 1

Block diagram of the beacon receiver system

Full size image

3 Method

3.1 The intensity scintillation index (S4)

The amplitude of received signal (i.e. radio beam) fluctuate about the mean level in certain manner. A typical parameter used to study scintillation is the S4 index (Briggs et al. 1963), which is defined as the ratio of the root-men-square of the intensity I to the mean intensity:

$${S}_{4}=\frac{\sqrt{\langle {I}^{2}\rangle -{\langle I\rangle }^{2}}}{\sqrt{{\langle I\rangle }^{2}}}.$$
(1)

S4 index is determined within a specific period. In this study, we used a one second sampling period for a sampling rate of 50 Hz. From here, we could identify the scintillation level as weak (S4 < 0.6) or strong (S4 > 0.6), with saturation level of S4 > 1.0. Identifying these levels for a given observation may indicate the behavior of irregularities and the level of disruption to radio communications. For instance, when the signal reaches saturation level, information content included in the signal phase and power is usually lost.

The ionospheric irregularities and the corresponding scintillation index can be characterized by a power-law spectrum, given by (Davies 1990)

$${S}_{4}= \alpha \cdot {f}^{-n},$$
(2)

where α is a proportionality factor and the exponent n = (p + 3)/4. Here, p is the spectral index, which is approximately equal to 3 for ionospheric scintillation (Wernik et al. 2007, 2003). Thus, the scintillation intensity scales are set as f−3/2. Equation (2) reveals that the amplitude scintillation spectrum displays a ‘corner frequency’ that represents the change from scattering to specular propagation. The corner frequency hinge on Fresnel scale and the drift speed of the irregularities. The power will tend to the slope if the frequencies are greater than the corner frequency (Umeki et al. 1977). This simple scaling is valid only for very intense scintillation. If scintillation is moderately strong to strong, the scintillation spectrum has a form close to Gaussian and therefore it is impossible to obtain the spectral index. On the other hand, the frequency exponent for S4 holds only for S4 < 0.5. With the strong scintillation (S > 0.5) these relationships do not apply for Eq. (2). Hence, The S4 > 0.6 is already in high S4-index value. Another important aspect of S4 index is that it provides reasonable estimates of signal disruption for a specific position on Earth.

3.2 The project method

As a general rule, modern observation techniques involve the measurement of scintillation activity by using multiple antenna and spaced receiver systems connected to digitizing systems for geostationary satellites (Joshi et al. 2019). For the purposes of ionospheric tomographic application (Raymond et al. 1994), these are considered polar orbit satellites. Different methods of scanning for scintillation observations are used for polar orbit satellites than with geostationary satellites. With the latter, the receiver obtains signals all the time, with a fixed penetration point. By contrast, the beacon or GNSS receiver system receives signals only when the polar orbit satellite overflies the station from north to south or contrariwise. Therefore, the penetration point is moving when the satellite is moving. As shown in Fig. 2a, the SIP (sub-ionosphere point) which is the projection point of IPP (ionospheric penetration point) is not coincide if the assumed height is wrong (Lin 2017; Ozeki 2010).

Assume a strong irregularity appears over the three stations as illustrated in Fig. 2b. The radio signals will start to fluctuate if the ray path starts to encounter the irregularity that lies in a north–south direction. Usually, it is assumed that the height of the irregularities that causes scintillation is around 350 km, because they largely occur in the F layer (about 225 km to 400 km) (Aarons et al. 1982). To improve our height assumptions, we use a project method to estimate the height of the irregularities. The three beacon receiver stations (S1, S2, and S3) that lie in a north–south direction, as shown in Fig. 2. We assume X1 is the height of penetration points lower than the height of strong irregularity h and X2 is the height of penetration points higher than the height of strong irregularity h. The projection line is \(\overline{A^{\prime}D^{\prime}}\) for S1 station, \(\overline{B^{\prime}E^{\prime}}\) for S2 station and \(\overline{C^{\prime}F^{\prime}}\) for S3 station if the height of penetration points is set as X2. The length of \(\overline{A^{\prime}D^{\prime}}\),\(\overline{B^{\prime}E^{\prime}}\) and \(\overline{C^{\prime}F^{\prime}}\) should be equal to the length of the irregularity Y if we assume the height of penetration points is equal the height of strong irregularity h. From the Fig. 2, we can see \(\overline{A^{\prime}D^{\prime}}\) is projected to the south for the northernmost station S1 and \(\overline{C^{\prime}F^{\prime}}\) is projected to the north for the southernmost station if we set the height of penetration points X2 are higher than strong irregularity h. Meanwhile, the length of each projection line is greater than the length of the irregularity Y.

Fig. 2
figure 2

a Two SIPs (sub-ionosphere point) from one satellite pass project different position of irregularities if the assumed height is wrong. b North–south view of the project method. By changing the height of the penetration points, it will cause the movements of the projection line. The projection lines remain the same if the correct height of the penetration points is set

Full size image

Conversely, the projection line is \(\overline{G^{\prime}J^{\prime}}\) for S3 station, \(\overline{H^{\prime}K^{\prime}}\) for S2 station and \(\overline{I^{\prime}L^{\prime}}\) for S1 station if the height of the penetration points is set X1 which is shorter than h. \(\overline{G^{\prime}J^{\prime}}\) is projected to the south for the southernmost station S3, and \(\overline{I^{\prime}L^{\prime}}\) is projected to the north for the northernmost station S1. Moreover, the lengths of these three projection lines are shorter than the length of the irregularity Y. The result of movement for X1 and X2 is on the contrary for the height of scintillation. Hence, we may estimate the height of ionospheric irregularity which the source of scintillation event from the above inference by shifting the height of the penetration points.

4 Results and discussion

4.1 The initial result of FORMOSAT-7/COSMIC-2 observation data

The first observation data by a new beacon receiver for FORMOSAT-7/COSMIC-2 was installed in March–April 2021 in Kenting (22.725N, 120.544E) which located at the southernmost of Taiwan island. Figure 3 shows the digital-receiver record of intensity, scintillation index (S4) of signals and relative slant TEC (total electron Content) from the FORMOSAT-7/COSMIC-2 satellite constellation. The satellite pass was on March 21 and time is 05:07 to 05:21 UT (the local time is + 8 h). The satellite FM4 of the FORMOSAT-7/COSMIC-2 constellation appeared from the south horizon at azimuth 300 degrees, reached the maximum elevation 75º at 05:14 UT, and set in the north horizon at azimuth 110º. The intensity of relative power was up about at 50 s from noise level and down to noise level after about at 1100 s. The maximum signal-to-noise ratio for 400 and 965 MHz of FORMOSAT-7/COSMIC-2 beacon transmitting signal are more than 40 and 30 db. The intensity of relative power is close to noise level if the elevation angle is below to 15º usually. Meanwhile the value of S4 index is unusual high (S4 > 1.5) for 400 and 965 MHz both, it means the data is useless during those periods. S4 index at 810 s is about 2.7 for 965 MHz, however we do not see the high S4 index at the same time for 400 MHz. So, we may understand the source of scintillation of 965 MHz is contributed from the local interference of background noise not from ionospheric irregularity.

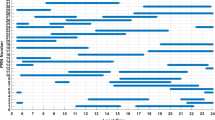
There are 83 scintillation days for Kenting station including from March 2020 to Sep 2021 (452 days) and occurred usually at 18 ~ 05 LT in the night time, especially at pre-midnight or post-midnight at Fig. 4. There are 78 scintillation events when Kp < 3 and there are 5 events when kp between 4 and 5. Figure 4 shows scintillations are happened at May–June and December–February less than the other months. On the contrary, scintillations are normally more frequent during the equinoctial months of August–October and March–April. Meanwhile there are 16 scintillation days happened when Kp > 3. Among those scintillations, there are 11 days happened at May–June and December–February which the scintillation occurred at low solar activity is less than the other months. We also check the magnetic activity at equinoctial months of August–October and March–April, only 5 days (Kp > 5) occurred scintillation at those periods. Of 12 scintillation days during December–January, when occurrence of scintillations is not as high as in the equinoctial months, subsequent to high magnetic activity (Kp > 5), scintillations were observed on 6 occasions (Kp < 3). Therefore, the rate of scintillations in during December–January is much large than equinoctial months of August–October and March–April at high magnetic activity.

Fig. 3
figure 3

Relative power (dB) (Top), S4 index (Middle) and Relative TEC (bottom) from FORMOSAT-7/COSMIC-2 FM4 on March 21, 2021 at 05:07:17 UT. Data of 400 and 965 MHz signals are shown by blue and red lines, respectively

Full size image

4.2 The results by the project method: a case study for FORMOSAT-/COSMIC data

As the mention at 3.2, with this characteristic of Beacon satellite system, we may roughly estimate the height of ionospheric irregularities that extend in a north–south direction. The radio signals will vary if the ray path starts to touch the strong irregularity that lies in a north–south direction, as shown in Figs. 5 and 6b. Figure 5 shows that the occurrence time of scintillation differs for each of the three stations. The scintillation signal was first received by the southern station (CheCheng), then by the northern station (NCU) later. Meanwhile, assuming a penetration height of 350 km, Figs. 2a, 6a, c depict the project issues. For each of the three stations, the scintillation region will be in a different location. The scintillation region of the southernmost station goes south in relation to the other stations, and so on. If the transmitting satellite is travelling from north to south, the southernmost station S3 receives the scintillation signals first, as shown in Fig. 2b. After the S3 station, the S2 and S1 stations will get scintillations. Station S3 will also complete the scintillation region scan first. The results for the three locations, however, are shown in Fig. 5. The scintillation signals were received first by the southernmost station (Che-Cheng, 2.7250N, 120.544E), and last by the northernmost station (Chung-li, 25.136N, 121.539E). The time series is displayed on the transverse axle, while the S4 index values are displayed on the vertical axle. The station has begun to receive scintillation signals, as evidenced by the rapid random variation of the S4 index. As a result, each receiver scans a separate area of the irregularity at the same moment, resulting in different ray trajectories. The scintillation time ranges for each station are shown in Fig. 5. Figure 7 shows the various projection lines to ground stations by adjusting the penetration points' height from 200 to 350 km. For the first recorded sampling point, the local time of observation is 12:46 LT on April 26th, 2006. The height of irregularity is around 250 km. At the same time, the Chung-li dynasonde (HF radar) collected the Spread F between 3 and 7 MHz at 12:45 LT local time. The height of the Spread F from the ionogram in Fig. 8 was compared. The Spread F reaches a height of 250–320 km. The dynasonde result validates the result calculated using the project approach and beacon data from the three sites.

Fig. 4
figure 4

The hourly occurrence and Kp index of scintillation events from Mar 2020 to Sep 2021 for 400 MHz signals

Full size image
Fig. 5
figure 5

The S4 index data of 3 stations for a case study of scintillation event. The time started at 16:40UT

Full size image
Fig. 6
figure 6

The S4 index distribution along the penetration line if the height of penetration points is set to 200 km (a), 250 km (b) and 350 km (c)

Full size image
Fig. 7
figure 7

The movement of shifting different heights for the penetration points from 200 to 350 km if the S4 index > 0.3. The blue color is for NCU station, black for TasoTun station and red for Checheng station

Full size image
Fig. 8
figure 8

The ionogram from the Chung-li dynaosnde 2006/4/26 16:45:00UT. The Range Spread F event occurred at the same time. The height of the Spread F is between 250 and 300 km

Full size image

According to single scatter scintillation theory scintillation theorem (Yeh and Liu 1982), there is a roll-off frequency at the Fresnel frequency. The Fresnel scale is \(\sqrt {2\lambda z}\). The Fresnel scale is an important parameter from the analysis of FFT spectrum for the physical specification of carry frequency. The λ is the wave length and \(z\) is the height of scintillation. The phase screen model assumes z is 350 km for the greatest possible height usually. Hence, the correct z is important parameter for Fresnel scale and phase screen model. From the results of Figs. 5, 6 and 7, we may change the height of penetration points from 350 to 200 km to check the height of scintillation region, based on the results of the project method.

The Slant Total Electron Content (TEC) is the integration of electron density along the ray path. The TEC of beacon system is produced by the differential Doppler technique. Another advantage of the beacon system is that the phase check can be used against moderate interference or noise. Thus, we do not have to consider about the phase unlock problem in the raw data for a moderate scintillation. However, it is impossible to obtain good phase when the scintillation saturates the receiver. This condition of saturation (S4 larger than 1) usually occurs around midnight of a strong magnetic activity when the KP index is larger than 5, in our experience. Fortunately, the scintillation of the special case at local time 12:45, April 26th, 2006, was a strong scintillation (Fig. 5). The S4 index was between 0.6 and 1.0, meaning that the quality of phase was still good enough to lock when the scintillation occurred. Hence, the TEC results in this case are reliable. Meanwhile we observed two TEC holes in the scintillation region, with characteristics similar to equatorial plasma bubbles (EPBs). Equatorial plasma bubbles, regions of depleted plasma densities, occur in the evening sector of the equatorial ionosphere. It is believed that the bubbles originate in the bottom of the F-region ionosphere, by the action of Rayleigh–Taylor instability, and are uplifted by drifts at a few 100 m/s through the F layer peak to the topside of the F region (Kelley 1989). It is also believed that EPBs are closely related to equatorial spread F (ESF).

5 Conclusion and future works

We upgraded the new beacon receiver by using an open-source software toolkit (GNU Radio) and open-source hardware for SDR (software-Defined Receiver) to receive both FORMOSAT-7/COSMIC-2 (400, 965, 2200 MHz) and FORMOSAT-3/COSMIC (150, 400, 1066.7 MHz). The data quality was confirmed by the preliminary results. However, the outcomes of our scintillation research, which include the project method, RTEC, and scintillation spectrum analysis, are limited to the region near Taiwan. As a result, we want to expand our beacon receiving stations in the South China Sea at Manila (Philippines), Dongsha, and Taiping Island.

The project approach might be used to calculate the height and length of the scintillation event's region. It is useful for monitoring the quality of satellite radio-communication for the FORMOSAT-7/COSMIC-2 multi-frequency form. For the scintillation event, we want to send our real-time data to the Space Weather Operation Office (https://swoo.cwb.gov.tw/V2/page/EN/index.html).