1 Introduction

Currently there is a continuous economic search for heat transfer devices, as well as their efficiency. Within these devices we find plate heat exchangers, which have an overall liquid-to-liquid coefficient efficiency of 2 to 3 times higher than other types of heat exchangers and energy storage units [1, 2]. Heat transfer coefficients are higher in plate type heat exchangers compared to shell and tube type heat exchangers due to Reynolds rates and thermal velocity [3-7]. Another outstanding aspect of plate heat exchangers is the capacity of using various viscous fluids and the fact that the presence of ice crystals generates an increase in the friction factor and hence an increase in the heat transfer process [8-11]. This is due to the conditions created by the rugged surface of the plates, which ensure the essential flow conditions for a higher efficiency of the dispersion coefficient in heat transfer, the roughness and type of material enable sub-cooling conditions [12-14].

In studies carried out by [15-21] analytical models based on numerical and experimental quantification were developed and validated, which relate to flow patterns and pressure drop models, some models represent storage rheology, which involve thermophysical states. Other studies analyzed the thermal performance of heat exchangers with 24 plates of 310 × 112 mm, using a propylene glycol concentration of 6% and ice slurry fractions between 0 and 11%, for flow rates of 1.7 m3h−1 and 3.6 m3h−1 and Reynolds of 1600 and 3350. The variation of heat exchange and pressure drop are a function of the ice slurry viscosity as well as the friction factor. Crystal size and ice fraction are very important, therefore also the Nusselt and Prandtl numbers [22]. With the studies carried out by [23-25] it is confirmed that at different flow rates, for glycol–water solutions with 6% for an ice slurry fraction from 0 to 20%, the global heat transfer coefficient remains constant, demonstrating the importance of ice concentrations and temperature variation, with pressure drops of approximately 5.5 kPa and 61.0 kPa as the flow increases from 0.414 m3h−1 and 1.1 m3h−1, also confirmed by [26].

The thermophysics of ice slurry is based on the solute. Experimenting with a mixture of ethanol/water and salt, a depression in the freezing point was observed, allowing the coexistence of the solid phase whose fluid complexity (multicomponent) generated studies of different regimes [14, 27, 28]. Enthalpy, density, thermal conductivity, viscosity, and freezing point are parameters that depend on the carrier fluid, as indicated by [5, 29], and seen in studies by [19, 30]. The methods of measuring temperature and density were carried out by the Coriolis effect. On the other hand, measurements of differential pressure, phase change and specific measurement of ions (based on carrier fluid concentrations) and their calorimetry [31] are conditions of latent heat absorbed as a function of initial and final temperatures of the fluid and the ice fractions [21, 32-34].

Fluid pumping must be ensured to avoid crystal agglomeration in the ice slurry production system [35-37]. All these studies lead us to understand that the application of potential energy systems in different areas can complement the behavior of ice slurry and consequently reduce energy consumption [23].

The use of ice slurry suspended in water has been the object of study in heat transfer and refrigeration due to its high heat capacity and its efficient cooling properties, therefore, a better thermal efficiency of the heat exchanger is generated and there is a better performance at certain concentrations [3-38]. With these conditions it is important to consider the flow stability of the ice slurry, as well as the distribution of its temperature and pressure as reported by [3, 26-50], where the use of a double flow circuit improved thermal efficiency, as well as the presence of the optimal fraction of ice slurry in suspension in the fluid [51, 52].

Overall, these studies suggest that the use of ice slurry in plate heat exchangers can significantly improve heat transfer. Because of this, it is important to collect information on its properties and its behavior, which may be different from that of conventional liquid fluids. Among the properties of ice slurry are viscosity, density, thermal conductivity, particle size, and Nusselts number, properties that affect heat transfer and heat exchanger efficiency, which can be beneficial for a variety of applications refrigeration and air conditioning applications. The present study focuses on the identification of the different parameters involved in heat transfer in a plate heat exchanger using ice slurry for different Reynolds’s regimes. Parameters such as the global heat transfer coefficient U, the proportionality of viscosity and Prandtl thermal diffusivity, the enhancement of heat transfer by conductance and surface Nusselts, have been studied to allow a better understanding of the system.

1.1 List of symbols

A

Area, m 2

\({\overline{P} }_{el}\)

Average electrical power of the calorimeter

\({A}_{c}\)

Channel area between exchanger plates, m 2

h

Convection heat transfer coefficient, W/m 2 K

H

Corrugated plate height, m

cf

Carrier Fluid

cd

Corrugated depth

c

Channel

v

Calorimeter

Cm

Convection coefficient constant for wáter

D

Diameter, m

µ

Dynamic viscosity, kg/sm

\({\mathrm Q}_{\mathrm{el}}\)  

Electrical energy absorbed by the calorimeter

f

Final

\(\dot{Q}_{w}\)

Flow water, W

U

Global coefficient of heat transfer, W/m2K

\({D}_{h}\)

Hydraulic diameter, m

W

Heat exchanger width, m

\({Q}_{el}\)

Heat absorbed by the calorimeter, J

h

Hydraulic

\(\mathop {Q_{is} }\limits^{.}\)  

Ice slurry cooling capacity, W

is

Ice slurry

i

Initial

\(\mathop {m_{is} }\limits^{.}\)  

Ice slurry mass flow rate, kg/s

\({\mathrm X}_{\mathrm{is}}\)  

Ice fraction of the calorimeter sample

LMTD

Logarithmic mean temperature difference

L

Latent heat of liquid ice, kJ/kg

F

Logarithmic mean temperature correction factor

\({\mathrm Q}_{\mathrm{lat}}\)  

Latent heat of the ice paste

m

Mass, kg

mfc

Mass flow per channel

Nu

Nusselt number

o

Out

\(\Delta P\)

Pressure drop, Pa

PR

Prandtl number

Re

Reynolds number

Cp

Specific heat, J/kg K

µ

Speed, m/s

\(\uprho\)

Specific mass, kg/m3

egs

Solution

\({Q}_{sen}\)

Sensible heat, W

k

Thermal conductivity, W/mK

T

Temperature, ºC

t

Time, s

\(\uplambda\)

Thermal conductivity, W/m K

Cn

Transfer coefficient for Ice Slurry

\(\mathop v\limits^{ \bullet }\)

Volumetric flow, m 3 /s

w

Water

2 Materials and methods

2.1 Ice slurry generation system

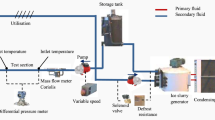
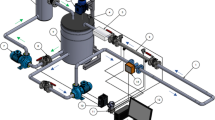
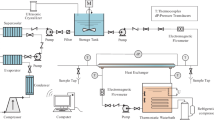
Ice slurry was generated continuously using a tube-type evaporator with a helical scraper from the company York Brasil-Integral-Energietechnik, see Fig. 1. This system was configured with a conventional refrigeration cycle (evaporator, condenser, compressor, and expansion device) and a secondary fluid (mixture of ethylene glycol and water through an agitator controlled by a frequency inverter).

Fig. 1
figure 1

Experimental diagram of the evaluation process of liquid ice in the heat exchanger

Full size image

The ice slurry was transported by a progressive cavity pump, to maintain the ice suspension from the tank to the bottom of the evaporator, it was stored in two tanks, one primary and one secondary, to maintain the ice slurry fraction after its passing through the heat exchanger, the ice fraction in the main tank did not change. A homogeneous temperature inside the tank was monitored, with type K thermocouples every 80 mm along the height of the tank, which was kept insulated to prevent heat loss. Due to the characteristics of ice slurry “ice crystals”, the flow was controlled using a 0.55-Hp peristaltic progressive cavity, with a frequency controller for the transport of the contents of the tank to the heat exchanger. The “crystal concentration” of the ice slurry fractions were measured using a calorimeter consisting of an electrical resistance (24 V), a temperature sensor and a mixer.

2.2 Thermal load system

This system was made up by an electric resistance, a water pump and a NESLAB model RTE-17 constant temperature bath with 1600 W electric power and 700 W cooling power at 0 °C. The temperature was controlled with a digital proportional, integral, and derivative “PID” controller with an error of ± 0.05 °C, which was connected to a data acquisition and processing system (Agilent Data Acquisition System and a PC). The variables involved in the study of the determination of the thermal load were the cooling capacity of the heat exchanger, obtained by measuring the temperature variation and fluid flow throughout the exchanger and the pressure drop obtained by a pressure translator (working range of 0–10 kPa). These variables were evaluated at different concentrations of ice slurry, thereby determining the Prandtl, Nusselt, and Reynolds numbers.

The tests were carried out in two stages: the preparation of the thermal load, maintaining a constant temperature of 30 ºC, and the generation of ice slurry, reaching a temperature of − 3.5 ºC, with a homogeneous concentration of ice. The tests were performed out with different flows of ice slurry.

The experimental section consisted of a plate heat exchanger, chosen for its thermal characteristics. The heat exchanger used was Alfa Laval and had 16 plates of 430 × 210 mm in AISI 316 L stainless steel, with a hydraulic diameter of 4 mm (variables), a heat transfer coefficient range between 3500 and 5500 W/m2 ºC and a National Pipe Thread “NPT” tapered threaded tube. The rugged plates have a ripple characteristic to increase area and fluid mix: each plate has 0.032 m2 of heat transfer area. Teflon-coated 0.17 mm diameter K-type thermocouples were placed between the plates through which the ice slurry flows. This configuration of thermocouples was based on studies on its location and its behavior within the plates and the pressure differential [44]. Thermocouples were also installed at the inlet and outlet of the heat exchanger and in the thermal water load to determine the energy balance in the exchanger, the cooling capacity in relation to ice slurry, and the relative thermal load. The gasket material was NBR, and the flow type was counter current for better heat exchange.

To measure the pressure, and drop caused by ice slurry, a differential pressure transducer was used, with a range of 0 to 10 kPa, fed by a high frequency received from the modulator. The signal generated (voltage) by the transducer is sent to the data acquisition system. To take the sample two valves A and B were installed, both at the entrance and exit.

3 Experimental method

The basic stage was the set-up of the test conditions, the generation of ice slurry and the conditioning of the load. The ice slurry was obtained with a 12% v/v ethylene glycol–water solution. The solution was pumped through the evaporator in a continuous process and at a defined volume, generating the ice slurry with the appropriate temperature and ice fraction conditions. The ice slurry was stored in a primary tank, with a capacity of 0.55 m3.

To avoid the agglomeration of the ice slurry inside the storage tank, a constantly working mixer was used, keeping the ice slurry required to proceed by pumping the plate heat exchanger. The speed of the mixer was adjusted with the frequency converter. Ice slurry was produced for the different ice fractions required in each test, from 3.0 to 21%. Each flow rate was determined by a calorimeter for each ice fraction condition. The established temperatures were between – 2 ºC and − 3.8 ºC. The generation time of the ice fraction varied between 1.5 h to 3 h. The thermal load was established for a volume of 0.4 m3, where it was heated from 18 ºC to 30 ºC with a bank of 2000 W electrical resistances. The time to condition the thermal load was 1 h. Once the experimental temperature was reached, the resistance bank was turned off and the thermal bath remained constant. The temperature had an error of ± 0.01 °C. Once the conditions of the ice slurry and the thermal load had been reached, the ice slurry generator was turned off. At this stage, the process of data acquisition, the temperature, the pressure, and the fraction of the ice slurry at the inlet and outlet of the plate heat exchanger were kept constant. The ice slurry flow rate was regulated using the frequency converter for values from 10 to 60 Hz, for 0.070 to 0.192 kg − 1, respectively. The ice slurry passes through the exchanger and then to the secondary tank. The water, after passing through the exchanger goes to the other storage tank. In this way the entry conditions of the water and the ice slurry remain constant. For each ice slurry flow rate, all the variables were observed at the outlet of the heat exchanger when the steady state was reached and then, the flow was varied increasing it until the process attained the highest flow. The thermal load flow and its temperature were kept constant throughout the tests.

3.1 Established data

Tests were initially performed to establish the performance of the heat exchanger using chilled water, to validate the results with the data published by the manufacturer, and to establish the thermodynamic properties of the ice crystal suspension in relation to the fraction of ice slurry and its enthalpy [45, 46].

Studies measuring the cooling capacity of ice slurry and water have been made. The temperature difference between the inlet and outlet fluids was measured, as well as the pressure drop across the heat exchanger, these measurements have allowed the evaluation of the ice slurry heat transfer efficiency and its comparison with water. Figure 2 shows the indirect measurement of the cooling capacity, showing a linear relationship between both systems (heat transfer from ice slurry and water); as one fluid increases, the other fluid also increases, thus suggesting that this phenomenon is related to the mentioned variables, as well as the correlation between both phenomena.

Fig. 2
figure 2

Cooling capacity in heat transfer for ice slurry and water

Full size image

The calculation of fluid properties was based on the average temperature of the fluid in each circuit of the heat exchanger. To avoid heat leakage from the heat exchanger, it was lined with Armaflex AC material (− 50/ + 110 ºC). The plate performance data was taken from the manufacturer Alfa Laval, the plate material was Nitrile Butadiene Rubber "NBR", and the heat balance between hot and cold-water flows revealed a difference of less than 5% according to the manufacturer’s conditions.

For the thermal power conditions of both fluids: ice slurry Eq. (1) and pure water Eq. (2) were used:

$$Q_{is} = m_{is} \left[ {Cp_{cf} (T_{f,i} - T_{f,o} ) + (x_{is,i} - x_{is,o} )L} \right]$$
(1)
$$\dot{Q}_{w} = \dot{m}_{w} Cp_{w\,} \Delta T$$
(2)

The concentration of ice slurry has a peculiar importance in heat transfer, the results of some investigations carried out regarding the concentrations of ice slurry indicated that the optimal fraction of ice in suspension generates a higher performance of the heat exchanger, this is shown in the graphs of [28, 36, 47] in relation to the flow of the ice slurry.

The equations referring to the thermal conductivity were made for each situation, considering the temperature of the heat exchanger film, the average electrical power of the calorimeter Eq. (3), the electrical energy absorbed by the calorimeter Eq. (4) and the ice fraction of the calorimeter sample Eq. (5).

$$\overline{P}_{el} = \overline{V}.\,\overline{I}$$
(3)
$$Q_{el} = \overline{P}_{el} .\,t$$
(4)
$${X}_{is}= \frac{{Q}_{el}- {Q}_{sen}}{{Lm}_{is}}$$
(5)

For the determination of the heat exchanger performance and for the definition of the global heat transfer coefficient, as a function of the logarithmic mean temperature, the area of the heat exchanger and the cooling capacity of the ice slurry were given by the following Eq. (6):

$$U = \frac{{\dot{Q}_{is} }}{ALMTD}$$
(6)

The viscosity of the ice slurry was determined by calorimetry. The samples were taken from a constant mixture of the ice slurry, where the peculiarity of the contact of the suspended ice particles was established. The following Eq. (7) was used:

$$\mu_{is} = \mu_{cf} \left[ {\left( {1.2,5c_{v,is} } \right) + 10,05c_{v,is}^{2} + 0,00273.e^{{16,6.c_{v,is} }} } \right]$$
(7)

To find the Reynolds number Eq. (6), the authors based the calculations on articles in which the experimental results show that the ice slurry is a function of crystals in aqueous solution:

$${\text{Re}}_{{D_{h} }} = \frac{{\rho uD_{h} }}{\mu } = \frac{{\dot{m}_{c} (2H)}}{{\mu A_{c} }} = \frac{{2\dot{m}_{c} }}{\mu W}$$
(6)

For the Nusselt number conditions, tests were carried out with water (thermal load) and with 12% v/v ethylene glycol aqueous solution, to obtain the following thermal equilibrium, Eq. (7):

$$\dot{m}_{w} \,Cp_{w} \,\Delta T_{w} \, = \,\dot{m}_{egs} \,Cp_{egs} \,\Delta T_{egs}$$
(7)

For the global coefficient of heat exchange, it was considered that the thermal resistance to heat exchange by conduction through the plate was negligible, thus the authors used the following Eq. (8):

$$\frac{1}{{\overline{U}}} = \frac{1}{{h_{w} }} + \frac{1}{{R_{F,w} }} + \frac{{e_{p} }}{{k_{F,is} }} + \frac{1}{{R_{F,is} }} + \frac{1}{{h_{is} }}$$
(8)

The calculation of the global coefficient of the plate heat exchanger establishes that the thermal resistance by conduction is negligible [46]. The parameters for each flow will be followed with the following Eq. (9):

$$\frac1U=\frac1{cm\;\mathrm{Re}_1^a}+\frac1{cn\;\mathrm{Re}_2^a}$$
(9)

For the convection transfer variables as a function of thermal conductivity, the following Eq. (10) was established:

$$h = \frac{Nu\,k}{{D_{h} }}$$
(10)

Considering the equation established by [48], to determine the magnitude of the plate heat exchangers, Eq. (11) is used and for the indistinct conditions of thermal load and ice slurry. Equations (12) and (13) were used:

$$Nu=c\;\mathrm{Re}^a\;\Pr^{0,4}$$
(11)
$${\overline h}_w=\frac{c\Pr_w^{0,4}k_w}{D_h}\text{Re}_w^a\,\, \text{for the thermal load}$$
(12)
$$\overline{h}_{egs} = \frac{{c\Pr_{egs}^{0,4} k_{egs} }}{{D_{h} }}{\text{Re}}_{egs}^{a} \, \, {\text{for the ice slurry}}$$
(13)

To determine the pressure drop referring to the friction factor, for each condition of the tests performed, Eq. (14) was used:

$$\Delta P = f\frac{{L_{e} u^{2} \rho }}{{2D_{h} }}$$
(14)

The mass flow was calculated with Eq. (15):

$$f = \frac{{4\rho h^{3} W^{2} \Delta P}}{{L_{e} \dot{m}^{2} }}$$
(15)

Equation (16) was used to calculate the latent heat of the ice paste:

$$Q_{lat} = m_{pg} x_{pg} L$$
(16)

4 Results and discussion

Variations were observed in the cooling capacity of the heat exchanger as a function of the mass flow rate according to Eqs. (1) and (2), as well as variations in the effectiveness of the temperature parameters, in the suspension of the ice slurry and in the cooling conditions viscosity (according to Eq. 7), conditions that determine the second performance [25, 49].

The initial and final fractions of ice slurry show a considerable increase in cooling capacity, compared to pure water tests: the cooling capacity increases up to 3 times. In each test, the fraction of ice at the outlet of the heat exchanger is shown, with initial fractions greater than 11% and mass flow rates greater than 0.16 kg−1. The fraction at the outlet of the exchanger is greater, indicating 0.05% the presence of ice crystals at the outlet.

The heat transfer coefficient is between 4357.7 W and 8643.3 W according to the variation of the ice slurry fraction, which is related to the critical values of ice fraction for different Reynolds regimes, for the viscosity and the evolution of the friction factor, whose behavior is established with Eq. (14) and studied in [50, 53].

As the flow increases, so does the measurement uncertainty, considering the flow rate and ice crystal suspension which are consistent with the literature [18, 54]. See Fig. 3.

Fig. 3
figure 3

Variation of the cooling capacity of the heat exchanger as a function of the mass flow

Full size image

4.1 Global heat exchange coefficient

Variations of the global coefficient of heat exchange with ice slurry mass flow rate were observe for higher initial concentrations. This global coefficient (Eqs. (6) and (7)) increases between the initial mass flow rates of 0.074 kg s−1, and output 0.184 kg s−1 for a global transfer coefficient of approximately 790 Wm−2 ºC−1, established for concentration fractions from 0.03 to 0.15%. These conditions are also shown in tubular exchangers where an increase in the global coefficient and in the distribution, ratio is observed [50, 55-57].

According to studies at temperatures below the freezing point, ice slurry has characteristics of thermophysical efficiency [9, 58]. The behavior of pure water can be seen in Fig. 4, which corresponds to expectations. It is very similar to the case of a small solid fraction, as proposed by [59], for a global transfer coefficient as referenced by [34, 45]. The behavior expected is confirmed in the present study.

Fig. 4
figure 4

Variation of global coefficient as a function of ice slurry mass flow

Full size image

In Fig. 4, the global heat transfer coefficient increases as the mass flow increases, according to [17]. It is seen that at initial ice fractions of 0.03%, the Fig. 4. shows behavior like that of pure water.

4.2 Pressure drop conditions

The differential pressure data in the plate heat exchanger was calculate using Eq. (14). The experimental results are based on the initial mass flow rate of 0.04 kg s−1, between the pressure ranges of 2500 Pa to 3500 Pa. Different initial fractions of the ice slurry were observed. See Fig. 5.

Fig. 5
figure 5

Variation in pressure drop for different flow rates of ice slurry

Full size image

In studies performed for higher initial concentrations of ice slurry, the pressure drops increase from 5500 to 8500 Pa. For heat exchanger outlet mass flow rates of 0.185 kg s−1, an increase corresponds to each outlet ice fraction of 0.03 to 0.15%, as shown by [3, 11, 20, 60]. Therefore, it is established that for a mass flow rate variation range of 21.60%, a pressure drops for initial conditions of 45.45% was observe. For the highest flow conditions, a differential of 41.17% was observed, coinciding with the bibliographic results.

Differential pressure is shown to increase with flow in all cases tested and different initial concentrations of ice slurry led to an increase of about 5% in pressure drop [23, 47].

The calculation of uncertainties indicates that, for this working range, the value of the uncertainty is considered constant. Likewise, the presence of ice particles in the fluid reduces the effective temperature of the mixture, this increases the temperature difference and the wall of the exchanger, generating an improvement in heat transfer; increasing the ice slurry fraction can increase fluid pressure and improve efficiency, this is also reported by [3, 26].

The variation of the friction factor (Eq. 14) is as a function of the Reynolds number (Eq. 6) for 600 < Re < 1810. The conditions of the pressure drop and the pumping power for the ice slurry were determined [61, 62]. The ranges of the Reynolds number are different when analyzing the cases with and without ice slurry [61, 63]. Based on this, the results show that the water curve shifts to the right. See Fig. 6. The adjustment of the curve was made for all the ice slurry tests and the adjustment curve has the same slope referred to the same exponent in Reynolds, but with a difference of a constant order of magnitude C, whose relation corresponds to f = CRea.

Fig. 6
figure 6

Variation of the friction factor with the Reynolds number in ice slurry

Full size image

4.3 Nusselt number with respect to the Reynolds regime

The results of the behavior of the Nusselt number show important extrapolation conditions for ice slurry at different concentrations. The highest initial ice slurry fractions reflect the loss condition for different Reynolds regimes. The physical properties of suspended crystals [16, 28] improve heat transfer [64] with an increase in Nusselt number. A decreasing behavior of the friction factor was observed with a higher ice fraction [65, 66] and the heat transfer coefficient of ice slurry showed an increase compared to pure water.

Compared to water with a Nusselt 7.98 < Nu, the Nusselt number is lower with the presence of ice slurry. This relationship is like the one observed by [67] using tubular type exchangers. In this case, there is also a shift of the pure water curve to the right, this is due to the highest Reynold among all the tests carried out. Significative differences between the values of the thermophysical properties of the different flow rates tested were found.

The constants "a", "b" of the Nusselt equation were evaluated by least squares methods on the mass of experimental data, obtaining the expression for the coefficients of the heat exchanger with the flow without phase change.

The results of the behavior of the Nusselt number are shown in Fig. 7, based on Eq. (7). This number corresponds to (4.21 < Nu), depending on the Reynolds number, reaching values of 1810 in the plate heat exchanger for the highest initial fractions of ice slurry. The physical properties of the fluid and the crystals in suspension [16] correspond to an improvement in heat transfer and a decrease in the friction factor with a higher ice fraction, respectively and according to [64]. The heat transfer coefficient of ice slurry shows an increase compared to pure water [26, 68].

Fig. 7
figure 7

Nusselt vs Reynolds for different concentrations of ice slurry and pure water

Full size image

In Fig. 7 it can be seen that as the concentration of the ice slurry increases, the Nusselt also increases, this suggests that a higher heat transfer efficiency of 0.15% is achieved, this is due to the fact that the ice particles in the fluid reduce the effective temperature of the mixture, generating an increase in the temperature difference between the fluid and the wall of the exchanger [68, 69], in the conduction and convection relationship that occurs in the system, improving the transfer of heat. This suggests that the use of ice slurry in plate heat exchangers can significantly improve heat transfer and increase the Nusselt number, being beneficial for a variety of refrigeration and air conditioning applications.

In the variation of the constant against Reynolds, it is observed that the value increases for water. This value also increases with the increase in the initial ice fraction, which was observed in each experiment, observing between 3 and 15%, it was determined that the latent heat given off by the ice crystals affects the Reynolds number as a function of the mass flow; therefore, the Nusselt at the surface and the global heat transfer coefficient related to the fraction of ice crystals, correspond to the local correlation of Nu and the coefficients obtained: a = 0.56 and c = 0.161, referring to the thermophysical properties of ice slurry [57, 63].

With the results, see Fig. 7, a clear approximation trend of the curves is observed, suggesting that the function should correctly correlate the parameters, which are related to the evidence of numerical studies under the dependence of different Reynolds and Prandtl regimes [69, 70]. However, these behaviors reflect the transport of ice slurry in plate heat exchangers and show the need for more experimental data to be able to propose a correlation. In other studies, the behavior at different regimes for Reynolds and ranges of (5.89 < Pr < 13.70), establish heat transfer coefficients in transient and turbulent regimes [71], such as the reduction of the thermal power of ice slurry and pure water, according to [21].

In Fig. 8 certain conditions are shown at constant variation NuPr−0.4 in relation to Reynolds. It is observed that the value increases the heat transfer to the water in relation to the increase in the ice fraction. The unestablished conditions for this phenomenon contribute to the conditioning of the limit term, which is a function of the speed of the turbulence [21, 72].

Fig. 8
figure 8

Reynolds vs Prandtl for different concentrations of ice slurry and pure water

Full size image

5 Conclusions

It is technically feasible to use ice slurry in plate heat exchangers. Due to the enhanced heat transfer, ice slurry shows favorable results and advantages compared to the water-water case. It was found that the cooling capacity and the global heat exchange coefficient increased up to three times.

In the behavior of ice slurry, a substantial pressure drops of 2.5 kPa and 8.5 kPa was observe. These results show a relationship to the friction factor for water and ice slurry at mass flows of 0.070 kg/s and 0.192 kg/s, respectively. For Reynolds (Re ≥ 600), the friction factor was low, and for dry ice inlets with concentrations greater than 11%, ice slurry fractions between 3 and 5% were observed at the outlet, which was related to the higher presented viscosity, with a pressure drop of 0.003 Pa. When the concentration of ice slurry was higher at the inlet, the number of Nu increased; compared to water, Nu was lower = 4.21, presenting ice fractions at the outlet of the heat exchanger.

From the experience, it is concluded that more information is required to understand the behavior of heat transfer in the different types of plate heat exchangers. The variation of the number of plates must be considered, the characteristics of the thermal load and the heat distribution can be varied, considering the use of other types of heat exchangers with different parameters of viscosity and friction. It is also concluded that with the increase in ice slurry, an increase in fluid pressure is also generated and the efficiency of the heat exchanger is improved. On the other hand, this effect could be attenuated as the ice concentration increases, due to the decrease in fluid flow in the exchanger and thus limit the improvement in heat transfer.