1 Introduction

In the real world, the data is occasionally missing, perplexing, ambiguous, or unclear. Probability theory is incapable of dealing with erroneous and ambiguous data, but fuzzy sets (FS) are capable of dealing with such unclear and imprecise data (Zadeh 1965). However, only FS carries a single membership value of ambiguous and imprecise information, which is insufficient in many actual scenarios to describe evidence of support and opposition together. To address this issue, the notion of an intuitionistic fuzzy set (IFS) was developed by Atanassov (1986), which takes into account both the truthiness and falsity of each piece of information. Over the last few decades, researchers and practitioners have concentrated their attention on IFS concepts, which have been widely implemented in a number of fields such as logic programming, medical diagnosis, pattern recognition, robotic systems, fuzzy topology, machine learning, and market prediction, to name a few. IFS theories are frequently being studied in depth, and the area of their applications is being expanded. As a result, intuitionistic fuzzy decision-making and intuitionistic fuzzy preference relations have been proven to be extremely essential. The IFSs and its extension sets have vast application opportunities in the disciplines of multi-attribute decision making (MADM) and multi-attribute group decision making (MAGDM), but they offer numerous fascinating and difficult research problems (Wan and Dong 2020; Sharma et al. 2022).

To handle uncertain information in a precise way, the possibility theory is used as the simplest mathematical theory among the contemporary uncertainty theories. Zadeh (1978) developed the possibility theory of fuzzy sets, which is comparable to probability theory since it is dependent on a set function, and that has been expanded by various academicians, including Yager (1992); Klir (1999), and others. Carlsson and Fullér (2001) defined the interval-valued probability mean, crisp probability mean value, and variance of continuous possibility distributions. Fullér and Majlender (2003) investigated the weighted interval-valued possibility mean value of fuzzy numbers. Liu and Yuan (2007) introduced the triangular intuitionistic fuzzy set by generalizing the IFS with respect to TFN. The possibility mean, variance, and covariance of TIFNs are introduced to solve MCDM problems (Wan et al. 2013; Wan 2013). Recently, the concept of the possibility mean, variance, and covariance of a generalized intuitionistic fuzzy number was proposed by Garai et al. (2018). The mean and variance are regarded as the most influential parameters in statistical analysis. In order to tackle real-world challenges, several academicians have employed the possibility mean and variance to express the mathematical features of fuzzy numbers.

The DEA is an essential tool for decision makers (DMs) to measure the performance of the DMUs. It is a non-parametric technique that studies the measurement of the efficiency score of the DMUs in the presence of multiple inputs and outputs. Charnes et al. (1978) studied the pioneer work (Farrell 1957) to measure the relative efficiency of the DMUs and developed the first DEA model, called the CCR model, under the assumption of constant return scale. Banker et al. (1984) developed the BCC model under the assumption of variable return scale. These two DEA models are extensively used to solve a variety of issues in business and economics, engineering, and industries including telecommunications, manufacturing, production, transportation, energy, finance, and marketing. The traditional DEA models required crisp inputs and outputs. But the real world usually contains some degree of uncertainty. Optimization under uncertainty is now one of the most interesting topics, which may be approached from several directions (probabilistic, stochastic, interval, fuzzy, etc.) and performed using various techniques. For the first time, Sengupta (1992) used fuzzy inputs and outputs in DEA to measure the performance of the DMUs. After that, many authors, researchers, and academicians presented different techniques to solve fuzzy DEA models, which appeared in the bibiliometic review papers (Emrouznejad et al. 2014; Zhou and Xu 2020). Recently, Mohanta et al. (2023) proposed a novel ranking approach to solve fuzzy LPP and fuzzy DEA models. To measure the performance of the DMUs in a highly uncertain environment, Gandotra et al. (2012) proposed the Intuitionistic fuzzy DEA model based on a weighted entropy approach. Hajiagha et al. (2013) used a logarithmic function to convert the intuitionistic fuzzy CCR and BCC models into corresponding crisp DEA models and evaluated the performance of the finance institutions. Puri and Yadav (2015) presented the optimistic and pessimistic efficiencies with intuitionistic fuzzy input/output data in DEA. Arya and Yadav (2018) proposed SBM and a super efficiency SBM model in the presence of intuitionistic fuzzy numbers to measure the efficiency of the hospitals. Fallahpour et al. (2016) developed an integrated DEA-artificial neural network (DEA-ANN) technique for supplier evaluation and selection. Otay et al. (2017) proposed an integrated IFDEA and intuitionistic fuzzy analytical hierarchy process (IF-AHP) for solving the performance evaluation problem of healthcare institutions. Singh (2018) proposed the intuitionistic fuzzy DEA/AR model in the presence of TIFN, and an expected value approach is used to solve it. Arya and Yadav (2019) proposed the intuitionistic fuzzy data envelopment analysis (IFDEA) and dual IFDEA (DIFDEA) models based on \(\alpha\) and \(\beta\)-cuts, and the index ranking approach is used to rank the DMUs. Liu et al. (2019) proposed two DEA cross-efficiency models to get the cross-efficiency values of all alternatives and the priority weight vector of the intuitionistic fuzzy preference relation. Edalatpanah (2019) proposed a ranking approach for solving the intuitionistic fuzzy DEA model. Shakouri et al. (2020) proposed the intuitionistic fuzzy network DEA model based on a parametric approach. Arya and Yadav (2020a) developed the intuitionistic fuzzy BCC model and intuitionistic fuzzy super efficiency BCC model with TIFNs input and output data and studied the infeasibility of IFDEA models. Arya and Yadav (2020b) proposed an intuitionistic FDEA model based on TIFN to measure the efficiencies of each DMU by using the \(\alpha\) and \(\beta\)-cut approaches. Javaherian et al. (2021) proposed the fuzzy network two-stage DEA model based on the expected value of the Intuitionistic fuzzy inputs and outputs. Arteaga et al. (2021) proposed a novel method for solving IFDEA. Sahil et al. (2021) proposed the parabolic intuitionistic fuzzy DEA model based on a parametric approach. Rasoulzadeh et al. (2022) proposed integrated Markowitz and cross-DEA models to measure the efficiency of the enterprises on the Tehran Stock Exchange. Ardakani et al. (2022) developed the two-stage network DEA model in the presence of trapezoidal intuitionistic fuzzy inputs and outputs to evaluate the efficiency of the DMUs in interval form. The given Table 1 compares the proposed technique with the existing techniques.

Table 1 Development of Intuitionistic Fuzzy DEA Models
Full size table

During the review of the literature, it was found that many authors studied different versions of the IFDEA model and solved them using different techniques, as shown in Table 1, but no one yet worked on IFDEA by applying the possibility mean approach. Possibility theory in fuzzy set, similar to probability theory in crisp set, helps in effectively representing highly uncertain data (Zadeh 1978; Carlsson and Fullér 2001). As a result, we have recommended here to use the possibility mean of the observed Intuitionistic fuzzy input and output data to appropriately depict the uncertainty. This is the first paper in which the weighted possibility mean for TIFN is applied to solve the IFDEA model. The weighted possibility mean function is associated with a risk factor that represents the decision-maker’s risk-taking attitude. The main contributions to this article are

  • A novel technique for solving Intuitionistic fuzzy DEA model is developed based on the weighted possibility mean approach, which converts it into the corresponding crisp DEA model.

  • The efficiency scores of the DMUs are obtained by solving the corresponding crisp DEA model with different risk factors, and DMUs are categorized into efficient and inefficient groups based on their overall efficiency score.

  • The proposed technique is used to measure the agricultural performance of Indian states.

The weighted possibility mean approach is used to covert the IFDEA model into the equivalent crisp DEA model, which is nothing more than a crisp LP problem. Any existing LP solution approach can be used to solve the crisp DEA model with different risk levels, and the efficiency score of each DMU is evaluated. The proposed approach is more adaptable and efficient than previous methods and is useful for ranking DMUs because it gives the exact value of the efficiency score of the DMUs rather than an interval value. Two numerical examples are considered here to demonstrate its validity and applicability, and the results obtained with the existing techniques are compared. Finally, a real-life case study is taken into consideration in order to assess the agricultural performance of Indian states by using agricultural input and output depicted as TIFN.

The remaining portions of this study are organized as follows: Sect. 2 provides an in-depth review of the literature on the application of DEA in the agricultural sector, both at the international and national levels. Section 3 presents some essential concepts of TIFS and the weighted possibility mean for TIFN. Section 4 presents a framework for the intuitionistic fuzzy DEA model and its step-wise solution technique. Section 5 presents two numerical examples to show the existence and applicability of the proposed technique, and the efficiency scores of the DMUs in the proposed approach are compared with the existing approach. Section 6 presents an application to measure the state-wise agricultural performance in India. Finally, Sect. 7 focuses on the conclusion and the direction of future studies.

2 DEA in agriculture: a literature review

Data Envelopment Analysis (DEA) is widely recognized as a prominent benchmarking method used for assessing performance in many industries and sectors (Liu et al. 2013; Sueyoshi et al. 2017; Mohanta et al. 2021; Kaffash et al. 2020; Camanho et al. 2023). Its versatility and effectiveness have contributed to its popularity among researchers and practitioners. Moreover, it has been shown that the use of DEA enables organizations to effectively identify specific areas within their operations that may be optimized, resulting in cost reduction and increased productivity. The use of the DEA and associated methodologies are employed by several researchers to assess agricultural efficiency and productivity in various regions. Here, we have conducted a comprehensive study of worldwide literature related to the analysis of agricultural performance. Aldaz and Millán (2003) proposed a new procedure for the measurement of efficiency and technical efficiency change by using DEA with full panel data of Spanish regional agriculture sectors. Balcombe et al. (2008) examined the sources of technical efficiency for rice farming in Bangladesh by using double bootstrap DEA model. Chiu et al. (2011) developed a modified two-stage DEA model based on the model to evaluate China’s agricultural efficiency and repaired efficiency. Adhikari and Bjorndal (2012) measured the technical inefficiency in Nepalese agriculture by using the DEA and SFA model. Moreira et al. (2011) performed production efficiency analysis for the 40 countries with largest value added by agricultural sector in 2005. Zamanian et al. (2013) investigated the levels of technical efficiency in agricultural sector of MENA countries by using DEA and Stochastic Frontier Analysis approaches in 2007–2008. Liu et al. (2015) applied DEA model to investigate the degree of efficiency and efficiency change of prefecture-level cities in the North-East China from 2000 to 2012. Assessment and selection of optimal schemes of agricultural industrial structure using DEA model gave a greater and better insight of agricultural industrial structure and was the first of such researches in Pakistan (Ahmad and Jun 2015). Nowak et al. (2015) used DEA for the measurement of the technical efficiency of agriculture in the 27 European Union (EU) countries in 2010. Kočišová (2015) investigated the relative technical efficiency of the agricultural sector in the European Union using the DEA during the period 2007–2011. Toma et al. (2015) applied DEA at regional level of 36 counties to analyze the performance of agriculture practiced in plain, hill and mountain areas. Atici and Podinovski (2015) measured the efficiency of the agricultural farms in different regions of Turkey by using DEA. An examination of the applicability of DEA method is used to measure the agriculture sectors efficiency of EU Country (Laurinavičius and Rimkuvienė 2017). Li et al. (2018) developed indices for the overall technical efficiency (OTE) and energy-saving target ratio (ESTR) using DEA to calculate the relative efficiency and energy-saving potential of 30 provinces in China from 1997–2014. Kocisova et al. (2018) examined the relative efficiency of agriculture in the European Union using SBM-DEA for the period 2005–2015. Horvat et al. (2019) examined the relative technical efficiency of agricultural production in 25 Serbian districts using two-stage data envelopment analysis. Wan and Zhou (2021) measures the total factor productivity (TFP) of agricultural management as well as technological change (TC) and technical efficiency change (EC) based on the Malmquist-DEA Modeling and drawing on the data from 12 cities in Hubei, a central province of China. Hsu et al. (2023) applied the dynamic slacks-based measure (DSBM) and the total-factor agricultural efficiency (TFAE) to explore the overall agricultural production efficiency of 30 administrative regions and the eastern, central, and western regions of China from 2012 to 2016. Atici et al. (2018) measured the agricultural productivity change of 34 OECD countries between years 1990 and 2014 by using DEA and MPI in the presence of Fuzzy agricultural data. Aye et al. (2018) measured the efficiency of agricultural production in South Africa from 1970 to 2014, using an integrated two-stage fuzzy approach. Nastis et al. (2019) proposed a novel estimation technique for solving fuzzy DEA and which is used to measure the organic farm efficiency of EU agricultural systems. Mardani and Salarpour (2015) used fuzzy DEA model to analyze the technical and scale efficiency of potato production in 23 Iranian provinces. Oukil (2023) presented a new application of inverse DEA for strategic decision making: mergers & acquisitions (M &A) in the agricultural sector. Recently, Kyrgiakos et al. (2023) did a literature study of 120 research papers that were all about how DEA could be used in agriculture, with a focus on sustainability. The results made it clear that the way data is collected needs to be more organised. This method should include a lot of different kinds of farming data, such as both quantitative and qualitative that have been neatly organized. A suggestion was also made to look into how the DEA method could be combined with data from GIS sources to make the whole study better.

Agriculture is the backbone of any third-world or developing country. Particularly to mitigate the demand of a large population in India, agriculture has played a vital role in food consumption. The concept of agriculture is based on the art and science of cultivating soil, raising crops, rearing animals, and fishing. After independence, in the first Five-Year Plan (FYP), the Indian government laid the foundation for development in the agricultural sector. The Planning Commission of India brought some policies for the reformation and development of Indian agriculture, primarily to enhance productivity (for example, the abolition of mahalwary and ryotwari and the implementation of land-celling). In the 1960s, the Green Revolution set a benchmark to prioritise the raising of some single crops like wheat and rice. The Indian government is now concerned about increasing food output to meet the needs of the world’s second-most populous country, with 1.3 billion people. The government is also encouraging farmers to practice organic farming. In 2020, the ’Self-Sufficient India’ mission India has taken the first step towards a major agricultural revolution, which aims to increase local food self-sufficiency in a sustainable manner in order to mitigate food crises. Agriculture is essential for the growth of the Indian economy, as the activities of employees in agriculture and related sectors account for 54.6% of the overall workforce. Subsidies for fertiliser and electricity were implemented to boost economic growth, enhance food security, extend access to these resources, and lower irrigation costs. Indeed, statistics show that agricultural subsidies have helped achieve some of these goals. The non-food part of agriculture is critical to the growth of numerous industries, including textile, food processing, and agro-based industries. Many authors investigated the Indian agricultural industry and measured its performance, efficiency, and productivity over different time periods. The DEA model was used to assess the allocative and technical efficiency of 300 wheat farms in Punjab (Jha et al. 2000) and the technical and scale efficiencies of tomato-producing farms in Karnataka with various output levels (Murthy et al. 2009). Ray and Ghose (2014) measured the technical efficiency of the agriculture sector of India in the years after the Green Revolution. Mathur and Ramnath (2018) examined the efficiency in food grain production in India for the period 1960–61 to 2013–14 using DEA and SFA. The DEA model was used to analyse the efficiency of all farms, and the RF approach was utilised to explore the factors important in predicting farm performance (Nandy and Singh 2020b). Again, Nandy and Singh (2020a) used a hybrid fuzzy DEA and machine learning algorithm to measure the efficiency of paddy producers in eastern India. Chaubey et al. (2023) measured the agricultural performances of Indian states using a non-parametric approach. Malmquist-DEA was used to measure the agricultural productivity and efficiency of Indian States (RL and Mishra 2022; Chaubey et al. 2022). However, there is a limited amount of literature in which the fuzzy DEA model is employed in agriculture. Furthermore, we could not find any research that employed an extended fuzzy set to effectively represent uncertainty and was used to measure agricultural performance.

3 Preliminaries

This section studies the preliminary results of IFS and develop the IFDEA model for evaluation performance of the DMUs.

Definition 1

(Zadeh 1965) The fuzzy set (FS) \(\hat{F}\) in \(\Omega\) is defined as

$$\begin{aligned} \hat{F}=\{ \langle x, \mu _F \rangle : x \in \Omega \} \end{aligned}$$
(1)

where the function \(\mu _F: \Omega \rightarrow [0,1]\) is the membership grade.

Definition 2

(Atanassov 1986) The Intuitionistic fuzzy set (IFS) \(\hat{I}\) in \(\Omega\) is defined as

$$\begin{aligned} \hat{I}=\{ \langle x, \mu _I, \nu _I \rangle : x \in \Omega \} \end{aligned}$$
(2)

where the functions \(\mu _I, \nu _I: \Omega \rightarrow [0,1]\) are the membership and non membership grades and defined as \(0 \le \mu _I+\nu _I \le 1\).

Definition 3

(Li 2010) Triangular intuitionistic fuzzy number (TIFN) is denoted by \(\widehat{A} = \langle a^L, a^M, a^U; \phi _a, \psi _a \rangle ,\) where the two membership functions for the truth, and falsity of x is defined as follows:

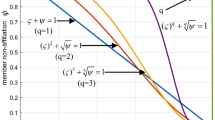
$$\begin{aligned} \mathfrak {T}(x)= {\left\{ \begin{array}{ll} \dfrac{x-a^L}{a^M-a^L} \phi _a,~~~ a^L \le x \le a^M \\ \phi _a, ~~~x=a^M\\ \dfrac{a^U-x}{a^U-a^M} \phi _a,~~~a^M \le x\le a^U\\ 0, ~~otherwise \end{array}\right. } \mathfrak {F}(x)= {\left\{ \begin{array}{ll} \dfrac{a^M-x+\psi _a (x-a^L)}{a^M-a^L},~~~ a^L \le x \le a^M \\ \psi _a, ~~~x=a^M\\ \dfrac{x-a^M+\psi _a(a^U-x)}{a^U-a^M}, ~~~ a^M \le x\le a^U\\ 1, ~~otherwise \end{array}\right. } \end{aligned}$$

where \(0 \le \mathfrak {T}(x)+ \mathfrak {F}(x) \le 1,~ x \in \mathbb {R}.\) Graphically it is represented in Fig. 1.

Fig. 1
figure 1

The truth and falsity membership grade for TIFNs

Full size image

Definition 4

(Li 2010) Suppose \(\widehat{A}_1=\langle a_1^L, a_1^M, a_1^U;\phi _{a_1}, \psi _{a_1} \rangle\) and \(\widehat{A}_2=\langle a_2^L, a_2^M, a_2^U; \phi _{a_2}, \psi _{a_2} \rangle\) are the two TIFNs. The arithmetic relations are defined as

  1. 1.

    \(\widehat{A}_1 \oplus \widehat{A}_2=\langle a_1^L+a_2^L,a_1^M+a_2^M,a_1^U+a_2^U; \phi _{a_1} \wedge \phi _{a_2}, \psi _{a_1}\vee \psi _{a_2} \rangle .\)

  2. 2.

    \(\widehat{A}_1 - \widehat{A}_2=\langle a_1^L-a_2^U,a_1^M-a_2^M,a_1^U-a_2^L; \phi _{a_1} \wedge \phi _{a_2}, \psi _{a_1}\vee \psi _{a_2} \rangle .\)

  3. 3.

    \(\widehat{A}_1 \otimes \widehat{A}_2=\langle a_1^L a_2^L,a_1^M a_2^M,a_1^U a_2^U; \phi _{a_1} \wedge \phi _{a_2}, \psi _{a_1}\vee \psi _{a_2} \rangle .\)

  4. 4.

    \(\lambda \widehat{A}_1 = {\left\{ \begin{array}{ll} \langle \lambda a_1^L, \lambda a_1^M, \lambda a_1^U; \phi _{a_1}, \psi _{a_1} \rangle , ~~\lambda > 0 \\ \langle \lambda a_1^U, \lambda a_1^M, \lambda a_1^L; \phi _{a_1}, \psi _{a_1} \rangle ,~~~\lambda < 0 \end{array}\right. }\) where \(a \wedge b=\min (a,b)\) and \(a \vee b=\max (a,b)\).

Definition 5

(Li 2010) The \(\alpha\) and \(\beta -\)cut for a TIFN \(\widehat{A} = \langle a^L, a^{M}, a^U; \phi _a, \psi _a \rangle ,\) can be defined as

$$\begin{aligned} \widehat{A}^{(\alpha ,\beta )}=\{ a: \phi _a \ge \alpha , \psi _a \le \beta \}, \end{aligned}$$
(3)

where \(0 \le \alpha \le \phi _a\) and \(\psi _a \le \beta \le 1\).

Using Definition 4 and Eq. (3), the lower limits \(\widehat{A}_L (\alpha )\) and \(\widehat{A}_L (\beta )\) and upper limits \(\widehat{A}_U (\alpha )\) and \(\widehat{A}_U(\beta )\) of \(\alpha\) and \(\beta\)-level cut for TIFN are defined as

$$\begin{aligned}&\widehat{A}_\alpha =[\widehat{A}_L (\alpha ), \widehat{A}_U (\alpha )]=\Big [a^L+\alpha (\frac{a^{M}-a^L}{\phi _a}), a^U-\alpha (\frac{a^U-a^{M}}{\phi _{a}})\Big ],\\&\widehat{A}_\beta =[\widehat{A}_L (\beta ), \widehat{A}_U (\beta )]=\Big [\frac{(\beta -\psi _a) a^L+(1-\beta )a^{M} }{1-\psi _a}, \frac{(\beta - \psi _a)a^U+(1-\beta )a^{M}}{1-\psi _{a}} \Big ], \end{aligned}$$

then

$$\begin{aligned} \widehat{A}^{(\alpha ,\beta )}=(\widehat{A}_\alpha , \widehat{A}_\beta ). \end{aligned}$$
(4)

Definition 6

(Wan et al. 2013) Let \(\widehat{A} = \langle a^L, a^M a^U; \phi _a, \psi _a \rangle ,\) be a TIFN.

  1. 1.

    The possibility mean of truth membership function for \(\widehat{A}\) is defined as follows:

    $$\begin{aligned} \mathcal {M}(\widehat{A}_\alpha )=\dfrac{m_L(\widehat{A}_\alpha )+m_U(\widehat{A}_\alpha )}{2} \end{aligned}$$
    (5)

    where

    $$\begin{aligned} m_L(\widehat{A}_\alpha )=2 \int _0^{\phi _a} Pos[\widehat{A} \le \widehat{A}_L(\alpha )] \widehat{A}_L(\alpha ) d \alpha =\dfrac{a^L+2a^M}{3}\phi _{a}^2 \end{aligned}$$

    and

    $$\begin{aligned} m_U(\widehat{A}_\alpha )=2 \int _0^{\phi _a} Pos[\widehat{A} \ge \widehat{A}_U(\alpha )] \widehat{A}_U(\alpha ) d \alpha =\dfrac{a^U+2a^M}{3}\phi _{a}^2 \end{aligned}$$
  2. 2.

    The possibility mean of falsity membership function for \(\widehat{A}\) is defined as follows:

    $$\begin{aligned} \mathcal {M}(\widehat{A}_\gamma )=\dfrac{m_L(\widehat{A}_\gamma )+m_U(\widehat{A}_\gamma )}{2} \end{aligned}$$
    (6)

    where

    $$\begin{aligned} m_L(\widehat{A}_\beta )&=2 \int _{\psi _a}^1 Pos[\widehat{A} \le \widehat{A}_L(\beta )] \widehat{A}_L(\beta ) d \beta \nonumber \\&= (a^M-\psi _a a^L)(1+\psi _{a}) - \dfrac{2(a^M- a^L)}{3}(1+\psi _{a}+\psi _a^2) \end{aligned}$$

    and

    $$\begin{aligned} m_U(\widehat{A}_\beta )&=2 \int _{\psi _a}^1 Pos[\widehat{A} \ge \widehat{A}_U(\beta )] \widehat{A}_U(\beta ) d \beta \nonumber \\&= (a^M-\psi _a a^U)(1+\psi _{a}) + \dfrac{2(a^U- a^M)}{3}(1+\psi _{a}+\psi _a^2) \end{aligned}$$

Definition 7

(Wan 2013) Let \(\widehat{A} = \langle a^L, a^M, a^U; \phi _a, \psi _a \rangle ,\) be a TIFNs, the weighted possibility means of truth and falsity degree can be defined as

$$\begin{aligned} \widetilde{ \mathfrak {K}} (\widehat{A})= \delta ~ \mathcal {M}(\widehat{A}_\alpha ) + (1-\delta ) \mathcal {M}(\widehat{A}_\beta ) \end{aligned}$$
(7)

and \(\delta \in [0,1]\) reflects the attitude of the decision maker towards the risk.

  1. 1.

    \(\delta \in [0, 0.5)\) shows that the expert is a risk taker who prefers uncertainty.

  2. 2.

    \(\delta =0.5\) shows that the expert’s decision on the parameter selection is neutral.

  3. 3.

    \(\delta \in (0.5, 1]\) shows that the expert’s sensitivity to taking risks while making a decision.

That implies

$$\begin{aligned} \widetilde{ \mathfrak {K} } (\widehat{A})= \delta \Big (\dfrac{a^L + 4a^{M}+ a^U}{6} \Big ) \phi _a^2 +(1-\delta ) \left( \dfrac{\begin{array}{l}{2[a^L + a^{M}+ a^U]-[a^L- 2a^{M} + a^U]\psi _a }\\ \qquad \qquad \qquad \qquad \quad {-[a^L +4 a^{M} + a^U]\psi _a^2}\end{array}}{6} \right) \end{aligned}$$
(8)

Example 3.1

If \(\widehat{A}=a\) be any real number, then it can be written in TIFN form \(\widehat{A}=\langle a,a,a;1,0 \rangle\) then \(\widetilde{ \mathfrak {K}} (\widehat{A})=\delta a+ (1-\delta ) a= a\).

Definition 8

Suppose \(\widehat{A_1}\) and \(\widehat{A_2}\) be two TIFNs, then the following are satisfy

  1. 1.

    \(\widehat{A_1}\preceq \widehat{A_2}\) if and only if \(\widetilde{ \mathfrak {K} } (\widehat{A_1}) \le \widetilde{ \mathfrak {K} } (\widehat{A_2}),\)

  2. 2.

    \(\widehat{A_1} \prec \widehat{A_2}\) if and only if \(\widetilde{ \mathfrak {K} } (\widehat{A_1}) < \widetilde{ \mathfrak {K} } (\widehat{A_2}),\)

  3. 3.

    \(\widehat{A_1} \approx \widehat{A_2}\) if and only if \(\widetilde{\mathfrak {K} } (\widehat{A_1}) = \widetilde{ \mathfrak {K} } (\widehat{A_2}),\)

where \(\widetilde{ \mathfrak {K} }(.)\) is the weighted possibility mean.

Theorem 1

Let us consider \(\widehat{A_i} = \langle a_i^L, a_i^{M}, a_i^U; \phi _{a_i}, \psi _{a_i} \rangle\) be n TIFNs and \(\lambda _i \in R\). Then the possibility mean of the aggregation of the following expression can be defined as

$$\begin{aligned} \widetilde{\mathfrak {K} }&\Bigg ( \sum _{i=1}^n \lambda _i \widehat{A_i} \Bigg )=\sum _{i=1}^n \Bigg [ \delta \Big (\dfrac{ a_i^L + 4 a_i^{M} + a_i^U}{6} \Big ) \Big (\bigwedge _{i=1}^n \phi _{a_i}\Big )^2 \nonumber \\&\quad +(1-\delta ) \Bigg ( \dfrac{\begin{array}{ll}{ 2 \Big [ a_i^L + a_i^{M}+ a_i^U\Big ] -\Big [ a_i^L - 2 a_i^{M} + a_i^U\Big ]\Big (\bigvee _{i=1}^n \psi _{a_i} \Big ) }\\ \qquad \qquad \qquad \qquad \quad { - \Big [ a_i^L +4 a_i^{M} + a_i^U\Big ]\Big (\bigvee _{i=1}^n \psi _{a_i} \Big )^2}\end{array}}{6} \Bigg ) \Bigg ]\lambda _i \end{aligned}$$
(9)

Proof

$$\begin{aligned} \sum _{i=1}^n \lambda _i \widehat{A_i}&= \langle \sum _{i=1}^n \lambda _i a_i^L, \sum _{i=1}^n \lambda _i a_i^{M}, \sum _{i=1}^n \lambda _i a_i^U; \bigwedge _{i=1}^n \phi _{a_i}, \bigvee _{i=1}^n \psi _{a_i} \bigg \rangle \end{aligned}$$

then from Definition 7, we have

$$\begin{aligned} \widetilde{ \mathfrak {K} } \Bigg (&\sum _{i=1}^n \lambda _i \widehat{A_i} \Bigg ) = \delta \Big (\dfrac{\sum _{i=1}^n \lambda _i a_i^L + 4 \sum _{i=1}^n \lambda _i a_i^{M}+ \sum _{i=1}^n \lambda _i a_i^U}{6} \Big ) \Big (\bigwedge _{i=1}^n \phi _{a_i}\Big )^2 \\&\quad +( 1-\delta ) \left( \dfrac{\begin{array}{ll}{ 2 \Big [\sum _{i=1}^n \lambda _i a_i^L + \sum _{i=1}^n \lambda _i a_i^{M}+ \sum _{i=1}^n \lambda _i a_i^U\Big ]}\\ \quad { \begin{array}{ll}{ -\Big [\sum _{i=1}^n \lambda _i a_i^L - 2 \sum _{i=1}^n \lambda _i a_i^{M} + \sum _{i=1}^n \lambda _i a_i^U\Big ]\Big (\bigvee _{i=1}^n \psi _{a_i} \Big )}\\ \quad \quad {- \Big [\sum _{i=1}^n \lambda _i a_i^L +4 \sum _{i=1}^n \lambda _i a_i^{M} + \sum _{i=1}^n \lambda _i a_i^U\Big ]\Big (\bigvee _{i=1}^n \psi _{a_i} \Big )^2}\end{array}}\end{array}}{6} \right) \end{aligned}$$

that implies

$$\begin{aligned} \widetilde{ \mathfrak {K} } \Bigg (&\sum _{i=1}^n \lambda _i \widehat{A_i} \Bigg )=\sum _{i=1}^n \Bigg [ \delta \Big (\dfrac{ a_i^L + 4 a_i^{M}+ a_i^U}{6} \Big ) \Big (\bigwedge _{i=1}^n \phi _{a_i}\Big )^2 \\ +(1-\delta )&\left( \dfrac{ \begin{array}{ll}{ 2 \Big [a_i^L + a_i^{M}+ a_i^U\Big ] -\Big [ a_i^L - 2 a_i^{M} + a_i^U\Big ]\Big (\bigvee _{i=1}^n \psi _{a_i} \Big ) }\\ \quad \quad \quad \quad \qquad \qquad \qquad {- \Big [ a_i^L +4 a_i^{M} + a_i^U\Big ]\Big (\bigvee _{i=1}^n \psi _{a_i} \Big )^2 }\end{array}}{6} \right) \Bigg ]\lambda _i . \end{aligned}$$

\(\square\)

4 Development of intuitionistic fuzzy data envelopment analysis (IFDEA) model

Suppose that there are n DMUs each having m inputs and r outputs as represented by the vectors \({\textbf {I}} \in R^m\) and \({\textbf {O}} \in R^{r},\) respectively. We define the input matrix I as \(I = [I_1,\cdots ,I_m] \in R^{m \times n},\) and the output matrix O as \(O =[O_1,\cdots ,O_r] \in R^{r \times n},~~ I_i \in R^m,~\forall ~ i=1,2,\cdots , m,~~O_k \in R^{r},~\forall ~ k=1,2,3,\cdots , r\) and assume that \(I > 0\) and \(O>0.\)Charnes et al. (1978) developed this model for measuring the efficiency of \(DMU_o\) i.e.

$$\begin{aligned} \max _{u,v}~&\theta =\dfrac{\sum _{k=1}^r u_{k}O_{ko}}{\sum _{i=1}^mv_i I_{io}}, \nonumber \\ \text {subject to~~}&\dfrac{\sum _{k=1}^r u_{k}O_{kj}}{\sum _{i=1}^mv_i I_{ij}} \le 1,~j=1,2,\cdots n,\\ \text {and }&u_k\ge 0,~~k=1,2,\cdots , r, \nonumber \\&v_i \ge 0,~~i=1,2,\cdots , m, \nonumber \end{aligned}$$
(10)

which is equivalent to the linear program (\(LP_o\)), i.e.

$$\begin{aligned} \max _{u,v}~&\theta =\sum _{k=1}^r u_{k}O_{ko}, \nonumber \\ \text {subject to~}&\sum _{i=1}^mv_iI_{io}=1,\nonumber \\&\sum _{k=1}^r u_{k} O_{kj} \le \sum _{i=1}^m v_i I_{ij}, ~~j=1,2,\cdots n, \nonumber \\ \text {and }&u_k\ge 0,~~k=1,2,\cdots , r, \nonumber \\&v_i \ge 0,~~i=1,2,\cdots , m, \end{aligned}$$
(11)

which is called the traditional DEA model or CCR model. The performance of DMUs may be incorrectly evaluated because the observational data for the given model is faulty, imprecise, or confusing. Furthermore, if the performance of a DMU is the best, then it will behave as a shaky reference unit for the other inefficient DMUs. A robust method is required to deal with this type of situation, utilising IFS theory. The following steps are followed to develop the IFDEA model by using TIFN as an input–output parameter, and the solution technique is also provided below.

  1. Step 1:

    Assuming inputs and outputs are TIFNs while the variables \(u_r\) and \(v_i\) are real numbers. Thus, the intuitionistic fuzzy DEA (IFDEA) model will be written as follows:

    $$\begin{aligned} \max _{u,v}~~&\theta =\sum _{k=1}^r u_{k} \widehat{O_{ko}}, \nonumber \\ \text {subject to~}&\sum _{i=1}^mv_i \widehat{I_{io}}=\widehat{1},\nonumber \\&\sum _{k=1}^r u_{k} \widehat{ O_{kj}} \le \sum _{i=1}^mv_i, \widehat{I_{ij}}, ~~j=1,2,\cdots n, \nonumber \\ \text { and }&u_k\ge 0,~~k=1,2,\cdots , r, \nonumber \\&v_i \ge 0,~~i=1,2,\cdots , m, \end{aligned}$$
    (12)

    where \(\widehat{ I_{ij}}=\langle I_{ij}^L,I_{ij}^{M}, I_{ij}^U, \phi _{I_{ij}}, \psi _{I_{ij}}\rangle\) and \(~\widehat{ O_{kj}}=\langle O_{kj}^L, O_{kj}^{M}, O_{kj}^U, \phi _{O_{kj}}, \psi _{O_{kj}} \rangle\), for \(i=1,2,3,\cdots ,n,~~j=1,2,3,\cdots ,m\) and \(k=1,2,3,\cdots ,r\). That is

    $$\begin{aligned} \max _{u,v}~~&\theta =\sum _{k=1}^r u_{k} \langle O_{ko}^L, O_{ko}^{M}, O_{ko}^U, \phi _{O_{ko}}, \psi _{O_{ko}} \rangle , \nonumber \\ \text {subject to~}&\sum _{i=1}^mv_i \langle I_{io}^L,I_{io}^{M}, I_{io}^U, \phi _{I_{io}}, \psi _{I_{io}}\rangle =\langle 1, 1, 1;1,0 \rangle ,\nonumber \\&\sum _{k=1}^r u_{k} \langle O_{kj}^L, O_{kj}^{M}, O_{kj}^U, \phi _{O_{kj}}, \psi _{O_{kj}} \rangle \nonumber \\&\qquad ~~ \le \sum _{i=1}^m v_i \langle I_{ij}^L,I_{ij}^{M}, I_{ij}^U, \phi _{I_{ij}}, \psi _{I_{ij}}\rangle , ~~j=1,2,\cdots n, \nonumber \\ \text { and }&u_k\ge 0,~~k=1,2,\cdots , r, \nonumber \\&v_i \ge 0,~~i=1,2,\cdots , m, \end{aligned}$$
    (13)
  2. Step 2:

    Applying possibility mean in the above Eq. (13), we have

    $$\begin{aligned} \max _{u,v} ~~&\theta = \widetilde{ \mathfrak {K} } \Big (\sum _{k=1}^r u_{k} \langle O_{ko}^L, O_{ko}^{M}, O_{ko}^U, \phi _{O_{ko}}, \psi _{O_{ko}} \rangle \Big ), \nonumber \\ \text {subject to~}&\widetilde{ \mathfrak {K} } \Big (\sum _{i=1}^mv_i \langle I_{io}^L,I_{io}^{M}, I_{io}^U, \phi _{I_{io}}, \psi _{I_{io}}\rangle \Big )=\widetilde{ \mathfrak {K} } \Big ( \langle 1, 1, 1;1,0 \rangle \Big ),\nonumber \\&\widetilde{\mathfrak {K}} \Big ( \sum _{k=1}^r u_{k} \langle O_{kj}^L, O_{kj}^{M}, O_{kj}^U, \phi _{O_{kj}}, \psi _{O_{kj}} \rangle \Big ) \nonumber \\&\qquad ~~ \le \widetilde{ \mathfrak {K} } \Big ( \sum _{i=1}^m v_i \langle I_{ij}^L,I_{ij}^{M}, I_{ij}^U, \phi _{I_{ij}}, \psi _{I_{ij}}\rangle \Big ), ~~j=1,2,\cdots n, \nonumber \\ \text { and }&u_k\ge 0,~~k=1,2,\cdots , r, \nonumber \\&v_i \ge 0,~~i=1,2,\cdots , m, \end{aligned}$$
    (14)

    Now from Theorem 1, we have

    $$\begin{aligned} \max _{u,v}~~&\theta = \dfrac{1}{6}\sum _{k=1}^r \Bigg [ \delta \Big ( O_{ko}^L + 4 O_{ko}^{M} + O_{ko}^U \Big ) \Big (\bigwedge _{k=1}^r \phi _{O_{ko}}\Big )^2 \\ +(1-\delta )&\left( \begin{array}{ll}{ 2 \Big [ O_{ko}^L + O_{ko}^{M} + O_{ko}^U\Big ] -\Big [ O_{ko}^L - 2 O_{ko}^{M} + O_{ko}^U \Big ]\Big (\bigvee _{k=1}^r \psi _{O_{ko}} \Big ) }\\ \qquad \qquad \qquad \quad \quad \quad \quad {- \Big [ O_{ko}^L + 4 O_{ko}^{M} + O_{ko}^U\Big ]\Big (\bigvee _{k=1}^r \psi _{O_{ko}} \Big )^2} \end{array} \right) \Bigg ] u_k, \\ \text {s.t } \sum _{i=1}^m&\Bigg [ \delta \Big ( I_{io}^L + 4 I_{io}^{M}+ I_{io}^U \Big ) \Big (\bigwedge _{k=1}^r \phi _{I_{io}}\Big )^2 \\ + (1-\delta )&\left( \begin{array}{ll}{ 2 \Big [ I_{io}^L + I_{io}^{M} + I_{io}^U\Big ] -\Big [ I_{io}^L - 2 I_{io}^{M} + I_{io}^U\Big ]\Big (\bigvee _{k=1}^r \psi _{I_{io}} \Big ) }\\ \qquad \qquad \qquad \quad \quad \quad \quad {- \Big [ I_{io}^L +4 I_{io}^{M} + I_{io}^U \Big ] \Big ( \bigvee _{i=1}^m \psi _{I_{io}} \Big )^2} \end{array} \right) \Bigg ] v_i =6,\\ \sum _{k=1}^r&\Bigg [ \delta \Big ( O_{kj}^L + 4 O_{kj}^{M} + O_{kj}^U \Big ) \Big (\bigwedge _{k=1}^r \phi _{O_{kj}}\Big )^2 \\ + (1-\delta )&\left( \begin{array}{ll}{ 2 \Big [ O_{kj}^L + O_{kj}^{M}+ O_{kj}^U\Big ] -\Big [ O_{kj}^L - 2 O_{kj}^{M} + O_{kj}^U\Big ]\Big (\bigvee _{k=1}^r \psi _{O_{kj}} \Big ) }\\ \qquad \qquad \qquad \quad \quad \quad \quad {- \Big [ O_{kj}^L + 4 O_{kj}^{M} + O_{kj}^U\Big ]\Big (\bigvee _{k=1}^r \psi _{O_{kj}} \Big )^2} \end{array} \right) \Bigg ] u_k \\&\le \sum _{i=1}^m \Bigg [ \delta \Big ( I_{ij}^L + 4 I_{ij}^{M}+ I_{ij}^U \Big ) \Big (\bigwedge _{k=1}^r \phi _{I_{ij}}\Big )^2 \\ + (1-\delta )&\left( \begin{array}{ll}{ 2\Big [ I_{ij}^L + I_{ij}^{M} + I_{ij}^U \Big ] -\Big [ I_{ij}^L - 2 I_{ij}^{M} + I_{ij}^U\Big ]\Big (\bigvee _{k=1}^r \psi _{I_{ij}} \Big ) }\\ \qquad \qquad \qquad \quad \quad {- \Big [ I_{ij}^L + 4 I_{ij}^{M} + I_{ij}^U \Big ] \Big ( \bigvee _{i=1}^m \psi _{I_{ij}} \Big )^2}\end{array} \right) \Bigg ] v_i, \\&\qquad \qquad ~~j= 1,2,\cdots , n,\\&\qquad \text {and } u_k\ge 0,~~k=1,2,\cdots , r, ~~v_i \ge 0,~~i=1,2,\cdots , m, \end{aligned}$$

    which is the corresponding crisp DEA model.

  3. Step 3:

    Solve this crisp DEA model and find the optimal solution \(\theta ^*\) for each \(\delta \in [0,1]\), which represents the attitude of the DM regarding the risk.

    1. (a)

      \(\delta \in [0, 0.5)\) shows that the expert is a risk taker who prefers uncertainty.

    2. (b)

      \(\delta =0.5\) shows that the expert’s decision on the parameter selection is neutral.

    3. (c)

      \(\delta \in (0.5, 1]\) shows that the expert’s sensitivity to taking risks while making a decision.

  4. Step 4:

    The performances of DMUs are evaluated and ranked based on the efficiency score obtained for each DMU with a risk factor. The overall efficiency scores are considered by taking the arithmetic mean of the efficiency scores of the DMUs with different risk factors.

The solution technique of the IFDEA model is represented by the flowchart in Fig. 2.

Fig. 2
figure 2

Flowchart for solving intuitionistic fuzzy DEA model

Full size image

Theorem 2

The DEA model given in Eq. (11) and the IFDEA model in Eq. (13) are equivalent.

Proof

When the aggregation operator and possibility mean approach is applied as shown in Step 2 of Sect. 4, it is easy to see that optimum feasible solution of every IFDEA model is also an optimum feasible solution for the DEA model, and vice versa. \(\square\)

Definition 9

A DMU is said to be efficient if its efficiency score 1; Otherwise, It is inefficient.

5 Numerical examples

There are two numerical examples that have been considered to demonstrate the applicability and validity of the proposed solution techniques and compared with the existing results.

Example 5.1

(Edalatpanah 2019)

This numerical example, given by Edalatpanah (2019), is taken into consideration to interpret the applicability and viability of the suggested method. It contains five DMUs, with two inputs and two outputs for each of them. These inputs and outputs are represented by TIFNs, as depicted in Table 2.

Table 2 The TIFN input–output data used by Edalatpanah (2019)
Full size table

Using the suggested approach, the intuitionistic fuzzy DEA model is converted into the corresponding crisp DEA model. MATLAB 2021 software is used to evaluate the relative efficiency scores of the DMUs by solving the corresponding crisp DEA model. The performances of the DMUs are evaluated with different risk factors based on the efficiency score (see Table 3). It is observed that the efficiency score of the DMUs decreases with an increase in the risk factor. When \(\delta =0\), the DMUs D1 and D4 are efficient and other DMUs are inefficient, and we rank them based on their efficiency score, i.e., \(D1=D4> D5> D2 >D3\). When \(\delta\) ranges from 0.25 to 0.75, the DMU D1 is efficient and other DMUs are inefficient, and we rank them as \(D1>D2> D4> D5 >D3\). When \(\delta =1\), the DMU D1 is efficient and other DMUs are inefficient, and we rank them as \(D1>D2> D3> D4 >D5\). The overall efficiency scores of the DMUs are calculated by taking the arithmetic mean of the efficiency scores of the DMUs with different risk factors and ranking them as \(D1>D2> D4> D5 >D3\). How the efficiency score changes with different risk factors is shown in Fig. 3.

The overall efficiency score of the DMU is obtained by using the proposed approach and is compared with the existing ranking approach (Edalatpanah 2019) as shown in Fig. 4 and Table 3. We have found the overall efficiency scores of the DMUs are similar to the existing ranking approach. But the results obtained with different risk factors are different from the existing ranking approach. The main advantage of the proposed probability mean approach is that it compares the performance of the DMUs with the risk-taking attitude of the decision-maker. Thus, our proposed approach for solving the IFDEA model has been implemented as a successful, robust technique and has the capability of completely ranking the DMUs.

Table 3 The efficiency score of the DMUs
Full size table
Fig. 3
figure 3

Efficiency score changes with risk factor

Full size image
Fig. 4
figure 4

Comparison with Edalatpanah ranking approach

Full size image

Example 5.2

(Puri and Yadav 2015)

This numerical example, given by Puri and Yadav (2015), is taken into consideration to interpret the applicability and viability of the suggested method. It contains twelve DMUs, with two inputs and two outputs for each of these. These inputs and outputs are represented by TIFNs, as depicted in Table 4. If the TIFN is in the form of \(\hat{A}=(a_1,a_2,a_3;~a_1',a_2,a_3')\), then the weighted possibility mean for \(\hat{A}\) defined in (8), will be

$$\begin{aligned} \widetilde{\mathfrak {K}}(\hat{A})= \delta (\frac{a_1+4a_2+a_3}{6})+ (1-\delta ) (\frac{a_1'+a_2+a_3'}{3}) \end{aligned}$$
(15)

and also \(\widetilde{\mathfrak {K}}(\lambda \hat{A})=\lambda \widetilde{\mathfrak {K}}(\hat{A}).\)

The weighted possibility mean function \((\widetilde{\mathfrak {K}})\) defined in Eq. (15), is employed in the preceding steps of Sect. 4 to transform the IFDEA model into the equivalent crisp DEA model. Similar to Example 5.1, the arithmetic mean of the ES of DMUs with different risk factors \((\delta \in [0,1])\) is used to compute the overall ES of each DMU. The DMUs are completely ranked based on the overall ES of the DMUs, as shown in Table 5. In the possibility mean approach, the DMUs are ranked as \(D2>D4>D12>D7> D3>D9>D1> D10>D11> D8>D5 > D6.\) The expected value approach is used by Puri and Yadav (2015) to evaluate the efficiency score (ES) of the DMUs and completely rank the DMUs based on the Supper efficiency score, as shown in Table 5. Figure 5 illustrates a comparison between the ES of the DMUs obtained by using the proposed approach and the expected value approach. The DMUs D1, D2, D4,  and D12 are efficient in the expected value approach; however, only D2 is efficient in the proposed approach.

Table 4 The TIFN input–output data used by Puri and Yadav (2015)
Full size table
Table 5 Efficiency Score of the DMUs and Ranking
Full size table
Fig. 5
figure 5

Comparison with Puri and Yadav expected value approach

Full size image

The observed input and output data in the real-world performance assessment problem are occasionally missing, unclear or partial, which causes the efficiency score to be erroneous. The fuzzy set is insufficient to effectively manage this kind of data and represent the ambiguity. Therefore, in uncertain data analysis, the Intuitionistic fuzzy set concept has benefits over fuzzy sets. TIFNs offer an improved and flexible way of representing uncertainty and imprecision by including measures of both membership and non-membership degrees in observed input and output data. It is evident from the preceding two examples that the proposed method can manage performance analysis problems in the presence of both linear and nonlinear TIFN inputs and outputs. Furthermore, the outcomes demonstrate that the suggested method gives decision-makers more freedom to take independent decisions when assessing the DMUs’ efficiency.

6 Case study: Indian agriculture sector

6.1 Data collection

The research was carried out in all 28 Indian states to measure agricultural performance. Around 70% of the rural population is dependent on agricultural production, and the majority of farmers are small landholders. The data was collected via the official website of the Reserve Bank of India (https://rbi.org.in), which published the report as Handbook of Statistics on Indian States in 2020–2021. The data includes four agricultural inputs: irrigated area, fertilizers utilized, cold storage, and workers, as well as four agricultural outputs: food grains, oil seeds, vegetables, and fruits. Table 6 contains a detailed description of the observed input–output data. The data are not uniformly distributed because of the distinctly diverse geographical distribution of the Indian States, as indicated in the statistical Table 7.

Table 6 About the input and output variable
Full size table
Table 7 Statistical analysis of the input and output data
Full size table

6.2 Results and discussion

To measure the performance of the states using the IFDEA model, follow the given steps in Sect. 4 and obtain the efficiency scores of the states obtained by solving the crisp LP problem given in Step 2. The efficiency scores of the states, obtained with different risk factors, are shown in Table 8. The overall efficiency scores of the states are obtained by taking the arithmetic mean of the ES of the states with different risk factors. The states are divided into efficient and inefficient groups based on the overall ES. The states “Andhra Pradesh, Arunachal Pradesh, Assam, Bihar, Jharkhand, Kerala, Madhya Pradesh, Maharastra, Manipur, Mizoram, Nagaland, Rajasthan, Sikkim, Tripura, and Uttar Pradesh” are considered efficient states because the overall ES is one. The other states whose overall ES is less than one are considered inefficient states. When the risk factor lies between 0 and 0.5, 60.71% of the states are efficient, and the rest are inefficient. After that, or the risk factor from 0.5 to 1, 53.57% of the states are efficient and other states are inefficient. The efficiency scores of the efficient states are one, which is unaffected by the risk factors. The efficiency scores of the inefficient states change with the risk factors. How the efficiency scores of the inefficient states are affected by the risk factors is shown in Fig. 6. The ES of Gujarat, Haryana, Punjab, and Uttarakhand rises when the risk factor rises, but it decreases in Chhatisgarh, Himachal Pradesh, Jammu & Kashmir, Karnataka, Meghalaya, and Tamil Nadu. The states of Odisha and West Bengal are efficient when the risk factor varies from 0 to 0.5, after that, these two states become inefficient.

Table 8 The efficiency score of the Indian States with different risk level
Full size table
Fig. 6
figure 6

Efficiency score of the inefficient States changes with risk factor

Full size image
Table 9 Efficiency score of the Indian state using traditional DEA model
Full size table

The agricultural performances of Indian states are assessed by calculating the efficiency score using the standard DEA model, namely the CCR model. The efficiency scores of different Indian states are presented in Table 9. The findings show that out of the 28 states, 17 are efficient with their efficiency score of 1, while the other 11 are inefficient with their efficiency score below 1. The efficiency scores of different Indian states are compared using both the proposed approach and the traditional DEA model, as shown in Fig. 7. The percentage of efficient Indian states in the suggested method is 50%, whereas it is 60.71% in the traditional DEA model. Out of India’s 28 states, 14 are efficient using the proposed approach; three more states-West Bengal, Odisha, and Meghalaya-are likewise efficient under the traditional DEA. On the other hand, these states are considered inefficient by the proposed approach because their overall efficiency scores are less than 1. But it has been shown that Odisha and West Bengal are efficient within the risk factor lambda range of [0, 0.5], but when the risk factor increases from 0.5 to 1, these states become inefficient. In both proposed approach and tradition DEA model the most inefficient states are Uttarakhand with efficiency score 0.3654 and 0.3101, respectively. In general, the suggested method combined intuitionistic fuzzy sets and the DEA model. It yielded impressive outcomes in comparison to the traditional DEA model, and it allowed decision-makers to take their own risks when determining the efficiency of DMUs.

Fig. 7
figure 7

Overall efficiency score of the Indian states

Full size image

The main advantage for policymakers to use the proposed approach for solving the IFDEA model is that it allows them to take their own risks when evaluating efficiency scores. The incorporation of intuitionistic fuzzy inputs and outputs in the DEA model enables decision-makers to properly estimate the agricultural performance of Indian states in an environment with a high level of uncertainty. The policymaker categorizes the Indian states into efficient and inefficient groups based on their efficiency scores and risk factors. The primary objective of decision-makers should be to carry out sensitivity studies in order to recognize important aspects that contribute to inefficiency and investigate possible improvement possibilities. Additionally, policymakers should undertake benchmarking and best practice sharing across Indian states in order to foster a culture of constant improvement and information transfer, which will ultimately result in better levels of efficiency.

7 Conclusions and future directions

The data in real-world performance measurement problems is typically inaccurate and unreliable. Fuzzy numbers offer a better representation of the data sets in uncertain circumstances. As a result, we used fuzzy DEA models to address these problems and measured the performance of the DMUs more effectively. In this paper, we have proposed a novel technique for solving the Intuitionistic FDEA model in order to evaluate the efficiency score of the DMUs, where the inputs and outputs are represented by TIFNs. The proposed possibility-mean approach directly converts the IFDEA model into the equivalent crisp LP problem, which can be solved by using any existing method. The possibility mean for TIFN is associated with a risk factor ranging from 0 to 1. The risk factor reflects the decision-maker’s risk-taking attitude, whether they are risk takers, risk adversers, or neutral. This proposed technique allows decision-makers to assume their own risks while evaluating the performance of the DMUs. We provided two existing examples and made a comparison between the obtained results and the existing results to demonstrate their effectiveness and validity. The overall ES is calculated by taking the arithmetic mean of the ES of DMUs with various risk factors, and the DMUs are ranked based on their overall ES. When evaluating the efficiency score and ranking the DMUs in an uncertain environment, we demonstrated that our proposed approach gives decision-makers more flexibility than existing approaches.

We have used the proposed technique to assess the relative efficiency of the agricultural data set of Indian states using an intuitionistic fuzzy DEA model. The performance of 28 states is measured using different risk variables, and how the efficiency score of inefficient states is impacted by risk factors is depicted visually. Out of the 28 Indian states, 53.71% are efficient, while the remaining states are inefficient. There are several factors affecting the agriculture industry that should be considered by decision-makers, which may provide different results while increasing the input and output data sets. One of the difficult tasks in this suggested technique is to completely rank the DMUs. This proposed approach may even be used to solve additional IFDEA models in order to evaluate the performance of DMUs.