Location optimization of on-campus bicycle-sharing electronic fences

Abstract

In the bicycle-sharing operation network, the mismatch between supply and demand as well as indiscriminate bicycle parking have caused the waste of resources and increased management costs for operators. This study presents design of a bike-sharing electronic fences location developed for Hunan University of Technology and Business. In this paper, we constructed Site Selection Model with Constrained Service Level and use Hybrid Genetic & Annealing algorithm (HGAA) to adjust the location of electronic fences to balance the supply and demand of sharing bicycles with the objective function of minimizing the cost and ensuring the service level, and we use Hunan University of Technology and Industry as an example to verify the effectiveness of the method.

1 Introduction

In recent years, the rapid development of bicycle sharing has effectively solved the "last mile" problem, and this low-carbon, economical, and convenient transportation mode is favored by teachers and students in universities. In the traditional bicycle-sharing system, customers must reach a fixed station to rent or return shared bicycles. However, the current station-free bicycle-sharing system allows riders to park bicycles anywhere, or just abandon them. Such a new system brings new optimization problems. In some areas, bicycles pile up and even block already-crowded streets and pathways. By contrast, the number of shared bicycles could not meet users' demands in other areas. But increasing the number of shared bicycles does not effectively solve above problems; it will lead to not only more idle bikes and waste of resources but also more serious road blockage. The unbalanced supply and demand of shared bicycles will affect the cost and revenue of operators. By setting electronic fences, operators could guide consumers to park shared bicycles to right locations which can effectively solve shared bicycle allocation problem. In addition, it can reduce operation cost and increase the utilization rate of shared bicycles. Therefore, this paper introduces the concept of electronic fence to solve the location optimization problem of shared bicycles. The electronic fence is a virtual site delineated based on satellite positioning, RFID, Bluetooth, etc. It obtains the current location information of a shared bicycle through a satellite positioning system and matches the obtained information with the critical threshold value of the electronic fence to determine whether the bicycle is parked in the correct location. It is an effective way to regulate the parking of shared bicycles.

This paper aims to improve the accessibility to shared bicycles on campus by finding the optimal locations of electronic fences based on the collected spatial and demand data. We define the problem as a Set Covering Problem (SCP); to solve the problem, we construct Site Selection Model with Constrained Service Level and consider the effect of users’ accessibility to parking locations on their willingness to ride shared bicycles. Besides, this paper takes Hunan University of Technology and Business as an example for research. We apply several data collection methods and HGAA to derive the final location optimization plan.

The innovation of this paper is mainly reflected in the following aspects: (1) using campus as a case study; (2) considering service level and cost comprehensively; (3) proving computational complexity; (4) using HGAA to solve the bike-sharing electronic fence location optimization problem.

The rest of this paper mainly includes: Sect. 2, literature review, literature review from different research on determining optimal station locations; Sect. 3, model construction, the optimal distribution model of location; Sect. 4, algorithm and solution, algorithm description and calculation steps; Sect. 5, data selection and processing, this part explains the data source and process; Sect. 6, numerical analysis, this part takes Hunan University of Technology and Business as an example to simulate the optimal station layout plan; Sect. 7, effectiveness verification, this part verifies the effectiveness and correctness of the algorithm; Sect. 8, conclusions, limitations, and future works, this part summarizes the whole paper and puts forward prospects for future research.

2 Literature review

At present, academic research on bicycle sharing mainly focuses on location optimization and scheduling. The current bicycle-sharing operation mode is divided into stake-based bike sharing (SBBS) and stake-free bike sharing (FBBS) (Cheng et al.2020).

In recent years, scholars have done a lot of research on the location optimization of public bicycle parking stations. Suleyman Mete et al. (2018) used Location-Allocation Models (LAMs) from Set covering problem, Maximal covering problem, and P-median problem, and applied them to the location decision of public bicycle stations at Gaziantep University. Jingyuan Liu et al. (2015) used an optimization model based on Genetic algorithm for site selection to maximize the usage of the selected stations and minimize the number of unbalanced stations. Liu et al. (2020) assumed that local governments had planned the number and alternative locations of bike parking sites and the total number of shared bicycles, and based on the idea of joint coverage site selection, they maximized the sum of covered demand points as well as the satisfied demand of parking and usage and minimized idle bicycles, then establish a multi-time, multi-objective optimization model with different weights.

The research on FBBS scheduling optimization is still imperfect. Liu et al. (2022) constructed the revenue function of shared bicycles based on Newsboy Model to provide decision-making suggestions for the scheduling of shared bicycles. Shi et al. (2022) proposed a shared bicycle scheduling under users’ incentive strategy to improve the long-term service rate and achieve shared bicycle rebalance; Jia and Wu (2020) introduced electronic fences as bicycle parking sites to address problems of disorderly parking and unbalanced distribution in the operation of shared bicycles, and achieved supply–demand balance by adjusting the number of bicycles in each electronic fence; Caggiani et al. (2018) used a BP neural network algorithm to predict the demand of each cluster, proposed a scheduling model focusing on the shortest overall scheduling time, and designed a two-stage VPR optimization algorithm for scheduling optimization.

In addition to the location and scheduling problems of shared bikes, scholars have also studied other problems of shared bikes. Guo et al. (2022) took the New York citibike system as an example and calculated the optimal customer satisfaction-oriented placement of each site based on the xgboost principle; Liu et al. (2021) proposed a deep network model based on bidirectional long- and short-term memory to predict future bike-sharing traffic; Xiaoji et al. (2021) designed a fusional projection localization schem based on inertial navigation system and nonholonomic constrain using MEMSIMU and bicycle motion characteristics to achieve continuous and reliable localization of shared bicycles under severe GNSS signal occlusion in urban environment.

3 Model construction

The paper studies a location optimization problem that highlights the exact number and location of electronic fences, aiming to minimize the cost and ensure the service level. This section proposes Site Selection Model with Constrained Service Level and gives the relevant mathematical notation.

3.1 Basic assumptions

• 1. The traffic of the study occurs in a limited number of subjects: teaching buildings, dormitory buildings, the sports hall.

• 2. Using questionnaires to obtain the threshold value, a certain percentage of students will choose to use shared bicycles if the distance exceeds the threshold value.

• 3. A certain percentage of students are assumed to go back to the dormitory after class, some of them stay in teaching buildings and some of them go to other places.

• 4. the demand part is derived from the class schedule, and the other part is assumed to be randomly distributed.

• 5. there is a limited and clear choice of locations for bike parking spots.

3.2 Mathematical notation

Y: the feasible set of alternative locations for the electronic fence points.

Y′: the set of points in Y that satisfy y_i = 1.

${\tau }_{i}$: alternative locations for the electronic fence points, with $i\in [\mathrm{1,2},3,\dots ,m]$

D: the set of locations of the demand points.

${\tau }_{j}$: the demand points, with $j \in [m+1,m+2,m+3,\dots ,m+n]$

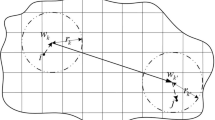
d_ij: the shortest distance between ${\tau }_{i}$ and ${\tau }_{j}$ after data cleansing.

d₀: the threshold.

T: service level.

T₀: minimum service level

$J\left({\tau }_{i}\right)=\left\{\begin{array}{c}1,\underset{{\tau }_{j}\in Y}{min} {d}_{ij}\le {d}_{0}\\ 0,\underset{{\tau }_{j}\in Y}{min} {d}_{ij}>{d}_{0}\end{array}\right.$

TC: total cost of electronic fence points i

TFC: total fixed cost.

TVC: total variable cost.

i: electronic fence point

$y_{i} = \left\{ \begin{array}{ll} 1, & \text{alternative point I selected as an electronic fence point} \\ 0, & \text{alternative point I not selected as an electronic fence point}\end{array} \right.$

TTC: total cost of all electronic fence points.

U: a full set.

S: a set containing n sets, the sum of these n sets is the full set.

C: a set, $C\in S$, and the union of the elements of C is U.

M: a very large number.

${\phi }_{0}$: initial solution.

${\Phi }_{0}$: initial solution space.

${\Phi }_{t}$: solution space after t-generation processing.

${\phi }_{i}$: solution.

${\phi }_{i}^{\prime}$: new solution.

$\alpha$: an average price.

${\alpha }_{1}$: a descent factor.

T_new: Temperature before iteration.

T_old: Temperature after iteration.

c_ij: the distance obtained directly using the API.

R_ij: the random number of building i and building j

R_j: the sum of random numbers in column j

N_i: the number of students in each building on weekdays.

P_ij: the possibility of students who choose to ride shared bicycles between building i and building j

E_ij: the estimated number of students needing bicycles between building i and building j

p: the number of people served.

x_ij: demand point ${\tau }_{i}$ is served by service point ${\tau }_{j}$

3.3 Model construction

For the site selection of electronic fences for shared bicycles, the following issues are mainly involved:

Problem 1.

The location and quantity of electronic fences.

Problem 2.

Capacity size of each electronic fence.

The demand to be considered are:

Demand 1.

Users’ perspective: we want to facilitate travel as much as possible, and the planned electronic fence should be as close to the demand point as possible.

Demand 2.

 Enterprise perspective: we hope the cost of the planned electronic fence is as low as possible (including fixed cost and maintenance cost).

First, we define the feasible set of alternative locations for the electronic fence points ${\tau }_{i}$:

$$Y=\left\{{\tau }_{1},{\tau }_{2},{\tau }_{3},\dots {\tau }_{m}\right\}$$

(1)

The set of feasible choices can be obtained by manual research and selection, or by extracting all the intersections from the map.

Then the set of locations of the demand points ${\tau }_{j}$ is defined:

$$D=\left\{{\tau }_{m+1},{\tau }_{m+2},{\tau }_{m+3},\dots ,{\tau }_{m+n}\right\}$$

(2)

Define the demand for ${\tau }_{i}$ is $D\left({\tau }_{i}\right)$ and the shortest distance between ${\tau }_{i}$ and ${\tau }_{j}$ as ${d}_{ij}$, and the specific calculation of this distance is given in the later section.

For Problem 1, students and teachers often want to be able to walk just a short distance to the parking spot, so this paper defines the service level based on:

$$T=\frac{\sum_{i\in D} D\left({\tau }_{i}\right)\times J\left({\tau }_{i}\right)}{\sum_{i\in D} D\left({\tau }_{i}\right)}$$

(3)

where J is a test function that checks whether the demand at a point can be satisfied within a certain distance, specifically:

$$J\left({\tau }_{i}\right)=\left\{\begin{array}{c}1,\underset{{\tau }_{j}\in Y}{min} {d}_{ij}\le {d}_{0}\\ 0,\underset{{\tau }_{j}\in Y}{min} {d}_{ij}>{d}_{0}\end{array}\right.$$

(4)

Thus $T$ is actually a calculation of the number of people who "can walk only a short distance to the nearest electronic fence point". It is reasonable to use this value to characterize Demand 1, provided that a suitable threshold ${d}_{0}$ is chosen.

For Demand 2, we have:

$$Total\,Cost\left(TC\right)=Total\,Fixed\,Cost\left(TFC\right)+Total\,Variable\,Cost\left(TVC\right)$$

(5)

The fixed cost is only related to whether or not to choose parking site $i$, while the variable cost is also related to the capacity of parking site $i$.

We set:

$$y_{i} = \left\{ \begin{array}{ll} 1, & \text{alternative point I selected as an electronic fence point} \\ 0, & \text{alternative point I not selected as an electronic fence point}\end{array} \right.$$

(6)

Then:

$$\begin{array}{*{20}l} {\left. {TC\left( {\tau _{i} } \right)} \right.} & = & {TFC + TVC\left( {D\left( {\tau _{i} } \right)} \right)} \\ {\left. {TTC} \right.} & = & {\sum\limits_{{\tau _{i} \in Y}} T C\left( {\tau _{i} } \right) = \sum\limits_{{\tau _{i} \in Y}} T FC + \sum\limits_{{\tau _{i} \in Y}} T VC\left( {D\left( {\tau _{i} } \right)} \right)} \\ & = & {\sum\limits_{{\tau _{i} \in Y}} {y_{i} } \times TFC_{i} + \sum\limits_{{\tau _{i} \in Y}} T VC\left( {D\left( {\tau _{i} } \right)} \right)} \\ \end{array}$$

(7)

This equation is complicated to calculate, but if we introduce an assumption that the change in variable cost is assumed to be linear with the change in demand.

Assumption: Variable costs are linear with size, i.e., we have:

$$TVC\left(a+b\right)=TVC\left(a\right)+TVC\left(b\right)$$

(8)

In fact, this assumption is reasonable in this case because the change in size is not very large. Based on this, we have:

$$TTC=\sum_{{\tau }_{i}\in Y} {y}_{i}\times TF{C}_{i}+TVC\left(\sum_{{\tau }_{i}\in Y} D\left({\tau }_{i}\right)\right)$$

(9)

And ${\tau }_{i}\in D\left({\tau }_{i}\right)$, which is the aggregate demand, is a constant, therefore:

$$minTTC\Leftrightarrow min\sum_{{\tau }_{i}\in Y} {y}_{i}\times TF{C}_{i}$$

(10)

Let us consider Problem 2 at this point. If we have already solved Problem 1: which locations have electronic fence points; then we can prove that in the optimal solution, each demand point must always be satisfied by its nearest electronic fence point.

This conclusion is almost obvious because, under the assumption of linearity of variable costs, the reallocation of demand does not cause a change in total cost, and being satisfied by the nearest electronic fence point maximizes the level of service.

Thus, our problem is only where to locate the electronic fences and how many to set, i.e., the value of each ${y}_{i}$. We formalize the problem:

$$\begin{array}{c}min\sum_{{\tau }_{i}\in Y} {y}_{i}\times TF{C}_{i}\\ maxT=\frac{\sum_{i\in D} D\left({\tau }_{i}\right)\times J\left({\tau }_{i}\right)}{\sum_{i\in D} D\left({\tau }_{i}\right)}\\ \, {\text{s.t.}} \, \left\{\begin{array}{c}{Y}^{\star }=\left\{{\tau }_{i}\in Y\mid {y}_{i}=1\right\}\\ J\left({\tau }_{i}\right)=\left\{\begin{array}{c}1,\underset{{\tau }_{j}\in {Y}^{\cdot }}{min} {d}_{ij}\le {d}_{0}\\ 0,\underset{{\tau }_{j}\in {Y}^{\cdot }}{min} {d}_{ij}>{d}_{0}\end{array}\right.\\ {y}_{i}\in \{\mathrm{0,1}\}\end{array}\right.\end{array}$$

(11)

This is a multi-objective planning problem. Considering that cost and service level jointly determine profit, we integrate the two objective functions. At the same time, considering a series of problems caused by low service level such as affect corporate image, we introduce a lower bound of service level ${T}_{0}$ as a constraint:

$$\begin{array}{c}minf=\alpha \sum_{i\in D} D\left({\tau }_{i}\right)\times J\left({\tau }_{i}\right)-\sum_{{\tau }_{i}\in {Y}^{\prime}} {y}_{i}\times TF{C}_{i}\\ \, {\text{s.t.}} \, \left\{\begin{array}{c}T\ge {T}_{0}\\ {Y}{^{\prime}}=\left\{{\tau }_{i}\in Y\mid {y}_{i}=1\right\}\\ J\left({\tau }_{i}\right)=\left\{\begin{array}{c}1,\underset{{\tau }_{j}\in {Y}^{\prime}}{min} {d}_{ij}\le {d}_{0}\\ 0,\underset{{\tau }_{j}\in {Y}{^{\prime}}}{min} {d}_{ij}>{d}_{0}\end{array}\right.\\ {y}_{i}\in \{\mathrm{0,1}\}\end{array}\right.\\ \end{array}$$

(12)

To build a modified model considering the effect of users’ accessibility to parking locations on their willingness to ride shared bicycles, we define a truncation function $J\left({\tau }_{i}\right)$, which means the needs beyond the radiation range ${d}_{0}$ will not be unsatisfied, while those within the radiation range ${d}_{0}$ will be completely satisfied. In order to improve the accuracy of the model, we consider constructing a demand loss function $f\left(d\right)$

$$J\left({\tau }_{i}\right)=f\left(\underset{{\tau }_{j}\in {Y}^{\prime}}{min} {d}_{ij}\right)$$

(13)

So in fact, the original $f\left(d\right)$ is a truncation function:

$$f\left(d\right)=\left\{\begin{array}{l}1,d<{d}_{0}\\ 0,d>{d}_{0}\end{array}\right.$$

(14)

we simply show a figure of original $f\left(d\right)$ by just setting $d\in \left[\mathrm{0,10}\right]$, ${d}_{0}=5$ to make the function more clear (Fig. 1).

Fig. 1

Plot of $f(d)=\{1, d<{d}_{0}; 0, d>{d}_{0}\}$

After modification, $f(d)$ is changed into a continuous function,

$$f\left(d\right)=\left\{\begin{array}{l}1,d<{d}_{0}\\ {e}^{-k\left(d-{d}_{0}\right)},d>{d}_{0}\end{array}\right.$$

(15)

The figure of modified $f\left(d\right)$ when $d\in \left[\mathrm{0,10}\right]$, ${d}_{0}=5$, $k=0.5$ is shown in Fig. 2:

Fig. 2

Plot of $f(d)=\{1,d<{d}_{0};e^{-k*(d-{d}_{0})},d>{d}_{0}\}$

3.4 Computational analysis

Theorem 1.

 The decisive problem in the first stage of Formular (11) is an NP-complete problem.

Proof:

We will prove that this problem can be reduced from a known NP-complete problem. Specifically, this problem is the Set covering problem (SCP).

Set covering problem (SCP): Given a full set $U$ and a set $S$ containing n sets, the sum of these n sets is the full set. The meaning of covering refers to a set $C$, $C \in S$, and the union of the elements of $C$ is $U$. The decisive problem of SCP is that given $\left(U,S\right)$ and an integer $k$, whether there exists a cover whose size does not exceed k. This is an NP-complete problem.

First, we construct our problem, denoted Problem P, using these SCP parameters.

Let the set of selectable points $Y=\left\{{\tau }_{1},{\tau }_{2},{\tau }_{3},\dots {\tau }_{m}\right\}=S$, that is, the set in $S$ corresponds to the set of selectable points one by one. Notice that after such a correspondence ${\tau }_{i}$ is a set, which is different from what it originally represented, but has no effect on the proof.

Then let $D=\left\{{\tau }_{m+1},{\tau }_{m+2},{\tau }_{m+3},\dots ,{\tau }_{m+n}\right\}=U$, which means that the elements in the full set U correspond to the demand points one by one. Unlike $Y$ where ${\tau }_{j}$ is an element rather than a set. Let ${TFC}_{i}= 1$, that is, the fixed cost of all selectable points is 1.

The next step is to set the distance matrix $d$. This is constructed according to the following rules:

$${d}_{ij}=\left\{\begin{array}{c}0,{\tau }_{j}\in {\tau }_{i}\\ 1,{\tau }_{j}\notin {\tau }_{i}\end{array}\right.$$

(16)

Then let ${d}_{0} = 0$ and the service level be restricted to 1.

The question is, does problem P have a solution for which the total fixed cost does not exceed k?

 Suppose the SCP problem gives a positive solution, i.e., construction of size is no more than k. Then for problem P, it is sufficient to take out optional points which suffice that do not exceed k and Y = S. Let this set be $y\in Y$, and let the subscript set of $I$ be $I = \{i| {\tau }_{i} \in y\}$. At this point, since$\cup y={\cup }_{i\in I}{\tau }_{i}=U$, that is, every element in $U$ can be found in ${\tau }_{i}$ which satisfies $i\in I$. Thus for ${d }_{ij}$, at fixed $j$ (i.e., for a particular element in $U$), there must be some $i$ satisfying ${d}_{ij}=0$, that is:

$$\forall j,\exists i,{\tau }_{j}\in {\tau }_{i}\Rightarrow\forall j,\exists i,{d}_{ij}=0$$

(17)

Then we could introduce $\forall j,{min}_{ i} {d }_{ij} = 0$, i.e., for any demand point, the distance to the nearest service point is 0, at which point the service level is 1, and the cost is less than k, so problem P also gives a positive result.

 Suppose that problem P gives a positive solution, i.e., there exists a solution with a total fixed cost not exceeding k and satisfying service level 1. Since the fixed cost of all optional points is 1, this means that the number of optional points does not exceed k. Let this set be $y \in Y$, and Let the subscript set $I = \{i| {\tau }_{i}\in y\}$ of i. Since the level of service is 1 and${d}_{ 0} = 0$, this means that$\forall j,{ min}_{ i} {d }_{ij }= 0$, which is equal to$\forall j, \exists i,{d}_{ ij }= 0$, i.e. that is $\forall j,\exists i,{\tau }_{j }\in {\tau }_{ i}$, then$\forall {\tau }_{j }\in U,{\tau }_{j}\in {\cup }_{i }{\tau }_{i }$. This proves that${\cup }_{i}{\tau }_{i } = U$. And$|I| \le k$, so the SCP problem will also give a firm solution.

4 Algorithm and solution

Since the Sect. 3.4 proved that the deterministic problem of Formular (11) is NP-complete and considering the large size of the problem, we use Heuristic algorithm to solve this problem. Specifically, we use a HGAA.

4.1 Coding approach

First, we need to properly encode the solution of the problem in order to use HGAA for iterative merit search. We simply encode the solution as a binary 0–1 string. The value of the $i-th$ bit $v\left(i\right)$ indicates whether the candidate point labeled $i$ is selected. That is to say $v\left(i\right)={y}_{i}$.

4.2 Objective function

The objective function of the original problem is the total fixed cost, i.e. $\sum_{{\tau }_{i}\in {Y}^{\prime}} {y}_{i}\times TF{C}_{i}$, but when using Iterative algorithm, the constraint can be put into the objective function as a penalty term as well, so as to avoid the process of verifying the feasibility of the solution. Specifically, we use:

$$c\left(x\right)=\sum_{{\tau }_{i}\in {Y}^{\prime}} {y}_{i}\times TF{C}_{i}+M\times max\left(0,{T}_{0}-T\right)$$

(18)

where M is a very large number. (But in other cases, such as setting the service level as a flexible constraint, it is possible to dynamically adjust the size of M).

So the overall objective function is:

$$\begin{array}{c}f\left(x\right)=\alpha \sum_{i\in D}D\left({\tau }_{i}\right)\times J\left({\tau }_{i}\right)-c\left(x\right)\end{array}$$

(19)

4.3 Algorithm

This paper uses a HGAA to solve this problem. The general process can be summarized as taking the initial solution ${\phi }_{0}$ and obtaining the initial solution space ${\Phi }_{0}$ by mutational operators.${\Phi }_{t}$ is obtained after t-generation processing ${\Phi }_{0}$ by mutational operators, crossover operators and selection operators. The final solution space is obtained after M iterations.

The initial solution contains all opened service points, that is, the initial solution ${\phi }_{0}=\left[1\dots 1\right]$.

Besides, the specific definition of each operator is as follows:

• Mutation operator. The process of mutation operator is that removes the solution ${\phi }_{i}$ from the solution space and obtains ${\phi }_{i }^{{\prime} }$ after the simulated Annealing algorithm, which is described in the following.

• Crossover operator. The procedure of the crossover operator is to first remove two solutions ${\phi }_{i}$, ${\phi }_{ j}$ from the solution space and randomly exchange some 0–1 pairs of them.

• Selection operator. The solutions in the solution space are sorted according to the objective function values, and a number of optimal solutions are selected to form a new next-generation solution space.

When the number of iterations reaches the upper limit M, the operation is terminated and the optimal solution in the final solution space is taken out.

4.4 Variational operator (simulated annealing algorithm)

For a solution ${\phi }_{i}$, it is a binary string. Randomly flip some bits, that is, randomly select some unopened service points to open, and randomly select some open service points to close, thus generating a new solution${\phi }_{i}^{\prime}$, and bring the new solution into the objective function to obtain$f({\phi }_{i}^{{\prime} })$. Based on $f({\phi }_{i}^{{\prime} }),$ $\Delta f = f({\phi }_{i}^{\prime}) - f({\phi }_{i })$ is calculated. If$\Delta f \le 0$, the new solution is accepted; if $\Delta f > 0$, the new solution is accepted according to the Metropolis criterion, i.e., the deteriorated solution is accepted with a certain probability, so that the algorithm has a global optimization ability to escape local extremes and avoid premature convergence, with probability:

$$p={e}^{-\frac{f\left({\phi }_{i}{^{\prime}}\right)-f\left({\phi }_{i}\right)}{KT}}$$

(20)

where a descent factor ${\alpha }_{1}$ is set for the temperature T.

$${T}_{\text{new }}={\alpha }_{1}{T}_{\text{old}}$$

(21)

The temperature is reduced iteratively until the number of iterations Q is reached.

5 Data selection and processing

For the demand data, considering the specificity of the school scenario, we have obtained some real data through surveys.

On the demand side, the demand for shared bicycles is projected from the number of students attending classes in academic buildings and the number of students living in each dormitory. In addition, by distributing nearly 400 questionnaires to university students, the relationship between walking time and willingness to ride shared bicycles among students is collected. We assumed that the average walking speed of a university student is 80 m/min, then we could obtain the threshold ${d}_{0}$. The set of demands and the set of alternative locations of electronic fence points will be used as input for distance calculation while performing route planning using the Gaode Map API. In the calculations later in this paper requires that ${d}_{ij}$ represents the shortest distance from $i$ to $j$, there is no $k$ such that ${d}_{ik}+{d}_{kj}<{d}_{ij}$, considering that:

• 1. there may be manually added/modified paths;

• 2. to ensure the robustness of the model, data cleaning should be performed.

The constraint ${x}_{ij}$ indicates whether node $ij$ is in the shortest path. In this step, the d matrix is processed, i.e., the shortest distance between any two nodes is obtained. Achieved using Freud's algorithm, the following model is designed to obtain the shortest distance between any two points in the network:

$$\begin{array}{c}min{d}_{ij}=\sum_{i=0}^{n} \sum_{j=0}^{n} {c}_{ij}{x}_{ij}\\ \, {\text{s.t.}} \, \left\{\begin{array}{c}\sum_{j:\left(i,j\right)\in G} {x}_{ij}-\sum_{j:\left(j,i\right)\in G} {x}_{ji}=\left\{\begin{array}{c}1,i=s\\ -1,s=t\\ 0,i\ne s,t\end{array}\right.\\ {x}_{ij}\ge 0\end{array}\right.\end{array}$$

(22)

The objective function is to minimize the total length of the planned path; constraint condition (1) ensures that the selected edge forms a chain from the starting point to the endpoint; constraint condition (2) is actually equivalent to ${x}_{ij}$ being a 0–1 variable.

In this paper, we use the Floyed algorithm to solve this problem.

The Floyed algorithm applies to APSP (All Pairs Shortest Paths), which is a dynamic planning algorithm.

Consider two possible shortest paths from any node $i$ to $j$:

• 1. directly from $i$ to $j$

• 2. from $i$ to $j$ through $k\left(k\le n\right)$ nodes.

Therefore, if the distance of the shortest path from node $i$ to $j$ is denoted by ${d}_{ij}$, for each node k, check that ${d}_{ik}+{d}_{kj}<{d}_{ij}$, and if this holds, let ${d}_{ij}={d}_{ik}+{d}_{kj}$; traverse through each $k$, updating the number of rows and columns except the $k th$ one each time. Performing this process n times will definitely lead to the optimal solution.

6 Numerical analysis

We took Hunan University of Technology and Business as an example to simulate the optimal station layout plan. The network map of the university is shown in Fig. 3. According to fieldwork findings, the number of students live in each dormitory is shown in Table 1. By using Gold Maps API, the latitude and longitude of main nodes are shown in Table 2. The latitude and longitude of candidate service points are collected on OpenStreetMap. By distributing 389 questionnaires, the relationship between walking time and willingness to ride shared bicycles among students is shown in Table 3. The number of questionnaires determined according to a criterion that the standard deviation of a recession should be less than 5% of its mean. We analyzed the school timetable and randomly select Lesson 2 on Monday as the example to draw the optimal layout of electronic fences; the number of students in each teaching building during that period is shown in Table 4.

Fig. 3

The network map of Hunan University of Technology and Business

Table 1 Number of students live in each dormitory

Table 2 Latitude and longitude of main buildings

Table 3 Relationship between walking time and willingness to ride shared bicycles among students

Table 4 Number of students attending Lesson 2 on Monday in each teaching building

To each building, we use normal distribution to derive a set of random numbers, each building has a random number corresponding to every other building, the fraction of the random number in the set is the fraction of students going to the corresponding building; between building $i$ and building $j$, we define ${R}_{ij}$ as the random number, and ${R}_{j}$ represents the sum of random numbers in column $j$.

Based on Table 1 and Table 4, let ${N}_{i}$ denote the number of students in each building on weekdays. Using Table 2 to calculate the distance between building $i$ and building $j$, and according to Table 3, we could tell the possibility of students who choose to ride shared bicycles between building $i$ and building $j$, which is denoted by ${P}_{ij}$.

Based on all results, we let ${E}_{ij}$ represent the estimated number of students needing bicycles between building $i$ and building $j$, Then, we get the formula as follows:

$${E}_{ij}=\frac{{R}_{ij}}{{R}_{j}}*{N}_{i}*{P}_{ij}$$

(23)

$${E}_{i}=\sum_{i=1}^{j}{E}_{ij}$$

${E}_{i}$ is the demand data we need to input to the algorithm; it represents the number of students needing bicycles in building $i$, and the final results are shown in Table 5:

Table 5 Number of students needing bicycles in building $i$

We set ${d}_{0}$=50 m, k = 1 and put all spatial and demand data to HGAA and the final results are shown in Fig. 4:

Fig. 4

The final layout plan of electronic fences

Please note that in Fig. 4, the blue nodes are demand nodes and the orange nodes are electronic fence points.

7 Effectiveness verification

We verify the effectiveness and correctness of our algorithm by computing the same case using a Mixed-integer Linear Programming (MILP) Solver. In order to use the solver, we first need to convert our problem into a mixed-integer programming (MIP) problem. Since the function $f(d)$ is non-linear, we start the conversion from $f(d)$ and consider the definition:

$${f}_{ij}=f\left({d}_{ij}\right)$$

(24)

We introduce several new decision variables: $p$ represents the number of people served, ${x}_{ij}$ indicates that demand point ${\tau }_{i}$ is served by service point ${\tau }_{j}$. Then the original problem can be written as:

$$\begin{array}{c}minf=\alpha p-\sum_{{\tau }_{i}\in {Y}^{\prime}} {y}_{i}\times TF{C}_{i}\\ \, {\text{s.t.}}\, \left\{\begin{array}{c}p\ge {T}_{0}\cdot \sum_{{\tau }_{i}\in Y} D\left({\tau }_{i}\right)\\ p=\sum_{i} \sum_{j} {x}_{ij}{f}_{ij}\\ {x}_{ij}\le {y}_{i},i=\mathrm{1,2},\dots ,m,j=m+1,m+2,\dots ,m+n\\ \sum_{j} {x}_{ij}=1,i=\mathrm{1,2},\dots ,m\\ {y}_{i}\in \{\mathrm{0,1}\},{x}_{ij}\in \{\mathrm{0,1}\}\end{array}\right.\end{array}$$

(25)

The objective function remains unchanged. The first constraint is the service level constraint. The second constraint is the calculation of the number of people served. The third constraint is that only open service points can provide services. The fourth constraint is the allocation of demand points to service points.

In this way, the problem is transformed into a mixed integer programming model, but the cost is that the number of decision variables and the number of constraints are greatly increased, which will bring difficulties to the accurate solution of the large-scale model.

The experimental results are as follows:

The red line is the result of MILP, and the blue line is the iterative process result of our HGAA. The horizontal axis is the iteration count, and the vertical axis is the value of objective function.

From Fig. 5, we can see that the convergence speed and convergence results are quite good. Moreover, the final result gap is only 0.085%.

Fig. 5

Comparison of the results of HGAA and MILP

8 Conclusion, limitations and future works

This paper uses campus as a case study to explore the optimal layout of electronic fences, considering service level and cost comprehensively. To solve the problem, computational complexity is proved and models are built based on SCP. By contrast to other researchers’ methods, we used HGAA to solve the problem. Moreover, Hunan University of Technology and Business was token as an example to validate the methods and gave guidance on school management and bicycle-sharing electronic fences location selection. Finally, this paper verified the effectiveness and correctness of the algorithms by computing the same case using a MILP Solver.

It should be noted that our research has some limitations and potential directions for future improvements. First, we assumed that variable costs are linear and did not consider the change of marginal utility. Second, the model overlooked practical constraints related to the actual limitations of each potential service point, such as restricted available space that limits the number of parked shared bicycles. However, if there is sufficient data, the algorithm could address this issue with minor modifications. Third, the algorithm's iteration speed may be affected when there is a large scale of optional service points. In future research, it might be possible to improve this issue by initially employing clustering for preliminary screening.