Introduction

Non-targeted analysis (NTA) is the characterization of the chemical composition of a sample without the prior knowledge of the composition [1]. In contrast to traditional targeted methods, which are generally well established, non-targeted approaches are newer and many challenges persist which are unique to the broad diversity of chemicals NTA is intended to address. Despite this, the utility of NTA is rapidly increasing and the concept has found use in characterizing the human exposome in a wide variety of sources including soil and sediment, air, water, dust, food, and consumer products such as medical devices [2].

The use of NTA for evaluation of medical devices, often described as chemical characterization testing, can be a powerful tool to address some biological endpoints when used in conjunction with toxicological risk assessment. This approach is advantageous because it can be a faster and cheaper method to assess the biocompatibility and safety of the device with fewer animal studies. Standards [3] and guidance [4] offer information regarding common approaches and starting points, however major gaps remain between current practices and universal agreement on the most appropriate non-targeted methods. Recent work discussed the challenges involved in NTA analyte recovery following liquid–liquid extraction, where liquid–liquid extraction is commonly used as a preparation method prior to instrumental analysis [5]. In that work, a proposed method for the selection of standards for evaluating a specific chemical subspace was presented. While the framework and predictive models described in the work were found to perform well for the evaluation of liquid–liquid extraction, other commonly used preparation techniques exist which may also significantly impact the recovery of chemicals intended to be detected by the NTA method and can benefit from similar treatment, such as concentration of liquid samples by evaporative methods.

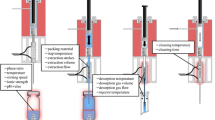
Evaporation, which is commonly accomplished under a stream of nitrogen or under vacuum, is a sample preparation technique commonly used in many fields including: chemical manufacturing [6], cannabinoid refinement [7], pharmaceuticals [8], and medical devices. For medical devices, evaporation is used to concentrate extracts prior to analysis if the extract is too dilute in order to achieve the toxicologically derived analytical evaluation threshold. In this context, extracts are often concentrated using nitrogen evaporation (NE, also known as nitrogen blowdown), or rotary evaporation (RE). Nitrogen evaporation consists of introducing direct nitrogen gas flow to the surface of the extract. This method is advantageous because the setup is often cheap, capable of evaporating multiple samples simultaneously using a single evaporator unit, able to evaporate at low temperatures, and able to evaporate high boiling point solvents. Rotary evaporation generally involves evaporating the solvent of a single sample in a closed system under vacuum. Rotary evaporation can be advantageous because it can evaporate much larger volumes (compatible with large volume glassware) and the evaporation rate is more consistent so evaporation can be reliably stopped at the desired final volume.

Evaporation of an extract as part of chemical characterization testing is often a necessary step to reach the analytical evaluation threshold, which allows for a more effective toxicological risk assessment. However, evaporative loss of any extractables which may be present remains a persistent concern for NTA. The recovery of these analytes can be estimated using basic thermodynamic principles. Ultimately, the impact of evaporation on recovery of extractables relates to the amount of analyte evaporated relative to the amount of solvent evaporated. Because the amount of solvent which needs to be evaporated greatly exceeds the amount of analyte present in the extract, the evaporation rate of solvent must be substantially higher than the analyte to prevent excessive evaporative loss during concentration. Using this concept, the recovery of an analyte from evaporation has been shown to be dependent on the air-solvent partition coefficient (\(K\)), which is the ratio of the concentration of the analyte in the solvent to the concentration of the analyte in the gas phase at equilibrium [9]. The recovery is also dependent on the post-evaporation final volume of the liquid (\({V}_{L,f}\)) and the gaseous volume of the evaporated solvent (\({V}_{G}\)) according to Eq. 1.

$$Recovery \left( \% \right) = 1 - \left[ {1 + K\left( {\frac{{V_{L,f} }}{V_G } } \right)} \right]^{ - 1} \times 100$$
(1)

The gaseous volume of the evaporated solvent can be determined from the change in liquid volume due to evaporation, the molecular volume of the liquid solvent (\({M}_{Vol,L}\)), and the molecular volume of the gaseous solvent (\({M}_{Vol,G}\)).

$$V_G = \Delta V_L /(M_{Vol,L} /M_{Vol,G} )$$
(2)

The molecular volumes in each state are trivially determined, where \({M}_{Vol,L}\) is the ratio of molecular weight to density and \({M}_{Vol,G}\) which can be derived from an equation of state, such as the ideal gas law.

$$M_{Vol,L} = MW/\rho$$
(3)
$$M_{Vol,G} = RT/P$$
(4)

Although all variables used in Eq. 1 are ideally known or may be estimated when performing evaporation for a targeted analyte, understanding the general impact on the extractables profile when using evaporation for chemical characterization is not as straightforward. A common approach to investigate the impact of sample preparation is to select a variety of surrogate chemicals of different chemical classes and conduct spike and recovery measurements. However, it is not always clear from these determinations what relevant properties were varied to probe recovery, and demonstration of the key recovery variables is necessary to extrapolate the recovery of a limited number of surrogates to the greater chemical space.

From the given equations relating to evaporation recovery, it is evident that all variables are parameters determined by the experimental method except \(K\). To extend predicted recoveries to all chemicals of a given chemical subspace, a model can be chosen to estimate this parameter. For estimating K, the Abraham solvation model has shown promise for its ability for liquid/gas partition systems [10]. Briefly, the partition coefficient (Eq. 5) is estimated by combining several products of solute descriptors (\(E\), \(S\), \(A\), \(B\), and \(L\)) and solvent system parameters (\(c\), \(e\), \(s\), \(a\), \(b\), and \(l\)). Each product of terms is specific to the system under study and corresponds to specific solute–solvent interactions. \(eE\) is the lone-pair interaction, \(sS\) is the dipole interaction, \(aA\) and \(bB\) are the hydrogen bond acidity and basicity interactions, and \(lL\) is the solute gas phase Ostwald partition coefficient into hexadecane at 298 K. The \(c\) term is a fitting parameter. Abraham solvation parameters can also be determined for a large dataset of chemicals using established Quantitative Structure Property Relationships (QSPR), which predict solvation parameters based on functional groups in the chemical structure.

$${\text{log}}K = c + eE + sS + aA + bB + lL$$
(5)

The purpose of this paper is to expand upon the previously described framework, which leverages the detectable space concept to guide method development and verification in chemical characterization, for determining the extent of recovery for medical device extractables due to evaporation. The described framework has been applied herein to evaporation specifically to demonstrate its utility as well as to present its potential as an expansion to the detectable space concept. However, the concepts employed remain adaptable to other extract processing or analytical methods. When applied as part of a robustness evaluation of the method verification process for NTA, the work also demonstrates how the model may guide experimental study design.

Materials and Methods

Chemicals

1,3-propanediol (98%), acetamide (99%), decamethyltetrasiloxane (DMTS; 97%), butylated hydroxytoluene (BHT; 99.9%), ε-caprolactam (99%), o-xylene (98%), octamethylcyclotetrasiloxane (OMCTS; 98%), cyclohexanone (99%), hexamethylenediamine (98%), pentylamine (99%), propionamide (97%), 1,8-octanediol (98%), toluene (99.8%), dichloromethane (DCM; 99.9%), and formic acid (98%) were purchased from Sigma-Aldrich (St. Louis, MO, USA). Liquid chromatography–mass spectrometry (LC–MS) grade water, 2-propanol (IPA; 99.9%), acetonitrile (ACN; 99.9%), and methanol (99.9%) were purchased from Thermo Fisher Scientific (Waltham, MA, USA). PLAS-CAL-001 calibration mix (including Erucamide, Irganox 1076, Irganox 3114, and Irganox 1010) was purchased from AccuStandard (New Haven, CT, USA).

Instrumentation

An Agilent 6890 GC and Agilent 5975B MSD with MSD ChemStation D.03.00.552 were used for analysis (Santa Clara, CA, USA). A split/splitless inlet was used in splitless mode using a 1 µL injection volume, 4 mm inner diameter single taper liner, and inlet temperature of 300 °C. For the chromatographic separation, a Restek Rxi-5Sil MS (cross bonded 5% 1,4-bis(dimethylsiloxy)phenylene 95% dimethyl polysiloxane) 30 m × 0.25 mm with 0.25 μm film thickness column (β = 250) with helium carrier (Ultra High Purity) at 1.0 mL/min constant flow was used. The oven temperature program was 40 °C (hold 1 min) to 280 °C at 15 °C/min. A 2.5 min solvent delay was implemented at the MSD and the transfer line temperature was 300 °C.

An Agilent Infinity II Liquid Chromatography (LC) and Agilent 6495 Triple Quadrupole Mass Spectrometer (MS) was used to analyze high boiling point compounds. The Agilent Jet Stream Technology Ion Source was run in positive ion mode electrospray ionization with a gas temperature at 230 °C, gas flow at 20 L/min, nebulizer at 35 psi, sheath gas temp at 325 °C, sheath gas flow at 1 L/min, and capillary at 4 kV. The injection volume was 5 μL. Solvent A was LC–MS grade water with 0.1% formic acid. Solvent B was LC–MS grade ACN with 0.1% formic acid. The gradient started at 80% B and increased to 95% B over 9 min. The gradient remained at 95% B for 5 min and reverted to 80% B over 1 min, remaining at 80% B for 1 min. The total run time was 16 min. The fragmentation information is included in the Supplemental Information.

An Organomation (Berlin, MA, USA) 12 position N-EVAP Nitrogen Evaporator system was run with a total flow rate of 5.0 L per min air. A water bath was used between 25 and 50 °C to heat the samples. The solution to be evaporated was placed in a water bath and the evaporator nozzles were lowered to within 3–4 cm of the surface of the liquid.

A Buchi (New Castle, DE, USA) R-215 Rotary Evaporator was used between 100 and 700 mbar (depending on the solvent and water bath temperature). The sample round bottom flask was rotated at 100 RPM. The chiller circulated 40/60 (v/v) ethylene glycol/water set between −10 and 10 °C. A water bath was used between 25 and 50 °C to heat the samples. The sample was transferred to a 100 mL round bottom flask. The flask was installed onto the RE unit and lowered into the water bath.

A Mettler (Columbus, OH, USA) AT250 analytical balance was used for mass measurements (initial and final volumes).

Chemical Space

To explore the application of the proposed framework, an initial chemical space was created from publicly available sources to encompass an array of chemicals that are applicable to medical device extractables, related to manufacture of plastics used in medical devices, or otherwise were of toxicological concern and may warrant consideration. The chemical space consisted of the Chemical and Products Database, Extractables and Leachables Safety Information Exchange database, California Proposition 65 list, and Toxic Substances Control Act list. The combined list contained approximately 125,000 individual chemical entries which was refined to remove duplicate chemicals and mixtures. Physicochemical parameters for the remaining chemical entries were generated from established QSPR using the EPA OPERA program [11], including boiling point, melting point, Henry constant, vapor pressure, pKa, octanol–air partition coefficient, octanol–water partition coefficient, and water solubility. This was supplemented with Abraham Solubility descriptors, which were generated using Poly-parameter Linear Free Energy Relationships (PPLFERs) previously described by Brown [12].

A “chemical subspace” was defined based on the application of the extract preparation method. In the case of evaporation, the method is often used prior to evaluation of extractable organic compounds by direct injection gas chromatography—mass spectrometry (GC–MS) and LC–MS. As such, inorganic elements and organometallic compounds were specifically excluded from the combined list to form the subspace applicable to evaporation.

Using the generated PPLFERs, \(K\) was estimated for all chemicals in the subspace by calculating the partition coefficient for various solvent/air mixes which was previously reported [10]. When available, experimental Abraham Solubility Parameters were obtained from the UFZ-LSER database and included with QSPR generated parameters for comparison [13]. The PPLFER model for estimation of Abraham Solubility Parameters has previously been well studied and validated [11, 12]. The model boundaries considered in the selected PPLFER model excludes inorganic solutes, most organometallic solutes, and any solutes which contained no carbon atoms. These were removed and excluded from the training set. Further, these chemical species were considered not applicable to the indicated chemical subspace.

Evaporation Recovery Method

To evaluate method parameters, an initial evaporation method was employed based on reducing the volume of hexanes by a factor of 5 at 35 °C. The selected standards were diluted to three concentrations representative of the linear ranges of the analytes. The sample was then evaporated in a water bath at the controlled temperature to the final volume under a stream of nitrogen or using RE. For RE, the evaporation pressure was set to 245 mbar and the condenser fluid was set to 0 °C. The RE pressure and condenser fluid temperature were modified according to the solvent and water bath temperature. For both evaporative methods, the sample was evaporated until approximately 2 mL of hexanes remained and the true final volume was measured gravimetrically. The samples were measured by GC–MS. The samples were weighed before and after evaporation to determine \({V}_{L,f}\) and \({\Delta V}_{L}\).

Concentration Impact

To evaluate the model prediction that recovery is not dependent on analyte concentration, and 100% recovery can still be achieved in specific combinations of evaporation conditions (analyte, solvent, and temperature) for low concentration and very low values of the ratio of final volume to change in volume (\({V}_{L,f}\)/\({\Delta V}_{L})\), analytes were selected with high log \(K\) values (Erucamide: 5.9, Irganox 1076: 7.4, Irganox 3114: 15.7, Irganox 1010: 20.9) and were evaporated by RE with a range of final volume to change in volume ratios. The RE method parameters were similar to those of the Evaporation Recovery Method above, however, the solvent used was 2-propanol, the water bath was set to 55 °C, and the pressure was set to 100 mbar. Samples were prepared by repeat tenfold concentration to a maximum concentration (2 µg/mL) to achieve a final \({V}_{L,f}\)/\({\Delta V}_{L}\) of 0.0014. To limit adsorption losses, the glassware was pretreated with 1 mL of the final mixture and air dried prior to the addition of the evaporation sample. Samples were weighed after each evaporation iteration to determine the final evaporation volume (\({V}_{L,f}\)). and analyzed by LC–MS.

Evaporation to Dryness

To evaluate the impact of evaporating a sample to dryness, which is outside of the model boundaries, a test method was employed to compare samples evaporated from 10 mL to dryness and reconstituted to 2 mL with samples evaporated from 10 to 2 mL. The selected standards were prepared at three concentrations representative of the linear ranges of the analytes. The solution was then evaporated in a water bath at 35 °C to the final volume (to dryness or to 2 mL) under a stream of nitrogen or using RE. The same NE and RE instrument parameters were used as in the Evaporation Recovery Method above. For both evaporative methods, the sample that was evaporated until approximately 2 mL of hexanes remained was then weighed to measure the true final volume. The samples evaporated to dryness were reconstituted with 2 mL of hexanes and sonicated for 1 min. The samples were weighed before and after evaporation to determine \({V}_{L,f}\) and \({\Delta V}_{L}\). The samples were measured by GC–MS.

Selection of Surrogate Chemicals and Evaporation Solvents

The model indicated for determining recovery can be separated into distinct components which must be considered when determining recovery following evaporation. Specifically, the range of estimated \(K,\) the ratio of final volume to change in volume (\({V}_{L,f}\)/\({\Delta V}_{L}\)), the solvent molecular weight, density, and vapor pressure, and the evaporation temperature must be evaluated. While \(K\), \({V}_{L,f}\)/\({\Delta V}_{L}\) and temperature are continuous and must be evaluated as such, the solvent-specific parameters are interrelated and categorically limited to the solvents which can generally be used in a chemical characterization study. An examination of common solvents which may be used is provided in Table 1.

Table 1 Properties of common extraction solvents
Full size table

Vapor pressures at alternative temperatures were estimated using the Antoine equation and the appropriate solvent-specific constants [15, 16]. Based on inspection of these solvents, the range of molecular weight, density, and vapor pressure were assessed through evaluation of recovery in dichloromethane, hexanes, and isooctane. Surrogate chemicals were then selected for each solvent to reflect a range of recoveries, which corresponded to log \(K\) values within the approximate range of 2–6 (Table 2). As necessary, consideration was also made to ensure the selected surrogate was soluble in the solvent under evaluation.

Table 2 Selection of surrogate standards per solvent
Full size table

While an empirical verification of the selected model is the primary focus of the framework, the analytical method was also validated for the nine analytes selected, which included assessment of the experimental parameters relevant to evaporation as a portion of the determination of method robustness. To address this aspect, the recovery was measured at three different temperatures which may be used under typical evaporation conditions (25, 35, and 50 °C). In addition, the surrogate chemicals selected were evaluated for linearity, precision, accuracy, limit of quantification, limit of detection, and specificity per guidance provided in ICH Q2(R2) [[17], p. 1]. These aspects are presented in the supplemental information. In all experiments, recovery of the selected analyte was determined by comparing the evaporated extract to the unevaporated standards prepared from the same stock.

Results and Discussion

Evaluation of the Selected Model

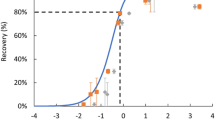
The results for the evaluation of the Evaporation Recovery Method using five surrogate chemicals are summarized in Fig. 1, along with a distribution of the theoretical recoveries. For all five chemicals selected, experimentally derived Abraham Solubility Parameters were available and were used to verify QSPR effectiveness. Throughout the recovery curve, \(K\) values determined using experimentally derived Abraham Parameters agreed with predicted recovery. In general, the QSPR model predicted experimental recoveries to within 20% above log \(K\) = 4 and below log \(K\) = 3. In the same manner as previously described an 80% cutoff for recovery was assigned as an acceptance value. Any chemicals within the subspace above this threshold were therefore considered adequately recovered, while chemicals with recovery less than 80% were considered inadequately recovered.

Fig. 1
figure 1

Recovery plot for the baseline evaporation method for hexanes at 35 °C. The orange circles and green squares are experimentally determined log \(K\) values using NE and RE, respectively. The gray triangles and purple diamonds are QSPR determined log \(K\) values using NE and RE, respectively. The black dashed line is the recovery cutoff (less than 80% recovery is considered unrecovered). The error bars are the standard error of the measurements. Points with error bars reaching 0% recovery were below the minimum measurable recovery, and the error bars indicate the range of possible recoveries

Full size image

A chemical characterization study which incorporates evaporation must select an evaporation method and the most effective parameters based on the intent of the study, such as to meet the analytical evaluation threshold. Although the process to achieve evaporation differs between RE and NE (and can significantly impact the absolute evaporation rate), the relative evaporation rate remains unaffected. The proposed model was shown to be equally effective at predicting evaporative loss under both conditions. Using either method, temperature is one of the most critical parameters for determining the most effective evaporation conditions. Practically, the evaporation temperature used in these methods could range from room temperature (approximated in the study as 25 °C) to 50 °C, above which the water bath temperature became difficult to maintain. As shown in Fig. 2, the choice of evaporation temperature in hexanes can shift the inflection of the recovery curve. This shift changes the method coverage (recovery > 80% of all chemicals in the chemical space) from 92 to 94%. The coverage is higher at higher temperature because the solvent vapor pressure increases faster than the temperature.

Fig. 2
figure 2

Theoretical recovery plots for various evaporation temperatures. The recovery increases at higher temperatures

Full size image

Another critical aspect is the evaporation volume ratio, which is defined from Eq. 1 as \({V}_{L,f}\)/\({\Delta V}_{L}\). Because the final volume following evaporation must logically be less than the initial volume, the change in volume should be reflected as the initial volume minus the final volume. Further, this ratio approaches infinity as \({\Delta V}_{L}\) approaches 0, implying the recovery of all analytes is 100% if no evaporation occurs. This finding is intuitively obvious, as there is no loss in recovery for any analyte due to evaporation if no evaporation occurs. While evaporation can still have significant impact even when the reduction in volume is small (1–10%), this impact is much more pronounced as the difference in volume increases. For example, if an extraction is performed in 100 mL hexanes and the extract must be reduced to 2 mL to achieve the necessary analytical evaluation threshold, this represents a 98% reduction of volume (\({V}_{L,f}\)/\({\Delta V}_{L}=1/49\)). With evaporation at 50 °C, such a reduction shifts the inflection by 2.7 orders of magnitude compared to a 10% reduction in volume (\({V}_{L,f}\)/\({\Delta V}_{L}=9\)), reducing the coverage of extractables from 99 to 86% based on the chemical space used in this study. It is therefore important to carefully consider the need to concentrate extracts and evaluate any chemicals which may be lost during evaporation using alternate means, such as headspace GC–MS. Further, efforts should always be made to minimize the extent of evaporation.

Additionally, the method should be verified for robustness as described, using the largest anticipated change in volume. Unlike other parameters, which can expand to both positive and negative infinity, volume reduction is unidirectional, spanning from 0 volume loss to 100% loss. Inherently, the recovery of all chemicals is 100% at 0 volume loss so assessment of this endpoint does not convey a greater understanding or control of the evaporation process. Instead, one should look toward the higher volume loss which they may encounter in their chemical characterization testing and evaluate that way. For the purposes of this work, an initial condition was established at 80% reduction (\({V}_{L,f}\)/\({\Delta V}_{L}=1/4\)). However, the effect of changing the evaporation volume ratio is demonstrated in Fig. 3, with the best recovery for the highest ratio (least evaporation).

Fig. 3
figure 3

Theoretical recovery plots for various evaporation volume ratios (\({V}_{L,f}\)/\({\Delta V}_{L}\)). The recovery increases at lower evaporation volume ratios

Full size image

The final critical aspect is the choice of solvent. The recovery will be highest for solvents with low molecular weight, high vapor pressure, and high density. Based on the properties listed in Table 1, the three solvents used in this study can be compared (DCM, hexanes, and isooctane). Isooctane has a slightly larger molecular weight than hexanes and DCM. DCM has twice the density of hexanes and isooctane. The most significant difference is the range of vapor pressures. DCM has ten times the vapor pressure of isooctane. As a result, for a given temperature and evaporation volume ratio, the recovery for DCM is higher than that of isooctane, as shown in Fig. 4. The coverage of Isooctane is 92%, while the coverage of DCM is 98%.

Fig. 4
figure 4

Recovery plot for evaporation from various solvents at the same temperature. The highest recovery was found for DCM

Full size image

Overall, 9 conditions were tested (three temperatures and three solvents) with a minimum of five analytes at three concentrations with two evaporation modes. This resulted in 70 concentration-averaged recovery measurements above the limit of detection, and the root-mean-square error was 12% for the experimental log \(K\) values and 12% for the QSPR values. This verified our assumption that it is reasonable to use the QSPR values to make general predictions concerning the chemical space.

Consideration of Matrix Effects and Mixtures in Evaporation

While the evaluations presented have considered simple solutions of analytes in ideal solvents, it is important to consider the practical implications of conducting an extract preparation step, such as evaporation, where the matrices can be complex and increasingly deviate from ideal behavior as the solution is concentrated. It is worth noting as well that these matrix effects and interferences from concentrating impurities in the solvent also significantly impact analysis. In fact, if deviation of recovery from the model due to matrix effects is expected and requires evaluation, a benefit of the proposed approach is the ability to systematically determine the appropriate standards which most effectively probe the potential for deviation from ideality. For example, with specified evaporation conditions (temperature, solvent, and evaporation volume ratio) the model can be used to determine values of log \(K\) that will show a range of recoveries from 0 to 100%, which present in a sigmoidal fashion where an inflection point is observed at a particular log \(K\) value. The compounds selected with log \(K\) values which bracket this inflection can be used for spike/recovery measurements to show the experimental recovery inflection point is unmoved. This presents substantial evidence that the matrix effect is not significantly impacting the evaporation. Alternately, if the inflection is moved, the information generated from the experiment can help ascertain to what degree and in what direction the recovery has shifted for all extractables. In addition to matrix effects impacting evaporation, it is also important to remain cognizant of the presence of precipitate following evaporation, which would indicate the extent of evaporation is not appropriate for a given extract. If these are noticed, evaporation should stop, and alternate means should be considered.

Additionally, this work evaluated the simpler case of evaporation from pure solvents. In practice, there is often a desire to perform extractions in mixtures, such as dilute alcohol solutions. Although such binary solutions can be advantageous when conducting extraction, evaluation of their impact on extract preparation becomes more complex. As indicated in the aforementioned equations, recovery of analyte from a solution following evaporation is strongly dependent on the solvent’s physicochemical properties as well as the analyte partition, represented by \(K\). The Abraham parameters for estimating \(K\) remain useful in evaluation of mixtures and have already been determined for several, including differing concentrations of ethanol in water. However, as an alcohol mixture evaporates, the mixture composition changes. Therefore, as an ethanol/water solution is evaporated, the amount of ethanol in the solution will decrease faster than the amount of water until the formation of an azeotropic mixture of ethanol and water. Additionally, as the composition changes so will the properties of the mixture as well as solubility of extractables. All of these considerations must be made in considering the use of such a dynamic situation.

Evaporating to Dryness

Evaporation to a specified final volume is complicated by non-linear evaporation kinetics, difficulty determining the remaining volume, and narrow “end-time” windows. It is much more convenient to evaporate a sample to dryness and then to reconstitute the sample to the desired volume. However, this procedure is likely in disagreement with the assumptions of the model presented in Eq. 1, namely that relative evaporation is the source of any recovery changes. This model does not account for thermal degradation, so thermally labile analytes are expected to have significant reductions in recovery. This concept is verified by Fig. 5, where some analytes were unaffected by evaporation to dryness (less thermally labile), while others saw marked reductions in recovery. This confirms that evaporation to dryness is outside the scope of the present work and a more complicated model would be required to predict the effects on the chemical space.

Fig. 5
figure 5

Recovery plot for the evaporation to dryness method. The orange circles and green squares are samples evaporated from 10 to 2 mL and have QSPR determined log \(K\) values using NE and RE, respectively. The gray triangles and purple diamonds are samples evaporated to dryness and have QSPR determined log \(K\) values using NE and RE, respectively. The black dashed line is the recovery cutoff (less than 80% recovery is considered unrecovered). The error bars are the standard error of the measurements. Points with error bars reaching 0% recovery were below the minimum measurable recovery, and the error bars indicate the range of possible recoveries

Full size image

Concentration Dependence

The idea that analytes at sufficiently small concentrations will eventually evaporate is often a cause for concern and can lead to setting concentration-based limitations on the degree of evaporation which may be deemed “acceptable” from anecdotal evidence rather than a rigorous evaluation of the evaporation method or parameters. As suggested in review of Eq. 1, no specific evaporation volume ratio is inappropriate, as the recovery is dependent on the combination of the variety of other variables. Although it is important to consider other effects outside of the act of evaporation, such as nonspecific surface adsorption at low concentration, and these should be demonstrated based on the concentration ranges applicable to the analytical method and study, evaporation itself remains independent of concentration. As an example of using more extreme evaporative conditions, analyte-solvent combinations were chosen with very high log \(K\) values such that very low values of the evaporation volume ratio could be used without any theoretical reduction in recovery (96–100% for all four chemicals for three iterations). Figure 6 shows the experimental verification of these conditions, where progressively smaller values of the evaporation volume ratio were used without any obvious reduction in recovery. The results demonstrate that no specific variable (analyte, temperature, solvent, or evaporation volume ratio) dominates the expected recovery. When considering a minimum applicable concentration, the evaporation method must instead be considered as part of the entire study to determine whether it is appropriate for the intended use.

Fig. 6
figure 6

Recovery plot for different evaporation volume ratios using the concentration impact method. The unevaporated sample was plotted as an evaporation volume ratio of 1. The symbols correspond to different chemicals. The error bars are the standard error of the measurements

Full size image

Selection and Expansion of the Chemical Space

In previous work, an effective chemical space for use in evaluating impact of recovery was considered comprehensive when it includes all chemicals which might be found in a chemical characterization study. While that work incorporated the combination of several sources of potentially relevant chemicals to create a reasonably comprehensive chemical space, it remains important to acknowledge that additional effort is needed in establishing a complete space. The creation of such a complete chemical space should incorporate known extractables as well as potential extractables generated through in silico methods. Known extractables could be efficiently incorporated into a singular, publicly accessible repository through the combined efforts of the NTA community, but even such a collective effort could not guarantee it would establish an exhaustive database which may be used as a suspect screening list to replace NTA. Instead, the effort to create such a repository for establishing chemical space would be continuously updated as new information and new chemical entities are discovered in chemical characterization studies. As the chemical space continuously improves, this inherently ensures the most up-to-date information is used uniformly across participants who conduct non-targeted analysis and help ensure the full range of physicochemical parameters associated with all extractables in a chemical characterization study is considered. As the chemical space grows, when new chemicals are discovered and added it becomes less likely these chemicals will alter to range of physicochemical parameters and the estimation of recovery impact from an extract processing step such as evaporation.

Application of the Selected Model

The experimentally verified model can be applied to a chemical space to predict the general effect of the evaporation. Without acceptance criteria, this approach is not capable of determining which evaporation methods are acceptable or unacceptable from a regulatory perspective, however comparison of coverage factors for different methods allows for a quantitative assessment of evaporation method variations. Ideally, an experimentally verified model will be applied to a sufficiently broad chemical space and the coverage factor will be 100% (all chemicals have a predicted recovery above 80%). In reality, this situation is very unlikely to ever occur. Instead, the framework can be used in study planning to choose an evaporation method that balances possible losses with practicability. Also, the chemicals lost during evaporation could be covered by another analytical method such that the total coverage factor is 100% (all chemicals in the chemical space have a recovery greater than 80% by at least one analytical technique used). These uses can help the biomedical community understand how extracts are changing due to sample concentration by evaporation.

Conclusions

Evaporation is an important step in the preparation of extracts prior to the use of an analytical instrument. In chemical characterization of medical devices, extracts are often concentrated by evaporation to reach sensitivity requirements. This is particularly important to consider because chemical characterization studies are intended to be non-targeted and as such any loss can significantly impact toxicological risk assessment. We have demonstrated that the use of a recovery model based on relative evaporation can be used to broadly predict losses. The significant variables include the air-solvent partition coefficient (\(K\)), the evaporation volume ratio (\({V}_{L,f}\)/\({\Delta V}_{L}\)), the solvent, and the temperature. Most of these are method dependent variables, but \(K\) is analyte and system specific. Good agreement was found between experiment and the theoretical recovery using experimentally measured log \(K\) values (12% root-mean-square error), and the same for modeled log \(K\) values (12% root-mean-square error). This included examining a variety of solvent and temperature conditions and used two different evaporation mechanisms. The model was then applied to the 39,000 chemicals of an extractables and leachables chemical space. Similar to the application of the framework on liquid–liquid extraction, when developing a method for chemical analysis which incorporates evaporation, an important aspect to address is understanding what the coverage of the chemical subspace will be given a specific set of experimental parameters. From application of the model to the entire chemical subspace and establishment of the 80% cutoff, the approach again demonstrates the advantage by allowing the user to quickly gauge the effect of adjusting extract preparation parameters on the overall potential chemical profile of an extract. Generalizing the results to the chemical space can be useful in comparing different evaporation methods and identifying chemicals that will be lost during evaporation. These lost chemicals will need to be detected by other means. Overall, this combination of an experimentally verified recovery model with a relevant chemical space is a powerful approach to characterize a non-targeted method.