1 Introduction

Because of its theoretical base and high generalization capability, a support vector machine (SVM) is an innovative and successful solution for data categorization and regression issues in the field of machine learning. SVM's main notion for binary classification problems is to find a hyperplane that can separate two classes with the greatest possible margin [5]. SVM [6, 33] is a convex quadratic programming problem that optimizes the margin between the nearest points of various classes while minimizing misclassification errors. In most cases, SVM is solved in dual space, resulting in a sparse and global solution [1]. Furthermore, SVM outperforms other machine learning algorithms such as artificial neural networks in terms of generalization instead of artificial neural networks, which suffer from overfitting and local minima. In a wide range of applications, such as human face detection, feature extraction, gene prediction, and several other classification issues, SVM beats most other learning techniques [12, 16, 23].

The hinge loss is used in SVM to maximize the shortest distance between classes; therefore, the final decision hyperplane is decided by the training points that are near to the decision boundary and are referred to as support vectors [29]. Normally, feature noise creates turbulence near the class boundaries [28]. As a result, feature noise may have a role in selecting the decision hyperplane as support vectors in SVM with hinge loss. Various approaches have been made to cope with feature noise ([4, 19, 30, 36, 37]; etc.). Huang et al. [14] presented the Pin-SVM (support vector machine with pinball loss), similar to SVM but using pinball loss rather than hinge loss. Unlike SVM, Pin-SVM applies penalties to correctly and incorrectly classified samples and learns the decision hyperplane by maximizing the quantile distance between classes resulting in noise insensitivity and resampling stability [14]. By incorporating the aggregation operators in hinge loss function and via Fuzzy logic, [20] proposed models that deal with the dataset shift. Xu et al. [34] presented a twin parametric SVM with pinball loss (Pin-TSVM) model that works faster than Pin-SVM and reduces noise sensitivity. Large-scale pinball twin SVM (TWSVM) provides the greater stability under sampling and tunable insensitivity to feature noise in comparison to TWSVM [32]. A novel twin bounded support vector machine classifier with squared pinball loss and its solution by functional iterative and Newton methods are proposed in [26].

For the regression problem, Asymmetric ν-twin support vector regression (Asy-v-TSVR) not only works faster than Asy-v-SVR but also employs the pinball loss to effectively reduce the disturbance of the noise and improve the generalization performance [35]. An improved regularization based Lagrangian asymmetric ν-TSVR using pinball loss function are proposed in [10]. An unconstrained variant of Asy-v-TWSVR, called robust asymmetric Lagrangian ν-TSVR using pinball loss function, that avoids the need to solve a pair of quadratic optimization problem thereby resulting in unique global solution [11].

Important data points can be fully allocated to one class in many real-world classification situations. In contrast, less meaningful data points, such as noise-corrupted data, cannot be assigned to any class. As a result, each data point should be treated differently depending on its significance; however, SVM doesn't have this capability. Lin and Wang [18] proposed the Fuzzy support vector machine (FSVM) to reduce the impact of noise and outliers in data. FSVM finds the ideal separation hyperplane by maximizing the margin between classes after assigning each sample a fuzzy membership value based on its relevance. Although FSVM has successfully avoided the negative impact of noise, it relies on the hinge loss and is ineffective in dealing with feature noise near the decision boundary.

Motivated by the works on Pin-SVM [14], FSVM [18], Functional and Newton method of solutions [2, 39], we propose a new fuzzy support vector machine with pinball loss (FPin-SVM whose solutions are obtained by two approaches: (i) obtaining its critical point by functional iterative algorithm, (ii) since it is not twice differentiable, either considering its generalized Hessian [8, 13] or introducing a smooth function [17] in place of the 'plus' function and applying Newton–Armijo algorithm. The effectiveness of the proposed FPin-SVM problem is demonstrated by performing experiments on a number of interesting synthetics and real-world datasets with different noises and comparing their results with SVM, FSVM, Pin-SVM, k-NN and OWAWA-FSVM.

In this work, all vectors are considered column vectors. For a vector \(x=({x}_{1},\text{...},{x}_{n}{)}^{t}\in {R}^{n}\), its transpose and 2-norm will be denoted by \({x}^{t}\) and \(||x||\) respectively. We define the plus function \({x}_{+}\) by \(({x}_{+}{)}_{i}={\text{max}}\left\{0,{x}_{i}\right\}\) where \(i=1,\text{...},n\). The \(m\) dimensional column vector of zeros and similarly the vector of ones will be denoted by 0 and \(e\) respectively and denote the identity matrix of appropriate size by .

The paper is organized as follows. Section 2 provides a brief review of the formulations of SVM, SVM with pinball loss (Pin-SVM), and fuzzy SVM (FSVM). Section 3 presents a new fuzzy SVM with pinball loss (FPin-SVM) in primal, whose solutions are obtained by functional and Newton-Armijo iterative methods. In Sect. 4, we investigate FPin-SVM properties. For comparison purposes, numerical tests on synthetic and benchmark datasets with different noises are performed in Sect. 5, while Sect. 6 concludes the paper.

2 Related work

In this section, we briefly describe the formulations of SVM, SVM with pinball loss, and Fuzzy support vector machine. For the binary classification problem, let the training set \({\left\{{x}_{i},{y}_{i}\right\}}_{i=1}^{m}\) be given where \({x}_{i}\in {R}^{n},{y}_{i}\in \left\{1,-1\right\}\).Let \(A\in {R}^{m\times n}\) represents the input matrix where the input example \({x}_{i}^{t}\) is its \({i}^{\text{th}}\) row and \(y=({y}_{1},\dots ,{y}_{m}{)}^{t}.\) Where \({x}_{i}^{t}\) the transpose of vector \({x}_{i}.\)

2.1 Support vector machine with hinge loss (SVM)

The linear SVM classifier attempts to find an optimal hyperplane \({w}^{t}x+b=0,w\in {R}^{n},b\in R;\) to maximize the margin and minimize the training error where wt is the transpose of vector w. The training error is measured by the hinge loss function defined as follows

$${L}_{\text{hinge}}(x,y,f(x))={\text{max}}(\mathrm{0,1}-{\text{yf}}(x))$$
(1)

By taking \(C>0\) as a trade-off parameter, \(\xi =({\xi }_{1},\dots ,{\xi }_{m}{)}^{t}\) as a vector of slack variables and \(e\) as a vector of ones of dimension m, the SVM model is obtained as

$$\underset{w,b,\xi }{\text{min}}\frac{1}{2}{w}^{t}w+{Ce}^{t}\xi $$
$$s.t.{y}_{i}({w}^{t}{x}_{i}+b)\ge 1-{\xi }_{i},{\xi }_{i}\ge 0,i=1,\dots ,m$$
(2)

Usually, dual of a problem (2) is solved and is obtained as

$$\underset{\alpha }{\text{min}}{\sum }_{i,j=1}^{m}{y}_{i}{y}_{j}{x}_{i}^{t}{x}_{j}{\alpha }_{i}{\alpha }_{j}-{\sum }_{i=1}^{m}{\alpha }_{i}$$
$$s.t.{\sum }_{i=1}^{m}{\alpha }_{i}{y}_{i}=0,0\le {\alpha }_{i}\le C,i=1,\dots ,m$$
(3)

where \(\alpha =({\alpha }_{1},\dots ,{\alpha }_{m}{)}^{t}\) is the vector of Lagrangian multipliers. The linear SVM decision function is given by

$$f(x)={\text{sign}}\left({\sum }_{i=1}^{m}{\alpha }_{i}{y}_{i}{x}^{t}{x}_{i}+b\right)$$
(4)

where \(b\) can be determined by Karush–Kuhn–Tucker (K.K.T.) conditions.

A nonlinear mapping is introduced in SVM to map the input example into a high dimensional feature space for the nonlinear case. Then SVM attempts to find the optimal separating hyperplane \({w}^{t}\phi ({x}_{i})+b=0\) in that feature space. By applying the kernel trick [6, 33] in (3), the minimization problem in dual for nonlinear SVM is obtained as

$$\underset{\alpha }{\text{min}}{\sum }_{i,j=1}^{m}{y}_{i}{y}_{j}k({x}_{i},{x}_{j}){\alpha }_{i}{\alpha }_{j}-{\sum }_{i=1}^{m}{\alpha }_{i}$$
$$s.t.{\sum }_{i=1}^{m}{\alpha }_{i}{y}_{i}=0,0\le {\alpha }_{i}\le C,i=1,\dots ,m$$
(5)

where \(\alpha =({\alpha }_{1},\dots ,{\alpha }_{m}{)}^{t}\) is the vector of Lagrangian multipliers,\(k({x}_{i},{x}_{j})=\phi ({x}_{i}{)}^{t}\phi ({x}_{j})\) and \(k(.,.)\) is a kernel function. The nonlinear SVM decision function is given by

$$f(x)={\text{sign}}\left({\sum }_{i=1}^{m}{\alpha }_{i}{\text{yk}}(x,{x}_{i})+b\right)$$
(6)

2.2 Support vector machine with pinball loss (Pin-SVM)

Since SVM with hinge loss is susceptible to noise and unstable with respect to resampling, Huang et al. [14] suggested using the pinball loss instead of hinge loss applied in SVM. The pinball loss function is defined as follows

$${L}_{\tau }(x,y,f({\varvec{x}}))=\left\{\begin{array}{c}1-y\,f(x),\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}1-y\,f(x)\ge 0\\ -\tau (1-y\,f(x),\hspace{1em}1-y\,f(x)<0\end{array}\right.$$
(7)

where \(0\le \tau \le 1\) is a user-defined parameter. The hinge loss and absolute \({L}_{1}\)-loss are the particular cases of pinball loss with \(\tau =0\) and \(\tau =1\), respectively. The support vector machine with pinball loss (Pin-SVM) model proposed by Huang et al. [14] is the following QPP,

$$\underset{w,b,\xi }{\text{min}}\frac{1}{2}{w}^{t}w+{Ce}^{t}\xi $$
$$\begin{array}{c}s.t.{y}_{i}({w}^{t}{x}_{i}+b)\ge 1-{\xi }_{i},\\ .{y}_{i}({w}^{t}{x}_{i}+b)\le 1+\frac{1}{\tau }{\xi }_{i},{\xi }_{i}\ge 0,i=1,\dots ,m\end{array}$$
(8)

The dual of problem (8) is derived as the following minimization problem

$$\underset{\alpha ,\beta }{\text{min}}\frac{1}{2}{\sum }_{i,j=1}^{m}{y}_{i}{y}_{j}{x}_{i}^{t}{x}_{j}({\alpha }_{i}-{\beta }_{i})({\alpha }_{j}-{\beta }_{j})-{\sum }_{i=1}^{m}({\alpha }_{i}-{\beta }_{i})$$
$$\begin{array}{c}s.t.{\sum }_{i=1}^{m}({\alpha }_{i}-{\beta }_{i}){y}_{i}=0,\\ {\alpha }_{i}+\frac{1}{\tau }{\beta }_{i}=C,{\alpha }_{i},{\beta }_{i}\ge 0,i=1,\dots ,m.\end{array}$$
(9)

where \(\alpha =({\alpha }_{1},\dots ,{\alpha }_{m}{)}^{t}\) and \(\beta =({\alpha }_{1},\dots ,{\alpha }_{m}{)}^{t}\) are the vectors of Lagrangian multipliers, respectively. The linear Pin-SVM decision function is given by

$$f(x)={\text{sign}}\left({\sum }_{i=1}^{m}({\alpha }_{i}-{\beta }_{i}){y}_{i}{x}_{i}^{t}{x}_{i}+b\right)$$
(10)

where \(b\) can be determined by K.K.T. conditions.

For the nonlinear case, the minimization problem in dual for nonlinear Pin-SVM can be obtained as

$$\underset{\alpha ,\beta }{\text{min}}{\sum }_{i,j=1}^{m}{y}_{i}{y}_{j}k({x}_{i},{x}_{j})({\alpha }_{i}-{\beta }_{i})({\alpha }_{j}-{\beta }_{j})-{\sum }_{i=1}^{m}({\alpha }_{i}-{\beta }_{i})$$
$$\begin{array}{c}s.t.{\sum }_{i=1}^{m}({\alpha }_{i}-{\beta }_{i}){y}_{i}=0,\\ {\alpha }_{i}+\frac{1}{\tau }{\beta }_{i}=C,{\alpha }_{i},{\beta }_{i}\ge 0,i=1,\dots ,m\text{.}\end{array}$$
(11)

where \(k({x}_{i},{x}_{j})=\phi ({x}_{i}{)}^{t}\phi ({x}_{j})\) and \(k(.,.)\) is a kernel function. Finally, the nonlinear Pin-SVM decision function is given by

$$f(x)={\text{sign}}\left({\sum }_{i=1}^{m}({\alpha }_{i}-{\beta }_{i}){y}_{i}k(x,{x}_{i})+b\right)$$
(12)

As the parameter \(\tau \) increases, the weights on the correctly classified points become great, so the margin width becomes large. Thus, the points near the boundaries of classes become less important in deciding the optimal decision hyperplane. The Effects of the feature noise are weakened, which leads to noise insensitivity.

2.3 Fuzzy support vector machine with hinge loss (FSVM)

In SVM, each data point is treated equally, but some data points can be more important than others for many real-world classification problems. Lin and Wang [18] proposed a fuzzy extension of SVM called fuzzy support vector machine (FSVM) to solve this problem. In FSVM, the fuzzy membership function assigns the fuzzy membership values to each data point based on its importance. We will use the class center method to generate the fuzzy membership [18].We denote \({x}_{+}\) and \({r}_{+}\) as the mean and radius of class + 1 and \({x}_{-}\) and \({r}_{-}\) as the mean and radius of class -1, respectively. The radius of each class is the farthest distance between its training points and its class center, namely \({r}_{+}=\underset{\left\{{x}_{i},{y}_{i}\text{=+}1\right\}}{\text{max}}\Vert {x}_{+}-{x}_{i}\Vert \) and \({r}_{-}=\underset{\left\{{x}_{i},{y}_{i}=-1\right\}}{\text{max}}\Vert {x}_{-}-{x}_{i}\Vert \). For any training point,\({x}_{i},\) its fuzzy membership \({s}_{i}\) is defined as follows:

$${s}_{i}=\left\{\begin{array}{c}1-\Vert {x}_{+}-{x}_{i}\Vert /({r}_{+}+d),\hspace{0.33em}if\hspace{0.33em}{y}_{i}=+1\\ 1-\Vert {x}_{-}-{x}_{i}\Vert /({r}_{-}+d),\hspace{0.33em}if\hspace{0.33em}{y}_{i}=-1\end{array}\right.$$

where \(d>0\) is used to avoid the case \({s}_{i}=0\text{.}\)

For the nonlinear classification problem, we will employ an improved fuzzy membership function studied (used) in [3, 15] and is defined as

$${s}_{i}=\left\{\begin{array}{c}1-\sqrt{{\Vert ({d}_{i}^{+})\Vert }^{2}/\left(({r}_{+}{)}^{2}+d\right)},\hspace{1em}if\hspace{0.33em}{y}_{i}=+1\\ 1-\sqrt{{\Vert ({d}_{i}^{-})\Vert }^{2}/\left(({r}_{-}{)}^{2}+d\right)},\hspace{1em}if\hspace{0.33em}{y}_{i}=-1\end{array}\right.$$

where

$$({d}_{i}^{+}{)}^{2}=k({x}_{i},{x}_{i})-\frac{2}{{m}^{+}}{\sum }_{({x}_{j},{y}_{j}\text{=+}1)}k({x}_{i},{x}_{j})+\frac{1}{({m}^{+}{)}^{2}}{\sum }_{({x}_{j},{y}_{j}\text{=+}1,{x}_{k},{y}_{k}\text{=+}1)}k({x}_{j},{x}_{k}),$$
$$({r}^{+}{)}^{2}=\underset{x,y\text{=+}1}{\text{max}}\left\{k(x,x)-\frac{2}{{m}^{+}}{\sum }_{({x}_{j},{y}_{j}\text{=+}1)}k(x,{x}_{j})+\frac{1}{({m}^{+}{)}^{2}}{\sum }_{({x}_{j},{y}_{j}\text{=+}1,{x}_{k},{y}_{k}\text{=+}1)}k({x}_{j},{x}_{k}),\right\}$$
$$({d}_{i}^{-}{)}^{2}=k({x}_{i},{x}_{i})-\frac{2}{{m}^{-}}{\sum }_{({x}_{j},{y}_{j}=-1)}k({x}_{i},{x}_{j})+\frac{1}{({m}^{-}{)}^{2}}{\sum }_{({x}_{j},{y}_{j}=-1,{x}_{k},{y}_{k}=-1)}k({x}_{j},{x}_{k}),$$
$$({r}^{-}{)}^{2}=\underset{x,y=-1}{max}\left\{k(x,x)-\frac{2}{{m}^{-}}{\sum }_{({x}_{j},{y}_{j}=-1)}k(x,{x}_{j})+\frac{1}{({m}^{-}{)}^{2}}{\sum }_{({x}_{j},{y}_{j}=-1,{x}_{k},{y}_{k}=-1)}k({x}_{j},{x}_{k}),\right\}$$

m+ and m- are the number of samples in positive and negative classes, respectively.

The formulation of FSVM in primal is written as:

$$\underset{w,b,\xi }{\text{min}}\frac{1}{2}{w}^{t}w+C{\sum }_{i=1}^{m}{s}_{i}{\xi }_{i}$$
$$s.t.{y}_{i}({w}^{t}{x}_{i}+b)\ge 1-{\xi }_{i},{\xi }_{i}\ge 0,i=1,\dots ,m$$
(13)

For a detailed discussion on the problem formulation of FSVM, its solution method, and its advantages, see [18].

3 Proposed Fuzzy support vector machine with pinball loss (FPin-SVM)

Following the work of Pin-SVM [14] and FSVM [18], a Fuzzy support vector machine with pinball loss (FPin-SVM) is proposed in this section to enhance the performance of FSVM with the attractive features of pinball loss including noise insensitivity and within-class scatter minimization. It is proposed to compute the solution of Pin–FSVM by iterative-based schemes [2, 39], which leads to lower training time.

Introducing the pinball loss function into the FSVM (13) with squared L2- norm of slack variables and adding the term \(({b}^{2}/2)\) into its objective function, we formulate the FPin-SVM for the linear case as the following QPP:

$$\underset{w,b,\xi }{\text{min}}\frac{1}{2}({w}^{t}w+{b}^{2})+\frac{C}{2}{\sum }_{i=1}^{m}{s}_{i}{\xi }_{i}^{2}$$
$$\begin{array}{c}s.t.{y}_{i}({w}^{t}{x}_{i}+b)\ge 1-{\xi }_{i},\\ \text{.}{y}_{i}({w}^{t}{x}_{i}+b)\le 1+\frac{1}{\tau }{\xi }_{i},i=1,\dots ,m\end{array}$$
(14)

where \(C>0\) and \(0\le \tau \le 1\) are the user-defined parameters;\({s}_{i}\) and \({\xi }_{i}\) are the fuzzy membership and slack variable corresponding to \({i}^{\text{th}}\) input example \({x}_{i}\), respectively.

Remark 1

Since \({y}_{i}({{\varvec{w}}}^{t}{{\varvec{x}}}_{i}+b)\ge 1-{{\xi }_{i}}_{\hspace{1em}}\Rightarrow \hspace{1em}{\xi }_{i}\ge 1-{y}_{i}({{\varvec{w}}}^{t}{{\varvec{x}}}_{i}+b)\) or \({\xi }_{i}=\mathit{max}(\mathrm{0,1}-{y}_{i}({{\varvec{w}}}^{t}{{\varvec{x}}}_{i}+b))\)

$${\mathrm{and} y}_{i}\left({{\varvec{w}}}^{t}{{\varvec{x}}}_{i}+b\right)\le 1+\frac{1}{\tau }{\xi }_{i}\hspace{1em}\Rightarrow \hspace{1em}{\xi }_{i}\ge \tau \left({y}_{i}\left({{\varvec{w}}}^{t}{{\varvec{x}}}_{i}+b\right)-1\right) or {\xi }_{i}=\tau \mathit{max}(0,{y}_{i}({{\varvec{w}}}^{t}{{\varvec{x}}}_{i}+b)-1)$$

Therefore, the empirical risk term with given constraints in optimization problem (14) can be equivalently written as a minimization problem of the form

$$\underset{{\varvec{w}},{\varvec{b}}}{min}\hspace{0.33em}\hspace{0.33em}\frac{C}{2}{\sum }_{i=1}^{m}{s}_{i}(\mathit{max}\{0,1-{y}_{i}({{\varvec{w}}}^{t}{{\varvec{x}}}_{i}+b){\}}^{2}+{\tau }^{2}\mathit{max}\{0,{y}_{i}({{\varvec{w}}}^{t}{{\varvec{x}}}_{i}+b)-1{\}}^{2})$$
$$=\underset{w,b}{\text{min}}\frac{C}{2}{\sum }_{i=1}^{m}{s}_{i}([(1-{y}_{i}({w}^{t}{x}_{i}+b){)}_{+}{]}^{2}+{\tau }^{2}[({y}_{i}({w}^{t}{x}_{i}+b)-1{)}_{+}{]}^{2})$$
$$=\underset{u}{\text{min}}\frac{C}{2}\left[((e-{\text{DG}}u{)}_{+}{)}^{t}S(e-{\text{DG}}u{)}_{+}+{\tau }^{2}(({\text{DG}}u-e{)}_{+}{)}^{t}S({\text{DG}}u-e{)}_{+}\right]$$

where \(u=[{w}^{t}b{]}^{t}\in {R}^{n+1},D={\text{diag}}({y}_{1},\dots ,{y}_{m}),S={\text{diag}}({s}_{1},\dots ,{s}_{m})\) and \(G=[Ae]\text{.}\)

Problem (14) can be written as an unconstrained minimization problem as follows

$$\underset{u}{\text{min}}\frac{1}{2}{u}^{t}u+\frac{C}{2}\left[((e-{\text{DG}}u{)}_{+}{)}^{t}S(e-{\text{DG}}u{)}_{+}+{\tau }^{2}(({\text{DG}}u-e{)}_{+}{)}^{t}S({\text{DG}}u-e{)}_{+}\right]$$
(15)

Remark 2

The unconstrained formulation (15) of the problem (14) is a strongly convex minimization problem because we considered the squared \(L2\) norm of slack variables instead of \(L1\) norm in (14). Further adding the \(({b}^{2}/2)\) term in the objective function of (14), effects in maximization of margin with respect to both orientation vector \(w\) and location parameter b of the separating decision hyperplane [22].

Once the solution vector \(u\) of the problem (15) is known, then given any input,\(x\) the linear decision function determines its class \(f(x)={\text{sign}}([{x}^{t}1]u)\text{.}\)

For the nonlinear extension of linear FPin-SVM to nonlinear FPin-SVM, we consider the kernel matrix \(K=K(A,{A}^{t})\) of order m having \(K(A,{A}^{t}{)}_{\text{ij}}=k({x}_{i},{x}_{j})\in R\) as its \((i,j{)}^{\text{th}}\) element. Further, for a given vector \(x\in {R}^{n}\), let \(K({x}^{t},{A}^{t})=(k(x,{x}_{1}),\dots ,k(x,{x}_{m}))\) be a row vector in \({R}^{m}\).Following the work of [22], we formulate the nonlinear Pin-SVM as the following QPP:

$$\underset{w,b,\xi }{\text{min}}\frac{1}{2}({w}^{t}w+{b}^{2})+\frac{C}{2}{\xi }^{t}S\xi $$
$$\begin{array}{c}s.t.D(K(A,{A}^{t})w+b)\ge e-\xi \\ \text{.}D(K(A,{A}^{t})w+b)\le e+\frac{1}{\tau }\xi \end{array}$$
(16)

where \(C>0\) and \(0\le \tau \le 1\) are the user-defined parameters;\(D={\text{diag}}({y}_{1},\dots ,{y}_{m}),S={\text{diag}}({s}_{1},\dots ,{s}_{m})\) and \(\xi =({\xi }_{1},\dots ,{\xi }_{m}{)}^{t}\text{.}\)

Problem (16) can be written as an unconstrained minimization problem as follows

$$\underset{u}{\text{min}}\frac{1}{2}{u}^{t}u+\frac{C}{2}\left[((e-{\text{DG}}u{)}_{+}{)}^{t}S(e-{\text{DG}}u{)}_{+}+{\tau }^{2}(({\text{DG}}u-e{)}_{+}{)}^{t}S({\text{DG}}u-e{)}_{+}\right]$$
(17)

where \(u=[{w}^{t}b{]}^{t}\in {R}^{m+1}\),\(G=[K(A,{A}^{t})e]\).

We propose to solve the primal problem (17) by obtaining its critical point through a functional iterative algorithm and the Newton method. Once the solution vector \(u\) of the problem (17) is known, then given any input \(x\), its class is determined by the nonlinear decision function:

$$f(x)={\text{sign}}([K({x}^{t},{A}^{t})1]u)\text{.}$$

3.1 Functional iterative method of solving FPin-SVM (FFPin-SVM)

Solving the unconstrained nonlinear FPin-SVM problem (17) in this subsection is proposed by computing its critical point, which becomes a root-finding problem by setting its gradient to zero.

The gradient vector of (17) can be obtained as

$$\nabla L(u)=u+{\text{CG}}^{t}{\text{DS}}\left[-(e-{\text{DG}}u{)}_{+}+{\tau }^{2}({\text{DG}}u-e{)}_{+}\right]$$
(18)

Using the inequality \({u}_{+}=\frac{u+\left|u\right|}{2},\nabla L(u)\) becomes

$$\nabla L(u)=u+\frac{C}{2}{G}^{t}{\text{DS}}\left[-\left(\left|e-{\text{DG}}u\right|+e\right)+{\tau }^{2}\left(\left|{\text{DG}}u-e\right|-e\right)+(1+{\tau }^{2}){\text{DG}}u\right]$$

Now, computing \(\nabla L(u)=0,\) we get

$$\left(\frac{2I}{C}+(1+{\tau }^{2}){G}^{t}{\text{DSDG}}\right)u={G}^{t}{\text{DS}}\left[\left(\left|e-{\text{DG}}u\right|+e\right)+{\tau }^{2}\left(-\left|{\text{DG}}u-e\right|+e\right)\right]$$
(19)

This leads to the following functional iterative scheme (FFPin-SVM), for \(i=\mathrm{0,1},\dots \)

$${u}^{i+1}={Q}^{-1}{G}^{t}{\text{DS}}\left[\left(\left|e-{\text{DG}}u\right|+e\right)+{\tau }^{2}\left(-\left|{\text{DG}}u-e\right|+e\right)\right]$$
(20)

where \(Q=\left(\frac{2I}{C}+(1+{\tau }^{2}){G}^{t}{\text{DSDG}}\right)\)

Since one can write the matrix product \({G}^{t}{\text{DSDG}}={G}^{t}{\text{DS}}^{1/2}{S}^{1/2}{\text{DG}}\) and it is of the form \({P}^{t}P\) where \(P={S}^{1/2}{\text{DG}}\) implies the matrix \({G}^{t}{\text{DSDG}}\) is positive semi-definite. Therefore, for the given parameters C > 0 and \(0\le \tau \le 1\), the matrix \(Q\) which is the sum of a positive definite matrix, and a positive semi-definite matrix is also a positive definite matrix.

Remark 3

The proposed iterative scheme (20) needs the inverse of a positive definite matrix Q having an order that equals to a number of input examples, but it is computed only once before the first iterative step begins the execution.

Remark 4

In FFPin-SVM (20), the time complexities for the matrix multiplications DG, SDG, GtDSDG, Q−1 GtDS and the matrix inversion Q−1 are m(m + 1), m(m + 1), m(m + 1)2 and (m + 1)3 respectively. Thus, the cumulative complexity of FFPin-SVM is O(2 m(m + 1) + m(m + 1)2 + (m + 1)3).

3.2 Newton method of solving FPin-SVM

In this subsection, we apply Newton iterative method with Armijo stepsize for solving the unconstrained nonlinear FPin-SVM problem (17), and it is defined as:

Newton method with Armijo stepsize [8, 21].

For solving (17), start with an initial guess \({u}^{0}\in {R}^{m+1}\)

  1. (i)

    Stop the iteration if \(g({u}^{i})=0\)

Else

Determine the direction vector \({d}^{i}\in {R}^{m}\) as the solution of the following linear system of equations in \(m\) variables:

$$\partial g({u}^{i}){d}^{i}=-g({u}^{i})$$
  1. (ii)

    Armijo stepsize. Define:where the stepsize \({\lambda }_{i}={\text{max}}\left\{1,\frac{1}{2},\frac{1}{4},\text{...}\right\}\) is such that:\(L({u}^{i})-L({u}^{i}+{\lambda }_{i}{d}^{i})\ge -\delta {\lambda }_{i}g({u}^{i}{)}^{t}{d}^{i}\) and \(\delta \in (0,\frac{1}{2})\text{.}\)

    $${u}^{i+1}={u}^{i}+{\lambda }_{i}{d}^{i},$$

Applying the Newton-Armijo algorithm to the problem (17) requires both gradient vector and Hessian matrix to be computed. For this purpose, the absolute value Eq. (19) is considered in the form

$${g}_{1}(u)=\left(\frac{2I}{C}+(1+{\tau }^{2}){G}^{t}{\text{DSDG}}\right)u-{G}^{t}{\text{DS}}\left[\left(\left|e-{\text{DG}}u\right|+e\right)+{\tau }^{2}\left(-\left|{\text{DG}}u-e\right|+e\right)\right]$$
(21)

Then, we compute a generalized Hessian [13] of \({g}_{1}(u)\) as.

$$\partial {g}_{1}\left(u\right)=\left(\frac{2I}{C}+{G}^{t}{\text{DSE}}_{1}\left(u\right){\text{DG}}+{\tau }^{2}{G}^{t}{\text{DSE}}_{2}\left(u\right){\text{DG}}\right),$$
(22)

where \({E}_{1}(u)=I+{\text{diag}}({\text{sign}}(e-{\text{DG}}u)),{E}_{2}(u)=I+{\text{diag}}({\text{sign}}({\text{DG}}u-e))\)

Remark 5

One can observe the matrices \({E}_{1}(u)\) and \({E}_{2}(u)\) with their diagonal values 0 or 1 or 2. By defining matrices \({P}_{1}={E}_{1}(u{)}^{1/2}{S}^{1/2}{\text{DG}}\) and \({P}_{2}={E}_{2}(u{)}^{1/2}{S}^{1/2}{\text{DG}}\), the matrices.

\({G}^{t}{\text{DSE}}_{1}(u){\text{DG}}\) and \({G}^{t}{\text{DSE}}_{2}(u){\text{DG}}\) can be written in the form \({P}_{1}^{t}{P}_{1}\) and \({P}_{2}^{t}{P}_{2}\) respectively. Therefore, for the given parameters C > 0 and \(0\le \tau \le 1\), the generalized Hessian matrix (22) which is the sum of a positive definite matrix, and two positive semi-definite matrices is also a positive definite matrix.

Since the gradient and generalized hessian defined by (21) and (22) of the proposed problem (17) are given, one can perform the Newton method with Armijo stepsize to obtain its solution. We call this generalized derivative approach of solution as NFPin-SVM1. It can be shown that [17] for any starting vector \({u}^{0}\) in \({R}^{m+1}\); the sequence \(\left\{{u}^{i}\right\}\) obtained using the Newton–Armijo algorithm described above converges globally and terminates at the global minimum in a finite number of iterations.

One can employ a popular smoothing technique as another approach for solving the proposed unconstrained nonlinear FPin-SVM. A smooth approximation function for the plus function introduced by Lee and Mangasarian [17] is defined as

$$p(x,\alpha )=x+\frac{1}{\alpha }(1+{\text{exp}}(-\alpha x))$$
(23)

where \(x\in R\) and \(\alpha >0\) is a smoothing parameter.

Now substituting \(p(x,\alpha )\) for \((x{)}_{+}\) in (18), its smooth reformulation is obtained as

$${g}_{2}(u)=u+{\text{CG}}^{t}{\text{DS}}\left[-p((e-{\text{DG}}u),\alpha )+{\tau }^{2}p(({\text{DG}}u-e),\alpha )\right]$$
(24)

The Hessian matrix corresponding to smooth approximation problem (24) can be obtained as

$$\partial {g}_{2}u=\left(I+{\text{CG}}^{t}{\text{DS}}\left[{\text{diag}}\left(\frac{1}{1+{\text{exp}}(-\alpha (e-{\text{DG}}u))}\right)+{\tau }^{2}{\text{diag}}\left(\frac{1}{1+{\text{exp}}(-\alpha ({\text{DG}}u-e))}\right)\right]{\text{DG}}\right)$$
(25)

Since the Hessian matrix (25) is positive definite, the Newton method with Armijo stepsize can be used to find the solution. We call this smooth approach to solution as NFPin-SVM2.Following the proof of [17], it can be shown that for any starting vector \({u}^{0}\) in \({R}^{m+1}\); the sequence \(\left\{{u}^{i}\right\}\) obtained using the Newton–Armijo algorithm described above converges globally and quadratically. Further, when the smoothing parameter \(\alpha >0\) converges to infinity, the unique solution converges to the unique solution of the original minimization problem (17) [17].

Remark 6

The key advantage in considering either the generalized Hessian or smooth approach for solving (17) is that a system of linear equations is solved instead of a QPP as in the case of SVM, FSVM, and Pin-SVM.

Remark 7

In NFPin-SVM1, for the evaluation of gradient (21) and generalized Hessian (22), compute the matrix multiplications DG, SDG, GtDSDG, E1(u)DG, GtDSE1(u)DG, E2(u)DG and GtDS E2(u)DG with complexities of m(m + 1), m(m + 1), m(m + 1)2, m(m + 1), m(m + 1)2, m(m + 1) and m(m + 1)2 respectively. Also, the system of linear equation i.e., \(\partial g({u}^{i}){d}^{i}=-g({u}^{i})\) (see step (i) of Newton iterative method) can be solved in (m + 1)3. In case of simple Newton algorithm terminates at p (< = itmax) iteration, its total complexity is: O(2 m(m + 1) + m(m + 1)2 + p[( 2 m(m + 1) + 2 m(m + 1)2,]. One can also compute the total complexity of NFPin-SVM2 algorithm as O(2 m(m + 1) + p[( 2 m(m + 1) + 2 m(m + 1)2).

4 Analysis of FPin-SVM

4.1 Noise insensitivity of FPin-SVM

We focus on the unconstrained FPin-SVM for the linear case for easy comprehension. Differentiating (15) with respect to variables \(u\) leads to the following K.K.T. condition

$$0\in \frac{1}{C}u+{\text{CG}}^{t}{\text{DS}}\left[-(e-{\text{DG}}u{)}_{+}+{\tau }^{2}({\text{DG}}u-e{)}_{+}\right]$$

Since \(u=[{w}^{t}b{]}^{t}\in {R}^{n+1},D={\text{diag}}({y}_{1},\dots ,{y}_{m}),S={\text{diag}}({s}_{1},\dots ,{s}_{m})\) and \(G=[Ae],\) the above optimality condition can be expressed as

$$0\in \frac{1}{C}\left[\begin{array}{c}w\\ b\end{array}\right]-{\sum }_{i=1}^{m}{y}_{i}{s}_{i}(1-{y}_{i}({w}^{t}{x}_{i}+b){)}_{+}\left[\begin{array}{c}{x}_{i}\\ 1\end{array}\right]+{\tau }^{2}{\sum }_{i=1}^{m}{y}_{i}{s}_{i}({y}_{i}({w}^{t}{x}_{i}+b)-1{)}_{+}\left[\begin{array}{c}{x}_{i}\\ 1\end{array}\right]$$
(26)

Defining the index sets \({T}_{1}^{+}=\left\{i:1-{y}_{i}({w}^{t}{x}_{i}+b)>0\right\}\) and \({T}_{2}^{-}=\left\{i:1-{y}_{i}({w}^{t}{x}_{i}+b)<0\right\}\) the Eq. (26) can be written as

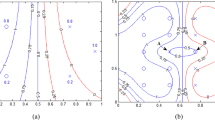
$$\frac{1}{C}\left[\begin{array}{c}w\\ b\end{array}\right]-{\sum }_{i\in {T}_{1}^{+}}{y}_{i}{s}_{i}(1-{y}_{i}({w}^{t}{x}_{i}+b))\left[\begin{array}{c}{x}_{i}\\ 1\end{array}\right]+{\tau }^{2}{\sum }_{i\in {T}_{2}^{-}}{y}_{i}{s}_{i}({y}_{i}({w}^{t}{x}_{i}+b)-1)\left[\begin{array}{c}{x}_{i}\\ 1\end{array}\right]=0$$
(27)

The parameter \(\tau \) in condition (27) controls the number of points in \({T}_{1}^{+}\) and \({T}_{2}^{-}\). When \(\tau \) is small, there are a lot of points in \({T}_{2}^{-}\) compared to \({T}_{1}^{+}\), and the result is sensitive. Both sets contain many points when \(\tau \) becomes large, and the result is less sensitive. This is also illustrated in Fig. 1. It is observed in Fig. 1a that the SVM is sensitive to the feature noise around the decision boundary, which results in an SVM classifier having a smaller margin. The linear decision boundaries obtained by the proposed FPin-SVM are shown in Fig. 1b, c. Here sets \({T}_{1}^{+}\) and \({T}_{2}^{-}\) contains the points within and outside the region defined by the positive and negative supporting hyperplanes, respectively. In Fig. 1b, FPin-SVM obtains a classifier with a margin slightly better and larger than SVM but still sensitive to feature noise because \({T}_{2}^{-}\) contains many points for smaller values \(0\text{.}1\) for \(\tau \).It can be seen that in Fig. 1c, for larger value 1 for \(\tau \) both sets contains many points, and the result is less sensitive to feature noise with larger margin width.

Fig. 1
figure 1

Illustrations of a SVM, b FPin-SVM with τ = 0.1, and c FPin-SVM with τ = 1 on a 2-D synthetic dataset

Full size image

4.2 Within-class scatter minimization

The proposed FPin-SVM formulation (14) can be equivalently transformed into \(\underset{w,b,\xi }{\text{min}}\frac{1}{2}({w}^{t}w+{b}^{2})+\frac{C}{2}{\sum }_{i=1}^{m}{s}_{i}\left[{\text{max}}{\left\{0,{e}_{i}\right\}}^{2}+{\tau }^{2}{\text{max}}{\left\{0,-{e}_{i}\right\}}^{2}\right]\)

$${\mathrm{s}.\mathrm{ t}. e}_{i}=1-{y}_{i}({w}^{t}{x}_{i}+b),i=1,\dots ,m$$
(28)

Note that when \(\tau =0,\) Eq. (28) reduces to the following L2 norm-Fuzzy support vector machine (L2-FSVM) [38]

$$\underset{w,b,\xi }{\text{min}}\frac{1}{2}({w}^{t}w+{b}^{2})+\frac{C}{2}{\sum }_{i=1}^{m}{s}_{i}{\text{max}}{\left\{0,{e}_{i}\right\}}^{2}$$
$${\mathrm{s}.\mathrm{ t}. e}_{i}=1-{y}_{i}({w}^{t}{x}_{i}+b),i=1,\dots ,m$$
(29)

and when \(\tau =1,\) Eq. (28) becomes Least square Fuzzy support vector machine (LS-FSVM) below

$$\underset{w,b,\xi }{\text{min}}\frac{1}{2}({w}^{t}w+{b}^{2})+\frac{C}{2}{\sum }_{i=1}^{m}{s}_{i}\left[{\text{max}}{\left\{0,{e}_{i}\right\}}^{2}+{\text{max}}{\left\{0,-{e}_{i}\right\}}^{2}\right]$$
$$\mathrm{s}.\mathrm{ t}. {e}_{i}=1-{y}_{i}({w}^{t}{x}_{i}+b),i=1,\dots ,m$$
(30)

Thus, FPin-SVM acts as a trade-off between the L2-FSVM and LS-FSVM:

$$\underset{w,b,\xi }{\text{min}}\frac{1}{2}({w}^{t}w+{b}^{2})+\frac{{C}_{1}}{2}{\sum }_{i=1}^{m}{s}_{i}^{2}{\text{max}}{\left\{0,{e}_{i}\right\}}^{2}+\frac{{C}_{2}}{2}{\sum }_{i=1}^{m}{s}_{i}^{2}\left[{\text{max}}{\left\{0,{e}_{i}\right\}}^{2}+{\text{max}}{\left\{0,-{e}_{i}\right\}}^{2}\right]$$
$${\mathrm{s}.\mathrm{ t}. e}_{i}=1-{y}_{i}({w}^{t}{x}_{i}+b),i=1,\dots ,m$$
(31)

Note that we obtain the FPin-SVM (28) with \(C={C}_{1}+{C}_{2}\) and \({\tau }^{2}=\frac{{C}_{2}}{C}\text{.}\) This observation also interprets the reasonable range of \(\tau \) is \(0\le \tau \le 1\text{.}\)

Remark 8

When membership values of all input points are equal, say 1, then Eq. (31) becomes.

$$\underset{w,b,\xi }{\text{min}}\frac{1}{2}({w}^{t}w+{b}^{2})+\frac{{C}_{1}}{2}{\sum }_{i=1}^{m}{\text{max}}{\left\{0,{e}_{i}\right\}}^{2}+\frac{{C}_{2}}{2}{\sum }_{i=1}^{m}\left[{\text{max}}{\left\{0,{e}_{i}\right\}}^{2}+{\text{max}}{\left\{0,-{e}_{i}\right\}}^{2}\right]$$

.

$${\mathrm{s}.\mathrm{ t}. e}_{i}=1-{y}_{i}({w}^{t}{x}_{i}+b),i=1,\dots ,m$$
(32)

and the FPin-SVM also becomes the trade-off between L2-SVM and LS-SVM [31]. L2-SVM focuses on the misclassification error because it maximizes the distance between positive and negative supporting hyperplanes \({w}^{t}{x}_{i}+b=\pm 1,\) and pushes the points to \({y}_{i}({w}^{t}{x}_{i}+b)\ge 1\text{.}\) LS-SVM also seeks the maximum margin hyperplane but pushes the positive and negative samples to be located around their respective supporting hyperplane, which results in small within-class scatter minimization and is related to Fisher discriminant Analysis [9, 31].

In Eq. (31), first-term maximizes the margin between the two supporting hyperplanes \({w}^{t}{x}_{i}+b=\pm 1,\) with respect to both orientation parameter \(w\) and location variable b; the second term minimizes the sum of squared misclassified sample's errors weighted by the corresponding sample's fuzzy membership value, and the third term minimizes the fuzzy membership weighted scatter of positive and negative samples from their respective supporting hyperplanes. Thus, FPin-SVM emphasizes misclassification error and focuses on within-class scatter minimization together, and incorporating the fuzzy membership of input points further improves its classification accuracy.

4.3 Comparison with other related methods

Both FSVM and FPin-SVM consider the importance of training data points in finding the optimal separating hyperplane between two classes but the loss function they employ are significantly different. FSVM employs the hinge loss function, while our proposed FPin-SVM uses the pinball loss function. Huang et al. [14] proposed the Pin-SVM that enjoys noise robustness but does not consider the importance of training samples, further improving its classification accuracy. Like Pin-SVM, our proposed FPin-SVM also adopts the pinball loss function, but we have made certain modifications to its objective function,first, we added b2/2 in the regularization term; second, in the empirical risk term, we considered the squared L2 norm of error variables and fuzzy membership function used to give different weightings to slack error variables. Unlike Pin-SVM, solutions of the FPin-SVM are obtained by functional and Newton-Armijo iterative algorithms, and it is proposed to solve the FPin-SVM directly in primal.

5 Experiments and results

To analyze the generalization performance and the computational efficiency of our proposed FPin-SVM formulation solved by functional iterative method (FFPin-SVM) and Newton method by considering generalized derivative approach (NFPin-SVM1) or Smooth approach (NFPin-SVM2), we compare the FFPin-SVM, NFPin-SVM1, and NFPin-SVM2 with SVM, FSVM, and Pin-SVM on well-known synthetic and benchmark datasets. All the classifiers are implemented on a P.C. running on Windows XP O.S. with a 64-bit, 3.20 GHz, Intel®core™2 Duo processor, having 8 G.B. of RAM under MATLAB R2015a environment. The MOSEK optimization toolbox solves the compared algorithms SVM, FSVM, and Pin-SVM for MATLAB, available at http://www.mosek.com; however, no external optimizer was used for solving FFPin-SVM, NFPin-SVM1, and NFPin-SVM2.

In implementing FFPin-SVM, NFPin-SVM1, and NFPin-SVM2, the values of the termination criteria tol and itmax were set to 0.001 and 10, respectively. Since smooth function approximation with parameter α = 5 has shown successful results [17]., we assumed α = 5 in implementingNFPin-SVM2.

Experiments are performed by choosing the popular Gaussian kernel function of the form: \(k(x,z)={\text{exp}}(-||x-z|{|}^{2}/2{\sigma }^{2})\) where \(x,z\in {R}^{n}\) and \(\sigma 0\) is the parameter. All the parameters are selected by employing the grid search using a ten-fold cross-validation methodology. The optimal regularization parameters \(C,{C}_{1}={C}_{2},{C}_{3}={C}_{4}\) and the kernel parameter \(\sigma \) are chosen from the set \(\left\{{2}^{i}|i=-9,-8,-7,\dots ,9\right\}\text{.}\) The optimal \(\tau \) is selected from the range{0.1, 0.2, 0.5, 1}. For optimal parameter values of k-NN and OWAWA-FSVM, we have taken parameter from the set as given in [20].

5.1 Performance on synthetic datasets

First, we consider a two-dimensional example used in [14]: positive and negative samples come from the Gaussian distributions: \({x}_{i},i\in I\text{ }N({\mu }_{1},\sum ),\) and \({x}_{j},j\in \text{II }N({\mu }_{2},\sum ),\) where \({\mu }_{1}=[0\text{.}\mathrm{5,3}],{\mu }_{2}=[0\text{.}5,-3]\) and \(\Sigma_{1} = \Sigma_{2} = diag(0.2,3).\) respectively. We also introduce the noise data points in the training set. The labels of noise points are selected from \(\left\{\mathrm{0,1}\right\}\) with equal probability, and the positions of the noise points follow the Gaussian distribution.

\(N({\mu }_{n},\sum )\) with \({\mu }_{n}=[\mathrm{0,0}{]}^{t}\text{.}\) We generate six different synthetic datasets with \((m={100},r=0),(m={100},r=0\text{.05}),(m={100},r=0\text{.}1),(m={200},r=0),(m={200},r=0\text{.05})(m={200},r=0\text{.}1)\text{.}\) where \(m\) the number of samples and \(r\) is the ratio of the noise data in the training set. To illustrate the performances of proposed algorithms, we repeat the resampling and training process 100 times, then report the average accuracy and training time in Table 1. One can observe that in all cases, the performance of SVM and FSVM are worse than all remaining algorithms, namely: Pin-SVM, FFPin-SVM, NFPin-SVM1, and NFPin-SVM2. In case of noisy data, our proposed algorithms FFPin-SVM, NFPin-SVM1, and NFPin-SVM2obtain the higher accuracies than compared algorithms SVM, FSVM, and Pin-SVM. Again, it is obvious from Table 1 that our proposed algorithms learning times are faster than compared algorithms which also validates the effectiveness of the proposed algorithms.

Table 1 The performance comparison of our proposed methods FPin-SVM, NPin-SVM1, and NPin-SVM2 with Pin-SVM, FSVM, and SVM on synthetic datasets with different noises. Time is for training in seconds
Full size table

As our second example, we consider the Ripley's Synthetic dataset [27], containing 250 training points and 1000 test points. Figure 2 shows the nonlinear decision boundaries obtained by all the algorithms on Ripley's dataset, where red and blue colors show positive and negative class points. The decision boundaries learned on a training set by proposed algorithms FFPin-SVM, NFPin-SVM1, and NFPin-SVM2 are similar but better than the compared algorithms SVM, FSVM, and Pin-SVM. The prediction accuracies and learning time of all the algorithms are listed in Table 2. It is evident from Table 2 that proposed algorithms obtained higher testing accuracies compared to SVM, FSVM, and Pin-SVM. Furthermore, the proposed algorithms are more computationally efficient than the compared algorithms, as shown in Table 2.

Fig. 2
figure 2

Classification results of the out proposed methods FFPin-SVM, NFPin-SVM1, and NFPin-SVM2 with nonlinear Pin-SVM, FSVM, and SVM on Example 2 (Ripley's dataset)

Full size image
Table 2 The performance comparison of our proposed methods FFPin-SVM, NFPin-SVM1, and NFPin-SVM2 with Pin-SVM, FSVM, and SVM on Example 2 (Ripley's dataset). Time is for training in seconds
Full size table

The third example is a two-dimensional synthetic checkerboard dataset consisting of a series of uniform points taken from 16 black and white squares of a checkerboard [25]. To test the learning ability of all algorithms on the checkerboard dataset, we consider the checkerboard dataset with 800 uniform points,each of the 16 squares consists of 50 points. Figure 2 shows the classification results of all the algorithms. It is observed in Fig. 3 that Pin-SVM, FFPin-SVM, NFPin-SVM1, and NFPin-SVM2 obtained the best separating decision hyperplane than SVM and FSVM because they simultaneously handle the within-class scatter minimization and misclassification error. To avoid the biased comparison, we make 10 independent runs on the checkerboard problem with 6400 uniform test sets, then report the average accuracies and training time of all the algorithms in Table 3. The results show that FFPin-SVM, NFPin-SVM1, and NFPin-SVM2 obtain the best test accuracies than Pin-SVM, FSVM, and SVM.

Fig. 3
figure 3

Classification results of our proposed methods FFPin-SVM, NFPin-SVM1, and NFPin-SVM2 with Pin-SVM, FSVM, and SVM on Examlpe3 (synthetic Checkerboard dataset)

Full size image
Table 3 The performance comparison of our proposed methods nonlinear FFPin-SVM, NFPin-SVM1, and NFPin-SVM2 with nonlinear Pin-SVM, FSVM, and SVM on Example3 (Synthetic Checkerboard dataset). Time is for training in seconds
Full size table

5.2 Performance on U.C.I. datasets

To further test the performance of the proposed methods, we perform experiments on several benchmark datasets, which are commonly used for testing the machine learning algorithms. These datasets are publically available at the U.C.I. repository of Machine Learning Datasets [24]. All the datasets are normalized so that features are located in [0, 1] before the training. We discussed the first example with labeled noise in the synthetic case, but classification problems may also have feature noise(Bi and Zhang, 2004). For this purpose, features of each dataset are corrupted by zero-mean Gaussian noise. For each feature, the ratio of the variance of noise to that of feature, denoted by \(r\), is set to be 0 (i.e., noise-free), 0.05, and 0.1. The same noise corrupted the training and testing datasets [14]. In order to compare the performance of the proposed algorithms (FF-PinSVM, NFPin-SVM1, NFPin-SVM2) with other algorithms (FSVM, Pin-SVM, k-NN, OWAWA-FSVM), we obtain their results on U.C.I. datasets where Gaussian kernel are employed in all the algorithms. We repeat the experiments ten times for each dataset and report the average test accuracies, standard deviation, and average learning time in Table 4.

Table 4 The accuracy as performance comparison of our proposed methods of nonlinear Fpin-SVM, Npin-SVM, and Spin-SVM with nonlinear Pin-SVM, FSVM, k-NN, OWAWA-FSVM and SVM in the Real world with different noises. Time is for training in seconds. Accuracy results are percent based
Full size table

Further, they are ranked according to the accuracy obtained for every dataset, and their average ranks are also reported in Table 4. Note that the average ranks of proposed algorithms are better than compared algorithms. To avoid any biasedness in comparison of the effectiveness with the compared algorithms, we statistically analyze the results of Table 4 by performing the popular Friedman test with the corresponding Nemenyi test recommended [7]. To validate that all the algorithms are significantly different against the null hypothesis, which states that all the algorithms are equivalent, we have

$${\chi }_{F}^{2}=\frac{{12}\times {33}}{8\times 9}\left[\begin{array}{c}6\text{.}{3030}^{2}+5\text{.}{5152}^{2}+{4.3182}^{2}+{7.3333}^{2}+{4.9091}^{2}\\ +{3.0303}^{2}+{2.0758}^{2}+{2.5303}^{2}-\frac{8\times {9}^{2}}{4}\end{array}\right]\simeq {1}{\text{3}}{5}\text{.}{0}{\text{9}}{50}$$
$${F}_{F}=\frac{32\times 135.0950}{33\times 7-135.0950}\simeq 45.0763$$

where \({F}_{F}\) is distributed according to \(F-\) distribution with \((\mathrm{7,7}\times {32})=(\mathrm{7,224})\) degree of freedom. Since the \({F}_{F}\) value is greater than the critical value of \(F(7,{224})=2\text{.}{0506}\) for the level of significance \(\alpha =0\text{.05}\), we reject the null hypothesis. We apply the Nemenyi post-hoc test to find the pair-wise comparison of algorithms. From [7], the critical value \({q}_{\alpha }\) for \(\alpha =0\text{.10}\) is 2.780, and the value of CD is \(2\text{.780}\sqrt{\frac{8\times 9}{6\times {33}}}\simeq 1\text{.6764}\text{.}\) Again, from Table 4, in terms of average ranks, the difference between (i). the best of SVM, FSVM, Pin-SVM, k-NN, OWAWA-FSVM and worst NFPin-SVM1, NFPin-SVM2 is: \(4.3182-2\text{.}\text{5303 = 1.7879}>1\text{.}{6764},\) the performance of NFPin-SVM1 and NFPin-SVM2 is better than SVM, FSVM, Pin-SVM, k-NN and OWAWA-FSVM; (ii). The best of SVM, FSVM, k-NN, OWAWA-FSVM and the value of FFPin-SVM are: \(4\text{.}\text{9091 - 3.0303}=1\text{.}{8788}>1\text{.6764,}\) the performance of FFPin-SVM is better than SVM, FSVM, k-NN, OWAWA-FSVM; (iii). The best and worst of FFPin-SVM, Pin-SVM is: \(4\text{.}{3182}-3\text{.}{0303}=1\text{.}{2879}<1\text{.}{6764},\) we conclude that the posthoc test is not powerful enough to detect any significant differences between these algorithms; (iv). The best and worst of SVM, Pin-SVM is: \(6\text{.3}{030}-4\text{.}{3182}=1.{9848}>1\text{.}{6764},\) the performance of Pin-SVM is better than SVM; (v).the best and worst of FSVM, Pin-SVM, OWAWA-FSVM is: \(\text{5.5152}-4.3182=1\text{.}{1970}<1\text{.}{6764},\) we conclude that the post hoc test could not find any significant differences between these algorithms.

The average AUC (area under curve) metric computed for real-world datasets on 10 different sets, and average rank is listed in Table 5. One can observe that our proposed methods have obtained largest AUC value for most of the datasets. Least average ranks of the proposed method show their effectiveness and applicability in comparison to SVM, FSVM, Pin-SVM, k-NN, OWAWA-FSVM.

Table 5 The AUC as performance comparison of our proposed methods of nonlinear FPin-SVM, NPin-SVM, and SPin-SVM with nonlinear Pin-SVM, FSVM, k-NN, OWAWA-FSVM, and SVM in the Real world with different noises
Full size table

With the above study of statistical comparison of all algorithms and their results reported in Table 4, it is evident that proposed algorithms result in superior classification performance on most of the datasets with the noise of different variances and obtain a lower learning time than those compared algorithms SVM, FSVM, Pin-SVM, k-NN and OWAWA-FSVM. Furthermore, the average rank for all datasets listed in the last row of the Table 4 shows that FFPin-SVM, NFPin-SVM1, and NFPin-SVM2 are ranked; third, first, and second, respectively, which also validates the effectiveness of the proposed algorithms.

6 Conclusions and future work

This paper proposes a Fuzzy support vector machine with pinball loss (Fpin-SVM) to enhance the generalization performance. The advantage of Fpin-SVM is that it is a strongly convex minimization problem whose solutions are obtained in primal by iterative based algorithms rather than solving QPP as is the case with the compared algorithms SVM, FSVM, Pin-SVM, k-NN and OWAWA-FSVM. We investigated Fpin-SVM properties, including noise insensitivity and within-class scatter minimization. In addition, we also compared Fpin-SVM with two related algorithms, FSVM and Pin-SVM. The numerical experiments conducted on several synthetic and benchmark datasets with different noises validate that the proposed algorithms are feasible and effective on both classification performance and computational speed. The main limitation of proposed method is that it is suitable for medium sized data because it requires inverse of positive definite matrix and due to use of pinball loss function it. Another issue is the sparsity because pinball loss function is not as sparse as hinge loss.

In addition to deal with limitation of proposed methods, our future work includes studying how to apply the pinball loss to other variants of SVM and develop faster algorithms to improve their computational speed. There is also room for the study of \(\varepsilon \)-insensitive pinball loss function to handle the unbalanced problem by weighting different sparseness parameters \(\varepsilon \) for each class.