Introduction

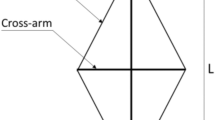
The use of slender steel columns in the construction industry is widespread. However, the main problem with the use of such structures is the reduction in load carrying capacity due to buckling. Buckling occurs due to instability in the structure and leads to a dramatic reduction in load carrying capacity. A system to improve the load carrying capacity of slender steel columns called a prestressed stayed column uses prestressed cable stays to enhance lateral stability. The stays are connected at the column ends and to cross-arms welded onto the column face (a typical system is shown in Fig. 1).

Fig. 1
figure 1

Prestressed stayed steel column with applied axial load P, length of column and cross-arm L and a respectively

Full size image

Prestressed stayed column buckling modes take the form of two distinct shapes; symmetric (half sine wave) and antisymmetric (full sine wave). In the post-buckling region, an interactive shape can occur as a combination of the first two distinct modes. Interactive post-buckling is generally observed when the critical loads of the first two modes are close together. This point is commonly referred to as the transition point.

There have been many studies attempting to develop design expressions for these structures. Earliest of these is the work by Chu and Berge [5] which sought to derive the buckling load expressions for these systems. Following this, Mauch and Felton [16] developed a method for optimising prestressed stayed steel columns by weight. However, these early works used a hinged connection between the column and cross-arms. A study by Ellis [7] was the first to use fixed connections between the column and cross-arms, resulting in a significant increase in buckling load. Further studies by Williams and Howson [39] and Hathout et al. [10] investigated the buckling behaviour of these systems with various configurations.

A major development in the analytical modelling of these systems by Hafez et al. [9] determined the relationship between the critical buckling load and initial prestress. They found that there are three distinct zones of behaviour: i) when the prestress is less than the minimum value, there is no increase in buckling load over the Euler load – zone 1; ii) when the prestress is between the minimum value and the optimum, there is a linear increase in buckling load – zone 2; and iii) when the prestress is above the optimum value, there is a linear decrease in buckling load – zone 3.

Several further studies have examined the buckling performance of prestressed stayed steel columns [11, 23, 24, 26, 28, 34, 40]. A study by Wadee et al. [37] prescribed design guidelines for prestressed stayed steel columns. They derived expressions to determine the maximum load carrying capacity for columns with symmetric and antisymmetric modes with varying prestress and initial imperfection. The validity of the expressions was checked by comparing the ultimate loads from the design procedure with various experimental results. However, this was for a limited number of data points, so they have not been fully validated, therefore, further research is required to validate the applicability of these expressions at other geometric scales.

Wang et al. [38] developed a method for determining the optimal cross-arm length of prestressed stayed columns through analytical modelling, validated by results obtained from finite element analysis. However, their analysis was limited to a single prestress level and the trends derived were not validated through physical experiments. A study by Tankova et al. [30] proposed a new method to determine the load carrying capacity of prestressed stayed columns through a series of design expressions. However, the method was only validated for prestressed stayed columns with a symmetric critical buckling mode. Krishnan [13] derived a Strength Enhancement Ratio (SER) to determine the benefit of using a prestressed stayed column system over a slender column. However, no guidance was provided to determine the load carrying capacity or reliability level of these structures.

The majority of previous studies concerned with the design of prestressed stayed columns have focused on developing expressions to be used in the design of these structures. However, the underlying presence of physical uncertainties has not been considered, and hence the reliability of prestressed stayed steel columns has not been understood. In this direction, this study will attempt to characterise the existing reliability levels of the design criteria and recommend partial safety factors to be used in the design of these structures. Results from a recently conducted experimental study will be used to characterise the uncertainty in the random variable distributions. In order to determine the reliability levels, the failure modes will be defined prior to establishing the baseline reliability levels through appropriate surrogate models. The associated partial safety factors will then be derived for defined target reliability.

Experimental studies

This section statistically analyses the material characteristics of tested specimens. The material characterisation formed part of the experimental study on the behaviour of small-scale prestressed stayed columns and were used to determine the material properties utilised in validating the numerical model. Tests were carried out on the main column material, cross-arms and the stay system. The outcomes from the material tests are used to determine the variation in the random variables for the reliability study leading to safety factor calibration.

Column testing

Testing of the main column material was performed using a method adopted by Osofero et al. [21], where a section of material was removed from either side of the coupon specimen. This ensured that failure of the specimen occurred within this section and enabled the material properties to be determined using a known cross-sectional area. An Instron 2620–601 dynamic clip-on extensometer was attached to this section to measure the deflection of the material. The cross-sectional area of this section was determined according to Eq. (1) from BS EN ISO 6892–1 [2] using the length of the extensometer. Half gauge lengths were also lightly scribed on the coupon specimen to ensure fracture occurred within the gauge length.

$$Gauge\;length=5.65\sqrt{A_c}$$
(1)

The specimens were tested in an Instron 4483 150kN load frame, with strain rate calculated according to the recommendations in BS EN ISO 6892–1 [2]. A total of 30 specimens were tested to obtain the Young’s modulus, yield stress, ultimate stress, strain at ultimate load and failure strain, with the mean, standard deviation and COV shown in Table 1. A large variation was observed in the strain at ultimate load εu and failure εf as in the experimental study of Serra et al. [27], although these variables are not relevant for the reliability calculations since they are not included in the identified limit states. The variation in diameter and wall thickness of the main column was measured on the supplied lengths of column material so the correlations for these variables were not considered. A typical stress–strain curve obtained for the main column testing is shown in Fig. 2.

Table 1 Statistical correlations for the column testing results. E is Young’s modulus, σy and σu are the Yield and Ultimate stresses respectively, εu and εf are the strains at ultimate load and at failure respectively, d is the column diameter and t is the wall thickness
Full size table
Fig. 2
figure 2

Stress–strain curve from the column testing

Full size image

Probabilistic modelling of experimental outputs

Following the completion of the column material testing, a statistical analysis was performed on the results. This allowed the correlation between different variables to be established as well as the goodness of fit for different distribution types. The dependency of the variables is computed by the Pearson’s linear correlation coefficient (ρ) as well as nonparametric correlation coefficients; Kendall’s coefficient (τ) and Spearman’s coefficient (ρs). Results for the correlations are presented in Table 1, which show a significant correlation between σy and σu as well as between εu and εf. A significant negative correlation is observed between σy and εu and also between σu and εu. However, there was no correlation between the variables E and σy, therefore this is not considered going forward. Analysis of the statistical distribution of each variable was then performed to determine the distribution types to be used in the reliability study. Typical histograms of each variable are shown with probability density plots for normal, Weibull and lognormal distributions in Fig. 3.

Fig. 3
figure 3

Probability densities of the random variables from column testing

Full size image

Typical probability plots for normal, Weibull and lognormal distributions are shown in Fig. 4. These plots identify any outliers for each distribution type and are then used to determine the goodness of fit of the random variables, shown in Table 2. The goodness of fit was calculated using the chi-square (CH), Kolmogorov–Smirnov (KSH) and the Anderson–Darling hypothesis (ADH) tests. A zero shows that the variable is sampled from the distribution, whereas a one rejects the hypothesis that the variable is from the assumed distribution. It was observed that Young’s modulus (E) is supported by all three tests for all distribution types, whereas other variables are supported by a different combination of tests for the three distribution types. Therefore, normal distribution was chosen for the random variables E, σy, d and t in the subsequent sections.

Fig. 4
figure 4

Probability plots for the column test results

Full size image
Table 2 Goodness of fit for the random variables
Full size table

Experimental investigation on the stay system

The experimental studies on stay system were performed according to the guidelines in BS EN ISO 6892–1 [2]. A total of 34 specimens were tested to obtain a range of values to determine the distribution properties. The stay system consisted of a mini rigging screw to apply the prestress, thimble eyes and ferrules to connect the cable, eye nuts and a quick link to connect to the load cell. Along with the stay components, the system was also made up of 3 mm 7 × 7 strand galvanised steel wire rope which accounts for approximately 50% of the total system length, shown in Fig. 5.

Fig. 5
figure 5

Stay system

Full size image

Testing of the stay system was performed in a 10kN Hounsfield uniaxial testing machine to determine the Young’s modulus, failure load and failure strain. The stress rate for the test was chosen according to the guidelines in BS EN ISO 6892–1 [2], and the material properties of the stay system were obtained from the resulting stress–strain curves (Fig. 6).

Fig. 6
figure 6

Stress–strain curves for the tensile testing of the stay system

Full size image

The mean, standard deviation and COV values for the Young’s modulus, failure strain, failure load and stay diameter are shown in Table 3. It was observed that the COVs for considered variables of the stay system are relatively small. The Young’s modulus was determined from the stress–strain curve up to around 2% strain.

Table 3 Statistical correlations for the cable testing results, where Es is the Young’s modulus of the stay system, εf is the failure strain, Ff is the failure load and ds is the stay diameter
Full size table

Probabilistic modelling

The correlation coefficients between the random variables from the experimental investigation on the stay system are shown in Table 3. It can be seen that significant correlation exists between Ff and εf, and a significant negative correlation exists between E and εf. There was no significant correlation observed between Es and ds, so these correlations were not included in the reliability modelling. Following the correlation results, the probability models for the random variables were studied and presented in Fig. 7. Example probability plots for normal, Weibull and lognormal distributions are shown in Fig. 8. Goodness of fit results for the stay system variables (shown in Table 4) highlight that the three tests support the use of any distribution type for all variables apart from the failure load. The variables used in the reliability studies are the stay diameter ds and the stay Young’s modulus Es, for which a normal distribution was chosen.

Fig. 7
figure 7

Probability densities for the stay system experimental investigation random variables

Full size image
Fig. 8
figure 8

Probability plots for the stay system experimental investigation random variables

Full size image
Table 4 Goodness of fit for the stay system experimental investigation random variables
Full size table

Development of the code calibration method

The calibration of partial safety factors considering the structural reliability is addressed extensively in the JCSS probabilistic model code [12]. Partial safety factors are used to adjust limit state functions in order to ensure the safe design of structures. The code calibration method used in this study is shown in the flow chart in Fig. 9, with the underlying steps described subsequently.

Fig. 9
figure 9

Flow chart of the code calibration method

Full size image

Limit states

Firstly, the failure modes of the system should be analysed and limit state functions for each system developed. The relevant explicit limit states can then be derived using existing expressions for the failure behaviour, while implicit limit states can be derived where no expressions exist.

Structure class

The next step of the code calibration procedure is to define the scope of the code as this will ensure that the class of structure being investigated has a defined range and scope.

Probabilistic model

Establishing the probabilistic models of underlying random variables is the next step in the code calibration procedure. This includes evaluating the distribution types of geometric, material and loading uncertainties along with relevant correlations.

Target reliability

Following the evaluation of the probabilistic model, the target reliability to be achieved through code calibration should be defined. The target reliability is set according to the consequences of failure and the cost to improve safety based on guidance from the JCSS probabilistic model code [12].

Partial safety factors

Partial factors are derived depending on the limit state function being analysed and initial values are chosen such that the existing reliability level can be determined.

Measure of fit

In order to investigate the closeness of the existing reliability to the target level, a penalty function is used as shown in Eq. (2).

$$Y={\left({\beta }_{i}-{\beta }_{t}\right)}^{2}$$
(2)

where βi is the reliability level and βt is the target reliability level. The reliability index determined for each run of the code calibration is compared with the target reliability level in Eq. (2) to find the closeness of fit to the target reliability. This measure of fit is used to optimise the partial safety factors as it penalises reliability levels if they deviate from the target level.

Failure modes

Following completion of the statistical analysis of the material test data, the failure modes of these structures were categorised. The main failure modes of prestressed stayed columns were initially established by Temple et al. [31] and are symmetric post-buckling, antisymmetric post-buckling, failure of the stays and yielding of the column. For each of these failure modes a limit state equation was then derived from relevant equations and available design expressions to obtain a baseline reliability level. The symmetric post-buckling limit state uses the ultimate load carrying capacity expressions derived by Wadee et al. [37], shown in Eq. (3), with an applied load P.

$${g}_{sym}=\left(\left(\frac{4{D}^{2}EI}{{L}^{2}}-2Tcos\alpha \right)\times {C}_{22}\right)\times \left(\left(\frac{{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{3Topt}-{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}}{2Topt}\right)\left(T-Topt\right)+{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}\right)-P$$
(3)

where D is a constant for prestressed stayed columns, E is the column Young’s modulus, I is the column second moment of area, L is the column length, T is the initial prestress, ⍺ is the angle between the column and cross-arm, C22 is an adjustment factor accounting for the change in stress in the stay, Topt is the optimal prestress, and \(\left(\frac{{N}_{max}}{{N}^{C}}\right)\) is a normalised maximum load carrying capacity for the prestress level 3Topt and Topt. Similarly, the antisymmetric post-buckling limit state, including the ultimate load carrying capacity expressions derived by Wadee et al. [37], can be expressed as:

$${g}_{anti}=\left(\left(\frac{4{D}^{2}EI}{{L}^{2}}-2Tcos\alpha \right)\times {C}_{22}\right)\times \left(\left(\frac{{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{3Topt}-{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}}{Topt}\right)\left(T-Topt\right)+{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}\right)-P$$
(4)

The mode corresponding to stay failure is added for completeness as in reality, for the configurations studied, it is highly unlikely that the tension would reach the stay failure load. The limit state for stay failure was considered to calculate the tension in the stays at the instant of buckling according to the equation derived by Hafez et al. [9]. This was chosen as the failure criteria as the principle failure mode will be either column buckling or material yielding, if it is assumed that the stay tension will reach its failure load after the ultimate load of the column is reached. The limit state function for stay failure is shown in Eq. (5), where Tu is the failure load for the stay and the right-hand side of the equation is the residual tension at the instant of buckling from Hafez et al. [9]. The residual tension expression uses the maximum load carrying capacity representation for symmetric post-buckling [37], including C3 as an additional geometric factor.

$${g}_{stay}={T}_{u}-\left(T-\left(\left(\left(\left(\frac{4{D}^{2}EI}{{L}^{2}}-2Tcos\alpha \right)\times {C}_{22}\right)\times \left(\left(\frac{{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{3Topt}-{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}}{2Topt}\right)\left(T-Topt\right)+{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}\right)-4Tcos\alpha \right){C}_{3}\right)\right)$$
(5)

The limit state function for yielding of the main column was chosen for comparison between the yield stress and the maximum Von Mises stress in the column. This is shown in Eq. (6), where σy is the yield stress of the column material and σVM is the maximum Von Mises stress in the column.

$${g}_{VM}={\sigma }_{y}-{\sigma }_{VM}$$
(6)

Two additional failure modes for yielding in the column are included. One for local buckling of the shell section due to the bending moment acting on the main column, shown in Eq. (7) and one comparing the maximum axial stress and the yield stress is shown in Eq. (8). The expression for local buckling is obtained from Morato and Sriramula [18] where it was used to approximate local buckling in an offshore wind turbine support structure:

$${g}_{LB}=\frac{1}{6}\left(1-0.84\frac{d}{t}\frac{{\sigma }_{y}}{E}\right)\left({d}^{3}-{\left(d-2t\right)}^{3}\right){\sigma }_{y}-SM$$
(7)
$${g}_{A}={\sigma }_{y}-{\sigma }_{A}$$
(8)

where σA is the maximum axial stress acting on the column, d is the column diameter, t is the wall thickness, E is the Young’s modulus and SM is the maximum bending moment in the column. The equation for local buckling is expected to be a more conservative expression for checking column yielding in most systems but may be more important for other column cross-section geometries. The failure modes in Eqs. (6)-(8) are implicit expressions, hence surrogate modelling was used to link outputs from relevant finite element models.

Surrogate modelling

Reliability levels of explicit limit state functions can be solved using a variety of methods, including Monte Carlo simulation and first order reliability methods. However, surrogate modelling is required to capture implicit limit state functions. This method is required as failure modes without a closed form expression rely on the output from the numerical models [8, 18]. This implies the use of an implicit limit state function being solved thousands of times, which would require an enormous amount of computation time. Surrogate modelling is a way to avoid this by constructing a relationship between the design variables and the output variable. This method allows a relatively small number of simulations to create a response surface that can be used in reliability calculations. This is required as the simulation of numerical model in the reliability analysis becomes impracticable. The limit state function is then no longer an implicit function with large computation time issues but an explicit function. As a result, traditional reliability methods can then be used to determine the reliability levels of the surrogate model. The first step in the development of the surrogate model is to create a sample of the design variables. There are many different sampling techniques available, and in this study the Latin Hypercube Sampling (LHS) technique was used as it gives a random sample across the distributions. A range of three times the standard deviation was chosen as it has been shown to cover 99% of the probabilities of the random variables [17]. Surrogate models can then be constructed from the output of the design variable sample. Various surrogate model types were investigated, including; Kriging, polynomial response surfaces, Radial basis functions (RBFs) and Artificial Neural Networks (ANNs).

Application example

An example system was chosen from the experimental study of Osofero et al. [21] as the design expressions in Wadee et al. [37] were derived from these test results. Specimen A4 which had an initial prestress value beyond the theoretical optimal was chosen. This theoretical optimal prestress value has been shown to give the highest load carrying capacity for configurations with symmetric critical modes [21, 25], Osofero et al. 22. Material and geometric properties for the application example are shown in Table 6. The ooDACE MATLAB toolbox was used to create the Kriging surrogate model expressions [6]. Limit state functions for the failure modes were analysed for the example system using the UQlab MATLAB toolbox [15]. The basic expressions were modelled initially for comparison with the surrogate models. The probability of stay failure was insignificant for this configuration and therefore was not considered for code calibration, although the failure mode is still included as a possible failure mode. A comparison between the reliability levels of the various surrogate models and the explicit limit state expressions was conducted to determine the most accurate surrogate modelling method. Table 5 shows a comparison of the reliability levels and probability of failures for the surrogate models and the basis expression for the symmetric limit state failure mode. It was found that the Kriging surrogate modelling method was most accurate so was used henceforth, as shown in Table 5.

Table 5 Comparison of surrogate modelling techniques and the basis expression
Full size table

Sensitivity analysis

Finite element analysis was used to investigate the sensitivity of each failure mode to various input parameters. Kriging surrogate modelling was used to create an explicit equation of all the input parameters to calculate the output load effect for each failure mode. A Sobol sensitivity analysis was then performed on each Kriging model, using the Matlab software UQlab [15] to investigate the relative influence of each input variable on the output of the finite element model. The total Sobol indices of each failure mode are shown in Fig. 10. The sensitivity results show that the relative influence of each of the input variables changes significantly for different failure modes. The area of the stay is seen to have the greatest influence on the output for the symmetric buckling, stay stress, shell buckling and axial load failure modes, whereas, the yield stress has the greatest influence for antisymmetric buckling and the magnitude of the Von Mises stress is mostly influenced by the column thickness (Table 6).

Fig. 10
figure 10

Total Sobol indices of each failure mode, where the variables are defined in Table 5

Full size image
Table 6 Material and geometric properties of specimen A4 from Osofero et al. [21]
Full size table

Probabilistic models

Uncertainties in the output of the surrogate models occur due to a combination of variables, these include stochastic variables and modelling uncertainties. The mean and COV values of the random variables (based on the experimental study discussed earlier) and modelling uncertainties considered in the present work are shown in Table 7.

Table 7 Stochastic variables and modelling uncertainties
Full size table

The paramaters XE and Xσ are standard modelling uncertainties for load effect calculations, taken from the JCSS probabilistic model code [12], XR is a resistance uncertainty for steel members used in the calibration of partial safety factors in Eurocode 3 [20], XFE is a parameter to account for inaccuracies introduced by the finite element model [35]. Lastly, Xsim was used as a measure to capture uncertainties introduced by the limited number of simulations performed [33]. By adding the modelling uncertainties to the probabilistic modelling, the limit state functions can now be written as follows.

$${g}_{sym}=\left(\left(\frac{4{D}^{2}EI}{{L}^{2}}-2Tcos\alpha \right)\times {C}_{22}\right)\times \left(\left(\frac{{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{3Topt}-{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}}{2Topt}\right)\left(T-Topt\right)+{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}\right){X}_{R}{X}_{FE}{X}_{sim}-{X}_{E}P$$
(9)
$${g}_{anti}=\left(\left(\frac{4{D}^{2}EI}{{L}^{2}}-2Tcos\alpha \right)\times {C}_{22}\right)\times \left(\left(\frac{{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{3Topt}-{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}}{Topt}\right)\left(T-Topt\right)+{\left(\frac{{N}_{max}}{{N}^{C}}\right)}_{Topt}\right){X}_{R}{X}_{FE}{X}_{sim}-{X}_{E}P$$
(10)
$${g}_{stay}={T}_{u}{X}_{R}-{X}_{\sigma }{X}_{FE}{X}_{sim}{T}_{r}$$
(11)
$${g}_{VM}={\sigma }_{y}{X}_{R}-{\sigma }_{VM}{X}_{E}{X}_{FE}{X}_{sim}{X}_{\sigma }$$
(12)
$${g}_{LB}=\frac{1}{6}\left(1-0.84\frac{d}{t}\frac{{\sigma }_{y}}{E}\right)\left({d}^{3}-{\left(d-2t\right)}^{3}\right){\sigma }_{y}{X}_{R}-SM{X}_{E}{X}_{FE}{X}_{sim}{X}_{\sigma }$$
(13)
$${g}_{A}={\sigma }_{y}{X}_{R}-{\sigma }_{A}{X}_{E}{X}_{FE}{X}_{sim}{X}_{\sigma }$$
(14)

The expression for the residual prestress is simplified by replacing the residual prestress from Eq. (11) with Tr.

The probability of failure and reliability level of the limit states including the modelling uncertainties are shown in Table 8. These values highlight the range of reliability level for various failure modes. From Table 8, the symmetric post-buckling limit state is the critical failure mode, followed by the Von Mises stress in the column reaching the yield stress value. Stay failure and local buckling of the column are the least critical modes for this application example as expected.

Table 8 Probability of failure and reliability level of the limit states
Full size table

Target reliability

Reference values for the reliability of structures are taken from the JCSS probabilistic model code [12]. These values are based on a reference period of one year and can be used as guidelines for the reliability of structures in general, as shown in Table 9. The value corresponding to moderate consequences of failure and normal cost was chosen as the target reliability for the present work, highlighted in bold in the table.

Table 9 Target reliabilities β according to the JCSS probabilistic model code [12]
Full size table

Calibration of safety factors

The method for improving the reliability level of these structures is to apply partial safety factors to the resistance and loading parts of the limit state functions and to optimise their values to reach the target reliability. The calibration procedure was performed on the symmetric post-buckling limit state equation as it is the critical failure mode of the explicit limit state failure functions. The symmetric limit state equation was replaced with the surrogate model to improve the accuracy of the expression as the design expressions do not account for change in yield stress. Loading was separated into dead load, leading live load and two accompanying variable actions according to Eurocode [3]. The factors for the combination of variable actions ψ = 0.7 is taken from BS EN 1990 [3]. The updated limit state equation is shown in Eq. (15). In this equation, the output from the surrogate model for the ultimate load, for system with symmetric buckling mode, is represented by Nu. Calibration of partial factors was also conducted for the three additional limit states that do not have closed forms. Optimisation of the partial factors is carried out until the penalty function is minimised. In the symmetric limit state, the partial factor for the dead load was fixed according to the recommendations in BS 5950–1 [1] (γD = 1.2). A dead load to live load ratio of 0.25 was used throughout, with 75% of the applied load being split equally between the live loads. This load combination was taken as an initial guess, although it can be adjusted depending on the load combinations of the structure being designed. Three optimisations were initially performed on Eq. (15) to compare the partial factors obtained with the values recommended in BS 5950–1 [1], as shown in Table 10. All three optimisations were performed with the material factor fixed at γm = 1.15, taken from BS EN 1992-1-1 (4). The first optimisation was done with only the leading live load; the second was done with the leading live load and the 1st accompanying live load; while the third optimised the leading, 1st and 2nd accompanying live load factors, in order to investigate different load combinations.

Table 10 Partial factor optimisation
Full size table
$${g}_{sym}={N}_{u}{X}_{R}{X}_{FE}{X}_{sim}/{\gamma }_{m}-{X}_{E}({\gamma }_{D}{G}_{D}+{\gamma }_{L}{G}_{L}+{\gamma }_{L1}\psi {G}_{L1}+{\gamma }_{L2}\psi {G}_{L2})$$
(15)

Following the calibration of the partial safety factors for different load combination cases, the values found were compared with those found in previous studies (Table 11). A comparison of the various partial safety factors in Table 11 highlights that there is a wide range of values for different structures. A study by Nadolski et al. [19] investigated the use of partial factors in the design of steel structures and highlighted that a range of different partial safety factor values could be used to obtain the same level of reliability.

Table 11 Partial safety factors obtained in previous studies for various types of structures
Full size table

A comparison of partial safety factors with three target reliability levels taken from Table 9 was then performed. The values for the material, leading live load and 1st accompanying live load partial safety factor were calibrated and are shown in Table 12. There were a range of possible solutions for the partial safety factors for each reliability level, but the values were chosen such that they minimised the penalty function.

Table 12 Calibrated partial safety factors for different levels of reliability
Full size table

Subsequently, the values in Table 12 were compared with the solutions presented in Table 13. Results for the partial safety factors with fixed material factor (γm = 1.15) show a trend of higher partial factors for lower levels of reliability. This highlights the variation in partial safety factors depending on the conditions used in the calibration.

Table 13 Calibrated partial safety factors for different levels of reliability, with fixed material factor γm = 1.15
Full size table

The calibration procedure was repeated using the three failure modes for column yielding with various target reliability levels. A resistance factor equal to 1.15 was used for these calibrations following the same procedure for the symmetric post-buckling limit state. A single load partial safety factor was calibrated for the three additional failure modes, with the values shown in Table 14.

Table 14 Load partial safety factor γL calibrated for the column yielding failure modes
Full size table

Results from this calibration highlight that the Von Mises stress in the column is the critical failure mode for column yielding in the application example, whereas the other two are more conservative limit states. Therefore, it should be ensured in the design of these structures that the maximum Von Mises stress is kept below the column yield stress. This is the case for the application example, although depending on the cross-section geometry, local buckling may become more important.

Conclusion

Due to the lack of previous studies into the reliability of prestressed stayed steel columns, this study has attempted to provide some guidance on reliability analysis of these systems. This work has presented a method to determine partial safety factors to be used to ensure the safe design of this type of structure. Also, this study has highlighted the possible failure modes of these structures. The random variables used to form the probabilistic model were taken from material characterisation tests from a recently conducted experimental study. It was found, through the investigation of existing reliability levels of the failure modes, that symmetric post-buckling and the Von Mises stress reaching column yield were the critical failure modes, whereas stay failure and local buckling were the least critical modes. A sensitivity analysis was also presented to determine the influence of each random variable on the output for each failure mode. Surrogate modelling was shown to be an effective method for developing limit state functions of the failure modes of these systems. Surrogate modelling was used in the calibration of partial factors for the symmetric failure mode as it was more accurate, while the column yielding failure modes used surrogate modelling to create closed form limit states.

It was found that the values of the partial safety factors vary greatly depending on the initial conditions used in the calibration procedure as well as the target reliability level. Values for the partial safety factors were shown for various calibration procedures and are recommended to be used under similar circumstances. The example shown above was performed on a system tested in the experimental study by Osofero et al. [21], so the partial safety factors derived are only applicable to a specific configuration. However, the procedure derived to obtain the partial safety factors is suitable for use on any system, and the range of values will provide guidance for general design purposes.