The Striatus bridge

Abstract

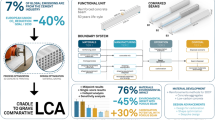
The paper describes the physical realisation of a 3D-concrete-printed, mortar-free, unreinforced masonry arched footbridge, designed for disassembly and reuse. The paper also details the novel integrated design, engineering and fabrication framework and the manufacturing and assembly processes used for the project. The research, motivated by the rapid growth in large-scale 3D concrete printing (3DCP), addresses the current lack of both design tools and integrated design-to-production solutions. It is guided by the insight regarding the applicability of design and analysis methods used in unreinforced masonry to large-scale, layered 3D printing with compression dominant materials such as concrete. Thus, the underlying computational framework and integrated design environment further extends and adapts advances in the computational design and analysis of unreinforced masonry structures to 3DCP masonry blocks. Adopting an unreinforced masonry paradigm for the design of 3DCP structures can make it possible to (i) reduce the amount of concrete used by allowing precise placement of concrete only where needed along the compressive flow of forces, (ii) reduce the amount of steel needed by reducing tensile and flexural strength requirements through a compression-appropriate design of both the global, shape and the block discretisation, and (iii) reuse components, repair the structures and recycle materials more easily. This paper builds on the relevance of the computational masonry paradigm to both delivering the ecological promises of 3DCP and to the development of a 3DCP-specific, design-to-production toolkit.

Design and construction of an unreinforced, 3d-concrete-printed masonry bridge

The research presented in this paper, motivated by the rapid growth in large-scale 3D concrete printing (3DCP), addresses the current lack of both design tools and integrated design-to-production solutions for this fabrication technology. It is guided by a novel insight regarding the applicability of design and analysis methods developed for unreinforced masonry to large-scale, layered 3D printing with materials favouring compression such as concrete [4, 5, 25]. The paper details a custom toolchain that enabled the integration of shape design, structural engineering, and robotic concrete printing for the design, production and construction of ProjectName - a discrete, dry-assembled, fully unreinforced, bifurcating, arched masonry footbridge composed of 53 3D-concrete-printed blocks and spanning 16 metres.(Figures 1 and 2)

Fig. 1

Design to production tool chain and physical demonstrator. (i-v) procedure to design a compression-only bridge structure and its stereotomy (a) robotic 3D concrete printing of blocks, (b) on site assembly, and (c) finished bridge

Fig. 2

Schematic drawings - (a) plan, (b) elevation A, (c) section BB, and (d) section CC

Promise of 3DCP and the masonry design paradigm

The positive aspects of concrete as a construction material include its low cost, ready availability, fire resistance, thermal mass, compressive strength, longevity and low embodied energy [2] and emissions [19] per unit mass. 3D Concrete Printing is generally anticipated to ameliorate the negative aspects of using concrete in construction including labour intensiveness, adverse effects of worker health and safety, excessive wastage due to the casting process, and significant carbon emissions when used in bulk [12, 14, 26]. It is widely recognised that, unlike desktop printing that admits a wide range of arbitrary shapes, only specific types of geometries that adhere to the constraints imposed by large-format 3DCP and incorporate the layer-by-layer deposition of linear filaments in the creation of the shapes, can be printed. Furthermore, the careful design of such shapes is critical to fully deliver the aforementioned benefits of 3DCP [12, 46].

The unreinforced masonry design paradigm and associated design and analysis techniques can specifically meet these requirements and are highly compatible with the compression-dominant, orthotropic material properties of layered 3DCP [5, 25]. Alignment of the printed layers orthogonal to expected compressive force flows engages the compressive strength of 3DCP whilst eliminating the need for tensile reinforcement [5, 7].

Furthermore, the wider benefits of structural geometry and the masonry paradigm to improve recyclability, and the repair and reuse of material and structural components due to dry assembly and clean separation of tensile and compressive materials have also been recently highlighted [10].

In summary, adopting an unreinforced masonry paradigm for the design of 3DCP structures can make it possible to

• 1. Reduce the amount of concrete used by allowing precise placement of concrete only and precisely where needed along the compressive flow of forces, which additionally reduces the stresses significantly [10].

• 2. Reduce the amount of steel needed by reducing tensile and flexural strength requirements through a compression-appropriate design of both the global, shape and the block discretization. Interestingly, the rate of carbonation of concrete is inversely proportional to the compressive strength of concrete. Therefore, low-strength concrete, as enabled by the funicular design, is more likely to be fully carbonated and, thus, reabsorb carbondioxide during the lifetime of the structure [34].

• 3. Repair structures more easily as the separation of concrete and steel allow for straightforward maintenance strategies. A major advantage of the masonry logic is that both structural action (compression versus tension) and the corresponding materials are separated. This offers a maintenance and repair strategy whereby all elements can be easily and separately accessed and inspected. The tension ties can be isolated and directly replaced. Furthermore, the lack of embedded reinforcement in the unreinforced concrete blocks means that corrosion of reinforcement and related long-term deterioration of the structure can be avoided [43, 45]. Importantly, any local damage can be isolated to a specific block, which can be reprinted and replaced. This could be done by propping the structure to relieve the thrust in the arch. Once the new part is placed, the arch can be reactivated. It can be noted that complete material failure and crushing of individual blocks is extremely unlikely and the non-fatal damages to be considered could be local crushing or cracking due to differential settlement of the foundations, or local damage due to impact such as by a vehicle.

• 4. Reuse components easily, due to the dry-assembled construction, glue-free connections, and thus non-destructive disassembly that masonry structures allow,

• 5. Recycle material easily and with low energy consumption due to both separation of materials and easy disassembly. Typical recycling of reinforced concrete involves the use of jaw and impact crushers that lead to increased powder by-products, reduced strength and quality of recycled aggregates that then have to be used in down-cycled applications such as road bottoming [20, 42]. Higher quality recycled aggregates and repeatable recycling, are two important parameters in achieving full, closed-loop recycling of concrete, similar to steel and plastics. This requires newer, more refined machines and processes [42]. Separation of materials by design, and thus the lack of embedded steel reinforcement in the concrete blocks is aligned with both these features of closed-loop recycling. On the other hand, dry assembly means discrete blocks can be dismantled with minimal falsework and moved to grinding stations without creating excessive dust. Importantly, dry assembly can lead to an ideal, so-called integrated inverse manufacturing that balances the workload in the construction and disassembly phases [42] (Tomosawa et al, 2005). Integrated inverse manufacturing is considered important to achieve closed-product lifecycles [32]. Lastly, absence of chemical bonding means recycling does not have to contend with material contamination and related complexities [20].

Lack of integrated design-to-production toolkits

To achieve the specific geometries that deliver the benefits of 3DCP, development of computer-aided-design (CAD) tools and design-to-production (DTP) solutions are needed. However, whilst potential features of a CAD pipeline are often discussed, attention is usually only to devoted to material and process aspects of 3DCP. Furthermore, even when shape-design related descriptions are given, they are typically restricted to simple geometries and practical CAD implementation details are absent. This is particularly so for non-parallel, inclined-plane printing [12, 17, 18, 30].

Both early pioneers and recent researchers have emphasised the relevance of the masonry-based design paradigm to address the critical, but often ignored need for a 3DCP-specific, integrated DTP toolkit. In particular, shape-design and analysis methods used for masonry structures along with recent advances in computational masonry and associated geometry processing methods can be combined to create a toolkit.

Furthermore, such a toolkit could provide

• 1. expressiveness of geometric modelling for designers whilst also being didactic regarding structural and process parameters,

• 2. possibilities of a rich variety of 3DCP-compatible shapes,

• 3. constructive guidance about the feasibility constraints imposed by the 3DCP process, and

• 4. methods to align inclined layers of material filaments orthogonal to compressive forces; [4, 7, 25]

Key contributions

This paper builds on the relevance of the computational masonry paradigm to both delivering the ecological, economical and productivity promises of 3DCP and to the development of a 3DCP-specific, DTP toolkit. Furthermore, the paper focuses attention on the hitherto ignored, but critically necessary aspects of computational design and practical implementation details of a CAD workflow, as described previously.

The main contribution of the paper is the development of a toolchain that enabled the design of an unreinforced, masonry bridge. The project that demonstrated both the concept and the toolchain, was physically realised by the dry assembly of 3DCP blocks that have each of their individual layers of printed concrete aligned orthogonal to the expected dominant compressive force flow. Specifically, the custom toolchain and the constituent, standalone applets enabled

• the use of the unreinforced masonry paradigm for the computational design of a 3DCP bridge, which is in contrast to both the paradigm and methods of design currently being used in practice and seen in recent examples of 3DCP bridge structures;

• the integration of user-guided, expressive shape-design, structural engineering, and robotic concrete printing;

• synthesis of force-aligned, continuously varying, inclined-plane print paths and the generation of robot instructions; and

• rapid iteration, refinement and collaboration. The novel, complex-geometry, large-scale bridge demonstrator was fully designed, coordinated between remotely located teams and produced on site in less than 6 months.

Limitations of scope

The toolkit is specific to the prefabrication paradigm offered by industrial robotic-arm-based, 6-degree-of-freedom (6-DOF) printing machines. Further, we assume the use of so-called two-component (2K) concrete formulations and printing setups to print along continuously varied inclinations and thicknesses.

We implemented the toolchain using a combination of custom C++ applications and the Python-based open-source framework COMPAS [44].

It can be noted that whilst rigorous computational structural design, verification and approval reports were needed for the realisation of the bridge, the detailed description of those aspects is beyond the focus and scope of this paper. However, a broad overview of the computational design and analysis of unreinforced masonry structures adapted to 3D-concrete-printed masonry bridge design is provided. This includes global form finding and discrete-element modelling for evaluation of structural mechanics and stability. Furthermore, COMPAS already implements all the masonry-related, structural design algorithms as used and outlined in this paper and prior work (Section “Prior work”). Similarly, details regarding material mix and printing processes receive only a cursory description.

Prior work

As described previously, the physical bridge demonstrator and the associated DTP toolkit operate at the intersection of two domains of research – 3D concrete printing and masonry design. Accordingly, the relevant prior work stems from those domains.

3DCP bridges

A notable precedent project is the very first 3DCP pedestrian bridge, installed in 2016, that used a micro-fibre reinforced cement and a particle bed fusion printer to generate bridge segments that were assembled onto a steel frame [22, 23, 46]. The fusion 3DCP method used in this bridge, is unlike all the other precedents and our demonstrator bridge. Although this technology was one of the pioneering efforts, it is recognised to have drawbacks in terms of being a dusty, human labour-intensive process [31].

There are three other relevant precedent 3DCP bridges which have been physically realised since 2018 - a bicycle bridge in Gemert, Netherlands [39], a bicycle bridge in Nijmegen, Netherlands [28] and a pedestrian bridge in Shanghai, China [47].

All three bridges are linear and composed of prefabricated, 3DCP blocks. It can be noted that none of the bridges use the unreinforced masonry paradigm in its structural design or for the alignment of the printed filaments orthogonal to expected compressive force flow. As a consequence, none of the bridges

• are dry-assembled, making disassembly, reuse or repair difficult.

• fully engage 3DCP material structurally. The Nijmegen Bridge, in fact, uses the 3DCP blocks as stay-in-place formwork into which steel reinforcement is placed and regular structural concrete is cast. The 3DCP deck blocks of the Shanghai bridge rest on structural steel arches. We understand from the authors that the original intention was to use the steel arches only as temporary supports. However, regulatory restrictions forced them to retain the steel structure (Weigou. X, personal communication, October 10, 2020). The Gemert bridge is heavily post-tensioned. Both the bridges in Gemert and Shanghai use predominantly hollow 3DCP blocks without any additional concrete casting.

• use unreinforced concrete mix for their 3DCP. The bridges in the Netherlands use a proprietary tensile filament embedding technique to reinforce the cement as the concrete filaments are printed. The bridge in Shanghai uses a fibre-reinforced concrete mix.

• fully align the 3DCP filament layers to expected force flow. The bridge in Shanghai comes closest to doing so, with the layers in the simple-arched deck blocks being non-parallel and aligned to a single-radius, circular arch. The bridges in the Netherlands use parallel, horizontal extrusion printing, which make them misaligned with structural force flow; hence, the need for heavy post-tensioning or use of the 3DCP elements as moulds of a formwork only.

• has a fully integrated, computational DTP pipeline. The bridges in Gemert and Shanghai are simple, single span geometries with repetitive cross-sectional shapes. The focus of the exercise seems to have been to demonstrate the viability of the technology and to validate material and process parameters. The Nijmegen bridge, on the other hand, appears to use a parametric workflow to generate the print-paths using a designer-specified, process-agnostic, mesh geometry. To the best of our knowledge, the shape-design of the bridge uses the expressive technique of the so-called subdivision modelling [41].

Our demonstrator bridge differs from the precedent bridges in all the aspects described above. It is dry-assembled and fully engages the 3DCP material structurally by discretizing the structure, based on a proper unreinforced-masonry stereotomy [38], and aligning the printed blocks and print-layers orthogonal to compressive force flows. The bridge, by directly using the hollow blocks as printed, without casting additional structural concrete in them, also fully utilizes the ability of 3DCP to save material by precisely placing material only where needed. In addition, we use a fully unreinforced concrete mix, without fibres or filament embedding. Furthermore, our demonstrator bridge design has complex geometry and multiple spans. Lastly, expressive design is an integral part of the demonstrator whilst also being process and structure-aware. We developed a fully integrated DTP toolchain to achieve these intentional differences.

Equilibrium and fabrication-aware computational design

Given the importance of the toolchain described above, the domains of computational masonry design and process-aware geometry processing are highly relevant fields. In this context, the Armadillo stone vault project and associated toolchain are an important precedent [38]. The project convincingly demonstrated an expressive, computational DTP pipeline for unreinforced stone masonry. Since, simply put, 3DCP blocks can be considered as artificial stone, we incorporate several of the structural geometry principles and algorithms from this project. In addition, for the physical demonstrator bridge, we followed a construction and assembly sequence of 3DCP blocks that was largely similar to the one used for Armadillo.

Prior work related to so-called mesh-based geometry processing for equilibrium-aware shape design are important precedents. [4, 6] describe the benefits of a mesh-based paradigm for intuitive design manipulation, computational handling of robotic fabrication constraints, etc. The structural relevance of the skeletal topology of meshes, automated procedures to generate them from structural boundary conditions, and their structurally informed manipulation is described in [33]. The so-called skeleton package of COMPAS demonstrates the automatic generation of compression-only, 3D mesh-surfaces from simple 2D graph description of a medial axis of the shape [3, 11, 15, 48]. We adapted the principles and data structures described in these references.

We used the constrained form finding of compression-only surfaces as described in [29], and discrete-element modelling of masonry structures as described in [37] for the structural heuristic, verification and analysis steps respectively (See Section “Structural threads of DTP toolchain”). Lastly, [4, 7] describe a Function Representation (FRep) based schema for inclined-plane print-path generation. We adopted the principles described by them to develop a full implementation and extension of the schema for practical, large-batch production. We also implemented specific extensions to generate the infill print-paths typically needed in 3D concrete printing.

Geometry processing

The DTP toolkit described in this paper uses a mesh-based geometry-processing paradigm. This paradigm is widely used in structure and fabrication-aware geometry processing [1, 13, 36]. We also adopt the use of JavaScript Object Notation (JSON) and half-edge mesh data structures that are common to this paradigm, to transmit and process 3D model information [24].

Design-to-Production Toolchain

The collaborative, multi-author, design-to-production (DTP) process that we developed to practically realise the demonstrator bridge, can be unrolled into a serial thread (Fig. 3a-c) and three structural guidance, verification and analysis threads that insert information into the serial thread via strategic data interfaces (Fig. 3i - iii).

Fig. 3

DTP Tool chain unrolled into threads. (a,b,c) serial thread, (i, ii, iii) parallel structural threads, (iv) material testing and prototyping thread, (v) foundation design thread & (vi) scaffold design thread

The serial thread includes three major process steps and outputs the print-paths, per 3DCP stone block. (Figure 3c):

• Shape-design: designer-guided shape-design of a medial surface (Fig. 3a).

• Stereotomy: decomposition of the medial surface into patches, thickening of the patches by offset, and synthesis of block geometries, including inter-block, planar interfaces (Fig. 3b).

• Print-path synthesis: Generation of the print-paths per block based on expected force flow and block interface planes as defined by the stereotomy. (Figure 3c).

Interleaved with each of the three process steps of the serial thread, are three corresponding parallel, structural verification processes:

• Best-fit TNA: A best-fitting TNA algorithm is used to take the user-provided, medial surface as a target and fits a nearest compression-only surface to it [29](Fig. 3i). This step modifies the shape of the user-provided medial surface.

• Discrete-element modelling is used to evaluate the structural stability of the discrete, rigid blocks produced as an outcome of the stereotomy. Through an iterative procedure, this step modifies the interface planes between blocks based on structural requirements (Fig. 3ii).

• Finite-element modelling is performed to verify the local bending stresses in the blocks, which inform the print-path synthesis (Fig. 3iii)

In addition to the design and structural threads above, there are three other threads- scaffold design, tension-tie and foundation design and material testing and printing prototyping (Fig. 3iv - vi). The first two output fabrication information to produce the timber falsework and the steel footings, tension ties and foundation information. These threads only receive information from the serial threads and output information. The third thread informs the blocks’ cross-section design and imposes angular limits on the inclinations of structural interfaces-planes between the blocks. Subsequently, the 3DCP blocks, timber falsework and steel supports are digitally manufactured using the information produced by the DTP toolchain. The parts are then transported independently and assembled on site (See Section “Printing, construction and assembly”).

It can be noted that each of the process steps described above are performed in stand-alone applications, are user-guided, and should not be viewed as single-step automation processes. However, the serial thread by itself can be used as a self-contained, parametric or user-guided design explorer if the structural and fabrication bounds, as established, are not violated. In other words, the three structural threads, and the foundation and material testing threads may or may not participate in every iteration of the serial thread, depending on the extent of change in the medial mesh surface. Thus, the serial thread can rapidly iterate whilst remaining within bounds of structural and printing feasibility.

Structural principles and printing constraints

The integrated design-to-production toolchain, as described, is informed by a global understanding of the structural mechanics of the bridge and the specific geometric constraints imposed by non-parallel, inclined-plane 3D concrete printing.

Striatus follows masonry structural logic on two levels. As a whole, the bridge behaves as a series of leaning unreinforced voussoir arches, with discretisations orthogonal to the dominant flow of compressive forces, following the same structural principles as arched Roman bridges in stone. Locally, on the level of the voussoir, the 3DCP layers behave as traditional brick masonry evident in the inclined rows of bricks within Nubian or Mexican vaulting (Fig. 4).

Fig. 4

(a) Arched balustrade and deck voussoirs, (b) start and end plane of a print block - P_s, P_e

Viewed from the top, the balustrade arches are leaning inward towards each other and are prevented from falling over by the deck. Because of the chosen stereotomy, they additionally provide a stabilising surcharge onto the thin deck, reducing the effect of live loads versus this increased dead load. The deck arches are also composed of voussoirs with discretisation orthogonal to compressive forces, which run along the spine (i.e., the skeleton) of the deck (Fig. 5).

Fig. 5

Structural principles. (a) stable, bifurcating deck arches, (b) inward leaning balustrade arches, (c) balustrade arches prevented from falling over by stable deck, (d) outward thrust resultants of masonry structure (e) tension ties to counter outward thrust resultants & (f) final geometry

Geometrically, the masonry structural logic at two levels means that it is critical to coordinate the interfaces planes between voussoirs, in both the balustrades and the deck arches, as the dominant compressive forces flow across these planes (Fig. 6). In terms of printing, each pairwise group of the interface planes determines the start and end plane of the printing (Fig. 4a). This means that the angular differences between start and end planes of all 53 printed blocks have to be globally coordinated to meet multiple criteria such as an appropriate structural contact, angle between adjacent blocks, and maximum print inclination.

Fig. 6

(a) block interface planes represented as a non-manifold mesh, (b) detail inset showing interface planes for one block - with adjacent blocks & internal left - right interface

As such, the main data interface between the serial thread and structural and prototyping threads are the interface planes These planes are represented and manipulated as a non-manifold mesh (Fig. 6) (see Section “Serial thread of DTP toolchain”).

File format and data structure

The collaborative design-to-production (DTP) toolchain described above is based on a mesh-based, geometry-processing paradigm. This allows for lightweight transmission and reconstruction of information by various participating tools in DTP. The DTP toolchain is supported by a custom file format that is loosely based on the GL Transmission Format (glTF), an increasingly widely used 3D file format. Similar to glTF, our file format uses JavaScript Object Notation (JSON) to store the 3D model information. The use of JSON enables the efficient transmission and loading of 3D scenes and models by applications, by minimising the size of 3D assets and the runtime processing needed to use those assets [27].

The main data structure that supports all the algorithmic operations in the DTP is a half-edge mesh. This data structure allows the run-time computing and storing of information per vertex, edge or face of the medial surface mesh that is created in the first step of the DTP process (Figs. 3a and 9). The data that is computed on the mesh using the half-edge data structure (Fig. 7), is then stored in the JSON file with the attributes and schema noted in Fig. 8 and transmitted throughout the serial and structural verification threads. At each consequent step of the DTP process, authors can parse relevant information and compute derivative information within their individual process threads. Any critical information that is relevant to the serial thread is added, as attributes, to the mesh vertices, edges or faces of the medial mesh surface. This information is mirrored in the JSON transmission file (see Fig. 12 and 21 for additional attributes added in the relevant serial thread).

Fig. 7

(a) key plan highlighting mesh patches of block b₂₂ & b₄₁; (b) Medial Spine, (c) list for left & right faces of the block (F_l,F_r), (c) Interpolated left & right print plane normals (PN_l,PN_r) , (d) block interface planes - start (P_sl, P_sr), end (P_el, P_er), sides (P_side) & internal (P_internal), (e) print contours left & right from start to end planes (C_sl, C_sr,C_el, C_er)

Fig. 8

(a) JSON attributes & schema stored on a half edge mesh - (b) list storing per face f_i one of its half-edge index he, (c) list storing per vertex v_i one of its outgoing half-edge index he, (d) list storing per half-edge he_i indicies for next half-edge (next), previous half-edge(prev), associated face f & associate start vertex index v, (e) attribute list storing face normal nf_i per face f_i, (f) attribute list storing vertex position vpos_i, vertex normal nv_i per vertex v_i

Implementation

The serial thread of the DTP toolchain was encapsulated in a lightweight, standalone C++ application of 800 Kilobytes. Similarly, on the structural thread, the best-fit TNA process was performed in a lightweight, standalone application produced using the COMPAS framework. The same lightweight application performed the translation of the JSON transmission file into DEM and FEM analysis friendly data. The application also controlled the batch processing of multiple analyses, subsequent parsing of the results and insertion of design-critical results into the JSON transmission file. The computationally expensive, well-established DEM and FEM analyses themselves were performed by commercially available software of 3DEC and SOFiSTiK, respectively.

Serial thread of DTP toolchain

The serial thread of the DTP toolchain takes a user-provided, 2D graph that represents the spine of the bridge, and outputs the printing information needed to 3DCP each of the discrete masonry blocks of the bridge. It comprises three major process steps: Shape design, stereotomy and print-path synthesis. It can be noted that, whilst the steps can proceed in an automated fashion, designer inspection and adjustment is currently required.

Shape design

The global shape design of the bridge begins with a user-specified, 2D graph representing the spine of the bridge (Fig. 9a).

Fig. 9

Shape design - (a) 2D spine graph, (b) coarse mesh, (c) subdivision mesh (d) form found mesh by manipulating the parameters of the force-density method [40] (e) design manipulated coarse mesh, (f) subdivision mesh using the Catmull-Clark subdivision algorithm [16], (g) guide mesh with balustrade for transmission via JSON format exchange file

By default, all 1-valence vertices of the graph are assumed to represent the footings of the bridge. Subsequently, the graph is converted into a corresponding coarse mesh (Fig. 9b). This is done by processing the vertices and half-edges of the graph to compute the vertex positions and face connectivity of coarse mesh [11].

The coarse mesh is subsequently subdivided using the Catmull-Clark subdivision algorithm [16] (Fig. 9c). The subdivided mesh is interactively shaped into a global, compressive surface by manipulating the parameters of the so-called force-density method [40] (Fig. 9d). Alternatively, the coarse mesh and the corresponding smooth, subdivided mesh can be interactively manipulated by the designer to be approximately arched 3D shapes. (Fig. 9e & f). Subsequently, the mesh faces representing the balustrade arches are added by extruding the boundary edges (Fig. 9g)

Both the 2D graph and the mesh are transmitted in the JSON-format exchange file. It can be noted that the procedural process of converting the graph into a coarse mesh and subsequently subdividing it, ensures that all the mesh vertices, half-edges and faces can be traced back to either a parent vertex or half-edge of the input graph. This enables both interactive, associative editing of the 3D shape using the graph vertices as control handles and computing derivative information such as the stereotomy, as described next.

Stereotomy

First, the mesh is decomposed into patches of faces (Fig. 10a-d). The half-edge data structure allows the original 2D graph to be traced on the 3D mesh as the spine of the bridge. The boundary edges of the balustrade faces can similarly be tracked as the spine of the balustrade faces (Fig. 10a). Subsequently, we start at the 1-valence vertices of the spine, ’walk’ along the edges of each spine, and collect the faces attached to each edge (Fig. 11a). The faces collected by this action, are grouped together for every four edges traversed on the spine (Fig. 10b). The number of edges of the spine traversed per group of faces, four in this case, is called the stride of the ’walk’. The action is repeated for the balustrade arches, except the stride is offset by two at the beginning (Fig. 10c). This creates a staggered set of patches along the deck and balustrade faces (Fig. 10d). This procedure is closely related to the algorithm of two colouring of meshes. For more see [33].

Fig. 10

Mesh two-colouring and stereotomy - (a) spine edges for deck and balustrade, (b) spine walk stride for deck, (c) spine walk stride for balustrade, (d) face coloured mesh & (e) thickened mesh

Fig. 11

(a) Mesh walks on spine and block face collections using the half edge data structure, (b) boundary representation of the solid voussoirs

The user-specified graph and the mesh derived from it serve as the inputs to compute the stereotomy or the discretisation of the mesh surface of the bridge into 3D blocks. The boundary edges of each patch of faces are extruded on both sides of the mesh surface to create the boundary representation of the solid voussoirs (Figs. 10e and 11b). The normal associated with each of constituent vertices is used for this operation. These additional stereotomy related information of each block is inserted into the JSON transmission file using the schema in Fig. 12.

Fig. 12

JSON attributes & schema added in the stereotomy thread - (a) block attribute stored as face colour, (b) thickness attribute storing corresponding vertex position of top v_itop and bottom v_ibottom per vertex v_i, (c) interface plane attribute storing plane origin o_i and normal pn_i per half-edge he_i

Block interface planarisation

The faces that represent the interface between the blocks are not planar after the block creation process described above (Fig. 13a). These are planarised (Fig. 13b) using a so-called perturbation procedure [3, 35](Fig. 14). The DEM step of the structural thread (Section “DEM Analysis”) updates the normal of the block interfaces and the thickness of each block, as deemed necessary by structural analysis. The information of each block is inserted into the JSON transmission file using the schema in Fig. 12. This completes the stereotomy of the bridge.

Fig. 13

Block interface planes (a) before and (b) after the perturbation procedure for planarisation

Fig. 14

(a) computing of the projection-based perturbation force F_i per vertex v_i of the interface planes -Plane_input, N_input - to make them planar using the best-fit target planes - Plane_target, N_target, (b) showing the iterative steps (Plane_iterations) of the solver for 6 interface planes

Print path synthesis

The planarised block interface planes (Fig. 13b), structurally verified 3D blocks (Fig. 10e), the spines of the deck and balustrade arches (Fig. 10a) are the input information needed to create the print-paths per block. Each block has a start and an end plane determined and assigned by the direction of the spine. First, the start and end planes are smoothly interpolated to create new planes (Fig. 15) and subsequently a print-path is generated on each of the interpolated planes using signed distance functions and the interpolation schema described by [7].

Fig. 15

Interpolation schemes to compute new planes between the start and end planes. (a) Linear interpolation scheme highlighting some print height is below the minimum printing height & (b) optimised weighted non-linear interpolation scheme to ensure all print heights lie in the specified printing height domain

Plane interpolation

The spine of edges associated with each block is subdivided at equal distances. New planes, centred at each of the subdivided points, are then generated (Fig. 15). The normals of the planes are computed by interpolating between the start and end planes. A weighted non-linear interpolation scheme was implemented to optimise and ensure that the print height between subsequent plane lies within the domain specified by the robotic printing constraint (see Section “Material and prototyping thread of DTP toolchain”).

It can be noted that all the deck blocks have two sets of start and end planes – a left (Fig. 16a) and right set (Fig. 16b). Consequently, there are two sets of interpolated planes. All the print paths on the left and right set of planes are first computed separately and merged in a post-processing step (Fig. 20). The balustrade blocks are simple, consisting of only one set.

Fig. 16

(a) Left Planes interpolated between start & end planes - P_sl, P_el, (b) right planes interpolated between start & end planes - P_sr, P_er. Base cross section profile computed as the zero contour of a signed distance field from each input plane mapped on the thickened mesh - (c) example left plane profile generation, (d) corresponding right plane profile generation & (e) combined left and right profiles

Cross-section interpolation

Next, a base cross-sectional profile is computed for the start, end and newly generated interpolated planes (Fig. 16c-e). The base cross-sectional profile curve for each of the planes is computed as the zero contour of a signed distance field (SDF) from each input plane mapped on the thickened mesh (Fig. 16e). After this, using the base profile subsequent 5 main SDFs are created on the interpolated planes to update the cross-sectional profile (Figs. 17a-e and 18a-e). The resultant SDF (Figs. 17f and 18f) is constituted as the Boolean of five individual SDFs. Each of the five SDFs serve a specific purpose - three boundary SDFs to control the cross-sectional thicknesses based on specified print width(Figs. 17a-c and 18a-c), and infill SDF to provide local stiffeners in each cross section (Figs. 17d and 18d) and a trim SDF aiding in the creation of one continuous print profile. Together, this step creates two sets of profile curves for the left and right planes, respectively for the deck blocks and a single set for the balustrade blocks.

Fig. 17

SDFs for deck blocks - (a) base profile polygonal SDF f₀, (b) offset polygonal SDF f₁ = f₀ + 0.5 * print width, (c) offset polygonal SDF f₂ = f₀ + 1.5 * print width, (d) Infill SDF f₃, (e) Trim SDF f₄ = line SDF at pattern points, (f) Resultant SDF f₅ =(f1 - (f2 - f3)) - f4

Fig. 18

SDFs for balustrade blocks - (a) base profile polygonal SDF f₀, (b) offset polygonal SDF f₁ = f₀ + 0.5 * print width, (c) offset polygonal SDF f₂ = f₀ + 1.5 * print width, (d) Infill SDF f₃, (e) Trim SDF f₄ = line SDF at brace points, (f) Resultant SDF f₅ = (f1 - (f2 - f3)) - f4

Post Processing

Lastly, the left and right sets of cross-sectional curves are post-processed and prepared for printing (Figs. 19a,b and 20). The artefacts created without appropriate post-processing can be noticed in Fig. 19c and its fixes with appropriate post processing in Fig. 19d. The information required to 3D print each block is inserted into the JSON transmission file using the schema in Fig. 21 and is subsequently parsed in the printing thread of the DTP (see Section “Printing, construction and assembly”).

Fig. 19

re-sampling of cross section profiles of the previous step to make it amenable to robotic print constraints of spacing and maximum number of points- (a) key map showing the number of re-sampling points per block sequence, (b) various re-sampling strategies tested on the contours - unsampled print profile (top), distance-based sampling (middle) and adaptive feature based sampling (bottom),(c,d) print result from distance based & adaptive feature based sampling respectively

Fig. 20

(a) Adaptive sampling of cross section profiles based on feature points. The feature point is computed as the nearest intersection of vector y_i with the cross-section profile, where y is the cross product of input guide vector x_i and the plane normal z. The cross section profiles are split at these feature point to maintain alignment with the planes below and the individual segments are sampled using adaptive distances - low sampling distance for segments on the outside and higher sampling distance for the internal parts of the block. (b) procedure to connect the left and right cross section profiles to create one continuous print path

Fig. 21

JSON attributes & schema added in the print path synthesis thread - (a) list storing per vertex of the print contour the position v_i, print normal n_i, print height h_i - computed as distance between v_i and the intersection point pt_i of n_i with the previous print plane - & (b) specified print width w_i

Structural threads of DTP toolchain

Interleaved between each of the three main processing steps of the serial thread of the DTP are three parallel, corresponding, structural analysis and verification threads.

Best-fit TNA

This structural evaluation thread takes the mesh surface as output from the shape-design step of the serial thread (Fig. 9c) and computes the nearest compression-only surface using the so-called best-fit Thrust Network Analysis (TNA) algorithm of [29] (Fig. 22). This thread then updates the positions of the vertices of the user-designed mesh surface and retains all the topological information. This thread may be skipped if the shape design includes a compression form-finding step or already has a reference, compression-only surface to inform the shape manipulation.

Fig. 22

Iterative solver for best-fit thrust network analysis (TNA) showing the form and force diagram - (a) iteration 1, (b) final iteration

DEM Analysis

This thread receives the stereotomy or the discretised 3D blocks from the serial thread, and performs various analyses to determine structural stability, mechanics etc., (Fig. 23). Discrete-element modelling (DEM) is the primary tool used to perform these analyses to evaluate structural performance such as response to loading, differential settlements of the footings, etc. This thread then updates both the normals of the interface planes between blocks (Figs. 13 and 14), and the thickness of each block to define the so-called intrados and extrados, which are the bottom and top surfaces, respectively, of each voussoir (Fig. 10e). This thread also informs the foundation and tension-tie design threads (Section “Design-to-Production Toolchain”).

Fig. 23

Discrete element modelling - (a) resultant force vectors at interface planes, (b) 3Dec Analysis, and (c) load testing

FEM Analysis

This thread performs local structural evaluation on the various cross-sectional profiles generated by the print-synthesis step of the serial thread. These analyses are performed using Finite-element modelling (FEM) and inform cross-sectional design parameters such as width of the print, maximum spacing between stiffeners, overall cross-sectional depth, etc (Figs. 24 and 25). It can be noted that these analyses are performed only on representative cross sections in the deck and balustrade arches.

Fig. 24

Finite element modelling and analysis

Fig. 25

Material testing and prototyping

Material and prototyping thread of DTP toolchain

Inclined-plane printing is a new capacity in 3D concrete printing. The so-called two-component (2K) mortar formulation and printing setup needed for enable such inclined-plane, variable thickness printing is in rapid development. As such, this particular thread of the DTP was necessary for the physical realisation of the bridge. In the future, as the concrete characterisation and the geometrical limits of the technology are better established, this thread may not be necessary.

We used the Tector 3D Build cement produced by [21]. However, several novel, proprietary formulations were developed and tried specifically for the project. Through several printing tests (Fig. 25), geometrical limits such as the maximum inclination of a print plane, maximum and minimum thickness of a print layer (i.e., the layer height), minimum and maximum width of printed filament (i.e., the layer width) etc. were established (Fig. 26a,b). The first two parameters of inclination and layer height impose angular limitations on the block planarisation step (Section “Block interface planarisation”) and the distance between planes in the plane-interpolation step of the serial thread, respectively (Section “Plane interpolation”). The layer-width parameter, as empirically established, informs the cross-section design (Section “Cross-section interpolation”).

Fig. 26

(a) initial stereotomy studies based on print constraints, (b) print recommendations for block orientation, layer height and width, and material calculation with various infill patterns

Printing, construction and assembly

The print-path synthesis step of the DTP outputs a print file per block. The file contains information about the position of every vertex of the print-path curve and the normal of the plane it sits on (Fig. 21). This information dictates the path that the print head will traverse to deposit material filaments. The positional and orientation information was converted into ABB-robot specific instructions. Proprietary printing-specific information such as pump rate, velocity control etc. were additionally included at this stage.

The structural design of the contact interfaces between the blocks assumed good contact and transfer of force across the interface. In the physically realised bridge, this was achieved by:

• placing at the bottom plane of each block a smooth plastic foil that separates the interface plane and the sacrificial raft that is printed to level out any imperfections in the print bed (Fig. 28a);

• slightly sanding off the top plane of each plane; and,

• insertion of neoprene pads between blocks. The neoprene material has a much lower Young’s modulus than the concrete offering a distribution of stress concentrations caused by interface irregularities. This strategy is similar to the traditional use of e.g. lead sheets in hard stone setting. Additionally, the friction properties of the neoprene-to-concrete interface could be quantified, and thus used in the engineering.

All constituent blocks of the bridge were produced using this DTP workflow and the resultant output files. In total, 53 blocks consisting of 7883 print planes and 58 kilometres of print path were 3D-concrete-printed in approximately 84 hours by one 6-DOF robot. The blocks weighed between 200 and 800 Kilograms each, and the total weight of all 3DCP blocks was approximately 24.5 tonnes (Fig. 27).

Fig. 27

data visualisations of (a) individual block metrics showing variation of print layer heights through the blocks, the print bounds, angle deviation between start and end plane, total number of points etc & (b) metrics for all 53 blocks

In addition to the robotically 3DCP blocks, timber falsework and steel supports were produced by Computer Numerically Controlled (CNC) machines. The manufacturing information and construction drawings for the timber falsework, steel footings, tension ties and for the foundation were produced by the ancillary threads of the DTP toolchain (Section “Design-to-Production Toolchain”).

The three main components of the bridge were then transported to site. The foundations, the steel footings and tension ties were first poured and installed. The timber falsework was then assembled. The printed blocks were subsequently assembled on top of the falsework – first, the deck blocks and then balustrade arches. In each case, the sequence of assembly was to start at the bottom of each of the deck or balustrade arch and proceed towards the keystones. Once all the blocks were assembled, the falsework was sequentially lowered until the blocks were fully structurally engaged (Fig. 28). The construction and assembly processes used is similar to the one used for the precedent Armadillo project. For more details, see [8, 38].

Fig. 28

(a) 3D printing of block, (b) preparation for transportation, (c,d,e) transportation and storage on site, (f) erection of scaffold, (g) placement of deck blocks & (h) placement of key stone balustrade block

The on-site manoeuvring and assembly of the 53 blocks required only one lightweight spider crane and a five-person construction team. The on-site construction and assembly spanned 35 days, including force-majeure logistical delays and full stoppage for approximately two weeks. The resulting, unreinforced masonry, 3D-concrete-printed bridge structure has a span of 16 metres.

Outlook

The proof of concept, the physically realised bridge and the associated design-to-production toolchain, together demonstrate the viability of applying unreinforced masonry paradigm and methods to the design of 3DCP bridges. The following areas of work could be improved to help its mainstream adoption:

• 1. Stereotomy and DEM for 3DCP blocks – Stereotomy or discretisation of the form-found, medial surface mesh into 3D solid blocks and the discrete element modelling (DEM) of the those blocks to structural verify their stability, are inter-related. Currently DEM evaluation happens entirely in the structural thread, at non-interactive rates. Developing a fast-approximation of the DEM evaluations within the serial thread will improve the interactive editing and didactic aspects of the design-to-production toolchain.

• 2. Print-path synthesis – The interpolation of the printing planes (Section “Print path synthesis”) results in non-parallel planes. In some cases, this causes the limits of inter-plane distance and the corresponding maximum or minimum layer-height to be exceeded. A fast, constrained optimisation routine to guarantee that interpolation will meet the layer-height limits will alleviate the need for manual intervention.

• 3. Interface design - development of male-female interface details to provide resistance against local sliding and resulting misalignment. The design of the interface can also consider reference and registration points that will aid the assembly process, including potentially full, unique and automatic registration.

• 4. Transport of unreinforced 3DCP blocks, starting from moving off the print bed is an important consideration. Since the blocks use an unreinforced cement fix, handling and transportation induced loads needs to be carefully considered and can be incorporated in the design process.

• 5. False-work design - the design of the false work can be optimised to minimise the amount of timber used, for repeated reuse of the timber parts, easy decentring etc.

• 6. Low-emissions concrete – the compressive stresses developed in the structure is very low given the unreinforced masonry structural principles. This opens a pathway for low-strength and thus low-carbon emissions concrete formulations that can be 3D printed along inclined planes. Currently, the printing-compatible mortar has high compressive strength.

The continued design development of the prototype of the footbridge itself may build upon disruptive improvements on sustainability and circularity that are offered by considering the use of 3DCP concrete as as artificial stone and the unreinforced masonry paradigm of design and construction. This is relevant to other structures such as floor slabs [9]. The structural design principles and structural behaviour features from unreinforced masonry, combined with the benefits of 3DCP could potentially pave the way for improvements in the so-called concrete ’ink’, such as reducing the requirement for high-strength concrete, reducing the amount of virgin materials used, alternative binders in the concrete etc.

Conclusions

The paper articulated the relevance of unreinforced masonry design to both achieve a sustainable use of concrete and realise the benefits of 3D concrete printing (3DCP). Furthermore, a practical pathway to design and construct bridge structures that reduce the amount concrete and steel used in addition to being repair, reuse and recycling friendly, was detailed.

The design-to-production (DTP) toolchain was critical for the collaborative, multi-author and integrated computational design, robotic 3DCP and construction of the arched bridge demonstrator. The DTP toolchain allowed for parallel investigations in design, structural engineering, material development and physical prototyping. These investigations fed into a serial thread of processes to produce a structurally informed, printing-feasible and expressive design.

In particular, the key contributions as described and practically demonstrated, suggest a clear pathway to incorporate the DTP toolchain into

• an end-to-end, industrial, integrated design-to-production solution for 3DCP bridges.

• an equilibrium and 3DCP aware, computational design pipeline for architects and other non-experts vis-à-vis 3DCP.

Furthermore, the paradigm, file format and data structure of this proof-of-concept DTP, based on COMPAS, makes it suitable for open-source publication and thus improve chances of its extension. These aspects are critical to fully realising the ecological, labour-saving and worker-safety benefits promised by 3DCP. Together, the work points to a new structural and architectural language of force-aligned, precision 3DCP emerging from the historic paradigm of unreinforced masonry