Though research in mathematics education on the relationships among humans and ideas is far different from research rooted in relationships among ideas (e.g., in mathematics), the investigative processes share some characteristics. First, one must start with a few axioms and definitions. In education, the locally useful axioms form what is called a theoretical framework, a foundational perspective on the nature of thinking and human experience. In collegiate mathematics education research, necessary definitions also include those for the methods of conducting a particular investigation (e.g., the ways that survey, interview, observation, and review of documents are used). Logico-deductive proofs do not exist in education research. Thus, as in medical research where the participants are people, empirical evidence of the nature of human experience is the basis of a compelling argument [1].

The work reported here has two purposes. First and foremost, the goal is to contribute to the undergraduate mathematics education research literature on mathematical motivation (more on this below). We also aim to offer the reader an experience of the reporting of educational research that defines technical terms and provides citations for further exploration. The terminology used in educational research is as nuanced as the human experiences it attempts to describe. To the uninitiated, the technical language can seem like unnecessary jargon. In most cases, it is not. For example, there are differences between mathematical motivation and mathematical engagement: the former is a sub-component of the latter. Such inclusion relationships matter when attempting to make sense of the experiences of instructors and their students. Moreover, it is the mathematical content and context that make the work mathematics education research. How people learn to know and do mathematics is different in large and small ways from how they learn in and through biology or astronomy or music. Contextually, a mathematics classroom offers different experiences (and constraints) than a laboratory with live specimens, an observatory, or a conservatory. What is important to know, and how it is known, also depend on what is valued in the discipline and on disciplinary traditions.

In what follows, we first provide the practical and theoretical background for the research. Then we present the results and close with a review of the implications of the work.

1 Background

Mathematics engagement involves the simultaneous recruitment of motivational and affective structures to guide sustained, productive learning behavior. Critical to this perspective is the idea that “productive learning behavior” is a social construct formed from the interaction of learners' personal learning states and mathematical dispositions, their home community, their classroom or learning environment community, and macro-cultural constraints such as curriculum, assessment, and cultural attitudes [2, p. 18].

Unpacking the classroom ecology of mathematics learning has been a goal for mathematics education for a long time [3]. Classroom ecology refers to the system of relations of people to one another and to the surroundings in which they operate. This complex system includes the dynamics of discipline-specific resources as well as the individual and collective goals and orientations of the people in the room. The classroom system is situated in and influenced by the circumstances of the larger environment of related classrooms (e.g., other sections of a calculus course), curricula, personal and department cultures, and larger institutional and social conditions [4].

There is a large research literature in K-12 education, and a smaller collection with similar results in college mathematics education, that has examined teaching effectiveness (as measured by student achievement) and good teaching (as measured by the qualities of instruction that lead to learning that is flexible, extensible, persistent, and resilient). Good teaching supports learning that includes missteps and stumbles—the humanity of those involved—to generate complex cognitive and socio-emotional connections built through human relationships [5,6,7,8,9]. This study contributes to the research on the qualities of good teaching by examining the perspectives of the humans involved, in the post-secondary classroom.

1.1 Driving Questions for the Research

This report is rooted in examples from a single calculus classroom considered as a case study and comes out of a larger project across multiple classrooms in the U.S. [10]. That project sought to gain insight into two questions: What are undergraduate student perceptions of the instructional processes they see as supporting their success in their first college mathematics course (e.g., calculus, finite mathematics, algebra-based statistics)? How do student perceptions of their learning needs compare to instructor assertions about what students need and to instructor perceptions of student assertions about what they (students) need? For this report, the research questions addressed are those of the larger project but considered specifically in the context of students and instructors in calculus:

RQ1. What are undergraduate student perceptions of the instructional processes they see as supporting their success in their calculus course?

RQ2. For students not in the upper grades quartile in a given case study class, how do student perceptions of their learning needs compare to those of other students, to instructor assertions about what students need, and to instructor perceptions of what students assert about what they (students) need in learning calculus?

Note that people define “success” in multiple ways, individually and collectively. The study of perceptions about what supports “success” does not depend on a single specific, uniform, definition of the success (e.g., as grades or intellectual satisfaction or “ownership” of ideas). Rather, it depends on acknowledging that what counts as “success” will vary from person to person and context to context.

1.2 Sources of Evidence

Empirical evidence in this report came from a focal calculus class (using survey, classroom observation, and interview data) and a more general view of student and instructor perspectives derived from analysis of questionnaires completed by calculus students and instructors across the U.S. The case study approach, including interviews of the instructor and five students in one calculus class, allowed digging to unearth examples illustrating some of the ideas in the survey, particularly perceptions among students who struggled to learn the subject. That is, the report is statistically and qualitatively descriptive, not predictive. Case study is a form of research and reporting aimed at credibility in portrayal of participants' intentions, perceptions, and actions, authenticity in representing participants views in their context, and transferability by giving detail that allows the reader to gauge the potential usefulness and potential stumbling blocks in attempting to interpret or replicate the work in a new context. Like all research, case study research also aims at dependability and confirmability by systematic and well-documented data collection, analysis, reporting, peer review, and clear connection to existing research and theory. The goal of transferability in qualitative work differs from the generalizability aimed for in quantitative studies (for more on the distinctions among types of qualitative and quantitative research, see [11]). Underpinning this case study are ideas about cognition, affect, and motivation drawn from the current knowledge base on human learning.

2 Theoretical Foundations

Researchers and practitioners care about student perceptions because these shape motivations, and motivations are drivers for engagement in mathematical learning activity [2]. After a brief overview of cognition, affect, and mathematical engagement, subsections return to each idea, providing and connecting theories related to these terms.

Cognition is concerned with the “what” of learning. It includes what knowledge is involved and what happens when the intellectual and psychological results of perception and reasoning coalesce into (for constructivists) persisting mental structures [12,13,14,15,16,17,18]. Affect is how experiences, knowledge, and information are perceived, including feelings aroused by these perceptions [19,20,21,22]. For example, when a student solves a word problem, selection and use of appropriate techniques will involve cognition, while aspects of affect such as the possible frustration or anxiety triggered by the task (or elation upon its completion) will also require attentional resources. Self-regulated behavior is the way a person acts, often in response to the acts and expectations of one or more other people and may or may not be linked consciously to intentions, perceptions, cognition, or affect [23,24,25,26]. Mathematical engagement refers to the in-the-moment relationship between a person and that person's immediate mathematical environment [2]. This relationship includes the tasks, as well as behaviors and internal states of self and others with whom a person interacts. For example, a student engaged in a mathematical task with a partner may be engaged in observable ways, like pulling a paper close or tipping the head forward and closing the eyes, as well as in mental ways that involve cognitive effort, motivation, and regulation of interaction with the task or with the person who is a partner in the task.

2.1 Mathematical Engagement and Mathematical Motivation

Viewed as more than the orientation and goal setting generally associated with motivation, mathematical motivation encompasses short-term volition of in-the-moment mathematical activity as well as longer-term structures of engagement that are the product of the accumulation of mathematically-dense in-the-moment experiences over time [2]. Mathematical motivations are made up of patterns of action and perceptions that interact to determine what a learner chooses to do, with whom, and toward what end. Hence, the importance of understanding student perceptions.

In the United States, research to date related to mathematical motivation in post-secondary settings has focused on students who are less skilled or less knowledgeable in mathematics. Part of the reason for this may lie in the nature of the educational system itself: students who are successful in mathematics at the university level may have already developed adeptness at identifying goals and managing affective response when engaged with mathematical tasks in the ways commonly offered in college classrooms. That is, many students have status quo success (e.g., passing grades) because they are effective at maintaining an intention to learn in the face of perturbing factors (e.g., internal and external messages about their skill, belonging, or likelihood of success [7]).

Learners in specific situations (e.g., when solving a mathematical problem) make decisions about assembling and allocating attentional resources and effort [27, 28]. Two kinds of intentions inform a person’s appraisal of a situation: learning intention or coping intention. Boekaerts' meta-analyses have indicated that learning intention and coping intention both account for the same proportion of variation in mathematical performance [29]. Learning and coping intentions co-exist. That is, the balance of the two categories of intention may lean more toward learning in one moment and then lean more toward coping in the next. Two types of strategies are used to achieve the goals aimed at when acting on intentions [27, 29]. Positive mental scenarios in which learners value a task and consider themselves competent to perform it, may be necessary (though not sufficient) for a learning intention. In fact, “low motivation control can be compensated by volition control (ability to initiate, persist, and disengage from a task)” [27, 30, 31]. Undergraduates just building skills and knowledge associated with a mathematical concept (e.g., the difference quotient or limit) must attend to multiple aspects. That is, there are multiple goals at stake during mathematical engagement, so monitoring and self-regulation may be required on many fronts simultaneously.

Research across cultures points to the ubiquity of self-regulation and self-efficacy as factors in mathematical motivations. Cultural embeddedness (the degree to which one identifies with a culture) affects the purposes, structure, distribution, and manifestations of self-efficacy and self-regulation [32, 33]. Consequently, depending on external and classroom cultures, perceptions of self and others can interact in different ways to shape intentions for classroom interaction [31]. This is true for both students and their teachers [34].

The twenty-first century move toward activity- or inquiry-based college instruction means “success” includes achieving goals for mathematical knowledge that are pursued alongside goals for belonging, self-determination, performance, well-being, and resource contribution/acquisition [35, 36]. All of these are subject to intrinsic and extrinsic forms of motivation regulation, informed by the perceptions the learner has about themselves and their environments [37].

We can adapt to our surroundings. We can try to change them. We can try a mixture of the two. Perceptions of self and of the environment will have an effect on choices about adaptation and change. It is particularly important to note that access to skills and understandings upon which new learning must build can greatly influence mathematical motivations: the kinds of self-image-preserving coping intentions recounted by Boekaerts et al. [29, 38] appear to be most likely when a learner's knowledge base is sparse, unstructured, or subjected to ambiguous, disruptive, or conflicting external messages. For example, deficit messaging and stereotype threat have emerged as important in research in undergraduate mathematics education [39,40,41].

The work reported here examined student and instructor perceptions in the post-secondary context in the U.S., through the lens of mathematical motivation and its constituent parts. Other theories applied to the same research data could explore other aspects of educational experience (e.g., expectancy, identity). The focus in this report is on classroom interactions and instructional approaches undergraduates viewed as supportive of their learning of calculus.

3 Methods

The larger project used a sequential exploratory design in which quantitative data collection and analysis informed and provided context for qualitative data collection, mixed-methods analysis, and reporting [42]. The quantitative aspect of this study used data from the larger project: student and instructor responses to a questionnaire from 675 calculus students and their 26 different instructors. The qualitative work involved review of video of a full term of meetings of a calculus class, surveys completed by the instructor and 27 students, and survey-response-based interviews with the instructor and five students from the class. In this section on methods, and again in the results section, we present the quantitative first, as context for the qualitative.

3.1 Survey

There were two questionnaires. One was for instructors, one for students. The questions were developed so that one endpoint of each survey item was a way of viewing mathematical teaching and learning valued in U.S. mathematics departments and the contrasting end represented a position commonly found among undergraduates. Based in part on the work of Hativa among undergraduates in the western United States [43], the development of the instrument was described elsewhere [44]. Nonetheless, we include some details here to orient the reader to the tool.

The pool of endpoint statements was from ethnographic work collecting utterances by students, mathematicians, educators, and administrators at U.S. colleges, comprehensive universities, research universities, and special institutions (e.g., technical colleges). To anyone familiar with college mathematics teaching in the U.S., many statements will be familiar, echoing what might be overheard in class, among students, or among colleagues (e.g., by faculty in mathematics department hallways or at professional meetings).

Statements were used on the questionnaire to create a comparative continuum for items (see Table 1 for an example). The two endpoint statements started as in vivo quotes. Most often, a statement from a student was juxtaposed to one originating from an instructor, sometimes the student quote was to the left, sometimes to the right.

Table 1 Instructions and sample comparative item from each survey
Full size table

3.1.1 National Survey Participants

Data collected in the national survey were from five different U.S. institutions (a two-year college, a comprehensive university, two doctorate-granting universities and a specialized technical institution). The 675 calculus students completing the survey did so in the classes of 26 different instructors in which enrollment ranged from 11 to 51 students (average 27 students per class). Although mathematics majors might have been in a class, most students (80%) were non-mathematics majors, taking calculus as part of their program or graduation requirements. Most of the classes (81%, 21 of 26) were part of a multi-section course. Geographically, the sample was from institutions in the eastern, central, and western United States.

3.1.2 Focal Items for Interviews

For the full project data set, there were statistically significant differences between instructor and student average responses on a subset of survey items. These items were the central content of the case study interviews (see Appendix). In what follows, we refer to this subset as the focal items.

3.2 Case Study

The case study institution was a public university with a student enrollment of about 4,000 (full-time equivalent). To protect the anonymity of participants, we have omitted some detail, and have included only a few of the demographic characteristics of the students, instructor, and institution. At the time of the study, the mathematics department had 13 faculty: 8 tenured or tenure-track (5 men, 3 women; 6 with doctorates in mathematics, 2 in education) and 5 non-tenure-track instructors (most teaching college algebra courses). The calculus course was coordinated in that there was a departmental statement of course objectives, a course outline of topics, and a common textbook (James Stewart's Calculus: Concepts and Contexts). There were three class sections of the Calculus I course in the term of the study.

The department practices around the course included regular communication among instructors. Faculty got together to discuss the content of the course and aspects of pacing—no instructor's class was substantially different from another's in terms of the nature and content of assignments and timing of tests (e.g., all gave tests on particular content in the same week). Faculty sometimes shared common test questions or projects and encouraged their students to visit other faculty members for help. For the purpose of teaching evaluation, the department practiced peer observation. Everyone in the department had been to others' classes.

3.2.1 Case Study Class Instructor and Participants

The instructor, Professor Green (a pseudonym) and all 30 students in his Calculus I class at the case study location consented to video recording of class meetings. A single video camera was at the back of the room and followed the instructor at the board as well as when he moved around to groups of students at work. The instructor and five of the students in the class each were interviewed about their responses to focal survey items.

The class met for ten weeks (known in the U.S. as a “quarter”). It was a first-calculus class, differential calculus, meeting four times a week for 50 min each time. The instructor was interviewed the second week of class and students during the seventh and eighth weeks. By then, students had done about five quizzes and one test.

At the time of the study, Professor Green was in his mid-50 s, had a bachelor's degree in mathematics, master's degree in a science, and a doctorate in mathematics education. He had taught Calculus I for more than five years at the university. Class met in a room with chalkboards on two walls. Seating for students was in four rows of three long tables each, each table had two to four chairs. The class started the quarter with 30 students, in the last few weeks of the term, 26 students were regularly present. The students were predominantly white, about half male and half female, and most had taken at least one mathematics course at the university before this calculus class. From the back of the classroom, it would have been easy to think that the students were all traditional university age, but that was not the case. There were several occasions when different students brought their children with them to class, and during a discussion on optimizing the light from a Norman window, one student said that in a former job in construction he had installed such a window. Starting with the second meeting, Professor Green occasionally handed out worksheets and had students work in groups in class to complete the sheet, or work on a problem from the text. Such working days happened roughly once per week. In week 6, Green began to ask students to present solutions to homework problems on the board. By the end of the quarter, about half, 13 different students, had gone to the board during class to do some or all of a problem. Students had a short project in the beginning to prepare them to work in groups and a larger group project assignment as part of the course. Each group project was a problem-solving task for which students were expected to meet and work together outside of class.

From the case study calculus class, we interviewed Alan, Barbara, Charles, Deborah, and Emily (pseudonyms). They had each taken other post-secondary mathematics courses before the calculus class: pre-calculus, college algebra, trigonometry, or a class in mathematics for prospective elementary teachers (grades for each course are included in Table 2).

Table 2 Information on interviewed students
Full size table

3.2.2 Interviews

Among the students who volunteered to be interviewed, we chose students based on their responses to the focal items from the questionnaire, seeking to represent different patterns of response. Individual interviews probed student and instructor thinking related to the focal items. The interviews were audio-recorded and transcribed and then reviewed for themes—ideas or experiences that recurred across interviews—as students told the stories behind why they rated an item as they had.

3.2.3 A Note on the Limitations of the Case Study

The main findings are from a case study and are not intended to be generalizable. Rather, the goal is transferability: giving sufficient detail to support the reader in interpreting the results for a situation similar to that of the case. This small study did not gather or analyze information about societal structures and systemic influences (and consequences) of student and instructor perceptions. The case was a single class (not a comparative case). Nonetheless, a useful example can anchor a lot of learning. The videos showed that the class had many mathematically adept students and the distribution of scores on tests was similar to that reported in other work on Calculus (low mean and large standard deviation). Researchers chose among undergraduate volunteers to provide insights into student thinking. The fact that the five volunteer students who were interviewed were not in the upper quartile of final grades for the class afforded the opportunity to explore perceptions of supports for success among students who struggled with “success” in terms of grades.

4 Results

The main results are about student perceptions of the instructional processes they saw as supporting their success in their first college course in calculus. Here, description of survey analysis for the national sample sets the stage for illustrative examples from the case interviews and classroom.

4.1 Survey

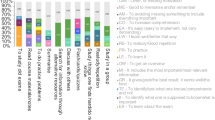
Factor analysis of the national survey data from calculus classrooms resulted in two main factors in student response (statistically correlated clusters of items). One factor was about behaviors and motivations associated with an effort to cope with a situation that was high-stakes and low agency. Simultaneously, the other group of survey items that clustered as having statistically similar responses that were also distinct from the first factor, represented statements that referred to managing responsibility, expectations, frustration, and abstracting ideas from specific content in the context of learning. Thus, we had the Coping factor of survey items related to the kinds of extrinsic motivation and external locus of control associated with coping intention, while the Learning factor was a group of items related to perceptions about aspects of effort and regulation connected to learning intention. Table 6 in the Appendix lists the items in each factor and the average ratings for each for calculus students and for instructors (recall that the instructors’ average was on the instructor version of the item). The results in Table 6 echo the literature on what upper high school and early undergraduate learners in the U.S. report as valuable (e.g., in research using the National Assessment of Educational Progress student perspectives data and the Mathematical Association of America’s national study of college calculus [45]).

4.1.1 Coping Factor: Valuing Predictability

Central to survival is identifying and controlling risk. As a collection, the items in the Coping factor indicated that students were seeking supports to reduce uncertainty, such as having predictable structures (e.g., knowing in advance something about types of test questions and test review; #15, #22), being told clearly, in concrete and precise ways about what to do and how to do it (#13, #14,), or having the extrinsic motivation of grades (#23). On items related to who was in control of the risk (e.g., agency), on average students were split between teacher and self as the locus when faced with being challenged (related to concepts #5, or self-confidence #11). Among the seven items in the Coping factor there were four with statistically significant differences between calculus instructor and student perceptions (see * entries in Table 6: #14, #15, #22, #23). The Coping factor consisted of items mainly about student perceptions of what to expect from (and how to cope with) class format and instructor behaviors.

4.1.2 Learning Factor: Effort and Persistence

The Learning factor was a group of items related to mathematical learning goals and motivational and volitional controls for achieving self-defined success in a mathematics class. Calculus students in the national sample were more likely, on average, to favor statements where the responsibility was with students for knowing prerequisite, or learning current, material (#9, #19) while also tending to favor statements suggesting there was more to success than effort (e.g., #1 and #21). Student responses also acknowledged effort related to persistence (#4), satisfaction (#7), and conceptual (as opposed to rote) interaction with mathematics (#6). There were statistically significant differences between calculus instructors and students on only two items in the Learning factor (#9, #21). On Item 9, the juxtaposition was between students' agreeing more with I have learned the mathematics required to take this course, while instructors had more agreement with Students in this class are not prepared mathematically for the course. On Item 21, the difference was between students' agreeing more that to emphasize mathematical thinking would intimidate me, while instructors had more agreement with I try to show the students how I think so that they may gain a better understanding of the subject. For the other items in the Learning factor, students and instructors had mixed responses with, on average, a mean about halfway along the continuum. Thus, across both factors, calculus students in the national sample had perceptions of what was supportive that differed from their instructors’ perceptions of what was supportive. At the same time, any individual student might have a response pattern that aligned with instructor views on items in either or both factors.

4.2 Case Study

Student and instructor perceptions arising from analysis of the case study classroom surveys, observations, and interviews resonated with the sentiments from the larger survey summarized above. Also, across the 10-week term, the tension between surviving and thriving (and who defined it) was evidenced in class in many ways, including requests by students to the teacher and in teacher replies to students.

4.2.1 Case Study Class Survey Responses

The survey responses in the case study class were like a “typical” class (represented by the averages in the national sample) in many ways but distinct in a few. Like the averages in the national sample, the case class averages on the Coping factor indicated differences between student and instructor perspectives. As in the national group, the case class students favored To help me learn, it is a good idea to have a worksheet with practice problems that I can match with test problems before a test and An instructor should do extensive reviewing before a test using class time (#15, #22). However, on these items instructors (including Professor Green) asserted Students need to learn to deal with test problems without a “preview” of practice problems and said they were unlikely to offer extensive review during class time. At the same time, unlike the national sample, students in the case class were in agreement with instructors (including Professor Green) that it was important to be motivated (by the instructor) to question, reason, and learn about abstraction, rather than work only with precise and concrete material (#14). The case class was also different from the national sample in favoring the idea that understanding the subject was more important than grades in the course (#23).

On the Learning factor, like the national sample, students in the case class asserted that they had learned the mathematics required to take the course which was significantly different from instructors’ (including Professor Green) assertion that students were not prepared mathematically for the course (#9). On all the other Learning factor items, the case class tended to agree with instructors, including Professor Green, even on the item on which there was a difference in the national sample: case students agreed that they would like to see how a mathematician thinks, to gain a better understanding of the subject (on average, the larger sample of calculus students did not favor this statement, #21).

Within the case class, among the five students interviewed, survey responses on two Coping factor items and one Learning factor item were statistically different from their case class peers and approaching significance on one additional Coping and one additional Learning factor. As detailed in Table 3, interviewed students were more likely than their classmates to not favor the idea of figuring things out on their own and did not find such independent work confidence building (#13, #5). The interviewed students also indicated in their surveys a greater tendency to give up when confronted with a problem for which they did not have an example to follow (#4) and were slightly more likely to indicate it was more common to feel frustration than satisfaction after working on a problem (#7) and to prefer explanation with many examples of problems being solved over general conceptual explanation (#6).

Table 3 Items on which interviewed student responses differed from the class average
Full size table

The analysis of the case class allowed delving into the details with specific examples from students and instructor. In interviews, student responses fell into seven themes, one of which grouped survey items in a cross-factor way: they spoke about being challenged as a unifying theme across Items #5, #13 (Coping factor) and #4, #7, #6 (Learning factor).

4.2.2 Case Study Theme: Test Practice and Test Review

Though Professor Green did not give out practice problems before each test, there was a review in class. Green handed out review sheets with summaries of the material and then invited students to make requests for problems he would work out on the board. In addition, Green regularly urged students to come to his office to work or get help.

On his survey, Professor Green did not choose a continuum value and filled out “Neither” on the item about review before a test. He wrote “I do some reviewing in class and sometimes offer a help session. Neither is ‘extensive.’” When asked whether he had taught classes in which he gave students a worksheet with practice problems before a test, Professor Green answered, “Yes.” Did he think it helped students to learn? He answered, “No,” and laughed softly. He thought that it was unwise because “it is an impossible goal to assume that students could be shown every problem they might encounter.” For Green, it was better to “give them tools that could apply to unfamiliar situations so that they were equipped to deal with them.” He also said there would always be students in the class who were not ready for unfamiliar problems on a test.

In student interviews, when discussing practice problems before a test (#15), all five students reported that in previous classes they had been given such materials before a test, under different names: review sheets, worksheets, homework assignments with answers, practice test, study guide. All said that in many cases problems were not exactly test problems, but they were “similar,” had the “same structure,” or “just used different numbers.” Students reported that these previews or reviews provided structure for content to be studied and time management:

Barbara: Gives me better focus.

Emily: Good so that you can figure out what you have to do…without it I have to read everything, didn't know what to focus on, takes a lot more time. [With it] I know exactly what the teacher wants you to focus on in the material.

Alan: Gives me a last look at it … helps you to kind of organize your thoughts about the whole subject.

Deborah: I know what to study and I study more too. I knew I wasn't wasting my time… have a grasp of what's in the test.

Though four interviewees felt that they learned better with practice problems, Charles was more circumspect and said that reviews “may miss some real complicated issues, in which case it would be better to have class discussions,”

Charles: Some people just focus on the stuff on them [review worksheets], and not further. …then …you're not exposed to different types of problems, you only did the problems in the worksheet. You kind of think that is that, what's on the test or what they want you to know. Because that might not be all that another teacher might want you to know. You might not be getting complete understanding of the whole course. Like my general chemistry class, going into another chemistry class, your upper division chemistry class teacher, thinks that one thing is important, …something in the class that's important that the general teacher did not focus on too much. So then if you didn't go on your own and learn all the stuff, then you'd be kind of lost in that other class. Like, my pre-calculus class in high school was different from the pre-calculus class here. Because my teacher did things differently than here, or focused on different things or explained things differently, … I think that's actually what happened to me. I only did what the teacher wanted me to do, I didn't go further. So, when I go to another class, a different professor, then I was lost.

Emily also noted that teachers who gave worksheets “take the time to help students see what things to focus on, they're trying to get the students to understand more…they are trying to help.”

Students did not decide a teacher was supportive solely based on whether practice problems were given before a test. The student interviewees who valued the practice problems said that instructors who did not give such problems had “a different teaching style.” Charles, who thought that class discussions would be better than a sheet of practice problems to bring out complicated issues, also thought that Professor Green, who did not give practice problems, was “harder to understand…but in general, he was a good teacher.”

4.2.3 Case Study Theme: Grades

Professor Green recognized the importance of grades to his students. In his interview, Green remarked on students' coping with the class format to get the grade they wanted or needed. He offered students chances to add points to their scores on quizzes and tests through various “deals” he made with them. Also, he adjusted their scores “using a curve” by adding points to each person's score (e.g., 18 points on the class’ second exam), saying to the class: “given where you are and where you ought to be, I think it is justified” (week 8, Class 33). Neither Professor Green nor his students discussed what it meant to say a curve was “justified.” On the survey, like the national pool of students, his students indicated a desire to gain confidence through both teacher guidance and independent learning. Interviewed students compared the value of “higher grade” with “better understanding,” saying:

Alan: At this point, I would say, probably a higher grade [is more important to me than understanding]. I'm more worried about my GPA [grade point average] right now. I don't think this is a course that I am going to use in my job type. …It depends on the course, it is in different courses that I'm going to use more that I'm worried about understanding the material and knowing it.

Barbara: I think understanding comes first, but it's pretty hard to get a low grade, because of the GPA [and negative consequences from it being low].

Charles: I'd say that you're better off with some solid understanding and a mediocre grade than you are with a mediocre understanding and a solid grade.

Deborah: Understanding the material, for future classes, is more important.

Emily: I know that understanding is more important. My parents think that grades are more important! (laughter). I think that a grade that a teacher gives you is based on the test rather than-, because they don't know exactly that you understand it more. Some people are lousy in taking a test, but they may be able to explain everything to somebody who may have messed up.

4.2.4 Case Study Theme: Concrete and Precise and Communicating About It

Professor Green saw and acknowledged that students wanted examples but urged them to learn about generalizations. For instance, after demonstrating examples on the board for finding the derivative of \(f\left(x\right)= {x}^{n}\) for the first few positive integers n, Green gave the generalized derivation of the power rule. He noted that the same answers could be found by using the new rule that he had worked through and told the class they were “seeing the power of generalization.” Meanwhile, interviews with the five students indicated their preference for concrete, numeric, real-world examples “that you could use later,”

Charles: I think I prefer a teacher that does more explaining on the assignment …does the homework [on the board].

Barbara: I like the material laid out, this is how you do it, and then explain it through problems, kind of in between, just because, then you can know why you are doing certain things to the problem. Because when they are showing you the concept, they explain to you why you are doing it, then when you're doing the problems, they are showing you how to do it.

Interviewees noted that it was important to have a chance to watch someone step through a problem and see/hear about the related sense-making and thinking of their (the problem-solver’s) success. The witnessing of success came when the instructor or other students worked examples on the board, narrating the solution pathway and noting, sometimes, potential pitfalls. Students said such witnessing was important so they could talk through working problems themselves. This emerged in interviews when students spoke of the value of learning to tell the story of solving as a part of understanding:

Alan: I learn a lot more through speaking than I do reading the book… so people who just ’say read the book and do the problems,' I don't learn nearly as well when people say that.

Charles: Learning well is being able to do the problems and actually understanding how they work, why they work.

Emily reported that sometimes the person she worked with in figuring things out was herself:

Emily: If I have one little problem, if I really understand, I find myself asking questions too… like you might ask, what if? What if it's this way. You know, like if it was minus sin x [ –sin x] rather than sin minus x [ sin –x ]… I'm trying to learn more, to understand. … I think that maybe if the instructor learns to, like take the time to help students see what things to focus on, they're trying to get the students to understand more.

4.2.5 Case Study Theme: Being Challenged

In the class observed, each week Professor Green told the class more than once that it was a challenging course both in terms of content and pace, encouraging them to see it as worthwhile. For example, he said in week 3 “look at it as challenges rather than obstacles…. Just like an arithmetic puzzle. Change a calculus problem from a threat to a puzzle. It's a nice feeling when you get there.” Professor Green tried to persuade the class to “buy into” the importance of understanding generalization (“it pays dividends”), reinforcing a coping intention related to grades while also supporting a learning intention of “understanding.”

Across class meetings, Professor Green mentioned some of the challenges students might have in studying calculus and provided recommendations to students for metrics they might use to determine whether they were doing what was needed to be successful by meeting those challenges. For example, he pointed to spending time on homework and reading the text as important and urged students to visit his office to work with him. For instance, in the second week of class he said:

Prof. Green: You need intelligence and hard work… You need a minimum of two hours every day for calculus, otherwise your chances of success are minimum even if you are a good student.

What is more, for students it was valuable to stumble through how to see it, say it, do it – important to have someone else to do that with or a habit of doing it with oneself, and to develop skill at prioritizing (“see what things to focus on”). The five case students said they learned by communicating. As indicated in earlier quotes, students who were interviewed felt that when they learned well, they asked and answered questions with others or internally. Emily said that when she studied “with somebody, even answering other people's questions, I tend to understand more.”

4.2.6 Case Study Theme: Responsibility

During class, Professor Green frequently said things to students to highlight what he felt was valuable like “it is important…” “for your own good…” “you need to see things in a certain way…” Green held an enculturative perspective—the goal of calculus instruction was to make students familiar with and seek to become functioning members of a community that valued fluency in the language, careful reasoning, and solving of mathematical problems. Green saw himself as guiding students through the course material with lectures and worksheet problem days; he expected students to learn independently through reading the textbook.

Observation of the classes indicated a shift in Green's teaching practices about halfway through the term. Green spent more class time on lecture that presented concepts in the first half of the term and more time on demonstrating how to solve problems in the second half of the term (at the board and when visiting groups of students as they worked on problems).

The observed and interviewed students echoed the common student view from the survey—that it was a student's responsibility to learn. At times a contrary perception of student intention from Professor Green was evidenced in class (e.g., he thought some students were not taking responsibility for learning, basing this conclusion on the evidence that they did not do well on quiz problems that were from the homework assignments).

Interviewee Alan had to miss class for sporting events because he was on a college team. He expected to be completely lost each time he returned. In discussing his progress in the seventh week of the course, Alan said “I think that’s mostly my fault at this point. Just because, I just haven't had time to do it, most of it.”

4.2.7 Case Study Theme: Prerequisites Plus

Students in the case study class had completed a course that appeared to be the necessary preparation for Calculus I: Pre-calculus. However, many in the case study calculus class did not do well on early quizzes and the first test. This would seem to confirm their survey responses: Though they had passed the prerequisite course, students did not express certainty that this was enough to do well in the subsequent course (#1, #9). As Deborah put it, learning well meant “having knowledge without going back to the book for help.” Barbara indicated that in the past she had not had to do much homework on her own. She succeeded (got passing grades) by practicing one concept and doing one or two problems. Charles said that his experience had been that the book had prescribed directions and that the teacher followed the book. Emily thought that algebra was “plug and chug” while calculus:

Emily: Is a completely different math that required a lot more information that needs to be learned in class…there is no knowledgeable person right there to ask questions when you are doing the homework at home. It went by a lot faster here. Every section went by just like that.

4.2.8 Case Study Theme: Mathematical Thinking

When asked about what might be intimidating to students in learning calculus, Professor Green said nothing would be intimidating if instruction relied on “interacting rather than lecturing at them” and it was important to “Listen to them in office hours and talk.” Professor Green continued, “it would be inexcusable [for an instructor] to walk into a class with a lack of preparation, be forced to think…think on your feet as you are teaching.” Green said it was essential to prepare and rely on the most “useful teaching tools: these are simply asking students, asking questions, telling how this applies.” However, said Green, for some students, the intimidation could not be completely eliminated.

Professor Green made efforts to elicit self-reliance and self-regulation. One example came in a cautionary lesson about relying too much on the calculator. In week 1 he had students use their graphing calculators to examine the limit as x approaches 0 of \(sin\left(\frac{\pi }{x}\right)\) [the course requirements included using a graphing calculator]. In class, he told students that learning was “worth the pain” and when students expressed a concern that some of the problems assigned did not have answers in the back of the book, he adjusted an assignment (Class #22), saying “That's a reasonable concern.”

In interviews, students responded that “mathematical thinking” meant:

Alan: Think more logically about everything. Everything happens for a reason.

Barbara: Math is like another language, numbers, equations.

Charles: It's about quantifying stuff.

Deborah: You go through a certain process? Different process for different problems…? Really, I have no idea.

Emily: Math is practically in every subject.

Generally, interviewed students saw “mathematical thinking” as not particularly connected to “how a mathematician thinks” and were not intimidated by either. At the same time, the mathematics itself, what was on a page as a mathematics problem, that could be intimidating:

Barbara: Yes, I think it does [intimidate me], because of all the memorizations, using that language that there is in math. You have to understand it before you can actually do the process to get the answers. There are two things, first there is memorization because you have to know the equations and you have to know laws and theorems to be able to solve the equations, then you have to know how to handle the theorems and laws in turn to get an answer.

Emily: I don't think the thinking intimidates me, but the math is pretty intimidating. ... If I just look at a math question in a calculus book, …I would be completely intimidated. I wouldn't have any idea of what's going on. But if you learned the material, like in a section, then everything works out, not everything, but you understand what the question is about… Like if I look at a problem, I have no knowledge of what it's asking …I would not know where to start, that would be intimidating.

Professor Green's response when asked, “What is mathematical thinking?” reflected the two parts Barbara mentioned (remembering rules and knowing how to handle them). He said: “a big part is understanding the techniques and definitions and so on. It's like playing chess, each game is different.” He felt learners needed to see specific things as tools and “apply different strategies to solve different things…you have to stop and think about it.”

5 Connections

Table 4 summarizes the relationships among the themes and survey items that emerged from interviews with students and instructor in the case class. As indicated in Table 3, interviewed students differed from the class average (and may or may not have aligned with the national sample) in their responses to five survey items (#4, #5, #6, #7, #13). Separate thematic coding of interviews grouped responses to these five survey items as a distinct component in student statements about “being challenged.” In this cross-factor theme, the importance of interaction with other people and relationships with mathematical ideas was most pronounced.

Table 4 Case study themes and associated survey items
Full size table

6 Discussion

As noted previously, in educational research the basis of a compelling argument is empirical evidence of the nature of human experience. For this research report, the evidence was quantitative (from survey analysis) and qualitative (from interviews and observations). The aim was to address the research questions about calculus student and instructor perceptions of what was seen as supportive of success in calculus, with a focus in the case study on reports by students not in the upper grades quartile. Seven themes of student perception and associated intentions (coping and learning), summarized in Table 4 and illustrated in the subsections of 4.2.1 through 4.2.7, exemplify student perceptions. Also, survey analysis provided the juxtapositions of average student and instructor responses, both in comparing the case class to the national sample and, digging down, in comparing the interviewees—who struggled with calculus—to their more traditionally “successful” classmates. Across the research questions, the main result is that students experienced aspects of both learning and coping as essential for success. The cross-factor theme of communication about ideas (with self and others) when being challenged was particularly important for interviewed students.

Depending on goals and intentions, people in a classroom make many choices in regulating their actions. At base, each decision is a balance of preserving well-being by devoting attention to coping with challenges or has the (possibly competing) aim of learning that embraces challenges. In a calculus class, some aspects of the environment—including local classroom norms and policies—may act as calls for compliance, while others are seen by students as opportunities to learn.

This study contributes to the mathematics education literature in two ways. First, the survey and case study allowed us to share the views of calculus students and faculty—giving them voice. In addition, the interviews allowed for examination of how these views were seen by five students and one instructor in calculus. Second, implicit and rather nebulous in the academic mathematics culture is the notion that the onus for making sense is on the student [46]. Certainly, the calculus faculty and students shared agreement that students have a responsibility to learn, but what was not shared was what supports for that learning were “reasonable” (as Professor Green would put it) to expect from the class context, content, teacher, and student. In part, Table 4 offers a listing of what came out of this study as appearing to be reasonable to the interviewed case class students.

6.1 Applications to and Implications for Practice

It is worth noting that for the vast majority of calculus students in both the national sample and in the case class, perceptions were based in experience of mathematics teaching that were limited to (at most) seven different mathematics instructors (four in high school and up to three in college). Instructors, on the other hand, had experience with hundreds of students across many classes.

Instructional change happens in the context of university and societal environments where many of the components, constraints, and conditions can be understood and manipulated [4]. Following calculus reform efforts in the 1990s, instructors have taken on the challenge of broadening and deepening student thinking, sometimes at the instructor’s own risk [47]. While the recent spread of inquiry- and activity-based approaches is promising, attention to how these are perceived by students and the ways instructional implementations support coping and/or learning intentions are an active area of current research in post-secondary education, including mathematics, science, and medical education (e.g., [48,49,50,51]).

Given that student engagement when being challenged emerged as important, what is the instructor’s role in that? What affect, motivation, self-regulation, and behaviors on the part of the instructor are influencing intentions (e.g., coping and learning) about instructional decision-making? Professor Green reported he was coping with what seemed to be pressure on him from students to be a performer of mathematics rather than to fulfill the role he saw for himself as a guide through mathematics as a coherent body of knowledge. Green perceived a high-stakes and low agency situation in his classroom because some of his students were not doing well on his tests, yet he and the other faculty members teaching calculus agreed the tests were an appropriate measure of his success as a teacher. As an example, one practical use of this work might be a four-step reflective process along the lines of recommendations in the MAA Instructional Practices Guide (IPG, [52]):

Step 1: Review the student survey items and make predictions about what local student response average values would be for each item.

Step 2: Have students complete the survey (anonymously).

Step 3: Compare predictions from Step 1 to results from Step 2 and examine any gaps larger than 1 (e.g., the gap of 2 on #15, the first item in Table 6).

Step 4: Identify ways that supporting students to cope with the course may be possible while also opening opportunities to learn. For instance, an instructor might have pairs of students generate review sheets for a test and share them, then structure a class discussion so students deliberate about what are the essential ideas to capture about the material since the last test.

Many valuable and practical ideas are discussed in the IPG and its companion book study guide for faculty. And, for considerations of the interplay among individuals, departmental cultures, and instructional change efforts, the Levers for Change report provides insights and research-based suggestions for instructional success across the variety of first-year courses, calculus included [53].

In his interview, Professor Green said he felt he knew what student perceptions were, and was not surprised by any of the student reactions. He also said, and it was visible in the classroom, that he sometimes communicated his anticipations in class to students and encouraged students to change their perceptions (e.g., the example of talking in class about students wanting examples but urging them to learn about generalizations). What he ended up doing would often be a split-second decision. He knew that when he responded to one group's needs he might make another group unhappy. Those decisions depended on his own instructional self-regulation and were informed by the norms in the department and whether he felt he could count on support from his colleagues.

This and related studies are valuable for increasing awareness and examination of assumptions we (as instructors) make regarding student perception. Recall that the interviewed students differed in their perceptions from the anticipated-by-Green perceptions of their peers (Table 3). One group in the case class (the interviewed struggling students) reported favoring teacher-led, directive, instruction over independently tackling intellectual challenges – in line with what Green anticipated. However, on average, the majority of students in Green’s class tended to view both guidance and independence, intellectual directives and intellectual challenges, with favor. That is, Professor Green anticipated and responded to the views of a particular subgroup of students, without also anticipating and responding to the perceptions of others. The implication for instructional practice is the value of considering multiple solution paths to an instructional problem. People with advanced mathematical training already have expertise in looking at a problem in multiple ways, starting by solving a simpler problem, and attending to goals while experimenting with potential routes to those goals. It may be worthwhile, particularly in the preparation of new college teachers/graduate students, to support the application of those methods to the problems of teaching [54, 55].

6.2 Future Research on Mathematics Teaching and Learning in Post-Secondary Settings

The five students in the case classroom who were interviewed—Alan, Barbara, Charles, Deborah, and Emily—are examples of the group Middleton et al. [56] identified as students whose interest (as a motivational factor) is based on fulfilling some other interest, such as requirements for their degree programs. Passing the calculus class was a stepping stone to some longer-term outcome, not of primarily intrinsic interest. The current national studies of calculus and persistence toward distant goals have done a broad quantitative sampling of course-taking patterns for “switchers” and “stayers” [54, 57]. Continuing research on success in college mathematics must also open the door for non-examples (i.e., where “success” does not happen or has a definition for students different from status quo expectations [15]).

Struggle and failure are important components of success but have been under-researched. For university calculus, for example, the results emerging from the national Progress Through Calculus study (available at http://www.maa.org/cspcc) suggest that what students experience in the calculus classroom makes a difference in the learning opportunities they have and decisions they make about proximal goals for courses to take and distal goals such as degree to pursue [58]. Post-secondary as well as secondary education research has documented that many students learn more deeply with higher frequencies of particular instructional practices: students working together on group-worthy tasks, students giving in-class presentations, and learners engaging in whole-class and group discussions where explanation and justification are required (e.g., see [59]). That is, research has demonstrated that what the case interviewees identified as supports for success when being challenged can, in fact, work. What is more, researchers have identified key structural components of successful calculus programs [57]. These include ways to support productive instructor intentions – from course coordination policies and scaffolds about teaching for novice instructors, to aspects of department culture such as encouraging experimentation with student-active classroom strategies.

The well-entrenched view that instructors are the active regulators of learning in mathematics and that the student’s job is to listen, compute, and get the right answer, fast, have been reported on and challenged for years in the United States [e.g., 3, 34, 50, 60]. However, how the teacher is “active” and student is “passive” view develops, persists, and may be regularly renegotiated has remained relatively unexplored in post-secondary mathematics contexts. We note here that depending on the school environment, the personal experiences of students, and what is valued in and from mathematical learning, a “student-active” classroom may or may not involve students speaking for the majority of class time [61].

The nature of awareness of goals and how students and instructors prioritize and balance goals while doing all this coping and learning, particularly at the university level, is a nascent area of research. For students in the U.S. the influences of external factors on isolated goals like encouragement by another person or social pressure (e.g., among students, between student and instructor, between an instructor and colleagues) may fade after a few weeks unless a person’s goal intentions are rooted in personal interests, perceived needs, or relationships [7, 19, 54, 62].

The qualitative work reported here has identified some particular student experience and perception to add to future research. For effective communication between instructor and student it is important that a shared lexicon for translation exists, otherwise “teaching is likely to remain a hit-or-miss affair” [63, p. 11]. Building on work about what students prefer [43, 64, 65], both the small study reported here and future work are needed to better understand the role of perceptions and intentions in the complex dynamics of cognition, affect, motivation, and regulation that support learning in post-secondary mathematics.

7 Researcher Perspectives

This background for the researchers is offered to allow the reader a glimpse of the orientations and experiences of the authors that might implicitly bias the research. For example, one author acknowledges the affinity she feels with math-avoiding and math-indifferent undergraduate students. On the other hand, both authors' backgrounds and experiences were distinct in many ways from those of the majority of the students in the research reported here – most student participants in this work were reared in majority culture, middle-class, suburban surroundings in the U.S. The authors were not.

The second author, Hsu, grew up outside the United States where, at that time, the language of instruction in her secondary school course of study was English (except for Chinese literature and history). She then came to the U.S., first completing a bachelor's degree in mathematics at a liberal arts women's college and then a master's at a major university. After teaching mathematics at women's colleges for three years, Hsu completed a PhD in mathematics at her master's institution. Hsu has held different tenure-track and contingent (contract) faculty positions and has 30 years of experience in teaching college mathematics at a variety of institutions (liberal arts, comprehensive universities, and a technical institute), with occasional research in mathematics. Though the challenges faced by a female, foreign-born, PhD responsible for teaching a classroom of predominantly white, sometimes mostly male U.S. students are beyond the scope of this report, Hsu acknowledges them and has deep interest in the teaching and learning of mathematics. In the earlier part of her teaching career, for more than 10 years, she participated annually in week-long short courses on mathematics curriculum and teaching. Then she turned to research in mathematics education. Hsu's own calculus learning was in a class of fewer than 10 students. Similar to Professor Green, Hsu's perspective on calculus instruction is that it is her job to guide students through a story in mathematics and to enculturate students to form mathematical habits of mind that are valued by mathematicians as students build understanding and competence in doing mathematics.

The first author, Hauk, is from an upbringing in the United States steeped in socio-cultural and ethnic diversity. Hauk completed a bachelor's degree in the arts, then did a teacher training program and became a certificated secondary school teacher of English and mathematics. After a few years, Hauk left K-12 teaching to do a PhD in mathematics and then a post-doctoral fellowship in mathematics education. As a faculty member in a university mathematics department over the last 15 years, Hauk has advised students completing PhDs in undergraduate mathematics education. Hauk's mathematical autobiography is filled with stories of great sadness, joy, pain, and loneliness in relation to mathematics: from the first grade where punishment for talking too much in class was to be slapped and ordered to teach Ruben how to add, to being the only woman in a sea of men at her doctoral graduation ceremony, to winning awards for teaching university mathematics. Hauk took differential calculus for the first time as a summer course in her third year as a licensed high school teacher. Her perspective on calculus instruction is responsive. A responsive university instructor actively models actions and approaches to engaging with mathematics that are culturally aware as well as socially and ethically informed. Instruction is the act of supporting students in critique, conversation, planning, and implementation of ideas. Calculus instruction is a collective practice of teacher and students engaging with and shaping the world through knowledge of mathematics and other content. This view is associated with the theory of critical pedagogy [45].