Thermal protection of a vertical plate using ethylene glycol film cooling flowing down on a vertical plate

Abstract

This paper concerns a numerical investigation of the evaporative cooling of liquid film falling along a vertical channel. The first plate is insulated and wetted by an ethylene glycol liquid film while the second one (y = d) is dry and isothermal. A marching procedure is employed for solution of the equation of mass momentum, energy and concentration in the flow. Numerical results for air-ethylene glycol system are presented. The effects of ambient gas temperature and inlet vapor mass fraction of ethylene glycol on the heat and mass transfer and on the ethylene glycol liquid film evaporation are investigated.

1 Introduction

The liquid film evaporation is found in many industrial applications such as evaporator, condensing devices, air-conditioning, refrigeration technology, absorber/generator heat exchange, nuclear technology and separation processes, heat pumps and drying technology. Cherif et al. [1] presented an experimental study of mixed convection heat and mass transfer in a vertical channel with film evaporation. The experimental results show that evaporation takes place on the majority of the surface of the two walls and, in some cases, evaporative cooling occurs especially for small heating flux and large air velocities. Ben Jabrallah et al. [2] studied numerically and experimentally the convective heat and mass transfer with the evaporation of a falling film in a cavity. They showed that the obtained results allow us to describe the thermodynamic state of the heated film by means of the liquid temperature and evaporation flow rate. Gorjaei et al. [3] presented an analysis of the effect of introduction of Al2O3 nanoparticles in the heat transfer inside a three-dimensional annulus. The convective heat transfer coefficient of the nanofluid can be improved with a lower volume concentration of CuO nanoparticles, as showed by Lazarus et al. [4]. The effects of nanoparticles dispersion on droplet evaporation were presented by Chen et al. [5]. They demonstrated an enhancement of droplet evaporation with nanoparticles adding. A study on heat transfer caused by free convection of nanofluid flowing on a vertical plate has been effected by Siddiqa et al. [6]. They demonstrated that the heat exchange was improved by the nanoparticles' dispersion. The free convective heat transfer within a porous wavy cavity with a nanofluid was numerically examined by Sheremet et al. [7]. They demonstrated that the local heat source affected the nanofluid flow and the heat transfer. Water droplets evaporation containing a low concentration of nanoparticles were examined by Askounis et al. [8]. They showed that the rate of droplet evaporation is unaffected by the dispersion of low concentration nanoparticles. Perrin et al. [9] presented a comparison between the theoretical and experimental results of nanofluid liquid drop evaporation. A numerical study by mixed convection of the falling liquid film evaporation was presented by Yan [10]. Experimental analysis of the liquid film evaporation was conducted by Huang et al. [11]. They showed that an increase in the temperature and air flow rate accelerated evaporation. Wei et al. [12] simulated the flow and heat transfer of CuO-water nanofluid in a tube using the single- and two-phase (mixture) models. Nasr and Alzahrani [13] presented a numerical study of liquid nanofilms’ evaporation inside a heat exchanger by mixed convection. Nasr et al. [14] studied the evaporation of binary liquid film by mixed convection inside heated vertical channel. Nasr and AL-Ghamdi [15] studied the liquid nanofilms’ condensation inside a heat exchanger by mixed convection. Nazir et al. [16] presented a thermal and mass species transportation in tri-hybridized Sisko martial with heat source over vertical heated cylinder. Nazir et al. [17] presented a significant Production of Thermal Energy in Partially Ionized Hyperbolic Tangent Material Based on Ternary Hybrid Nanomaterials. They showed that the thermal energy expression is derived by the contribution of Joule heat and viscous dissipation. They presented a model of flow equations by using the concept of boundary layer theory, which occurs in the form of a coupled system of partial differential equations (PDEs). Muhammad Sohail et al. [18] presented a finite element analysis for ternary hybrid nanoparticles on thermal enhancement in pseudo-plastic liquid through porous stretching sheet. Muhammad Sohail et al. [19] presented a study of triple-mass diffusion species and energy transfer in Carreau–Yasuda material influenced by activation energy and heat source. Nazir et al. [20] presented finite element analysis for thermal enhancement in power law hybrid nanofluid.

As regards the prior research, the numerical study of ethylene glycol liquid film evaporation is no considered. The main purpose of the present work is to analyze the effect of ambient gas temperature and inlet vapor mass fraction of ethylene glycol on the heat and mass transfer and on the ethylene glycol film evaporation.

2 Analysis

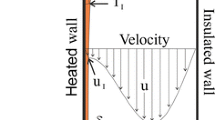
The present work deals with a numerical analysis of evaporation of pure liquid film by mixed convection flowing along one of the channel vertical plates (Fig. 1). The studied channel is made up of two vertical and parallel plates. The first plate is subjected to a uniform heat flux q₁ and wetted by a pure ethylene glycol liquid film while the second one (y = d) is dry and isothermal. The pure liquid film flowing down with an inlet temperature T_0L and an inlet mass flow rate m_L0.The air enters the channel with a temperature T₀, a water and ethylene–glycol vapour concentrations c₀₁ and c₀₂ and velocity u₀.

Fig. 1

Physical model

3 Governing equations

3.1 For The liquid phase

The Continuity equation, x-momentum equation, Energy equation, diffusion equation are respectively:

Continuity equation

$$\frac{{\partial \rho_{L}^{{}} u_{L}^{{}} }}{\partial \xi } - \frac{{\eta_{L} }}{{\delta^{{}} }}\frac{{\partial \delta^{{}} }}{\partial \xi }\frac{{\partial \rho_{L}^{{}} u_{L} }}{{\partial \eta_{L} }} + \frac{H}{{\delta^{{}} }}\frac{{\partial \rho_{L}^{{}} v_{L} }}{{\partial \eta_{L} }} = 0$$

x-momentum equation

$$\begin{gathered} u_{L}^{{}} \frac{{\partial u_{L}^{{}} }}{\partial \xi } + \left( {v_{L} \frac{H}{{\delta^{{}} }} - u_{L}^{{}} \frac{{\eta_{L} }}{{\delta^{{}} }}\frac{\partial \delta }{{\partial \xi }}} \right)\frac{{\partial u_{L}^{{}} }}{{\partial \eta_{L} }} = - \frac{1}{{\rho_{L} }}\frac{dP}{{d\xi }} - \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{H}{{\rho_{L}^{{}} \delta^{2} }}\frac{\partial }{{\partial \eta_{L} }}\left[ {\mu_{L}^{{}} \frac{{\partial u_{L}^{{}} }}{{\partial \eta_{L} }}} \right] + gH \hfill \\ \end{gathered}$$

Energy equation

$$u_{L} \frac{{\partial T_{L} }}{\partial \xi } + \left( {u_{L} \frac{\eta - 1}{\delta }\frac{\partial \delta }{{\partial \xi }} + \frac{H}{\delta }v_{L} } \right)\frac{{\partial T_{L} }}{\partial \eta } = \frac{1}{{\rho_{L} C_{pL}^{{}} }}\frac{H}{{\left( \delta \right)^{2} }}\frac{\partial }{\partial \eta }\left( {\lambda_{L} \frac{{\partial T_{L} }}{\partial \eta }} \right)$$

Overall mass equation

$$\int\limits_{0}^{1} {\delta \rho_{L}^{{}} u_{L}^{{}} d\eta_{L} } = \left[ {\mathop m\limits^{{}}_{0L} - H\int\limits_{0}^{\xi } {\rho v(\xi ,\eta = 0)d\xi } } \right]$$

3.2 For the gaseous phase

Continuity equation

$$\frac{\partial \rho u}{{\partial \xi }} + \frac{\eta - 1}{{d - \delta }}\frac{\partial \delta }{{\partial \xi }}\frac{\partial \rho u}{{\partial \eta }} + \frac{H}{d - \delta }\frac{\partial \rho v}{{\partial \eta }} = 0$$

x-momentum equation

$$\begin{gathered} u\frac{\partial u}{{\partial \xi }} + \left( {\frac{\eta - 1}{{d - \delta }}\frac{\partial \delta }{{\partial \xi }}u + \frac{H}{d - \delta }v} \right)\frac{\partial u}{{\partial \eta }} = - \frac{1}{\rho }\frac{dP}{{d\xi }} - g\beta H(T - T_{0} ) - g\beta^{*} H\sum\limits_{i = 1}^{2} {(c_{i} - c_{0} )} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{\rho }\frac{H}{{\left( {d - \delta } \right)^{2} }}\frac{\partial }{\partial \eta }\left( {\mu \frac{\partial u}{{\partial \eta }}} \right)\, \hfill \\ \end{gathered}$$

Energy equation

$$\begin{gathered} u\frac{\partial T}{{\partial \xi }} + \left( {u\frac{\eta - 1}{{d - \delta }}\frac{\partial \delta }{{\partial \xi }} + \frac{H}{d - \delta }v} \right)\frac{\partial T}{{\partial \eta }} = \frac{1}{{\rho C_{p}^{{}} }}\left\{ {\frac{H}{{\left( {d - \delta } \right)^{2} }}\frac{\partial }{\partial \eta }\left( {\lambda \frac{\partial T}{{\partial \eta }}} \right)} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left. {\rho \sum\limits_{i = 1}^{2} {\left( {D_{g,im} C_{pi}^{{}} - D_{g,am} C_{pa}^{{}} } \right)\frac{H}{{(d - \delta )^{2} }}\frac{\partial T}{{\partial \eta }}\frac{{\partial c_{i} }}{\partial \eta }} } \right\} \hfill \\ \end{gathered}$$

Species equation

$$u\frac{{\partial c_{i} }}{\partial \xi } + \left( {u\frac{\eta - 1}{{d - \delta }}\frac{\partial \delta }{{\partial \xi }} + \frac{H}{d - \delta }v} \right)\frac{{\partial c_{i} }}{\partial \eta } = \frac{1}{\rho }\frac{H}{{\left( {d - \delta } \right)^{2} }}\frac{\partial }{\partial \eta }\left( {\rho D_{g,im} \frac{{\partial c_{i} }}{\partial \eta }} \right);\,\,\,\,\,\,\,i = 1,2,3$$

Overall mass equation

$$\int\limits_{0}^{1} {\rho (d - \delta )u(\xi ,\eta )d\eta } = \left[ {(d - \delta_{0} )\rho_{0} u_{0} + H\int\limits_{0}^{\xi } {\rho v(\xi ,\eta = 0)d\xi } } \right].$$

3.3 Boundary conditions

*For ξ = 0 (inlet conditions):

T (0, η) = T₀; ci(0, η) = c_0i; u(0, η) = u₀; P = P₀.

T_L(0, η_L) = T_{0L;δ(0) = δ0;} $\int\limits_{0}^{1} {\rho_{0L} \delta_{0} u_{L} (0,\eta_{L} )d\eta_{L} } = m_{0L}$.

*At η = 1(dry plate):

$$u(\xi ,1) \, = \, 0 ; \, v \, (\xi ,1) \, = \, 0 ; \, T \, (\xi ,1) = \, T_{w } ; \left( {\frac{{\partial c_{i} }}{\partial \eta }} \right)_{\eta = 1} = 0$$

*At η_L = 0 (wet plate):

$$u_{L} (\xi ,0) = 0;v_{L} (\xi ,0) = 0;0 = - \lambda_{L} \frac{1}{\delta }\left. {\frac{{\partial T_{L} }}{{\partial \eta_{L} }}} \right)_{{\eta_{L} = 0}}$$

*At $\eta = 0$( η_L = 1) (liquid–gas interface):

The continuities of the velocities and temperatures give:

$$u_{L} \left( {\xi ,\eta_{L} = 1} \right) = u\left( {\xi ,\eta = 0} \right);\ T_{L} (x,h_{L} = 1) \, = \, T_{{}} (x,h = 0)$$

The heat balance at the interface implies

$$- \frac{1}{\delta }\lambda_{L} \left. {\frac{{\partial T_{L} }}{{\partial \eta_{L} }}} \right)_{{\eta_{L} = 1}} = - \frac{1}{d - \delta }\lambda \left. {\frac{\partial T}{{\partial \eta }}} \right)_{\eta = 0} - \dot{m}L_{v}$$

with

$$\dot{m} = - \frac{{\rho \sum\nolimits_{i = 1}^{2} {D_{g,im} \left. {\frac{{\partial c_{i} }}{\partial \eta }} \right)_{\eta = 0} } }}{{\left( {d - \delta } \right)\left( {1 - \sum\nolimits_{i = 1}^{2} {c_{i} \left( {\xi ,\eta = 0} \right)} } \right)}}$$

$$\,\,c_{1} \left( {\xi ,0} \right) = \frac{{p^{*}_{vs,1} }}{{p^{*}_{vs,1} + \left[ {p^{*}_{vs,2} \,\,\frac{{M_{2} }}{{M_{1} }}} \right] + \left[ {p - p^{*}_{vs,1} - p^{*}_{vs,2} \,} \right]\frac{{M_{a} }}{{M_{1} }}}};c_{2} \left( {\xi ,0} \right) = \frac{{p^{*}_{vs,2} }}{{p^{*}_{vs,2} + \left[ {p^{*}_{vs,1} \,\,\frac{{M_{1} }}{{M_{2} }}} \right] + \left[ {p - p^{*}_{vs,1} - p^{*}_{vs,2} } \right]\frac{{M_{a} }}{{M_{2} }}}}$$

The continuities of shear stress and local evaporated mass flux of species i give:

$$\frac{1}{\delta }\mu_{L} \left. {\frac{{\partial u_{L} }}{{\partial \eta_{L} }}} \right)_{{\eta_{L} = 1}} = \frac{1}{d - \delta }\mu \left. {\frac{\partial u}{{\partial \eta }}} \right)_{\eta = 0}$$

The latent heat flux of mixture is given by:$q_{l} = q_{l1} + q_{l2} = \dot{m}L_{v} = - \frac{{\rho L_{v} \,\sum\nolimits_{i = 1}^{2} {D_{g,im} \left. {\frac{{\partial c_{i} }}{\partial \eta }} \right)_{\eta = 0} } }}{{\left( {d - \delta } \right)\left( {1 - \sum\nolimits_{i = 1}^{2} {c_{i} \left( {\xi ,\eta = 0} \right)} } \right)}}$.

The sensible heat flux is given by:

$$q_{s} = - \lambda \frac{1}{d - \delta }\left. {\frac{\partial T}{{\partial \eta }}} \right)_{\eta = 0} .$$

The total cumulated evaporation rate of mixture at the interface is given by:

$$Mr = \int\limits_{0}^{\xi } {\dot{m}} (\xi )d\xi = Mr_{1} + Mr_{2} .$$

4 Results and discussions

All the results of this study have been obtained for the case of c₀₂ = 0, T₀ = 293.15 K, T_0L = 293.15 K,T_w = 293.15 K,m_0L = 0.015 kg/m.s,u₀ = 1 m/,the geometrical ratio is d/H = 0.015 and the imposed wall heat flux is q₁ = 0W/m².

Figure 2 illustrates the effect of the inlet temperature of the gas on the interfacial temperature. It is clear from this figure that a decrease of the inlet temperature of the gas induces a slightly increase of the interfacial temperature.

Fig. 2

The evolution of the interfacial temperature with different values of the inlet gas temperature: C₀₁ = C₀₂ = 0, T_w = 25 °C, T₀ = 25 °C, m_0L = 0.015 kg/m.s, u₀ = 1 m/s, q1 = 0

The evolution of the sensible heat flux of mixture along the channel for several values of inlet temperature of the gas is illustrated in Fig. 3a. This figure shows that the sensible heat flux exchange increases with the inlet temperature of the gas. This result has been explained by the fact that the interfacial temperature increase with the inlet temperature and consequently the sensible heat flux exchange increases. It is observed from Fig. 3b that the latent heat flux exchange increases with the inlet temperature of the gas. Apparently, the values of the latent heat flux are all positive, and this indicates that the direction of the latent heat flux is from the interface to the hot gas stream. It is noted that the latent heat flux increases in the flow direction.

Fig. 3

The evolution of the sensible and latent heat flux of water and ethylene glycol along the channel with different values of the inlet gas temperature: c₀₁ = c₀₂ = 0, T_w = 25 °C, T_0L = 25 °C, m_0L = 0.015 kg/m.s, u₀ = 1 m/s, q1 = 0

It is apparent that from Fig. 4 that the local mass evaporation rate increases with the inlet temperature of the gas. The axial distributions of non-dimensional accumulated mass evaporation rate are shown in Fig. 5. It is clear that an increase in T₀ causes a larger Mr. This can be explained by the fact that when we increase the inlet temperature of the gas, the latent heat flux is from the interface increases and consequently the accumulated mass evaporation rate increases. Figure 6 shows that an increase in the inlet gas mass fraction of ethylene glycol induces an increase of the temperature at the interface liquid–gas. It is shown from Fig. 7 that an increase in the inlet gas mass fraction of ethylene glycol inhibits the ethylene glycol evaporation causing an increase in the temperature at the interface liquid–gas. This result has been confirmed in the Fig. 6.

Fig. 4

The evolution of the local evaporation rate of ethylene glycol along the channel with different values of the inlet gas temperature: c₀₁ = c₀₂ = 0, T_w = 25 °C, T_0L = 25 °C, m_0L = 0.015 kg/m.s, u₀ = 1 m/s, q1 = 0.

Fig. 5

The evolution of the total cumalated evaporation rate of ethylene glycol with different values of the inlet gas temperature: c₀₁ = c₀₂ = 0, T_w = 25 °C, T_0L = 25 °C, m_0L = 0.015 kg/m.s, u₀ = 1 m/s, q1 = 0

Fig. 6

The evolution of the temperature at the interface for different values of the inlet vapor ethylene glycol mass fraction of the gas: c₀₁ = c₀₂ = 0, T_w = 25 °C, T_0L = 25 °C, T₀ = 25 °C, m_0L = 0.015 kg/m.s, u₀ = 1 m/s, q1 = 0

Fig. 7

The evolution of the total cumulated evaporation rate of ethylene glycol for different values of inlet vapor mass fraction of ethylene glycol: c₀₁ = c₀₂ = 0, T_w = 25 °C, T_0L = 25 °C, T₀ = 25 °C, m_0L = 0.015 kg/m.s, u₀ = 1 m/s, q1 = 0

5 Conclusions

We presented a numerical study of evaporation of ethylene glycol liquid film by mixed convection flowing along one of the channel vertical plates (Fig. 1). The studied channel is made up of two vertical and parallel plates. The first plate is insulated and wetted by a pure liquid film (ethylene glycol) while the second one (y = d) is dry and isothermal. The liquid film flowing down with an inlet temperature T_0L and an inlet mass flow rate m_L0.The air enters the channel with a temperature T₀, a water and ethylene–glycol vapour concentrations c₀ and velocity u₀. It is shown that an augmentation in the gas temperature induces an increase in the temperature and ethylene glycol mass fraction at the interface and a decrease in the latent and sensible heat fluxes. The increase in the inlet gas temperature enhances the ethylene glycol film evaporation.