1 Introduction

The generation of waves in the realm of thermoelasticity and nonlinear mechanics has recently attracted significant interest for its feeling of the naturalness of synergy between the thermal effect and the stress fields. Numerous authors and researchers have discussed their works and efforts in the nonlinear study of hyperbolic-parabolic differential equations based on the thermoelasticity hypothesis, concentrating their efforts on the issues that lead to the being, the singularity, and the immovability of the solutions to such issues [1].

In essence, it is simple to determine if the dejection restraint of heat is strong enough to provide false solutions, even for irregular beginning and boundary data, or is too soft to prevent discontinuities from occurring, or else in between. As a result, thinking about the nonlinear waves that can be imagined in solids became a significant point of continuity dynamics [1]. Mathematical models describing the nonlinear phenomenon were derived by Maugin [2] treated the propagation of the nonlinear mechanical waves in elastic crystals [3]. The nonlinear thermoelasticity offers abundant research for investigation the coupling status between the mechanical and thermal fields. The essential differential equations of thermoelasticity causes embarrassing the type of nonlinear biased special differential equations of mixed represent for that few true solutions exist. Numbers of contributions in this field are in [3,4,5,6,7,8,9,10,11,12,13,14].

The traditional theory of thermoelasticity depends on Fourier’s law of heat conduction. Because of the nature of the parabolic differential equation of the energy, infinite diffusion speeds for the heat disturbances are expected. Maxwell found out that the nature concept of the hyperbolic differential equation generates thermal disturbances with finite speeds, is known as the second sound phenomenon. Chester noted some justification to the second sound phenomenon that must exist in any solid material. Many of the methods and approaches that induced to overcome the rejected prediction of the classical model in the context of the general definition of relaxation time the heat flux in the classical Fourier’s heat conduction law, accordingly, introducing the non-Fourier heat conduction law [15, 16].

The novelty of this work is introducing a new theory of nonlinear generalized thermoelasticity for anisotropic thermoelastic homogeneous materials, to examine the temperature produced by the deviatory components of strain and the general formulation of the energy equation. An isotropic and homogeneous one-dimensional thermoelastic half-space will be solved using the governing equations of the computational model.

2 Nonlinear generalized thermoelasticity theory

The well-known energy equation for an isotropic thermoelastic material takes that form [15, 16]:

$$\rho \dot{\varepsilon } = \sigma_{ij} \dot{e}_{ij} - \,q_{i,i} ,$$
(1)

and

$$e_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right),$$
(2)

where \(e_{ij}\) gives the tensor components of a small strain where the products of the displacement gradients have been obsoleted,\(\rho\) is the density of the material,\(\varepsilon\) is the internal energy, \(\sigma_{ij}\) are the stress components tensors, \(q_{i}\) gives the heat flux vector, and \(u_{i,j}\) is the displacement gradient vector.

We consider the stress–strain relation in nonlinear form is more significant than in the strain–displacement relations as in the most theories of elasticity and it is also satisfied in thermoelasticity.

The Helmholtz’s equation (free energy equation) for unit mass as [15, 16]:

$$\phi = \varepsilon - TS,$$
(3)

where S defines the entropy and T is the absolute value of temperature.

The thermoelastic material has been assumed to be a function of the displacement gradient and the absolute temperature as [15, 16]:

$$\phi = \phi \left( {e_{ij} ,T} \right).$$
(4)

Hence, we have:

$$\rho \dot{\phi } = \rho \frac{\partial \phi }{{\partial e_{ij} }}\dot{e}_{ij} + \rho \frac{\partial \phi }{{\partial T}}\dot{T}.$$
(5)

From Eq. (3), we have:

$$\rho \dot{\phi } = \rho \dot{\varepsilon } - \rho T\dot{S} - \rho \dot{T}S.$$
(6)

Substitute from Eq. (1) into Eq. (6), we obtain:

$$\rho \dot{\phi } = \sigma_{ij} \dot{e}_{ij} - \rho S\dot{T} - \rho T\dot{S} - \,q_{i,i} .$$
(7)

From Eqs. (5) and (7), we get the following:

$$\sigma_{ij} = \rho \frac{\partial \phi }{{\partial e_{ij} }},$$
(8)
$$S = - \frac{\partial \phi }{{\partial T}},$$
(9)

and

$$\,q_{i,i} = - \rho T\dot{S} + Q,$$
(10)

where there is heat generated through the material at a rate of Q per unit time and unit volume.

From Eqs. (9) and (10), we can deduce the following equation:

$$\,q_{i,i} = T\left( {\rho \frac{{\partial^{2} \phi }}{{\partial T^{2} }}\dot{T} + \rho \frac{{\partial^{2} \phi }}{{\partial T\partial e_{ij} }}\dot{e}_{ij} } \right) + Q.$$
(11)

We can expand the free energy function in a power series in the strain components and the temperature increment as follows:

$$\rho \,\phi \left( {e_{ij} ,\theta } \right) = \frac{1}{2}c_{ijkl} e_{ij} e_{kl} - \gamma_{ij} e_{ij} \theta + \beta \,\theta^{2} + \frac{1}{2}a_{ijkl} e_{ij} e_{kl} \theta ,$$
(12)

where \(\theta = T - T_{0}\), defines the temperature increment and \(T_{0}\) is reference temperature (constant). \(c_{ijkl} ,\,\,\gamma_{ij} ,\,\,\beta \,\,and\,\,a_{ijkl}\) are some of the material parameters.

The free energy equation in (12) gives that

$$\rho \frac{\partial \,\phi }{{\partial \,T}} = \rho \frac{\partial \,\phi }{{\partial \,\theta }} = - \gamma_{ij} e_{ij} + 2\beta \theta + \frac{1}{2}a_{ijkl} e_{ij} e_{kl} ,$$
(13)
$$\rho \frac{{\partial^{2} \phi }}{{\partial T\partial e_{ij} }} = a_{ijkl} e_{kl} - \gamma_{ij} ,$$
(14)
$$\,\rho \frac{{\partial^{2} \phi }}{{\partial \,T^{2} }} = 2\beta ,$$
(15)

and

$$\rho \frac{\partial \phi }{{\partial e_{ij} }} = c_{ijkl} e_{kl} - \gamma_{ij} \theta + a_{ijkl} e_{kl} \theta .$$
(16)

Substitute from Eqs. (14) and (15) into Eq. (11), we get:

$$\,q_{i,i} = 2\beta T\dot{\theta } + a_{ijkl} Te_{kl} \dot{e}_{ij} - \gamma_{ij} T\dot{e}_{ij} + Q.$$
(17)

Since the specific heat based on constant strain of the material is given by:

$$C_{E} = \frac{T}{\rho }\dot{S} = - \frac{T}{\rho }\frac{{\partial^{2} \phi }}{{\partial \,T^{2} }}.$$
(18)

Hence, from Eq. (15) we have:

$$2\beta = - \frac{{\rho C_{E} }}{T}.$$
(19)

Then Eq. (17) will be in the form:

$$\,q_{i,i} = - \rho C_{E} \dot{\theta } - T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) + Q.$$
(20)

From the non-Fourier heat conduction law [16], we have

$$- K\theta_{,ii} = q_{i,i} + \tau_{o} \dot{q}_{i,i} .$$
(21)

Thus, we get the equation of the heat conduction as:

$$\begin{aligned} K\theta_{,ii} & = \rho C_{E} \dot{\theta } + T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) + \rho C_{E} \tau_{o} \ddot{\theta } \\ & \quad + \tau_{o} \dot{\theta }\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) \hfill \\ & \quad + \tau_{o} T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \ddot{e}_{ij} - a_{ijkl} \dot{e}_{kl} \dot{e}_{ij} - a_{ijkl} e_{kl} \ddot{e}_{ij} } \right) \\ & \quad- Q - \tau_{o} \dot{Q}\,. \hfill \\ \end{aligned}$$
(22)

In general, for anisotropic and non-homogeneous material, Eq. (22) of heat conduction takes the following form

$$\begin{aligned} \left( {K_{ij} \theta_{,i} } \right)_{,j} & = \rho C_{E} \dot{\theta } + T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) + \rho C_{E} \tau_{o} \ddot{\theta }\\ & \quad + \tau_{o} \dot{\theta }\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) \hfill \\ & \quad + \tau_{o} T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \ddot{e}_{ij} - a_{ijkl} \dot{e}_{kl} \dot{e}_{ij} - a_{ijkl} e_{kl} \ddot{e}_{ij} } \right) \\ & \quad - Q - \tau_{o} \dot{Q}\,, \hfill \\ \end{aligned}$$
(23)

and for the anisotropic and homogeneous material, it could be written in the form

$$\begin{aligned} K_{ij} \theta_{,ij} & = \rho C_{E} \dot{\theta } + T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) + \rho C_{E} \tau_{o} \ddot{\theta } \\ & \quad + \tau_{o} \dot{\theta }\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) \hfill \\ & \quad + \tau_{o} T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \ddot{e}_{ij} - a_{ijkl} \dot{e}_{kl} \dot{e}_{ij} - a_{ijkl} e_{kl} \ddot{e}_{ij} } \right) \\ & \quad - Q - \tau_{o} \dot{Q}\,. \hfill \\ \end{aligned}$$
(24)

The second term of the above Eqs. (22)–(24) gives the effect of the strain components on the heat generation and this term is nonlinear so that positive and negative shearing strains generate the same temperature rise [1].

From Eqs. (8) and (16), the constitutive relations take the form

$$\sigma_{ij} = c_{ijkl} e_{kl} - \gamma_{ij} \theta + a_{ijkl} e_{kl} \theta .$$
(25)

The equations of motion with body force components Fi take the forms [15, 16]

$$\sigma_{ij,j} + F_{i} = \rho \ddot{u}_{i} .$$
(26)

Finally, the above equations of motion by using Eq. (26) take the form

$$c_{ijkl} e_{kl,j} - \gamma_{ij} \theta_{,j} + a_{ijkl} \left( {e_{kl} \theta } \right)_{,j} + F_{i} = \rho \ddot{u}_{i} ,$$
(27)

3 Special cases

3.1 Anisotropic nonlinear generalized thermoelastic material with a small temperature increment

If the thermoelastic material is anisotropic and non-homogeneous with small temperature increment then, \(\left( {1 + \frac{\theta }{{\,T_{0} }}} \right) \approx 1\) and the heat conduction equation in (23) be in the form:

$$\begin{aligned} \left( {K_{ij} \theta_{,i} } \right)_{,j} & = \rho C_{E} \dot{\theta } + T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) + \rho C_{E} \tau_{o} \ddot{\theta } \\ & \quad+ \tau_{o} \dot{\theta }\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) \hfill \\ & \quad + \tau_{o} T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \ddot{e}_{ij} - a_{ijkl} \dot{e}_{kl} \dot{e}_{ij} - a_{ijkl} e_{kl} \ddot{e}_{ij} } \right) \\ & \quad - Q - \tau_{o} \dot{Q}\,.\, \hfill \\ \end{aligned}$$
(28)

When the material is homogeneous, it takes the following form:

$$\begin{aligned} K_{ij} \theta_{,ij} & = \rho C_{E} \dot{\theta } + T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) + \rho C_{E} \tau_{o} \ddot{\theta } \\ & \quad + \tau_{o} \dot{\theta }\left( {\gamma_{ij} \dot{e}_{ij} - a_{ijkl} e_{kl} \dot{e}_{ij} } \right) \hfill \\ & \quad + \tau_{o} T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma_{ij} \ddot{e}_{ij} - a_{ijkl} \dot{e}_{kl} \dot{e}_{ij} - a_{ijkl} e_{kl} \ddot{e}_{ij} } \right) \\ & \quad - Q - \tau_{o} \dot{Q}\,. \hfill \\ \end{aligned}$$
(29)

3.2 Isotropic nonlinear and homogeneous generalized thermoelastic material with a large temperature increment

For an isotropic nonlinear and homogeneous thermoelastic materials, the Eqs. (20), (22), (25) and (27) be in the forms

$$\,q_{i,i} = - \rho C_{E} \dot{\theta } - T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma \,\delta_{ij} \dot{e}_{ij} - a_{1} \delta_{ij} \,e_{ij} \,\dot{e} - a_{2} \,e\,\delta_{ij} \,\dot{e}_{ij} } \right) + Q,$$
(30)
$$\begin{aligned} K\theta_{,ii} & = \rho C_{E} \dot{\theta } + T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma \,\delta_{ij} \dot{e}_{ij} - a_{1} \dot{e}\,\delta_{ij} \,e_{ij} \, - a_{2} \,e\,\delta_{ij} \,\dot{e}_{ij} } \right) \\ & \quad + \tau_{o} \rho C_{E} \ddot{\theta } + \gamma \tau_{o} T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\,\delta_{ij} \ddot{e}_{ij} \hfill \\ & \quad + \gamma \,\tau_{o} \dot{\theta }\,\delta_{ij} \dot{e}_{ij} - \,\tau_{o} \dot{\theta }\left( {a_{1} \dot{e}\,\delta_{ij} \,e_{ij} \, + a_{2} \,e\,\delta_{ij} \dot{e}_{ij} } \right) \hfill \\ &\quad - \,\,\tau_{o} T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left[ {a_{1} \left( {\dot{e}\,\delta_{ij} \,\dot{e}_{ij} \, - \ddot{e}\,\delta_{ij} \,e_{ij} \,} \right) + a_{2} \,\left( {\dot{e}\,\delta_{ij} \dot{e}_{ij} - \,e\,\delta_{ij} \ddot{e}_{ij} } \right)} \right]\\ & \quad - Q - \tau_{o} \dot{Q}\,, \hfill \\ \end{aligned}$$
(31)
$$\sigma_{ij} = 2\mu e_{ij} + \lambda \delta_{ij} e - \gamma \,\delta_{ij} \theta + \left( {a_{1} e_{ij} + a_{2} \delta_{ij} e} \right)\,\theta ,$$
(32)
$$2\mu e_{ij,j} + \lambda \delta_{ij} e_{,j} - \gamma \,\delta_{ij} \theta_{,j} + \left[ {\left( {a_{1} e_{ij} + a_{2} \delta_{ij} e} \right)\,\theta } \right]_{,j} + F_{i} = \rho \ddot{u}_{i} .$$
(33)

We can get this case of small temperature increment when we set \(\left( {1 + \frac{\theta }{{\,T_{0} }}} \right) \approx 1\).

4 Computational model

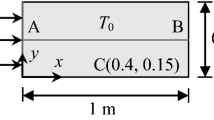
The essential equations of the model of nonlinear generalized thermoelasticity will be applied and solved for a homogenous, isotropic, one-dimensional, and thermoelastic half-space \(0 \le x < \infty \quad and\;a_{1} = a_{2} = \frac{a}{2}.\)

We will consider the medium has not any external heat sources or body forces. The half-space will be subjected to a thermal shock and traction free and considering it is at rest initially.

The displacement components take the forms:

$$u_{x} = u\left( {x,t} \right),\,\,\,u_{y} = u_{z} = 0.$$
(34)

The equation of motion is in the form:

$${\left( {\lambda + 2\mu } \right) \frac{{\partial^{2} u}}{{\partial \,x^{2} }} - \gamma \frac{{\partial^{2} \theta }}{{\partial \,x^{2} }} + a\left( {\theta \frac{{\partial^{2} u}}{{\partial \,x^{2} }} + \frac{\partial u}{{\partial x}}\frac{\partial \theta }{{\partial x}}} \right) = \rho \frac{{\partial^{2} u}}{{\partial \,t^{2} }}}.$$
(35)

The heat equation takes the form:

$$\begin{gathered} K\frac{{\partial^{2} \theta }}{{\partial \,x^{2} }} = \rho C_{E} \frac{\partial \theta }{{\partial t}} + T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma \,\frac{{\partial^{2} u}}{\partial \,t\,\partial x} - a\,\frac{\partial u}{{\partial x}}\,\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x}} \right) + \rho C_{E} \tau_{o} \frac{{\partial^{2} \theta }}{{\partial \,t^{2} }} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\tau_{o} \frac{\partial \,\theta }{{\partial \,t}}\left( {\gamma \,\frac{{\partial^{2} u}}{\partial \,t\,\partial x} - a\,\frac{\partial u}{{\partial x}}\,\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x}} \right) + \tau_{o} T_{0} \left( {1 + \frac{\theta }{{\,T_{0} }}} \right)\left( {\gamma \,\frac{{\partial^{3} u}}{{\partial \,t^{2} \,\partial x}} - a\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x}\,\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x} - a\,\frac{\partial u}{{\partial x}}\,\,\frac{{\partial^{3} u}}{{\partial \,t^{2} \,\partial x}}} \right). \hfill \\ \end{gathered}$$
(36)

The constitutive equation asl follows:

$$\sigma_{xx} = \left( {2\mu + \lambda } \right)\frac{\partial u}{{\partial x}} - \gamma \,\theta + a\,\frac{\partial u}{{\partial x}}\,\theta .$$
(37)

For a simple form, we can use the following dimensionless variables:

$$\left( {x^{\prime}_{{}} ,u^{\prime}} \right) = c_{0} \eta \left( {x,u} \right),\left( {t^{\prime},\tau^{\prime}_{o} } \right) = c_{0}^{2} \eta \left( {t,\tau_{o} } \right),\sigma^{\prime}_{xx} = \frac{{\sigma_{xx} }}{2\mu + \lambda },\theta^{\prime} = \frac{\theta }{{T_{0} }},a^{\prime} = a\frac{{T_{0} }}{\lambda + 2\mu },$$
(38)

where \(c_{0}^{2} = \frac{2\mu + \lambda }{\rho }\) and \(\eta = \frac{{\rho C_{E} }}{K}\).

Hence, we have (the primes have been canceled for simplicity)

$${\frac{{\partial^{2} u}}{{\partial \,x^{2} }} - \beta_{1} \frac{{\partial^{2} \theta }}{{\partial \,x^{2} }} + a\left( {\theta \frac{{\partial^{2} u}}{{\partial \,x^{2} }} + \frac{\partial u}{{\partial x}}\frac{\partial \theta }{{\partial x}}} \right) = \frac{{\partial^{2} u}}{{\partial \,t^{2} }}},$$
(39)
$$\begin{gathered} \frac{{\partial^{2} \theta }}{{\partial \,x^{2} }} = \frac{\partial \theta }{{\partial t}} + \tau_{o} \frac{{\partial^{2} \theta }}{{\partial \,t^{2} }} + \left( {1 + \theta + \tau_{o} \frac{\partial \theta }{{\partial t}}} \right)\left( {\beta_{2} \,\frac{{\partial^{2} u}}{\partial \,t\,\partial x} - a\beta_{3} \,\frac{\partial u}{{\partial x}}\,\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+ \beta_{2} \tau_{o} \left( {1 + \theta } \right)\,\frac{{\partial^{3} u}}{{\partial \,t^{2} \,\partial x}} - a\tau_{o} \left( {1 + \theta } \right)\beta_{3} \left( {\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x}\,\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x} + \,\frac{\partial u}{{\partial x}}\,\,\frac{{\partial^{3} u}}{{\partial \,t^{2} \,\partial x}}} \right), \hfill \\ \end{gathered}$$
(40)

and

$$\sigma_{xx} = \frac{\partial u}{{\partial x}} - \beta_{1} \theta + a\,\frac{\partial u}{{\partial x}}\,\theta ,$$
(41)

where \(\beta_{1} = \frac{{\gamma \,T_{0} }}{\lambda + 2\mu }\), \(\beta_{2} = \frac{\,\gamma }{{\rho \,C_{E} }}\) and \(\beta_{3} = \frac{{\left( {\lambda + 2\mu } \right)}}{{\rho C_{E} T_{0} \,}}\) are non-dimensional constants.

The thermoelastic solution for the present medium can be completed by the application of the initial and boundary conditions.

The initial conditions can be considered as:

$$\theta = \frac{\partial \theta }{{\partial t}} = 0,\,\,u = \frac{\partial u}{{\partial t}} = 0\quad at\;t = 0.$$
(42)

Assume that the boundary plane \(x = 0\) is thermally loaded by a thermal shock, which takes the form

$$\theta \left( {0,t} \right) = \theta_{0} H\left( t \right),$$
(43)

where H (t) is the Heaviside unit step function and \(\theta_{0}\) is the shock intensity(constant).

Consider the bounding plane \(x = 0\) traction free, so we have

$$\sigma_{xx} \left( {0,t} \right) = 0.$$
(44)

5 Numerical scheme

A finite element method has been applied to obtain the numerical solutions of the nonlinear Eqs. (39) and (40). The Finite element method is an original computational technique where it is developed to get the numerical solution of the complex, nonlinear, and hard problems in mechanical structural. The advantage of this method is that it allows physical effects to be visualized and quantified with respect to its experimental limitations [17,18,19,20,21,22].

Throughout the finite element method, we chose the displacement component \(u\) and temperature \(T\) to be jointed to the corresponding nodal values by

$$u = \sum\limits_{i = 1}^{m} {N_{i} u_{i} (t)} ,\,\,T = \sum\limits_{i = 1}^{m} {N_{i} T_{i} (t)} ,$$
(45)

where \(m\) is the number of nodes per element, while \(N\) is the shape functions. In the framework of standard Galerkin approach, the shape functions and the weighting functions coincide. Hence,

$$\delta u = \sum\limits_{i = 1}^{m} {N_{i} \delta u_{i} } ,\,\,\delta T = \sum\limits_{i = 1}^{m} {N_{i} \delta T_{i} } .$$
(46)

Then, the finite element equations of (43) and (44) can be obtained as:

$$\int\limits_{\Gamma } {\delta u\left( { \frac{{\partial^{2} u}}{{\partial \,x^{2} }} - \beta_{1} \frac{{\partial^{2} \theta }}{{\partial \,x^{2} }} + a\left( {\theta \frac{{\partial^{2} u}}{{\partial \,x^{2} }} + \frac{\partial u}{{\partial x}}\frac{\partial \theta }{{\partial x}}} \right) - \frac{{\partial^{2} u}}{{\partial \,t^{2} }}} \right)} \,dx = 0,$$
(47)
$$\int\limits_{\Gamma } {\delta T\left( \begin{gathered} \frac{{\partial^{2} \theta }}{{\partial \,x^{2} }} - \frac{\partial \theta }{{\partial t}} - \tau_{o} \frac{{\partial^{2} \theta }}{{\partial \,t^{2} }} - \left( {1 + \theta + \tau_{o} \frac{\partial \theta }{{\partial t}}} \right)\left( {\beta_{2} \,\frac{{\partial^{2} u}}{\partial \,t\,\partial x} - a\beta_{3} \,\frac{\partial u}{{\partial x}}\,\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x}} \right) - \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\beta_{2} \tau_{o} \left( {1 + \theta } \right)\,\frac{{\partial^{3} u}}{{\partial \,t^{2} \,\partial x}} + a\tau_{o} \left( {1 + \theta } \right)\beta_{3} \left( {\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x}\,\,\frac{{\partial^{2} u}}{\partial \,t\,\partial x} + \,\frac{\partial u}{{\partial x}}\,\,\frac{{\partial^{3} u}}{{\partial \,t^{2} \,\partial x}}} \right) \hfill \\ \end{gathered} \right)} \,dx = 0.$$
(48)

6 Numerical results and discussion

Copper material has been taken due to its high thermal conductivity and has excellent wear characteristics against steel. So, the physical data for which is given below [15, 23,24,25]:

\({\text{k }} = {386}\,{\text{N/K sec}}\), \(\alpha_{T} = 1.78\,\left( {10} \right)^{ - 5} \text{K}^{ - 1}\), \(C_{E} = 383.1\,\text{m}^{2} /\text{K}\), \(\mu = \,3.86\,\left( {10} \right)^{10\,}\text{ N/m}^{2}\), \(\lambda = \,7.76\,\left( {10} \right)^{10\,}\text{ N/m}^{2}\), \(\rho = 8954\,\text{kg/m}^{3}\), \({\text{T}}_{{0}} = {\text{293 K}}\), \({\text{a}} = 0.5\).

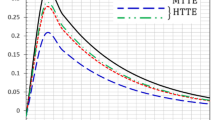
In Figs. 1, 2, 3, 4, the computations were carried out when \(t = 0.1\), \(\theta_{0} = 1\) and the temperature, the stress, the strain, and the displacement distributions are represented graphically with respect to the wide range of x \(\left( {0 \le x \le 1} \right)\) and for a small increment of temperature \(\theta_{0} /T \ll 1\). The solid lines represent the linear generalized thermoelasticity, while the dotted lines represent the nonlinear generalized thermoelasticity.

Fig. 1
figure 1

The temperature distribution for a small increment of temperature

Full size image
Fig. 2
figure 2

The stress distribution for a small increment of temperature

Full size image
Fig. 3
figure 3

The displacement distribution for a small increment of temperature

Full size image
Fig. 4
figure 4

The strain distribution for a small increment of temperature

Full size image

In Fig. 1, the temperature distribution in this figure shows that the value of the temperature decreases in the nonlinear case than the linear case and it has a finite speed of propagation. In Fig. 2, the nonlinear parameter “\(a\)” has a significant effect on the stress distribution, and it makes the peak point decreases. The nonlinear terms causse decreasing to the value of the temperature increment and the thermal wave.

In Figs. 3 and 4 the nonlinear parameter “\(a\)” has significant effects on the displacement and the strain distributions. The mechanical wave has a finite speed of propagation. The absolute values of the peak points of the displacement, and the strain distributions increase based on the nonlinear model. Thus, the mechanical waves have a smaller speed of propagation in the context of the nonlinear model than in the context of linear model.

In Figs. 5, 6, 7, 8, the computations were carried out when \(t = 0.05,\,0.1\,,\,0.15\), \(\theta_{0} = 100\) and the temperature, the stress, the strain, and the displacement distributions are represented graphically with respect to a wide range of x \(\left( {0 \le x \le 1} \right)\) and for a large increment of temperature \(\theta_{0} /T \gg 1\) for the nonlinear generalized thermoelasticity. In those figures, we can see that time has a significant effect on all the studied fields.

Fig. 5
figure 5

The temperature distribution for a large increment of temperature and different time

Full size image
Fig. 6
figure 6

The stress distribution for a large increment of temperature and different time

Full size image
Fig. 7
figure 7

The displacement distribution for a large increment of temperature and different time

Full size image
Fig. 8
figure 8

The strain distribution for a large increment of temperature and different time

Full size image

7 Conclusion

The governing equations of the nonlinear thermoelasticity with one relaxation time model which have been constructed in this work succeeded to offer the same physical behavior of the thermal and the mechanical waves of the linear thermoelasticity with one relaxation time model through the thermoelastic materials with more accurate results.

The parameter of the nonlinear term of has significant effects on the temperature increment, stress, displacement, and strain distributions.

The speeds of propagation of the thermal and mechanical waves have a smaller values based on the nonlinear theorem of thermoelasticity than based on the linear theorem of thermoelasticity.