1 Introduction

Boundary value models of ordinary differential equations (ODEs) arise in modeling diverse science and technological processes. In particular, we discuss the two-point boundary value models in favor of their great relevance in many areas, including theoretical physics, engineering, optimization theory, fluid dynamics, and control theory to state but a few. Further, since not all ODEs possess exact analytical structures as solutions, through the application of analytical methods—which is usually the most common step taken to analyze a given differential equation; thus, the need to greatly search for an optimal numerical approach. In this regard, a lot of mathematicians have endeavored to propose various efficient numerical approaches that rapidly converge to the available exact solution with an utmost level of exactitude. In fact, we mention the shooting methods as one of such vibrant numerical approaches in this circle. Besides, as the method possesses so many benefits, nevertheless, the method is found to require an enormous computational space, as a drawback in obtaining perfect approximation, more particularly, with regard to nonlinear models. Furthermore, Attili et al. [1] presented an efficient method based on the use of the shooting method for solving a special two-point boundary value model, which takes the following pattern

$$R\left(t\right){w}^{^{\prime\prime} }\left(t\right)+{R}^{\prime}\left(t\right){w}^{\prime}\left(t\right)=f\left(t,w,{w}^{\prime}\right),$$
(1)

subject to the following prescribed two-point boundary data \(w\left(a\right)=\alpha , w\left(b\right)=\beta ,\) where \(R\left(t\right)\), \({R}^{\prime}\left(t\right)\), and \(f\) are continuous functions, and the inverse operator was considered to take the following expression

$${L}^{-1}\left(t,D\right)=\underset{a}{\overset{t}{\int }}\frac{dx}{R\left(x\right)} \underset{a}{\overset{x}{\int }}\frac{ds}{\xi \left(s\right)}w\left(s\right).$$

In [2], Al-Zaid et al. utilized the technique to third-order linear equations and obtained good results. The present paper deploys the mixture of the shooting method and the ADM [3,4,5,6,7,8,9] to deeply examine the class of boundary value models accompanied by two-point boundary data. In this paper, we study the shooting technique with the standard ADM and the normal form of the inverse operator, which reduces the computing operations, for the general form of the second order BVPs for both linear and nonlinear cases. Moreover, it is relatable to mention here that due to the efficiency of the shooting method, many variants of the method exist, including its mixture with the finite difference method; likewise, there exist multiple shooting techniques, for more on this recap, one may read [10,11,12,13,14,15,16,17,18] and the references therein for more related studies. Therefore, as the coupling between the shooting method and the ADM is named as Efficient Decomposition Shooting Method (EDSM) in this study, the coupled EDSM method will be proposed for the linear and nonlinear models with different operator \(D\) and different inverse operator \({L}^{-1}.\) Also, we shall be demonstrating the method on some test models, and further establish a comparative study between the approximate solutions posed by the proposed method and those of the exact analytical solutions, together with others from the available open literature. Lastly, we would give some concluding notes about the performance of the proposed method.

2 Traditional ADM for solving initial value models

The traditional ADM [2,3,4,5,6,7,8,9] has been greatly used in the literature to tackle a variety of ODEs, featuring both boundary and initial value problems. Without much delay, the following generalized two-point second-order nonlinear (linear inclusive) ODEs is expressed as follows

$${w}^{{\prime}{\prime}}= f\left(x,w,{w}^{\prime}\right), a\le x\le b,$$
(2)

together with the following two-point boundary data

$$w\left(a\right)= \alpha , w\left(b\right)=\beta ,$$

the above model is the governing model of concern in this study. However, with the targeted coupling between the ADM and shooting method, we first present the ADM procedures on both the nonlinear and linear ODEs. Therefore, to present the method on nonlinear models, we make consideration to the following generalized initial value problem, derived from Eq. (2), and expressed in an operator form as follows

$$Lw+Rw+Nw=g\left(x\right),$$
(3)

together with following initial data

$$w\left(a\right)= \alpha , {w}^{\prime}\left(a\right)=t.$$
(4)

More, in the above equations, L represents the highest-order derivative, which is a second-order linear operator, while \(R\) and \(N\) are the linear operator with order lower than that of L, and the nonlinear differential operator, respectively. In addition, \(g(x)\) is a prescribed forcing term; while \(\alpha\) and \(t\) are given real constants. Furtherer, consider the new differential operator from Eq. (3) as follows

$$L\left(.\right)=\frac{{d}^{2}}{{dx}^{2}}\left(.\right),$$
(5)

together with its inverse linear operator \({L}^{-1}\), expressed using a twofold integral operator as follows

$${ L}^{-1}\left(.\right)=\underset{a}{\overset{x}{\int }}\underset{a}{\overset{x}{\int }}\left(.\right)\,dx\,dx.$$
(6)

Additionally, according to the traditional ADM, the solution \(w(x)\) should be divided into the following infinite series of components

$$w\left(x\right)=\sum_{n=0}^{\infty }{w}_{n}\left(x\right),$$
(7)

while the nonlinear term \(Nw\) is acquired using the subsequent recurrent formula

$${A}_{n}=\frac{1}{n!}\frac{{d}^{n}}{{d\lambda }^{n}}{\left[N\left(\sum_{i=0}^{n}{\lambda }^{i}{w}_{i}\right)\right]}_{\lambda =0} , n=0, 1, 2,\dots .$$

upon which the ADM reveals the recurrent components \({w}_{n}\left(x\right)\) as follows

$$\genfrac{}{}{0pt}{}{{w}_{0}=\phi \left(x\right)+{L}^{-1}\left(g\left(x\right)\right), }{{ w}_{n+1}=-{L}^{-1}\left({Rw}_{n}\right)-{L}^{-1}\left({A}_{n}\right), n\ge 0,}$$
(8)

that further yields the resulting approximate solution of the governing model in Eqs. (3) and (4) as \({w}_{m+1}=\sum_{n=0}^{m}{w}_{n}\left(x\right).\) In the same fashion, the linear case follows the same steps of the solution as in the nonlinear case, only that we should exclude the nonlinear term. Thus, we rewrite Eq. (3) in the following form

$$Lw+Rw=g\left(x\right),$$
(9)

with the same initial data as

$$w\left(a\right)= \alpha , {w}^{\prime}\left(a\right)=t.$$
(10)

Therefore, the ADM posed the recurrent scheme of components \({w}_{n}\left(x\right)\) for Eqs. (9) and (10) as follows

$$\genfrac{}{}{0pt}{}{{w}_{0}=\phi \left(x\right)+{L}^{-1}\left(g\left(x\right)\right), }{{ w}_{n+1}=-{L}^{-1}\left({Rw}_{n}\right), n\ge 0,}$$
(11)

that satisfies the linear model expressed in Eqs. (9) and (10) when the net sum of the components \({w}_{n}\left(x\right)\) is calculated as \({w}_{m+1}=\sum_{n=0}^{m}{w}_{n}\left(x\right) .\)

3 Proposed EDSM

A potential strategy that begins by converting the governing boundary value problem into a related system of starting value issues with defined initial value conditions is the shooting method [10,11,12,13,14,15,16,17,18]. The initial value problems are then solved by guessing these unknown initial conditions; the accuracy of the guesses for the missing initial conditions is then determined by comparing the calculated value of the dependent variable with the given value at the terminal point. Additionally, if these two values don't match, a fresh value should be estimated again until the two agree on a number with a predetermined level of accuracy. Indeed, none of the resulting initial value models is solved exactly; so, the solution will be approximately determined using the one-step methods or multistep methods or even directly upon using the ADM [2,3,4,5,6,7,8,9] as in the present study.

The shooting method theoretical treatment of convergence has been examined in [19, 20]. Granas et al. conducted a convergence analysis. The weaker hypotheses necessary to ensure the boundary value problem's existence and uniqueness were the first ones they analyzed. The analysis established the shooting method's convergence without requiring any extra limitations.

It must be demonstrated that the initial value problem has a unique solution defined on the interval in order for the previously mentioned numerical approach to be workable. Noteworthy, however, is the fact that a number of researchers have already demonstrated the Adomian series convergence such as [21].

In fact, shooting techniques are highly appropriate and advantageous for a variety of problems. For the solution of initial value difficulties, they rely on dependable and easily accessible procedures. The shooting method for boundary value problems uses a very small amount of computer storage compared to global approaches; the discretized version's mesh is typically automatically tuned to the behavior of the solution, and subject to the method’s inherent limitations, increasing the accuracy of a solution is simple. The study bounds on the shooting method inherent error in [22].

3.1 Linear case

Let us make consideration to the linear ODEs of second order that follows

$${w}^{{\prime}{\prime}}= p\left(x\right){w}^{\prime}+q\left(x\right)w+r\left(x\right), a\le x\le b,$$
(12)

together with the following two-point boundary data

$$w\left(a\right)= \lambda , w\left(b\right)=\beta .$$
(13)

The second-order model mentioned above will now be divided into two initial value models depending on the shooting method’s application, and the boundary conditions listed in Eq. (13) will be changed to particular initial conditions for each initial value problem, say

$${u}^{{\prime}{\prime}}= p\left(x\right){u}^{\prime}+q\left(x\right)u+r\left(x\right), a\le x\le b,$$
(14)
$$u\left(a\right)= \lambda , {u}^{\prime}\left(a\right)=0,$$
(15)

and

$${v}^{{\prime}{\prime}}= p\left(x\right){v}^{\prime}+q\left(x\right)v, a\le x\le b,$$
(16)
$$v\left(a\right)= 0, {v}^{\prime}\left(a\right) =1.$$
(17)

Additionally, Eq. (14) can be expressed using operator notation as follows

$$Lu= p\left(x\right){u}^{\prime}+q\left(x\right)u+r\left(x\right),$$
(18)

once \({L}^{-1}\) is applied previously supplied in Eq. (6) to Eq. (18), one obtains.

$$u\left(x\right)= {\phi }_{1}\left(x\right)+{ L}^{-1}\left(p\left(x\right){u}^{\mathrm{^{\prime}}}\right)+{ L}^{-1}\left(q\left(x\right)u\right)+{ L}^{-1}\left(r\left(x\right)\right),$$
(19)

such that \(L{\phi }_{1}\left(x\right)=0.\) Next, as in the ADM steps, the components \({u}_{n}\left(x\right)\) are recurrently determined as follows

$$\begin{gathered} u_{0} = \phi_{1} \left( x \right) + L^{ - 1} \left( {r\left( x \right)} \right), \hfill \\ u_{1} = L^{ - 1} \left( {p\left( x \right)u_{0}^{\prime} \left( x \right) + q\left( x \right)u_{0} \left( x \right)} \right), \hfill \\ u_{2} = L^{ - 1} \left( {p\left( x \right)u_{1}^{\prime} \left( x \right) + q\left( x \right)u_{1} \left( x \right)} \right), \hfill \\\qquad\qquad\qquad\qquad\;\,\cdot \hfill \\\qquad\qquad\qquad\qquad\;\,\cdot \hfill \\\qquad\qquad\qquad\qquad\;\,\cdot \hfill \\ \end{gathered}$$
(20)

Additionally, the \(m + 1\) -term approximant is regarded for the purposes of numerical computation as

$$u = \psi_{1,m + 1} \left( x \right) = \mathop \sum \limits_{k = 0}^{m} u_{k} \left( x \right).$$
(21)

Likewise, with reference to the second initial value model provided by Eq. (16), we can similarly calculate

$$v = \psi_{2,m + 1} \left( x \right) = \mathop \sum \limits_{k = 0}^{m} v_{k} \left( x \right),$$
(22)

where the components \(v_{k} \left( x \right)\) are obtained in the same way as \({v}_{0}= {\phi }_{2}\left(x\right),\)

$$\begin{gathered} v_{1} = L^{ - 1} \left( {p\left( x \right)v_{0}^{\prime} \left( x \right) + q\left( x \right)v_{0} \left( x \right)} \right), \hfill \\ v_{2} = L^{ - 1} \left( {p\left( x \right)v_{1}^{\prime} \left( x \right) + q\left( x \right)v_{1} \left( x \right)} \right), \hfill \\\qquad\qquad\qquad\qquad\;\,\cdot \hfill \\\qquad\qquad\qquad\qquad\;\,\cdot \hfill \\\qquad\qquad\qquad\qquad\;\,\cdot \hfill \\ \hfill \\ \end{gathered}$$
(23)

Subsequently, we construct \(z\) as follows

$$\begin{gathered} z_{1} \left( x \right) = u_{1} \left( x \right) + \theta v_{1} \left( x \right), \hfill \\ z_{2} \left( x \right) = u_{2} \left( x \right) + \theta v_{2} \left( x \right), \hfill \\ z_{3} \left( x \right) = u_{3} \left( x \right) + \theta v_{3} \left( x \right), \hfill \\\qquad\qquad\quad\;\cdot \hfill \\\qquad\qquad\quad\;\cdot \hfill \\\qquad\qquad\quad\;\cdot \hfill \\ \hfill \\ \end{gathered}$$
(24)

where \(\theta\) is a fixed number.

Hence, if we assume \(u\left(x\right)\) and \(v\left(x\right)\) to stand for the solutions of the second-order linear initial value models given in Eqs. (14)–(15) and (16)–(17), respectively, then, we define

$$z\left( x \right) = u\left( x \right) + \frac{\beta - u\left( b \right)}{{v\left( b \right)}}v\left( x \right), v\left( b \right) \ne 0,$$
(25)

where \(z(x)\) represents the solution to the second-order linear boundary value problem given in Eqs. (12)–(13).

3.2 Nonlinear case

Let us make consideration to the nonlinear ODEs of second order that follows

$${w}^{{\prime}{\prime}}= f\left(x,w,{w}^{\prime}\right), a\le x\le b,$$
(26)

together with the following specified two-point boundary data

$$w\left(a\right)= \lambda , w\left(b\right)=\beta .$$
(27)

Nevertheless, since the shooting method procedures for solving both the cases of linear and nonlinear models remain the same, with the exception of the fact that the solution of the nonlinear model could not be represented as a linear combination of the solutions of the resulting initial value models. As such, the solution of the original boundary value model is approximated by that of the system of the resulting initial value problems, having t as a parameter. So, we will convert the second-order boundary value model into a system of initial value problems, where we will be replacing the boundary data with specific initial conditions. In this regard, we consider the model to take the following form

$${w}^{{\prime}{\prime}}= f\left(x,w,{w}{^\prime}\right), a\le x\le b,$$
(28)

where the initial data is now prescribed as follows

$$w\left(a\right)= \lambda , {w}^{\prime}\left(a\right)=t.$$
(29)

However, as the mixture of the traditional ADM with the shooting method is to be employed to solve the above model in Eqs. (28) and (29), we start off by selecting the parameters \(t = {t}_{k}\) in such a way that the following limit

$$\underset{k\to \infty }{{\text{lim}}}w(b,{t}_{k})=w\left(b\right)=\beta ,$$
(30)

is guaranteed, where \(w\left(x,{t}_{k}\right)\) presents the solution to the initial value problem in Eqs. (28), (29) with \(t ={t}_{k}\), while \(w(x)\) is the solution of the original boundary value model in Eqs. (26), (27). For that reason, the expected solution to the resulting first initial value problem is required in a sequence form after constraining initial guess \({t}_{0}=\frac{\beta -\alpha }{b-a}\). Therefore, we may find the value of \({t}_{1}\) as follows by applying Newton's approach

$${ t}_{1}={t}_{0}-\frac{w\left(b,{t}_{0}\right)-\beta }{\frac{dw}{dt}\left(b,{t}_{0}\right)}.$$
(31)

Next, to determine the value of \(\frac{dw}{dt}\left(b,{t}_{0}\right)\), we scale the initial value problem expressed in Eqs. (28) and (29) to depend on \(x\) and \(t\) variables as follows

$${w}^{{\prime}{\prime}}(x,t)=f\left(x,w\left(x,t\right),{w}{^\prime}\left(x,t\right)\right) ,$$
(32)

with the initial data

$$w\left(a,t\right)= \lambda , {w}^{\prime}\left(a,t\right)=t.$$
(33)

We then proceed to differentiate Eq. (32) and (33) partially in \(t\). So, if we let \(z(x,t)=\frac{\partial w}{\partial t}\left(x,t\right)\), the above model now becomes

$${z}^{{\prime}{\prime}}=\frac{\partial f}{\partial w}\left(x,w,{w}{^\prime}\right) z\left(x,t\right)+\frac{\partial f}{\partial {w}{^\prime}}\left(x,w,{w}{^\prime}\right) {z}{^\prime}\left(x,t\right), a\le x\le b,$$
(34)

with

$$z\left(a\right)= 0, {z}^{\prime}\left(a\right)=1.$$
(35)

Lastly, the initial value problem given above will be directly solved at \({t}_{k}\) using the traditional ADM, which gives \(\frac{dw}{dt}\left(b,{t}_{0}\right)=z(x,{t}_{0})\). Also, to determine the complete sequence, the guessed points \({t}_{k}\) for \(k=2, 3,\dots\) together with the nonlinear function \(y\left(b,t\right)-\beta =0\) are thus determined through the utilization of the Secant iterative method as follows

$${t}_{k}={t}_{k-1}-\frac{\left(w\left(b,{t}_{k-1}\right)-\beta \right)\left({t}_{k-1}-{t}_{k-2}\right)}{w\left(b,{t}_{k-1}\right)-w\left(b,{t}_{k-2}\right)}, k=\mathrm{2,3},\dots$$
(36)

Notably, the numerical process in the present study is to be ended upon attainment of the following stopping criteria

$$\left|w\left(b,{t}_{k}\right)-\beta \right|\le tolerance.$$
(37)

4 Numerical examples

This section shows how the suggested methodology applies to some chosen test models, allowing it to be examined for both second-order linear and nonlinear two-point boundary value models. Precisely, two linear and two nonlinear models are considered as test models, where the methodology is fully implemented on the first and third examples, for the linear and nonlinear cases, respectively. To further assess the effectiveness of the developed scheme, the method is compared to a combination of the shooting method and the fourth-order Runge–Kutta approach. We will also contrast our findings with those of other numerical techniques found in the literature [1, 23,24,25,26,27,28,29,30,31,32,33,34,35,36].

In addition, we offer some supporting Tables 1, 2, 3, 4, 5, 6, 7, 8 and Figs. 1, 2, 3, 4 that show the absolute error differences between the corresponding exact analytical solutions and, conversely, the suggested numerical solutions utilizing EDSM (\({{\varvec{E}}}_{\mathbf{E}\mathbf{D}\mathbf{S}\mathbf{M}})\) and further verified by the fourth-order Runge–Kutta method \(({{\varvec{E}}}_{\mathbf{S}\mathbf{R}\mathbf{K}\mathbf{M}4})\).

Table 1 The absolute error for EDSM, SRKM4 when \(h=0.1\) and \(h=0.05.\)
Full size table
Table 2 Comparison between different methods described in [23,24,25,26,27] when \(h = 0.1\)
Full size table
Table 3 The absolute error for EDSM, SRKM4 when \(h=0.1\) and \(h=0.05.\)
Full size table
Table 4 Comparison between different methods described in [28,29,30,31] when \(h=0.1\)
Full size table
Table 5 The absolute error for EDSM, SRKM4 when \(h=0.1\) and \(h=0.05.\)
Full size table
Table 6 Comparison between different methods described in [32,33,34] when \(h=0.1\)
Full size table
Table 7 The absolute error for EDSM, SRKM4 when \(h=0.1\) and \(h=0.05\)
Full size table
Table 8 Comparison between different methods described in [1, 35, 36] when \(h = 0.5\)
Full size table
Fig. 1
figure 1

Graphical comparison, depicting the exact and contending approximate solutions with \(h=0.1\)

Full size image
Fig. 2
figure 2

Graphical comparison, depicting the exact and contending approximate solutions with \(h=0.1\)

Full size image
Fig. 3
figure 3

Graphical comparison, depicting the exact and contending approximate solutions with \(h=0.1\)

Full size image
Fig. 4
figure 4

Graphical comparison, depicting the exact and contending approximate solutions with \(h=0.05\)

Full size image

Example 1

We make consideration to the inhomogeneous second-order linear two-point boundary value problem as follows [23,24,25,26,27]

$$w^{\prime\prime} - w^{\prime} = - e^{x - 1} - 1, 0 \le x \le 1,{ }w\left( 0 \right) = 0, w\left( 1 \right) = 0,$$

that satisfies the following exact analytical solution \(w\left( x \right) = x\left( {1 - e^{x - 1} } \right)\)

We now consider the following two initial value problems based on the proposed EDSM

$$u^{\prime\prime} = u^{\prime} - e^{x - 1} - 1,$$
(38)
$$u\left(0\right)=0, {u}^{\prime}\left(0\right)=0,$$
(39)

and

$${v}^{{\prime}{\prime}}= {v}^{\prime},$$
(40)
$$v\left(0\right)= 0, {v}^{\prime}\left(0\right)=1.$$
(41)

Equations (38) and (39) operator versions can be expressed as

$$Lu={u}^{\prime}-{e}^{x-1}-1,$$
(42)

and

$$Lv={v}^{\prime}.$$
(43)

After applying \(L^{ - 1}\) to both sides of Eq. (42) and using the conditions given in Eq. (39), we obtain

$$u\left(x\right)={e}^{-1}+{e}^{-1}x-\frac{1}{2}{x}^{2}-{e}^{x-1}+{L}^{-1}\left({u}^{\prime}\right).$$
(44)

Likewise, applying \({L}^{-1}\) to both sides of Eq. (43) and using the conditions given in Eq. (41), we obtain

$$v\left(x\right)=x+{L}^{-1}\left({v}^{\prime}\right).$$
(45)

Furthermore, by breaking down the corresponding solutions in Eqs. (44) and (45) using the conventional ADM process, the corresponding recursive relationships are thus derived as follows

$$\left\{\begin{array}{c}{ u}_{0}\left(x\right)=-\frac{1}{2}{x}^{2}+{e}^{-1}+x{e}^{-1}-{e}^{x-1}, \\ \\ {{u}_{n+1}\left(x\right)= L}^{-1}\left({u}_{n}^{\prime}\right), n\ge 0,\end{array}\right.$$

and

$$\left\{\begin{array}{c} {v}_{0}\left(x\right)=x, \\ \\ {{v}_{n+1}\left(x\right)= L}^{-1}\left({v}_{n}^{\prime}\right), n\ge 0.\end{array}\right.$$

Then, the solutions of the initial value models in Eqs. (38, 39, 40, 41) are thus obtained from the above schemes upon taking the respective series summations. Finally, the approximate solution \(z\left(x\right)\) \(\mathrm{with } \hfill m=10\hfill and \hfill m=20,\) when \(h=\frac{1}{10} \hfill and \hfill h=\frac{1}{20}\), respectively, will be computed in Table 1 and 2 by using

$$z\left({x}_{k}\right)= u\left({x}_{k}\right)+\frac{-u\left(1\right)}{v\left(1\right)}v\left({x}_{k}\right),$$

where \({x}_{k}=kh\) for \(k=\mathrm{0,1},\dots ,m\).

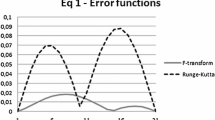
The absolute error difference between the proposed \({{\varvec{E}}}_{\mathbf{E}\mathbf{D}\mathbf{S}\mathbf{M}}\) solution and the exact analytical solution, which was further confirmed with \({{\varvec{E}}}_{\mathbf{S}\mathbf{R}\mathbf{K}\mathbf{M}4}\), is presented in Table 1. Table 2 demonstrates that, when compared to the approaches employed in [23,24,25,26,27] and the SRKM4, EDSM is the most proficient strategy for solving the governing model. Once more, we depict the exact analytical and competing approximation answers in Fig. 1, where the solutions exhibit perfect agreement.

Example 2

We make consideration to the inhomogeneous second-order linear two-point boundary value problem as follows [28,29,30,31]

$${w}^{{\prime}{\prime}}+\frac{2}{x}\left({w}^{\prime}-\frac{1}{x}w\right)=\frac{{\text{sin}}\left(ln x\right)}{{x}^{2}}, 1\le x\le 2, w\left(1\right)=1, w\left(2\right)=2,$$

that satisfies the following exact analytical solution.

$$w\left(x\right)={k}_{1}x+{k}_{2}{x}^{-2}-\frac{1}{10}{\text{cos}}\left(ln x\right)-\frac{3}{10}{\text{sin}}\left(ln x\right),$$

where

$$k_{1} = \frac{11}{{10}} - k_{2} , \hfill and\; \hfill k_{2} = \frac{1}{70} \left[ {8 - 4\cos \left( {\ln 2} \right) - 12\sin \left( {\ln 2} \right)} \right].$$

Thus, without loss of generality, the approximate solution \(z\left(x\right)\) with \(m=10\) and \(m=20\) is obtained for \({x}_{k}=kh\) for \(k=\mathrm{0,1},\dots ,m\) using the following scheme

$$z\left( {x_{k} } \right) = u\left( {x_{k} } \right) + \frac{2 - u\left( 2 \right)}{{v\left( 2 \right)}}v\left( {x_{k} } \right),$$

see also Table 3 and 4 for the numerical results.

The absolute error difference between the proposed solution \({{\varvec{E}}}_{\mathbf{E}\mathbf{D}\mathbf{S}\mathbf{M}}\), and the exact analytical solution, which was further confirmed with \({{\varvec{E}}}_{\mathbf{S}\mathbf{R}\mathbf{K}\mathbf{M}4}\), is presented in Table 3. Table 4 demonstrates that, when compared to the approaches in references [28,29,30,31] and SRKM4, EDSM is the most proficient strategy for resolving Example 2. Furthermore, we show the precise analytical and approximative solutions in Fig. 2, where a perfect agreement between the solutions is observed.

Example 3

We make consideration to the inhomogeneous second-order nonlinear two-point boundary value problem as follows [32,33,34]

$${w}^{{\prime}{\prime}}=\frac{1}{2}(1+{x+w)}^{3}, 0\le x\le 1, w\left(0\right)=0, w\left(1\right)=0,$$
(46)

that satisfies the following exact analytical solution

$$w\left(x\right)=-\left(x+1\right)+2{\left(2-x\right)}^{-1}.$$

First, we consider the following initial value problems are

$${y}^{{\prime}{\prime}}=\frac{1}{2}({1+x+y)}^{3}, y\left(0\right)= 0, {y}^{\prime}\left(0\right)={t}_{k},$$
(47)

and

$${ z}^{{\prime}{\prime}}=\frac{3}{2}({1+x+y)}^{2}z, z\left(0\right)= 0, {z}^{\prime}\left(0\right)=1.$$
(48)

Moreover, the operator forms of Eqs. (47) and (48) can be expressed as follows

$$Ly=\frac{1}{2}({1+x+y)}^{3}, y\left(0\right)= 0, {y}^{\prime}\left(0\right)={t}_{k},$$
(49)

And

$$Lz = \frac{3}{2}(1 + x + y)^{2} z, z\left( 0 \right) = 0, z^{\prime}\left( 0 \right) = 1.$$
(50)

On applying \({L}^{-1}\) to both sides of Eq. (49) and (50), and upon using the respective initial conditions, then the recursive relationships are

$$\left\{\begin{array}{c} {y}_{0}\left(x\right)={t}_{k}x+\frac{1}{4}{x}^{2}+\frac{1}{4}{x}^{3}+\frac{1}{8}{x}^{4}+\frac{1}{40}{x}^{5}, \\ \\ {y}_{n+1}\left(x\right)=\frac{1}{2}{L}^{-1}\left({A}_{n}+{B}_{n}\left(3x+3\right)+{y}_{n}(3{x}^{2}+6x+3)\right), n\ge 0,\end{array}\right.$$

and

$$\left\{\begin{array}{c} {z}_{0}\left(x\right)=x, \\ \\ {z}_{n+1}\left(x\right)=\frac{1}{2}{L}^{-1}\left(3{{y}_{n}}^{2}{z}_{n}+2{y}_{n}{z}_{n}\left(3x+3\right)+(3{x}^{2}+6x+3){z}_{n}\right), n\ge 0,\end{array}\right.$$

where the solution Eq. (47) with \(m=10\) and \(m=20\) can be computed from the following series

$$y\left(x\right)=\sum_{k=0}^{m}{y}_{k}={y}_{0}+{y}_{1}+\dots +{y}_{m}.$$

Lastly, if \(tolerance={10}^{-15}\) is considered, that is, when \(|w\left(b,{t}_{k}\right)-\beta |\le {10}^{-15}\), then \(w\left(x,{t}_{k}\right)\) reveals the solution of the governing model earlier given in Eq. (46) with \(t ={t}_{k}\); see Table 5 and 6 for the numerical results.

The absolute error difference between the proposed solution \({{\varvec{E}}}_{\mathbf{E}\mathbf{D}\mathbf{S}\mathbf{M}}\) and the exact analytical solution is presented in Table 5 and is further confirmed with \({{\varvec{E}}}_{\mathbf{S}\mathbf{R}\mathbf{K}\mathbf{M}4}\). Additionally, based on Table 6 comparison with the findings presented in [32,33,34] and SRKM4, it is evident that EDSM is the most proficient method for solving the current model. Furthermore, Fig. 3 shows the precise analytical and approximative answers; a high degree of agreement between the solutions is evident.

Example 4

We make consideration to the homogeneous second-order nonlinear two-point boundary value problem as follows [1, 35, 36]

$${w}^{{\prime}{\prime}}+w{w}^{\prime}-{w}^{3}= 0, 1\le x\le 2, w\left(1\right)=1/2, w\left(2\right)=1/3,$$
(51)

that satisfies the following exact analytical solution \(w\left(x\right)=1/\left(x+1\right)\).

We consider the two initial value problems with initial conditions are

$${y}^{{\prime}{\prime}}={y}^{3}-y{y}^{\prime}, y\left(1\right)=\frac{1}{2}, {y}^{\prime}\left(1\right)={t}_{k},$$
(52)

and

$${ z}^{{\prime}{\prime}}=\left(3{y}^{2}-{y}^{\prime}\right)z -y{z}^{\prime}, z\left(1\right)= 0, {z}^{\prime}\left(1\right)=1.$$
(53)

Then the recursive relationships are

$$\left\{\begin{array}{c} {y}_{0}\left(x\right)=\frac{1}{2}+{t}_{k}x-{t}_{k}, \\ \\ {y}_{n+1}\left(x\right)={L}^{-1}\left({A}_{n}-{B}_{n}\right), n\ge 0,\end{array}\right.$$

and

$$\left\{\begin{array}{c} {z}_{0}\left(x\right)=x-1, \\ \\ {z}_{n+1}\left(x\right)={L}^{-1}\left(3{y}^{2}z-y{z}^{\prime}-{y}^{\prime}z \right), n\ge 0.\end{array}\right.$$

Further, from the above equations, \({A}_{n}\) and \({B}_{n}\) represent the Adomian polynomials in favor of the nonlinear terms \({y}^{3}\) and \(yy{\prime}\), respectively. Moreover, the latter equations reveal the solution of Eq. (52) with \(m=10\) and \(m=20\) via the following series

$$y\left(x\right)=\sum_{k=0}^{m}{y}_{k}={y}_{0}+\dots +{y}_{m}.$$

Lastly, if \(tolerance={10}^{-30}\) is considered, that is, when \(|w\left(b,{t}_{k}\right)-\beta |\le {10}^{-30}\), then \(w\left(x,{t}_{k}\right)\) reveals the solution of the governing model earlier given in Eq. (51) with \(t ={t}_{k}\); see Table 7 and 8 for the numerical results.

The absolute error difference between the exact analytical solution and the suggested solution \({{\varvec{E}}}_{\mathbf{E}\mathbf{D}\mathbf{S}\mathbf{M}}\), which is further verified with \({{\varvec{E}}}_{\mathbf{S}\mathbf{R}\mathbf{K}\mathbf{M}4}\), is shown in Table 7. Table 8 further shows that, when compared to the approaches in [1, 35, 36] and SRKM4, EDSM is the most competent technique for solving the model under consideration. Additionally, Fig. 4 displays a good degree of exactitude in the graphical representation of the exact analytical and approximation solutions.

5 Conclusions

In conclusion, a numerical method has been introduced in the present study to efficiently tackle the class of second-order ODEs, more specifically, the two-point boundary value problems of both the linear and nonlinear forms. After being used on some test problems, the suggested approach performed better than the compared numerical methods. As such, we may conclude that our approach is robust, low-cost, and applicable to various physical models. Finally, we have provided graphical illustrations and tables to visualize the efficacy of the proposed method. In practical applications, we advise applying the Efficient decomposition shooting method to solve boundary value problems because its error is quite slight compared to other methods. These approaches are appealing since most computers have reasonably good subroutines for solving initial value models numerically.