1 Introduction

The global burden of dengue is substantial, with an estimated 50 million infections occurring annually across more than 100 countries [1]. The sickness usually appears 4–7 days after contact, with fever starting suddenly in most cases. The incubation period can last anywhere from 3 to 14 days. It is assumed that viremia, which can be detected by mosquito inoculation, begins two to three days before symptoms appear and peaks at the onset of sickness [2, 3]. Mosquitoes, when feeding on individuals in this febrile, viremic state, can become infected, though the virus is generally cleared from the bloodstream within approximately 7 days of fever onset, largely through intricate immune mechanisms [4, 5]. Mathematical epidemiology employs two primary approaches: homogeneous and heterogeneous modeling [6, 7]. Homogeneous models utilize ordinary differential equations to represent an average of spatial and age structures, providing a simplified understanding of disease spread. Conversely, heterogeneous models offer more nuanced and detailed descriptions of how diseases propagate within populations. In mathematical epidemiology, the heterogeneous modeling paradigm recognizes variations among people in immune responses and population interactions [10], aligning with the perspectives presented by the proposed model. By incorporating elements such as immune cells and dengue-infected monocytes, the model captures the wide range of reactions individuals may exhibit when infected with the virus. Moreover, the model’s realism is enhanced over homogeneous approaches by employing a Caputo-type fractional-order derivative operator, which encapsulates the complexity of interactions between the virus and the host immune system [10]. By considering the diverse immune responses within the population, the model provides a more accurate depiction of dengue virus dynamics overall.Dengue fever, a significant viral mosquito-borne illness, poses a substantial global health threat. Severe manifestations of the disease are associated with the antibody-dependent enhancement (ADE) phenomenon, wherein pre-existing antibodies to dengue can exacerbate subsequent infections [8, 9].The absence of a targeted treatment for dengue underscores the critical importance of vaccine development endeavors, with a primary focus on creating a tetravalent vaccine. Notably, two vaccines, Dengvaxia and DENVax, have successfully completed phase 3 trials [10]. Dengvaxia, administered to seronegative individuals, has raised concerns due to its association with an elevated risk of severe cases, prompting discussions regarding its safety and advocating for pre-vaccination screening tests [11,12,13]. Conversely, DENVax’s efficacy is dependent on individual aerostats [10]. The advancement of vaccines can profoundly contribute to disease eradication through the modeling of within-host interactions. This avenue seeks to deepen our comprehension of how vaccine strategies may be significantly influenced by insights derived from such modeling, particularly in the absence of specific therapies. Ultimately, it underscores the crucial necessity of integrating within-host dynamics modeling into vaccine development endeavors. The intricate dynamics of dengue pose considerable challenges in devising effective control models, necessitating the incorporation of realistic assumptions and robust data [14,15,16,17]. Mathematical models play a pivotal role in forecasting disease dynamics and assessing the efficacy of public health interventions. Fractional-order modeling has gained acceptance in the field of epidemiology for its ability to capture complex and nonlinear disease processes, as many researchers have demonstrated [18,19,20,21,22]. By including memory effects, such as immunity among recovered people, and factoring variable infection and recovery rates over time, as described by previous research [23,24,25], this modeling technique offers an alternative to classic integer-order models. Notable examples of fractional-order models include the Caputo–Fabrizio model and the Atangana–Baleanu model, both of which provide insights into disease dynamics and the influence of healthcare capacity on disease transmission. Nevertheless, additional research is imperative to validate and enhance these models for precise forecasting of disease spread. The model presented in references [26, 27] elucidates the dynamics of dengue virus infection within monocytes, taking into account the immune response. It elucidates the phenomenon of rapid virus clearance approximately 7 days post-symptom onset and demonstrates that higher rates of viral invasion result in diminished levels of free virus and a notable decrease in the basic reproduction ratio. Through numerical simulations, the pivotal role of the immune response in constraining virus proliferation is underscored. Dengue fever presents a significant public health challenge, affecting more than a third of the global population, as noted in references [28,29,30,31]. The disease is caused by four closely related yet antigenically distinct serotypes. Disease severity is intricately linked to an individual’s immunological status, categorized as either seronegative or seropositive, prior to a natural infection with dengue.[36].Introduces the multistep Laplace optimized decomposition method for modeling COVID-19 dynamics, offering a more effective approximation than traditional methods. It uses Caputo-type fractional-order derivatives and graphical analysis to assess growth patterns and computational efficiency, demonstrating high accuracy in understanding COVID-19 dynamics [37]. Presents TFMIADM, a method integrating Dirichlet constraints in the RKHSM framework. It employs Caputo’s partial time derivative and constructs method spaces, discussing convergence and error. Numeric-analytic solutions are expressed through Fourier function expansion in A(H) and B(H) spaces. Algorithms tackle model solving in time and space domains, demonstrated effectively. Concluding remarks emphasize key insights and references [38]. Investigates social media addiction dynamics using the Caputo differential operator, emphasizing its significance. They develop the model with the Caputo scheme and use the Hilbert reproducing scheme to derive numerical solutions. Convergence-error behavior is analyzed, and computational algorithms showcase results. The study concludes with a summary and recommendations for future research [39]. Examines modeling diseases like infectious diseases and cancer, focusing on the interaction between the immune system and cancer cells using fractional differential equations. It covers key aspects such as mathematical framework, solution representation, and error analysis, concluding with summaries of findings and future research suggestions. By employing a novel fractional-order modeling technique to comprehend how the virus propagates within a host with adaptive immunity, the work fills in research gaps regarding the dengue virus.The fractional-order system’s response to different model parameters is examined using the normalized forward sensitivity approach. The generalized mean value theorem is applied to help investigate the model’s solutions, and positivity and boundedness theory are employed. Moreover, the existence and uniqueness of solutions are established using the Banach fixed-point method. It examines several aspects of the immune system and highlights the significance of adaptive immune responses and transmission rates. It also examines how memory affects immunological dynamics, providing information for managing illness. The study presents a novel fractional-order model for understanding dengue virus dynamics within hosts with adaptive immunity, offering original contributions compared to existing models. It comprehensively analyzes immune system components, emphasizing transmission rates and adaptive immune responses, and investigates memory’s impact on immune dynamics to optimize disease control strategies. Compared with traditional integer-order models, the Caputo-type fractional-order derivative operator was used for this model in order to offer a more realistic depiction of dengue viral dynamics within hosts with adaptive immunity. This decision makes it possible to use a more adaptable framework to represent the intricate relationships, such as memory effects and long-range interactions, that exist between the virus and the immune system. The model can more accurately explain derivatives that are common in biological systems but are frequently overlooked in conventional integer-order models by adding fractional-order derivatives. expanding on our knowledge of immune responses and viral dissemination. Overall, the utilization of the Caputo-type fractional-order derivative operator is beneficial since it provides a more accurate representation of the dynamics of the dengue virus and can provide insights that are not possible with conventional models.

2 Preliminaries

2.1 Some fundamental definition from fractional-order within-host Dengue virus model

Following the concepts presented in Refs. [32,33,34,35], it is essential to first provide some fundamental concepts of fractional calculus.

Definition 1

The Riemann–Liouville fractional \(\theta\)-order integral operator of function \(g:\Re_{ + } \to \Re\), denoted \(J^{\theta } g(t)\) is defined as

$$ J^{\theta } (g) = \frac{1}{\Gamma (\theta )}\int\limits_{0}^{t} {\frac{g(\xi )}{{(t - \xi )}}} d\xi . $$

where \(\theta \in \Re_{ + }\) such that \(\theta \in (0,1)\) and \(\,t > 0\).The gamma function.\(\Gamma (\theta )\), is given by

$$ \Gamma (\theta ) = \int\limits_{0}^{\infty } {\chi^{\theta - 1} \ell^{ - \chi } d\chi .} $$

Definition 2

The Caputo fractional \(\theta\)-order derivative of \(g:\Re_{ + } \to \Re\),denoted \(J^{\theta } g(t)\) is defined as

$$ {}^{C}J^{\theta } (g) = \frac{1}{\Gamma (1 - \theta )}\int\limits_{0}^{t} {\frac{{g^{:} (\xi )}}{(t - \xi )}} d\xi . $$

where \(\,0 < \theta \le 1\) and \(J^{\theta } (g) = {\raise0.7ex\hbox{${d^{\theta } }$} \!\mathord{\left/ {\vphantom {{d^{\theta } } {dt^{\theta } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${dt^{\theta } }$}}.\)

Lemma 1

Generalized Mean Value Theorem

Let \(f(t) \in C[0,t^{ * } ]\) and \({}^{C}J^{\theta } f(t) \in C[0,t^{ * } ]\)\(for\,\,\,\,0 < \theta \le 1\), then \(f(t) = f(0) + \frac{{{}^{C}J^{\theta } f(\phi )t^{\theta } }}{\Gamma (\theta )}\),\(\phi \in [0.t],\forall \,\,t \in (0,t^{ * } ),\)

\((i)\,\,if\,\,\,{}^{C}J^{\theta } f(\phi ) \ge 0\,\,\,\,\forall \,\,t \in (0,t^{ * } )\,\,\,\,then\,\,f(t)\,\,is\) non-decreasing for each \(\forall \,\,\,t \in (0,t^{ * } ).\)

\((ii)\,\,if\,\,\,{}^{C}J^{\theta } f(\phi ) \le 0\,\,\,\,\forall \,\,t \in (0,t^{ * } )\,\,\,\,then\,\,f(t)\,\,is\) non-decreasing for each \(\forall \,\,\,t \in (0,t^{ * } ).\)

Lemma 2

let \(\,\varpi (t) \in C(0,\infty )\) satisfies

$$ \,{}^{C}J^{\theta } \zeta (t) + b_{1} \zeta (t) \le a_{2} ,\,\zeta (0) = \zeta_{0} , $$

where \(\theta \in \,(0,1]\,\,\,and\,\,b_{1} ,b_{2\,} \, \in \Re \,\,\,\,with\,\,b_{1} \ne 0\) then \(\zeta (t) \le \left( {\varpi_{0} - \frac{{b_{2} }}{{b_{1} }}} \right)\,\,E_{b.1} ( - b_{1} t^{\theta } ) + \frac{{b_{2} }}{{b_{1} }}.\)

Where \(E_{b.1}\)(.) is a Mittag-Leffer operator given by \(E_{b.1} (y) = \sum\limits_{n = 0}^{\infty } {\frac{{y^{n} }}{\Gamma (bn + 1)}} .\)

Definitions 3

  1. i.

    The Laplace transform of a positive real function \(\chi (\psi )\) given by \(L\chi (\psi ) = \chi (s)\):\(\chi (s) = \int\limits_{0}^{\infty } {e^{ - s\tau } \chi (\psi )} d\psi .\)

  2. ii.

    If \(\chi (\psi )\) s of order \(\alpha\), then its Laplace transform is given by:\(L[\chi^{\alpha } (\psi )] = \xi^{\alpha } L[\chi (\psi )] - \xi^{\alpha - 1} \chi (0) - \xi^{\alpha - 2} \chi ^{\prime}(0) - \xi^{\alpha - 3} \chi ^{\prime\prime}(0).\)

  3. iii.

    The inverse Laplace transform of the function \(\frac{\chi (s)}{s}\) is \(L^{ - 1} \frac{\chi (s)}{s} = \int\limits_{0}^{\tau } {\chi (\psi )d\psi } .\)

Definition 4

The Adomian polynomials denoted by \(X_{0} ,X_{1...} X_{k}\), consists in the decomposition of the unknown function \(\chi (\psi ))\) whose series can be expressed as \(\chi (\psi ) = \chi_{0} + \chi_{1} + \chi_{2} + \chi_{k}\) is given as:

$$ X_{k} = \frac{1}{k}\frac{{d^{k} }}{{d\Psi^{k} }}\left[ {\chi (\psi )\sum\limits_{m = 0}^{j} {X_{m} \Psi^{m} } } \right]_{\chi = 0} . $$

2.2 Steps of solutions of Laplace–Adomian decomposition method

Consider the subsequent fractional-order differential equation given by;

$$ {}^{C}J^{\alpha } P(t) = L_{i} (P_{1} ,P_{2} ,P_{3} , \cdots P_{i} ) + Z_{i} (P_{1} ,P_{2} ,P_{3} , \cdots P_{i} ).Y $$

Subject to

\(P^{\alpha } (0) = c_{k}^{i}\), for \(i = 1,2,3...m,\) and \(\,n_{i - 1} \le \alpha \le n_{i}\).

Where \(L_{i}\), \(Z_{i}\) respectively denotes the linear and nonlinear differential operators and \({}^{C}J^{\alpha } P_{i} (t)\) is Caputo–Fabrizio operator of \(i\) number of unspecified functions \(P(t)\).

To apply the Laplace–Adomian decomposition method on the described system we start by performing the Laplace transform on Eq. (1).\(L\left[ {\,{}^{C}J^{\alpha } w_{i} (t)\,} \right] = L\left[ {\,\,L_{i} (P_{1} ,P_{2} ,P_{3} , \cdots P_{i} ) + Z_{i} (P_{1} ,P_{2} ,P_{3} , \cdots P_{i} )\,\,} \right]\).

Applying Definition 3, on (2) yields:

$$\frac{{sL\left[ {P_{i} \left( t \right)} \right] - P_{i} \left( 0 \right)}}{{s + \alpha \left( {1 - s} \right)}} = L\left[ {\,\,L_{i} (P_{1} ,P_{2} ,P_{3} , \cdots P_{i} ) + Z_{i} (P_{1} ,P_{2} ,P_{3} , \cdots P_{i} )\,\,} \right]. $$

Utilizing the Adomian decomposition method, the unknown function is decomposed as:

$$P_{i} (t) = \sum\limits_{j = 0}^{\infty } {P_{ij} (t),} \quad i = 1,2,3 \cdots ,m, $$

While the nonlinear terms are given by:

\(Z_{i} (w_{1} ,...w_{i} ) = \sum\limits_{j = 0}^{\infty } {X_{ij} (t),}\)\(i = 1,2,...m\).

And \(A_{ij}\) is the Adomian polynomial defined in definition yields:

$$ L\left[ {\sum\limits_{j = 0}^{\infty } {P_{ij} (t)} } \right]\, = \frac{{P_{i}^{{k_{i} }} (0)}}{s} + \frac{{s + \alpha \left( {1 - s} \right)}}{s}\left( {L\,\,\left[ {L_{i} \left( {\sum\limits_{j = 0}^{\infty } {P_{1j} (t),...,\sum\limits_{j = 0}^{\infty } {P_{mj} (t)} } } \right)} \right] + L\left[ {\sum\limits_{j = 0}^{\infty } {X_{ij} (t)} } \right]} \right) $$

Applying the inverse Laplace transform to both sides of (6) yields \(w_{1j} ,w_{2j} , \ldots w_{n,j} ,\,j \ge 0\):

\(P_{i(j + 1)} (t) = L^{ - 1} \left( {\frac{{P_{i}^{{k_{i} }} (0)}}{s}} \right) + L^{ - 1} \left( {\frac{{s + \alpha \left( {1 - s} \right)}}{s}L\left[ {\,\,L_{i} \left( {\sum\limits_{j = 0}^{\infty } {P_{1j} (t),...,\sum\limits_{j = 0}^{\infty } {P_{mj} (t)} } } \right)} \right] + L\left[ {\sum\limits_{j = 0}^{\infty } {X_{ij} (t)} } \right]} \right)\).

Which simplifies to the required recurrence relation given by

$$ P_{i(j + 1)} (t) = c_{k}^{i} + L^{ - 1} \left( {\frac{{s + \alpha \left( {1 - s} \right)}}{s}L\left[ {\,\,L_{i} \left( {\sum\limits_{j = 0}^{\infty } {P_{1j} (t),...,\sum\limits_{j = 0}^{\infty } {P_{mj} (t)} } } \right)} \right] + L\left[ {\sum\limits_{j = 0}^{\infty } {X_{ij} (t)} } \right]} \right) $$

3 Method

3.1 Formulation of model

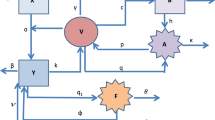
In this section, reference [26] presents Eq. (1) to model the growth of the dengue virus population in the human body, starting from detectable viremia, about two days before symptoms appear. We assume a single serotype of the virus targeting monocytes. Denoted as S(t), I(t), V(t), and Z(t), the model represents densities of susceptible and infected monocytes, free virus particles, and immune cells. We then derive Eqs. (2) and (3) by reformulating the classical derivative in (1) using fractional order and Caputo-derivative methods.

$$ \left. \begin{gathered} \frac{dS}{{dt}} = \mu - \alpha S - aSV, \hfill \\ \frac{dI}{{dt}} = aSV - \beta_{1} I - \upsilon IZ, \hfill \\ \frac{dV}{{dt}} = kI - \gamma V - \alpha SV, \hfill \\ \frac{dZ}{{dt}} = c_{1} I + dIZ - \delta Z. \hfill \\ \end{gathered} \right) $$
(1)

3.2 Potential limitations and assumptions of the proposed model

The dengue viral population growth model that has been suggested implies that there is only one virus serotype that targets monocytes. To reformulate classical derivatives, fractional order and Caputo-derivative methods are employed. Potential oversimplification in describing virus dynamics, ambiguities in parameter estimates, and a restricted emphasis on monocytes are some of the limitations. By addressing these issues, the applicability of the model becomes evident, and potential areas for improvement are highlighted.

From Eq. (1), Ref. [26]

$$ \left. \begin{gathered} \frac{{d^{\alpha } S(t)}}{dt} = \mu - \alpha S(t) - aS(t)V(t), \hfill \\ \frac{{d^{\alpha } I(t)}}{dt} = aS(t)V(t) - \beta_{1} I(t) - \upsilon I(t)Z(t), \hfill \\ \frac{{d^{\alpha } V(t)}}{dt} = kI(t) - \gamma V(t) - aS(t)V(t), \hfill \\ \frac{{d^{\alpha } Z(t)}}{dt} = c_{1} I(t) + dI(t)Z(t) - \delta Z(t). \hfill \\ \end{gathered} \right) $$
(2)

where \(\beta_{1} = \beta + \frac{\eta \upsilon }{\delta }\) and \(c_{1} = c + \frac{\eta d}{\delta }\).

For biological factors, the region of model (2) is restricted by \(\chi = \{ (S,I,V,Z):S,I,V,Z \ge 0\}\),

Furthermore, all of the parameters in model (2) are positive. If we substitute \(S = 0\) into the first equation of model (2), we get \(\frac{{d^{\alpha } S(t)}}{dt} \ge 0\). Substituting \(I = 0,\,V = 0\,,\,\,\,and\,\,\,\,Z = 0\) into model (2) second, third, and fourth equations, accordingly.

We get \(\frac{{d^{\alpha } I(t)}}{dt} \ge 0\),\(\frac{{d^{\alpha } V(t)}}{dt} \ge 0\) and \(\frac{{d^{\alpha } Z(t)}}{dt} \ge 0\) respectively. In other words, the vector field on the boundary of \(\chi\) does not point to the exterior of \(\chi\). Hence the region \(\chi\) is positively invariant under the flow induced by model (2).

The process of reformulating and analyzing the derivative in the caputo fractional order mathematical model of equation leads to Eq. (3).

$$ \left. \begin{gathered} {}^{C}J^{{\alpha_{1} }} S(t) = \mu - \alpha S(t) - aS(t)V(t), \hfill \\ {}^{C}J^{{\alpha_{1} }} I(t) = aS(t)V(t) - \beta_{1} I(t) - \upsilon I(t)Z(t), \hfill \\ {}^{C}J^{{\alpha_{1} }} V(t) = kI(t) - \gamma V(t) - aS(t)V(t), \hfill \\ {}^{C}J^{{\alpha_{1} }} Z(t) = c_{1} I(t) + dI(t)Z(t) - \delta Z(t). \hfill \\ \end{gathered} \right) $$
(3)

With initial conditions

$$ S(0) = S_{0} ,\,\,I(0)\, = I_{0} ,\,\,V(0)\, = V_{0} ,\,\,Z(0) = Z_{0} \,. $$
(4)

where \({}^{{{{}{}}c}}J^{\alpha } 0 \le \alpha \le 1\) for the fractional order Caputo derivative and \(\alpha\) for the fractional time derivative. This model’s initial conditions Eq. (4) satisfy a predetermined relationship and are mutually independent.

Numerical solutions are investigated by applying the Adomian decomposition method (ADM) in combination with Laplace transform on the given fractional-order model. To validate the generated results, both initially conditions and parameters are assigned random values.

The following Table 1 presents the definition of each compartment and provides a description of each parameter utilized in the model.

Table 1 Variables and parameters descriptions
Full size table

3.3 Analysis of the fractional model

In this section, we will use integer-order methods to quantitatively evaluate the mathematical model. This will allow us to assess its characteristics and practical uses, to examine the characteristics of solutions to the non-integer order within-host Dengue virus model.

3.3.1 Positivity and boundedness properties

Theorem 1

The solution \(S(t)\),\(I(t)\),\(V(t)\) and \(Z(t)\) of the fractional-order within-host Dengue virus model (3) are non-negative for all t > 0, if the initial conditions (4) are non-negative.

Proof

It is implied from system (3) that

$$ {}^{C}J^{{\alpha_{1} }} S(t)\left| {_{S = 0} } \right.\,\,\,\,\,\,\,\, = \mu > 0. $$
$$ {}^{C}J^{{\alpha_{1} }} I(t)\left| {_{I = 0,S,V \ge 0} } \right.\,\,\,\,\, = aS(t)V(t) \ge 0. $$
(5)
$$ {}^{C}J^{{\alpha_{1} }} V(t)\left| {_{V = 0,I \ge 0} } \right.\,\,\,\,\, = KI(t) \ge 0. $$
$$ {}^{C}J^{{\alpha_{1} }} Z(t)\left| {_{Z = 0,I \ge 0} } \right.\,\,\,\,\, = c_{1} I(t) \ge 0. $$

Given that the Caputo derivatives in Eq. (5) are non-negative on the bounding planes \(\Re_{ + }^{4}\), we may apply the modified mean value theorem (see Lemma 1). When the initial conditions (4) are non-negative, this theorem implies that the solutions S(t), I(t), V(t), and Z(t) are non-decreasing for all t > 0.

3.3.2 Existence and uniqueness of solution

In this subsection, existence and uniqueness of solution of the fractional-order dengue virus model (2) is investigated by employing Banach fixed point theory technique [33].other possible methods as presented in [33] can also be employed to establish existence and uniqueness results for fractional models. Let the fractional system (2) be re-written in compact form.

$$ {}^{C}J^{\theta } (g(t)) = H(t,g(t)),0 \le t \le \varphi . $$
$$ g(0) = g_{0} . $$

where \(g(t) = (S(t),I(t),V(t),Z(t))^{T}\), and \(H(t,g(t)):[0,0] \times \Re_{ + }^{4} \to \Re .[0,0]\)\( \times \Re_{ + }^{4} \to \Re .\)

Defined by \(H(t,g(t)) = (H,(S,I,V,Z))^{T} i = 1,2,.......4\) so that

$$ \left. \begin{gathered} H_{1} (t,S,I,V,Z) = \mu - \alpha S(t) - aS(t)V(t), \hfill \\ H_{2} (t,S,I,V,Z) = aS(t)V(t) - \beta_{1} I(t) - \upsilon I(t)Z(t), \hfill \\ H_{3} (t,S,I,V,Z) = kI(t) - \gamma V(t) - aS(t)V(t), \hfill \\ H_{4} (t,S,I,V,Z) = c_{1} I(t) + dI(t)Z(t) - \delta Z(t). \hfill \\ \end{gathered} \right) $$
(6)

Integrating system (6) fractionally using Definition 1, the following Voltterra integral equation is obtained.

$$ g(t) = g_{0} + \frac{1}{\Gamma (\theta )}\int_{0}^{t} {(t - \phi )^{\theta - 1} } H(\phi ,g(\phi ))d\phi . $$
(7)

Let \({\rm B} = (C[0,\varphi ].\left\| . \right\|)\) be a Banach space for all continuous \(\Re\)- valued function with the supremum norm defined by \(\left\| {g(t)} \right\| = \sup \{ \left| {g(t)} \right|:t \in [0.\phi ].\) it requires to show that \(H(t,g(t))\) satisfies Lipschitz continuity. To do this, the next result is claimed.

Theorem 3

If there exists a constant \(\kappa \ge 0\) such that

$$ \left\| {H(t,g_{1} (t)) - H(t,g_{2} (t))} \right\| \le \kappa \left\| {g_{1} (t) - g_{2} (t)} \right\|. $$
(8)

then \(H(t,g_{1} (t))\) is Lipschitz continuous for all \(g_{1} (t),g_{2} (t),g_{2} (t)\)) in \(C([0,\phi ] \times \Re_{ + }^{4} ,\Re \,\,and\,\,t \in [0,\phi ]\).

Proof

Recall that solutions of the fractional-order dengue model (2) are bounded in a positively invariant set \(\Phi\). Now, for \(S_{1} (t)\) and \(S_{2} (t)\), one has

$$ \left\| {H_{1} (t,S_{1} ,I,V,Z) - H_{1} (t,S_{2} ,I,V,Z)} \right\| \le \left\| {\alpha - a} \right\|\,\left\| {S_{1} - S_{2} } \right\|. $$
(9)

Consequently, since \(V \le P_{1} \,\,\,\,in\,\,\Phi\)

$$ \left\| {H_{1} (t,S_{1} ,I,V,Z) - H_{1} (t,S_{2} ,I,V,Z)} \right\| \le \kappa_{1} \,\left\| {S_{1} - S_{2} } \right\|. $$
(10)

where \(\kappa_{1} = \alpha - a > 0\).

In a similar way

$$ \left\| {H_{2} (t,S,I_{1} ,V,Z) - H_{2} (t,S,I_{2} ,V,Z)} \right\| \le \kappa_{2} \,\left\| {I_{1} - I_{2} } \right\|. $$
(11)

where \(\kappa_{2} = \beta_{1} - \upsilon Z > 0\), since \(Z \le \upsilon Z\)

$$ \left\| {H_{3} (t,S,I,V_{1} ,Z) - H_{3} (t,S,I,V_{2} ,Z)} \right\| \le \kappa_{3} \,\left\| {V_{1} - V_{2} } \right\|. $$
(12)

where \(\kappa_{3} = \gamma - \alpha S > 0\), since \(S \le \alpha S\)

$$ \left\| {H_{4} (t,S,I,V,Z_{1} ) - H_{4} (t,S,I,V,Z_{2} )} \right\| \le \kappa_{4} \,\left\| {z_{1} - z_{2} } \right\|. $$
(13)

where \(\kappa_{4} = \delta - dI > 0\), since \(I \le dI\).

Therefore, condition (8) is satisfied, where \(\kappa = \max \{ \kappa_{1} ,\kappa_{2} ,\kappa_{3} ,\kappa_{4} \}\) is the Lipschitz constant.

Next, define the fixed point of an operator \(G:{\rm B} \to {\rm B}\) by \(G(g(t) = g(t)\) so that

$$ G(g(t) = = g_{0} + \frac{1}{\Gamma (\theta )}\int_{0}^{t} {(t - \phi )^{\theta - 1} } H(\phi ,g(\phi ))d\phi . $$
(14)

Theorem 4

The fractional-order within-host Dengue model (2) (equivalently, system (8)) has a unique solution if \(\phi^{\theta } \kappa < \Gamma (\theta + 1).\)

Proof.

It suffices to prove that \(G\) is a contraction. Since \(H(t,g(t))\) is Lipchitz continuous as shown in Theorem 3, then for \(g_{1} (t),g_{2} (t) \in {\rm B}\) and \(0 \le t \le \phi\).

$$ \begin{gathered} \left\| {G(t,g_{1} (t)) - G(t,g_{2} (t))} \right\| = \left\| {\frac{1}{\Gamma (\theta )}\int_{0}^{t} {(t - \phi )^{\theta - 1} } [H(\phi ,g_{1} (\phi )) - H(\phi ,g_{2} (\phi ))]d\phi } \right\|, \hfill \\ \le \frac{1}{\Gamma (\theta )}\int_{0}^{t} {(t - \phi )^{\theta - 1} } [H(\phi ,g_{1} (\phi )) - H(\phi ,g_{2} (\phi ))]d\phi , \hfill \\ \le \frac{\kappa }{\Gamma (\theta )}\left\| {[g_{1} (\phi ) - g_{2} (\phi ))]} \right\|\int_{0}^{t} {(t - \phi )^{\theta - 1} } d\phi , \hfill \\ \le \Omega \left\| {[g_{1} (\phi ) - g_{2} (\phi ))]} \right\|. \hfill \\ \end{gathered} $$
(15)

where \(\Omega = \phi^{\theta } \kappa /(\theta \,\Gamma (\theta ))\).It follow that \(\Omega < 1\) if \(\phi^{\theta } \kappa < \Gamma (\theta + 1)\), Hence. \(G\) is a contraction, and a unique solution exist for the fractional-order within-host model of Dengue virus.

3.3.3 Basic reproduction number

The reproduction ratio of the SIVZ model (3) is associated with the reproduction power of the fever.

$$ R_{0} = \sqrt {\frac{\kappa }{\beta }} \frac{{{\raise0.7ex\hbox{${a\mu }$} \!\mathord{\left/ {\vphantom {{a\mu } \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}}{{\gamma + {\raise0.7ex\hbox{${a\mu }$} \!\mathord{\left/ {\vphantom {{a\mu } \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}}. $$
(16)

4 Sensitivity analysis on basic reproduction number

It is important to know how the parameters of the model affect the dynamical behavior of the within-host Dengue system. This will help provide effective measure that can be targeted at controlling the spread of infected cells and virus in the host system.to achieve this, sensitivity analysis of the model is conducted as follow, using Ref. [26].By definition, the normalized forward sensitivity index \(\Phi\) of a variable n that depends differentiable on a parameter q is defined as

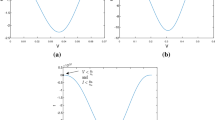
$$ \Phi_{q}^{{R_{0} }} = \frac{{\partial R_{0} }}{\partial q} \times \frac{q}{{R_{0} }}. $$

The threshold quantity for the fractional –order within-host Dengue model (2) is the basic reproduction number \(R_{0}\) with respect to each of all its associated parameters are calculated, and the results are depicted in Fig. 1 it can be seen

$$R_{0} = \sqrt {\frac{\kappa }{\beta }} \frac{{a\mu /\alpha }}{{\gamma + a\mu \$ /\alpha }}. $$
Fig. 1
figure 1

Sensitivity chart of essential parameters contained in \(\Re_{0}\)

Full size image

The outlines of the sensitivity of each parameter’s impact on the basic reproduction number \(\Re_{0}\). Both \(\kappa\) and \(a\) have a significant influence, \(\beta\) denote a reduction in the likelihood of transmission, suggesting factors that mitigate the spread of the virus. Contribution make \(\Re_{0}\) high. This highlights the need to address their roles by implementing factors potentially capable of lowering their value because positive sensitivity on \(\Re_{0}\), we have graphical representation in Fig. 1.

Table 2 provides a comprehensive overview of indices, both positive and negative, pertaining to \(\Re_{0}\). Positive indices within this table signify an increased potential for virus transmission, indicating a higher risk of spreading the infection. Conversely, negative indices denote a reduction in the likelihood of transmission, suggesting factors that mitigate the spread of the virus. Our analysis delves deeply into the intricate dynamics of virus propagation, shedding light on the pivotal role played by susceptible cell responses to incoming virus particles. It becomes evident that these responses significantly influence the spread of the virus. In particular, we observe a strong correlation between a higher invasion rate parameter ‘a’ and an elevated likelihood of contracting the virus. This highlights the importance of considering host susceptibility when assessing the risk of viral transmission. Furthermore, our study unveils intriguing insights into the impact of antigenic immune responses on virus propagation. Notably, cytotoxic T lymphocytes (CTLs) and antibodies, crucial components of the immune system’s defense mechanism, exhibit a negative impact on virus propagation. This suggests their ability to effectively combat the proliferation of infected cells and Dengue virus (DENV) particles, thereby curbing the spread of the infection. To visually depict the sensitivity of these factors on \(\Re_{0}\), Fig. 1 presents a Sensitivity chart showcasing key parameters. This graphical representation aids in understanding the relative influence of different variables on virus transmission dynamics.Moreover, our findings are further elucidated through Fig. 2, which depict dynamic responses to variations in essential parameters. These 2-D plots provide a detailed visualization of how factors such as the invasion rate parameter ‘a’ and the impact of antigenic immune responses shape the trajectory of virus propagation over time.

Table 2 Sensitivity index of each parameter on \(\Re_{0}\)
Full size table
Fig. 2
figure 2

2D of Essential parameters contained in \(\Re_{0}\)

Full size image

This study underscores the critical importance of considering both host susceptibility and immune responses when assessing the risk and dynamics of virus transmission. By highlighting key parameters and their influence on virus propagation, we contribute valuable insights to the understanding of viral spread and the development of effective control strategies.

4.1 Simulated response of \(\Re_{0}\) to model parameters

We study and observe the impact and contribution of each parameter on the basic reproduction number \(\Re_{0}\). Figures 3, 4, 5, 6 and 7. From an epidemiological standpoint, while antigenic immunity is crucial in restricting the replication of viral particles by bolstering the presence of Cytotoxic T-Lymphocytes and antibodies, there is a requirement to enhance initiatives and treatments specifically aimed at suppressing the replication of infected cells during the invasion of DENV particles on susceptible cells.

Fig. 3
figure 3

Impact and contribution of parameters \(\beta\) contained in \(\Re_{0}\)

Full size image
Fig. 4
figure 4

Impact and contribution of parameters \(a\) contained in \(\Re_{0}\)

Full size image
Fig. 5
figure 5

Impact and contribution of parameters \(\gamma\) contained in \(\Re_{0}\)

Full size image
Fig. 6
figure 6

Impact and contribution of parameters \(\mu\) contained in \(\Re_{0}\)

Full size image
Fig. 7
figure 7

Impact and contribution of parameters \(\alpha\) contained in \(\Re_{0}\)

Full size image

5 Laplace–Adomian Decomposition Method Application to Model

Using Laplace transforms and Adomian polynomials to provide a numerical solution for Eq. (3) is widespread in physics, engineering, and biology, particularly in scenarios where alternative methods are inefficient. Taking the Laplace transform of Eq. (3), we obtain the following:

$$ \left. \begin{gathered} L\{ {}^{C}J^{\theta } S(t)\} = L\{ \mu - \alpha S(t) - aS(t)V(t)\} , \hfill \\ L\{ {}^{C}J^{\theta } I(t)\} = L\{ aS(t)V(t) - \beta_{1} I(t) - \upsilon I(t)Z(t)\} , \hfill \\ {}^{C}J^{\theta } V(t) = L\{ kI(t) - \gamma V(t) - aS(t)V(t)\} , \hfill \\ {}^{C}J^{\theta } Z(t) = L\{ c_{1} I(t) + dI(t)Z(t) - \delta Z(t)\} . \hfill \\ \end{gathered} \right\} $$
(17)
$$ \left. \begin{gathered} S^{\theta } S(t) - S^{\theta - 1} S(0) = L\{ \mu - \alpha S(t) - aS(t)V(t)\} , \hfill \\ S^{\theta } I(t) - S^{\theta - 1} I(0) = L\{ aS(t)V(t) - \beta_{1} I(t) - \upsilon I(t)Z(t)\} , \hfill \\ S^{\theta } V(t) - S^{\theta - 1} V(0) = L\{ kI(t) - \gamma V(t) - aS(t)V(t)\} , \hfill \\ S^{\theta } Z(t) - S^{\theta - 1} Z(0) = L\{ c_{1} I(t) + dI(t)Z(t) - \delta Z(t)\} . \hfill \\ \end{gathered} \right\} $$
(18)
$$ \left. \begin{gathered} S^{\theta } S(t) = S^{{\theta_{1} - 1}} S(0) + L\{ \mu - \alpha S(t) - aS(t)V(t)\} , \hfill \\ S^{\theta } I(t) = S^{\theta - 1} I(0) + L\{ aS(t)V(t) - \beta_{1} I(t) - \upsilon I(t)Z(t)\} , \hfill \\ S^{\theta } V(t) = S^{\theta - 1} V(0) + L\{ kI(t) - \gamma V(t) - aS(t)V(t)\} , \hfill \\ S^{{\theta_{1} }} Z(t) = S^{\theta - 1} Z(0) + L\{ c_{1} I(t) + dI(t)Z(t) - \delta Z(t)\} . \hfill \\ \end{gathered} \right\} $$
(19)
$$ \left. \begin{gathered} S(t) = S^{ - 1} S(0) + \frac{1}{{S^{\theta } }}L\{ \mu - \alpha S(t) - aS(t)V(t)\} , \hfill \\ I(t) = S^{ - 1} I(0) + \frac{1}{{S^{\theta } }}L\{ aS(t)V(t) - \beta_{1} I(t) - \upsilon I(t)Z(t)\} , \hfill \\ V(t) = S^{ - 1} V(0) + \frac{1}{{S^{\theta } }}L\{ kI(t) - \gamma V(t) - aS(t)V(t)\} , \hfill \\ Z(t) = S^{ - 1} Z(0) + \frac{1}{{S^{\theta } }}L\{ c_{1} I(t) + dI(t)Z(t) - \delta Z(t)\} . \hfill \\ \end{gathered} \right\} $$
(20)

Assuming that the solution \(S(t),I(t),V(t),Z(t).\) are in form infinite series by

$$ \begin{gathered} S(t) = \sum\limits_{n = 0}^{ \propto } {S_{n} } ,I(t) = \sum\limits_{n = 0}^{ \propto } {I_{n} ,} .V(t) = \sum\limits_{n = 0}^{ \propto } {V_{n} } , \hfill \\ Z(t) = \sum\limits_{n = 0}^{ \propto } {Z_{n} } . \hfill \\ \hfill \\ \end{gathered} $$
(21)

And nonlinear term involved in the model are \(S(t)V(t)\), \(I(t)Z(t)\) are decomposed by Adomain.

$$ S(t)V(t) = \sum\limits_{n = 0}^{ \propto } {A_{n} } \,\,\,\,\,\,\,\,\,\,I(t)Z(t) = \sum\limits_{n = 0}^{ \propto } {B_{n} } .$$
(22)

where \(A_{n} ,\,B_{n}\) are Adomain polynomial given by:

$$ \begin{gathered} A_{n} = \frac{1}{\Gamma (n + 1)}\frac{{d^{n} }}{dt} \left[\sum\limits_{k = o}^{n} {^{{}} } \lambda^{k} S_{K} \sum\limits_{k = 0}^{n} {\lambda^{n} } V_{k} \right]\lambda ,\,\,\,\, \hfill \\ B_{n} = \frac{1}{\Gamma (n + 1)}\frac{{d^{n} }}{dt}\left[\sum\limits_{k = o}^{n} {^{{}} } \lambda^{k} I_{K} \sum\limits_{k = 0}^{n} {\lambda^{n} } Z_{k} \right]\lambda . \hfill \\ \end{gathered} $$
(23)

Substitute Eq. 21, 22 and 23 in the Eq. (20)

$$ \left. \begin{gathered} S(t) = S^{ - 1} S(0) + \frac{1}{{S^{\theta } }}L\{ \mu - \alpha S_{n} (t) - aA_{n} \} , \hfill \\ I(t) = S^{ - 1} I(0) + \frac{1}{{S^{\theta } }}L\{ aA_{n} - \beta_{1} I_{n} (t) - \upsilon B_{n} \} , \hfill \\ V(t) = S^{ - 1} V(0) + \frac{1}{{S^{\theta } }}L\{ kI_{n} (t) - \gamma V_{n} (t) - aA_{n} \} , \hfill \\ Z(t) = S^{ - 1} Z(0) + \frac{1}{{S^{\theta } }}L\{ c_{1} I_{n} (t) + dB_{n} - \delta Z_{n} (t)\} . \hfill \\ \end{gathered} \right\} $$
(24)

Using initial condition in Eq. (24),

We have

$$ \left. \begin{gathered} S(t) = \frac{{n_{1} }}{S} + \frac{1}{{S^{\theta } }}L\{ \mu - \alpha S_{n} (t) - aA_{n} \} , \hfill \\ I(t) = \frac{{n_{2} }}{S} + \frac{1}{{S^{\theta } }}L\{ aA_{n} - \beta_{1} I_{n} (t) - \upsilon B_{n} \} , \hfill \\ V(t) = \frac{{n_{3} }}{S} + \frac{1}{{S^{\theta } }}L\{ kI_{n} (t) - \gamma V_{n} (t) - aA_{n} \} , \hfill \\ Z(t) = \frac{{n_{4} }}{S} + \frac{1}{{S^{\theta } }}L\{ c_{1} I_{n} (t) + dB_{n} - \delta Z_{n} (t)\} . \hfill \\ \end{gathered} \right\} $$
(25)

To get the solution of each compartment, we iterate term in Eq. (25) and taking the Laplace inverse gives general formula for the model

$$ \left. \begin{gathered} \sum\limits_{n = 0}^{\infty } {S_{n + 1} } (t) = L^{ - 1} [\frac{1}{{S^{\theta } }}L\{ \mu - \alpha S_{n} (t) - aA_{n} \} ], \hfill \\ \sum\limits_{n = 0}^{\infty } {I_{n + 1} } (t) = L^{ - 1} [\frac{1}{{S^{\theta } }}L\{ aA_{n} - \beta_{1} I_{n} (t) - \upsilon B_{n} \} ], \hfill \\ \sum\limits_{n = 0}^{\infty } {V_{n + 1} } (t) = L^{ - 1} [\frac{1}{{S^{\theta } }}L\{ kI_{n} (t) - \gamma V_{n} (t) - aA_{n} \} ], \hfill \\ \sum\limits_{n = 0}^{\infty } {Z_{n + 1} } (t) = L^{ - 1} [\frac{1}{{S^{\theta } }}L\{ c_{1} I_{n} (t) + dB_{n} - \delta Z_{n} (t)\} ]. \hfill \\ \end{gathered} \right\} $$
(26)

The followings were obtained from (26);

$$ S_{0} = n_{1} ,I_{0} = n_{2} ,V_{0} = n_{3} ,Z_{0} = n_{4} . $$
(27)

When n = 0, from first equation of (26)

$$ \begin{aligned} S_{1} & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {\mu - \alpha S_{0} - aA_{0} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {\mu - \alpha Sn_{1} - an_{1} n_{3} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}*\frac{1}{S}\left\{ {\mu - \alpha Sn_{1} - an_{1} n_{3} } \right\}} \right],\, \hfill \\& = L^{ - 1} \left[ {\left\{ {\mu - \alpha Sn_{1} - an_{1} n_{3} } \right\}\frac{1}{{S^{\theta + 1} }}} \right], \hfill \\ & = (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)}. \hfill \\ \end{aligned} $$
(28)

When n = 0, in second equation of Eq. (26) to obtain the following;

$$ \begin{aligned} I_{1} & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {aA_{0} - \beta_{1} I_{0} - \upsilon B_{0} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}*\frac{1}{S}\left\{ {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\left\{ {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right\}\frac{1}{{S^{\theta + 1} }}} \right], \hfill \\ I_{1} & = \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)}. \hfill \\ \end{aligned} $$
(29)

Also, when n = 0, in third equation of (26) to obtain this;

$$ \begin{aligned} V_{1} & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {kI_{0} - \gamma V_{0} - \alpha A_{0} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}*\frac{1}{S}\left\{ {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\left\{ {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right\}\frac{1}{{S^{\theta + 1} }}} \right], \hfill \\ V_{1} & = \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)}. \hfill \\ \end{aligned} $$
(30)

Similarly, when n = 0, from fourth equation of (26) to obtain this;

$$ \begin{aligned} Z_{1} & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {c_{1} I_{0} + dB_{0} - \delta Z_{0} } \right\}} \right], \hfill \\& = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}*\frac{1}{S}\left\{ {c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\left\{ {c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} } \right\}\frac{1}{{S^{\theta + 1} }}} \right], \hfill \\ Z_{1} & = (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)}. \hfill \\ \end{aligned} $$
(31)

When n = 1, from first equation of (26)

$$ \begin{aligned} S_{2} & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {\mu - \alpha S_{1} (t) - aA_{1} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ \begin{gathered} \mu - \alpha (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)} - a(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)} \hfill \\ + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)}) \hfill \\ \end{gathered} \right\}} \right], \hfill \\ & = L^{ - 1} \left[ \begin{gathered} \frac{1}{{S^{\theta } }}*\{ \mu - \alpha (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} - a(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} \hfill \\ + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }})\} \hfill \\ \end{gathered} \right], \hfill \\ & = L^{ - 1} \left[ \begin{gathered} \frac{1}{{S^{\theta } }}*\{ \mu - \alpha (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{1}{{S^{\theta + 1} }} - a(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{1}{{S^{\theta + 1} }} \hfill \\ + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{1}{{S^{\theta + 1} }})\} \hfill \\ \end{gathered} \right],\, \hfill \\ & = L^{ - 1} \left[ {\left\{ \begin{gathered} \{ \mu - \alpha (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{1}{{S^{2\theta + 1} }} - a(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{1}{{S^{2\theta + 1} }} \hfill \\ + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{1}{{S^{2\theta + 1} }} \hfill \\ \end{gathered} \right\}} \right], \hfill \\ S_{2} & = \left\{ \mu - \alpha (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} - a \left(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} \right. \right. \hfill \\ &\quad \left. \left. + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}\right)\right\}. \end{aligned} $$
(32)

When n = 1, from second equation of (26).

$$ \begin{aligned} I_{2} & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {aA_{1} - \beta_{1} I_{1} - \upsilon B_{1} } \right\}} \right], \hfill \\& = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}\left\{ \begin{gathered} a(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)}) \hfill \\ - \beta_{1} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)} - \upsilon (n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)}) \hfill \\ + n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)}) \hfill \\ \end{gathered} \right\}} \right]& = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}\left\{ \begin{gathered} a(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }}) \hfill \\ - \beta_{1} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} - \upsilon (n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }}) \hfill \\ + n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} \hfill \\ \end{gathered} \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}\left\{ \begin{gathered} a(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{1}{{S^{\theta + 1} }} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{1}{{S^{\theta + 1} }}) \hfill \\ - \beta_{1} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{1}{{S^{\theta + 1} }} - \upsilon (n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{1}{{S^{\theta + 1} }}) \hfill \\+ n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{1}{{S^{\theta + 1} }}) \hfill \\ \end{gathered} \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\left\{ \begin{gathered} a(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{1}{{S^{2\theta + 1} }} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{1}{{S^{2\theta + 1} }}) \hfill \\ - \beta_{1} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{1}{{S^{2\theta + 1} }} - \upsilon (n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{1}{{S^{2\theta + 1} }}) \hfill \\+ n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{1}{{S^{2\theta + 1} }}) \hfill \\ \end{gathered} \right\}} \right],\, \hfill \\ I_{2} & = a \left(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} \right) \hfill \\ & \quad - \beta_{1} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} - \upsilon \left(n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} \right. \hfill \\ & \quad \left. + n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} \right). \hfill \\ \end{aligned} $$
(33)

When n = 1, from third equation of (26).

$$ \begin{aligned} V_{2} & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {kI_{1} - \gamma V_{1} - aA_{1} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ \begin{gathered} k\left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)} - \gamma \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)} \hfill \\ - a(n_{3} (\mu - \alpha n_{1} - an_{1} n_{3} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)}) \hfill \\ \end{gathered} \right\}} \right], & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}\left\{ \begin{gathered} k\left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} - \gamma \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} \hfill \\ - a(n_{3} (\mu - \alpha n_{1} - an_{1} n_{3} )\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }}) \hfill \\ \end{gathered} \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}\left\{ \begin{gathered} k\left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{1}{{S^{\theta + 1} }} - \gamma \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{1}{{S^{\theta + 1} }} \hfill \\ - a(n_{3} (\mu - \alpha n_{1} - an_{1} n_{3} )\frac{1}{{S^{\theta + 1} }} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{1}{{S^{\theta + 1} }}) \hfill \\ \end{gathered} \right\}} \right], \hfill \\ & = L^{ - 1} \left[ \begin{gathered} k\left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{1}{{S^{2\theta + 1} }} - \gamma \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{1}{{S^{2\theta + 1} }} \hfill \\ - a(n_{3} (\mu - \alpha n_{1} - an_{1} n_{3} )\frac{1}{{S^{2\theta + 1} }} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{1}{{S^{2\theta + 1} }}) \hfill \\ \end{gathered} \right], \hfill \\ V_{2} & = k\left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} - \gamma \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} \hfill \\ & \quad - a \left(n_{3} (\mu - \alpha n_{1} - an_{1} n_{3} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} \right). \hfill \\ \end{aligned} $$
(34)

When n = 1, from fourth equation of (26) to obtain the following;

$$ \begin{aligned} & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ {c_{1} I_{1} + dB_{1} - \delta Z_{1} } \right\}} \right], \hfill \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}L\left\{ \begin{gathered} c_{1} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)} + d \left(n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)}\right) \hfill \\ + n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)} - \delta (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)} \hfill \\ \end{gathered} \right\}} \right], \\ & = L^{ - 1} \left[ {\frac{1}{{S^{\theta } }}\left\{ \begin{gathered} c_{1} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} + d \left(n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} \right) + \hfill \\ n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} - \delta (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{\Gamma (\theta + 1)}{{\Gamma (\theta + 1)S^{\theta + 1} }} \hfill \\ \end{gathered} \right\}} \right], \hfill \\ Z_{2} & = c_{1} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} + d\left(n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}\right) \hfill \\ & \quad + n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} - \delta (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} \hfill \\ \end{aligned} $$
(35)
$$ \begin{aligned} S_{1} &= (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)}. \hfill \\ I_{1} &= \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)}. \hfill \\ V_{1} &= \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{\theta } }}{\Gamma (\theta + 1)}. \hfill \\ Z_{1}& = (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{\theta } }}{\Gamma (\theta + 1)}. \hfill \\ S_{2} &= \{ \mu - \alpha (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} - a \left(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}\right) \hfill \\ & \quad + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}.\,\,\,\,\, \hfill \\ I_{2} & = a\left(n_{3} (\mu - \alpha Sn_{1} - an_{1} n_{3} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}\right) \hfill \\ & \quad - \beta_{1\,\,} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} - \upsilon \left(n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} \right. \hfill \\ & \quad \left. + n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}\right) \hfill \\ V_{2} & = k\left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} - \gamma \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} \hfill \\ &\quad - a\left(n_{3} (\mu - \alpha n_{1} - an_{1} n_{3} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} + n_{1} \left( {kn_{2} - \gamma n_{3} - \alpha n_{1} n_{3} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}\right). \hfill \\ Z_{2} & = c_{1} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)} + d(n_{4} \left( {an_{1} n_{3} - \beta_{1} n_{2} - \upsilon n_{2} n_{4} } \right)\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}) \hfill \\ & \quad + n_{2} (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}) - \delta (c_{1} n_{2} + dn_{2} n_{4} - \delta n_{4} )\frac{{t^{2\theta } }}{\Gamma (2\theta + 1)}.\,\, \hfill \\ \end{aligned} $$
(36)

6 Results and discussion

6.1 Results

In order to gain a better understanding of the dynamics and control of the dengue virus, we present a numerical simulation. Following the simulations initial values and parameters in Table 1 to evaluate the results we have obtained the following series solution of arbitrary order;

$$ S = 84 + \frac{{79.53716t^{\alpha } }}{\Gamma (\theta + 1)} - \frac{{26.31671192t^{2\theta } }}{\Gamma (2\theta + 1)}. $$
(37)
$$ I = - \frac{{0.59916t^{\alpha } }}{\Gamma (\theta + 1)} + \frac{{0.720419120t^{2\theta } }}{\Gamma (2\theta + 1)}. $$
(38)
$$ V = \frac{{15.51916t^{\alpha } }}{\Gamma (\theta + 1)} - \frac{{24.46712t^{2\theta } }}{\Gamma (2\theta + 1)}. $$
(39)
$$ Z = - \frac{{0.5040t^{\alpha } }}{\Gamma (\theta + 1)} + \frac{{0.51909180t^{2\theta } }}{\Gamma (2\theta + 1)}. $$
(40)

6.2 Numerical simulation

For the subsequent numerical simulations, we utilize T-cell parameters as the basis for immune cell characteristics, where μ = 80 cells/(day·μL), α = 3 days (Ref. [26]). The estimated value of η is derived under the assumption that the equilibrium density of immune cells in the absence of infection is 2000 cells. In this model, the disease’s endemic status hinges on individual responses to incoming viruses. A higher invasion rate a increases the likelihood of contracting the disease, while a greater elimination rate ν of infected cells reduces the infection risk. The fractional-order behavior is depicted in Figs. 7, 8, 9, and 10, illustrating the dynamics of S, I, V, and Z for varying successful virus invasion rates. Initially, the susceptible monocyte S decreases, reaches a minimum value, and then returns to equilibrium. The patterns of free virus, V, and infected cells, I, are similar, initially increasing to maximum values before decreasing to equilibrium levels. Higher values of a correspond to elevated virus loads, but critical conditions emerge after symptom onset. The abundance of immune cells, Z, increases with age. Figures 11, 12, 13 and 14 show the dynamics of S, V, and Z for different contact rates between infected monocytes and immune cells. The variation of d has a contrasting effect on the densities of S, I, and V compared to the variation of a. increasing the parameter d.

Fig. 8
figure 8

Fractional order \(\theta\) effect on susceptible monocytes

Full size image
Fig. 9
figure 9

Fractional order \(\theta\) effect on infected monocytes

Full size image
Fig. 10
figure 10

Fractional order \(\theta\) effect on dengue particles

Full size image
Fig. 11
figure 11

Fractional order \(\theta\) effect on immune response CTL

Full size image
Fig. 12
figure 12

Infection rate \(a\) effect on susceptible monocytes

Full size image
Fig. 13
figure 13

Infection rate \(a\) effect on free dengue particles

Full size image
Fig. 14
figure 14

Rate of Infected monocytes to virus particles \(\upsilon\) effect on infected monocytes

Full size image

6.3 Discussion

A fractional-order model examines dengue virus dynamics within a host, focusing on adaptive immune memory. The basic reproductive threshold (R0 = 3.535) indicates the virus’s threat. Figures 1 and 2 underscore the importance of the sensitivity of each parameter’s impact on the basic reproduction number through 2-D plots depicting the responses to two variations in parameters. Figures 3, 4, 5, 6 and 7 observe the parameter impact on the reproduction number.

Antigenic immunity restricts viral replication by boosting cytotoxic T-lymphocytes and antibodies. It’s crucial to suppress infected cell replication during DENV invasion. Figures 8, 9, 10 and 11 analyze cell dynamics using fractional-order Caputo derivatives, focusing on immune memory’s impact.Results show reinforcing viral invasion measures increase susceptible cells and decrease infected cells, enhancing the immune response. Figures 12 and 13 reveal the infection rate’s effect. Figures 14 and 15 show the rate of infected monocytes effect on virus particles. Figure 16a–d compare cell distribution at fractional and classical orders.

Fig. 15
figure 15

Rate of Infected monocytes to free virus particles \(\upsilon\) effect on immune response

Full size image
Fig. 16
figure 16

a Classical order \(\theta\) effect on susceptible monocytes. b Fractional order \(\theta\) effect on susceptible monocytes. c Classical order \(\theta\) effect on infected monocytes. d Fractional order \(\theta\) effect on infected monocytes

Full size image

Figure 16a–d suggest reduced viral dispersion at α = 0.75 compared to α = 1, potentially leading to faster infected cell concentration declined. This approach reveals strategies for reducing dengue virus concentration, crucial in understanding infection dynamics. with the help of the Maple 18 software package’s Range-Kutta module that used to perform calculations, simulations, and data analysis in the study.

7 Conclusion

In this study, similar to previous investigations on dengue fever models, within-host dengue fever has been described in the literature [32,33,34,35].

The transmission model was fractionalized with the Caputo derivative operator and qualitatively examined using several analytical approaches. The fractional-order model illustrates the interplay of four mutually exclusive compartments: healthy (density of susceptible monocytes), infected monocytes, free dengue particles, immune cells, and two adaptive immunological immune responses (cytotoxic T-lymphocytes (CTLs)). The basic qualitative analysis utilizing the well accepted a positively invariant region containing limited and non-negative solutions is defined by the mean value theorem Banach fixed point.

The fractional-order within-host dengue fever model’s existence and uniqueness were established through the application of theory. The normalized forward sensitivity approach was used to conduct a sensitivity analysis, which indicated that the parameter values should be increased. The work presents a fractional-order within-host dengue fever model and investigates the relationships between immune cells, free dengue particles, susceptible monocytes, and infected monocytes. Important details consist of: Understanding Dynamics, The concept helps to explain how diseases spread among their hosts. Targets for therapeutic actions are identified by treatment insights. The development of vaccines aids in assessing vaccination tactics and efficacy. Result Anticipation: Sensitivity analysis forecasts changes in parameters. Interventions to reduce the burden of disease are guided by public health consequences. To sum up, the model improves understanding of the dynamics of dengue fever and provides information for future research, medical interventions, and public health campaigns.