1 Introduction

Mathematics is integrally involved in every aspect of our life. Especially in every aspect of our real life, mathematics has applications. Differential equations (DE) are used as tools to solve many difficult problems in our real life. With the help of differential equations we can find the formula to solve many important problems in many areas of our life like mental, physical, medical principles etc. Differential equations are linear, non-linear, dependent or independent. Non-linear differential equations (NLDE) play many important roles in the area of science and engineering.

Solving linear differential equations (LDEs) is rather simple. But, due to the nonlinear terms are present, it is exceedingly complicated and challenging to solve nonlinear differential equations (NLDEs). Due to this fact, it is common practice to solve nonlinear differential equations by converting them into linear differential equations from a variety of perspectives. But to transform all NLDEs into LDEs is not often feasible. In these situations, there are some key methods that can be used to solve the NLDEs without transforming them into LDEs, including the perturbation method, the harmonic balance method, and the iteration method.

The perturbation method is appropriate for solving nonlinear differential equations where the nonlinearities are small, whereas the harmonic balance method is appropriate for solving nonlinear differential equations where the nonlinearities are strong, and the iteration method is appropriate for solving nonlinear differential equations with both strong and small nonlinearities. Mickens was the first to suggest the Harmonic Balance Method (HBM) in 1984. Then Gottlieb, Hu & Tang, and other mathematicians contributed to develop the method. Iteration Method is a powerful analytical method that can be solved truly nonlinear differential equations. R. E. Mickens introduced the iteration method for the first time in 1987. The HBM and the iteration method are fundamentally different from each other. As for instance in the harmonic balance method, the variable has to be initially gauged up to a certain label but cannot be changed later. But it is overcome in iteration method. At different stages in the iteration method we can even take different types of harmonics for our advantage. For example if we are working with 5th harmonic and for our convenience we can also work with 3rd harmonic at the next stage. So it is an advantage for us that we do not see this kind of limitation in the case of iteration method as a method of perturbation and harmonic balance.

The third-order derivative of displacement is called ‘jerk’ and it was first introduced by Schot [26] in 1978. In other words jerk is named as the rate of change of acceleration. Clearly, considering time, first, second and third derivative are respectively referred to velocity, acceleration and jerk. This type of equation is called nonlinear jerk equation.

Jerk equation form is generally

$$ \dddot x = J(x,\dot{x},\ddot{x})\, $$
(1)

where \(J(x,\dot{x},\ddot{x})\) denotes the jerk functions.

Among the researchers who presented analytical solutions to these oscillators, Gottlieb [6] used the inferential periodic solution and the lowest order harmonic balance method for the corresponding angular frequency. Gottlieb found that solution and the angular frequency was not accurate enough. To solve the nonlinear jerk equations and their higher order approximations, Wu et al. [8] and Leung et al., [7] conducted an advanced HBM and a residual harmonic balance method respectively. The objective of their method was to obtain accurate results for large amplitude oscillators. To describe higher order probabilistic solutions of the non-linear jerk equation Ma et al. [5] and Hu [1] conducted the homotopy perturbation method. But their results were not good. Ramos [2,3,4] presented some procedures to solve nonlinear jerk equations. It has been observed that the second reduction procedure yields good solutions in the case of unit or tends to unit initial velocities. In [2], Ramos provided very good results for the first and second differential equations that were obtained by four approximate methods based on order reduction; this result was as good to or more good than the results obtained by the parameter perturbation method. A modified method of Mickens for a nonlinear jerk equation was presented by Hu et al. [18], and Newton's method of approximate angular frequency helped to obtain the second order. With cubic nonlinearities, a residual harmonic balance method has been introduced by Leung et al. [7] for describing the boundary cycles of the parity. Recently Haque [9] introduced a new method of direct iteration [19] with a view to solving the nonlinear jerk oscillator, which contained acceleration and velocity of displacement time. Mohammadian et al. [21], Mohammadian & Shariati [22], Mohammadian & Akbarzade [23], Mohammadian [24, 25], Akgül & Hijaz [27], Luqman et al. [28], Safdar et al. [29], Bansi et al. [30], Partohaghighi et al. [31], Akgül et al.[32], Chen, & Xing [33], Cao et al. [34], Gao et al. [35], Chen et al. [36], Liu et al. [37], Yin et al. [38], Plastino et al. [39] solved various nonlinear problems using some effective and important methods.

Some restrictions have been placed on the mathematical form of the superlative oscillator for achieving a periodic solution for jerk-oscillators. Gottlieb [6] taken into consideration only the third order nonlinear function \(\dot{x}\ddot{x}^{2}\).

Based on invariance of time-reversal and space-reversal, generalized jerk function is written following the form [6] because it carries only third order nonlinearity

$$ \dddot x = \alpha x\dot{x}\ddot{x} - \beta \dot{x}\ddot{x}^{2} - \gamma \dot{x} - \delta x^{2} \dot{x} - \varepsilon \dot{x}^{3} $$
(2)

Over dot’s are denoted by derivatives with respect to time \({\text{t}}\) and the parameters \(\alpha ,\,\,\beta ,\,\,\gamma ,\,\,\delta\) and \(\varepsilon\) the actual constant is given. Any one or two of these parameters (aside from \(\alpha \) and \(\delta \) simultaneously) may be set to unity by rescaling \(x\) and/or \(t\) to produce standard equations with fewer control parameters appropriate for more in-depth analysis. (Of course, a parameter shouldn't be "normalized" in this way if the behavior of a specific term that has a very small coefficient needs to be examined.)

The relevant prerequisites are:

$$ x(0) = 0,\,\,\dot{x}(0) = A\;and\;\ddot{x}(0) = 0\,. $$
(3)

Three initial conditions in Eq. (4) periodic requirements must be fulfilled. Here at least one of \(\alpha ,\,\,\beta ,\,\,\gamma ,\,\,\delta\) and \(\varepsilon\) should be non-zero.

In this article, it has been presented Haque’s approach with Mickens’ iteration method to obtain the approximate analytical solutions of the nonlinear jerk oscillator including displacement time velocity and acceleration. Following the application of the suggested method, more accurate, workable, and compatible results were discovered. Effective simplification has been discovered from the change, ensuring that the solution is free of algebraic complications. The computed results produced by the suggested method have been compared to the exact result as well as the outcomes of other approaches that are currently in use. The results obtained exhibit a rapid convergence towards the exact values, with errors far less than those found in the literature.

2 The approach

Let's have a look at a nonlinear oscillator that is described by

$$ \ddot{x} + f(\dot{x},\,\ddot{x}) = 0,\,\,\,x(0) = 0,\,\,\dot{x}(0) = A $$
(4)

where the over-dots represent the time-related differentiation, t, over dash denotes integration with respect to time. Also Ω is the frequency. By adding \(\Omega^{2} x\) of both sides of Eq. (5), we have

$$ \ddot{x} + \Omega^{2} x = \Omega^{2} x - f(\dot{x},\ddot{x}) \equiv G(\dot{x},\ddot{x}) $$
(5)

Following [17], we formulate the iteration scheme as

$$ \ddot{x}_{k + 1} + \Omega_{k}^{2} x_{k + 1} = G(\dot{x}_{k} ,\ddot{x}_{k} );k = 0,1,2....... $$
(6)

combined with

$$ x_{0} (t) = A\cos (\Omega_{0} t) $$
(7)

Herein satisfies the conditions

$$ x_{k + 1} (0) = A,\dot{x}_{k + 1} (0) = 0 $$
(8)

The requirement that secular words shouldn't appear in the solution at any point during the iteration determines \(\Omega_{k}\). For further information, see [18]. The solutions are provided in the following order: \(x_{0} (t),\,x_{1} (t),\,.......\). The approach can be applied to any level of approximation, but the solution is limited to a lower order, typically the second [15] due to increased algebraic complexity.

3 Process for a solution

We have measured the function \(\dot{x}\ddot{x}^{2}\) containing velocity times acceleration squared i.e. jerk function.

The model of nonlinear jerk oscillator is.

$$ \dddot x + \dot{x} = x\dot{x}\ddot{x} $$
(9)

Let \(\dot{x} = y\) where is the space variable \(y(t)\). Then the Eq. (9) becomes.

$$ \ddot{y} + y = y\dot{y}y^{\prime} $$
(10)

Apparently, Eq. (10) becomes

$$ \ddot{y} + \Omega^{2} y = (\Omega^{2} - 1 + \dot{y}y^{\prime})y $$
(11)

Now the iteration scheme is according to.

$$ \ddot{y}_{k + 1} + \Omega_{k}^{2} y_{k + 1} = (\Omega_{k}^{2} - 1 + \dot{y}_{k} y^{\prime}_{k} )y_{k} $$
(12)

Equation (7) becomes.

$$ y_{0} = y_{0} (t) = A\cos \theta $$
(13)

where \(\theta = \Omega \,t\), for k = 0 the Eq. (12) becomes.

$$ \ddot{y}_{1} + \Omega_{0}^{2} y_{1} = (\Omega_{0}^{2} - 1 + \dot{y}_{0} y^{\prime}_{0} )y_{0} $$
(14)

Substituting the right-hand side of Eq. (14) into the elementary function Eq. (13) and expanding it into a cosine series, we get

$$ \ddot{y}_{1} + \Omega_{0}^{2} y_{1} = a_{11} \cos \theta + a_{13} \cos 3\theta $$
(15)
$$ {\text{where}}\;a_{11} = \, \frac{A}{4}( - 4 - A^{2} + 4\Omega_{0}^{2} )\;a_{13} = \frac{{A^{3} }}{4} $$
(16)

We must remove \(\cos \theta\) from the right side of the Eq. (15) to evade secular terms in the solution, and we get

$$ \Omega_{0}^{2} = \frac{{4 + A^{2} }}{4} $$
(17)

After solving Eq. (15) and meeting the initial requirement \(y_{1} (0) = A\) we have,

$$ y_{1} (t) = (A + a_{13} \frac{1}{{8\Omega_{0}^{2} }})\cos \theta + a_{13} \frac{1}{{ - 8\Omega_{0}^{2} }}\cos 3\theta $$
(18)

It is necessary to determine \(\Omega_{1}\) in relation to this first approximation of the solution to Eq. (11). The solution will reveal the value of \(\Omega_{1}\).

$$ \ddot{y}_{2} + \Omega_{1}^{2} y_{2} = (u^{2} - 1 + z_{1} w_{1} )y_{1} $$
(19)

where \(u={\Omega }_{1}\)

Substituting \(y_{1}\) into the Eq. (19) from Eq. (18) and then trigonometrically expanding we obtain

$$ \ddot{y}_{2} + \Omega_{1}^{2} y_{2} =\,a_{21} \cos \theta + a_{23} \cos 3\theta + a_{25} \cos 5\theta + a_{27} \cos 7\theta + a_{29} \cos 9\theta $$
(20)

where

$${a}_{21}=-\frac{64A}{{(4+{A}^{2})}^{3}}-\frac{66{A}^{3}}{{(4+{A}^{2})}^{3}}-\frac{76{A}^{5}}{3{(4+{A}^{2})}^{3}}-\frac{275{A}^{7}}{64{(4+{A}^{2})}^{3}}-\frac{279{A}^{9}}{1024{(4+{A}^{2})}^{3}}+\frac{64A{u}^{2}}{{(4+{A}^{2})}^{3}}+\frac{50{A}^{3}{u}^{2}}{{(4+{A}^{2})}^{3}}+\frac{13{A}^{5}{u}^{2}}{{(4+{A}^{2})}^{3}}+\frac{9{A}^{7}{u}^{2}}{8{(4+{A}^{2})}^{3}}$$
$${a}_{23}=\frac{18{A}^{3}}{{(4+{A}^{2})}^{3}}+\frac{31{A}^{5}}{2{(4+{A}^{2})}^{3}}+\frac{287{A}^{7}}{64{(4+{A}^{2})}^{3}}+\frac{223{A}^{9}}{512{(4+{A}^{2})}^{3}}-\frac{2{A}^{3}{u}^{2}}{{(4+{A}^{2})}^{3}}-\frac{{A}^{5}{u}^{2}}{{(4+{A}^{2})}^{3}}-\frac{{A}^{7}{u}^{2}}{8{(4+{A}^{2})}^{3}}$$
$${a}_{25}=-\frac{13{A}^{5}}{6{(4+{A}^{2})}^{3}}-\frac{241{A}^{7}}{192{(4+{A}^{2})}^{3}}-\frac{93{A}^{9}}{512{(4+{A}^{2})}^{3}}$$
$${a}_{27}=\frac{13{A}^{7}}{192{(4+{A}^{2})}^{3}}+\frac{39{A}^{9}}{2048{(4+{A}^{2})}^{3}}$$
$${a}_{29}=-\frac{{A}^{9}}{2048{(4+{A}^{2})}^{3}}$$
(21)

We must remove \(\cos \theta\) from the right side of the Eq. (20) to evade secular terms in the solution, and we get

$${\Omega }_{1}=\frac{\sqrt{196608+202752{A}^{2}+77824{A}^{4}+13200{A}^{6}+837{A}^{8}}}{\sqrt{196608+153600{A}^{2}+39936{A}^{4}+3456{A}^{6}}}$$
(22)

Satisfying the initial condition \(y_{2} (0) = A\), after solving equation and we have

$${y}_{2}=\left(A-{\text{a}}23\frac{1}{-8{u}^{2}}-{\text{a}}25\frac{1}{-24{u}^{2}}-{\text{a}}27\frac{1}{-48{u}^{2}}-{\text{a}}29\frac{1}{-80{u}^{2}}\right){\text{Cos}}\left[\theta \right]+{\text{a}}23\frac{1}{-8{u}^{2}}{\text{Cos}}\left[3\theta \right]+ {\text{a}}25\frac{1}{-24{u}^{2}}{\text{Cos}}[5\theta ]+{\text{a}}27\frac{1}{-48{u}^{2}}{\text{Cos}}[7\theta ]+{\text{a}}29\frac{1}{-80{u}^{2}}{\text{Cos}}[9\theta ]$$
(23)

It is necessary to determine \({\Omega }_{2}\) in relation to this second approximation of the solution to Eq. (10). The solution will reveal the value of \({\Omega }_{2}\)

$$ \ddot{y}_{3} + \Omega_{2}^{2} y_{3} = (v^{2} - 1 + z_{2} w_{2} )y_{2} $$
(24)

where \(v={\Omega }_{2}\)

Substituting \(y_{2}\) from Eq. (23) into the Eq. (24) and then expanding in a trigonometric reduce we get,

$$ \ddot{y}_{3} + \Omega_{2}^{2} y_{3} = \sum\limits_{i = 1}^{5} {a_{2(2i - 1)} \cos (2i - 1)\theta } $$
(25)

where

$${\text{a}}31=-\frac{14843406974976A}{{\left(4+{A}^{2}\right)}^{3}{\left(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6}\right)}^{3}}-\frac{48704929136640{A}^{3}}{{\left(4+{A}^{2}\right)}^{3}{\left(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6}\right)}^{3}}-\frac{73635603677184{A}^{5}}{{\left(4+{A}^{2}\right)}^{3}{\left(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6}\right)}^{3}}-\dots \dots \dots \dots +\frac{453505107{A}^{23}{v}^{2}}{10{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}+\frac{303605847{A}^{25}{v}^{2}}{320{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}$$
$${\text{a}}33=\frac{4174708211712{A}^{3}}{{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}+\frac{13045963161600{A}^{5}}{{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}+\frac{93366515662848{A}^{7}}{5{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}+\dots \dots \dots -\frac{57316365{A}^{23}{v}^{2}}{8{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}-\frac{10768005{A}^{25}{v}^{2}}{64{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}$$
$$\dots \dots \dots $$
$$\dots \dots \dots .$$
$${\text{a}}323=\frac{1062763{A}^{23}}{1548288000{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}+\frac{535081{A}^{25}}{1376256000{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}+\frac{3232683{A}^{27}}{58720256000{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}$$
$${\text{a}}325=-\frac{2509{A}^{25}}{1101004800{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}-\frac{7527{A}^{27}}{11744051200{(4+{A}^{2})}^{3}{(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})}^{3}}$$
(26)

We must remove \(\cos \theta\) from the right side of the Eq. (25) to evade secular terms in the solution, and we get

$${\Omega }_{2}=(\surd (1470839609502185029632000+4826192468679044628480000{A}^{2}+7296583778952951103488000{A}^{4}+6729655286686996758528000{A}^{6}+4224062453812034745139200{A}^{8}+1905190794429295126118400{A}^{10}+635148579378340823040000{A}^{12}+158430275820381536256000{A}^{14}+29559820082388423147520{A}^{16}+4072969446127757557760{A}^{18}+402650199557972162560{A}^{20}+27028701991773424000{A}^{22}+1103351520402981540{A}^{24}+20664999056050911{A}^{26}))/(\surd (1470839609502185029632000+4458482566303498371072000{A}^{2}+6185793448860155117568000{A}^{4}+5195136748778629890048000{A}^{6}+2942060899402643197132800{A}^{8}+1183763398031645972889600{A}^{10}+347054002037317435392000{A}^{12}+74713245367727554560000{A}^{14}+11723452070119656652800{A}^{16}+1307822024910333542400{A}^{18}+98471182016367820800{A}^{20}+4493801696683622400{A}^{22}+94013857927987200{A}^{24}))$$
(27)

Satisfying the initial condition \(y_{3} (0) = A\), after solving Eq. (25) we have

$$ y_{3} = \sum\limits_{j = 1}^{13} {b_{2j - 1} \cos (2j - 1)\theta } $$
(28)

where

$${\text{b}}1=(A(15390791571754665742385707116134400000+66372788653191996014038361938329600000{A}^{2}+134560875748061218770912364462080000000{A}^{4}+\dots \dots +67570451934855362616032854200{A}^{32}+989314829845834376935281807{A}^{34}))/(425779200(4+{A}^{2})(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})(1470839609502185029632000+4826192468679044628480000{A}^{2}+\dots \dots +1103351520402981540{A}^{24}+20664999056050911{A}^{26}))$$
$${\text{b}}3=({A}^{3}(17350730036700335658353295360000+72113971715035770080030883840000{A}^{2}+140446403027324546431397658624000{A}^{4}+\dots \dots +476625556767476625248088{A}^{30}+7833777738590256505155{A}^{32}))/(15360(4+{A}^{2})(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})(1470839609502185029632000+\dots \dots +27028701991773424000{A}^{22}+1103351520402981540{A}^{24}+20664999056050911{A}^{26}))$$
$$\dots \dots \dots $$
$$\dots \dots \dots $$
$${\text{b}}23=({A}^{23}(1088269312+616413312{A}^{2}+87282441{A}^{4})(23592960+24330240{A}^{2}+9397760{A}^{4}+1618520{A}^{6}+105309{A}^{8}))/(8110080(4+{A}^{2})(6144+4608{A}^{2}+1136{A}^{4}+93{A}^{6})(1470839609502185029632000+4826192468679044628480000{A}^{2}+\dots \dots +27028701991773424000{A}^{22}+1103351520402981540{A}^{24}+20664999056050911{A}^{26}))$$
$${\text{b}}25=-(193{A}^{25}(32+9{A}^{2})(23592960+24330240{A}^{2}+9397760{A}^{4}+1618520{A}^{6}+ 105309{A}^{8}))/(16384(4+{A}^{2})(6144+4608{A}^{2}+1136{A}^{4}+ +93{A}^{6})(1470839609502185029632000+\dots \dots +27028701991773424000{A}^{22}+ 1103351520402981540{A}^{24}+20664999056050911{A}^{26}))$$
(29)

It is necessary to determine \({\Omega }_{3}\) in relation to this second approximation of the solution to Eq. (10). The solution will reveal the value of \({\Omega }_{3}\)

Similarly the method can be obtained by higher order approximation and respectively Eqs.(17, 22, 27),.… represent the approximate frequencies of the oscillator (10).

4 Findings and discussion

The proposed method is advanced based on Mickens’ iteration method [20] for solving several classes of nonlinear jerk equations. To compare the obtained results to exact results and others existing results obtained from different methods of the nonlinear jerk equations, and to calculate the percentage error (prevail by %) of our obtained results compared to the exact results, we have used the following formula

$$ Error = \left| {\frac{{T_{e} - T_{k} }}{{T_{e} }}} \right| \times 100\% $$

where the various approximate periods obtained by \(T_{0} ;k = 0,1,2.....\) is illustrated the modified method and the oscillator's exact period, denoted by the letter h, is indicated \(Te\).

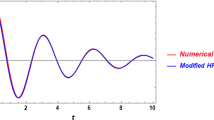
We now want to show a comparison of oscillator results. That is, the velocity of the displacement time is for the acceleration of time and the jerk function containing the velocity. Nowadays, without the iteration method, Ramos [2], Ma et al. [5] and Gottlieb [6] have found approximate solutions, frequency and time approximations to the nonlinear jerk oscillators (given in Eq. 10). Here we have used modified iteration method to get neighboring solutions, which is quite simple. In most cases our results yielded better results than those obtained by other researchers and in many cases almost matched other researchers. Here we have considered the first, second and third nearest frequencies \(\Omega_{0} ,\Omega_{1}\) and \(\Omega_{2}\) respectively and corresponding periods are \(T_{0} ,T_{1}\) and \(T_{2}\).Our results are shown in Tables 1 and 2. Besides we have also provided the results of Gottlieb [6], Ma et al. [5] and Ramos [2] respectively to compare the estimated frequencies. A graph is provided in the Fig. 1 where the comparative graph of our obtained result and exact result is presented.

Table 1 Analyzing the differences between the approximate and exact periods \({T}_{e}\) of \(\dddot x + \dot{x} = x\dot{x}\ddot{x}\)
Full size table
Fig. 1
figure 1

The third-order approximate solutions for A = 1 of \(\dddot x + \dot{x} = x\dot{x}\ddot{x}\) compare with the corresponding exact solution

Full size image

5 Conclusion

In this study, the majority of solutions are synthesized to be much better. The modified solutions demonstrate that the modification is more accurate than other existing approaches and is valid for the large amplitude of oscillation in the jerk system. The adopted modification is determined to be stable, efficient, and compliant. Additionally, it offers a significant number of appropriate solutions to the nonlinear jerk equations that occur in applied mathematics, mathematical physics, and other engineering disciplines, including mechanical, electrical, and space engineering. After considering every angle of all the ways examined in Table 2, we get to the conclusion that the adopted method is much superior to each equivalent level demonstrated by other methods. We concluded by summarizing:

  1. (i)

    The suggested approach is an effective strategy for examining random oscillations. A severely nonlinear oscillator's approximate frequencies and related periodic solutions can be easily and effectively obtained using this technique.

  2. (ii)

    The suggested method outperforms previous existing findings in terms of approximate frequencies and related periodic solutions as well as high validity for both small and large beginning oscillation amplitudes.

  3. (iii)

    The maximum percentage error for the third order approximate period of nonlinear Jerk oscillator containing displacement time velocity and time acceleration is 1.40 e-1.

  4. (iv)

    It has been determined that the majority of researchers have used the procedure to alter the method in order to enhance the solutions in the iteration method, but we have focused on rearranging the leading oscillators with their own merit and selecting appropriate harmonic terms from trigonometric expansion. These two have been determined to be equally important for obtaining better answers.

  5. (v)

    The suggested strategy also yields outstanding results for higher-order, while most strategies yield good results for first-order answers but not good results for higher-order.

Table 2 Approximate periods obtained by the proposed method compare with exact periods \({T}_{e}\) and other existing periods of \(\dddot x + \dot{x} = x\dot{x}\ddot{x}\)
Full size table