Further insights into steady three-dimensional MHD Sakiadis flows of radiating-reacting viscoelastic nanofluids via Wakif’s-Buongiorno and Maxwell’s models

Abstract

Keeping in mind the stress relaxation tendency of many viscoelastic multi-phase flows (e.g., polymer solution flows and transport phenomena of red cell suspensions within blood media), the present research investigation intends principally to develop a realistic model for revealing properly the aspects of reacting-radiating Maxwell nanofluids during their laminar boundary layer flows in the steady regime over a horizontal impermeable surface under a transversal magnetic influence. For this purpose, the principal leading differential formulation is derived theoretically by linking Wakif’s-Buongiorno approach with Maxwell’s model. By invoking fundamentally the general boundary layer assumptions and the passive control strategy for the nanoparticles, the governing PDEs’ formulation is simplified accordingly and then stated properly for the case of the convective heating condition at the impermeable bi-stretching surface. By executing a feasible non-dimensionalization technique, the monitoring ODEs’ system is achieved successfully, whose solutions are presented precisely in different illustrative scenarios using Richardson’s extrapolation method. After carrying out successfully several validating tests, it is demonstrated that the weakly viscoelastic feature has generally a slight delaying effect on the nanofluid motion. This dynamical weakening can be reinforced more with the generation of thermal energy by intensifying the external magnetic field source. Additionally, these physical factors show an intensifying influence on the surface drag forces. However, a dropping impression is seen for the local heat transfer at the contact surface. Contrary to the broadening impact of the radiative heat transfer as well as the convective heating and thermophoresis mechanisms on the thermal and mass boundary layer regions, it is witnessed that the first-order chemical reaction mechanism and Brownian’s motion exhibit a shrinking impact on the mass boundary layer region.

1 Introduction

Nowadays, the exceptional features of nanofluids [1, 2] have gained much attention from pioneering researchers in the field of thermal sciences and fluid dynamics [3,4,5,6,7] owing to their useful applications in different vital fields (e.g., heat exchangers, cooling of microelectronic devices and engine.

vehicles, computers, pharmaceutical productions, biomedicine areas, chemical engineering, drug delivery, and photovoltaic thermal collectors). Experimentally, the stable nanofluidic mixtures are obtained principally by the feeble volumetric addition of one kind (i.e., for the monotype nanofluids) or more than two types (i.e., for the hybrid nanofluids) of insoluble nano-sized particles (e.g., graphene, metal oxides, carbon nano-tubes, metals, ceramic oxides, and metal alloys) into an appropriate hosting fluid (e.g., water, ethylene, oil, bio-fluids, and lubricants). Compared with alumina and copper oxide nanoparticles, Eastman et al. [8] demonstrated that the existence of 0.3% copper species (i.e., a small volumetric fraction of nano-sized nanoparticles having a mean diameter less than 10 nm) in ethylene glycol can provide an important enhancement of about 40% in the thermal conductivity of the hosting fluid. Comhenesive meta-analyses on the contribution of nanoparticles in the happening transport phenomena were performed quantitatively by Animasaun et al. [9] and Wakif et al. [10] to evidence the crucial roles Brownian’s motion and the thermophoresis mechanism in the heat and mass transfer enhancements within nanofluidic media.

Because of the numerous applications of nanofluids and boundary layer flows in different domains (e.g., heat transfer enhancements, aerodynamics, aeroacoustics, meteorology, aeronautics, hydrodynamics, and polymer industries), considerable attention has been devoted recently to these attractive research topics. In this context, Khan and Pop [11] invoked the approximation of the boundary layer theory to quantify the heat and mass transfer enhancements via steady two-dimensional nanofluid boundary layer flows over an extending surface based on the active nanoparticles’ control strategy [12, 13] in the case where the horizontal contact surface is assumed to be impermeable and heated isothermally. The same scrutinization was updated by Makinde and Aziz [14] for the convectively heating nanofluid flows. In another related research work, Das [15] introduced the slippery concept on the boundary layer nanofluid flows over a nonlinear stretching sheet under a uniform transversal through-flow effect. By adopting the non-homogeneous nanofluid approach and Falkner’s-Skan flow model in the case of constant boundary conditions for the temperature and the concentration at a static wedge surface, Wubshet and Tulu [16] used the spectral method to simulate steady forced convective flows of viscous dissipative nanofluids in a porous medium under the driven impact of an external magnetic field source. In an extensive statistical analysis, Mahanthesh and Mackolil [17] approximated quadratically the buoyancy and radiative heat flux terms in the conservation equations to conduct a comprehensive sensitivity analysis of mixed convective boundary layer flows of radiating nanofluids. The possibility of obtaining dual solutions for the velocity and the temperature was discussed in detail by Zainal et al. [18] during the two-dimensional flow of copper-alumina/water over a non-isothermal permeable sheet under the influences of an external magnetic field, a non-uniform transversal through-flow, and a nonlinear stretching/shrinking process by carrying out multi-linear regression tests and Lie’s group analyses, Mamatha et al. [19] elucidated numerically the triple diffusive phenomenon within a convectively heated fluidic medium during its steady laminar motion over a permeable stretching sheet under the dynamical influences of suction and injection processes. Based on the single-phase nanofluid approach, Zhang et al. [20] exploited the possibility of hybridizing experimentally the silver and titanium dioxide nanoparticles in an aquatic medium to optimize numerically the thermal enhancement within radiating water-based hybrid nanofluids during their steady MHD mixed convective Falkner’s-Skan flow in a porous medium under the influence of an internal heat generation. To understand the other aspects of boundary layer nanofluid flows, interested readers can refer to the recent innovative research works cited in the references [21,22,23,24,25,26,27,28].

Indeed, the majority of lotions (e.g., shampoos, creams, gels, and toothpaste), food liquids (e.g., soaps, ketchup, honey, and sauce), biological fluids (e.g., synovial liquid, blood, saliva, and urine), natural materials (e.g., drilling mud, liquid petroleum derivatives, and trees' rubber), as well as the most fluids used in today's industries and daily life (e.g., pharmaceutical products, lubricants, detergents, and paints) behave as non-Newtonian media (i.e., due to their complex molecular structures) and can exhibit different rheological trends (e.g., viscolestic, pseudoplastic, and viscoplastic tendencies), in which the viscosity of such a medium is a function of the shear stress. Keeping in mind the importance of these kinds of substances in many applications (e.g., petroleum industries, biomedical sciences, geophysics, and chemical engineering), several investigations [29, 30] have been reported in this context to provide a sufficient scientific background about the rheological constitutive models that can be adopted in a complex flow problem. By invoking the boundary layer assumptions, Sadeghy et al. [31] deliberated dynamically and rheologically Sakiadis’s viscoelastic flows of upper-convected Maxwell fluids over a horizontal moving plate. From another point of view, Hayat et al.[32] ignored the occurred heat transfer process within the fluidic medium to inspect steady two-dimensional MHD stagnation point flows of reacting upper-convected Maxwell fluids towards a horizontal stretching sheet by applying semi-analytically the homotopy analysis procedure on the streamlined momentum and concentration equations. Methodically, Patil et al. [33] provided the cases where similar or non-similar solutions are possible theoretically for the boundary layer flows of some non-Newtonian fluids (e.g., Sutterby fluids, power-law fluids, Powell-Eyring fluids, Reiner-Philipoff fluids, Ellis fluids, second-grade fluids, third-order fluids, Eyring fluids, Prandtl-Eyring fluids, Sisco fluids, and Williamson fluids) over a body shape. Similarly, Khan et al.[34] discussed the similar and non-similar solutions of the boundary layer equations of Powell-Eyring fluid flows over a heated stretching surface. Under the assumption of a strong transversal suction process, Zaydan et al. [35] employed a robustness differential quadrature algorithm to determine the flow pattern and heat transfer feature of EMHD dissipative flows of internally heated fluids over a moving isothermal electromagnetic actuator (i.e., Riga plate). Due to the importance of biofluids in biomedicine sciences, Wajihah and Sankar [36] reviewed several non-Newtonian models for modeling blood flows within arteries. Other crucial nanofluid investigations can be found in the references [37,38,39,40,41,42].

Contrary to the other previous attempts dealing with the boundary layer flow problems of viscoelastic nanofluids, the present numerical scrutinization provides further insights into three-dimensional flows of Maxwell nanofluids in the case where the laminar nanofluid motion takes place in the steady regime over a bi-stretching surface under the impacts of a uniform transversal magnetic field source, a chemical reaction process, and a linear radiative heat transfer mechanism. By adopting a newly developed nanofluid formulation and introducing acceptable simplifications, the boundary layer equations of the studied flows are solved accurately for realistic boundary conditions, whose solutions are presented for the proposed nanofluid flow problem in terms of the streamwise velocity, the spanwise velocity, the temperature, and the nanoparticles’ moar concentration after several validations.

2 Nanofluid flow formulation

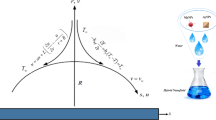
As sketched schematically in Fig. 1, the proposed three-dimensional boundary layer flow problem is well-described for the case of a chemically reacting viscoelastic nanofluid during its radiating motion near a horizontal surface. Physically, the transversal exertion of an external uniform magnetic field ${\text{B}} = \left( {0,0,B} \right)$ induces Lorentz’s forces due to the electrical behavior of the nanofluid medium. Due to the higher temperature $T_{hf} \left( { > T_\infty } \right)$ of the heating fluid, sufficient thermal energy is transported transversally to the nanofluidic medium across the contact surface via the convective heat transfer coefficient $h$. Moreover, the viscoelastic nanofluid motion has happened in the steady regime thanks to the application of a bi-extending process on the impermeable horizontal surface by adjusting accordingly the surface velocity vector ${\text{V}}_w = \left( {\hat{u}_w ,\hat{v}_w ,\hat{w}_w } \right)$, in which $\hat{w}_w = 0$. Keeping in mind the non-permeability tendency of the bi-stretching surface, the molar concentration of the solid phase is controlled passively in this analysis. By imposing the constant conditions $\left\{ {\hat{T}\left( {\hat{x},\hat{y},\hat{z} \to \infty } \right) \to T_\infty ,\hat{C}\left( {\hat{x},\hat{y},\hat{z} \to \infty } \right) \to C_\infty } \right\}$ for the free-stream temperature and nanoparticles' molar concentration, the viscoelastic nanofluid initiates its laminar motion transversally with zero streamwise and spanwise velocities from the free-stream region towards the horizontal bi-stretching surface.

Fig. 1

Proposed three-dimensional boundary layer flow problem

By combining theoretically Wakif’s-Buongiorno approach and [43,44,45,46,47,48,49,50] Maxwell’s model [51] along with the assumptions of the boundary layer theory [52] and the linearized law of Rosseland [53], the leading PDEs’ formulation is stated:

$$\left\{ {\begin{array}{*{20}l} {PDEs:\left\{ {\begin{array}{*{20}l} {Eq_0 :\left\{ {\frac{{\partial \hat{u}}}{{\partial \hat{x}}}\left( {\hat{x},\hat{y},\hat{z}} \right) + \frac{{\partial \hat{v}}}{{\partial \hat{y}}}\left( {\hat{x},\hat{y},\hat{z}} \right) + \frac{{\partial \hat{w}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right) = 0} \right\},} \hfill \\ {Eq_1 :\left\{ {\underline{\Omega } \hat{u}\left( {\hat{x},\hat{y},\hat{z}} \right) = \upsilon \frac{{\partial^2 \hat{u}}}{{\partial \hat{z}^2 }}\left( {\hat{x},\hat{y},\hat{z}} \right) - \hat{\lambda }F_1 \left( {\hat{x},\hat{y},\hat{z}} \right) - \frac{\sigma B^2 }{\rho }\left[ {\hat{u}\left( {\hat{x},\hat{y},\hat{z}} \right) + \hat{\lambda }\hat{w}\left( {\hat{x},\hat{y},\hat{z}} \right)\frac{{\partial \hat{u}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right)} \right]} \right\},} \hfill \\ {Eq_2 :\left\{ {\underline{\Omega } \hat{v}\left( {\hat{x},\hat{y},\hat{z}} \right) = \upsilon \frac{{\partial^2 \hat{v}}}{{\partial \hat{z}^2 }}\left( {\hat{x},\hat{y},\hat{z}} \right) - \hat{\lambda }F_2 \left( {\hat{x},\hat{y},\hat{z}} \right) - \frac{\sigma B^2 }{\rho }\left[ {\hat{v}\left( {\hat{x},\hat{y},\hat{z}} \right) + \hat{\lambda }\hat{w}\left( {\hat{x},\hat{y},\hat{z}} \right)\frac{{\partial \hat{v}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right)} \right]} \right\},} \hfill \\ {Eq_3 :\left\{ {\underline{\Omega } \hat{T}\left( {\hat{x},\hat{y},\hat{z}} \right) = \alpha^* \frac{{\partial^2 \hat{T}}}{{\partial \hat{z}^2 }}\left( {\hat{x},\hat{y},\hat{z}} \right) + \,\frac{{\partial \hat{T}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right)\left[ {\,\frac{\tau D_B }{{\delta_W }}\frac{{\partial \hat{C}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right) + \frac{\tau D_T }{{T_\infty }}\frac{{\partial \hat{T}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right)} \right]} \right\},} \hfill \\ {Eq_4 :\left\{ {\underline{\Omega } \hat{C}\left( {\hat{x},\hat{y},\hat{z}} \right) = D_B \frac{{\partial^2 \hat{C}}}{{\partial \hat{z}^2 }}\left( {\hat{x},\hat{y},\hat{z}} \right) + \,\,\,\frac{\delta_W D_T }{{T_\infty }}\frac{{\partial^2 \hat{T}}}{{\partial \hat{z}^2 }}\left( {\hat{x},\hat{y},\hat{z}} \right) - K_{\hat{C}} \left[ {\hat{C}\left( {\hat{x},\hat{y},\hat{z}} \right) - C_\infty } \right]\,} \right\}} \hfill \\ \end{array} } \right\},} \hfill \\ {BCs:\left\{ {\begin{array}{*{20}l} {BCs_0 :\left\{ {{\hat{\text{V}}}\left( {\hat{x},\hat{y},\hat{z} = 0} \right) = \left( {\hat{u}_w ,\,\hat{v}_w ,\,0} \right),\,\,\frac{{\partial \hat{T}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z} = 0} \right)\, = \frac{h}{k}\left[ {\hat{T}\left( {\hat{x},\hat{y},\hat{z} = 0} \right) - T_{hf} } \right],\,J\left( {\hat{x},\hat{y},\hat{z} = 0} \right)\, = 0} \right\},} \hfill \\ {BCs_\infty :\left\{ {\hat{u}\left( {\hat{x},\hat{y},\hat{z} \to \infty } \right) \to 0,\,\hat{v}\left( {\hat{x},\hat{y},\hat{z} \to \infty } \right) \to 0,\,\hat{T}\left( {\hat{x},\hat{y},\hat{z} \to \infty } \right) \to T_\infty ,\,\hat{C}\left( {\hat{x},\hat{y},\hat{z} \to \infty } \right) \to C_\infty } \right\}} \hfill \\ \end{array} } \right\},} \hfill \\ \end{array} } \right\},$$

(1)

where

$$\left\{ \begin{gathered} \left\{ {\underline{\Omega } \equiv \hat{u}\left( {\hat{x},\hat{y},\hat{z}} \right)\frac{\partial }{{\partial \hat{x}}} + \hat{v}\left( {\hat{x},\hat{y},\hat{z}} \right)\frac{\partial }{{\partial \hat{y}}} + \hat{w}\left( {\hat{x},\hat{y},\hat{z}} \right)\frac{\partial }{{\partial \hat{z}}},\alpha^* = \alpha + \frac{{16\sigma_{SB} \hat{T}_\infty^3 }}{{3\left( {\rho C_P } \right)\beta_R }},\tau = \frac{{\left( {\rho C_P } \right)_{np} }}{{\left( {\rho C_P } \right)}}} \right\}, \hfill \\ \left\{ {\begin{array}{*{20}l} {F_1 \left( {\hat{x},\hat{y},\hat{z}} \right)} \hfill \\ {F_2 \left( {\hat{x},\hat{y},\hat{z}} \right)} \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {\underline{L}^2 \hat{u}\left( {\hat{x},\hat{y},\hat{z}} \right) + \hat{w}^2 \left( {\hat{x},\hat{y},\hat{z}} \right)\frac{{\partial^2 \hat{u}}}{{\partial \hat{z}^2 }}\left( {\hat{x},\hat{y},\hat{z}} \right) + 2\hat{w}\left( {\hat{x},\hat{y},\hat{z}} \right)\underline{L} \frac{{\partial \hat{u}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right)\,\,} \hfill \\ {\underline{L}^2 \hat{v}\left( {\hat{x},\hat{y},\hat{z}} \right) + \hat{w}^2 \left( {\hat{x},\hat{y},\hat{z}} \right)\frac{{\partial^2 \hat{v}}}{{\partial \hat{z}^2 }}\left( {\hat{x},\hat{y},\hat{z}} \right) + 2\hat{w}\left( {\hat{x},\hat{y},\hat{z}} \right)\underline{L} \frac{{\partial \hat{v}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right)\,} \hfill \\ \end{array} } \right\}, \hfill \\ \left\{ {J\left( {\hat{x},\hat{y},\hat{z}} \right) = \frac{D_B }{{\delta_W }}\frac{{\partial \hat{C}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right) + \frac{D_T }{{T_\infty }}\frac{{\partial \hat{T}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z}} \right),\underline{L} \equiv \hat{u}\left( {\hat{x},\hat{y},\hat{z}} \right)\frac{\partial }{{\partial \hat{x}}}\, + \,\,\hat{v}\left( {\hat{x},\hat{y},\hat{z}} \right)\frac{\partial }{{\partial \hat{y}}}} \right\} \hfill \\ \end{gathered} \right\}.$$

(2)

As shown in Eq. (1) and Fig. 1, several expressive symbols are utilized especially in this scrutinization, like $\left( {\hat{x},\hat{y},\hat{z}} \right)\left[ m \right]$ for the position coordinates, ${\hat{\text{V}}}\left( {\hat{x},\hat{y},\hat{z}} \right)\left\langle { = \left( {\hat{u},\hat{v},\hat{w}} \right)} \right\rangle \left[ {m.s^{ - 1} } \right]$ for the nanofluid velocity vector, $\left\{ {\hat{u}_w \left\langle { = a\hat{x}} \right\rangle ,\,\hat{v}_w \left\langle { = b\hat{y}} \right\rangle } \right\}\left[ {m.s^{ - 1} } \right]$ for the stretching velocities along the $\left( {\hat{x},\hat{y}} \right) -$ directions, $\left\{ {a,\,b} \right\}\left[ {s^{ - 1} } \right]$ for the stretching rates $\left\{ {\frac{{d\hat{u}_w }}{{d\hat{x}}},\,\frac{{d\hat{v}_w }}{{d\hat{y}}}} \right\}$ along the $\left( {\hat{x},\hat{y}} \right) -$ directions, $\upsilon \left[ {m^2 .s^{ - 1} } \right]$ for the nanofluid kinematic viscosity, $\hat{\lambda }\left[ s \right]$ for the rheological relaxation time, $\rho \left[ {kg.m^{ - 3} } \right]$ for the nanofluid density, $\sigma \left[ {S.m^{ - 1} } \right]$ for the nanofluid electrical conductivity, $B\left[ {kg.s^{ - 2} .A^{ - 1} } \right]$ for the magnetic field strength, $h\left[ {W.K^{ - 1} .m^{ - 2 } } \right]$ for the convective heat transfer factor, $\hat{T}\left( {\hat{x},\hat{y},\hat{z}} \right)\left[ K \right]$ for the nanofluid temperature distribution, $T_\infty \left[ K \right]$ for the free-stream temperature, $T_{hf} \left[ K \right]$ for the temperature of the heating fluid, $\Delta T\left\langle { = T_{hf} - T_\infty } \right\rangle \left[ K \right]$ for the temperature difference, $k\left[ {W.K^{ - 1} .m^{ - 1 } } \right]$ for the nanofluid thermal conductivity, $\left( {\rho C_P } \right)_{np} \left[ {J.m^{ - 3} .K^{ - 1} } \right]$ for the nanoparticles’ heat capacitance, $\delta_W \left[ {mol.m^{ - 3} } \right]$ for Wakif’s corrective coefficient, $\left( {\rho C_P } \right)\left[ {J.m^{ - 3} .K^{ - 1} } \right]$ for the nanofluid heat capacitance, $\alpha^* \left\langle { = \alpha + \frac{{16\sigma_{SB} \hat{T}_\infty^3 }}{{3\left( {\rho C_P } \right)\beta_R }}} \right\rangle \left[ {m^2 .s^{ - 1} } \right]$ for the apparent nanofluid thermal diffusivity of the nanofluidic medium, $\alpha = \left\langle {\frac{k}{{\left( {\rho C_P } \right)}}} \right\rangle \left[ {m^2 .s^{ - 1} } \right]$ for the nanofluid thermal diffusivity, $\sigma_{SB} \left[ {W.K^{ - 4} .m^{ - 2} } \right]$ for Stefan’s-Boltzmann constant, $\tau = \left\langle {\frac{{\left( {\rho C_P } \right)_{np} }}{{\left( {\rho C_P } \right)}}} \right\rangle \left[ - \right]$ for the heat capacitance ratio, $D_B \left[ {m^2 .s^{ - 1} } \right]$ for Brownian’s diffusive coefficient, $\beta_R \left[ {m^{ - 1} } \right]$ for the mean radiative absorption factor, $D_T \left[ {m^2 .s^{ - 1} } \right]$ for the thermophoresis diffusive coefficient, $\hat{C}\left( {\hat{x},\hat{y},\hat{z}} \right)\left[ {mol.m^{ - 3} } \right]$ for the molar concentration distribution of nanoparticles, $C_\infty \left[ {mol.m^{ - 3} } \right]$ for the molar concentration of nanoparticles in the free-stream region, and $K_{\hat{C}} \left[ {s^{ - 1} } \right]$ for the chemical reaction constant.

From a physical point of view, the above PDEs’ system can be simplified mathematically by introducing the following modifications [54]:

$$\left\{ {\begin{array}{*{20}c} {\left\{ {\hat{u}\left( {\hat{x},\hat{y},\hat{z}} \right),\hat{v}\left( {\hat{x},\hat{y},\hat{z}} \right),\hat{w}\left( {\hat{x},\hat{y},\hat{z}} \right)} \right\} \to \left\{ {\sqrt {a\upsilon } U\left( {\xi ,\varsigma } \right),\sqrt {a\upsilon } V\left( {\eta ,\varsigma } \right), - \sqrt {a\upsilon } H\left( \varsigma \right)} \right\},} \\ {\left( {\hat{x},\hat{y},\hat{z}} \right) \to \sqrt {{\frac{\upsilon }{a}}} \left( {\xi ,\eta ,\varsigma } \right),\hat{T}\left( {\hat{x},\hat{y},\hat{z}} \right) \to \Delta T\Theta \left( \varsigma \right) + T_\infty ,\frac{{\hat{C}\left( {\hat{x},\hat{y},\hat{z}} \right)}}{C_\infty } \to \Phi \left( \varsigma \right) + 1} \\ \end{array} } \right\},$$

(3)

in which

$$H\left( \varsigma \right) = G\left( \varsigma \right) + F\left( \varsigma \right),$$

(4)

$$U\left( {\xi ,\varsigma } \right) = \xi F^{\prime}\left( \varsigma \right),$$

(5)

$$V\left( {\eta ,\varsigma } \right) = \eta G^{\prime}\left( \varsigma \right).$$

(6)

Keeping in mind that $\hat{u}\left( {\hat{x},\hat{y},\hat{z}} \right) \ge 0$, $\hat{v}\left( {\hat{x},\hat{y},\hat{z}} \right) \ge 0$, and $\hat{w}\left( {\hat{x},\hat{y},\hat{z} = 0} \right) = 0$, we have:

$$\left\{ {F\left( \varsigma \right) \ge 0,G\left( \varsigma \right) \ge 0,G\left( {\varsigma = 0} \right) = 0,F\left( {\varsigma = 0} \right) = 0} \right\}.$$

(7)

Accordingly, Eq. (1) can be reduced to the following ODEs’ system:

$$\left\{ \begin{gathered} ODEs:\left\{ \begin{gathered} Eq1:\left\{ {F^{\prime\prime\prime}\left( \varsigma \right) + \left( {1 + \lambda M} \right)H\left( \varsigma \right)F^{\prime\prime}\left( \varsigma \right)- F^{\prime2} \left( \varsigma \right) + \lambda H\left( \varsigma \right)\left| {\begin{array}{*{20}c} {2F^{\prime}\left( \varsigma \right)}\quad {F^{\prime\prime\prime}\left( \varsigma \right)} \\ {H\left( \varsigma \right)}\qquad{F^{\prime \prime}\left( \varsigma \right)} \\ \end{array} } \right| - MF^{\prime}\left( \varsigma \right)} \right\}, \hfill \\ Eq2:\left\{ {G^{\prime\prime\prime}\left( \varsigma \right) + \left( {1 + \lambda M} \right)H\left( \varsigma \right)G^{\prime \prime}\left( \varsigma \right) - G^{\prime2} \left( \varsigma \right) + \lambda H\left( \varsigma \right)\left| {\begin{array}{*{20}c} {2G^{\prime}\left( \varsigma \right)}\quad{G^{\prime\prime\prime}\left( \varsigma \right)} \\ {H\left( \varsigma \right)}\qquad{G^{\prime \prime}\left( \varsigma \right)} \\ \end{array} } \right| - MG^{\prime}\left( \varsigma \right)} \right\}, \hfill \\ Eq3:\left\{ {\left( {1 + R_D } \right)\Theta^{\prime \prime}\left( \varsigma \right) + \Pr H\left( \varsigma \right)\Theta^{\prime}\left( \varsigma \right) + \Pr Nb\Phi^{\prime}\left( \varsigma \right)\Theta^{\prime}\left( \varsigma \right) + \Pr Nt\Theta^{\prime2} \left( \varsigma \right) = 0} \right\}, \hfill \\ Eq4:\left\{ {\Phi^{\prime \prime}\left( \varsigma \right) - ScK_\Phi \Phi \left( \varsigma \right) + \frac{Nt}{{Nb}}\Theta^{\prime \prime}\left( \varsigma \right) + Sc\,H\left( \varsigma \right)\Phi^{\prime}\left( \varsigma \right) = 0} \right\}, \hfill \\ \end{gathered} \right\} \hfill \\ BCs:\left\{ {\begin{array}{*{20}l} {BCs_0 :\left\{ {H\left( \varsigma \right) = 0,F^{\prime}\left( \varsigma \right) = 1,G^{\prime}\left( \varsigma \right) = S,\,\Theta^{\prime}\left( \varsigma \right) = Bi_T \left[ {\Theta \left( \varsigma \right) - 1} \right],\Phi^{\prime}\left( \varsigma \right) = - \frac{Nt}{{Nb}}\Theta^{\prime}\left( \varsigma \right) \, at \, \varsigma = 0} \right\},} \hfill \\ {BCs_\infty :\left\{ {F^{\prime}\left( \varsigma \right) \to 0,G^{\prime}\left( \varsigma \right) \to 0,\Theta \left( \varsigma \right) \to 0,\Phi \left( \varsigma \right) \to 0\; as \, \varsigma \to \infty } \right\}} \hfill \\ \end{array} } \right\}, \hfill \\ where \hfill \\ \left\{ {\begin{array}{*{20}l} {S = \frac{b}{a},M = \frac{\sigma B^2 }{{\rho a}},\lambda = a\hat{\lambda },\Pr = \frac{{\upsilon \left( {\rho C_P } \right)}}{k},R_D = \frac{{16T_\infty^3 \sigma_{SB} }}{3\beta_R \kappa },Bi_T = \frac{h}{\kappa }\sqrt {{\frac{\upsilon }{a}}} ,} \hfill \\ {\tau = \frac{{\left( {\rho C_P } \right)_{np} }}{{\left( {\rho C_P } \right)}},Nb = \frac{\tau D_B C_\infty }{{\upsilon \delta_W }},Nt = \frac{{\tau \left( {T_{hf} - T_\infty } \right)D_T }}{T_\infty \upsilon },Sc = \frac{\upsilon }{D_B },K_\Phi = \frac{{K_{\hat{C}} }}{a}} \hfill \\ \end{array} } \right\} \hfill \\ \end{gathered} \right\}$$

(8)

Before dealing with the developed ODEs’ formulation, several prior examinations were performed computationally to choose the ranging values of the parameters $\left\{ {S,M,\lambda ,\Pr ,R_D ,Bi_T ,Nt,Nb,Sc,K_\Phi } \right\}$ as shown in Table 1. This preliminary process is necessary for creating clear and discussable graphical illustrations.

Table 1 A list of the pertinent parameters along with their selected values

3 Important quantities of interest

From an engineering point of view, the performance of the present nanofluid flow problem can be quantified locally through the skin friction coefficients $\left\{ {C_{F\hat{x}} ,C_{G\hat{y}} } \right\}$, the surface temperature $T_w$, and Nusselt’s number $Nu_{\hat{x}}$ only due to the vanishing mass flux condition of nanoparticles along the $\hat{z} -$ direction (i.e., Sherwood’s number is zero). Besides, the crucial physical quantities of interest $\left\{ {C_{F\hat{x}} ,C_{G\hat{y}} ,Nu_{\hat{x}} ,T_w } \right\}$ are given along with their reduced expressions $\left\{ {C_{Fr} ,C_{Gr} ,\Theta_w ,Nu_r } \right\}$ by the following relationships [54, 55]:

$$C_{F\hat{x}} = \frac{{\mu \left( {1 + \lambda } \right)}}{{\rho \hat{u}_w^2 }}\frac{{\partial \hat{u}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z} = 0} \right),$$

(9)

$$C_{G\hat{y}} = \frac{{\mu \left( {1 + \lambda } \right)}}{{\rho \hat{v}_w^2 }}\frac{{\partial \hat{v}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z} = 0} \right),$$

(10)

$$T_w = \hat{T}\left( {\hat{x},\hat{y},\hat{z} = 0} \right),$$

(11)

$$Nu_{\hat{x}} = - \frac{{\hat{x}}}{k\Delta T}\left( {k + \frac{{16\sigma_{SB} \hat{T}_\infty^3 }}{3\beta_R }} \right)\frac{{\partial \hat{T}}}{{\partial \hat{z}}}\left( {\hat{x},\hat{y},\hat{z} = 0} \right),$$

(12)

$$C_{Fr} = - \sqrt {{Re_{\hat{x}} }} C_{F\hat{x}} = - \left( {1 + \lambda } \right)F^{\prime \prime}\left( {\xi = 0} \right),$$

(13)

$$C_{Gr} = - \sqrt {{Re_{\hat{y}} }} C_{G\hat{y}} = - S^{ - \frac{3}{2}} \left( {1 + \lambda } \right)G^{\prime \prime}\left( {\xi = 0} \right),$$

(14)

$$\Theta_w = \frac{T_w - T_\infty }{{\Delta T}},$$

(15)

$$Nu_r = \frac{{Nu_{\hat{x}} }}{{\sqrt {{Re_{\hat{x}} }} }} = - \left( {1 + R_D } \right)\Theta^{\prime}\left( {\xi = 0} \right).$$

(16)

Here, the symbols $\left\{ {Re_{\hat{x}} ,Re_{\hat{y}} } \right\}$ refer to Reynolds’s numbers, whose expressions are written as:

$$\left\{ {Re_{\hat{x}} = \frac{{\hat{u}_w \hat{x}}}{\upsilon },Re_{\hat{y}} = \frac{{\hat{v}_w \hat{y}}}{\upsilon }} \right\}.$$

(17)

4 Solution methodology with validation of results

In this investigation, the resulting differential system of Eq. (8) is solved easily in Maple’s software using Richardson’s extrapolation method as a numerical procedure. Further, the computational efficiency of the employed numerical method is well evidenced in Table 2 and Table 3 via multiple comparisons with the existing outcomes of certain special cases. As expected, the obtained tabular results prove quantitatively the credibility of the following computational methodology.

Table 2 Dynamical validation of Richardson’s extrapolation results

Table 3 Thermal validation of Richardson’s extrapolation results

5 Results and discussion

Keeping in mind the principle objectives of the present investigation, several impressive findings are deliberated comprehensively hereafter in terms of the dimensionless quantities $U\left( {\xi ,\varsigma } \right) -$ Streamwise nanofluid velocity, $V\left( {\eta ,\varsigma } \right) -$ Spanwise nanofluid velocity, $F^{\prime}\left( \varsigma \right)\left\langle { = U\left( {\xi = 1,\varsigma } \right)} \right\rangle -$ Streamwise nanofluid velocity function, $G^{\prime}\left( \varsigma \right)\left\langle { = V\left( {\eta = 1,\varsigma } \right)} \right\rangle -$ Spanwise nanofluid velocity function, $\Theta \left( \varsigma \right) -$ Nanofluid temperature distribution, $\Phi \left( \varsigma \right) -$ Nanoparticles’ molar concentration repartition, $C_{Fr} -$ Skin friction coefficient along the streamwise direction, $C_{Gr} -$ Skin friction coefficient along the spanwise direction, $\Theta_w -$ Surface temperature, and $Nu_r -$ Nusselt number. Practically, the aspects of the inspected nanofluid flow problem are evidenced adequately in this study by adjusting a sole control parameter and keeping the others fixed in their default values as specified in Table 1. Herein, the operating control parameters $M -$ Magnetic parameter, $\lambda -$ Deborah number, $R_D -$ Thermal radiation parameter, $Bi_T -$ Biot number, $Nt -$ Thermophoresis parameter, $Nb -$ Brownian motion parameter, and $K_\Phi -$ Chemical reaction parameter are selected as the main influencing parameters. However, the effects of the involved control parameters $S -$ Stretching ratio parameter, $\Pr -$ Prandtl number, and $Sc -$ Schmidt number are ignored in this examination (i.e., because their impressions are already discussed in the basic references [54,55,56]), whose assigned values are kept unchanged in all subsequent physical scenarios.

By exploiting accordingly the generated data sets corresponding to the nanofluid velocity functions $\left\{ {F^{\prime}\left( \varsigma \right),G^{\prime}\left( \varsigma \right)} \right\}$, the dynamical patterns of the present nanofluid flow are revealed three-dimensionally as well as two-dimensionally as shown in Fig. 2(a) and (b). These dynamical illustrations are obtained graphically by quantifying numerically the expressions of the streamwise and spanwise nanofluid velocities $\left\{ {U\left( {\xi ,\varsigma } \right),V\left( {\eta ,\varsigma } \right)} \right\}$ in MATLAB’s software. Moreover, it is important to mention here that the contours of the two-variable functions $\left\{ {U\left( {\xi ,\varsigma } \right),V\left( {\eta ,\varsigma } \right)} \right\}$ represent also the velocity boundary layers’ shapes along the streamwise and spanwise directions. As preliminary remarks, it is observed that the streamwise nanofluid motion speeds up noticeably with the increasing values of the streamwise variable $\xi$ $\left( {i.e., \, \frac{\partial U}{{\partial \xi }}\left( {\xi ,\varsigma } \right) > 0} \right)$ and slows down independently of the spanwise variable $\eta$ as long as the magnitude of transversal variable $\varsigma$ is heightened progressively towards its asymptotical value $\varsigma_\infty$$\,\left( {i.e., \, \frac{\partial U}{{\partial \eta }}\left( {\xi ,\varsigma } \right) = 0,\frac{\partial U}{{\partial \varsigma }}\left( {\xi ,\varsigma } \right) < 0} \right)$. Similarly, it is found that the spanwise nanofluid motion hastens remarkably $\left( {i.e., \, \frac{\partial V}{{\partial \eta }}\left( {\eta ,\varsigma } \right) > 0} \right)$ with the augmenting values of the spanwise variable $\eta$ and decelerates independently of the streamwise variable $\xi$ when the transversal variable $\varsigma$ is increased gradually in the transversal computational domain $\left( {i.e., \, \frac{\partial V}{{\partial \xi }}\left( {\eta ,\varsigma } \right) = 0,\frac{\partial V}{{\partial \varsigma }}\left( {\eta ,\varsigma } \right) < 0} \right)$. Physically, the application of a transversal magnetic field on the three-dimensional nanofluid motion generates locally Lorentz’s forces within the electrically conducting medium, whose streamwise and spanwise components can be strengthened/weakened accordingly through the growing/lessening values of the magnetic parameter $M\left\langle { = \frac{\sigma B^2 }{{\rho a}}} \right\rangle$. Generally, Fig. 3(a) and (b) confirm that the induced electromagnetic forces act resistively on the nanofluid flow along the streamwise and spanwise directions, in which the streamwise and spanwise velocity profiles $\left\{ {F^{\prime}\left( \varsigma \right),G^{\prime}\left( \varsigma \right)} \right\}$ descent significantly with the rising values of the magnetic parameter $M$. From a rheological point of view, the viscoelastic tendency of the flowing Maxwell nanofluid is examined dynamically in Fig. 4(a) and (b) by adjusting Deborah’s numbers $\lambda$. In this respect, it is proved that the weakly viscoelastic feature of the nanofluidic medium $\left( {i.e., \, 0 < \lambda \le 0.06} \right)$ has a slight falling impact on the streamwise and spanwise velocity profiles $\left\{ {F^{\prime}\left( \varsigma \right),G^{\prime}\left( \varsigma \right)} \right\}$ due to the occurred temporal relaxation phenomenon, in which the fluidity behavior of the nanofluidic medium diminishes. In this situation, the nanofluidic medium requires more time to recover its equilibrium state after being stressed.

Fig. 2

a Pattern of the streamwise velocity $U\left( {\xi ,\varsigma } \right)$ and its contour. b Pattern of the spanwise velocity $V\left( {\eta ,\varsigma } \right)$ and its contour

Fig. 3

a $F^{\prime}\left( \varsigma \right)$ versus $M$. b $G^{\prime}\left( \varsigma \right)$ versus $M$

Fig. 4

a $F^{\prime}\left( \varsigma \right)$ versus $\lambda$. b $G^{\prime}\left( \varsigma \right)$ versus $\lambda$

Thermally, Figs. 5, 6, and 7 disclose respectively that the magnetic parameter M, the thermal radiation parameter $R_D$, Biot’s number $Bi_T$, and the thermophoresis parameter Nt have an enhancing impression on the temperature distribution $\Theta \left( \varsigma \right)$ throughout the nanofluidic medium. Indeed, the heating effect of the control parameters $\left\{ {M,R_D ,Bi_T ,Nt} \right\}$ can be explained as follows:

• The advanced values of the magnetic parameter $M$ reinforce strongly the resistive role of Lorentz’s forces, which leads to the generation of an extra amount of thermal energy within the nanofluidic medium.

• The higher values of the thermal radiation parameter $R_D$ strengthen enormously the heat transfer mechanism within the nanofluidic medium by improving its apparent thermal diffusivity $\alpha^* \left\langle { = \alpha + \frac{{16\sigma_{SB} \hat{T}_\infty^3 }}{{3\left( {\rho C_P } \right)\beta_R }}} \right\rangle$.

• The grander Biot’s numbers $Bi_T$ reduce notably the thermal resistance between the heating fluid and the bi-stretching surface and facilitate enormously the convective heat exchange rate across the contact surface.

• The superior values of the thermophoresis parameter $Nt$ support dynamically the ascendant thermo-migration of the nanoparticles from the hot region (i.e., near the convectively heated surface) to the cold zone (near the free-stream region).

Fig. 5

$\Theta \left( \varsigma \right)$ versus $M$

Fig. 6

$\Theta \left( \varsigma \right)$ versus $\left\{ {R_D ,Bi_T } \right\}$

Fig. 7

$\Theta \left( \varsigma \right)$ versus $Nt$

In addition to the thermally enhancing aspect of the thermophoresis parameter $Nt$, the curves $\Phi \left( \varsigma \right)$ of Fig. 8 (i.e., the nanoparticles’ molar concentration repartition) reveal that the increasing values of the thermophoresis parameter $Nt$ broaden the concentration boundary layer region and diminish the surface nanoparticles’ molar concentration due to the upward thermo-migration of the nanoparticles within the nanofluidic medium from the hot zone to the cold region (i.e., the thermophoresis process). Besides, the mass outcomes of Fig. 9 demonstrate that the intensifying values of the thermal radiation parameter $R_D$ and Biot’s number $Bi_T$ reinforce significantly the thermophoresis mechanism. However, the mass results of Fig. 10 ascertain that the intensifying values of the nanofluid parameter $Nb$ shrink the concentration boundary layer region and upsurge the surface nanoparticles’ molar concentration because of the downward mass migration of the nanoparticles (i.e., Brownian’s motion) within the nanofluidic medium from the more concentrated region (i.e., the cold region) to the less concentrated zone (i.e., the hot zone). Moreover, the mass upshots of Fig. 11 show that the chemical reaction parameter $K_\Phi$ has the same mass impact on the nanoparticles’ molar concentration repartition $\Phi \left( \varsigma \right)$ due to the destructive trend of the imposed chemical reaction process.

Fig. 8

$\Phi \left( \varsigma \right)$ versus $Nt$

Fig. 9

$\Phi \left( \varsigma \right)$ versus $\left\{ {R_D ,Bi_T } \right\}$

Fig. 10

$\Phi \left( \varsigma \right)$ versus $Nb$

Fig. 11

$\Phi \left( \varsigma \right)$ versus $K_\Phi$

Sequel to the above inclusive qualitative analyses, other computational executions are carried out successfully to quantify the skin friction coefficient $C_{Fr}$ along the streamwise direction, the skin friction coefficient $C_{Gr}$ along the spanwise direction, the surface temperature $\Theta_w$, and Nusselt’s number $Nu_r$ as demonstrated in Table 4 and Table 5. For the sake of clearness, the behaviors of the reduced physical quantities $\left\{ {C_{Fr} ,C_{Gr} ,\Theta_w ,Nu_r } \right\}$ towards the operating control parameters $\left\{ {M,\lambda ,R_D ,Bi_T ,Nt} \right\}$ are also provided in these tabular depictions.

Table 4 Numerical values of the frictional coefficients $\left\{ {C_{Fr} ,C_{Gr} } \right\}$ when $\varsigma_\infty = 5$

Table 5 Numerical values of the thermal quantities $\left\{ {\Theta_w ,Nu_r } \right\}$

6 Closing remarks

In this informative simulation, the flow pattern, as well as the heat and mass aspects of a convectively heated viscoelastic nanofluid have been evidenced realistically during its steady three-dimensional laminar motion near a horizontal bi-stretching surface under the assumption of zero nanoparticles’ mass flux at the contact surface. By considering the dynamical resistive effect of a transversal magnetic field in the momentum equation and including effectively the radiative heat transfer contribution in the thermal balance equation along with the destructive impression of a first-order chemical reaction in the nanoparticles’ molar concentration equation, interesting outcomes have been derived properly from the present numerical analysis based on Wakif’s-Buongiorno approach, whose main conclusions can be itemized beneath as follows:

• The nanoparticles’ molar concentration distribution can be revealed properly within a nanofluidic medium via Wakif’s-Buongiorno approach.

• The present numerical results are computed accurately with the help of MAPLE’s software using Richardson’s extrapolation technique.

• The viscoelastic and magnetic effects show a decelerating trend on the streamwise and spanwise nanofluid motions.

• A significant temperature rise can be achieved transversally across the nanofluidic medium by intensifying the magnetic field source, the radiative heat transfer mechanism, the convective heating process, and the thermophoresis diffusion.

• The upper values of the thermophoresis parameter, the thermal radiation parameter, and Biot’s number exhibit a remarkable widening effect on the mass boundary layer region with a noticeable lessening in the surface nanoparticles’ molar concentration. However, a reverse propensity is observed for the chemical reaction and Brownian motion parameters.

• The higher viscoelastic and magnetic strengths can intensify considerably the surface frag forces along the streamwise and spanwise directions.

• The heat transfer mechanism can be ameliorated practically at the bi-stretching surface either by strengthening the radiative heat transfer at convective heating processes or by diminishing the viscoelastic and magnetic effects.

• The nanoparticles’ molar concentration shows a declining tendency at the bi-stretching surface by magnifying the radiative heat transfer mechanism, the convective heating process, and the thermophoresis diffusion. However, a reverse inclination is depicted for the chemical reaction and Brownian motion parameters.

• No mass transfer is assessed in this scrutinization at the impermeable bi-stretching surface.