1 Introduction

Albert Einstein once said, "The most incomprehensible thing about the world is that it is at all comprehensible. But how do we fully understand incomprehensible things?" In this sense, nonlinear science offers some hints[1]. The environment we live in is intrinsically nonlinear. In several scientific disciplines, such as fluid mechanics, solid-state physics, plasma physics, plasma waves, and biology, nonlinear evolution equations (NEEs) are frequently employed as models to describe complicated physical events.

Academics are currently focusing on nonlinear wave equations for the mathematical description and examination of real-world occurrences. To have a deeper understanding of actual events, the exact solutions of the conforming mathematical models should be obtained. Many scholars have worked hard to provide a universal approach to dealing with all types of NLEEs.

In particular, a variety of techniques have been used to investigate distinct physical model solutions that are modeled by nonlinear partial differential equations (NPDEs)., notably the Exp(-Phi)-Expansion method[2, 3], Bifurcation Analysis [4], the unified technique[5], Sine–Gordon expansion method [6], Kudryashov schemes [7], Jacobi elliptic task technique [8], the Jacobi elliptic ansatz technique [9], fractional iteration algorithm [10, 11], variation of \(\left( {{{G^{\prime}} \mathord{\left/ {\vphantom {{G^{\prime}} G}} \right. \kern-0pt} G}} \right)\)-expansion method [12], modified decomposition schemes [13], the hyperbolic and exponential ansatz method [14], natural transformation technique [15], Hirota’s simple schemes [16, 17], the modified extended tanh expansion system [18], and significantly more[19,20,21,22,23,24]. Previous papers handled the solution procedure of nonlinear Riccati equations, Jimbo–Miwa equation, the Kadomtsev–Petviashvili equation [25,26,27,28,29], more systematically and conveniently, and these solutions are close to the aforementioned equation and helped us in this study to investigate more novel soliton solutions.

In order to convey the reasonability and simplicity of the cycle, we instrument the modified \((G{\prime}/G)-\)-expansion schemes in the current study to produce accurate solutions to the Zoomeron equation. The key advantage of this cycle over other designs is that it contributes more innovative precise solutions, including additional independent factors, and we also produce a few novel results. The exact reactions are crucial in disclosing the key element of the real events. In addition to its considerable significance, fractional order nonlinear population's particular responses.

To the best of our knowledge, modified \((G{\prime}/G)-\)expansion method has not been previously employed in the derivation of soliton solutions for the nonlinear Zoomeron equation. To provide a visual representation, select instances are graphically illustrated through the utilization of Maple, a widely used commercial software platform. This innovative approach serves as a potent tool for generating traveling wave solutions across a broad spectrum of nonlinear partial differential equations.

2 The modified (G'/G)-expansion method

We are considering:

$$ T\left( {u,u_{x} ,u_{xx} ,u_{t} ,u_{tt} ,u_{xt} ,.....} \right) = 0, $$
(1)

where \(T\) is a polynomial in \(u\).

Family I: Implement the traveling variable:

$$u=u\left(x,t\right)=u\left(\xi \right),\xi ={p}_{3}\left(x-Vt\right),$$
(2)

where \(p_{3}\) and \(V\) are a constant to be determined later. Implementing Eq. (2) into Eq. (1), we find:

$$S\left(u,{p}_{3}u{\prime},{p}_{3}^{2}u{\prime}{\prime},-{p}_{3}Vu{\prime},...\right)=0.$$
(3)

Family II: Considering the ansatz form:

$$u\left(\xi \right)={\sum }_{i=-N}^{N}{V}_{i}{\Delta }^{i},$$
(4)

where \(\Delta =\left(\frac{{G}{\prime}}{G}+\frac{\lambda }{2}\right),\left|{A}_{-N}\right|+\left|{A}_{N}\right|\ne 0\) and \(G=G\left(\xi \right)\) satisfies the equation

$${G}^{^{\prime\prime} }+\lambda {G}{\prime}+\mu G=0,$$
(5)

where \({V}_{i}\left(\pm 1,\pm 2,......,\pm N\right)\), \(\lambda \) and \(\mu \) are coefficient constants later. Implementing homogeneous balance principle in Eq. (3), the positive integer \(N\) can be determined. From the Eq. (5), we find that

$$\Delta =r-{\Delta }^{2},$$
(6)

where \(r=\frac{{\lambda }^{2}-4\mu }{4}\) and \(r\) is calculated by \(\lambda \) and \(\mu \). So, \(\Delta \) satisfies (6), which produces:

Family III: By implementing Eq. (5) and Eq. (4) and Eq. (3) and collecting all terms with the same order of Δ together, the left-hand side of Eq. (3) is converted into polynomial in Δ. Equating each coefficient of the polynomial to zero, we can get a set of algebraic equations which can be solved to find the values of the studied method.

3 Application of the modified (G'/G)-expansion method

The modified (G'/G)-expansion approach is used in this subsection to solve the Zoomeron equation in the form.

$${\left(\frac{{u}_{xy}}{u}\right)}_{tt}-{\left(\frac{{u}_{xy}}{u}\right)}_{xx}+2{\left({u}^{2}\right)}_{xt}=0$$
(7)

where u(x,y,t) is the amplitude of the relative wave mood. This equation is one of incognito evolution equation. The equation was introduced by Calogero and Degasperis [21]. Using the wave variable

$$u\left(x,y,t\right)=U\left(\xi \right),\xi =x+sy-wt,$$

Equation (7) is carried to an ODE

$$s\left({w}^{2}-1\right)U"-2w{U}^{3}-RU=0,$$
(8)

where the prime denotes the derivation with respect to Δ and \(R\) is the integration constant.

Balancing the highest- order derivative term U′′ with the nonlinear term \(U^{3}\) of Eq. (8) yields N = 1 According to modified \({\raise0.7ex\hbox{${G^{\prime}}$} \!\mathord{\left/ {\vphantom {{G^{\prime}} G}}\right.\kern-0pt} \!\lower0.7ex\hbox{$G$}}\) expansion method,

Now the solution of Eq. (8) is,

$$U\left(\xi \right)={V}_{-1}{\Delta }^{-1}+{V}_{0}+{V}_{1}\Delta $$
(9)

Putting Eq. (9) in Eq. (8) with the help of the proposed methods we get,

Set of solutions:

Case-1:

$$S=\pm \sqrt{\frac{R}{W({\lambda }^{2}-4\mu )}}\frac{W}{{W}^{2}-1},{V}_{0}=0,{V}_{-1}=\pm \sqrt{\frac{R}{W({\lambda }^{2}-4\mu )}},{V}_{1}=\pm \frac{1}{4}\frac{\sqrt{R({\lambda }^{2}-4\mu )}}{W}$$

Substituting the values of case (1) into Eq. (9) then we achieve,

$${U}_{1}(\xi )=\pm \sqrt{\frac{R}{W}} \frac{1}{\left({\lambda }^{2}-4\mu \right)}\left[2{\left\{\mathit{tan}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right\}}^{-1}+{\left({\lambda }^{2}-4\mu \right)}^{2}\mathit{tan}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right]$$
(10)
$${U}_{2}(\xi )=\pm \sqrt{\frac{R}{W}} \frac{1}{\left({\lambda }^{2}-4\mu \right)}\left[2{\left\{\mathit{cot}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right\}}^{-1}+{\left({\lambda }^{2}-4\mu \right)}^{2}\mathit{cot}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right]$$
(11)
$${U}_{3}(\xi )=\pm \sqrt{\frac{R}{W}} \left[\frac{1}{\sqrt{{\lambda }^{2}-4\mu }}\left\{\frac{4{\xi }^{2}+{\lambda }^{2}-4\mu }{4\xi }\right\}\right]$$
(12)
$${U}_{4}(\xi )=\pm \sqrt{\frac{R}{W}} \frac{1}{\sqrt{{\lambda }^{2}-4\mu }}\left[2{\left\{\mathit{tan}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right\}}^{-1}+{\left({\lambda }^{2}-4\mu \right)}^{2}\mathit{tan}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right]$$
(13)
$${U}_{5}(\xi )=\pm \sqrt{\frac{R}{W}} \frac{1}{\sqrt{{\lambda }^{2}-4\mu }}\left[2{\left\{\mathit{cot}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right\}}^{-1}+{\left({\lambda }^{2}-4\mu \right)}^{2}\mathit{cot}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right]$$
(14)

Case-2:

$$S=-\frac{2R}{{W}^{2}{\lambda }^{2}-4{W}^{2}\mu -{\lambda }^{2}+4\mu },{V}_{0}=0,{V}_{-1}=\pm \sqrt{\frac{2R}{W\left({\lambda }^{2}-4\mu \right)}}i,{V}_{1}=0$$

Substituting the values of case (2) into Eq. (9) then we achieve,

$${U}_{6}\left(\xi \right)=\pm \left[i\sqrt{\frac{R}{2W}} {\left\{\mathit{tan}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right\}}^{-1}\right]$$
(15)
$${U}_{7}\left(\xi \right)=\pm \left[i\sqrt{\frac{R}{2W}} {\left\{\mathit{cot}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right\}}^{-1}\right]$$
(16)
$${U}_{8}\left(\xi \right)=\pm \left[i\sqrt{\frac{2R}{W\left({\lambda }^{2}-4\mu \right)}}\xi \right]$$
(17)
$${U}_{9}\left(\xi \right)=\pm \left[i\sqrt{\frac{R}{2W}} {\left\{\mathit{tan}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right\}}^{-1}\right]$$
(18)
$${U}_{10}\left(\xi \right)=\pm \left[i\sqrt{\frac{R}{2W}} {\left\{\mathit{cot}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right\}}^{-1}\right]$$
(19)

Case-3:

$$S=-\frac{2R}{{W}^{2}{\lambda }^{2}-4{W}^{2}\mu -{\lambda }^{2}+4\mu },{V}_{0}=0,{V}_{-1}=0,{V}_{1}=\pm \sqrt{\frac{R\left(4\mu -{\lambda }^{2}\right)}{8W}}$$

Substituting the values of case (3) into Eq. (9) then we achieve,

$${U}_{11}\left(\xi \right)=\pm \left[\sqrt{\frac{R\left(4\mu -{\lambda }^{2}\right)}{8W}}\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\left\{\mathit{tan}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right){\xi }^{-1}\right\}\right]$$
(20)
$${U}_{12}\left(\xi \right)=\pm \left[\sqrt{\frac{R\left(4\mu -{\lambda }^{2}\right)}{8W}}\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\left\{\mathit{cot}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right){\xi }^{-1}\right\}\right]$$
(21)
$${U}_{13}\left(\xi \right)=\pm \left[\sqrt{\frac{R\left(4\mu -{\lambda }^{2}\right)}{8W}}{\xi }^{-1}\right]$$
(22)
$${U}_{14}\left(\xi \right)=\pm \left[\sqrt{\frac{R\left(4\mu -{\lambda }^{2}\right)}{8W}}\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\left\{\mathit{tan}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right){\xi }^{-1}\right\}\right]$$
(23)
$${U}_{15}\left(\xi \right)=\pm \left[\sqrt{\frac{R\left(4\mu -{\lambda }^{2}\right)}{8W}}\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\left\{\mathit{cot}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right){\xi }^{-1}\right\}\right]$$
(24)

Case-4:

$$S=\pm \sqrt{\frac{R}{2W\left({\lambda }^{2}-4\mu \right)}}\frac{W}{{W}^{2}-1}i,{V}_{0}=0,{V}_{-1}=\sqrt{\frac{R}{2W\left({\lambda }^{2}-4\mu \right)}}i,{V}_{1}=-\frac{1}{8}\frac{R}{W}\sqrt{\frac{R}{2W\left({\lambda }^{2}-4\mu \right)}}i$$

Substituting the values of case (4) into Eq. (9) then we achieve,

$${U}_{16}\left(\xi \right)=\pm \frac{i}{2}{\left\{\mathit{tan}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right\}}^{-1}\left[\sqrt{\frac{R}{2W}} +\frac{1}{8}\frac{R}{W}\frac{1}{\sqrt{\frac{R}{2W\left({\lambda }^{2}-4\mu \right)}}}\left(\sqrt{{\lambda }^{2}-4\mu }\right)\right]$$
(25)
$${U}_{17}\left(\xi \right)=\pm \frac{i}{2}{\left\{\mathit{cot}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right\}}^{-1}\left[\sqrt{\frac{R}{2W}} +\frac{1}{8}\frac{R}{W}\frac{1}{\sqrt{\frac{R}{2W\left({\lambda }^{2}-4\mu \right)}}}\left(\sqrt{{\lambda }^{2}-4\mu }\right)\right]$$
(26)
$${U}_{18}\left(\xi \right)=\pm i\left(1+\frac{R}{8W}\right)\left[\sqrt{\frac{R}{2W\left({\lambda }^{2}-4\mu \right)}}\frac{1}{\xi }\right]$$
(27)
$${U}_{19}\left(\xi \right)=\pm \frac{i}{2}{\left\{\mathit{tan}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right\}}^{-1}\left[\sqrt{\frac{R}{2W}} +\frac{1}{8}\frac{R}{W}\frac{1}{\sqrt{\frac{R}{2W\left({\lambda }^{2}-4\mu \right)}}}\left(\sqrt{{\lambda }^{2}-4\mu }\right)\right]$$
(28)
$${U}_{20}\left(\xi \right)=\pm \frac{i}{2}{\left\{\mathit{cot}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right\}}^{-1}\left[\sqrt{\frac{R}{2W}} +\frac{1}{8}\frac{R}{W}\frac{1}{\sqrt{\frac{R}{2W\left({\lambda }^{2}-4\mu \right)}}}\left(\sqrt{{\lambda }^{2}-4\mu }\right)\right]$$
(29)

4 Graphical representation

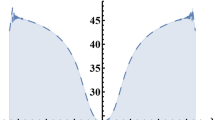
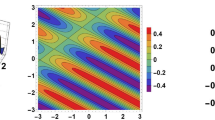
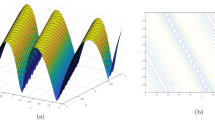
Graphs are a useful tool for advising and for calling problems' solutions calmly. A blueprint is a visible depiction of incomplete or imperfect solutions, or other data, typically used for allusive purposes. When assuming addition in routine activity, we need the fundamental capacity to use graphs effectively. We will discuss the graphical depiction of the discovered solutions in this section. Figure 1 exhibits the unique presentation of Eq. (11) using the parameters \(\lambda = - 4,\,\mu = 2,\,\,R = 2,W = 0.5,y = 0.5.\) Specifically, Fig. 1 shows the 3D form (real and complex), 2D form (real and complex), and density form (real and complex) of.Eq. (11). The real part of this shape addresses the wave profile, and complex part represents the anti-kink wave profile. The solution attributes of Eq. (10) are displayed in Fig. 2 using \(\lambda = 3,\,\mu = 1,\,\,R = 0.5,W = - 0.9,y = 0.5.\) This shape addresses the bell shape and kink wave profile. The nature of the result of Eq. (13) is shown in Fig. 3 using \(\lambda = 2,\,\mu = 2,\,\,R = 0.5,W = 0.9,y = 0.5.\) This shape addresses the periodic wave profile. The solution attributes of Eq. (11) are displayed in Fig. 4 using \(\lambda = 3,\,\mu = 1,\,\,R = 0.5,W = - 0.9,y = 0.5.\) This shape addresses cusp wave of multiple wings shape and kink wave profile.

Fig. 1
figure 1

The graphical representation of Eq. (11): a real 3D shape, b real 2D shape, c complex 3D shape, d complex 2D shape

Full size image
Fig. 2
figure 2

The graphical representation of Eq. (10): a real 3D shape, b real 2D shape, c complex 3D shape, and d complex 2D shape

Full size image
Fig. 3
figure 3

The graphical representation of Eq. (13): a real 3D shape, b real 2D shape, c complex 3D shape, and d complex 2D shape

Full size image
Fig. 4
figure 4

The graphical representation of Eq. (11): (a) real 3D shape, (b) real 2D shape, (c) complex 3D shape, and (d) complex 2D shape

Full size image

5 Comparison

The paper compares the findings of the Zoomeron equation obtained by the proposed approach with solutions discovered in past research in this section. The comparison, as shown in Table, reveals differences between the obtained results and those documented by Reza Abazari et al. [30] obtained by \((G{\prime}/G)-\)expansion method. The table shows that for some values of arbitrary parameters, the derived solutions deviate from those described in previous literature [30]. This highlights the consistency with previous results while emphasizing the novelty of the remaining outcomes. This work provides several innovative soliton solutions to the aforementioned equation utilizing the modified \((G{\prime}/G)-\)expansion strategy, as illustrated by the comparison table below.

Solutions of Reza Abazari et al.[30]

Solutions attained in this study

(i) If \({{C}_{1}}^{2}>{{C}_{2}}^{2}\) then

\({u}_{H}\left(\xi \right)=\pm \frac{1}{2}\sqrt{\frac{-2R}{w}}{\text{tanh}}\left(-\frac{1}{2}\sqrt{\frac{2R}{c({w}^{2}-1)}}\left(\xi -{\eta }_{H}\right)\right)\)

(ii) If \({{C}_{1}}^{2}<{{C}_{2}}^{2}\) then

\({u}_{H}\left(\xi \right)=\pm \frac{1}{2}\sqrt{\frac{-2R}{w}}{\text{coth}}\left(-\frac{1}{2}\sqrt{\frac{2R}{c({w}^{2}-1)}}\left(\xi -{\eta }_{H}\right)\right)\)

(iii) For rational function

\({u}_{rat}\left(\xi \right)=\pm \frac{c({w}^{2}-1){C}_{2}}{w({C}_{1}+{C}_{2}\xi )\sqrt{-\frac{c({w}^{2}-1)}{w}}}\)

(i) For case1

\({U}_{1}(\xi )=\pm \sqrt{\frac{R}{W}} \frac{1}{\sqrt{{\lambda }^{2}-4\mu }}\left[2{\left\{\mathit{tan}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right\}}^{-1}+{\left({\lambda }^{2}-4\mu \right)}^{2}\mathit{tan}\left(\frac{\sqrt{4\mu -{\lambda }^{2}}}{2}\right)\xi \right]\)

(ii) For case 2

\({U}_{6}\left(\xi \right)=\pm \left[i\sqrt{\frac{R}{2W}} {\left\{\mathit{tan}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right\}}^{-1}\right]\)

(iii) For case 3

\({U}_{11}\left(\xi \right)=\pm \left[\sqrt{\frac{R\left(4\mu -{\lambda }^{2}\right)}{8W}}\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\left\{\mathit{tan}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right){\xi }^{-1}\right\}\right]\)

(iv) For case 4

\({U}_{16}\left(\xi \right)=\pm \frac{i}{2}{\left\{\mathit{tan}h\left(\frac{\sqrt{{\lambda }^{2}-4\mu }}{2}\right)\xi \right\}}^{-1}\left[\sqrt{\frac{R}{2W}} +\frac{1}{8}\frac{R}{W}\frac{1}{\sqrt{\frac{R}{2W\left({\lambda }^{2}-4\mu \right)}}}\left(\sqrt{{\lambda }^{2}-4\mu }\right)\right]\)

6 Conclusion

Our study thoroughly evaluated the innovative computational solutions related with the Zoomeron equation using the proposed approaches. We have shown a plethora of new computational outcomes over a spectrum encompassing hyperbolic, rational, and trigonometric equations, showing patterns such as the king-type form, singular king shape, periodic waves, and bell-shaped wave profiles. Utilizing Maple, this study employs the powerful capabilities of the software to present captivating two- and three-dimensional (2-D and 3-D) visual representations of these solutions. To emphasize the uniqueness of our study, we conducted comparison analyses, comparing our observed responses to those published in recent research papers. The demonstration of the efficacy of these established methodologies highlights its appropriateness, impact, and adaptability in dealing with various nonlinear models, necessitating additional investigation and inspection.