1 Introduction

Lagrange, Laplace, Euler, Bernoulli, and d’Alembert conducted the first studies of the partial differential equation (PDE) in the eighteenth century as an essential tool for understanding the physical properties of solids, fluids and, more widely, as the primary approach for analytical examination of real-world models in many fields. The analysis of physical models is still a prime concern in evolving PDEs. In the middle of the nineteenth century, mainly due to Riemann’s work, PDEs were often utilized in many different branches of mathematics. This distinction significantly impacted the development of PDEs in the nineteenth and twentieth centuries. A fractional partial differential equation (FPDE) is a generalized version of an integer-ordered partial differential equation. The order of integrals and derivatives is arbitrary in fractional-order calculus. Leibniz, Riemann, Liouville, Grunwald, and Letnikov developed the fractional calculus theory, which has since found several uses in science and engineering. It has been an active area of research to find accurate and effective ways to solve fractional differential equations. The applications that preceded its development, fractional calculus, particularly fractional partial differential equations, have garnered much interest from mathematics and physics researchers. Fractional derivatives are a helpful tool for describing some physical difficulties since they offer more accurate representations of real-world problems than integer-order derivatives. Fractional calculus is a highly significant branch of mathematics and plays a severe and critical role in describing complex dynamical behavior in various application fields. Due to its numerous applications in studying a variety of real-world spectacles in bioengineering [1,2,3], viscoelasticity [4], electronics [5, 6], robotic technology [7], control theory [8], signal processing [9], diffusion model and relaxation processes [10, 11], chemistry [12], and physics [13, 14]. Fractional-order calculus is widely used as an essential tool in many areas of physical, mathematical, biological, and engineering sciences [15,16,17,18,19,20]. Thus, fractional-order nonlinear partial differential equations have established a fundamental interest in generalizing integer-order nonlinear PDEs to represent complex problems in optical physics, thermodynamics, engineering, and fluid dynamics [21,22,23].

Oscar Klein and Walter Gordon introduced the Klein-Gordan (KG) equation in 1927 as a fascinating differential equation. Schrodinger initially considered the KG equation as a quantum wave equation in his research for an equation defining de Broglie waves. The KG equation is essential in mathematical physics and many scientific applications, including solid-state physics, elementary particle behavior, dispersive wave phenomena, dislocations propagation in crystals, nonlinear optics, relativistic physics, and quantum field theory [24, 25]. Wazwaz has achieved compactons, solitons, and periodic solutions using the tanh technique [26]. The equation has received a lot of interest in the research of solitons and condensed matter physics [27,28,29], in investigating the interaction of solitons in a collisionless plasma, in the repetition of starting states, and in the study of nonlinear wave equations [30]. The classical (integer-order) spatial–temporal Klein–Gordon equation was created based on homogeneous space and time. Homogeneous space and time were the foundation for developing the classical (integer-order) spatial–temporal Klein–Gordon equation. Since space and time are not homogeneous enough to be handled by classical calculus at mesoscopic and microscopic scales, this equation could not explain both chargeless and single-particle systems. Thus, the abovementioned drawback can be solved using the spatial–temporal fractional KG equation.

The traditional approach KG equation appears as

$$\frac{{\partial^{2} y\left( {x,t} \right)}}{{\partial t^{2} }} + \lambda \frac{{\partial^{2} y\left( {x,t} \right)}}{{\partial x^{2} }} = F\left( {x,t,y} \right), \left( {x,t} \right) \in \left[ {a,b} \right] \times \left[ {0,T} \right],$$
(1)

with initial conditions

$$y\left( {x,0} \right) = h_{1} \left( x \right), y_{t} \left( {x,0} \right) = h_{2} \left( x \right),$$

and the Dirichlet boundary conditions

$$y\left( {a,t} \right) = g_{1} \left( t \right), y\left( {b,t} \right) = g_{2} \left( t \right),$$

where \(y\) stands for an unknown function in the variables \(x\) and \(t\), \(\lambda\) is a real number, and \(F\) indicates the source term. The numerical analysis of the KG equation has received much attention in recent years. We will use an arbitrary order derivative instead of an integer order derivative to investigate the problem's physical behavior. There are numerous methods to find the solutions to the fractional Klein–Gordon equation, including the Clique polynomial method [31], the Modified double Laplace decomposition method [32], the Adomian decomposition method, and Daftardar-Jafari method [33], the Chebyshev polynomials-based collocation method [34], Fractional Reduced Differential Transform Method [35]. The following kind of Caputo fractional derivative of order \(1 < \alpha \le 2\) is used in the current work to examine a generalized version of Klein-Gordon:

$${}_{}^{C} D_{t}^{\alpha } y\left( {x,t} \right) + \lambda D_{xx} y\left( {x,t} \right) = F\left( {x,t,y} \right).$$
(2)

The wavelet theory is a recently revived and developing approach in mathematics. Wavelets are based on Joseph Fourier's fundamental hypothesis, which states that a complex function can be expressed by a collection of self-similar functions superimposed on one another. In evaluating physical conditions when the signal involves discontinuities and abrupt spikes, the wavelets offer an advantage over conventional Fourier approaches because of their ability to extract both local spectral and temporal data. Wavelets are mathematical operations that separate data into distinct frequency components. Each frequency component is subsequently examined with a resolution appropriate to its scale. Orthogonality and efficient localization are the main wavelet requirements that attract researchers. Wavelets can be a mathematical tool to extract data from various formats. These properties of wavelets help to draw the attention of many researchers to solve partial differential equations by wavelet-based methods. In the literature, some wavelet-based numerical techniques have been successfully solved, including the Laguerre wavelet-Adomian method [36], the Chebyshev wavelet operational matrix method [37], the Fibonacci wavelet method [38], Shannon-Cosine wavelet spectral method [39], Laguerre wavelet method [40], Chebyshev wavelet-Picard technique [41], Hermite wavelet method [42], Bernoulli wavelet collocation technique [43].

Fibonacci wavelets are a recent addition to the wavelet family and are produced by Fibonacci polynomials. Numerous applications in applied sciences use the famous Fibonacci numbers and the golden ratio. The book [44] extensively discusses Fibonacci polynomials' traits, benefits, applications, and various generalizations. Several scholars have become interested in Fibonacci wavelets due to their unique characteristics and advantages over other wavelets. The operational matrix of integration of Fibonacci wavelets is sparse, so that the computational time will be less. Due to properties like compact support, orthogonality, and vanishing moment, the Fibonacci wavelet is a function that may be created at many scales and has a variety of applications. This method does not require any regulating parameters, unlike some semi-analytical approaches that depend upon the regulating parameters. It is quite easy to obtain the Fibonacci polynomials using computer tools, such as the \(Fibonacci\left[ {m,t} \right]\) command in the software Mathematica. Several researchers are interested in studying Fibonacci wavelets because of their advantages and unique qualities. The researchers used this polynomial-based wavelet method as a consequence to solve different types of equations, including the hyperbolic partial differential equation [45], time-fractional telegraph equations [46], fractional optimal control problems [47], time-fractional bioheat transfer model [48], fractional order partial differential equations which are arising in the financial market [49], fractional dispersive partial differential equation [50].

The paper is organized as described in the paragraph that follows. Section 2 discusses Fibonacci wavelets, the concept of a fractional derivative, and wavelet results. The operational matrix of integration is discussed in Sect. 3. Section 4 describes the method of the proposed technique. Section 5 carries out projected method applications. Section 6 provides a conclusion of the paper.

2 Basic concepts

Definition 2.1:

The \(\alpha\)-order Caputo fractional derivative of \(f\left( t \right) \in C_{\mu }\) is defined by [17],

$$\frac{{\partial^{\alpha } f\left( t \right)}}{{\partial t^{\alpha } }} = \frac{1}{{{\Gamma }\left( {m - \alpha } \right)}}\mathop \int \limits_{0}^{t} \left( {t - x} \right)^{m - \alpha - 1} \frac{{\partial^{m} f\left( x \right)}}{{\partial x^{m} }}dx,$$
(3)

for \(m - 1 < \alpha \le m\), where \(m = \alpha\) be a positive integer, \(t > 0, f\left( t \right) \in C_{\mu }^{m} ,\mu \ge - 1\).

Definition 2.2:

The \(\alpha\)-order fractional integral of \(f\left( t \right)\) is defined by [51]

$$I^{\alpha } f\left( t \right) = \frac{1}{{{\Gamma }\left( \alpha \right)}}\mathop \int \limits_{0}^{t} \left( {t - x} \right)^{\alpha - 1} f\left( x \right)dx,$$
(4)

for \(\alpha > 0\) and \(t > 0, \forall\, \alpha ,t \in {\mathbb{R}}\).

Definition 2.3:

The Fibonacci wavelets are defined as [46],

$$\zeta _{{n,m}} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{{2^{{\frac{{k - 1}}{2}}} }}{{\sqrt {w_{m} } }}\phi _{m} \left( {2^{{k - 1}} x - n + 1} \right),} \hfill & {\frac{{n - 1}}{{2^{{k - 1}} }} \le x < \frac{n}{{2^{{k - 1}} }},} \hfill \\ {0,} \hfill & {{\text{Otherwise}},} \hfill \\ \end{array} } \right.$$
(5)

with

$$w_{m} = \mathop \int \limits_{0}^{1} \left( {\phi_{m} \left( x \right)} \right)^{2} dx,$$
(6)

where \(k\) indicates the resolution level \(k = 1, 2, \ldots\), the translation parameter \(n = 1, 2, \ldots , 2^{k - 1}\), the Fibonacci polynomial \(\phi_{m} \left( x \right)\) has a degree \(m = 0, 1, \ldots ,M - 1\), and \(\frac{1}{{\sqrt {w_{m} } }}\) is the normalization factor. The Fibonacci polynomials are represented as follows using the recurrence relation for each \(x \in {\mathbb{R}}^{ + }\) [45]:

$$\phi_{m + 2} \left( x \right) = x\phi_{m + 1} \left( x \right) + \phi_{m} \left( x \right),\; \forall\, m \ge 0$$
(7)

with the initial conditions are \(\phi_{0} \left( x \right) = 1\) and \(\phi_{1} \left( x \right) = x\). The Fibonacci polynomials have the following general formula [45]:

$$\phi _{m} \left( x \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {m = 0,} \hfill \\ {x,} \hfill & {m = 1,} \hfill \\ {x\phi _{{m - 1}} \left( x \right) + \phi _{{m - 2}} \left( x \right),} \hfill & {m > 1,} \hfill \\ \end{array} } \right.$$
(8)

3 Operational matrix of integration

We have simplified a few Fibonacci wavelet basis here at \(k = 1\):

$$\zeta_{1,0} \left( x \right) = 1,$$
$$\zeta_{1,1} \left( x \right) = \sqrt 3 x,$$
$$\zeta_{1,2} \left( x \right) = \frac{1}{2}\sqrt{\frac{15}{7}} \left( {1 + x^{2} } \right),$$
$$\zeta_{1,3} \left( x \right) = \sqrt {\frac{105}{{239}}} x\left( {2 + x^{2} } \right),$$
$$\zeta_{1,4} \left( x \right) = 3\sqrt {\frac{35}{{1943}}} \left( {1 + 3x^{2} + x^{4} } \right),$$
$$\zeta_{1,5} \left( x \right) = \frac{3}{4}\sqrt {\frac{385}{{2582}}} x\left( {3 + 4x^{2} + x^{4} } \right),$$
$$\zeta_{1,6} \left( x \right) = 3\sqrt {\frac{5005}{{1268209}}} \left( {1 + 6x^{2} + 5x^{4} + x^{6} } \right),$$
$$\zeta_{1,7} \left( x \right) = 3\sqrt {\frac{5005}{{2827883}}} x\left( {4 + 10x^{2} + 6x^{4} + x^{6} } \right),$$
$$\zeta_{1,8} \left( x \right) = \frac{3}{2}\sqrt {\frac{85085}{{28195421}}} \left( {1 + 10x^{2} + 15x^{4} + 7x^{6} + x^{8} } \right),$$
$$\zeta_{1,9} \left( x \right) = 3\sqrt {\frac{1616615}{{5016284989}}} x\left( {5 + 20x^{2} + 21x^{4} + 8x^{6} + x^{8} } \right),$$
$$\zeta_{1,10} \left( x \right) = 3\sqrt {\frac{1616615}{{11941544471}}} \left( {1 + 15x^{2} + 35x^{4} + 28x^{6} + 9x^{8} + x^{10} } \right),$$
$$\zeta_{1,11} \left( x \right) = \frac{3}{8}\sqrt {\frac{37182145}{{10276002038}}} x\left( {6 + 35x^{2} + 56x^{4} + 36x^{6} + 10x^{8} + x^{10} } \right).$$

And

$$\zeta_{10} \left( x \right) = \left[ {\zeta_{1,0} \left( x \right),\zeta_{1,1} \left( x \right),\zeta_{1,2} \left( x \right),\zeta_{1,3} \left( x \right),\zeta_{1,4} \left( x \right),\zeta_{1,5} \left( x \right),\zeta_{1,6} \left( x \right),\zeta_{1,7} \left( x \right),\zeta_{1,8} \left( x \right),\zeta_{1,9} \left( x \right)} \right]^{T} .$$

By integrating the basis mentioned above with respective \(x\) from 0 and \(x\) and then expressing integrated wavelet basis as a linear combination is given by;

$$\mathop \int \limits_{0}^{x} \zeta_{1, 0} \left( {x } \right)dx = \left[ {\begin{array}{*{20}c} 0 & {\frac{1}{\sqrt 3 }} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \zeta_{1,1} \left( x \right)dx = \left[ {\begin{array}{*{20}c} { - \frac{\sqrt 3 }{2}} & 0 & {\sqrt{\frac{7}{5}} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \zeta_{1,2} \left( x \right)dx = \left[ {\begin{array}{*{20}c} 0 & {\frac{\sqrt 5 }{{6\sqrt 7 }}} & 0 & {\frac{{\sqrt {239} }}{42}} & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \zeta_{1,3} \left( x \right)dx = \left[ {\begin{array}{*{20}c} { - \frac{{\sqrt {105} }}{{2\sqrt {239} }}} & 0 & {\frac{7}{{2\sqrt {239} }}} & 0 & {\frac{{\sqrt {1943} }}{{4\sqrt {717} }}} & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \zeta_{1,4} \left( x \right)dx = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {\frac{{\sqrt {717} }}{{5\sqrt {1943} }}} & 0 & {\frac{{4\sqrt {2582} }}{{5\sqrt {21373} }}} & 0 & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \zeta_{1,5} \left( x \right)dx = \left[ {\begin{array}{*{20}c} { - \frac{{\sqrt {385} }}{{4\sqrt {2582} }}} & 0 & 0 & 0 & {\frac{{\sqrt {21373} }}{{24\sqrt {2582} }}} & 0 & {\frac{{\sqrt {1268209} }}{{24\sqrt {33566} }}} & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \zeta_{1,6} \left( x \right)dx = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & {\frac{{4\sqrt {33566} }}{{7\sqrt {1268209} }}} & 0 & {\frac{{\sqrt {2827883} }}{{7\sqrt {1268209} }}} & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \zeta_{1,7} \left( x \right)dx = \left[ {\begin{array}{*{20}c} { - \frac{{3\sqrt {5005} }}{{4\sqrt {2827883} }}} & 0 & 0 & 0 & 0 & 0 & {\frac{{\sqrt {1268209} }}{{8\sqrt {2827883} }}} & 0 & {\frac{{\sqrt {28195421} }}{{4\sqrt {48074011} }}} & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \zeta_{1,8} \left( x \right)dx = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\frac{{\sqrt {48074011} }}{{18\sqrt {28195421} }}} & 0 & {\frac{{\sqrt {5016284989} }}{{18\sqrt {535712999} }}} \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \zeta_{1,9} \left( x \right)dx = \left[ {\begin{array}{*{20}c} { - 3\sqrt {\frac{323323}{{25081424945}}} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\frac{{\sqrt {535712999} }}{{5\sqrt {5016284989} }}} & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right) + \frac{{\sqrt {11941544471} }}{{10\sqrt {5016284989} }}\zeta_{1,10} \left( x \right).$$

Hence,

$$\mathop \int \limits_{0}^{x} \zeta \left( x \right)dx = B_{10 \times 10} \zeta_{10} \left( x \right) + \overline{{\zeta_{10} \left( x \right)}} ,$$

where,

$${B}_{10\times 10}=\left[\begin{array}{cccccccccc}0& \frac{1}{\sqrt{3}}& 0& 0& 0& 0& 0& 0& 0& 0\\ -\frac{\sqrt{3}}{2}& 0& \sqrt{\frac{7}{5}} & 0& 0& 0& 0& 0& 0& 0\\ 0& \frac{\sqrt{5}}{6\sqrt{7}}& 0& \frac{\sqrt{239}}{42}& 0& 0& 0& 0& 0& 0\\ -\frac{\sqrt{105}}{2\sqrt{239}}& 0& \frac{7}{2\sqrt{239}}& 0& \frac{\sqrt{1943}}{4\sqrt{717}}& 0& 0& 0& 0& 0\\ 0& 0& 0& \frac{\sqrt{717}}{5\sqrt{1943}}& 0& \frac{4\sqrt{2582}}{5\sqrt{21373}}& 0& 0& 0& 0\\ -\frac{\sqrt{385}}{4\sqrt{2582}}& 0& 0& 0& \frac{\sqrt{21373}}{24\sqrt{2582}}& 0& \frac{\sqrt{1268209}}{24\sqrt{33566}}& 0& 0& 0\\ 0& 0& 0& 0& 0& \frac{4\sqrt{33566}}{7\sqrt{1268209}}& 0& \frac{\sqrt{2827883}}{7\sqrt{1268209}}& 0& 0\\ -\frac{3\sqrt{5005}}{4\sqrt{2827883}}& 0& 0& 0& 0& 0& \frac{\sqrt{1268209}}{8\sqrt{2827883}}& 0& \frac{\sqrt{28195421}}{4\sqrt{48074011}}& 0\\ 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{48074011}}{18\sqrt{28195421}}& 0& \frac{\sqrt{5016284989}}{18\sqrt{535712999}}\\ -3\sqrt{\frac{323323}{25081424945}} & 0& 0& 0& 0& 0& 0& 0& \frac{\sqrt{535712999}}{5\sqrt{5016284989}}& 0\end{array}\right]$$

and \(\overline{{\zeta }_{10}\left(x\right)}=\left[\begin{array}{c}\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \frac{\sqrt{11941544471}}{10\sqrt{5016284989}}{\zeta }_{\mathrm{1,10}}\left(x\right)\end{array}\end{array}\right]\).

Integrate the above basis once again. Then we have,

$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,0} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} { - \frac{1}{2}} & 0 & {\sqrt{\frac{7}{15}} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,1} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{3}} & 0 & {\frac{{\sqrt {239} }}{{6\sqrt {35} }}} & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,2} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} { - \frac{\sqrt 5 }{{2\sqrt {21} }}} & 0 & \frac{1}{4} & 0 & {\frac{{\sqrt {1943} }}{168\sqrt 3 }} & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,3} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} 0 & { - \frac{{5\sqrt {35} }}{{12\sqrt {239} }}} & 0 & \frac{2}{15} & 0 & {\frac{{\sqrt {2582} }}{{5\sqrt {7887} }}} & 0 & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,4} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} { - \frac{{\sqrt {35} }}{{2\sqrt {1943} }}} & 0 & {\frac{7\sqrt 3 }{{10\sqrt {1943} }}} & 0 & \frac{1}{12} & 0 & {\frac{{\sqrt {1268209} }}{{30\sqrt {277849} }}} & 0 & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,5} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} 0 & { - \frac{{\sqrt {385} }}{{4\sqrt {7746} }}} & 0 & {\frac{{\sqrt {2629} }}{{40\sqrt {7746} }}} & 0 & \frac{2}{35} & 0 & {\frac{{\sqrt {2827883} }}{{168\sqrt {33566} }}} & 0 & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,6} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} { - \frac{{\sqrt {5005} }}{{4\sqrt {1268209} }}} & 0 & 0 & 0 & {\frac{{\sqrt {277849} }}{{42\sqrt {1268209} }}} & 0 & \frac{1}{24} & 0 & {\frac{{\sqrt {28195421} }}{{28\sqrt {21559553} }}} & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,7} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} 0 & { - \frac{{\sqrt {15015} }}{{4\sqrt {2827883} }}} & 0 & 0 & 0 & {\frac{{\sqrt {16783} }}{{7\sqrt {5655766} }}} & 0 & \frac{2}{63} & 0 & {\frac{{\sqrt {5016284989} }}{{72\sqrt {913406209} }}} \\ \end{array} } \right]\zeta_{10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,8} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} { - \frac{{3\sqrt {17017} }}{{8\sqrt {140977105} }}} & 0 & 0 & 0 & 0 & 0 & {\frac{{\sqrt {21559553} }}{{144\sqrt {28195421} }}} & 0 & \frac{1}{40} & 0 \\ \end{array} } \right]\zeta_{10} \left( x \right) + \frac{{\sqrt {11941544471} }}{{180\sqrt {535712999} }}\zeta_{1,10} \left( x \right),$$
$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta_{1,9} \left( x \right)dxdx = \left[ {\begin{array}{*{20}c} 0 & { - \sqrt {\frac{969969}{{25081424945}}} } & 0 & 0 & 0 & 0 & 0 & {\frac{{\sqrt {913406209} }}{{90\sqrt {5016284989} }}} & 0 & \frac{2}{99} \\ \end{array} } \right]\zeta_{10} \left( x \right) + \frac{{4\sqrt {10276002038} }}{{55\sqrt {115374554747} }}\zeta_{1,11} \left( x \right).$$

Hence,

$$\mathop \int \limits_{0}^{x} \mathop \int \limits_{0}^{x} \zeta \left( x \right)dxdx = B^{\prime}_{10 \times 10} \zeta_{10} \left( x \right) + \overline{{\zeta_{10} \left( x \right)}}^{\prime} ,$$

where

$${B}^{\prime}_{10\times 10}=\left[\begin{array}{cccccccccc}-\frac{1}{2}& 0& \sqrt{\frac{7}{15}} & 0& 0& 0& 0& 0& 0& 0\\ 0& -\frac{1}{3}& 0& \frac{\sqrt{239}}{6\sqrt{35}}& 0& 0& 0& 0& 0& 0\\ -\frac{\sqrt{5}}{2\sqrt{21}}& 0& \frac{1}{4}& 0& \frac{\sqrt{1943}}{168\sqrt{3}}& 0& 0& 0& 0& 0\\ 0& -\frac{5\sqrt{35}}{12\sqrt{239}}& 0& \frac{2}{15}& 0& \frac{\sqrt{2582}}{5\sqrt{7887}}& 0& 0& 0& 0\\ -\frac{\sqrt{35}}{2\sqrt{1943}}& 0& \frac{7\sqrt{3}}{10\sqrt{1943}}& 0& \frac{1}{12}& 0& \frac{\sqrt{1268209}}{30\sqrt{277849}}& 0& 0& 0\\ 0& -\frac{\sqrt{385}}{4\sqrt{7746}}& 0& \frac{\sqrt{2629}}{40\sqrt{7746}}& 0& \frac{2}{35}& 0& \frac{\sqrt{2827883}}{168\sqrt{33566}}& 0& 0\\ -\frac{\sqrt{5005}}{4\sqrt{1268209}}& 0& 0& 0& \frac{\sqrt{277849}}{42\sqrt{1268209}}& 0& \frac{1}{24}& 0& \frac{\sqrt{28195421}}{28\sqrt{21559553}}& 0\\ 0& -\frac{\sqrt{15015}}{4\sqrt{2827883}}& 0& 0& 0& \frac{\sqrt{16783}}{7\sqrt{5655766}}& 0& \frac{2}{63}& 0& \frac{\sqrt{5016284989}}{72\sqrt{913406209}}\\ -\frac{3\sqrt{17017}}{8\sqrt{140977105}}& 0& 0& 0& 0& 0& \frac{\sqrt{21559553}}{144\sqrt{28195421}}& 0& \frac{1}{40}& 0\\ 0& -\sqrt{\frac{969969}{25081424945}} & 0& 0& 0& 0& 0& \frac{\sqrt{913406209}}{90\sqrt{5016284989}}& 0& \frac{2}{99}\end{array}\right]$$
$${\text{and}}\;{\mkern 1mu} \overline{{\zeta _{{10}} \left( x \right)}}^{\prime} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ {\frac{{\sqrt {11941544471} }}{{180\sqrt {535712999} }}\zeta _{{1,10}} \left( x \right)} \\ {\frac{{4\sqrt {10276002038} }}{{55\sqrt {115374554747} }}\zeta _{{1,11}} \left( x \right)} \\ \end{array} } \\ \end{array} } \right].$$

In this manner, we can produce the matrices for our expediency.

4 Convergence and error analysis

Theorem 1

[45]: Let \(y\left( {x,t} \right)\) in \(L^{2} \left( {{\mathbb{R}} \times {\mathbb{R}}} \right)\) be a continuous bounded function defined on \(\left[ {0,1\left] \times \right[0,1} \right]\), then Fibonacci wavelet expansion of \(y\left( {x,t} \right)\) is uniformly converges to it.

Proof:

Let \(y\)\(\left( {x,t} \right)\) in \(L^{2} \left( {{\mathbb{R}} \times {\mathbb{R}}} \right)\) be a continuous function defined on \(\left[ {0,1} \right] \times \left[ {0,1} \right]\) and bounded by a real number \(\mu\). The approximation of \(y\left( {x,t} \right)\) is;

$$y\left( {x,t} \right) = \mathop \sum \limits_{i = 1}^{\infty } \mathop \sum \limits_{j = 0}^{\infty } a_{i,j} \zeta_{i,j} \left( x \right) \zeta_{i,j} \left( t \right),$$

where, \(a_{i, j} = \,<y\left( {x,t} \right),\zeta_{i,j} \left( x \right)\zeta_{i,j} \left( t \right)>\), and \(<,>\) represents inner product. Since \(\zeta_{i,j} \left( x \right),\zeta_{i,j} \left( t \right)\) are functions on \(\left[ {0,1} \right]\). Then,

$$a_{i,j} = \mathop \int \limits_{0}^{1} \mathop \int \limits_{0}^{1} y\left( {x, t} \right)\zeta_{i,j} \left( x \right)\zeta_{i,j } \left( t \right)dxdt,$$

\(a_{i, j} = \mathop \int \limits_{0}^{1 } \mathop \int \limits_{I}^{ } y\left( {x,t} \right)\frac{{2^{{\frac{k - 1}{2}}} }}{{\sqrt {w_{m} } }}\phi_{m} \left( {2^{k - 1} x - n + 1} \right)\zeta_{i,j} \left( t \right)dxdt,\)

where \(I = \left[ {\frac{n - 1}{{2^{k - 1} }},\frac{n}{{2^{k - 1} }}} \right]\). Put \(2^{k - 1} x - n + 1 = r\) then,

$$a_{i,j } = \frac{{2^{{\frac{k - 1}{2}}} }}{{\sqrt {w_{m} } }}\mathop \int \limits_{0}^{1} \mathop \int \limits_{0}^{1} y\left( {\frac{r - 1 + n}{{2^{k - 1} }},t} \right)\phi_{m} \left( r \right)\frac{dr}{{2^{k - 1} }}\zeta_{i,j} \left( { t} \right)dt,$$

\(a_{i,j} = \frac{{2^{{ - \left( {\frac{k - 1}{2}} \right)}} }}{{\sqrt {w_{m} } }}\mathop \int \limits_{0}^{1} \left[ {\mathop \int \limits_{0}^{1} y\left( {\frac{r - 1 + n}{{2^{k - 1} }}, t} \right)\phi_{m} \left( r \right)dr} \right]\zeta_{i,j} \left( { t} \right)dt.\)

By generalized mean value theorem for integrals,

$$a_{i,j} = \frac{{2^{{ - \left( {\frac{k - 1}{2}} \right)}} }}{{\sqrt {w_{m} } }}\mathop \int \limits_{0}^{1} y\left( {\frac{ \xi - 1 + n}{{2^{k - 1} }} ,t} \right)\zeta_{i,j} \left( { t} \right)dt\left[ {\mathop \int \limits_{0}^{1} \phi_{m} \left( { r} \right)dr} \right],$$

where \(\xi \in \left( {0,1} \right)\) and choose \(\mathop \int \limits_{0}^{1} \phi_{m} \left( r \right)dr = A\),

$$a_{i,j} = \frac{{A 2^{{ - \left( {\frac{k - 1}{2}} \right)}} }}{{\sqrt {w_{m} } }} \mathop \int \limits_{{\frac{n - 1}{{2^{k - 1} }}}}^{{\frac{n}{{2^{k - 1} }}}} y\left( {\frac{\xi - 1 + n}{{2^{k - 1} }},t} \right)\frac{{2^{{\frac{k - 1}{2}}} }}{{\sqrt {w_{m} } }}\phi_{m} \left( {2^{k - 1} t - n + 1} \right)dt,$$

\(a_{i,j} = \frac{A}{{w_{m} }} \mathop \int \limits_{{\frac{n - 1}{{2^{k - 1} }}}}^{{\frac{n}{{2^{k - 1} }}}} y\left( {\frac{\xi - 1 + n}{{2^{k - 1} }},t} \right)\phi_{m} \left( {2 ^{k - 1} t - n + 1} \right)dt.\)

Put \(2^{k - 1} t - n + 1 = s\) then,

$$a_{i,j} = \frac{ A}{{w_{m} }} \mathop \int \limits_{0}^{1} y\left( {\frac{\xi - 1 + n}{{2^{k - 1} }},\frac{s - 1 + n}{{2^{k - 1} }}} \right)\phi_{m} \left( s \right)\frac{ds}{{2^{k - 1} }},$$

\(a_{i,j} = \frac{{A2^{ - k + 1} }}{{w_{m} }} \mathop \int \limits_{0}^{1} y\left( {\frac{\xi - 1 + n}{{2 ^{k - 1} }},\frac{s - 1 + n}{{2 ^{k - 1} }}} \right)\phi_{m} \left( s \right)ds.\)

By generalized mean value theorem for integrals,

$$a_{i,j} = \frac{{A2^{ - k + 1} }}{{w_{m} }}y\left( {\frac{\xi - 1 + n}{{2^{k - 1} }},\frac{{\xi_{1} - 1 + n}}{{2^{k - 1} }}} \right)\mathop \int \limits_{0}^{1} \phi_{m} \left( s \right)ds,$$

where, \(\xi_{1} \in \left( {0,1} \right)\) and \(\mathop \int \limits_{0}^{1} \phi_{m} \left( s \right)ds = B\) then

$$a_{i,j} = \frac{{AB2^{ - k + 1} }}{{w_{m} }} y\left( {\frac{\xi - 1 + n}{{2^{k - 1} }},\frac{{\xi_{1} - 1 + n}}{{2^{k - 1} }}} \right),\;\forall\, \xi ,\xi_{1} \in \left( {0,1} \right).$$

Therefore,

$$\left| {a_{i,j} } \right| = \left| {\frac{{AB2^{ - k + 1} }}{{w_{m} }}} \right|\left| {y\left( {\frac{\xi - 1 + n}{{2^{k - 1} }},\frac{{\xi_{1} - 1 + n}}{{2^{k - 1} }}} \right)} \right|.$$

Since \(y\) is bounded by \(\mu\),

$$\left| {a_{i,j} } \right| = \frac{{\left| A \right|\left| B \right|\left| {2^{ - k + 1} } \right|\mu }}{{\left| {w_{m} } \right|}},$$

where \(w_{m} = \mathop \int \limits_{0}^{1} \left( {\phi_{m} \left( t \right)} \right)^{2} dt\). Therefore \(\mathop \sum \limits_{i = 1}^{\infty } \mathop \sum \limits_{j = 0}^{\infty } a_{i,j}\) is convergent. Hence, the Fibonacci wavelet expansion of \(y\left( {x,t} \right)\) converges uniformly.

Error analysis: Error estimation for continuous bounded function \(y\left( {x,t} \right)\) by using the above theorem 1.

\(y\left( {x,t} \right)\) is the exact solution and \(y_{app} \left( {x,t} \right)\) is the Fibonacci wavelet approximate solution.

Where, \(y\left( {x,t} \right) = \mathop \sum \nolimits_{n = 1}^{\infty } \mathop \sum \nolimits_{m = 0}^{\infty } a_{n,m} \zeta_{n,m} \left( x \right) \zeta_{n,m} \left( t \right)\) and \(y_{app} \left( {x,t} \right) = \mathop \sum \nolimits_{n = 1}^{{2^{k - 1} }} \mathop \sum \nolimits_{m = 0}^{M - 1} a_{n,m} \zeta_{n,m} \left( x \right) \zeta_{n,m} \left( t \right).\)

$$y\left( {x,t} \right) - y_{app} \left( {x,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 0}^{\infty } a_{n,m} \zeta_{n,m} \left( x \right) \zeta_{n,m} \left( t \right) - \mathop \sum \limits_{n = 1}^{{2^{k - 1} }} \mathop \sum \limits_{m = 0}^{M - 1} a_{n,m} \zeta_{n,m} \left( x \right) \zeta_{n,m} \left( t \right)\, = \mathop \sum \limits_{{n = 2^{k} }}^{\infty } \mathop \sum \limits_{m = M}^{\infty } a_{n,m} \zeta_{n,m} \left( x \right) \zeta_{n,m} \left( t \right).$$

Now,

$$||E_{n}||^{2} = ||y\left( {x,t} \right) - y_{app} \left( {x,t} \right)||^{2} = \,<y\left( {x,t} \right) - y_{app} \left( {x,t} \right),y\left( {x,t} \right) - y_{app} \left( {x,t} \right)>,$$
$$\Rightarrow ~||E_{n}|| ^{2} = \mathop \sum \limits_{{n = 2^{k} }}^{\infty } \mathop \sum \limits_{{m = M}}^{{\infty ~~}} a_{{n,m~}}^{2} \zeta _{{n,m}}^{2} \left( x \right)~\zeta _{{n,m}}^{2} \left( t \right).$$

But from the theorem 1, we have, \(\left| {a_{n,m} } \right| \le \left| {\frac{{2^{ - k + 1}\mu A B }}{{w_{m} }} } \right|.\)

$$\Rightarrow ~||E_{n}|| ^{2} \le \mathop \sum \limits_{{n = 2^{k} }}^{\infty } \mathop \sum \limits_{{m = M}}^{{\infty ~~}} \frac{{2^{{ - 2\left( {k - 1} \right)}} }}{{w_{m}^{2} }}~\mu ^{2} ~A^{2} ~B^{2} \zeta _{{n,m}}^{2} \left( x \right)~\zeta _{{n,m}}^{2} \left( t \right).$$

Theorem 2

[45]: Let the Fibonacci wavelet sequence \(\left\{ {\zeta_{n,m} \left( x \right)} \right\}\) which are continuous functions defined in \(L^{2} \left( {\mathbb{R}} \right)\) in \(x\) on \(\left[ {a,b} \right]\) converges to the function \(\zeta \left( x \right)\) in \(L^{2} \left( {\mathbb{R}} \right)\) uniformly in \(x\) on \(\left[ {a,b} \right]\). Then \(\zeta \left( x \right)\) is continuous in \(L^{2} \left( {\mathbb{R}} \right)\) in \(t\) on \(\left[ {a,b} \right]\).

Proof:

Since the Fibonacci wavelet sequence \(\left\{ {\zeta_{n,m} \left( x \right)} \right\}\) is uniformly converges to \(\zeta \left( x \right)\) in \(L^{2} \left( {\mathbb{R}} \right)\). Therefore, for every \(\varepsilon > 0\), there exists a number \(k = k_{\varepsilon }\) such that,

$$||\zeta_{n,m} \left( x \right) - \zeta \left( x \right)|| < \frac{\varepsilon }{3},\; \forall\, t \in \left[ {a,b} \right],$$
(9)

Also, \(\{{\zeta }_{n,m}(x)\}\) is continuous in \(L_{2} \left( {\mathbb{R}} \right)\) in \(t \in \left[ {a,b} \right]\). Then there exists a number \(\delta = \delta_{\varepsilon }\) such that,

$$||\zeta_{n,m} \left( x \right) - \zeta \left( x \right)|| < \frac{\varepsilon }{3} ,\,{\text{whenever}}\,||x^{\prime} - x|| < \delta\;\; \forall\, x^{\prime},x \in \left[ {a,b} \right],$$
(10)

By Minkowski’s inequality, we have

$$||\zeta \left( {x^{\prime}} \right) - \zeta \left( x \right)|| = ||\zeta \left( {x^{\prime}} \right) - \zeta_{n,m} \left( {x^{\prime}} \right) + \zeta_{n,m} \left( {x^{\prime}} \right) + \zeta_{n,m} \left( x \right) - \zeta_{n,m} \left( x \right) - \zeta \left( x \right)||,$$
$$||\zeta \left( {x^{\prime}} \right) - \zeta \left( x \right)|| \le ||\zeta \left( {x^{\prime}} \right) - \zeta_{n,m} \left( {x^{\prime}} \right)|| + ||\zeta_{n,m} \left( {x^{\prime}} \right) - \zeta \left( x \right)|| + ||\zeta_{n,m} \left( x \right) - \zeta_{n,m} \left( x \right)||,$$

\(< \frac{\varepsilon }{3} + \frac{\varepsilon }{3} + \frac{\varepsilon }{3} = \varepsilon\),

\(||\zeta \left( {x^{\prime}} \right) - \zeta \left( x \right)|| < \varepsilon\) for all \(||x^{\prime} - x|| < \delta\) with \(x^{\prime},x \in \left[ {a,b} \right]\). Hence \(\zeta \left( x \right)\) is continuous in \(L^{2} \left( {\mathbb{R}} \right)\) in \(x\) on \(\left[ {a,b} \right]\).

Theorem 3

[45]: Let the Fibonacci wavelet sequence \(\left\{ {\zeta_{n,m}^{k} \left( x \right)} \right\}_{k = 1}^{\infty }\) converges itself in \(L^{2} \left( {\mathbb{R}} \right)\) uniformly in \(x\) on \(\left[ {a,b} \right].\) Then there is a function \(\zeta \left( x \right)\) is continuous in \(L^{2} \left( {\mathbb{R}} \right)\) in \(x\) on \(\left[ {a,b} \right]\) and \(\mathop {\lim }\limits_{k \to \infty } \zeta_{n,m}^{k} \left( x \right) = \zeta \left( x \right)\; \forall\, x \in \left[ {a,b} \right]\).

Theorem 4

[50]: Let \(\left\{ {x_{i} = t_{i} /i = 1, 2, \ldots , 2^{k - 1} M^{2} } \right\}\) be any set of \(\frac{2i - 1}{{2^{k} M^{2} }}\) distinct points in \(\left[ {a,b} \right]\) and \(y\left( {x,t} \right) \in c\left[ {a,b} \right],\) where \(c\left[ {a,b} \right]\) is a set of all continuous functions defined in \(\left[ {a,b} \right]\). \(y\left( {x,t} \right)\) be the solution of the given partial differential equation; then there is exactly one linear combination \(\varphi \left( {x,t} \right)\) of polynomial-based wavelet functions that satisfy

\(y\left( {x_{i} ,t_{i} } \right) = \varphi \left( {x_{i} ,t_{i} } \right)\; \forall\, i = 1, 2, \ldots , 2^{k - 1} M^{2}\).

5 The proposed method

The primary goal of this part is to introduce a novel method based on Fibonacci wavelets for solving the time-FKGE. Consider the fractional nonlinear PDE of the following type:

$$\frac{{\partial^{\alpha } y\left( {x,t} \right)}}{{\partial t^{\alpha } }} = F\left( {x,t,y\left( {x,t} \right),\frac{{\partial y\left( {x,t} \right)}}{\partial x},\frac{{\partial^{2} y\left( {x,t} \right)}}{{\partial x^{2} }}} \right),$$
(11)

where \(x,t\) are the independent variables, and \(y\) is a dependent variable with the given physical conditions.

$$y\left( {x,0} \right) = G_{1} \left( {x } \right), y\left( {0,t} \right) = G_{2} \left( t \right), y\left( {r,t} \right) = G_{3} \left( t \right),$$
(12)

where \(r\) be any constant, \(G_{1} \left( x \right), G_{2} \left( t \right),\) and \(G_{3} \left( t \right)\) are the real-valued and continuous functions. Let's assume,

$$\frac{{\partial^{3} y\left( {x,t} \right)}}{{\partial x^{2} \partial t}} \approx \zeta^{T} \left( x \right)H\zeta \left( t \right),$$
(13)

where, \(\zeta^{T} \left( x \right) = \left[ {\zeta_{1,0} \left( x \right), \ldots ,\zeta_{1, M - 1} \left( x \right), \ldots ,\zeta_{{2^{k - 1} ,0}} \left( x \right), \ldots ,\zeta_{{2^{k - 1} ,M - 1}} \left( x \right)} \right],\)

\(H = \left[ {s_{i,j} } \right]\) be \(2^{k - 1} M \times 2^{k - 1} M\) unknown matrix such that \(i, j = 1, \ldots ,2^{k - 1} M\).

$$\zeta \left( t \right) = \left[ {\zeta_{1,0} \left( t \right), \ldots ,\zeta_{1,M - 1} \left( t \right), \ldots ,\zeta_{{2^{k - 1} ,0}} \left( t \right), \ldots ,\zeta_{{2^{k - 1} ,M - 1}} \left( t \right)} \right]^{T} ,$$

By integrating Eq. (13) concerning \(t\) from limit 0 to \(t\).

$$\frac{{\partial^{2} y\left( {x,t} \right)}}{{\partial x^{2} }} = \frac{{\partial^{2} y\left( {x,0} \right)}}{{\partial x^{2} }} + \zeta^{T} \left( x \right)H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right],$$
(14)

Now integrate Eq. (14) twice concerning to \(x\) from 0 to \(x\).

$$\frac{{\partial y\left( {x,t} \right)}}{\partial x} = \frac{{\partial y\left( {0, t} \right)}}{\partial x} + \frac{{\partial y\left( {x,0} \right) }}{\partial x} - \frac{{\partial y\left( {0 ,0} \right)}}{\partial x} + \left[ {B\zeta \left( x \right) + \overline{\zeta \left( x \right)} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right],$$
(15)
$$y\left( { x,t} \right) = y\left( {0,t } \right) + y\left( { x,0} \right) - y \left( {0,0} \right) + x\left[ {\frac{{\partial y \left( {0,t} \right)}}{\partial x} - \frac{{\partial y \left( {0,0} \right)}}{\partial x}} \right] + \left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right],$$
(16)

Put \(x = r\) in Eq. (16) along with the given physical conditions in Eq. (12). We attain,

$$G_{3} \left( t \right) = G_{2} \left( t \right) + G_{1} \left( r \right) - G_{1} \left( {0 } \right) + r\left[ {\frac{{\partial y\left( {0,t} \right)}}{\partial x} - \frac{{\partial y\left( {0,0} \right)}}{\partial x}} \right] + \mathop {\lim }\limits_{x \to r} \left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right],$$
$$\left[ {\frac{{\partial y \left( {0,t} \right)}}{\partial x} - \frac{{\partial y\left( {0,0} \right)}}{\partial x}} \right] = \frac{1}{r}\left[ {G_{3} \left( t \right) - G_{2} \left( t \right) - G_{1} \left( r \right) + G_{1} \left( 0 \right) - \mathop {\lim }\limits_{x \to r} \left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right]} \right],$$
(17)

Substitute Eq. (17) in Eqs. (15) and (16)

$$\frac{{\partial y\left( {x,t} \right)}}{\partial x} = \frac{{\partial G_{1} \left( x \right)}}{\partial x} + \frac{1}{r}\left[ {G_{3} \left( t \right) - G_{2} \left( t \right) - G_{1} \left( r \right) + G_{1} \left( 0 \right) - \mathop {\lim }\limits_{x \to r} \left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right]} \right] + \left[ {B\zeta \left( x \right) + \overline{\zeta \left( x \right)} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right],$$
(18)
$$y\left( {x,t} \right) = G_{2} \left( t \right) + G_{1} \left( x \right) - G_{1} \left( 0 \right) + \left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right] + \frac{x}{r}\left[ {G_{3} \left( t \right) - G_{2} \left( t \right) - G_{1} \left( r \right) + G_{1} \left( 0 \right) - \mathop {\lim }\limits_{x \to r} \left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right]} \right],$$
(19)

Case I: If \(\alpha = 2\) in Eq. (11), then differentiate Eq. (19) twice with concerning \(t\). We obtain,

$$\frac{{\partial^{2} y\left( {x,t} \right)}}{{\partial t^{2} }} = \frac{{d^{2} }}{{dt^{2} }}G_{2} \left( t \right) + \frac{{d^{2} }}{{dt^{2} }}\left[ {\left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right]} \right] + \frac{x}{r}\frac{{d^{2} }}{{dt^{2} }}\left[ {G_{3} \left( t \right) - G_{2} \left( t \right) - G_{1} \left( r \right) + G_{1} \left( 0 \right) - \mathop {\lim }\limits_{x \to r} \left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right]} \right],$$
(20)

Now fit the \(y,y_{tt} ,y_{x} ,\) and \(y_{xx}\) into Eq. (11), and discretise with their respective collocation points in Eq. (21).

$$x_{i} = t_{i} = \frac{2i - 1}{{2^{k} \left[ M \right]^{2} }}, i = 1, 2, \ldots ,2^{k - 1} \left[ M \right]^{2} .$$
(21)

We solve the nonlinear system of algebraic equations using the Newton–Raphson method to ascertain the values of the unknown coefficients. In Eq. (19), substitute the obtained values of the unknown coefficients to get the deserved approximate solution for the given PDE.

Case II: Utilizing the notion of Caputo derivative (2.1), differentiate Eq. (19) fractionally of order \(\alpha \in \left( {1,2} \right)\) for the given equation. Then we obtain,

$$\frac{{\partial^{\alpha } y\left( {x,t} \right)}}{{\partial t^{\alpha } }} = \frac{{d^{\alpha } }}{{dt^{\alpha } }}G_{2} \left( t \right) + \frac{{d^{\alpha } }}{{dt^{\alpha } }}\left[ {\left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right]} \right] + \frac{x}{r}\frac{{d^{\alpha } }}{{dt^{\alpha } }}\left[ {G_{3} \left( t \right) - G_{2} \left( t \right) - G_{1} \left( r \right) + G_{1} \left( 0 \right) - \mathop {\lim }\limits_{x \to r} \left[ {B^{\prime}\zeta \left( x \right) + \overline{\zeta \left( x \right)}^{{^{\prime}}} } \right]^{T} H\left[ {B\zeta \left( t \right) + \overline{\zeta \left( t \right)} } \right]} \right],$$
(22)

To collocate with the collocation points \(x_{i} = t_{i} = \frac{2i - 1}{{2^{k} \left[ M \right]^{2} }}, i = 1, 2, \ldots ,2^{k - 1} \left[ M \right]^{2}\), by replacing \(y,\frac{{\partial^{\alpha } y\left( {x,t} \right)}}{{\partial t^{\alpha } }},y_{x} ,\) and \(y_{xx}\) in Eq. (11). For finding the unknown coefficients by applying the Newton–Raphson method to the obtained system of nonlinear algebraic equations. Substitute the calculated values for the unknown coefficients in Eq. (19), which produces the FWCM solution for the FKGE.

6 Applications of the projected method

Different types of error norms are given below:

$${\text{L}}^{\infty }\, {\text{error}} = {\text{Max}}\left( {{\text{W}}_{{\text{i}}} } \right), 1 \le {\text{i}} \le {\text{n}} - 1,\,{\text{L}}^{2}\, {\text{error}} = \sqrt {\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} {\text{W}}_{i}^{2} } ,\,{\text{RMS error}} = \sqrt {\mathop \sum \limits_{i = 1}^{n} \frac{{W_{i}^{2} }}{n}} ,\,{\text{where}},\,{\text{W}}_{i} = |{\text{y}}_{{\text{i}}} \left( {\text{exact solution}} \right) - {\text{y}}_{{\text{i}}} \left( {\text{approximate solution}} \right)|.$$

Example 1

Consider the nonlinear FKGE [31],

$${}_{.}^{{\text{C}}} {\text{D}}_{{\text{t}}}^{{\upalpha }} {\text{y}}\left( {{\text{x}},{\text{t}}} \right) - {\text{D}}_{{{\text{xx}}}} {\text{y}}\left( {{\text{x}},{\text{t}}} \right) + {\text{y}}^{2} \left( {{\text{x}},{\text{t}}} \right) = - 6{\text{xt}}^{3} + {\text{x}}^{6} {\text{t}}^{6} + \frac{{6{\text{x}}^{3} {\text{t}}^{3 - \alpha } }}{{{\Gamma }\left( {4 - \alpha } \right)}} ,$$

with initial conditions

$${\text{y}}\left( {{\text{x}},0} \right) = 0, {\text{y}}_{{\text{t}}} \left( {{\text{x}},0} \right) = 0,$$

and the Dirichlet boundary conditions

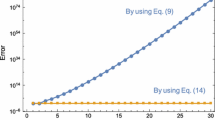
$${\text{y}}\left( {0,{\text{t}}} \right) = 0, \,{\text{y}}\left( {1,{\text{t}}} \right) = {\text{t}}^{3} .$$

The analytical solution is \({\text{y}}\left( {{\text{x}},{\text{t}}} \right) = {\text{x}}^{3} {\text{t}}^{3}\) when \(\alpha = 2\). We apply the FWCM to find the solution for the time fractional Klein-Gordan equation. Figure 1 displays a graphical presentation of the numerical results of the projected technique. Tables 1 and 2 explain the FWCM solution at distinct values of \(t\) and \(x\), respectively, for the values of \({\text{M}} = 3, 6\). Figure 2 shows the present method solution at distinct \(\alpha\) values. Table 3 compares the error norms of the present technique with the Clique polynomial method (CPM) [31], and CPU time is also calculated for the distinct values of \(t\) for \(\alpha = 2, M = 12\). Figure 3 reflects the 1-dimensional graph of the exact and FWCM solutions at distinct values of \(t\). Figures 4 and 5 show the graphical exhibition of the numerical results of the projected technique for the distinct values of \(\alpha\) at \(t = 0.1\) and \(x = 0.1\), respectively. Table 4 compares the present method solution with the Legendre and Jacobi polynomial solutions.

Fig. 1
figure 1

Graphical interpretation, for example, 1

Full size image
Table 1 The absolute error at \(\alpha = 2\) for the distinct values of \(t\) and \(M\), for example, 1
Full size table
Table 2 The absolute error at \(\alpha = 2\) for the distinct values of \(x\) and \(M\), for example, 1
Full size table
Fig. 2
figure 2

Graphical presentation of FWCM solution for fractional \(\alpha\) order, for example, 1

Full size image
Table 3 Different types of error norms at \(\alpha =2\), for example, 1
Full size table
Fig. 3
figure 3

1-dimensional graphical representation of FWCM solution at distinct \(t\) values, for example, 1

Full size image
Fig. 4
figure 4

1-dimensional representation of FWCM solution at distinct \(\alpha\) values at \(t = 0.1\), for example, 1

Full size image
Fig. 5
figure 5

1-dimensional representation of FWCM solution at distinct \(\alpha\) values at \(x = 0.1\), for example, 1

Full size image
Table 4 The absolute error at \(\alpha = 2\), and \(M = 6\) for the distinct values of \(t\), for example, 1
Full size table

Example 2

Consider the nonlinear FKGE [31],

$${}_{.}^{{\text{C}}} {\text{D}}_{{\text{t}}}^{\alpha } y\left( {{\text{x}},{\text{t}}} \right) - \frac{5}{2}{\text{D}}_{{{\text{xx}}}} {\text{y}}\left( {{\text{x}},{\text{t}}} \right) + {\text{y}}\left( {{\text{x}},{\text{t}}} \right) + \frac{3}{2}{\text{y}}^{3} \left( {{\text{x}},{\text{t}}} \right) = 0,$$

with initial conditions

$${\text{y}}\left( {{\text{x}},0} \right) = \sqrt{\frac{2}{3}} {\text{tan}}\left( {\frac{10}{3}\sqrt{\frac{2}{111}} {\text{x}}} \right), {\text{y}}_{{\text{t}}} \left( {{\text{x}},0} \right) = \frac{{{\text{sec}}\left( {\frac{10}{3}\sqrt{\frac{2}{111}} {\text{x}}} \right)^{2} }}{{9\sqrt {37} }},$$

and the Dirichlet boundary conditions

$${\text{y}}\left( {0,{\text{t}}} \right) = \sqrt{\frac{2}{3}} {\text{tan}}\left( {\frac{10}{{3\sqrt {222} }}{\text{t}}} \right), {\text{y}}\left( {1,{\text{t}}} \right) = \sqrt{\frac{2}{3}} {\text{tan}}\left( {\frac{10}{3}\sqrt{\frac{2}{111}} \left( {1 + \frac{1}{20}{\text{t}}} \right)} \right).$$

The analytical solution is \(y\left( {x,t} \right) = \sqrt{\frac{2}{3}} {\text{tan}}\left( {\frac{10}{3}\sqrt{\frac{2}{111}} \left( {x + \frac{1}{20}t} \right)} \right)\) when \(\alpha = 2\). Figure 6 shows the 3-dimensional time–space graph of the exact solution, FWCM solution, and error analysis. Tables 5 and 6 describe the absolute error of the present method at distinct \(t\) and \(x\) values, respectively, for the values of \(M = 3, 6\). For the distinct values of \(\alpha\), the present method solution is drawn in Fig. 7. Figure 8 displays the 1-dimensional graph of the exact solution and the FWCM solution at distinct values of \(t\). Table 7 compares the \(L^{\infty }\), \(L^{2}\) and Root Mean Square (RMS) error norms of the current technique with the CPM [31], and CPU time is also calculated for the distinct values of \(t\) for \(\alpha = 2, M = 10\). Figures 9 and 10 explain the graphical evaluation of the numerical results of the present method for the distinct values of \(\alpha\) at \(t = 1\) and \(x = 1\), respectively.

Fig. 6
figure 6

Graphical interpretation, for example, 2

Full size image
Table 5 The absolute error at \(\alpha = 2\) for the distinct values of \(t\) and \(M\), for example, 2
Full size table
Table 6 The absolute error at \(\alpha = 2\) for the distinct values of \(x\) and \(M\), for example, 2
Full size table
Fig. 7
figure 7

Graphical presentation of FWCM solution for fractional \(\alpha\) order, for example, 2

Full size image
Fig. 8
figure 8

1-dimensional presentation of FWCM solution at distinct \(t\) values, for example, 2

Full size image
Table 7 Different types of error norms at \(\alpha = 2\), for example, 2
Full size table
Fig. 9
figure 9

1-dimensional representation of FWCM solution at distinct \(\alpha\) values at \(t = 1\), for example, 2

Full size image
Fig. 10
figure 10

1-dimensional representation of FWCM solution at distinct \(\alpha\) values at \(x = 1\), for example, 2

Full size image

Example 3

Consider the nonlinear FKGE [31],

$${}_{.}^{C} D_{t}^{\alpha } y\left( {x,t} \right) - D_{xx} y\left( {x,t} \right) + y\left( {x,t} \right) + \frac{3}{2}y^{3} \left( {x,t} \right) = \frac{{{\Gamma }\left( {3 + \alpha } \right)}}{2}\sin \left( {\pi x} \right)t^{2} + \left( {1 + \pi^{2} } \right)\sin \left( {\pi x} \right)t^{2 + \alpha } + \frac{3}{2}\left( {\sin \left( {\pi x} \right)t^{2 + \alpha } } \right)^{3} ,$$

with the initial conditions:

$$y\left( {x,0} \right) = 0, y_{t} \left( {x,0} \right) = 0,$$

and boundary conditions:

$$y\left( {0,t} \right) = 0, y\left( {1,t} \right) = 0.$$

The analytical solution is \(y\left( {x,t} \right) = {\text{sin}}\left( {\pi x} \right)t^{2 + \alpha }\). Figure 11 shows the 3-dimensional graphical presentation of the exact solution, FWCM solution, and an error graph is drawn. Tables 8 and 9 express the absolute error of the projected technique at distinct \(t\) and \(x\) values, respectively, for the value of \(M = 6\). For the distinct values of \(\alpha\), the present method solution is drawn in Fig. 12. Tables 10 and 11 compare the absolute error of the present technique with the CPM [31] at \(M = 8\) and distinct values of \(\alpha\). Figures 13 and 14 display the 1-dimensional graph of the exact solution and the FWCM solution at distinct \(t\) and \(x\) values, respectively. Figure 15 explains the graphical illustration of the numerical results of the current technique for the distinct values of \(\alpha\) at \(t = 0.1\). Figure 16 represents a graphical demonstration of the present method solution for different of \(\alpha\) at \(x = 0.1\).

Fig. 11
figure 11

Graphical interpretation, for example, 3

Full size image
Table 8 The absolute error at \(\alpha = 2\) for the distinct values of \(t\), for example, 3
Full size table
Table 9 The absolute error at \(\alpha = 2\) for the distinct values of \(x\), for example, 3
Full size table
Fig. 12
figure 12

Graphical presentation of FWCM solution for fractional \(\alpha\) order, for example, 3

Full size image
Table 10 Comparison of absolute errors for the distinct values of \(\alpha\) at \(t = 1\), for example, 3
Full size table
Table 11 Comparison of absolute errors for the distinct \(\alpha\) values, for example, 3
Full size table
Fig. 13
figure 13

1-dimensional illustration of FWCM solution at distinct \(t\) values, for example, 3

Full size image
Fig. 14
figure 14

1-dimensional illustration of FWCM solution at distinct \(x\) values, for example, 3

Full size image
Fig. 15
figure 15

1-dimensional representation of FWCM solution at distinct \(\alpha\) values at \(t = 0.1\), for example, 3

Full size image
Fig. 16
figure 16

1-dimensional representation of FWCM solution at distinct \(\alpha\) values at \(x = 0.1\), for example, 3

Full size image

7 Conclusion

In this paper, we describe a numerical technique for estimating the approximate solution based upon FWCM for a class of Klein-Gordon fractional model. This method is a direct and attractive tool for studying and solving linear and nonlinear fractional partial differential equations without using any controlling parameter. Several illustrative examples have been used to test the effectiveness and capacity of the current method. The results demonstrate this method's total reliability and enormous potential for scientific applications. To illustrate the efficiency of the projected technique, we compare the numerical results of the FWCM approximation with the Clique polynomial method [31]. Ultimately, we conclude that the FWCM is highly strong, simple, and successful in obtaining numerical solutions to various FPDE-related problems in mathematics, physics, and engineering. The present method can be extended to models with higher-order PDEs, higher-order fractional PDEs, time-delay PDEs, and systems of PDEs with minor adjustments.