1 Introduction

The complexity of the climate system comes from the diversity of its determining parameters [1, 2]. It is essentially composed of the atmosphere, the hydrosphere (oceans, seas, rivers, lakes, groundwater…), the cryosphere (snow, glaciers, ice pack…), the continental surfaces, and the biosphere (living beings) [3, 4]. It is also defined as a set of diverse phenomena (pressure, temperature, humidity, precipitation, sunshine, wind, etc.) [4]. According to IPCC 2007, Climate change refers to the different, statistically significant variations of the average state of the climate or its variability, persisting over a long period of time [5]. This can be due to natural internal processes, natural external forces, or to human impacts.

The IPCC group highlighted in its fifth report in 2013 that the global warming of the climate system is undeniable, adding that human influence is the main cause [6]. Globally, 2020 was the hottest year with + 0.6 °C compared to a reference period of 1981–2010, and + 1.25 °C compared to the preindustrial period 1850–1900) [7, 8]. Also, the average global temperature showed a warming of around 0.85 °C over the period 1880–2012 [6, 8], accompanied by a reduction in ice caps by a rate of 3.5–4.1% per decade, leading to a sea level rise of about 19 cm [6]. On the other hand, the 5th report of the IPCC shows that the increase in global temperature is causing changes in all the regions of the world: the atmosphere and oceans are warming, the surface area and volume occupied by snow and ice is decreasing, and sea levels are rising, and the weather conditions are changing. Climate models predict a global average temperature 2.6 to 4.8 degrees Celsius (°C) higher than at present, a sea level rise of 0.45–0.82 m (m) and a weather disruption [6]. There is also an estimated probability of about 66% that the Arctic Ocean would be completely ice-free in the summer before the middle of the twenty-first century.

General circulations Models (GCMs) are the main tools for predicting climate change’s the greenhouse gas emission scenarios [9,10,11]. These models are based on a large grid scale (250 to 600 km) [12]. However, a very fine spatial resolution is necessary for the assessment of climate change impact both at the regional and local scale. To establish a relationship between the local climate variables and the those simulated by GCM, several methods have been developed and are known as “downscaling methods”, which are differentiated into Dynamic Descent Scale (DD) and Statistical Descent Scale (SD) methods [13].

Recently, many statistical models are developed of which Statistical Downscaling Models (SDSM) are widely used [12]. And which principal objective is the assessment of the hydrological responses under climate change scenarios by the downscaling of the most important climate variables [12]. As a consequence, several works have been carried out to evaluate and predict climate change related to the different RCP scenarios [10, 14,15,16,17].

The main objective of this work is to assess and predict the climate change for the 2015–2100 period in a semi-arid zone such as the case of the Boufakrane watershed located in the central part of Morocco. To achieve this goal, the SDSM method was used to reduce the climate variables such as: rainfall and temperature and to assess the future climate change related to various RCP scenarios. For this purpose, the annual, monthly, and daily rainfall and the temperature were analyzed. A rainfall index was calculated to differentiate between dry and humid years of the climate series. Thereafter, the non-parametric Pettitt test was applied to determine the trend of the projected rainfall.

2 Methodology and used data

2.1 Study area

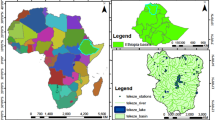
The Boufakrane river watershed located in the central north part of Morocco has a surface of about 399 Km2. Its latitude ranges from 33°50′22″N to 33°55′22″N, and longitude from 5°27′07″W to 5°36′22″W with an altitude varying from 276 to 1379 from the north to the south of the basin (Fig. 1). It is characterized by a semi-arid climate with a rainfall of around 500 mm/year, and a dry period extending from June to October. The area is characterized by a very high quality and quantity of water resources and soils allowing for farming practices with a high level of efficiency [18]. The latter is considered as the main sector contributing to the economic and social activity in the region.

Fig. 1
figure 1

Localisation of Study area

Full size image

2.2 Adopted methodology

A 15-year climate database from September 01, 2001 to September 01, 2015, was taken as a reference period. Two climatic factors were chosen which are rainfall and minimum temperature, minimum temperature, and average temperature. An analysis of this period was carried out based on the rainfall index, the weighted rainfall index, and the non-parametric test Pettitt’s test. To select the appropriate variables for the prediction of the different climate factors, a correlation study of these factors and the predictor variables integrated in the second-generation Earth System Model (CanESM2), developed by the Canadian Centre for Climate Modelling and Analysis (CCCma) of Environment Canada was applied. After the model calibration the prediction of climate factors was made based on the three RCP scenarios (i.e., RCP 2.6, RCP 4.5, and RCP 8.5) for the period of 2015–2100. Finally, the rainfall index and the weighted rainfall index were calculated for the same period to distinguish dry from wet periods. The methodology adopted in this work is given in Fig. 2.

Fig. 2
figure 2

Flowchart of the adopted methodology

Full size image

2.3 Rainfall and weighted rainfall indices

The annual rainfall index (RI) measures the deviation from an average established over a long period by referring to the observation station’s data. This index is obtained using the rainfall in the year, the mean and the standard deviation of the series (Eq. 1) [19].

$$\mathrm{RI}=\frac{{\mathrm{X}}_{\mathrm{i}}-{\mathrm{X}}_{\mathrm{m}}}{\upsigma }$$
(1)

\({X}_{i}\) Rainfall in year; \({X}_{m}\): the mean of the series; σ the standard deviation of the series.

To visualize inter-annual fluctuation of rainfall, seasonal variations are eliminated by applying a weighting (low-pass filter of order 2 or 2-year moving average method) to the annual rainfall totals through the equations recommended by [20]:

$${X}_{t}=0.06 {X}_{\left(t-2\right)}+0.25 {X}_{\left(t-1\right)}+0.38 {X}_{\left(t\right)}+0.25 {X}_{\left(t+1\right)}+0.06 {X}_{(t+2)}$$
(2)

With 3 ≤ t ≤ (n-2), \({X}_{t}\) is the weighted rainfall value of the term t, \({X}_{\left(t-2\right)}\) and \({X}_{\left(t-1\right)}\) are the observed rainfall immediately before the term t, and \({X}_{(t+2)}\) and \({X}_{\left(t+1\right)}\) are the observed rainfall totals of two terms immediately after the term t.

The weighted rainfall totals for the first two [\({X}_{\left(1\right)}\) and \({X}_{\left(2\right)}\)] and last two [\({X}_{\left(n-1\right)}\) and \({X}_{\left(n\right)}\)] terms in the series were calculated as follows:

$${X}_{(1)}=0.54{X}_{(1)}+0.46{X}_{(2)}$$
(3)
$${X}_{(2)}=0.25{X}_{(1)}+0.50 {X}_{(2)}+0.25 {X}_{(3)}$$
(4)
$${X}_{(n-1)}=0.25{X}_{(n-2)}+0.50 {X}_{(n-1)}+0.25 {X}_{(n)}$$
(5)
$${X}_{(n)}=0.54{X}_{(n)}+0.46 {X}_{(n-1)}$$
(6)

2.4 Pettitt’s test

The Pettitt’s test [21] is a non-parametric test for a shift in the central tendency of the time series. The H0-hypothesis, no change, is tested against the HA-Hypothesis, change. This test rests on the calculation of the variable UtT defined by Eq. 7:

$${\text{U}}_{{{\text{tT}}}} = \mathop \sum \limits_{{{\text{I}} = 1}}^{{\text{T}}} \mathop \sum \limits_{{{\text{J}} = {\text{I}} + 1}}^{{\text{T}}} {\text{D}}_{{{\text{IJ}}}}$$
(7)
$$D_{IJ} = - 1\;si\;({\text{xi}} - {\text{xj}}) < 0);\;D_{IJ} = 0\;si\;({\text{xi}} - {\text{xj}}) = 0;\;D_{IJ} = 1\;si\;({\text{xi}} - {\text{xj}}) > 0$$

3 Results and discussions

3.1 Rainfall analysis

The analysis of the inter-annual precipitation in the Meknes station from 1974/75 to 2015/16 was carried out to understand the climatic regime in the Boufakrane watershed. The series showed a high spatial and temporal variability with an alternation of dry and wet periods. This is confirmed by the statistical calculated parameters, with an average value of 538.61 mm, a maximum value of 1124 mm, and a minimum value of 237.9 mm recorded respectively in 2000/2001 and 2013/2014. The standard deviation of the series is about 185.70 mm while the coefficient of variation is about 34.47% (Fig. 3a).

Fig. 3
figure 3

a Inter-annual rainfall in Meknes; b Rainfall index; c weighted rainfall index for Meknes station; d Pettitt’s test

Full size image

The rainfall and weighted rainfall indices were calculated to better differentiate humid from dry periods. The evolution of these indices shows an alternation of dry and humid periods during the studied period. There was a humid period from 1974/75 until 1979/80 followed by a dry period from 1980/81 until 1994/95. Then the region witnessed an unstable period until 2006/07 characterized by an alternation of humid and dry years. The year 2007/08 represents the beginning of a humid period until the year 2010/11. Therefore, after the hydrological year of 2011/12 the river basin experienced a dry period until 2015/16 (Fig. 3b, c).

To better identify the breaks in the rainfall series, the non-parametric Pettitt’s test has been applied with a confidence interval of 99% and a significance level of 0.05 or 5%. The results showed a break in the rainfall series in the hydrological year of 1979/80with an average before and after the break of 675.78 mm and 511.94 respectively. The estimated deficit is 24.24% (Fig. 3d).

3.2 Predictors variables selection and model validation

The objective here is to select the different predictor variables that are suitable for the elaboration of the model that will allow the prediction of the different climatic factors. Therefore, the atmospheric predictor variables from the National Center for Environmental Prediction (NCEP)/National Center for Atmospheric Research (NCAR) downloaded from (http://ccds-dscc.ec.gc.ca/) were used (Table 1). A correlation study has been made for the choice of atmospheric variables, which are correlated with climatic variables. Two statistical parameters were considered in the choice of predictor variables, namely: the correlation index (r2) and p value. Table 1 shows the different predictor variables with their descriptions.

Table 1 Predictor variables of NCEP and NCAR
Full size table

The predictors of the NCEP/NCAR were chosen to be used in creating the calibrated model. The final set of predictors was selected after analyzing the correlation coefficient (r2) and verifying the association of predictors and predictands via scatter plot. The selected predictor variables for precipitation are surface meridional velocity, wind direction, divergence, and surface precipitation. For the maximum temperature, the mean sea level pressure, surface meridional velocity, meridional velocity, surface-specific humidity, and surface mean temperature were selected. Whereas mean sea level pressure, surface-specific humidity and surface mean temperature were selected for the average and minimum temperature. Table 2 shows the predicted variables, the selected predictors variable, and both the correlation coefficient and p value for each one of them.

Table 2 Selected set of predictor variables
Full size table

3.3 Prediction of the temperature

The representation of the monthly temperature for the study period along with that extracted from the RCP scenarios shows an upward trend for all the three scenarios RCP 2.6, RCP 4.5, and RCP 8.5. For the RCP 8.5 scenario, it showed an upward trend for the monthly temperature in most of the months with values approaching 1.67 °C. Similarly, for the RCP 4.5 scenario, an upward trend has been recorded with up to 1.20 °C for some months while the RCP 2.5 scenario has shown no trend (Figs. 4 and 5).

Fig. 4
figure 4

Predicted monthly temperature

Full size image
Fig. 5
figure 5

Predicted annual temperature

Full size image

3.4 Prediction of the rainfall

3.4.1 Monthly rainfall

The representation of the monthly rainfall for the study period with that extracted from the RCP scenarios shows a downward trend for all the three scenarios RCP 2.6, RCP 4.5, and RCP 8.5. For the RCP 8.5 scenario, for some months, this downward trend reaches 10 mm for the monthly rainfall (Fig. 6). The difference between the average annual rainfall value for the period 1981–2015 and the average value for the three scenarios. All the three scenarios showed a decrease in monthly rainfall in most of the months except for June and September, with an average of 5.9 mm, 6.37 mm, and 4.63 mm respectively for RCP 2.6, RCP 4.5 and RCP 8.5. For the RCP 2.6 scenario, a maximum decrease is expected in the months of December, January, and April with a rate of over 11 mm, while for the month of June a rate of 3 mm more is foreseen. Similarly, for the RCP 4.5 scenario, a decrease of almost 13 mm is expected for the months of December and January, and more than 10 mm for May, while for the month of June a rate of 1 mm more is predicted. For the RCP 8.5 scenario, a decrease of 11 mm is expected for the month of December, and more than 6 mm for January and August (Fig. 6).

Fig. 6
figure 6

Predicted monthly rainfall

Full size image

3.4.2 Annual rainfall

Figure 7 shows the results of the rainfall prediction according to the different RCP scenarios for the 2015–2099 period. They show a downtrend for the different scenarios. For scenario RCP 2.6, the rainfall variability shows a decreasing downward trend towards 2099, and this is well illustrated in the annual average rainfall. Both other scenarios RCP 4.5 and RCP 8.5 show the same pattern, a downward trend and a rainfall decrease towards the end of the century except for a few years, which show a significant amount of rainfall.

Fig. 7
figure 7

Predicted annual rainfall according to the RCP scenarios

Full size image

3.4.3 Rainfall and weighted rainfall (RI and WRI)

To better understand the hydrological regime and precipitation patterns, the rainfall index and the weighted rainfall index were calculated for the predicted period (Figs. 8 and 9). The positive values for both indices represent humid years, while the negative values represent dry years. For the RCP 2.5 scenario, the results show a secession of humid and dry episodes for the period 2015–2050, whereas after 2050, it is expected to see only dry years until the end of the century. For the two other scenarios (RCP 4.5, and RCP 8.5), the results show a secession of humid and dry periods during all the estimated periods.

Fig. 8
figure 8

Predicted Rainfall Index (RI) according to the RCP scenarios

Full size image
Fig. 9
figure 9

Predicted Weighted Rainfall Index (WRI) according to the RCP scenarios

Full size image

3.4.4 Pettitt’s test

The application of Pettitt's test on the predicted rainfall for the different climate scenarios showed a break for the RCP 2.5 scenario while it showed no break for the other two scenarios (RCP 4.5 and RCP 8.5). For the RCP 2.6 scenario, the break in the series was recorded for the year 2050 with an average of 523.283 mm and 433.499 mm respectively before and after the break (Fig. 10).

Fig. 10
figure 10

Applied Pettitt’s test for the annual rainfall according to the RCP 2.6

Full size image

4 Discussion

In the Mediterranean context, the rainfall prediction is very difficult due to its limitation and variability in time and space. Melki and his collaborators in 2017 [22] have conducted research in the region of Gafsa (Southwest of Tunisia) The analysis is based on annual precipitation of 18 stations during the period 1960–2015. The results showed extremely variable rainfall regime, low recurrence of rainy days, and daily rainfall anomalies with intensities varying between 50 and 423 mm/day. This variation was influenced by different parameters including the presence of a mountainous range.

In Morocco, agriculture has a very important position, and it is considered as a very important socio-economic sector. However, this sector is exposed to several challenges such as: the spatio-temporal variability of rainfall, the succession of drought periods, and extreme phenomena. Therefore, given the direct relationship of crop production to the annual rainfall balance, agriculture is directly impacted, and is subsequently reflected in the disruption of agricultural ecosystems [18, 23,24,25,26,27,28,29].

In this national context, several parameters have increased pressure on water resources, such as: the harsh climatic conditions, the rapid urbanisation and the population increase, the socio-economic development, as well as the development of the techniques used in the agricultural field [27, 30,31,32,33,34,35,36,37,38,39]. In the Saïss plain, to which the study area belongs, an increase in the consumption of water resources has been recorded. According to the study on the updating of the Integrated Water Resources Development Master Plan carried out by the Sebou hydraulic basin agency [40], the plain has experienced a water deficit of 100 Mm3yr−1 with an estimated annual input of around 242 Mm3yr−1, and an output of around 342 Mm3yr−1, for the period 1939–2002. Of which, 22% is assigned to domestic use while the remaining 78% is allocated to the agriculture.

In a similar background, the SDSM model has been applied in Morocco in the Essaouira basin by Ouhamdouch et al. in 2017 [10]. A combined application of the SDSM results and the non-parametric Pettitt’s test of trend was performed for the period 2018–2050. The results showed a decreasing trend in annual precipitation for the RCP 4.5 (17.29%) and increasing trends for RCP 2.6 and RCP 8.5 by 12.50% and 21.33%, respectively. Meanwhile, the annual mean temperature is expected to have an increase of 0.72 °C, 0.57 °C and 0.69 °C under RCPs 2.6, 4.5 and 8.5, respectively.

In this study, the results of the SDSM and the non-parametric Pettitt test the for the study period 2015–2100 showed a downward trend of annual rainfall of (17.29%) for RCP 2.6 while no trend was recorded for the two scenarios RCP 4.5, and RCP 8.5. The results of this work showed that a disturbance of the climate system is expected, which will influence the crop and livestock systems as directly related to the water balance. The analysis of daily rainfall showed that the wet years indicated for the rainfall and weighted rainfall indices are only disturbances of the climate system and are generally characterised by extreme events.

5 Conclusion

The main objective of this work is to assess the future climate change for the 2015–2100 period in a semi-arid zone such as the case of the Boufakrane river watershed, Morocco. Therefore, the Statistical DownScaling Model (SDSM) method has been used to reduce maximum temperatures, minimum temperatures and rainfall in order to predict future climate change related to various RCP scenarios such as RCP 2.6, RCP 4.5, and RCP 8.5. For this purpose, the annual, monthly, and daily rainfall as well as the minimum, the maximum, and the average temperature records of the region were analyzed.

The analysis of the prediction data for rainfall and temperature showed that it is expected to witness a perturbation in the climate system. This will influence the spatial and temporal distribution of water resources along with a negative impact on the crucial sectors in the region, such as agriculture. Considering the scarcity and limitation of water resources in the region, an investigation of the future rainfall situation is particularly crucial and imperious. Therefore, this quantification will contribute to the understanding of the amount of water resources available in the future, and consequently the implementation of an adequate strategy for water resources management.