1 Introduction

Solitary waves, or solitons as they are also known, are nonlinear waves that have the ability to propagate through media over a prolonged period while maintaining key properties; for example, velocity and shape [1]. As solitons remain stable when they collide with other solitons, they have found widespread application in a range of areas including optics, fluid mechanics, finance, biology, physics, engineering sciences, and neuroscience. Nonlinear partial differential equations are used to model solitons. For example, the regularized long wave (RLW) equation, which was originally presented by Peregrine [2] and Benjamin et al. [3], is as follows:

$$\begin{aligned} u_t +u_x +\delta uu_x -\mu u_{xxt}=0,\quad x\in {\mathfrak {R}}, \quad 0\le t\le T, \end{aligned}$$
(1)

where \(\delta\) and \(\mu\) are positive constants. It is considered with the homogeneous Dirichlet boundary conditions \(u\rightarrow 0\) as \(x\rightarrow \pm \infty\).

The RLW equation is particular case of the generalized long wave (GRLW) equation which has the form

$$\begin{aligned} u_{t}+u_{x}+\delta u^{p}u_{x}-\mu u_{xxt}=0, \end{aligned}$$
(2)

where p is a positive integer by setting \(p=1\). In our paper, we consider another particular case of the GRLW equation called the modified regularized long wave (MRLW) equation when \(p=2\) and is given by

$$\begin{aligned} u_{t}+u_{x}+\delta u^{2}u_{x}-\mu u_{xxt}=0. \end{aligned}$$
(3)

The GRLW equation and its particulars cases: RLW equation and MRLW equation were initially suggested as a means of modeling phenomena that exhibited dispersion waves in combination with weak nonlinearity; for example, pressure waves in a liquid gas bubble mixture, ion-acoustic and magnetohydrodynamic waves in plasma, phonon packets in nonlinear crystals, and nonlinear transverse waves in shallow water. The analytical solution that underpins the MRLW equation is limited to single solitary waves under the restricted initial and boundary conditions. Scholars have yet to develop formulae for other cases, for example, within the context of the Maxwellian initial condition and situations involving the interaction of more than one soliton. As such, the development of accurate numerical approximations remains critical such as finite difference methods [4,5,6,7,8,9], finite element method [10,11,12,13], mixed finite element method [14, 15], collocation method [16,17,18], spectral method [19, 20] and Adomian decomposition method [21, 22].

Numerous finite difference schemes for the MRLW problem have been documented in the extant literature, with many scholars placing a specific focus on the finite difference methods and the MRLW equation. The MRLW problem, for instance, was solved using the finite difference approach by Khalifa et al. [6], who also investigated other aspects of the MRLW equation, including the interaction of solitary waves. Additionally, Fourier analysis was performed to demonstrate the stability of the scheme. The truncation error was also well controlled.

The generalized regularised long wave (GRLW) problem was solved by Akbari and Mokhtari using a new compact finite difference method (CFDM) [23]. The stability analysis of the energy method was explored, and an error estimate was presented. The method was validated using two solitary waves interaction and the propagation of single solitons. To ascertain the method conservation properties, three motion invariants were assessed.

A fully implicit finite difference technique for the numerical solution of the MRLW equation was presented by Inan and Bahadir [24]. The validity of the approach was tested using several MRLW equation examples. A comparison of the results with analytical and other numerical invariants demonstrated the accuracy and dependability of the outcomes achieved utilizing the fully implicit finite difference scheme.

In the current study, we suggest a finite difference approach to solve the MRLW equation that has three levels in time and a five-point stencil in space. The stability of the Fourier analysis-based method is considered, and the accuracy of the convergence rate of \(O(h^4+k^2)\) is also proved. The remainder of this paper is structured as follows. The analytical solution of the MRLW equation and its conservative laws are reviewed in Sect. 2. The creation of the suggested scheme is the focus of Sect. 3. The stability and convergence rates of the scheme are examined in Sect. 4. To validate our theoretical findings, Sect. 5 presents various numerical experiments for single and interaction of solitons. Finally, our concluding remarks are contained in Sect. 6.

2 Analytical solution and conservation laws

The analytical solution of the MRLW equation Eq. (3) is given in the form [6]

$$\begin{aligned} u(x,t)=\sqrt{\frac{6c}{\delta }}sech \left(\sqrt{\frac{c}{\mu (c+1)}}(x-(c+1)t-x_{0})\right), \end{aligned}$$
(4)

where \(\sqrt{\frac{6c}{\delta }}\) is the amplitude of the MRLW solitary wave. The solitary wave is initially centred at \(x_0\) and its speed and its width are represented by c and \(\sqrt{\frac{c}{\mu (c+1)}}\), respectively.

The validity of the numerical methods can be determined using the three invariants of the motion that the MRLW equation has; that is, the mass, momentum, and energy conservative laws given as [6, 25]:

$$\begin{aligned} I_{1}= & {} \int _{-\infty }^{\infty }u(x,t)dx, \end{aligned}$$
(5)
$$\begin{aligned} I_{2}= & {} \int _{-\infty }^{\infty }(u^2+\mu u_{x}^{2})dx, \end{aligned}$$
(6)

and

$$\begin{aligned} I_{3}=\int _{-\infty }^{\infty }(u^4-\frac{6 \mu }{\delta }u_{x}^{2})dx. \end{aligned}$$
(7)

The use of these invariants can be particularly pertinent in situations for which there are no analytic solutions or during soliton interactions [25].

3 Construction of the finite difference scheme

To construct the finite difference scheme of the MRLW equation Eq. (3) with a three-level scheme in time and a five-point stencil in space, the following notations for the derivatives are used:

$$\begin{aligned} (u_j^n)_t= & {} \frac{u_j^{n+1}-u_j^{n-1}}{2k}\nonumber \\ (u_j^n)_x= & {} \frac{-u_{j+2}^n+8u_{j+1}^n-8u_{j-1}^n+u_{j-2}^n}{12h}\nonumber \\ (u_j^n)_{xxt}= & {} \frac{-u_{j+2}^{n+1}+16u_{j+1}^{n+1}-30u_j^{n+1} +16u_{j-1}^{n+1}-u_{j-2}^{n+1}}{24kh^2}\nonumber \\{} & {} \qquad +\frac{u_{j+2}^{n-1}-16u_{j+1}^{n-1}+30u_j^{n-1}-16u_{j-1}^{n-1}+u_{j-2}^{n-1}}{24kh^2}, \end{aligned}$$
(8)

where \(k=\Delta t\) is the time step and \(h=\Delta x\) represents the spatial step size. The superscript n denotes a quantity associated with time level \(t_n\) and subscript j denotes a quantity associated with space mesh point \(x_j\). The grid points are \(t_{n}=nk,\, n=0,1,2,\ldots ,N\) for time and \(x_{j}=jh,\, j=0,1,2,\ldots ,M\) for space, where M and N are positive integers. The finite difference scheme therefore becomes

$$\begin{aligned} (u_j^n)_t+(1+\delta (u_j^n)^{2})(u_j^n)_x-\mu (u_j^n)_{xxt}=0. \end{aligned}$$
(9)

Then substituting Eq. (8) into Eq. (9) yields

$$\begin{aligned}{} & {} \mu u_{j-2}^{n+1}-16\mu u_{j-1}^{n+1}+(30\mu +12h^2)u_j^{n+1} -16\mu u_{j+1}^{n+1}+\mu u_{j+2}^{n+1}\nonumber \\{} & {} \quad =-Q_j^nu_{j-2}^{n}+8Q_j^nu_{j-1}^{n}-8Q_j^nu_{j+1}^{n}+Q_j^nu_{j+2}^{n}\nonumber \\{} & {} \qquad +\mu u_{j-2}^{n-1}-16\mu u_{j-1}^{n-1}+(30\mu +12h^2)u_j^{n-1} -16\mu u_{j+1}^{n-1}+\mu u_{j+2}^{n-1}, \end{aligned}$$
(10)

where \(Q_j^n=kh(1+\delta (u_j^n)^{2})\). The scheme (10) is a tridiagonal system that can be easily simulated using MATLAB platform. From now in our work, we take \(\delta =1\).

4 Convergence and linear stability analysis

Lemma 1

The finite difference scheme (10) is marginally stable.

Proof

In the case of applying the Von Neumann stability theory, the solution of Eq. (10) can be written as

$$\begin{aligned} u_{j}^{n}=\xi ^{n}e^{ilx_{j}}, \,\, i=\sqrt{-1}, \end{aligned}$$
(11)

where l is a mode number. Now, set

$$\begin{aligned} \xi ^{n+1}=g\xi ^{n}\Longrightarrow \xi ^{n+1}=g^2\xi ^{n-1}, \end{aligned}$$
(12)

and then inserting Eqs. (11) and (12) into Eq. (10) yields

$$\begin{aligned} g^2-(2i\sin \theta ) g-1=0, \end{aligned}$$
(13)

where g is the growth factor and

$$\begin{aligned} \sin \theta =\frac{kh(1+u^2)(\sin 2\phi -8\sin \phi )}{2\mu \cos 2\phi -32\mu \cos \phi +30\mu +12 h^2},\quad \phi =lh, \end{aligned}$$
(14)

with assuming that \((u_j^n)^{2}\) in Eq. (10) is locally constant, and for simplicity, we write it as \(u^{2}\). To verify Eq. (14), we must show that

$$\begin{aligned} \bigl |\frac{kh(1+u^2)(\sin 2\phi -8\sin \phi )}{2\mu \cos 2\phi -32\mu \cos \phi +30\mu +12 h^2}\bigr |\le 1. \end{aligned}$$

To do this, we have

$$\begin{aligned} \bigl |\frac{kh(1+u^2)(\sin 2\phi -8\sin \phi )}{2\mu \cos 2\phi -32\mu \cos \phi +30\mu +12 h^2}\bigr |=\bigl |\frac{kh(1+u^2)\sin \phi (\cos \phi -4)}{16\mu (1-\cos \phi )-2\mu \sin ^2 \phi +6 h^2}\bigr |. \end{aligned}$$

Now, we set \(y=1-\cos \phi\) and so \(\sin \phi = \sqrt{y(2-y)}.\) Then we have

$$\begin{aligned} \sup _{\forall \phi } &{} \frac{k^2h^2(1+u^2)^2\sin ^2 \phi (\cos \phi -4)^2}{(16\mu (1-\cos \phi )-2\mu \sin ^2 \phi +6 h^2)^2}&= \sup _{0\le y \le 2} \frac{k^2h^2(1+u^2)^2 y(2-y) (3+y)^2}{(16\mu y-2\mu (y(2-y)) +6 h^2)^2} \\ &= \frac{16k^2h^2(1+u^2)^2}{(14\mu +6 h^2)^2} \le 1, \end{aligned}$$

for small spatial step size h and small time step k, and \(\mu\) is practically taken to be unity.

Now, Eq. (13) yields that \(g_1=-e^{i\theta }\) and \(g_2=e^{-i\theta }\), which implies that \(\Vert g_1\Vert =\Vert g_2\Vert =1\), and therefore the finite difference scheme (10) is marginally stable. \(\square\)

Lemma 2.

If u(x, t) is smooth enough, then the local truncation error of finite difference scheme (10) is \(O(h^4+k^2)\).

Proof

Let \(v_j^n=v(x_j,t_n)\) represents the exact solution for the Eq. (3) with independent variables x and t. The local truncation error of Eq. (9) is thus as follows:

$$\begin{aligned} T_j^n=(v_j^n)_t+(1+(v_j^n)^{2})(v_j^n)_x-\mu (v_j^n)_{xxt}. \end{aligned}$$
(15)

Now, using Tylor expansion, it is easily shown that \(T_j^n\) at the point \((x_j,t_n)\) can be written as

$$\begin{aligned} T_{j}^n=[v_t+(1+(v)^{2})v_x-\mu v_{xxt}]\Vert _{(x_j,t_n)} +\frac{k^2}{6}v_{ttt}\Vert _{(x_j,t_n)}-\frac{h^4}{30}[(1+v^2)v_{xxxxx}]\Vert _{(x_j,t_n)}+\cdots , \end{aligned}$$
(16)

and hence we have

$$\begin{aligned} T_j^n=O(h^4+k^2). \end{aligned}$$
(17)

\(\square\)

5 Numerical experiments

In this section, we present some numerical experiments to verify our theoretical results obtained in the previous section. The accuracy of the proposed scheme is measured using the \(L_{\infty }\) and \(L_{2}\) errors at \(t=t_N\) that are approximated by

$$\begin{aligned} L_{\infty }= & {} \max _{1\le j\le M}\Vert v(x_j,t_N)-u(x_j,t_N)\Vert , \end{aligned}$$
(18)
$$\begin{aligned} L_{2}= & {} \sqrt{h\sum _{j=1}^{M}(v(x_j,t_N)-u(x_j,t_N))^2}. \end{aligned}$$
(19)

In addition, the invariants of mass, momentum, and energy for the MRLW equation are calculated for a single soliton and during the interaction of two and three solitary waves to measure the conservation properties of the proposed scheme.

5.1 Motion of single solitary waves

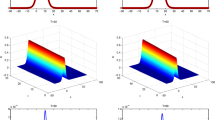
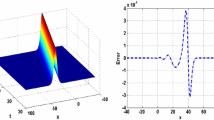
With \(h=0.4\) and \(k=0.05\) fixed, two experiments were performed to demonstrate the viability of our scheme in the situation of a single soliton motion. Calculations up to \(T=20\) were performed. In line with the work of [23], the model parameters were selected as \(x_0=0\), \(c=0.1\) with range \([-40,60]\) for the first example and \(x_0=0\), \(c=0.03\) with range \([-80,120]\) for the second example. Tables 1 and 2 show the values of \(L_{\infty }\) and \(L_{2}\) errors and the invariants \(I_1\), \(I_2\), and \(I_3\). The invariant \(I_1\) is changed by less than \(10^{-5}\) in both circumstances, whilst the changes for the invariants \(I_2\) and \(I_3\) approach zero, demonstrating the reasonable conservatism of our proposed scheme. At \(T=20\), the errors for the first example are reasonably minimal, at \(1.182044\times 10^{-4}\) for \(L_{\infty }\) error and \(2.93952\times 10^{-4}\) for \(L_{2}\) error. Given that our approach is highly accurate, similar results are obtained for the second example as \(2.09146\times 10^{-5}\) for \(L_{\infty }\) error and \(5.92125\times 10^{-5}\) for \(L_{2}\) error. In Fig. 1 for the first example, the motion of the single wave is plotted at various time levels with an amplitude of 0.3, and in Fig. 2 for the second case, with an amplitude of 0.17. The fact that the waves at \(t=16\) and \(t=20\) adequately agree with those at \(t=4\) demonstrates the reliability and accuracy of our scheme.

Table 1 Invariants and errors for single solitary wave on \([-40,60]\) with \(h=0.4\), \(k=0.05\), \(c=0.1\)
Full size table
Fig. 1
figure 1

Single solitary wave on \([-40,60]\) with \(h=0.4, k=0.05,c=0.1\) at times: \(T=4,T=8,T=12,T=16\) and \(T=20\)

Full size image
Table 2 Invariants and errors for single solitary wave on \([-80,120]\) with \(h=0.4, k=0.05,c=0.03\)
Full size table
Fig. 2
figure 2

Single solitary wave on \([-80,120]\) with \(h=0.4, k=0.05,c=0.03\) at times: \(T=4,T=8,T=12,T=16\) and \(T=20\)

Full size image

Furthermore, we compare our results in terms of maximum errors with the obtained results in [8, 9, 12, 13] to examine the validity of our scheme. For the purpose of comparisons, the parameters are chosen as \(h=0.2\), \(k=0.025\), \(c=1\), \(x_0=40\), and \(\delta =6\), with a range [0, 100]. The computations are performed up to \(T=10\) and are listed in Table 3. It is clearly observed that \(L_{\infty }\)-errors obtained by our scheme are marginally smaller than those obtained by others, indicating that our scheme is more accurate.

Table 3 Comparison of our results with some of recent results using maximum error (\(L_{\infty }\times 10^3\)) for single solitary wave on [0, 100] with \(h=0.2\), \(k=0.025\),\(c=1\), \(x_0=40\) and \(\delta =6\)
Full size table

5.2 Convergence rate

To calculate the convergence rates in space and in time, we use the following formula [23]

$$\begin{aligned} Order=\log _2\left(\frac{L_{\infty }(h,k)}{L_{\infty }(\frac{h}{2},\frac{k}{4})}\right) \end{aligned}$$

for the convergence rate in space, and

$$\begin{aligned} Order=\log _2\left(\frac{L_{\infty }(h,k)}{L_{\infty }(\frac{h}{4},\frac{k}{2})}\right) \end{aligned}$$

for the convergence rate in time, with respect to the maximum norm errors. With the other parameters remaining the same as in Table 1, we started with \(h=k=0.8\), and reduced the spatial and temporal variables by 2 and 4, respectively, to calculate the spatial convergence rates. The resultant \(L_{\infty }\) errors and the corresponding convergence rates of our scheme are recorded in Table 4, which reveals that the fourth order of convergence in the spatial direction was achieved. Table 5, in contrast, displays the temporal convergence rates, as we first set \(h=k=0.8\), then scaled them back by a factor of 2 for k and 4 for h. Other parameters are chosen as in Table 1. Based on the proposed scheme, the accuracy of order 2 in the temporal direction is obtained. These spatial and temporal rates are aligned with the theoretical conclusions in Lemma 2.

Additionally, the log-log scale depicted in Fig. 3. shows the resultant \(L_{\infty }\) errors on the solitary wave solutions with regard to spatial variable h and temporal variable k. In Fig. 3a and b, lines of slope 4 and 2 are added as references. As can be observed in these figures, our scheme achieved an \(O(h^4+k^2)\) accuracy, coinciding with the theoretical predictions.

Table 4 The convergence rates in space and maximum errors at \(T=20\) for single solitary wave of MRLW equation on \([-40,60]\) with \(c=0.1\) and \(x_0=0\)
Full size table
Table 5 The convergence rates in time and maximum errors at \(T=20\) for single solitary wave of MRLW equation on \([-40,60]\) with \(c=0.1\) and \(x_0=0\)
Full size table
Fig. 3
figure 3

a The \(L_{\infty }\) errors with respect to h at time \(T=20\) with parameters chosen as in Table 4. b The \(L_{\infty }\) errors with respect to k at time \(T=20\) with parameters chosen as in Table 5

Full size image

5.3 Interaction of solitary waves

The interaction of two and three solitary waves travelling in the same direction is discussed in this section. The initial conditions in these scenarios can be described by a linear sum of two and three well-separated solitary waves of different amplitudes, as follows:

$$\begin{aligned} u(x,0)=\sum _{i=1}^{p}\sqrt{6c_i}sech \left(\sqrt{\frac{c_i}{\mu (c_i+1)}}(x-x_i) \right), \end{aligned}$$
(20)

where \(p=2\) and \(p=3\) for the interaction of two and three solitary waves, respectively. We performed the simulations up to \(T=200\) and on the range [0, 300], with fixed \(h=0.4\) and \(k=0.05\) to enable the interaction to take place. Two solitary waves with \(c_1=\frac{4}{21}\), \(c_2=\frac{9}{91}\), \(x_1=15\) and \(x_2=35\) interacted at various time levels, as shown in Fig 4. Table 6 lists the outcomes of the conservation of three laws. Fig 5 presents a plot of the interaction of three solitons at various time levels, where \(c_1=\frac{4}{21}\), \(c_2=\frac{9}{91}\), \(c_3=\frac{15}{301}\), \(x_1=15\), \(x_2=35\) and \(x_3=55\). Table 7 lists the three invariants for this case. The outputs of the experiments reveal that the three invariants held relatively steady throughout the interaction process. Our approach effectively maintains the soliton properties because the waves interact and maintain their shape.

Table 6 Invariants for interaction of two solitary waves on [0, 300] with \(h=0.4, k=0.05,c_1=\frac{4}{21},c_2=\frac{9}{91}\)
Full size table
Fig. 4
figure 4

Interaction of two solitary waves on [0, 300] with \(h=0.4, k=0.05\) at times: \(T=0,T=80,T=160,T=200\)

Full size image
Table 7 Invariants for interaction of three solitary waves on [0, 300] with \(h=0.4, k=0.05,c_1=\frac{4}{21},c_2=\frac{9}{91},c_3=\frac{15}{301}\)
Full size table
Fig. 5
figure 5

Interaction of three solitary waves on [0, 300] with \(h=0.4, k=0.05\) at times: \(T=0,T=80,T=160,T=200\)

Full size image

6 Conclusion

In this paper, we described the use of a finite difference method based on a three-level temporal scheme and a five-point space stencil to solve the initial boundary-value problem for the MRLW equation. Based on the maximum norm, the scheme is shown to be marginally stable and convergent with second-order accuracy in time and fourth-order accuracy in space. In order to demonstrate the effectiveness and accuracy of the proposed method, numerical experiments using single and solitary waves interaction were described. Investigations into the conservation quantities for mass, momentum, and energy were also conducted, and the results were deemed satisfactory. Comparisons with other previous results are given to show the accuracy and the efficiency of the proposed scheme.