1 Introduction

A high penetration of various renewable energy sources is an effective solution for the deep decarburization of electricity production [1,2,3]. Renewable generation plants (wind turbines, Photovoltaics, etc.), electric vehicles, and other related infrastructures must be largely developed on a large scale to realize the target of carbon-neutrality [4, 5]. Wind energy is the most widespread and economic renewable energy at present [6]. While wind electricity supply still suffers from significant variations, over daily and monthly/seasonal scales, because of the fluctuation of the wind resource [7, 8]. Energy storage is considered as an effective technology to improve renewable penetration and quality, and to reduce greenhouse gas emissions which is an extra reduction compared with non-storage renewable generation scenario [9,10,11,12,13]. The added energy storage system to renewables as a baseload could further reduce the CO2-emission from 72% to 90% compared with a zero-renewable scenario [9]. The report of The UN Climate Conference (COP27) by IPCC pointed out that “Mitigation response options: energy storage for low-carbon grids” [14]. The MIT published ‘The Future of Energy Storage’ and stated “the important role of energy storage in future decarbonized electricity systems that will be central to the fight against climate change” [15].

The economic performance by integrating energy storage technologies into wind generation has to be analyzed for commercial development [16]. One solution is to implement the electricity price arbitrage strategy. The real-time pricing (RTP) varies in the market throughout a single day due to the different patterns of supply and demand. A wind farm with an energy storage device is considered as a whole to be connected to the grid market. Firstly, the energy storage device stores abandoned wind generation to eliminate curtailment. Secondly, it stores wind generation when the price of electricity is pretty low. Then the energy storage system releases electricity to the grid during high price time. Through the arbitrage strategy, the energy storage coupled with wind generation can produce benefits which in turn supports the installation of energy storage system [17,18,19].

Researchers from around the world have analyzed the arbitrage through energy storage, especially with intermittent renewable energy. Many energy storage technologies were analyzed for energy arbitrage in real-time electric markets in USA [20]. Pumped hydro storage (PHS), Lithium-ion battery storage, Compressed air energy storage (CAES) and some other technologies were considered as promising technologies in terms of profitability through the price arbitrage [20]. The value of arbitrage for energy storage in European electric markets was investigated considering different European power markets and different energy storage technologies. The net revenue was of €110–125/MWh. It was suggested that energy storage system may play vital roles as a necessary positioning to produce more benefits [21]. The intertemporal arbitrage of Lithium battery energy storage system (BESS) within German-Austrian market was assessed using a mixed-integer linear programming (MILP) model [22]. A 1.1MW/1.078MWh LiFePO4 battery was considered for arbitrage, and after around 1.5 years the storage system reach the break-even point and generate a positive NPV (net present value) [22]. In Ontario, Canada, a 1MW/1MWh storage system was simulated through 2015 for generating profits through the energy arbitrage [23]. A gross revenue of $21,686 was generated, and ancillary service by this energy storage can add $155,798 revenue per MW per year. The research suggested that energy storage technologies need to evolve for lower cost, and other ancillary service and energy policies should also implemented to make the energy storage more economically feasible [23].

Energy storage system is also considered as enablers of several possibilities. Except energy arbitrage enabler, it can also provide ancillary services as well as deferral of infrastructure investment [24]. Along with the development trend of new electricity system of more renewable energy sources, more flexible and adjustable requirements, it increases the need of energy storage for ancillary services such as spin / non-spin reserves, frequency regulation, voltage support, and participating markets for energy and ancillary services [24]. Installing a battery energy storage in a hospital in Northern Ireland for arbitrage and providing ancillary services, the payback period is 3.1 years [25]. Large scale energy storage technologies, e.g. Liquid air energy storage (LAES), can provide more predictable and reliable source of energy by providing ancillary services [26]. Especially, when the grid is with high shares of intermittent renewable sources, it provides multi-time scale ancillary services such as frequency regulation and spinning reserves leading to decrease of consumer’s cost. Taking the UK as an example, it will solve problems of transmission network congestion and abating wind power curtailment through LAES, and save about 400 million pounds per year [26].

Energy storage in concert with wind energy have become attractive for grid and electricity customers which can increase system stability and efficiency, and moreover facilitate penetration of renewable energy and reduction of their costs [27, 28]. More complex and general optimization methods and dispatching strategies have been proposed and analyzed aiming to reduce electricity costs. A BESS participating in an electricity market (Spanish Day-Ahead Market) for arbitrage was investigated through a Mixed Integer Linear Programming (MILP) optimization [17]. The daily price difference is among 5~50€/MWh. The objective of the optimization is to schedule the charging-discharging to maximize revenues of reduce the cost of use. For a 1MW/1MWh BESS system, the annual accumulated profits were about €1000~2100 when the accumulated storage energy was about 400~800MWh [17]. A particle swarm optimization (PSO) algorithm was utilized to figure out the buildings’ optimal operation strategy with renewable energy and battery energy storage system to minimize the cost of energy [29]. The cost is reduced by 12.1%-58.3% under the proposed operation strategy with various electricity prices [29]. Electricity cost saving potentials are affected by the size of renewable energy or battery bank. A distributed generation (DG) system with renewable energy (wind turbine, PV) that is connected to the grid is proposed in reference [30]. Different energy portfolios (PV, PV with government subsidies, PV with Wind generation) and capacity were investigated through an optimization algorithm to reduce the distributed generation lifecycle cost. The analysis showed that exploring wind power can realize cost-savings in locations where the average wind speed was above 4.8 m/s [30]. Given the real-time pricing in Spanish electricity market, a grid-connected storage system is modelled to minimize the levelized cost of energy (LCE) by optimizing the size and control of the storage system [31]. In case of the 2013 Spanish electricity market, the battery storage system was not profitable due to small price difference in a whole day, unless the cost was no more than 0.045 €/kWh in the near future [31]. A grid-connected BESS with wind energy was studied on scheduling the storage size to minimize energy cost using a whole year data. For a factory, the electricity cost was decreased by 54% in a day in summer time considering the time-of-use (TOU) price, while it is 0.7% reduction in winter time. And the whole year saving of electricity payment could be as much as 28.1% with optimal schedules [32]. The above-mentioned research mainly aimed to reduce electricity cost when purchasing electricity from grid. A few publications presented methodology to schedule charging-discharging for maximizing electricity sales under TOU tariff. Sioshansi et al. analyzed the arbitrage revenue of a price-taking storage system with different storage capacities in considering various technologies and applications for PJM electric market in USA [33]. These factors were considered including locations, fuel price, energy storage efficiency and size, and load profile. The arbitrage revenue in PJM with an energy storage roundtrip efficiency of 80% and a storage time of 12 hours can reach $110/kW-year [33]. A method of price signal prediction for energy arbitrage scheduling of energy storage plant was developed based on feature selection tools and classification techniques [34]. A case of arbitrage was studied utilizing the utility-scale Lithium battery that participated in the Ontario wholesale market in Canada. A 5-MW, 1-h Lithium battery with round-trip efficiency of 78% was analyzed. The total profit through arbitrage of the energy storage plant was as much as 78,723 US dollars for 8 months [34]. An optimal charging scheduling was investigated for electric vehicles (EV) with wind power generation [35]. Some factors including whether the wind power sufficient, electricity price, SOC of an EV, wind generation pattern were considered. The study revealed an adaptive principle to better install the wind generation among EVs [35]. As the energy storage system can be at states of charging, discharging, and still storage, it provides spinning reserve service (charging and discharging processes), and non-spinning reserve service (still storage state) [36]. Energy storage to provide reserve services plays vital role in reducing several uncertainties in the power systems with high shares of renewable sources [37]. In an IEEE-30 bus test system case study, the energy and spinning reserve requirements are 13.53 GW/day and 1.355 GW/day, respectively. The value of $2395/day can be saved when energy storage providing spinning reserve service [38].

Researchers have studied the optimization configuration methods and economy of energy storage systems. Based on the current results, further research is needed: (1) The previous research on the value of ESS either considers the electricity price arbitrage or analyzes the benefits of providing ancillary services. There is still a gap in the research on how to establish the optimization model of ESS and the operation control strategy of the charging and discharging process that considers both electricity price arbitrage and reserve ancillary services. (2) Currently, most studies have set the optimization time step to 1 hour. However, when energy storage provides auxiliary services, the corresponding time is often in the minute level. (3) Few studies regard the RE and ESS coupling system as an independent system operator (ISO) to participate in the power market. (4) At present, most studies focus on specific energy storage. Due to the differences in the characteristics of different energy storage (e.g., CAES, BESS, PHS), the conclusions are not universal.

The economic viability of electricity storage is a key factor for its large-scale application. In this study, we carried out the optimization and the economic viability of energy storage applications especially when it is connected to the wind generation. A newly developed model based on particle swarm optimization (PSO) was introduced to optimize the capacity of electricity storage when integrated into a wind generation considering electricity price arbitrage. The study examines the profitability of different energy storage systems considering various roundtrip efficiencies, cost, and lifetime (service time). Moreover, reserve ancillary services were considered and analysed. Thus, this can add extra benefit to the wind-storage coupled system. The benefits of reserve ancillary services and its sensitivity were analysed. It is to obtain the best scheduling strategy, and to compare their net revenue of electricity with and without storage system. Thus, the optimal capacity and its operation strategy will be obtained. This study can be of help for both renewable energy development and energy storage application when commercially installed.

2 System description

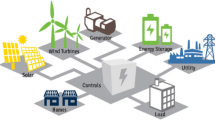
The system integrated with a wind farm, energy storage system and the electricity users is shown in Fig. 1. The energy storage plant stores electricity from the wind generation and releases it to the load when needed. Electricity can also be transmitted directly from the wind farm to the load.

Fig. 1
figure 1

Schematic diagram of the integrated system

Full size image

The electricity price is of three categories which are peak, mid-peak, and off-peak periods according to time-of-use (TOU) tariff. The operation strategy is that at off-peak time (low price), the energy storage system stores electricity; at on-peak time (high price), it releases electricity. Benefits are generated through the electricity price arbitrage.

3 Methodology

3.1 Objective function

3.1.1 Revenue without energy storage

The revenue of generation from a wind farm without energy storage was calculated by equation (1) throughout a whole year.

$$f_1=\sum\limits_i\left[WG\left(i\right)\times price\left(i\right)\times t\right]$$
(1)

where, WG(i) is the power generated by wind generation at i time period, MW; price(i) is the grid electricity price at i time period, $/kWh; t is the time step, and it is assumed to be 10 min.

3.1.2 Revenue with energy storage through energy arbitrage

After energy storage is integrated into the wind farm, one part of the wind power generation is sold to the grid directly, and the other part is purchased and stored with a low price, and then is sold with a high price through the energy storage system.

The revenue from direct sales from wind farm to the grid without energy storage is calculated as follows:

$${\mathrm{IC}}_1=\sum\limits_i\left\{\left[WG(i)-P_{\mathrm{st}}^{\mathrm c}\mathit{(i)}\right]\times t\times price{(i)}\right\}$$
(2)

where, \(P_{\mathrm{st}}^{\mathrm c}\left(i\right)\) is the charging power of the energy storage system during i time period, MW.

The revenue from the energy storage system that sells electricity to the grid is calculated as follows:

$${\mathrm{IC}}_2=\sum\limits_i\left[P_{\mathrm{st}}^{\mathrm d}{(i)\times price{(i)}}\times t\right]$$
(3)

where, \(P_{\mathrm{st}}^{\mathrm d}\left(i\right)\) is the discharging power at i time step, MW.

Thus, the 1-year electricity sales revenue of storage integrated with wind farm is calculated as follows:

$$f_2={\mathrm{IC}}_1+{\mathrm{IC}}_2$$
(4)

3.1.3 Additional revenue with energy storage through ancillary service

The energy storage system may provide spinning reserve service (charging and discharging processes) and non-spinning reserve service (still storage state) to the grid which pay for the service to the owner of the energy storage system. When charging, the spinning reserve capacity equals the current charging power value. When discharging, the spinning reserve capacity is calculated by subtracting the current discharging power (partial load) from maximum discharging power value. When still storage state, the non-spinning power equals the maximum discharging power of the energy storage system.

The additional revenue through spinning reserve service can be calculated as follows:

$${\mathrm{IC}}_3=\sum\limits_1^i\left[R_{\mathrm{st}}^{\mathrm{sr}}\left(i\right)\times c^{\mathrm{sr}}\times t\right]$$
(5)

where, \(R_{\mathrm{st}}^{\mathrm{sr}}\left(i\right)\) represents the available capacity of the spinning reserve by energy storage system within period i, MW; csr is the price of spinning reserve ancillary services from the grid to the owner of the storage pant, $/MW.

The additional revenue through non-spinning reserve service is calculated as follows:

$${\mathrm{IC}}_4=\sum\limits_1^i\left[R_{\mathrm{st}}^{\mathrm{nsr}}\left(i\right)\times c^{\mathrm{nsr}}\times t\right]$$
(6)

where, \(R_{\mathrm{st}}^{\mathrm{nsr}}\left(i\right)\) is the capacity of non-spinning reserve within the time period i, MW; cnsr is the price of non-spinning reserve ancillary services from the grid to the owner of the energy storage system, $/MW.

Thus, the 1-year income by reserve ancillary service of energy storage system is calculated as follows:

$$f_3={\mathrm{IC}}_3+{\mathrm{IC}}_4$$
(7)

3.1.4 Energy storage plant cost

The annual cost of investment of the energy storage plant is calculated as follows:

$$f_{\mathrm{cap},\mathrm a}=f_{\mathrm{cr}}\times s_{\mathrm{storage}}\times c_{\mathrm{storage}}$$
(8)
$$f_{\mathrm{cr}}=\frac{\beta\times\left(1+\beta\right)^T}{\left(1+\beta\right)^T-1}$$
(9)

where, fcr is the depreciation factor; cstorage is the total installed cost, $/MWh; sstorage stands for the power size of energy storage, MWh; β stands for the discount rate; T stands for the operation time of the energy storage system, year.

The annual spending for operation and maintenance (O&M) is as follows:

$$f_{\mathrm O\&\mathrm M,\mathrm a}=0.02\times s_{\mathrm{storage}}\times c_{\mathrm{storage}}$$
(10)

The annual cost for O&M is the expenditure of normal O&M of the system, which is estimated as 2% of the initial investment cost [39].

Energy storage system annual cost calculation:

$$f_{\text{storage,one}\_\mathrm{year}}=f_\text{cap,a}+f_{{O}\And{M,a}}$$
(11)

The objective function is to achieve maximum revenue of the energy storage system integrated with wind farm of 1 year.

When only electricity sales revenue is considered, and the objective function is:

$$f = {f_2} - f_{\text{storage,one}\_\mathrm{year}}$$
(12)

When considering both electricity sales revenue and reserve ancillary service, the objective function is:

$$f = {f_2} + {f_3} - f_{\text{storage,one}\_\mathrm{year}}$$
(13)

3.2 Constraints of energy storage system

3.2.1 Constraints for discharging process

  1. a)

    The power constraint of energy storage system.

$$P_{{\text{st}}}^{\text{d}}\left( i \right) + R_{{\text{st}}}^{\text{sr,d}}(i) \leq U_{{\text{st}}}^{\text{d}}\left( i \right) \times \overline P_{{\text{st}}}^{\text{d}}$$
(14)

where, \(\overline P_{\mathrm{st}}^{\mathrm d}\) is the maximum power of the energy release process, MW; \(U_{\mathrm{st}}^{\mathrm d}\left(i\right)\) is the running state during energy release, 1 for discharging, 0 for non-discharging.

  1. b)

    State of charge (SOC)

$${E_{{\text{st}}}}\left( {i - 1} \right) - {1 \mathord{\left/ {\vphantom {1 {\eta_{{\text{st}}}^{\text{d}} \times {\text{t}} \times \left[ {P_{{\text{st}}}^{\text{d}}\left( i \right) + R_{{\text{st}}}^{\text{sr,d}}(i)} \right]}}} \right. \kern-0pt} {\eta_{{\text{st}}}^{\text{d}} \times {\text{t}} \times \left[ {P_{{\text{st}}}^{\text{d}}\left( i \right) + R_{{\text{st}}}^{\text{sr,d}}(i)} \right]}}\geq {\underline E_{{\text{st}}}}$$
(15)

where, Est(i) is the stored capacity of the energy storage plant at time i, MWh; \(\underline E_{st}\) is the lowest limit storage capacity, MWh; \(\eta_{\mathrm{st}}^{\mathrm d}\) is discharging efficiency.

3.2.2 Constraints for charging process

  1. a)

    The power constraint of energy storage system.

$$R_{{\text{st}}}^{\text{sr,c}}(i) \leq P_{{\text{st}}}^{\text{c}}\left( i \right) \leq U_{{\text{st}}}^{\text{c}}\left( i \right) \times \overline P_{{\text{st}}}^{\text{c}}$$
(16)

where, \(\overline P_{\mathrm{st}}^c\) is the maximum power of the charging process, MW; \(U_{\mathrm{st}}^{\mathrm c}\left(i\right)\) is the operation state during charging process, 1 for charging, 0 for non-charging.

  1. b)

    SOC constraint of energy storage system.

$${E_{{\text{st}}}}\left( {i - 1} \right) + \eta_{{\text{st}}}^{\text{c}} \times {\text{t}} \times P_{{\text{st}}}^{\text{c}}\left( i \right) \leq {\overline E_{{\text{st}}}}$$
(17)

where, \({\overline E}_{\mathrm{st}}\)  is the highest limit storage capacity, MWh; \(\eta_{\mathrm{st}}^{\mathrm c}\) is the charging efficiency.

  1. iii)

    The constraint of wind generation

$$P_{{\text{st}}}^{\text{c}}\left( i \right) \leq WG\left( i \right)$$
(18)

3.2.3 Constraints for non-charging and non-discharging processes

  1. a)

    Power constraints for non-spinning reserve

$$R_{{\text{st}}}^{{\text{nsr}}}(i) \leq \overline P_{{\text{st}}}^{\text{d}} \times \left[ {1 - U_{{\text{st}}}^{\text{d}}(i) - U_{{\text{st}}}^{\text{c}}(i)} \right]$$
(19)

Where, \(U_{\mathrm{st}}^{\mathrm d}\) and \(U_{\mathrm{st}}^{\mathrm c}\) can only be either 1 or 0 which means operating state or storage state. When either one equals 1, the energy storage can not provide non-spinning service.

  1. b)

    Energy constraints for non-spinning reserve

$$R_{{\text{st}}}^{{\text{nsr}}}(i) \leq {{\eta_{{\text{st}}}^{\text{d}} \times {E_{{\text{st}}}}(i - 1)} \mathord{\left/ {\vphantom {{\eta_{{\text{st}}}^{\text{d}} \times {E_{{\text{st}}}}(i - 1)} t}} \right. \kern-0pt} t}$$
(20)

When requiring the non-spinning reserve during period i, there should be enough energy stored before that.

Equations (14) and (16) limit the total energy that can be stored or released from the storage system within time step i. Equations (15) and (17) confine the stored energy that is between the maximum and minimum storage capacity. Equations (18) ensures the power stored by the energy storage plant at time i is no more than wind power. Equations (19) and (20) are set to restraint the non-spinning reserve capacity through the energy storage system in the non-discharging and non-charging processes.

3.3 Optimization method

Particle swarm optimization (PSO) algorithm which is a population-based search algorithm is developed based on the simulation of the social behavior of birds within a flock. The algorithm is applied to solve the nonlinear problem. Compared with genetic algorithm, which is evolved into a relatively efficient optimization algorithm. The movement of particles in the search space is shown in Fig. 2. The implementation of PSO includes four evaluation criteria: firstly, it is to initial the swarm to make sure the initial point of the particle is in the search space; secondly, it is to examine whether each particle group position satisfies the constraints; thirdly, it is to update the best position of the particle when its fitness value is better than the previous one; fourthly, it is to verify if the particle optimal value is better than the global optimal value, and if so, to update the global optimal position of the particle swarm. The parameters of the particle swarm optimization algorithm used in this study are shown in Table 1 [40].

Fig. 2
figure 2

Schematic diagram of particle swarm optimization algorithm

Full size image
Table 1 Parameters of particle swarm optimization algorithm
Full size table

4 Results and discussion

4.1 Energy storage operation strategy

A new model based on PSO was developed to optimize the capacity of energy storage plant when integrated into a wind farm considering electricity price arbitrage. The energy storage device of wind-storage coupled system operates charging or discharging according to the electricity price difference for a certain time period. Annual data of wind generation and electricity data was considered. It aims to analyze the optimal storage capacity and operation strategy to generate the most benefits from the coupled system. Fig. 3 presents the yearly power output data of a 50MW wind farm. The electricity price data in this area within 1 year is shown in Table 2 [41]. The low price of electricity is 0.0401 $/kWh (23:00-7:00); the flat price of electricity is 0.1111 $/kWh (7:00-10:00; 15:00-18:00; 21:00-23:00); the high price of electricity is 0.1899 $/kWh (10:00-15:00; 18:00-21:00), and the peak price of electricity is 0.2093 $/kWh (11:00-13:00; 16:00-17:00).

Fig. 3
figure 3

Wind generation profile of a year

Full size image
Table 2 Electricity price
Full size table

All the electricity from the wind farm without energy storage is sold to the grid and users. The annual revenue is 12.78 million US dollars. When integrating the energy storage plant, it stores the wind power when the electricity price is low, and releases it when the price is high. The total income of the wind-storage coupled system can be significantly increased. However, it will increase the initial investment by adding energy storage system. Thus, the method to best allocate the capacity of energy storage plant should be developed with respect to the energy storage round-trip efficiency, cost, lifetime, and other factors to acquire the optimization capacity and operation strategy for a certain wind farm. The revenue of wind-storage system is composed of wind generation revenue, energy storage income and its cost. With the TOU price, the revenue of the wind-storage system is determined by the total generated electricity and energy storage performance. By calculating the investment cost and arbitrage income of the energy storage plant, the configuration capacity of the energy storage plant is obtained when the wind-storage system’s net income of the reaches the maximum.

There are various types of electricity storage technologies: pumped hydro storage (PHS), Lithium-ion batteries (Li-ion), compressed air energy storage (CAES), lead-acid batteries, nickel-cadmium batteries (Ni-Cd), flywheels, sodium-sulphur batteries (NaS), supercapacitors, etc [42, 43]. These technologies can be categorized into three groups: bulk energy storage type which can operate a few hours to weeks; load shifting energy storage type which operates a few minutes to hours; and power quality energy storage type which operate a few seconds to several minutes [44]. As PHS and CAES tend to be of lower cost, they are suitable for application of large scale capacity, and operated as an arbitrage device. Li-ion batteries are of more maturity, higher efficiency as many battery storage stations are under operation [45]. PHS, CAES and Li-ion battery are the most promising technologies of all electric energy storage systems in terms of technology maturity, charging-discharging performance and cost. The economic parameters for these three energy storage technologies are given in Table 3.

Table 3 Economic parameters for large scale energy storage technologies [42, 44, 46]
Full size table

4.2 Optimization results considering energy arbitrage

This study evaluates the best energy storage allocation capacity under various energy storage system lifetime, cost and efficiencies for coupling with a wind farm of 50MW. As shown in Table 4 and Fig. 4, the energy storage system lifetime is set as 10, 15, 20, 25 and 30 years, respectively. The energy storage and release efficiencies are 70%, 75%, 80%, 85%, 90% and 95%, respectively. The energy storage plant cost is set as 150, 225, 300, 375 and 450$/kWh respectively. The energy storage plant’s optimum capacity of for a wind generation is calculated considering energy arbitrage, so is the annual benefit of wind-storage coupled system with the optimal capacity.

Table 4 Optimization results of wind-storage system based on electricity price arbitrage
Full size table
Fig. 4
figure 4

Annual revenue of wind-storage coupled system considering price arbitrage

Full size image

Table 4 and Fig. 4 show that with the increase of the lifetime, the increase of the efficiency, and the decrease of the cost, the optimization storage capacity and the annual revenue of the wind-storage coupled system increase. When the energy storage system lifetime is of 10 years, and the cost is equal to or more than 375 $/kWh, the optimization configuration capacity is 0 MWh, which means no energy storage installation. The annual revenue of the simulated wind-storage system is 12.78 million dollars, which is purely from the sale of wind generation. When the energy storage plant lifetime is of 10 years, and the cost is equal to or less than 300 $/kWh, with the increased efficiencies of both charging and discharging processes, the installed storage capacity and the annual revenue of the wind-storage coupled system increase. When the energy storage plant lifetime is of 15, 20, 25 and 30 years, respectively, the change trend of the optimization capacity and the annual revenue of the wind-storage coupled system versus the cost and the efficiency of the energy storage plant is similar to that when the lifetime of the energy storage plant is of 10 years.

Figure 5 shows the optimal storage capacity under different lifetime, and the annual income of the wind-storage coupled system under the optimal allocation capacity when the charging and discharging efficiencies are 80%, and the cost of 150 $/kWh. Figure 5 shows that with longer lifetime, the optimal allocation capacity of the energy storage plant and the annual revenue of the wind-storage coupled system increase. For example, when the lifetime is 20 years and 30 years, respectively, the optimal installed storage capacity is 16MWh and 23MWh, respectively. And the annual revenue of the wind-storage coupled system is 12.83 million dollars and 12.87 million dollars, respectively.

Fig. 5
figure 5

Energy storage optimal capacity and annual revenue versus lifetime

Full size image

Figure 6 shows the optimal storage capacity under different charging and discharging efficiencies, and it also shows the annual income of the wind-storage coupled system under the optimal storage capacity when the energy storage cost is 150 $/kWh, and the lifetime is 20 years. Figure 6 shows that the optimal storage capacity and the annual revenue of the wind-storage coupled system increase significantly with the improvement of the charging and discharging efficiencies. For instance, when both the charging and discharging efficiencies are 80%, the optimal storage capacity is 16MWh. While, when both charging and discharging efficiencies are 90%, the best allocation storage capacity is of 42MWh. And the wind-storage system annual revenue is 12.83 million dollars and 13.12 million dollars, respectively (Fig. 6).

Fig. 6
figure 6

Energy storage optimal capacity and annual revenue versus efficiency

Full size image

Figure 7 shows the optimal allocation storage capacity under different energy storage system costs, and the annual income of the wind-storage coupled system under the optimal installation capacity when the efficiency for both charging and discharging processes is 90% and the lifetime of 20 years. As can be seen from Fig. 7, with the decrease of the energy storage cost, the optimal installation capacity of energy storage plant and the annual revenue of wind-storage coupled system are significantly improved. For instance, when the energy storage plant cost is 300$/kWh and 150$/kWh, respectively, the optimal allocation capacity is 7MWh and 42MWh, respectively. And the annual revenue of wind-storage system is 12.80 million dollars and 13.12 million dollars, respectively.

Fig. 7
figure 7

Energy storage system optimal capacity and annual revenue versus cost

Full size image

As shown in Fig. 8 and Table 5, the efficiencies for charging and discharging are set to be 85%, and the influence of the energy storage cost and lifetime on the optimal installation capacity and annual income is analyzed. The results in Table 5 present the optimal storage capacity under various cost and lifetime. The related results about annual revenue are given in Fig. 8. The results of Table 5 and Fig. 8 reveal that when the energy storage cost is equal to or greater than 375 $/kWh, the calculated capacity of the energy storage system is 0 MWh, which means no energy storage installation. The annual revenue of the wind-storage coupled system is 12.78 million dollars which is the income of wind generation only sold to the grid or customer. With the decrease of energy storage plant cost and the increase of lifetime, the best storage capacity and the corresponding annual income of wind-storage coupled system increase. When the energy storage system lifetime is 30 years and the cost is 150 $/kWh, the optimal storage capacity is 42 MWh, and the annual revenue of wind-storage system is 13.01 million dollars.

Fig. 8
figure 8

Wind-storage system annual revenue versus cost and lifetime

Full size image
Table 5 Optimal storage capacity considering ancillary services under various cost and lifetime
Full size table

As shown in Fig. 9 and Table 6, the cost of energy storage plant is set to be 300 $/kWh. The influence of charging/discharging efficiencies and lifetime on the best allocation storage capacity and the annual revenue of wind-storage coupled system is analyzed. Table 6 presents the optimal storage capacity under different charging and discharging efficiencies and lifetime. Figure 9 shows the wind-storage system annual revenue corresponding to the optimal storage capacity under different conditions. Table 6 and Fig. 9 reveal that when the efficiencies of charging and discharging processes are equal to or less than 80%, the optimal storage capacity is 0MWh, which means no enenergy storage utlized. And the wind-storage system annual revenue is 12.78 million dollars. With the increase of charging and discharging efficiencies and lifetime, the best storage capacity and the corresponding annual income of the wind-storage coupled system increase. When efficiencies for charging and discharging processes are 95%, and the energy storagel ifetime is 30 years, it can be installed 20MWh energy storage as the best capacity in this case. And the annual revenue of the wind-storage coupled system is 12.96 million US dollars.

Fig. 9
figure 9

Wind-storage system annual revenue versus energy storage/release efficiency and lifetime

Full size image
Table 6 Optimal storage capacity considering ancillary services under various efficiency and lifetime
Full size table

As shown in Fig. 10 and Table 7, the energy storage plant lifetime is set to be 15 years. The optimal storage capacity and annual revenue of the wind-storage coupled system are analyzed with various charging/charging efficiencies and costs. Table 7 presents the optimal storage capacity under different charging and discharging efficiencies and costs. Figure 10 reveals the annual income of the wind-storage system corresponding to the optimal energy storage capacity under different conditions. Table 7 and Fig. 10 reveal that when the efficiencies for charging and discharging processes are equal to or less than 75%, and the cost is equal to or more than 450 $/kWh, the optimal storage capacity is calculated as 0MWh, which means no energy storage utilized. Thus, the annual revenue of the wind-storage coupled system is 12.78 million dollars only from the sale of wind generation. The optimal energy storage capacity and the corresponding annual revenue of wind-storage system increase when increasing the charging and discharging efficiencies and decreasing the energy storage system cost. The optimal storage capacity is 38MWh when the charging and discharging efficiencies are 95%, the energy storage cost is 150 $/kWh. The total annual income is calculated as 13.23 million US dollars from the wind-storage coupled system.

Fig. 10
figure 10

Wind-storage system annual revenue versus energy storage/release efficiency and cost

Full size image
Table 7 Optimal storage capacity considering ancillary services under various efficiency and cost
Full size table

4.3 Optimization results considering spinning / non-spinning reserve service

In addition to the arbitrage income, the energy storage system can also generate extra revenue by providing reserve ancillary service to the grid. In this section, the following factors are taken into account including the electricity sales of wind-storage system, the reserve ancillary services of the energy storage system, and the investment cost of the energy storage system. The value of spinning / non-spinning reserve service is set as 2.25 $/MW per hour.

As shown in Fig. 11 and Table 5, the efficiencies for charging and discharging are set to be 85%. Under different energy storage system cost and lifetime, the optimal configuration capacity of the energy storage plant and the annual comprehensive revenues of the wind-storage system considering only electricity price arbitrage and the electricity price arbitrage plus reserve service are compared. From Table 5 and Fig. 11, when the energy storage plant cost and lifetime are the same, the optimal configuration capacity of the energy storage system considering electricity price arbitrage and reserve service, and the annual comprehensive revenues of the wind-storage system are both greater than or equal to the situation that only electricity price arbitrage is considered. For example, when the lifetime of the energy storage system is 30 years and the cost is 150 $/kWh, the optimal configuration capacity of the energy storage system that only considers the electricity price arbitrage and also considers the energy arbitrage and reserve service is 42MWh and 48MWh, respectively. The annual comprehensive revenue is 13.015 million US dollars and 13.240 million US dollars respectively.

Fig. 11
figure 11

Wind-storage system annual revenue considering ancillary services versus cost and lifetime

Full size image

As shown in Fig. 12 and Table 6, the cost of energy storage system is set to be 300 $/kWh. Under different energy storage system efficiency and lifetime, the optimal configuration capacity of the energy storage plant and the annual comprehensive revenues of the wind-storage system considering only electricity price arbitrage mode, and the mode of electricity price arbitrage plus reserve service are compared. From Table 6 and Fig. 12, when the energy storage system efficiency and lifetime are the same, for the mode of electricity arbitrage plus ancillary services, the energy storage optimal configuration capacity, and the annual comprehensive revenues of the wind-storage system are both greater than or equal to the mode that only electricity price arbitrage is considered. For example, when the storage plant’s lifetime is 30 years, and the charging and discharging efficiencies are 85%, respectively, the storage system optimal configuration capacities for both modes (electricity price arbitrage only and the electricity price arbitrage plus reserve service) are 20MWh and 28MWh, respectively. The annual comprehensive revenue are 12.961 million US dollars and 13.097 million US dollars, respectively.

Fig. 12
figure 12

Wind-storage system annual revenue considering ancillary services versus efficiency and lifetime

Full size image

As shown in Fig. 13 and Table 7, the lifetime system is set to be 15 years. Under different energy storage system efficiency and cost, the optimal configuration capacity of the energy storage plant and the annual comprehensive revenues of the wind-storage system considering two modes (only electricity price arbitrage mode, and the mode of electricity price arbitrage plus reserve service) are compared. From Table 7 and Fig. 13, when the energy storage system efficiency and cost are the same, the energy storage optimal configuration capacity and the annual comprehensive revenues of the wind-storage system considering the mode of electricity price arbitrage plus ancillary services are both greater than or equal to the mode that only electricity price arbitrage is considered. For example, when the cost of the energy storage system is 150 $/kWh and the charging and discharging efficiencies are 95%, respectively, the optimal configuration capacities for both modes (only electricity price arbitrage mode, and the mode of electricity price arbitrage plus reserve service) are 38MWh and 58MWh, respectively. The annual comprehensive revenue is 13.231 million US dollars and 13.497 million US dollars, respectively.

Fig. 13
figure 13

Wind-storage system annual revenue considering ancillary services versus efficiency and cost

Full size image

5 Conclusions

This study aims to clarify how the energy storage combines with wind generation and what benefits can be generated through the combination. According to the time of use electricity price, the energy storage system can store electricity when the price is low, and release it when the price is high. The optimization objective is the maximum annual revenue of the wind-storage coupled system, and the constraints include charging and discharging power, state of charge and stored wind power by the energy storage plant. The complicated optimization model for the wind-storage coupled system is developed, which also includes the storage and release operation control strategy considering the price arbitrage. The optimum storage capacity and its annual revenue under different conditions are calculated by particle swarm optimization (PSO) algorithm. In order to further improve the economic benefits of wind-storage system, this study also evaluates the comprehensive benefits of the wind-storage system when considering both modes (only electricity price arbitrage mode, and the mode of electricity price arbitrage plus reserve service). The optimization results show that when the energy storage cost is low, the operation lifetime is long and the charging and discharging efficiencies are high, the optimal allocation storage capacity can be found through the capacity optimization method. Thus, the proper range of energy storage system investment and best economic performance can be calculated.

Take a 50 MW wind farm as an example, the total revenue without energy storage is 12.78 million dollars. There are differences in the cost, lifetime, and efficiency of different energy storage technologies in wind-storage coupled system. This study analyzes the optimal energy storage capacity and annual revenue of wind-storage coupled system under different energy storage systems. For the wind-storage coupled system, as only electricity price arbitrage is considered: (1) the optimal capacity of the compressed air energy storage is 5MWh, and the annual revenue of the wind-storage coupled system is 12.79 million dollars; (2) the optimal configuration capacity of the battery energy storage system is 10MW, and the annual revenue of the wind-storage coupled system is 12.83 million dollars; (3) the optimal capacity of the pumped hydro energy storage is 15MW, and the annual revenue of the wind-storage coupled system is 12.84 million dollars. For the wind-storage coupled system, as the electricity price arbitrage plus reserve service is considered: (1) the optimal capacity of the compressed air energy storage is 16MWh, and the annual revenue of the wind-storage coupled system is 12.84 million dollars; (2) the optimal configuration capacity of the battery energy storage system is 16MW, and the annual revenue of the wind-storage coupled system is 12.90 million dollars; (3) the optimal capacity of the pumped hydro energy storage is 29MW, and the annual revenue of the wind-storage coupled system is 12.95 million dollars.