Role of CCUS in carbon neutral power system

Abstract

Achieving carbon neutrality by 2060 is an ambitious goal to promote the green transition of economy and society in China. Highly relying on coal and contributing nearly half of CO₂ emission, power industry is the key area for reaching carbon-neutral goal. On basis of carbon balance, a criterial equation of carbon neutral for power system is provided. By means of the equation, the different effects of three technical approaches to achieve carbon neutrality, including energy efficiency improvement, shifting energy structure and CO₂ capture, utilization and storage (CCUS) technology, had been evaluated. The results indicate that building a carbon-neutral power system requires comprehensive coordination between energy efficiency, renewable energy and CCUS technology. In particular, the unique role of CCUS in achieving carbon neutral target was investigated. For any power systems with fossil energy input, CCUS and negative emission technologies is indispensable to reach carbon neutrality. However, rather high energy consumption and costs is the critical gas deterring the large scale deployment of CCUS. Considering the specific conditions of China’s power industry, before the time window between 2030 and 2040 being closed, CCUS would either be ready for large scale deployment by reducing energy consumption and costs, or be phased out along with the most coal power plants. Conclusively, carbon neutral scenario will give CCUS the last chance to decarbonize the fossil fuel, which has great significance for China.

Background information

Anthropogenic CO₂ emissions, especially the utilization of fossil fuels for power generation, is the leading cause of global warming. Reduction of CO₂ emissions is crucial in our efforts towards mitigation global warming. Among all the mitigation strategies, CO₂ capture, utilization and storage (CCUS) is an efficient and reliable technology especially for high carbon fuels, while there is no alternative yet existing for mitigating emissions from the continued use of fossil fuel for electricity generation [1,2,3,4,5].

By the end of 2020, most countries in the world have successively proposed carbon-neutral targets. Among them, the major economies in the world, such as the United States, the European Union, Japan, and Canada, have proposed to achieve carbon-neutral targets by 2050 [6,7,8]. As the world’s largest carbon emitter, China has a total carbon emissions of more than 11.3 billion tons, accounting for about 30% of global carbon emissions [9]. Therefore, the carbon emission reduction required for China is much higher than that of other economies, and its carbon-neutral tasks are obviously more complex and diversified. Recently (22 September 2020), the Chinese government announced in the 75th session of the UN General Assembly (New York, USA) that China aims to achieve carbon neutrality before 2060. The announcement of the carbon neutral target clearly indicated that China needs to carry out a self-revolution to achieve zero CO₂ emissions before 2060 [10].

Among all the fields, power industry is the key area for carbon emission reduction due to the large amount of CO₂ emissions [9]. The carbon neutral target challenges traditional energy systems, where energy saving, renewable energy and carbon removal technologies (CCUS) are three pathways in achieving carbon neutral goal. China is home to over half the world’s existing coal capacity and projects under construction. Whereas the announcement of the carbon neutrality clearly indicated that fossil fuel should be either decarbonized or replaced by renewable energy before 2060. Considering the large amount of and the highly reliance on coal, the role of CCUS has to be shifted or significantly enhanced in the scenario of carbon neutrality, otherwise the coal has to be phased out to achieve carbon neutral target.

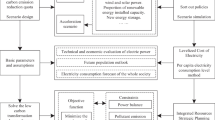
Thus, in order to better understand and achieve the goal of carbon neutrality, this paper provided the criterial equation of carbon neutrality for power systems with discussion the pathways in achieving carbon neutral target. More seriously, the important role of CCUS was discussed, and correspondingly, the challenges and possible path for the deployment of CCUS were explored.

Criterion equation of carbon neutral for power system

Formula derivation

The concept of carbon neutrality is essentially a balance between carbon sources and carbon sinks. The carbon source is the process of releasing CO₂ into the atmosphere, and the carbon sink is the process of absorbing CO₂ from the atmosphere. Investigating the atmospheric system within a certain period of time, when the amount of CO₂ emitted by all carbon sources into the system is equal to the amount of CO₂ absorbed by all carbon sinks from the system, carbon neutrality can be achieved. There are various carbon sources and sinks in nature with complicated relationships. Among them, the most important carbon source related to human activities is energy production. In 2020, China’s power sector emitted about 4 billion tons of CO₂ per year, which is close to 40% of the total emissions. Thus, the power sector is one of the key areas in emission reduction to achieve the carbon-neutral goal. To this end, this article focuses on the issues of carbon neutrality in the power industry.

According to the amount and sources of carbon elements, energy can be divided into three types: Carbonaceous energy [11], Carbon free energy and Carbon-neutral energy [12]. Carbonaceous energy mainly refers to fossil fuel, which contains carbon elements mined underground (the carbon elements in the ancient atmosphere are transformed into biomass through photosynthesis, and then become fossil fuels through long geological years). And in the process of utilization, the carbon element emitted to the atmosphere in the form of CO₂. In addition, carbon free energy refers to renewable energy such as solar energy and wind energy, which contain no carbon elements and does not directly emit CO₂ during utilization. Moreover, carbon-neutral energy refers to biomass, whose carbon elements come from the atmosphere. During the short period of growth and utilization, the carbon element is absorbed by biomass from the atmosphere and transferred to the atmosphere. Thus, the net CO₂ content in the atmosphere is not changed by carbon-neutral energy.

Carbonaceous and carbon-neutral energy are the most important carbon sources in the power industry. And the CO₂ cycle in the atmosphere will be affected by both of them during the utilization processes. According to characteristics of different energy and diverse energy utilization technologies, the carbon emissions during the utilization process can be obtained by the following equation [13]:

$$E=\frac{44}{12} FCO$$

(1)

E is the amount of CO₂ emissions; F is the total energy of the fuel consumed, depending on the amount of fuel consumed and the heating value of the fuel; C is the carbon content per unit of fuel energy, depending on the type of fuel; O is oxidant factor, indicating the percentage of carbon in the fuel that is eventually converted to CO₂, depending on whether the fuel is burned adequately. Considering the professional technology of boilers and with the advancement of combustion technology, the oxidation factor of most energy conversion processes have approached to 1 [14]. Thus, the oxidation factor will be assumed to be 1 in the following discussion [13].

The net carbon emissions of power system can be expressed as Eq. (2) based on carbon balance:

$$\mathrm{NE}=\mathrm{Source}+\mathrm{Sink}$$

(2)

Source refers to the amount of carbon emissions from carbon sources in the system, sink represents the carbon absorption from carbon sinks in the system.

Define K as the carbon recovery ratio, representing the proportion of CO₂ emitted by carbon sources that is absorbed by carbon sinks. According to the elemental balance, the carbon-balanced equation for different types of energy can be established as follows. The subscripts C, CN, and CF represent carbonaceous energy, carbon-neutral, and carbon free energy, respectively:

As for carbonaceous energy:

$${\mathrm{NE}}_{\mathrm{C}}=\frac{44}{12}{F}_C{C}_C+\left(-\frac{44}{12}{F}_C{C}_C{K}_C\right)$$

(3)

The carbon recovery ratio K_C < 1 and NCE_C > 0 due to the technical limitation;

For carbon neutral energy:

$${\mathrm{NE}}_{\mathrm{CN}}=\frac{44}{12}{F}_{\mathrm{CN}}\kern0.1em {C}_{\mathrm{CN}}+\left(-\frac{44}{12}{F}_{\mathrm{CN}}\kern0.1em {C}_{\mathrm{CN}}\kern0.1em {K}_{\mathrm{CN}}\right)+\left(-\frac{44}{12}{F}_{\mathrm{CN}}\kern0.1em {C}_{\mathrm{CN}}\right)$$

(4)

Considering that the amount of CO₂ emitted (${F}_{CN}\cdot {C}_{CN}\cdot \frac{44}{12}$) and absorbed ($-{F}_{CN}\cdot {C}_{CN}\cdot \frac{44}{12}$) by carbon-neutral energy are equal. Thus, Eq. (4) can be simplified as:

$${\mathrm{NE}}_{\mathrm{CN}}=-\frac{44}{12}{F}_{\mathrm{CN}}\kern0.1em {C}_{\mathrm{CN}}\kern0.1em {K}_{\mathrm{CN}}$$

(5)

when the carbon recovery ratio K_CN > 0, the carbon recovery technology is equipped in biomass power plants and the negative emission can be obtained (NE_CN < 0).

However, for carbon free energy, the net carbon emission NE_CF always equal to 0 due to its carbon free characteristics (C_F = 0), as shown in Eq. (6):

$${\mathrm{NE}}_{\mathrm{CF}}=\frac{44}{12}{F}_{\mathrm{CF}}\kern0.1em {C}_{\mathrm{CF}}\kern0.4em {\displaystyle \begin{array}{c}\underline {\underline {\kern0.6em {C}_{\mathrm{CF}}=0\kern0.7em }}\\ {}\end{array}}\kern0.4em 0$$

(6)

Based on Eqs. (3), (5) and (6), the total net carbon emission of the power system composed of fossil energy (carbonaceous energy), carbon free energy (non-biomass renewable energy) and carbon neutral energy (biomass energy) is:

$$\mathrm{NE}=\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}{\mathrm{NE}}_i=\frac{44}{12}{F}_{\mathrm{C}}\kern0.1em {C}_{\mathrm{C}}+\sum \limits_{i=\mathrm{C},\mathrm{CN}}\left(-\frac{44}{12}{F}_i\kern0.1em {C}_i\kern0.1em {K}_i\right)$$

(7)

NE is the net carbon emission of power system. If the dimensionless parameter R is defined as the proportion of carbon contained in carbonaceous energy among the total carbon input of the system:

$$R=\frac{F_{\mathrm{C}}\kern0.1em {C}_{\mathrm{C}}}{F_{\mathrm{C}}\kern0.2em {C}_{\mathrm{C}}+{F}_{\mathrm{C}\mathrm{N}}\kern0.1em {C}_{\mathrm{C}\mathrm{N}}}$$

(8)

Equation (7) can be simplified as:

$$\mathrm{NE}=\frac{44}{12}\left[R\left(1-{K}_{\mathrm{C}}\right)-\left(1-R\right){K}_{\mathrm{C}\mathrm{N}}\right]\sum \limits_{i=\mathrm{C},\mathrm{CN}}\left({F}_i\kern0.1em {C}_i\right)$$

(9)

Obviously, the power system can achieve carbon neutrality when NE ≤ 0. But in fact, the realization of carbon neutrality must meet the demand for energy products. In other words, carbon neutrality is a carbon balance under the premise of a certain power output. Therefore, carbon emission intensity is required to be adopted to characterize the carbon emission of the power system:

$${I}_{\mathrm{c}}=\mathrm{NE}/\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}\left({F}_i\kern0.1em {\eta}_i\right)=\frac{44}{12}\left[R\left(1-{K}_{\mathrm{C}}\right)-\left(1-R\right){K}_{\mathrm{C}\mathrm{N}}\right]\sum \limits_{i=\mathrm{C},\mathrm{CN}}\left({F}_i\kern0.1em {C}_i\right)/\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}\left({F}_i\kern0.1em {\eta}_i\right)$$

(10)

where I_c is the carbon emission intensity of the power system, which represents the amount of CO₂ emitted per unit of power generated by the power system. η_i represents the power supply efficiency, $\sum \limits_i{F}_i\cdot {\eta}_i$ is the total power generation of the power system.

The carbon emission intensity I_c ≤ 0 must be met by power systems achieving carbon neutrality. Thus, the formula (6) can be further simplified, and the following carbon-neutral formula can be obtained:

$$\left[R\left(1-{K}_{\mathrm{C}}\right)-\left(1-R\right){K}_{\mathrm{C}\mathrm{N}}\right]\sum \limits_{i=\mathrm{C},\mathrm{CN}}\left({F}_i\kern0.1em {C}_i\right)/\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}\left({F}_i\kern0.2em {\eta}_i\right)\le 0$$

(11)

For power systems with multiple energy inputs, the above carbon neutrality equation must be satisfied to achieve the goal of carbon neutrality.

The different effects of emission reduction approaches

As a major carbon emitter, the power industry will play a key role in achieving carbon neutrality. According to the criterial equation of carbon neutrality derived above, there are three major ways to establish a carbon-neutral power system: (1) Improve energy efficiency thus to save the consumption of carbonaceous energy; (2) Shift the energy structure and reduce the proportion of carbonaceous energy (3) Rebuild the balance of sources and sinks by adopting CO₂ capture, utilization and storage technology to achieve low-carbon utilization of carbonaceous energy.

Energy efficiency improvement - potential

According to the Eq. (10), the consumption of carbonaceous energy can be reduced by improving the utilization efficiency, thereby reducing carbon emissions from the power system. Taking coal power plants as an example, Fig. 1 shows the trend of average standard coal consumption and its corresponding carbon emission intensity in the past 20 years in China. It can be seen from the figure that with the development of power generation technology focusing on thermal cycle upgrading, such as the improvement of initial steam parameters and the introduction of reheating and recuperation, the power generation efficiency of coal power plants has risen from ~ 20% in the middle of the twentieth century to the current ~ 47% power generation efficiency. At the same time, the average standard coal consumption of electricity has been declining year by year, dropping to 304.7 g/kWh by 2020. The reduction in coal consumption has also significantly reduced the carbon emission intensity of coal power plants. As shown in the green curve in Fig. 1, in the past 20 years, the carbon emission intensity of coal power plants in China has dropped from 1078 gCO₂/kWh to 838 gCO₂/kWh (the carbon content of coal is assumed to be 75 wt.% [12] and the oxidant factor as 1.0). However, it can also be found that the declining trend of power generation energy consumption has gradually flattened. The reason for this trend comes from the following reality, super-critical or ultra-super-critical power plants had already accounted around 70% of installed capacity, while “650 °C” or “700 °C” technologies are still in research due to material limitation. Thus, the potential for continuing to reduce carbon emissions through energy saving is confined.

Fig. 1

The trend of average coal consumption and carbon emission intensity of thermal power plants in China

Shifting the energy structure - reliability

Coal, natural gas and oil are the most widely used carbonaceous energy at present. Due to composition and energy characteristics of fossil fuels and technical utilization efficiency, different fossil fuels have various CO₂ emission characteristics. Among fossil fuels, coal has the highest carbon content ranging from 0.024 kg /MJ to 0.026 kg /MJ [13], which means that 0.08 kg ~ 0.1 kg CO₂ will be produced by direct combustion of coal with every 1 MJ energy released. CH₄ is the main component of natural gas with the carbon content about 0.015 kg/MJ, which is only half of that of coal. Obviously, natural gas is lower carbon than coal from the perspective of CO₂ emission characteristics. On the other hand, the average efficiency of coal-based power generation technology is only about 40%, while combined cycle burning natural gas can reach higher than 60%. Correspondingly, about 1 kg of CO₂ will be emitted into the atmosphere for every 1 kWh of electricity output by traditional coal power plants, and natural gas power plants adopting combined cycle only emit about 0.35 kg of CO₂ to the environment for every 1 kWh of electricity output, which is about 1/3 of that of coal power plants. Figure 2 shows the carbon emission intensity of different fossil fuels with different power efficiency, and renewable energy. Peat and coking coal represent two typical coals with low and high carbon content per calorific value, respectively. When power generation efficiency (η) equals to 100%, the value of carbon emission intensity equals to the carbon emissions per unit of fuel energy (44/12C). It’s naturally that the net carbon emission intensity are both 0 gCO₂/kWh for carbon-neutral and carbon free renewable energy. Although biomass will produce a certain amount of CO₂ emissions during collection, processing (~ 20 gCO₂/kWh emissions) and transportation (about 3 gCO₂/kWh emissions for 50 km) processes [15], the emission amount is very small and can be ignored. Thus, carbon emission reduction can be achieved by increasing the proportion of renewable energy in the power system.

Fig. 2

Carbon emission intensity of different energy resources and technologies

From 2000 to 2020, the electricity installed capacity and generation ratio of renewable energy in China increased from 24.9% and 16.4% to 26.8% and 41.2%, respectively. This change in the energy structure has reduced the carbon emission intensity of the power system by about 30-35%. The temperature control plan of the 13th Five-Year Plan mentioned that CO₂ emissions intensity need to be controlled within 550 g/kWh, mainly by increasing the proportion of renewable energy [16]. At present, most strategic studies suggest that in a carbon-neutral scenario by 2060, renewables will be the main source of electricity accounted for more than 80% electricity generation ratio [17, 18].

CO₂ capture, utilization and storage technology – energy penalty

CO₂ Capture, Utilization and Storage (CCUS) is the only technology that can achieve low-carbon utilization of high-carbon fuel and realize negative emissions. As shown in Fig. 3, for carbonaceous energy, CCUS constructs a carbon cycle, capturing CO₂ released from carbonaceous energy and storing it in the ground. For carbon-neutral energy, CCUS breaks the original carbon cycle by storing the CO₂ absorbed from the atmosphere into the ground, creating a negative emission effect. The more fossil energy power plants or biomass power plants equipped with CCUS technology, the higher the recovery ratio K_C or K_CN in the carbon neutral formula. For a power plant, K_C or K_CN represents the CO₂ recovery rate of the specific power plant, or it represents the proportion of the power plants equipped with CCUS in a regional energy system after comprehensive consideration the CCUS deployment conditions.

Fig. 3

The impact of CCUS technology on the carbon cycle

At present, the average carbon emission intensity of 600 MW newly-built power generation plants are about 770 gCO₂/kWh and 350 gCO₂/kWh for ultra-supercritical power plants and gas-fired power plants, respectively. The carbon emission intensity is close to or even better than that in the United States and the United Kingdom [19]. Under the carbon neutral scenario, the role of CCUS has to be shifted or significantly enhanced. After installing CCUS, the average carbon emission intensity of coal power plants can be reduced to about 80 gCO₂/kWh when the carbon capture rate reaches 90%. However, it’s inevitable that some coal fired power plants are un-retrofitable, due to practical reasons like lacking of space for CO₂ separation unit, or no matched storage sites. So, it will be difficult to install CCUS for all power plants in a specific region, which also means that K_C for a regional power system could not reach 100%. For biomass power plants, the average carbon emission intensity is about 1200 gCO₂/kWh without considering the carbon source of the biomass itself [20, 21]. If CCUS (90% carbon capture rate) is further introduced, the average carbon emissions will drop to about − 1080 gCO₂/kWh under 90% capture rate, creating so called negative emission effect. Correspondingly, an capture rate K for an energy system with both K_C and K_CN can be defined, indicating the ratio of the total amount of CO₂ captured of the power system with CCUS to the total CO₂ emissions of the power system without CCUS. Similarly, K can be derived from Eq. (10) as follows:

$$K=R-\left[R\left(1-{K}_{\mathrm{C}}\right)-\left(1-R\right){K}_{\mathrm{C}\mathrm{N}}\right]$$

(12)

By defining K, the overall contribution and the importance of CCUS to carbon neutral system can be reflected. Thus, Eq. (9) can be further written as:

$${I}_{\mathrm{c}}=\frac{44}{12}\left(R-K\right)\sum \limits_{i=\mathrm{C},\mathrm{CN}}\left({F}_i\kern0.1em {C}_i\right)/\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}\left({F}_i\kern0.1em {\eta}_i\right)$$

(13)

R represents the ratio of system carbon emissions to the total carbon input, and K represents the ratio of captured carbon to input carbon. When R = K, the energy system achieves carbon neutrality.

It is worth noting that although increasing capture rate can directly reduce carbon emissions, the capture rate and η_i are not independent of each other. As CO₂ capture requires additional energy consumption, the power generation efficiency of power plants equipped with CCUS technology will be significantly reduced, which is currently one of the key obstacles hindering the large-scale promotion of CCUS technology. Therefore, the influence of the capture rate K on η_i should be further considered for I_c. Assuming that the capture energy consumption per CO₂ (EC_CO2) is the same for carbon neutral and carbonaceous energy, the carbon emission intensity I_c after modifying η_i can be written as follows:

$${\displaystyle \begin{array}{l}{I_{\mathrm{c}}}^{'}=\frac{44}{12}\left(R-K\right)\sum \limits_{i=\mathrm{C},\mathrm{CN}}\left({F}_i\cdot {C}_i\right)/\left[\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}\left({F}_i\cdot {\eta}_i\right)-\frac{44}{12}\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}\left({F}_i\cdot {C}_i\cdot K\cdot {EC}_{\mathrm{CO}2}\right)\right]\\ {}\kern1.3em =\frac{44}{12}\left(R-K\right)\sum \limits_{i=\mathrm{C},\mathrm{CN}}\left({F}_i\cdot {C}_i\right)/\left[\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}{F}_i\cdot \left({\eta}_i-\frac{44}{12}{C}_i\cdot K\cdot {EC}_{\mathrm{CO}2}\right)\right]\\ {}\kern1.3em =\frac{44}{12}\left(R-K\right)\sum \limits_{i=\mathrm{C},\mathrm{CN}}\left({F}_i\cdot {C}_i\right)/\left[\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}{F}_i\cdot \left({\eta}_i-{\eta_i}^{\hbox{'}}\right)\right]\end{array}}$$

(14)

$\frac{44}{12}\sum \limits_{i=\mathrm{C},\mathrm{CN},\mathrm{CF}}\left({F}_i\cdot {C}_i\cdot K\cdot {EC}_{\mathrm{CO}2}\right)$ represents the total capture energy consumption of CCUS, η_i’ is the reduction in power generation efficiency of the original system caused by the adoption of CCUS.

The relationship and trend of I_c and I_c^’ are shown in Fig. 4. Considering the deterioration of system performance due to CCUS, the carbon emission intensity I_c^’ of the system after the introduction of CCUS will be higher than that under the ideal situation I_c (the impact of CCUS on system performance is not considered). When R = K, the energy system achieves carbon neutrality.

Fig. 4

The relationship between K and I_c

As discussed above, the contribution of each technical approach on carbon neutrality can be further evaluated by Eq. (10). From 2000 to 2020, the total CO₂ emission intensity of China’s power sector decreased by 317.3 gCO₂/kWh (from 878.6 gCO₂/kWh to 561.3 gCO₂/kWh), whose calculation is based on generation data of China Electricity Council (CEC) and fuel emission factor data from Intergovernmental Panel on Climate Change (IPCC) [13, 22] with the oxidant factor being assumed to be 1.0. The share of power generation from non-fossil fuel had increased from 19% to 32.2%, contributing 157 gCO₂/kWh of CO₂ emission reduction. Meanwhile, average coal consumption of fossil fuel power plants had been decreased from 392 g/kWh to 305 g/kWh with the power generation proportion of that decreased to 67.8%, which leads to 160.3 g CO₂/kWh of CO₂ mitigation. It can be seen that the increment of renewable share and energy saving of fossil fuel power plants play the similar role (nearly half to half contribution for total CO₂ emission reduction) for decarbonization of power sector in China in the past two decades. Due to the immaturity of CCUS technology, the contribution of it is negligible in the absence of domestic CCUS demonstration projects.

In addition, as renewable energy is expected to account for about 80% electricity generation ratio in 2060 [17, 18], which will definitely become the main contributor. At the same time, if the average coal consumption of thermal power plant declines to about 200-250 g/kWh in 2060 with around 20% electricity generation ratio, about 10-20% of the carbon emission intensity reduction of power system can be anticipated by improving energy efficiency. Finally, the left part of carbon emissions will be covered by CCUS technology on the scenario of carbon neutrality.

Indispensable role of CCUS in carbon neutral target

Due to the high reliance of carbonaceous energy in China and the instability and unsafety of high portion of renewable energy, it’s really difficult to imagine an energy system totally phasing out the utilization of carbonaceous energy over a long period of time, which means R will not be 0. Correspondingly, according to Eq. (13), it’s apparently that I_c could not reach 0 when R is not 0, only if K equals R, and naturally, the CCUS technology for both carbonaceous energy and carbon neutral energy is indispensable in achieving carbon neutral target. However, K_C and K_CN play the different role in power system reaching carbon neutral target.

Based on Eq. (11), the relationship of capture rates between fossil fuel (K_C) and biomass (K_CN) can be derived as follows in the carbon neutral scenario:

$${K}_{CN}=\frac{R}{1-R}-\frac{R}{1-R}{K}_C$$

(15)

K _C and K_CN represents the capture rates of carbonaceous energy and carbon neutral energy for an area or an energy system. On the basis of Eq. (15), Fig. 5 depicts the relationship between energy inputs and capture rates of different CO₂ capture technologies in the carbon neutral scenario. Considering that the typical or the optimized value of K_C for fossil fuel power plants is around 0.7 ~ 0.9 [23,24,25], K_C is adopted as a variable parameter with specific value of 0.7, 0.8 and 0.9 in the analysis. As shown in Fig. 5, with the increase of R, the ratio of K_CN / K_C increases dramatically as its growth rate increases under a specific K_C, which implies a much higher demand for negative emission technology if more coal fired power plants are deployed. The left side of Fig. 5 indicates the optimum area for CCUS retrofit under a comparatively lower capture rates. However, carbon neutrality is difficult to be achieved even with negative emission technology when R increases to a certain value (as shown in the shaded areas in Fig. 5), such as R > 0.9 under K_C = 0.9 condition, due to the unreachable value of K_CN (K_CN ≥ 0.9). Similarly, when K_C increases (less than 0.9), the demand of carbon neutral system for negative emission technology declines, and a higher proportion of carbonaceous energy can be input into energy system under carbon neutral scenario.

Fig. 5

The relationship between energy inputs and capture rates of different CO₂ capture technologies in the carbon neutral scenario

Challenge for CCUS

The rather high energy consumption and cost is widely recognized as the leading gap deterring the development and deployment of CCUS. In order to better understand the compositions of the energy consumption or cost of CCUS, the thermodynamic and economic analysis for the representative demonstration power plant will be conducted in this section.

The Boundary Dam Carbon Capture, Sequestration and Utilization (CCUS) facility is the world’s first industrial-scale post-combustion CCUS project [26]. It is located outside Estevan, Saskatchewan and commenced operations in October 2014. Thus, this section goes to give a detailed analysis of Boundary Dam to help understand the energy consumption and cost of CCUS. In May 2011, SaskPower retrofitted the existing plant and installed CO₂ capture facilities in this project. The total investment of the project is about $1.24 billion, of which 50% is for capture facilities, 30% for renovation of existing power plants, and about 20% for emission control and other facilities.

Table 1 summarizes the thermodynamic and economic performance of this project. As shown in Table 1, the system power generation efficiency can reach 37.8% after retrofitting without considering CCUS. However, a drop of 10.1-13.9% points of system efficiency will be caused after the installation of CCUS, decreasing to about 23.9-27.7%. It is obviously that the introduction of CCUS highly deteriorates the thermodynamic performance of the Boundary Dam. As the major energy penalty is caused by CO₂ desorption process, nearly accounting for 80% among CO₂ capture energy consumption, the large improvement of CO₂ separation process may be expected to reduce the efficiency penalty of CCUS to 5-8% points when the desorption energy consumption declines to 2-2.5 GJ/t CO₂ [28].

Table 1 Technical and economic analysis of the retrofitted Boundary Dam demonstration project [27]

Similarly, as indicated by Table 1, CO₂ capture cost reaches 100-130 $/t CO₂, which is unaffordable for the long-time operation. Fortunately, the considerable benefits of EOR (60.8 $/t CO₂) have helped the Boundary Dam survive successfully. Among CCUS full chain, the cost of CO₂ capture is undoubtedly the leading cause of the dilemma of Boundary Dam, accounting for around 90% of the total cost of CCUS. Thus, cutting down the energy consumption and cost of the CO₂ capture process may be the only way to rescue CCUS from the current dilemma.

Although the CO₂ capture cost of Boundary Dam is around 130 $/t-CO₂, as high as 67% cost reduction will be anticipated in the second demonstration project (Shand Power station) according to the pre-feasibility study of Saskpower with the technology progress [26]. In addition, as indicated by the roadmap issued by China in 2015 [29] and 2019 [28], the avoidance cost of the first-generation CO₂ capture technology, mainly post-combustion capture, is anticipated to be reduced to around 40 $/t CO₂ by 2030, mainly driven by the improvement of separation technologies and accumulation of engineering experience, etc.

Further, the challenges CCUS faces in achieving carbon neutrality also come from other low-carbon power generation technologies. Green Premium is a crucial indicator for evaluation of the cost of CO₂ avoidance of low-carbon technologies [30]. In power industry, the Green Premium for electricity amounts to the additional cost of getting all power in the grid from non-emitting sources like wind, solar, nuclear power, and fossil fuel plants equipped with carbon-capture technology over one that emits a greater amount of greenhouse gases. It can be calculated by the following equation:

$$GP=\frac{COE_{LC}-{COE}_C}{CE_C-{CE}_{LC}}$$

(16)

where GP refers to Green Premium, COE is the cost of electricity of the specific power generation technology, CE is the amount of CO₂ emissions, LC and C represent the low-carbon technology and carbon emission technology (reference case), respectively.

Take the current cost of low-carbon technologies in China as an example. Considering that the coal power plant is the most common and traditional power generation technology with great amount of carbon emissions in China, it is set as the reference case for the calculation of GP. Table 2 shows the costs of diverse power generation technologies in China. The data of COE comes from the report of IEA in 2020 [31], and the median value is adopted. The amount of CO₂ emission of coal power plants is around 800 g CO₂/kWh in 2020 according to Fig. 1, and 90% CO₂ capture rate is assumed for CCS. For solar and wind technologies, due to the large load fluctuations, energy storage technology is often needed to ensure its safe and stable operation. Assuming that when the annual energy storage capacity accounts for ~ 20% of the total electricity production [32,33,34], the stability of a fully-renewable power supply can be achieved. And the cost of energy storage is assumed to be 100 $/MWh [35]. Based on the above information and assumptions, the GP can be obtained following the Eq. (16), as shown in Table 2. The results show that half of renewable energies show obviously advantage in GP, due to the lower COE, even with considering the cost of energy storage technology. CCUS may not be competitive with most of the renewable energy technologies at present in China, even if it has lower GP than solar CSP and biomass. Thus, it is imperative to reduce the energy consumption and cost of CCUS technology under the carbon neutral scenario as soon as possible.

Table 2 Comparison of the costs of diverse power generation technologies in China (2020)

Time window for CCUS retrofitting is closing

With the fast development of renewable energy, the role of coal is being knocked out, especially in some developed countries. Figure 6a shows the trend of installed capacity of coal-fired power plants in China. The growth rate of that has decreased from > 10% between 2003 and 2008 to > 5% between 2008 and 2020 mainly due to market and the energy revolution policy mentioned by the Chinese Government in 2016 with the aims of achieving low-carbon and clean energy structure by adjusting the energy mix, reducing the energy consumption, innovating the energy technologies and strengthening the role of market. More seriously, the carbon neutral target proposed recently by Chinese government will undoubtedly accelerate the reduction of living space for coal power plants in the power industry.

Fig. 6

The installed capacity and service life of coal power plants in China

However, the coal power plants in China are still very young, much shorter than its service life, as shown in Fig. 6b. Currently, more than 80% of 300-400 MW (the largest proportion) coal-fired power plants have been in service for less than 20 years (most of them were put into operation after 2000). For the 500-999 MW units, no more than 5% are in service for more than 20 years. And the maximum service life of 1000 MW units is 12 years at present. In other words, there are 530 million kW units in China that have been in service for less than 10 years, and the proportion of units with service life of more than 30 years is less than 1.1%. By contrast, in the world, more than 24% of the coal power units have been in service for more than 30 years. Among them, the longest service life has reached more than 60 years. In some countries, more than 90% of coal power units have been in service for 30 to 60 years. Therefore, most of the installed capacity of coal power plants in China is still in the “youth” stage.

As China’s coal power units are still very young, most of them will still have a large residual value before 2030 ~ 2040, even considering a rather short designed life like 30 years. But facing the goal of carbon neutrality, most coal power plants will have to face two choices: (1) Forced to decommission, to be replaced by either renewable power or new coal power plants with CCUS; (2) Low-carbon retrofit. It’s obviously that retrofitting the original power station before decommissioning can extend its service life and save investment, compared with building new low-carbon power stations with lower energy penalty. In other words, almost all existing coal power units in China are bound to face the challenge of low-carbon retrofit, if power industry want to reduce the sunk cost. Under the goal of carbon neutrality, the critical time window for coal power plants to make choices will be around 2030 ~ 2040, which is also the peak for low-carbon retrofitting of coal power plants. Before the “window” closed, it is imperative to make CCUS ready for large scale deployment. If CCUS can be ready with competitive low energy consumption and cost compared with other low-carbon technologies, the coal power plant is anticipated to remain a certain amount of installed capacity with CCUS even until 2060. Otherwise, most of the retrofittable coal power plants in the youth stage will be forced to decommission.

Finally, some possible countermeasures can be anticipated to support the technology innovation of CCUS. The innovation of CCUS technology can be conducted from two aspects: the improvement of CO₂ separation technologies (mainly indicate the innovation of the first-generation of CCUS technology [28, 29]) and the exploration of new CO₂ capture technologies (mainly indicate the second-generation of CCUS technology [28, 29]). The rather high energy consumption of CO₂ separation technologies, like chemical absorption, causing even more than 10% points efficiency penalty. With the innovation of separation technology, the power system efficiency penalty is expected to be reduced to 5% points. In addition to the improvement of separation processes, the innovation of energy conversion methods can facilitate CO₂ separation or directly realize fully enrichment of CO₂ to avoid separation. From the systematic perspective, this technical direction can be referred to as source control technologies, which possess the following technical characteristics: (1) Different from the direct combustion in which 1/3 of fuel chemical exergy will be destructed, source control technology try to find new path to transform the chemical energy of fuel in cascade way. Just like polygeneration system [36,37,38,39] or chemical looping combustion [40, 41], the exergy destruction of fuel conversion will be reduced owing to the cascade utilization of chemical energy of fuel, which leads to improvement in efficiency of energy utilization; (2) and meanwhile, the carbon components will be partially (in polygeneration system) or fully concentrated (in chemical looping combustion), instead of being diluted by air. Concentration of CO₂ along with the fuel conversion will facilitate or even cancel the separation process; (3) and finally, the efficiency of source control system can profit from both efficient utilization of chemical energy of fuel and reduced energy consumption in separation. Finally, zero or even negative penalty for CO₂ capture can be expected.

Conclusions

This paper introduced the critical equation of carbon neutral for power system based on the carbon balance principle. According to the carbon-neutral equation, three technical approaches to achieve carbon neutrality are discussed, including improving energy efficiency, shifting energy structure and adopting CCUS technology. And the role of CCUS in achieving carbon neutral target is focused on in this paper. Some conclusions can be drawn as follows:

• (1) Building a carbon-neutral power system in the future requires a combination of energy efficiency, renewable energy and CCUS technology, nevertheless, the role of each approach will be different. For power systems that use fossil energy, CCUS technologies will be indispensable to achieve the goal of carbon neutrality. Considering the limitation of capture ratio, negative emission technology, like BECCS, will play the key role in neutralizing the carbon emission of power system with fossil fuel input.

• (2) The coal power plants in China are still “young”, and almost all the existing power plants are bound to face the challenge of CO₂ emission reduction. Under the goal of carbon neutrality, the critical time window for coal power plants to make choices will be around 2030 ~ 2040, which is also the peak for low-carbon retrofitting of coal power plants.

• (3) Compared with renewable energy, the costs of CCUS have fallen far less than expected. As the fossil fuel with CCUS and renewable energy are both the promising technologies in low carbon pathways, if the CCUS technology cannot make a breakthrough before the window closing, much more energy, environment and economic penalty will be paid for coping with the climate change.

• (4) Carbon neutral scenario may be the last chance for CCUS to get a foothold in the future emissions-reduction portfolio. Greatly reducing the energy consumption and costs of CCUS technology by accelerating the innovation of new-generation capture technology may be the breakthrough point for CCUS.