Optimal reaction pathways of carbon dioxide hydrogenation using P-graph attainable region technique (PART)

Abstract

The attainable region interpretation of the thermodynamic principles has indicated that carbon dioxide (CO₂) can be either hydrogenated directly to form dimethyl ether (DME) or gasoline. The process that converts CO₂ to DME is more thermodynamically favourable at lower temperature. A certain thermodynamic temperature range (25 to 300 °C) is suggested for the conversion of CO₂ to DME via a methanol intermediate pathway without addition of work. Optimal synthesis routes derived from P-graph's mutual exclusion solver were compared with reactions reported in literature and showed great correlation. The reactions collectively possess Gibbs free energy of less than zero, and negative enthalpy of reaction. With P-graph attainable region technique, the case studies have demonstrated that the synthesis of DME and gasoline using CO₂ hydrogenation via methanol intermediate and carbon monoxide intermediate from Fischer–Tropsch synthesis is feasible with no work and heat requirement. Both case studies have demonstrated visual advantage of P-graph and data-driven applications. The benefit of integrating the P-graph framework with machine learning model like decision tree classifier was also demonstrated in the second case study as it solves topological optimisation problems without scaling constraints.

1 Introduction

Carbon capture, sequestration and utilisation techniques were driven by the urgent need to reduce net carbon dioxide (CO₂) emissions. If the advantages of CO₂ utilisation outweigh the costs of carbon capture and sequestration, large-scale carbon capture and utilisation techniques may be feasible. In recent years, there has been a lot of interest in the catalytic methods of using CO₂ as a carbon source for the synthesis of fuels such as methanol or dimethyl ether (DME) [1]. In addition, research on catalysis for CO₂ hydrogenation to single-carbon (C₁) products has advanced significantly. Significant advancements have recently been made in the heterogeneous catalytic hydrogenation of CO₂ to a variety of highly valuable and readily available fuels and chemicals that contain two or more carbon atoms (C₂₊), such as DME, olefins, liquid fuels, and higher alcohols [2]. Due to the extreme inertness of CO₂, high C–C coupling barrier and the numerous competing reactions, the synthesis of C₂₊ products is more difficult than that of C₁ products [3]. The insights on CO₂ hydrogenation to C₂₊ products are required to facilitate researchers working in this field.

In general, methanol or a Fischer–Tropsch synthesis (FTS) is used to hydrogenate CO₂ into C₂₊ compounds [4, 5]. The dehydration of methanol can serve as the foundation for the large-scale manufacture of DME. Methanol is transformed into DME by an acid catalyst following a purification stage in a later reactor [6]. Two consecutive reactions can be coupled over a bifunctional catalyst to achieve methanol reaction-based CO₂ hydrogenation. Through a carbon monoxide (CO) or formate route, CO₂ and hydrogen (H₂) can be transformed to methanol [7]. Methanol is then coupled over zeolites or alumina, dehydrated, or both [3]. Hence, methanol synthesis catalysts and methanol dehydration or coupling catalysts are combined to form bifunctional or hybrid catalysts, which may convert CO₂ into high-value C₂₊ chemicals like DME and hydrocarbons [8]. As a result of CO₂ hydrogenation using FTS, liquid fuels like gasoline and diesel as well as other compounds with added value like aromatics and isoparaffins can also be produced [9]. To optimise the yield of C₂₊ generated, CO₂ hydrogenation should ideally take place close to equilibrium, such as under high pressure or at lower temperatures settings [10]. More CO₂ and H₂ are used by the reverse water gas shift (RWGS) reaction when the temperature is high [11]. However, this might lead to the rise in H₂O concentration which inhibits the production of desired products for both thermodynamic and competitive adsorption reasons. The direct approach is still being tested non-commercially at research facilities up to pilot demonstration scale [12]. Therefore, the current focus is directed towards the conversion of CO₂ on a large scale, and consequently a better comprehension of this conversion from a thermodynamic point of view is needed in order to establish appropriate reaction conditions.

The attainable region (AR) is referred to as the collection of all outcomes that are feasible for the system under study and are compatible with all of the system’s restrictions when they are reached utilising the system’s core mechanisms [13]. Glasser et al. [14] has demonstrated how a geometrical method may be used to identify this zone for reaction and mixing. For constant flow reactors, the AR was initially discovered in a two-dimensional concentration space [15]. The AR has been expanded to processes instead of only reactors [16]. Patel et al. [16] provided details on the feed and a list of potential product species. Following the determination of the set of independent material balances from this, the AR was discovered in the space of reaction extents [17]. According to Sempuga et al. [18], this area reflects the set of all potential outputs from all feasible processes and can be informational in discovering and synthesising desirable products. Phase transitions in a CO₂ conversion system may be built and optimised with the use of the AR approach. High-level design process flow sheets that depict the thermodynamically possible maximum have been created using this method [19]. The resultant process flow sheets operate as closely to reversibility as feasible while efficiently converting raw materials into desired products [13]. The AR is bounded in the space of reaction extents after a number of separate material balances are calculated. This area can be helpful in locating desirable processes since it represents the set of all potential outputs from all potential processes [20]. The AR is also known as the Gibbs free energy-Enthalpy attainable region (G–H AR) and may be discovered in the space of enthalpy of formation versus Gibbs free energy [21].

To display the direction of speciation in the AR space, the Gibbs free energy minimisation method can be used [22]. These AR diagrams may be thought of as forecasting instruments that provide information on catalyst speciation in the reactor under any particular circumstance [23]. Finding the ideal conversion condition requires understanding how the reaction is impacted by variations in Gibbs free energy under various conditions [24]. G–H AR can specify the heat and work requirements for all feasible reaction processes in a Gibbs free energy-Enthalpy (G-H) space after obtaining mass balance attainable region (MB AR) [20].

The P-graph framework’s material and operational node sets are defined through workflow modelling (Figure A1). Maximal structure generation (MSG) and solution structure generation (SSG) are the names of the algorithms that carry out these actions [25, 26]. The accelerated branch-and-bound (ABB) technique may also be used to generate the optimal network utilising the P-graph structure [27]. In general, P-graph is an excellent substitute for mathematical programming because its algorithmic framework eliminates the risk of formulation error [28]. It has recently been combined with the attainable region technique [29]. P-graph Studio is an online software implementation of this computing framework (http://p-graph.org/) [30]. A framework which introduces the integration of machine learning algorithms in P-graph was developed by Teng et al. for process network synthesis (PNS) and network topology optimisation [31].

It should be noted that there has not been any research done yet using P-graphs to depict optimal reaction pathways of CO₂ hydrogenation. Therefore, this study is designed to address this research gap by determining optimal reaction pathways for conversion of CO₂ to C₂₊ products using P-graph attainable region technique (PART). For PART, the AR technique was first used to determine possible chemical pathway with complete raw material consumption and zero CO₂ emissions. Other process paths that adhere to these standards and use various chemical component combinations are yet to be developed. In addition, even if AR determines a region for all potential reaction paths, not every pathway is ideal. P-graph is therefore integrated into the framework to produce optimal reaction points in the feasible region [29]. Two case studies in this work which investigate CO₂ hydrogenation via methanol and CO intermediate used PART to derive the optimal and sub-optimal reaction pathways.

The reaction of CO₂ hydrogenation to produce octane is a complex process that involves multiple steps and parameters [2]. The reactant concentrations of CO₂ and H₂ concentrations in the feedstock, and any other reactants or co-reactants that may be used are difficult to determine based on thermodynamic attainable region approach due to greater degrees of freedom [32]. Therefore, this PART framework helps predicting the amount of octane produced, as well as any other products that may be formed, such as water (H₂O), methane (CH₄), or other hydrocarbons present in the reaction system. The technique outlined in this study for identifying the best thermodynamic conditions for CO₂ hydrogenation is based on the measurement of minimum Gibbs free energy at various temperatures. Predicting the ideal temperatures at ambient pressure for the chosen phase should be possible using the results of this thermodynamic analysis.

The aim of this work is to present the usability of PART in determining optimal and sub-optimal pathways based on process constraints like complete material consumption to reduce CO₂ emissions as well as increasing the economic viability of the process. This study also aims to present the visualization of network synthesis problem in graph structure and allowed for manual modification in P-graph studio using hydrogenation of CO₂ to produce DME and gasoline as case studies.

To demonstrate the reliability of PART in finding optimal reaction pathways, this paper presents two case studies. For the first case study (methanol-based CO₂ hydrogenation) which has less components with lower degrees of freedom, the optimal pathways derived from PART are compared to reported reactions in literature. The second case study (FTS-based CO₂ hydrogenation) which has higher degrees of freedom is demonstrated to show how P-graph with embedded machine learning models may be directly applied to find optimal reaction pathways accurately.

2 Methods

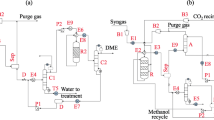
Due to the limited technical readiness of majority of CO₂ conversion processes, this study intends to give a more pedagogical thermodynamic analysis of certain CO₂ conversion chemical pathways (Fig. 1). Thermodynamic analysis was conducted on a CO₂ hydrogenation reaction system to produce DME and gasoline. Finally, in order to achieve complete CO₂ consumption, a constraint of zero CO₂ flowrate in final product stream is emphasized.

Fig. 1

Application flow of P-graph Attainable Region Technique (PART) in this study

Therefore, utilising the thermodynamic characteristics of Gibbs free energy and enthalpy at a certain temperature and pressure, the G-H AR may be generated from the MB AR. The feed composition is obtained from the AR, and the optimal and nearly optimal reaction paths are produced using the P-graph. Based on material, energy, and work balances, the strategy entails selecting the right combinations of species that react in order to optimise the intended result [24]. Hence, creating a CO₂ reaction network and even construction of a conceptual process design would offer many routes for producing the desired products.

2.1 Creating MB AR in the extent of reaction space

The matrix containing the stoichiometric coefficients of the independent material balances that depict the process or reaction system is referred to as v in Eq. (1), where N is the amount of substances in the system, and j represents the number of independent material balances for the reaction [33].

$$\bf v=\left(\begin{array}{ccc}{\mathrm v}_{11}& \dots .& {\mathrm v}_{\mathrm {1N}}\\ \vdots & \ddots & \vdots \\ {\mathrm v}_{\mathrm {j1}}& \cdots & {\mathrm v}_{\mathrm {jN}}\end{array}\right)$$

(1)

The following equations shown in Eqs. (2, 3, 4, 5) provide the moles of each component at any time throughout the reaction [33].

$${{\text {n}}_{\text {i}}}={{\text {n}}}_{\text {i}}^{\circ }+{\text {v}}^{\text {T}} \mathbf \upepsilon$$

(2)

$$\mathbf \upepsilon = \left[ {\begin{array}{*{20}c} {\upepsilon_{1} } \\ \vdots \\ {\upepsilon_{2} } \\ \end{array} } \right]$$

(3)

$$\mathrm{N}=\left[\begin{array}{c}\begin{array}{c}{\mathrm{n}}_{1}\\ \vdots \end{array}\\ {\mathrm{n}}_{\mathrm{N}}\end{array}\right]$$

(4)

$${\text{n}}_{{\text{i}}}^{^\circ } = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{n}}_{1}^{^\circ } } \\ \vdots \\ \end{array} } \\ {{\text{n}}_{{\text{N}}}^{^\circ } } \\ \end{array} } \right]$$

(5)

where i is the component in reaction j, AR was plotted by determining the column vector of extents (ε) to which a j reaction is taking place, N is the column vector of number of moles at extent j, ${\mathbf{n}}_{\mathbf{i}}^{^\circ }$ is the column vector of initial moles of components, and v^T is the transposition of the stoichiometric matrix v of the size ($\mathrm{j}\times \mathrm{N}$).

To depict the AR for a particular feed of CO₂ and H₂, a set of extents where the number of moles of each component is greater than or equal to zero (${\mathbf{n}}_{\mathbf{i}}\ge 0$) needs to be determined. The inequality is expressed in Eq. (6) [24].

$$\mathbf{Ax}\ge \mathbf{b}$$

(6)

where x represents the set of extents (ε), b denotes ${\mathbf{n}}_{\mathbf{i}}^{^\circ }$ in the form of negative, and matrix can be represented in Eq. (7) [24].

$${\mathbf{A}}\;{ = }\;{\mathbf{vx}}^{{\mathbf{T}}}$$

(7)

where v is the matrix containing the stoichiometric coefficients of the independent material balances, and x^T is the transposition of the set of extents.

This enables the plotting of AR as well as examining scenarios where alteration and evaluation of various feeds can be performed. 2D and 3D plots were illustrated to display the closed convex areas of two and three separate mass balances from methanol reaction-based CO₂ hydrogenation and FTS-based CO₂ hydrogenation, respectively.

2.2 Constructing AR in a G-H space

Using the Gibbs free energy and enthalpy at a certain temperature and pressure, the G-H AR (or AR in a G-H space) may be created from the MB AR. The MATLAB algorithms used to generate the AR plots in Figs. 2, 3, 4, and 9 are included in Supplementary Information (A1).

Fig. 2

Change in MB AR in extent space for a feed 1 mol CO₂ when the H₂ supplied is increased, a 0.5 mol, b 1 mol, c 2 mol, d 3 mol

Fig. 3

G-H AR for the DME synthesis system at 25 °C

Fig. 4

G-H AR for DME synthesis system at higher temperatures of: (a) 25 °C, (b) 200 °C, (c) 300 °C, (d) 400 °C, (e) 500 °C, (f) 600 °C

Enthalpy and Gibbs free energy, respectively, reflect the lowest energy needs of the process or reaction and the work potential of the process. Negative numbers of these energies indicate that work and energy are discharged from the process, whilst positive values indicate that effort and energy must be given to the process. Brinkley provided the first algorithm for computing the equilibrium state of a multicomponent system numerically [34]. The approach was based on the stoichiometric approach, which involved assessing equations for the equilibrium constants of the reactions.

The first step of the stoichiometric method is to calculate the heat generated in thermodynamic equilibrium conditions for a given reaction. The reaction properties of standard enthalpy (${\Delta \text{H}}_{ }^{0})$ and standard enthalpy (${\Delta \text{G}}^{0}$) which are varied with different temperature settings (T) in a function of universal gas constant (R) and equilibrium constant (K) can be represented in Equations (A1) and (A2) [1]. Hence, the enthalpy of formation (${\Delta \text{H}}^{0}$) and Gibbs free energy (${\Delta \text{G}}^{0}$) were derived from ${\Delta \text{H}}_{ }^{0}$ and ${\Delta \text{H}}_{ }^{0}$ of various species from Equations (A3) and (A4) [20]. This can be generalised for species i in reactions j in Equations (A5) and (A6) [13].

To estimate the values of aH and aG for the combined process, various reaction extents are considered concurrently with the enthalpy and Gibbs free energy at optimal reaction temperature obtained from G-H AR. The aH and aG for the combined process on each substance were validated using Hess’s law, which stipulates that heat released or absorbed in a chemical process is equal whether the process occurs in one or multiple phases [15]. The following sections present the specific methodology for case study 1 [Sect. (2.3)] and 2 [Sect. (2.4)].

2.3 Case study 1: methanol-based CO ₂ hydrogenation

2.3.1 Stoichiometric material balance

The five chemical species involved in this case study are DME (CH₃OCH₃), CO₂, H₂O, H₂, and methanol (CH₃OH). In this study, the matrix algebra technique created by [35] to identify separate reactions was applied. The system is set up as a matrix function (Table 1), and Gaussian elimination is used to discover the independent material balances (Table 2). This is done by making all other entries zero and attempting to get a single ‘‘1’’ in each column (in any row, but not the same row). The independent reactions in Table 2 are the balance equations involving each component in the reaction system which equals to the corresponding amount of atoms “C”, “H”, and “O” indicated in the left columns.

Table 1 Atomic matrix form of the DME synthesis compounds

Table 2 Independent material balances for DME production by using gaussian elimination

2.3.2 Changes in temperature on G-H AR Plot

Changes in operational circumstances and their impact on the G-H space for a single reaction was used to show how the operational factors, such as temperature and pressure, affect a reaction. This demonstrates how temperature fluctuation at constant pressure is impacted by various enthalpy and Gibbs free energy values. The performance of the methanol synthesis process at the ambient conditions of 25 °C and 1 bar and reported reaction temperatures was demonstrated using the temperature range of 200–600 °C.

The changes in enthalpy ($\Delta \text{H}$) and changes in Gibbs free energy ($\Delta \text{G}$) in regard to the respective extents of the two separate material balances under the specified parameters of temperature and pressure were represented in Equations (A7) and (A8), respectively [24]. From Equations (A7) and (A8), a linear relationship will be obtained for each of the chemical species. Therefore, the limits of each species involved in the reaction can be analysed in a G–H space using Equations (A9) and (A10). The G-H diagram shows the areas in the AR where heat may be added to or released from [24].

2.3.3 P-graph for optimal pathways prediction

The method is based on describing the system using Gibbs free energy-based work, heat, and elemental mole balances. The input of the raw material node is the feed of the reactions. Process edges were used to create the elemental constituents of the raw material (for example, for CO₂, the edge produces 1 atom of C and 2 atoms of O connected to the elemental nodes) is used to create the product component. The same process edge was utilised to estimate the side products of the process, with the input nodes serving as the elemental nodes and the output node serving as the side product. A constraint of zero side products was set to enable maximum flowrate of desired product.

The system’s heat balance was represented as intermediate nodes with values of standard enthalpy of formation and Gibbs free energy of each component. The flowrates of the intermediate nodes denoted the system’s overall changes in enthalpy and Gibbs free energy, which provided information of the reaction’s spontaneity and amount of heat released or required. Setting specific information in the process nodes served as a representation of the limitations and optimisation goal in the process. In this case, by setting the flow rate of the CO₂ side product node to zero, the limitation of CO₂ formation in the final product was imposed. By establishing an arbitrary price for DME, the goal of maximising product selectivity and CO₂ consumption was achieved using ABB algorithm in P-graph studio.

2.4 Case study 2: FTS-based CO ₂ hydrogenation

2.4.1 Stoichiometric material balance

Gasoline-range hydrocarbons have a high octane number [36]. Therefore, gasoline is represented by octane in this case study for theoretical analysis since octane has thermodynamic data for Gibbs free energy and enthalpy of formation that is readily available. The thermodynamic data was required to perform minimal Gibbs free energy calculations to determine the AR of the process. Similar to the case study of methanol reaction-based hydrogenation, 1 mol of CO₂ (${\mathrm{N}}_{\mathrm{o},{\mathrm{CO}}_{2}}$) with H₂ (${{\mathrm{N}}_{\mathrm{o},{\mathrm{H}}_{2}})}$which varied between 0 and excess were assumed to be converted into products.

The six chemical species in the FTS system under study are gasoline (C₈H₁₈), CO₂, H₂O, H₂, CO, and CH₄. The system was set up as a matrix function (Table 3), and Gaussian elimination was used to determine the independent material balances (Table 4).

Table 3 Atomic matrix form of the gasoline synthesis compounds

Table 4 Independent material balances for gasoline production by using gaussian elimination

2.4.2 G-H attainable region at ambient temperature

Plotting the total Gibbs and enthalpy values for H₂O, H₂, and CO, CH₄, and C₈H₁₈ revealed the points where all the product species are less than 0. Since the thermodynamic data of CO is unavailable at other temperature besides 25 °C, the effect of higher temperatures on G-H attainable region for this reaction is not demonstrated in this case study.

Stoichiometric balance of the chemical species performed helped determining the point at which the molar flow rate in the reactor is higher than or equal to zero. This enabled the establishment of a linear relationship for the corresponding species for various feeds. Therefore, a linear relationship that satisfied the requirements of the G-H ARs for each of the species (CO, CH₄, CO₂, H₂, H₂O, and C₈H₁₈) was plotted by eliminating extents (ε₁, ε₂, and ε₃) and number of moles for each of the species in terms of the enthalpy and Gibbs free energy determined for the combined process. A G-H plot was then used to show the final enthalpy and Gibbs free energy limits for each species in the overall process [21].

2.4.3 Molar composition profile with changes in temperatures

Chemical equilibrium can be solved numerically using stoichiometric or non-stoichiometric techniques. Non-stoichiometric methods directly minimise the Gibbs free energy of formation of chemical species to solve reaction equilibrium, with the functions being bound by mass balance equations, whereas stoichiometric method converge on the solution of a set of material balance equations [37].

The stoichiometric approach which requires the information of equilibrium constant to determine values of Gibbs free energy and enthalpy of each species at certain temperature as described in Sect. 2.2 is applicable for this case study at ambient temperature. However, for reactions that contain species with incomplete equilibrium data at temperatures other than ambient settings like this case study, the Gibbs free energy minimisation approach demonstrated in this section can be used to assess the molar composition of species under higher temperatures.

The goal of this method is to identify the set of n_i (amount of substances of each component in the overall reaction) that minimises Gibbs free energy for given temperature and pressure within the restrictions of the material balance. The formulas that govern for Gibbs free energy minimisation are described by Abbott et al. [38]. A single-phase system’s overall Gibbs free energy (${\mathrm{G}}^{\mathrm{t}}$) based on temperature (T) and pressure (P) is provided in Equation (A11). The approach of Lagrange’s indeterminate multipliers was used to solve the Gibbs free minimisation problem (Equations (A12)–(A16)). The constraining material balance equations can be produced as the total amount of atoms in each element is constant [39]. If the standard Gibbs free energy for species i (${\mathrm{G}}_{\mathrm{i}}^{0}$) is arbitrarily set equal to zero for all elements in their standard states, then for any compound, ${\mathrm{G}}_{\mathrm{i}}^{0}$ is equivalent to the standard Gibbs free energy change of formation for species i (${\Delta {\text{G}}_{\mathrm{fi}}^{0}})$ [1]. The equation governing chemical equilibrium at constant pressure is denoted in Equation (A17). Gibbs free energy of formation of any components (${\Delta \text{G}}_{\mathrm{fi}}$) at varying temperatures can be expressed using the Gibbs–Helmholtz equation in Equation (A18) [40]. Hence governing equations for reactive species can be represented using Equations (A19) and (A20) [40].

There are now nine non-linear equations and nine unidentified variables (${\mathrm{n}}_{{\mathrm{CO}}_{2}},{\mathrm{n}}_{{\mathrm{H}}_{2\mathrm{O}}},{\mathrm{n}}_{{\mathrm{H}}_{2}},{\mathrm{n}}_{\mathrm{CO}},{\mathrm{n}}_{{\mathrm{CH}}_{4}},{\mathrm{n}}_{{\mathrm{C}}_{8}{\mathrm{H}}_{18}},\mathrm{\lambda_{C}},\uplambda_{H},\mathrm{ and \, \lambda_{O}}$) to be solved. Isqnonlin function in MATLAB was used to solve nonlinear least-squares curve fitting problems in Equation (A19) of each species. The equations were solved by determining the minimum of constrained nonlinear multivariable function. Constrained minimisation determines vector x that is a local minimum to a scalar function f(x) subject to constraints. The minimum of the problem was specified by Eq. (8) [41].

$$\mathrm{minf}\left(\mathrm{x}\right) \left\{\begin{array}{c}\mathbf{k}(\mathbf{x})\le 0\\ \mathbf{keq}\left(\mathbf{x}\right)=0\\ \begin{array}{c}\mathbf{A}\bullet \mathbf{x}\le \mathbf{b}\\ \mathbf{Aeq}\bullet \mathbf{x}=\mathbf{beq}\\ \mathrm{lb}\le \mathrm{x}\le \mathrm{ub}\end{array}\end{array}\right.$$

(8)

where, k(x) and keq(x) are the functions that return vectors, b and beq represent the vector components, A and Aeq are the matrices, lb and ub are the lower and upper boundary respectively, and f(x) is a function that returns a scalar. f(x), k(x), and keq(x) can be nonlinear functions.

2.4.4 Data retrieval for machine learning derived P-graph

A dataset is required to train the decision tree classifier for predicting the presence of CO₂ in product stream depending on the amount and types of reactants used. The dataset of all possible reactions of hydrogenation of CO₂ with C₈H₁₈ as the target product was created using a reaction network model developed by McDermott et al. [42] with imported thermodynamic data for each chemical species involved from Materials Project, which is an open-access database. However, the possible sets of all pathways required manual inspection to ensure C₈H₁₈ is formed as the main product.

The C-H–O chemical system’s phases were first obtained from the database. The collection of all N phases p_i(i = 1, 2,…, N) that may be created from a specific set of chemical components is referred to as the chemical system in this context. In order to generate each reactant or product node on the graph, different phase combinations up to a maximum size, n, were taken into account. The collection of all nodes, P can be produced by Eq. (9) [42].

$$\mathrm{P}=\left\{{\mathrm{p}}_{\mathrm{i}}|\mathrm{i}\le \mathrm{N}\right\}$$

$$\cup \left\{{\mathrm{p}}_{\mathrm{i}}+{\mathrm{p}}_{\mathrm{i}}|\mathrm{i},\mathrm{j}\le \mathrm{N};\mathrm{i}\ne \mathrm{j}\right\} \cup \dots \dots$$

(9)

$$\cup \left\{{\mathrm{p}}_{\mathrm{i}}+{\mathrm{p}}_{\mathrm{j}}+\dots {\mathrm{p}}_{\mathrm{n}}|\mathrm{i},\mathrm{j}\dots \mathrm{n}\le \mathrm{N};\mathrm{i}\ne \mathrm{j}\dots \ne \mathrm{n}\right\}$$

The chemical reactions were combined via mass conservation. Reaction steps discovered via pathfinding can be linearly coupled to fulfil the stoichiometric mass limitations of the overall reaction when a net reaction is known from the beginning. When the linear system of equations provided by is numerically solved, these restrictions translate to Eq. (10) [43].

$$\mathbf{Am}=\mathbf{c}$$

(10)

where c is a vector containing the stoichiometric coefficients of the net synthesis reaction, m is a vector containing the multiplicity of each reaction (i.e., the factor by which the entire reaction is multiplied), and A is the matrix that included the stoichiometric coefficients of all phases that are present in all reactions where reactants/products have negative/positive coefficients, respectively.

This set of equations was solved using a matrix pseudoinverse in the SciPy package for the multiplicity vector, m [44]. An enumerator algorithm in Supplementary Information (A2) was used to retrieve all possible reactions which involved C₈H₁₈ as the main product. The downloaded computed structure entry objects from the Materials Project’s database can be automatically transformed into Gibbs computed entry objects, where all entries’ Gibbs free energies of formation, have been derived from AI-estimated equivalent values based on DFT-computed energies for all entries at the specified temperature [45]. The Gibbs entry set class provides a function which automatically eliminates entries that have a given energy per atom above the convex hull of stability. There were several enumerator classes used to find all possible reactions in a collection of entries, and to find all open reactions inside a group of entries and a list of specified open entries or elements [46].

All reactions within a set of entries can be determined by minimising the Gibbs free energy between a pair of reacting phases that are interacting at an interface using a thermodynamic technique. To identify all predicted responses inside a set of entries, the grand potential between a set of two reacting phases engaging at an interface with an open element was minimised. The basic enumerator class accepts a variety of inputs to enable output customisation. In this case, CO₂ is listed as the precursor, and C₈H₁₈ is the target product. The algorithm only considers reactions whose reactants are a subset of the list of precursors and eliminate unbalanced reactions. Therefore, every reaction predicted is stoichiometrically balanced. The minimise enumerators build reactions by reducing the free energy using thermodynamic methods rather than only utilising a combinatorial approach. This suggests that reactions start out as a new convex hull uniting two compositions inside either a closed (Gibbs) or open (Grand Potential) system on the compositional phase diagram [47].

All initial reactions produced by the minimise enumerators must have a negative reaction energy and produce a set of product phases that are stable with regard to one another. These requirements are imposed on the minimise enumerators. However, these enumerators will also provide the opposite (positive energy) response if they are allowed to operate without restrictions. Therefore, a constraint of minimisation of great potential (Φ) is set to prevent enumerators for generating positive energy response Eq. (11) [48].

$$\phi = G - \mu_{i} N_{i}$$

(11)

where G is the Gibbs free energy of the species, i is an open species with a molecular quantity (N_i) and chemical potential (μ_i).

The potential reaction paths that incorporate interdependent reactions found from the procedure above were then used to train a decision tree classifier to determine gasoline product stream with or without the presence of CO₂ in final product stream with P-graph. The correlation between variables within a dataset for this case study is presented in a pairwise plot in Supplementary Information (A6).

2.4.5 Decision tree classifier and P-graph generation for optimal pathways prediction

Questions that divide into subnodes are contained in the root (raw material) and decision (intermediate) nodes. The highest decision node is all that the root node is. In other words, it is the point at which the classification tree traversal begins. The terminal nodes are nodes that do nor divide into more nodes which represent the product nodes in this case. Classes are assigned by majority voting in leaf nodes. The entropy of the distribution across classes is known as cross-entropy [49]. In order for the trees to be absolutely positive about which class each leaf belongs to, the entropy over the classes should be minimised, a highly spikey distribution in the classes, where it’s predominantly one class and fewer of the others is preferred. Finding the attribute that yields the largest information gain (i.e., the branches with the most homogenous branches) is the key to building a decision tree. The impurity criterion (${\mathrm{H}}_{\mathrm{CE}}$) equation of the decision tree used is shown in Eq. (12). The information gain ($\mathrm{IG}$) can be calculated using Eq. (13) [50].

$${\mathrm{H}}_{\mathrm{CE}}\left({\mathrm{X}}_{\mathrm{m}}\right)=-\sum_{\mathrm{k\epsilon y}}{\mathrm{p}}_{\mathrm{mk}}\mathrm{log}({\mathrm{p}}_{\mathrm{mk}})$$

(12)

where ${\mathrm{X}}_{\mathrm{m}}$ is the observations in node m, $\mathrm{y}$ is the classes, and ${\mathrm{p}}_{\mathrm{m}}$ is the distribution over classes.

$$\mathrm{IG}\left({\mathrm{D}}_{\mathrm{p}},\mathrm{f}\right)=\mathrm{I}\left({\mathrm{D}}_{\mathrm{p}}\right)-\frac{{\mathrm{N}}_{\mathrm{left}}}{\mathrm{N}}\mathrm{I}\left({\mathrm{D}}_{\mathrm{left}}\right)-\frac{{\mathrm{N}}_{\mathrm{right}}}{\mathrm{N}}\mathrm{I}\left({\mathrm{D}}_{\mathrm{right}}\right)$$

(13)

where f is the feature split on, ${\mathrm{D}}_{\mathrm{p}}$ is the dataset of the parent node, ${\mathrm{D}}_{\mathrm{left}}$ is the dataset of the left child node, ${\mathrm{D}}_{\mathrm{right}}$ is the dataset of the right child node, I is the impurity criterion, N is the total number of samples, ${\mathrm{N}}_{\mathrm{left}}$ is the number of samples at left child node, and ${\mathrm{N}}_{\mathrm{right}}$ is the number of samples at right child node.

The trained decision tree classifier is shown in Supplementary Information (A5). An open-sourced P-graph python library developed by Teng et al. [31] was utilised to specify the problem network in a graph structure. The P-graph initialization function then accepts the solver information, which includes problem network, the solver type, the maximum number of solutions, and the mutual exclusion list, as an input. The backend P-graph solver is activated by the run function, which reads the solution from initialised objects. The algorithms used to gather data used in this case study as well as the generation of P-graph with embedded decision tree classifier algorithm are included in Supplementary Information (A2) and (A3), respectively.

The problem network was exported to P-graph studio after problem setup which was used to initialize the network problem solving in P-graph. For manual editing in the P-graph file, the feed of the reactions was added to the input of the process nodes and an arbitrary operating cost was set for the stream with CO₂ product so that solver chooses product stream with complete CO₂ consumption. An arbitrary cost of 0.001 EUR/g was set at the product nodes. The P-graph generated by machine learning contains intermediate nodes which represent the branches of the decision tree model leading to the process with highest economic value.

2.4.6 Identification of reaction pathways predicted by machine learning

In P-graph studio, all potential reactant species in the system (CO₂, CO, H₂) were added as raw material nodes connected to the input of the machine learning-derived intermediate nodes “C”, “H”, “O”, “dH”, and “dG”. It should be noted that the product nodes derived were only gasoline-rich stream. The exact moles of final products were determined by adding a set of product nodes which contain all the side and desired products from the reaction (“CO”, “H₂O”, “CH₄”, “C₈H₁₈”). The moles of final products were defined via elemental or stoichiometry balances and the changes in enthalpy and Gibbs energy were also calculated by P-graph using Eqs. (12, 13).

3 Case studies

3.1 Case study 1: methanol reaction-based CO₂ hydrogenation

Attributing to its physicochemical characteristics, DME as one of the compounds produced from methanol, can be used as fuel [51]. It is also a crucial chemical step in the synthesis of light olefins and petrol and is comparable to liquefied petroleum gas with minimal emissions of NOx, SOx, and particles [52].

The procedure described here to generate the MB AR is comparable to that derived by Okonye et al. for the synthesis of methanol [21]. The first step in configuring the MB AR for the CO₂ hydrogenation system is to generate three potential material balances, as shown by Eqs. (14, 15, 16), and then determining the desired products for a system incorporating these material balances under various circumstances. The reactions occurring throughout the CO₂ hydrogenation process have usually been defined by the three material balances according to literature, which are two-step synthesis of DME which consists of CO₂ hydrogenation [Eq. (14)] and methanol dehydration to DME over the acid function [Eq. (15)], and direct hydrogenation of CO₂ [Eq. (16)] [3].

$${\mathrm{CO}}_{2}+{3\mathrm{H}}_{2}\to {\mathrm{CH}}_{3}\mathrm{OH}+{\mathrm{H}}_{2}\mathrm{O}$$

(14)

$$2{\mathrm{CH}}_{3}\mathrm{OH}\to {\mathrm{CH}}_{3}{\mathrm{OCH}}_{3}+{\mathrm{H}}_{2}\mathrm{O}$$

(15)

$$2{\mathrm{CO}}_{2}+{6\mathrm{H}}_{2}\to {\mathrm{CH}}_{3}{\mathrm{OCH}}_{3}+{3\mathrm{H}}_{2}\mathrm{O}$$

(16)

There were two key considerations being taken into account in this case study, where the thermodynamic analysis assesses all three reactions simultaneously, and all species were combined in a single vapour phase. To assess the theoretical temperature effect on these reactions from a qualitative standpoint, high-temperature ranges were investigated. Comparisons between the predicted reaction pathways and the reactions given in the literature were made.

3.2 Case study 2: FTS-based CO₂ hydrogenation

FTS-based CO₂ hydrogenation may be achieved in either one or two reactors. Attributing to its simplicity of implementation and hence reduced cost of CO₂ conversion, the direct one-reactor conversion method has received considerable interest. This method combines the hydrogenation of CO into hydrocarbons via the FTS reaction with the conversion of CO₂ to CO via the RWGS reaction [53]. Under identical circumstances, an effective catalyst should be active for both RWGS and FTS, which commonly correspond to light olefins, liquid fuels, and higher alcohols. The researchers are interested in a system with a feed of CO₂ and H₂, which resembles the hydrogenation process in FTS to produce liquid fuels [54]. Therefore, this section explores the synthesis of gasoline from FTS-based CO₂ hydrogenation with PART technique. The chemical formula for gasoline can be approximated as C₈H₁₈ (n-octane) [55]. There are four common material balances of the system, namely direct CO₂ hydrogenation [Eq. (17)], RWGS reaction [Eq. (18)], methanation [Eq. (19)], and FTS as the final step [Eq. (20)] [3].

$$8{\text{CO}}_{2} + 25{\text{H}}_{2} \to {\text{C}}_{8} {\text{H}}_{18} + 16{\text{H}}_{2} {\text{O}}$$

(17)

$${\mathrm{CO}}_{2} + {\mathrm{H}}_{2} \to \mathrm{CO }+ {\mathrm{H}}_{2}\mathrm{O}$$

(18)

$$\mathrm{CO }+ {3\mathrm{H}}_{2}\to {\mathrm{CH}}_{4} + {\mathrm{H}}_{2}\mathrm{O}$$

(19)

$$8\mathrm{CO }+ {17\mathrm{H}}_{2} \to {\mathrm{C}}_{8}{\mathrm{H}}_{18} + {8\mathrm{H}}_{2}\mathrm{O}$$

(20)

4 Results and discussion

4.1 Results and discussion for case study 1

4.1.1 MB AR of methanol reaction-based CO₂ hydrogenation

MB AR plots the region in extent space contains all conceivable sets of the extent of reactions or material balances. As precise chemical reactions are not always known in reactive systems, the idea of independent reactions or material balances might be helpful. Five chemical species, including CO₂, H₂, methanol, DME, and H₂O, make up the CO₂ conversion system under study.

The independent material balances [Eqs. (21, 22)] which are derived from .

Table 2 can be stated in terms of extent of reaction (ε).

$${\mathrm{CO}}_{2} + {3\mathrm{H}}_{2} \to {\mathrm{CH}}_{3}\mathrm{OH }+ {\mathrm{H}}_{2}\mathrm{O}\quad\mathrm{\varepsilon }_{1}\quad\Delta \text{H}=-49.208\quad\Delta \text{G}= 3.588$$

(21)

$${\mathrm{CH}}_{3}\mathrm{OH }\to 0.5{\mathrm{CH}}_{3}{\mathrm{OCH}}_{3}+ 0.5{\mathrm{H}}_{2}\mathrm{O}\quad\mathrm{\varepsilon }_{2}\quad\Delta \text{H}=-20.459\quad\Delta \text{G}=-33.186$$

(22)

To calculate the MB AR in extended space, extent of reaction was employed. The feasible zone, in which the amount of each component is either zero or a positive quantity, is determined by using mole balances in terms of the extent of reactions. Hence, the MB AR in the extent space is the obtained feasible region. Table 5 demonstrates that at initial stage, the moles of all components, are a function of the MB AR. The MB AR is offered for the various species and feed ratios. Two components of CO₂ and H₂ are designated as feed in the context of this study, where ${N}_{o,{CO}_{2}}$ equals to 1 mol and ${{N}_{o,{H}_{2}}}$ varies between 0 and excess.

Table 5 Stoichiometric material balance denoting the extent of reactions

By solving the inequalities in Table 5, vertices of the MB AR in terms of extents (ε₁, ε₂) can be determined using Equations (A9, A10). The vertices are important as one of them contains the minimal Gibbs free energy in the G-H space for every given set of conditions.

The initial feed composition affects the MB AR. Hence, it is vital to look at how the initial conditions of our system influences MB AR. In this process, H₂ is utilised as the main feedstock to reduce CO₂ and produce C₁ and C₂₊ products. The CO₂ and H₂ feed system is of interest to the researchers because it helps to emphasise reaction mechanisms for producing C₂₊ materials [3]. Therefore, this section will examine these two components as feed in various compositions. At the initial stage, several feed material combinations were examined using a base of 1 mol of CO₂ for various quantities of H₂ provided. The effects of varying the H₂ quantity in the system’s feed combination are shown in Fig. 2, where nox = [CO₂; H₂; H₂O; CH₃OH; CH₃OCH₃] is a vector that represents the initial compositions of feed and products. A separate composition is represented by each corner or vertex.

Figure 2 illustrates the impact of variations in the quantity of H₂ given, which contains variations of 0.5 (Fig. 2(a)), 1 (Fig. 2(b)), 2 (Fig. 2(c)) and 3 mol (Fig. 2(d)). The formation of the MB AR is altered by increasing the H₂ feed while keeping a feed of 1 mol CO₂. The mass balance MB AR in Fig. 2(d) does not alter in form when more than 3 mol of H₂ are added. Hence, the stage of total reduction of CO₂ is achieved with 3 mol of H₂ supplied as depicted by the MB AR in Fig. 2(d).

The three vertices in each MB AR are produced from (ε₁, ε₂) = Feed (0, 0), A (1, 0), and B (1, 1) which sets the constraints of MB AR. The G-H AR is shown in Fig. 3 using these vertices, with changes in Gibbs free energy and enthalpy of formation. Since the molar extent of the reaction (ε) were determined by the compositions of reactants and products in the system, the enthalpy and Gibbs free energy of the reaction at any point can be determined using Equations (A7, A8).

Figure 3 which displays the total consumption of CO₂ is produced by translating the MB AR in Fig. 2(d) to the G-H space with the determined vertices. Based on Fig. 3, the composition at A can be attained in one of two ways: either directly via $\overrightarrow{\mathrm{FA}}$ which is analogous to reaction in Eq. (16), or indirectly via $\overrightarrow{\mathrm{FB}}$ then to $\overrightarrow{\mathrm{BA}}$ as shown in Eqs. (14, 15). Hess’s law states that regardless of the method or procedures used to create the final composition, the energy needs for a chemical process remain constant [56]. This implies that for the two paths, Gibbs free of energy and enthalpy of formation for the composition at A will always be the same. In other words, $\overrightarrow{\mathrm{FA}}$ should result from the combination of $\overrightarrow{\mathrm{FB}}$ and $\overrightarrow{\mathrm{BA}}$.

The changes of standard Gibbs free of energy and enthalpy of formation of the reactions in Fig. 3 are negative, indicating that the reactions are exothermic and create work. The reaction is more spontaneous when Gibbs free energy is more negative. This indicates that CO₂ may be thermodynamically reduced to CH₃OCH₃ directly without the input of work. In comparison to $\overrightarrow{\mathrm{FB}}$, $\overrightarrow{\mathrm{FA}}$ will dominate the reaction as the Gibbs free energy of reaction of this reaction pathway is more negative, enabling product formation to be more thermodynamically stable and releases work from the reactor system simultaneously. The G-H AR (Fig. 3) predicts that, in the presence of both CO₂ and H₂ in the reaction, the reduction to CO₂ can occur at 25 °C. Whilst a reaction could be thermodynamically possible at 25 °C, it might take a very long time to take place because of kinetic barriers. It should also be noted that reaction kinetics and the available driving force to produce the products at equilibrium, reactor type, and reaction temperature will dictate the choice of the specific path adopted in the reacting system.

4.1.2 G–H attainable region at higher temperatures for methanol reaction-based CO₂ hydrogenation

Depending on the kind of catalyst and support utilised, CO₂ is typically hydrogenated to create C₁ and C₂₊ products at temperatures between 200 °C and 400 °C. In order to demonstrate the appropriate thermodynamically viable phases in this temperature range, it is first required to observe how the G-H AR evolves. It is crucial to observe how the system's heat, work, and product needs vary as the temperature rises.

From Fig. 4, it is shown that two potential reaction routes ($\overrightarrow{FA}$ and $\overrightarrow{FB}$) that convert feed material to CH₃OCH₃ and CH₃OH products exhibit deviations in enthalpy of formation and Gibbs free energy. This suggests that both reactions do not share the same driving force and might not take place simultaneously. This also indicates it is not likely to have the mixture of intermediate and unreacted products in the final product spectrum. Figure 4(a)–(c) suggested that $\overrightarrow{FA}$ rather than $\overrightarrow{FB}$ is the favoured pathway below 300 °C since it exhibits a steeper gradient. If the reaction travels along the G-H AR’s borders, the pathway that provides the feed’s steepiest gradient will most likely to occur at minimum Gibbs free energy. This is due to the hypothesis that a steeper gradient is the path where the system has the highest driving power available to produce desired or intermediate products. From Fig. 4(a)–(f), it can be seen that Gibbs free energy of reaction of $\overrightarrow{FB}$ moves further away from the system’s minimum Gibbs free energy as temperature increases, which decreases its selectivity and the likelihood of intermediate products formed from this material balance being present in the reaction’s final product.

The G-H AR in Fig. 4(b) and Fig. 4(c) illustrate the temperature increase to 200 and 300 °C. The first thing to notice is that the system’s minimal Gibbs free energy still allows for the production of DME directly from CO₂ reduction. This avoids the need for work addition to the process under temperatures no more than 300 °C. The plot shows that when the temperature rises to 400 °C and above, the reaction’s positive slope also rises, shifting the mass balance area into positive Gibbs free energy space as a result. Therefore, greater temperatures are not favourable for forward reactions due to its more positive Gibbs free energy, as the reaction will opt to stay at the feed point which is more stable thermodynamically. Therefore, higher pressure on the system is required in order to make the reaction possible at higher temperatures. The G-H AR in this work demonstrated that the conversion of CO₂ to CH₃OCH₃ at 400 °C and above is endergonic and is not possible without the addition of work to the process. This finding agrees well with the literature, as the reported hydrogenation reactions of CO₂ to CH₃OH and CH₃OH to C₂₊ compounds normally occur at 200–300 °C and 400 °C, respectively, over bifunctional catalysts [57].

Table 6 also shows that this range of temperatures studied do not require additional heat to be supplied to the reactor, as negative enthalpy leads to formation of exothermic reactions which transfers energy to the surroundings. However, as the temperature rises, the Gibbs free energy has grown more positive. This also indicates that conversion of CO₂ to CH₃OCH₃ is less stable at high temperatures. In general, the attainable region approaches minimum Gibbs free of energy at 25 °C, resulting in a more spontaneous forward reaction and is more favourable for exothermic reaction. This indicates that the reaction in this case study is most likely to take place at 25 °C.

Table 6 Standard heat enthalpy and Gibbs free of formation at different temperatures of the G-H AR

4.1.3 P-graph to predict optimal pathways

To determine the stoichiometry chemical equations of the main reaction route ($\overrightarrow{\mathrm{FA}}$), the initial reaction with formation of intermediates ($\overrightarrow{\mathrm{FB}}$) and the secondary reaction which forms the final product ($\overrightarrow{\mathrm{BA}}$), P-graph is employed which helps estimating all feasible reactions in the system with identified process constraints. The maximal structure of P-graph is denoted in Figure A2. The SSG algorithm of P-graph was used to generate all possible solution structures while the ABB method was then subsequently used derive optimal structures for a given set of process constraints. The process constraints in this reaction are: (1) Full consumption of feed (1 mol of CO₂ and 3 mol of H₂). (2) Maximum flowrate of CH₃OCH₃ (by setting an arbitrary proportional investment cost for CH₃OCH₃ product node).

As a result, 182 structures were generated using the SSG algorithm which denoted all configurations for the DME synthesis. The set of these structures resembles the attainable region of the process. The two optimal solution structures were then selected by the ABB algorithm and are depicted in Fig. 5 and Fig. 6.

Fig. 5

P-graph of optimal reaction pathway #1 generated by ABB algorithm with specified process constraints

Fig. 6

P-graph of optimal reaction pathway #2 generated by ABB algorithm with specified process constraints

The material balances for direct conversion of CO₂ ($\overrightarrow{\mathrm{FA}})$ (Fig. 5), and indirect conversion of CO₂ ($\overrightarrow{\mathrm{FB}}$ and $\overrightarrow{\mathrm{BA}}$) (Fig. 6) determined from P-graph modelling are demonstrated in Eqs. (23, 24, 25). The process block diagrams to represent $\overrightarrow{\mathrm{FA}}$ and $\overrightarrow{\mathrm{FB}}$ and $\overrightarrow{\mathrm{BA}}$ are presented in Figs. 7 and 8, respectively.

Fig. 7

Process block diagram of $\overrightarrow{FA}$

Fig. 8

Process block diagram of $\overrightarrow{FB}$ and $\overrightarrow{BA}$

$$\overrightarrow {{FA}} :{\text{CO}}_{2} \, + \,3{\text{H}}_{2} \, \to \,0.5{\text{CH}}_{3} {\text{OCH}}_{3} \, + \,1.5{\text{H}}_{2} {\text{O}}\,\,\Delta {\text{H}}\, = \, - \,{\text{61}}{\text{.267}}\,{\text{kJ/mol;}}\quad \Delta {\text{G}}\,{\text{ = }}\, - \,{\text{4}}{\text{.948}}\,{\text{kJ/mol}}$$

(23)

$$\overrightarrow{\mathrm{FB}} :{\mathrm{CO}}_{2}+ {3\mathrm{H}}_{2} \to {\mathrm{CH}}_{3}\mathrm{OH }+ {\mathrm{H}}_{2}\mathrm{O }\,\,{{\Delta \text{H}}} = - \text{49.208 kJ/mol; }{\Delta \text{G=3.588 kJ/mol}}$$

(24)

$$\overrightarrow{\mathrm{BA}} :{\mathrm{CH}}_{3}\mathrm{OH }\to 0.5{\mathrm{CH}}_{3}{\mathrm{OCH}}_{3} + 0.5{\mathrm{H}}_{2}\mathrm{O }\,\,{\Delta \text{H}} = - \text{12.059 kJ/mol; }{\Delta \text{G}} = - \text{8.536 kJ/mol}$$

(25)

The ratio of CO₂ consumption in H₂ for $\overrightarrow{\mathrm{FA}}$ and $\overrightarrow{\mathrm{FB}}$ to $\overrightarrow{\mathrm{BA}}$ is 1:3, suggesting $\overrightarrow{\mathrm{FBA}}$ as the possible pathway, which shows great correlation to the reported ratios and reaction pathways in literature [Eqs. (14, 16)]. The compositions of feed and products in $\overrightarrow{\mathrm{FA}}$ which was derived from P-graph is analogous to the direct hydrogenation reaction in Eq. (16). This shows that the prediction of optimal pathways of other C₂₊ products is possible with P-graph modelling.

In order to decide which reaction pathway may be favoured, either $\overrightarrow{\mathrm{FA}}$ or ($\overrightarrow{\mathrm{FB}}$→$\overrightarrow{\mathrm{BA}}$), Le-Chatelier’s principle can be applied which assesses the effect of changes in temperatures to the equilibrium of the reaction system. According to Fig. 6(a), direct conversion ($\overrightarrow{\mathrm{FA}}$) is a more favoured pathway at 25 °C since it occurs at the system’s minimum Gibbs free energy. In additional, since both direct and indirect hydrogenation reactions produce the equal amount of CH₃OCH₃ while the unit operations required in direct hydrogenation are much less, direct hydrogenation [Eq. (23)] is determined to be the most optimal pathway in this case study.

4.2 Results and discussion for case study 2

4.2.1 Attainable region approach of FTS-based CO₂ hydrogenation

When all components (C, H, and O) in Table 4 are equivalent to zero, three independent mass balances can be found in Eqs. (26, 27, 28). This enabled the quantity of the product and side product and the unreacted reactant to be determined. The overall equation of the three reactions can be generalised in Eq. (29).

$${\mathrm{CO}}_{2}+ {\mathrm{H}}_{2}\to \mathrm{CO }+ {\mathrm{H}}_{2}\mathrm{O}\quad {\upepsilon }_{1} \quad \Delta \text{H}= 41.192\quad\Delta \text{G}= 28.588$$

(26)

$${\mathrm{CO}}+ {3\mathrm{H}}_{2} \to {\mathrm{CH}}_{4} + {\text{H}}_{2}\mathrm{O}\quad \upepsilon_{2}\quad \Delta \text{H}= -205.818\quad \Delta \text{G}= -141.872$$

(27)

$$8\mathrm{CO }+ 17\mathrm{H}_{2} \to {\mathrm{C}}_{8}{\mathrm{H}}_{18} + 8{\mathrm{H}}_{2}\mathrm{O}\quad {\upepsilon }_{3} \quad \Delta \text{H}= -1259.344\quad\Delta \text{G}= -747.276$$

(28)

$$9{\mathrm{CO}}_{2}+29 {\mathrm{H}}_{2}\to 18{\mathrm{H}}_{2}\mathrm{O}+{\mathrm{CH}}_{4}+{\mathrm{C}}_{8}{\mathrm{H}}_{18} \quad \Delta \text{H}= -1094.434 \quad \Delta \text{G}= -631.496$$

(29)

The independent mass balances expressed in the form of extent of reaction was utilised to determine the MB AR of FTS mechanism in extent space. Table 7 demonstrates the MB AR in terms of initial number of moles of the components.

Table 7 Stoichiometric material balance denoting the extent of reactions

To study the effect of introduction of CO₂ and H₂ as feed to the system at different composition, different combinations of feed materials were considered where a basis of 1 mol of CO₂ was employed for various amounts of H₂ supplied. Figures 9(a)–(d) delineates the changes of extent space by varying the H₂ amount in the initial conditions of the system. The feed composition vector is represented by nox = [CO₂; H₂; H₂O; CO; CH₄; C₈H₁₈].

Fig. 9

Changes in MB AR in extent space of FTS system for a feed 1 mol CO₂ when the H₂ is increased, a 0.1 mol, b 0.5 mol, c 0.8 mol, d 1 mol

Figure 9 illustrates the impact of variations in the quantity of H₂ given, which ranged from 0.1 mol ((Fig. 9(a)) to 1 mol (Fig. 9(d)). The form and region of the MB AR are altered by increasing the H₂ feed while keeping a feed of 1 mol CO₂. The point at which all of the CO₂ is reduced is depicted by the MB AR in Fig. 9(d). The bounds of the MB AR are formed by the three vertices in the corresponding MB AR, which are produced as (ε₁, ε₂, ε₃) = Feed (0, 0, 0), A(0.25, 0.25, 0), B(0.32, 0, 0.04), and C(1, 0, 0).

4.2.2 G–H attainable region for FTS-based CO ₂ hydrogenation

The G-H AR space is created by integrating the enthalpy and Gibbs free energy limits of each distinct species. The sides of the extent plot in Fig. 10 were translated to the G-H limits of the attainable region in Fig. 10, which is denoted as the green shaded area. Because the parameters needed to optimise the process in a steady state system are met and all the species are positive, this is the region where viable reactions are possible at 25 °C. This area represents all conceivable combinations of the species participating in the reactions, contains the feed point, and is zero on the intersections.

Fig. 10

G-H diagram demonstrating AR at 25 °C and 1 bar using a feed of 1 mol of CO₂

Each species’ solid line depicts the points in the G–H space where the flowrate is zero for that species. The dashed line next to each solid line shows the direction that each species forms, which is towards the positive extents. Heat and work addition are both necessary for the process in quadrant “B” (where H > 0 and G > 0). The process is exothermic in quadrant “A” (G > 0 and H < 0), however work addition is necessary.

As a result, since operating in quadrants “A” and “B” requires more effort, hence these regions are not practical to carry out the reaction. Work is lost in quadrants “C” and “D” since Gibbs free energy is less than zero. While the operations in quadrant “C” need to remove heat, those in quadrant “D” need to be supplied with heat energy. The size distribution of the G-H AR demonstrates the huge variety of mass balancing combinations that might be used to produce various products from each feed. It is crucial to remember that when mixing is taken into account, the Gibbs free energy must be smaller than zero for the entire reaction to be thermodynamically possible.

The G-H AR provides information on the thermodynamic boundaries of what is feasible. More specifically, as illustrated in Fig. 10, the AR is restricted at the top by the requirement that Gibbs free of energy be non-positive and then anticlockwise by the conditions that CH₈H₁₈, H₂, H₂O, CO, and CH₄ moles are equivalent to zero. This G-H AR plot shows that the FTS-based CO₂ hydrogenation reaction (green shaded region) which occurs in quadrant “C” does not require any heat and work input at a reaction temperature of 25 °C. The point “x” (Fig. 10) which resembles the lowest point of the shaded attainable region is where flowrates of H₂O and CH₄ are equal to zero. Since the slopes of these lines are rather steep, it is assumed that if gas mixing were considered, these species would not be zero but rather some lesser amount.

4.2.3 Effect of temperature on molar composition

This section demonstrates the effect of temperature on the hydrogenation of CO₂ and CO. The molar composition of reacting species (${\mathrm{n}}_{{\mathrm{CO}}_{2}}$, ${\mathrm{n}}_{{\mathrm{H}}_{2\mathrm{O}}}$, ${\mathrm{n}}_{{\mathrm{H}}_{2}}$, ${\mathrm{n}}_{\mathrm{CO}}$, ${\mathrm{n}}_{{\mathrm{CH}}_{4}}$, ${\mathrm{n}}_{{\mathrm{C}}_{8}{\mathrm{H}}_{18}}$) against temperature range (298 K to 873 K) were obtained using lsqnonlin function in MATLAB as demonstrated in Supplementary Information (A4).

As it was already indicated that CO is produced via dehydration of CO₂ [Eq. (26)], followed by dehydration of CO [Eqs. (27, 28)] which produces the desired product, C₈H₁₈. Hence, the reaction under study has two possible outcomes: (1) the production of C₈H₁₈, which has economic appeal; (2) the conversion of CO₂, which has environmental significance. The opposing impact of feedstock composition on these two goals is seen in Fig. 11. The composition of CO increases at higher temperature as CO₂ conversion is more significant. A simultaneous reduction in the compositions of H₂O and C₈H₁₈ can be observed as temperature increases.

Fig. 11

Molar composition profile at different temperatures

Higher temperatures are particularly favourable for CO₂ and H₂ conversion and CO and CH₄ production. They also reduce the amount of by-products H₂O significantly. These findings are in line with the experimental evidence that has been published in the literature [1]; [58]. However, the increment of CO in the reaction requires more H₂ to convert to C₈H₁₈ and H₂O. Therefore, if H₂ feed is not increased in the system, the effect on hampering C₈H₁₈ yield upon increasing the CO content at higher temperature can be observed. Therefore, the yield of hydrogenation products, C₈H₁₈ and H₂O falls as temperature increases. As a result, the generation of C₈H₁₈ and H₂O are both favoured to a greater extent at temperature 25 °C.

4.2.4 Machine learning derived P-graph to predict optimal pathways

Since this reaction involves six chemical species and multiple intermediate reactions, machine learning is implemented to derive different combinations of feed to produce optimal reaction pathways with the highest economic value. The combination of feed must be considered for synthesis of gasoline with zero CO₂ emission. In order to accurately estimate the stoichiometric ratio of optimal reaction pathway with maximum flow of gasoline product formation and complete consumption of CO₂, a decision tree classifier was trained using elements of C, H, and O, and enthalpy of heat formation and Gibbs free energy to predict amount of CO₂ in final product stream.

Figure A3 illustrates the machine learning-derived P-graph model, which is divided into parts that deal with raw materials allocation, decision trees, and choices related to unconsumed CO₂. The product node on the left contains zero CO₂ product while the product node on the right contains CO₂. To ensure P-graph modelling selects reaction pathways with full consumption of CO₂, a constraint was imposed in the stream with unconverted CO₂ by setting a penalty (operating cost) to reduce the economic value of the streams with unreacted CO₂. From the mutual exclusion solver of P-graph with ABB algorithm, 14 solutions were derived and ranked as highest profit to lowest. Solution 1 shows that the feed which contains 9 mol of CO₂ and 29 mol of H₂, producing 18 mol of H₂O, 1 mol of CH₄ and 1 mol of C₈H₁₈ gives the highest economic value of 3109.5 EUR/y where all CO₂ were consumed (Fig. 12). The molar feed predicted from the P-graph model is analogous to the overall reaction in Eq. (29). Figure 13 delineates the process block diagram of solution 1. Moreover, it should be noted that the enthalpy and Gibbs free energy of this reaction estimated by the machine learning model are − 3495.13 kJ/h and 0 kJ/h, respectively. This shows that the reaction is exothermic with no requirement of work.

Fig. 12

Solution 1 pathway with the highest economic value and attained full consumption of CO₂. Raw material nodes are depicted as CO₂ (red), H₂ (green), CO (blue). Product nodes are CO (purple), H₂O (orange), CH₄ (yellow), C₈H₁₈ (grey)

Fig. 13

Process block diagram of solution 1 pathway

In general, the optimal reaction pathway deduced from P-graph integrated with decision tree classifier algorithm has shown agreement with the overall reaction reported in literature. This shows that machine learning-derived P-graph can be used as a tool to solve topological reaction optimisation problems without scaling constraints.

5 Conclusion

The optimal and sub-optimal reaction pathways for CO₂ hydrogenation technology can be determined using this PART framework with a minimum amount of heat and Gibbs free energy of formation data. When using the P-graph method, it is possible to frame the AR technique as a tool for mathematical programming by considering the reactant and product economic values as well as flow rate constraints. By using the enthalpy of formation Gibbs free energy minimisation strategy, as shown in the AR space, the AR technique was successfully used to gain a deeper understanding of CO₂ hydrogenation. For each certain reaction zone in the reactor, the AR spaces can be used to estimate the product composition. The optimal temperatures for a desired phase may be predicted using this thermodynamic technique. It has been demonstrated the derivation of two potential reaction routes, one of which converts CO₂ directly to CH₃OCH₃, and the other of which uses CH₃OH as an intermediate product. The chemical route of $\overrightarrow{\mathrm{FA}}$ is thermodynamically advantageous throughout the process, according to the G-H AR. $\overrightarrow{\mathrm{FA}}$ is also favourable in industrial settings since short reaction pathway will involve less unit operations hence resulting in minimal operating cost. The amount of substances involved in the reaction estimated by P-graph modelling showed great correlation to the reactions in reported literature. The automation of P-graph generated with machine learning algorithms was also demonstrated in this study which enabled minimal manual editing in P-graph Studio. However, this method limits the applicability to reactions involving recently discovered materials as its implementation requires data from conduct experiments or previous studies on the reaction to retrieve information of reaction conditions, reactant concentrations, product yield and selectivity and so on for data training in prior to predictive modelling.