Improving membrane filtration performance through time series analysis

Abstract

For ultrafiltration, and membrane filtration more generally, the quantitative determination of the modes of fouling remains a subject of great interest. Herein an integral method for determining the modes from a time series of volumetric flux $J\left(t\right)$ is given and illustrated with previously published filtration data of bergamot juice (Ruby-Figueroa et al (J Membr Sci 524:108-116, 2017)). The integral method of fouling analysis has the potential to become the cornerstone of a robust empirical process. In addition to determining, in a clear-cut manner, the point at which there is a switch from one mode to another, the robust methodology yields characteristic $J\left(t\right)$ equation for each mode that are an excellent fit to the data. The emphasis is upon the creation of a robust methodology which is best viewed as being a semi-empirical method that is indicative of the modes of fouling. For the example chosen, the initial 4 L/m² generates some pore blocking after which the main mode of fouling is cake build-up. The variation of overall resistance with time is also informative and analysis of this series was used to check the result for the initial phase of fouling as determined from the time series of volumetric flux. A comparison against the ARIMA (Autoregressive integrated moving average) method, which has never been previously undertaken, is given herein. The integral method of fouling analysis was found to be superior, in part because of the quality of fit to the data and in part because it enables one to establish whether the initial fouling is different in character from the subsequent fouling. Having this information can improve membrane selection and overall membrane filtration performance.

1 Introduction

Over the past four decades numerous sets of membrane filtration data have been assessed to determine the modes of fouling. These data, often presented graphically, are a time series of fluxes which are often determined from having measured the mass of permeate collected as a function of time. Since ultrafiltration membranes in industry are operated in a cross-flow mode, it is essential that allowance is made in the governing equations for the removal of foulants from the membrane surface. In a previous contribution to the literature [1] three inter-linked areas were advanced. One concerned a re-evaluation of the derivation of the flux decline relationships given in the seminal paper outlining the concept of critical flux [2]. Linked to this an alternative hydrodynamic dependency for the removal term was suggested. Instead of the removal term being simply proportional to shear stress (and independent of flux) it was suggested that the removal term could be a function of both factors by being proportional to shear stress and inversely proportional to flux (this being consistent with a model for micro-sieves [3]). Whilst the hydrodynamic dependency of the removal term is still worth of further investigation, it is important to be able to differentiate between the various phases of fouling and this differentiation might be considered a prerequisite. Thus this contribution is focussed almost exclusively upon the third area, namely use of the integral method of fouling analysis to make this differentiation. This method enables one to determine (a) the modes of fouling; (b) the switch point from one mode of fouling to another and (c) the characteristic equation for each mode. The implicit restriction inherent in the integral method is that the different membrane fouling modes are sequential and not simultaneous. For example, it is useful when fouling might initially be dominated by a phase of pore blocking and then by a phase in which cake formation is predominant.

The previous work mentioned above [1] dissipated its efforts across the aforementioned three areas which is probably why the authors of a recent paper [4] did not compare their approach with the integral method of analysis. They used fruit juice ultrafiltration to explore the applicability of using ARIMA (Autoregressive integrated moving average) models and other models. The nature of ARIMA—auto regressive (AR), integrated (I), moving average (MA) models will be outlined later. At this point it is simply noted that later a few points of commonality between the integral analysis approach and the ARIMA models will be mentioned in Sect. 2.6. Before reaching this point, the reader is reminded about the four fouling mechanisms for porous membranes (namely (i) complete pore blocking; (ii) internal pore blocking; (iii) partial pore blocking; and (iv) cake filtration), then some analytical approaches from the 1990s are summarised. Section 2.4 provides a detailed derivation of the integral method of fouling analysis and thereby answer the question “What is the integral method”. Subsequently in Sect. 3, the filtration data for bergamot juice [4] is used to detail how the application of the integral approach can readily be made in practice. Demonstrating how the integral method of fouling analysis can be applied readily and accurately is the principal aim of this paper. A strength of this integral approach is that it enables one to establish whether the initial fouling is different in character from the subsequent fouling. Such information can improve membrane selection. Such selection is key to the wider penetration of membrane processes. The special collection to which this paper belongs has noted that molecular engineering is “concerned with the development of advanced materials with specific functions or performance characteristics that are governed by nano- and micro-scale physicochemical attributes” [5]. Furthermore, properties and architecture at the nano- and micro-scale are increasingly being recognised as key to in-use performance. Relating process-scale output of membranes to their surface architecture and physico-chemical properties is important particularly as the advances in molecular engineering will permit the tailoring of membranes to specific applications.

2 Theory

2.1 Early work on fouling in dead-end filtration

With regard to dead-end filtration, Hermia was the first person to provide a single equation linking the four blocking filtration laws for porous media, and the first to give a physical derivation of the so-called intermediate blocking law [6]. In his seminal paper on constant pressure filtration he references the development of these laws over the period from the 1930s to the 1960s and showed that the expressions for (i) complete pore blocking; (ii) internal pore blocking; (iii) partial pore blocking; and (iv) cake filtration can be linked, for constant pressure filtration, by a single equation:

$$\frac{{d}^{2}t}{d{V}^{2}}{{=k}_{n}\left(\frac{dt}{dV}\right)}^{n}$$

(1)

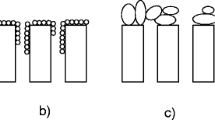
where t is time, V is filtrate volume, n is an index characteristic of a particular mode of blocking and ${k}_{n}$ is a constant that is dependent upon the mode of blockage—see Table in [6]. A schematic of the modes of blockage is given in Fig. 1.

Fig. 1

Source is [1]

Illustration of the principal mechanisms for the fouling of porous membranes. Adsorption is not included.

In earlier work (e.g. [6]) the expression relating to internal pore blocking was referred to as the Standard Blocking Filtration Law. When this relationship is applicable in dead-end mode, $t/V$ is linearly related to t. The other classic relationship for dead-end filtration is the so-called Cake Filtration Law. Here $t/V$ is linearly related to V.

Writing $dV/dt$ for convenience as $y$, Eq. (1) can be re-written to introduce flux due to $y=AJ$. Developing the left-hand side of (1)

$$\frac{d(1/y)}{dV}={\frac{-1}{{y}^{2}}{\frac{dy}{dV}= \frac{-A}{{\left(AJ\right)}^{2}}\frac{dJ}{dV}=\frac{-A}{{\left(AJ\right)}^{2}}\frac{dJ}{dt}\frac{dt}{dV}=\frac{-A}{{\left(AJ\right)}^{3}}\frac{dJ}{dt} =k_n}\left(\frac{1}{y}\right)}^{n}$$

(2)

Substituting $y=AJ$ on the right-hand side:

$$\frac{-dJ}{dt}=\frac{{k}_{n}}{A}{\left(AJ\right)}^{3-n}$$

(3)

For dead-end filtration, Eq. (3) relates flux decline to flux and the mode of fouling. Unlike Eq. (1), there is a physical significance to this equation. Furthermore, anticipating the developments in Sect. 2.4, flux can be related to volume of filtrate:

$$-{\int }_{{J}_{0}}^{J}{J}^{n-2}dJ={k}_{n}{A}^{2-n}{\int }_{0}^{t}Jdt={k}_{n}{A}^{1-n}V$$

(4)

In writing the above note was taken of the fact that $V=A{\int }_{0}^{t}Jdt$. Later use is made of the term specific volume, $v=V/A$.

2.2 Early work on fouling in cross-flow membrane filtration

The remainder of this paper will use the term ‘fouling’ instead of ‘blockage’ and refer to ‘permeate volume’ rather than ‘filtrate volume’ because the focus is upon flux decline in membrane application. By including a removal term into the basic differential equations which represent three of the four fouling mechanisms Field et al. [2] extended Hermia’s analysis to cross-flow filtration. The fourth fouling mechanism is the so-called standard blocking mechanism which involves intra-pore fouling. As this mechanism by definition cannot be mediated by solute/particle back diffusion from the membrane surface Hermia’s expression for the n = 1.5 mode does not need to be modified for cross-flow. Overall the equations can be elegantly unified into the following generic equation:

$$\frac{-dJ}{dt}={K}_{n}{J}^{2-n}(J-{J}_{R}) \quad \text{for}\, J>{J}_{R}$$

(5)

where J is volumetric flux, n is an index characteristic of a particular mode of blocking and ${K}_{n}$ is a constant that is dependent upon the mode of blockage and ${J}_{R}$ is related to the cross-flow removal from the surface of the membrane as discussed elsewhere [2]. Herein flux decline is modelled empirically and this term is taken to be a modelling constant. Also, and the importance will become apparent in Sect. 2.4, Eq. (5) can be developed in a manner akin to Eq. (4):

$$-{\int }_{{J}_{0}}^{J}{J}^{n-2}dJ={K}_{n}{\int }_{0}^{t}\left(\right(J-{J}_{R})dt={K}_{n}(v-{J}_{R}t)$$

(6)

where $v$ is a specific volume; the volume of permeate per unit area of membrane.

Arnot et al. [7] used Eq. (5) to determine the dominant fouling mechanism in a system treating an oily-water emulsion. They found that fouling was either by incomplete pore blocking (n = 1) or ‘cake’ filtration (n = 0) and depended on the membrane used and the operating conditions. In order not to give undue emphasis to early or late times, the data were fitted in both flux and resistance form simultaneously. It will be immediately apparent from the following equation that as the flux declines the fouling resistance will increase so that if one is minimising the sum of the square of errors more weight will be given to fluxes at early times (because these fluxes are larger) and to resistances at later times because resistances increase with time. In the absence of an osmotic pressure difference across the membrane, the classic expression for volumetric flux is:

$$J=\frac{\varDelta P}{\mu ({R}_{m}+{R}_{f})}$$

(7)

where $\varDelta P$ is the pressure difference across the membrane, $\mu$ is the viscosity of the permeate, ${R}_{m}$ is the hydraulic resistance of the clean membrane, and ${R}_{f}$ is the resistance due to fouling. For use in Sect. 2.3, it is noted that from Eq. (7) it follows that:

$$\frac{d{R}_{f}}{dt}=\frac{\varDelta P}{\mu {J}^{2}}\left(\frac{-dJ}{dt}\right)$$

(8)

2.3 Evaluation of the rate of change of resistance

For a positive flux the value of $\frac{dJ}{dt}$ will always be negative or zero; this is both intuitively obvious and a clear consequence of Eq. (5). Furthermore $\frac{{d}^{2}J}{d{t}^{2}}$is always negative or zero thus $\frac{dJ}{dt}$ always decreases with respect to time until it is zero. However, the behaviour of, $d{R}_{f}/dt$, is not necessarily a mirror image of $\frac{dJ}{dt}$ [8]. Combining Eqs. (5) and (8) it is found that:

$$\frac{d{R}_{f}}{dt}=\frac{\varDelta P{K}_{n}\left(J-{J}_{R}\right)}{\mu {J}^{n}}$$

(9)

The term $d{R}_{f}/dt$ is always positive or zero, but the change in it with respect to flux (or time) can be positive as well as negative. Further differentiation yields:

$$\frac{{d}^{2}{R}_{f}}{d{t}^{2}}=\frac{\varDelta P{K}_{n}}{\mu {J}^{n+1}}\left[\left(1-n\right)J+n{J}_{R}\right]\frac{dJ}{dt}$$

(10)

For cake and intermediate cases (or more generally for 0 ≤ n ≤ 1), ${d}^{2}{R}_{f}/d{t}^{2}$ will, for all time values, be negative because the right-hand side of Eq. (10) reduces to a positive term multiplied by $\frac{dJ}{dt}$, which is negative. However for ‘complete’ pore blocking one obtains from Eq. (10) that:

$$\frac{{d}^{2}{R}_{f}}{d{t}^{2}}=\frac{\varDelta P{K}_{n}}{\mu {J}^{3}}\left[2{J}_{R}-J\right]\frac{dJ}{dt}$$

(11)

Thus when $J$ is more than $2{J}_{R}$ the value given for Eq. (11) is positive and $d{R}_{f}/dt$ initially increases with time. As discussed elsewhere [8], if the fouling mechanism is characterised by ‘complete’ pore blocking (and $J>{J}_{R})$there should be a maximum in a plot of $d{R}_{f}/dt$ versus time plot. This method for determining the modes of fouling is not the focus of this paper; here it is used as a secondary check.

2.4 Integral method of fouling analysis

The principal advantage of this method over that in Sect. 2.3 or say the one used by others e.g. [9, 10] is the avoidance of the need to numerically differentiate data and thereby introduce uncertainties. The integral method is a practical method for identifying whether the initial fouling of a membrane is by the same mode as the subsequent fouling. The left-hand side of Eq. (6) takes four forms depending upon the value of n. The generic form is written as $fn\left(J,n\right)$ and the specific forms are given in Table 1.

Table 1 Specific forms of $fn\left(J,n\right)$ as determined by the mode of fouling

In summary, the method consists of five stages: (1) The time evolution of volumetric flux (J) is plotted so as to capture the trend in the data, and to establish a suitable first estimate of the cross-flow removal term, ${J}_{R}$ from the flux asymptote. Label this estimate ${J}_{Re}$.

(2) Using the data from Stage 1, a time series of $v-{J}_{Re}t$ values is created and these become the abscissa values on the x-axis. The ordinate values are the four $fn\left(J,n\right)$ functions as given in Table 1.

(3) If one $fn\left(J,n\right)$ function fits the data well, one can explore the possibility that there is just one mode of fouling, but the four curves are likely to indicate points of inflection at a common value of $v-{J}_{Re}t$ [1].

(4) Using data up to the point of inflection candidate values of n for the first phase of fouling are obtained.

(5) Next data beyond the inflection point is used to establish the possible modes of fouling in the second phase.

(6) Assuming that there is just one change in mode, the final stage is optimisation of the parameter values so as to have expressions for flux as a function of time.

Returning to Eq. (6), and dividing through by t it readily seen that it can be written as:

$$\frac{fn\left(J,n\right)}{t}=\frac{{K}_{n}v}{t}-{K}_{n}{J}_{R}$$

(12)

For each putative value of n, the left-hand side can be established from the data, likewise $\frac{v}{t}$. Hence Eq. (12) can be used to form four equations of the form $y=mx+c$ and one can readily establish the form that gives the best fit to the data and hence the appropriate value of n (establishing the mode) and the corresponding values of ${K}_{n}$ and ${J}_{R}$. Therefore, the integral method enables one to determine (a) the modes of fouling; (b) the switch point from one mode of fouling to another and (c) the characteristic equation for each mode.

2.5 Application of ARIMA models to ultrafiltration

The Box-Jenkins ARIMA approach is named after the two statisticians, George Box and Gwilym Jenkins, and is well established in the statistical literature. It is “essentially an exploratory data-oriented approach that has the flexibility of fitting an appropriate model, which is adapted from the structure of the data itself” [4]. Typically, four ARIMA models (211, 112, 212 and 111) are built to find which gives the best fit to the experimental data. The main differences between them is the order of the autoregression and the order of the moving average. This is reflected in the first and last digits of the labelling. Hence the ARIMA 111 model is first order autoregressive and has a first order moving average whereas the ARIMA 212 model is second order with respect to both the autoregression and the moving average. The ARIMA 211 model includes is second order for autoregression but the moving average is first order while the ARIMA 112 model includes a first order autoregressive element and a second order moving average. For membrane models concerned with fruit juice filtration one only need to consider non-seasonal ARIMA models. The ARIMA (p, d, q) categorisation refers, in sequence to the order of the autoregressive model (p), the degree of differencing (d), and the order of the moving-average (q). The application of this approach to ultrafiltration has until recently been limited.

2.6 Comparison of modelling approaches

Whilst a detailed comparison of the integral method of flux analysis with other methods is not the main focus of this paper, a few remarks will be made. Unlike Hermia’s approach there is due allowance in the integral method for cross-flow through the inclusion of a removal term in the underlying mass balance. As with the method evaluating the rate of change of resistance (Sect. 2.3) there is an endeavour to establish whether there is an initial mode of fouling distinct from a later mode, but they differ in that one involves numerical differentiation and the other numerical integration. The ARIMA model, is not a black-box in the same sense as artificial neural networks (ANNs) but any link to physical phenomena is missing. Interesting the main study on the use of ARIMA models for ultrafiltration of fruit juices found that the data for three different fruit juices were fitted by three different ARIMA models, the 111, 211 and 212 models [4]. Although the integral method was formulated from the physical models of Hermia, the four forms of Eq. (6) like the four principal ARIMA models can be viewed just in empirical terms, i.e. as expressions verifiable by observation or experience rather than theory or mechanistic modelling. Certainly, the output from the integral analysis is not restricted to a particular type of feed suspension and/or a single back-transport mechanism. This is a key point of commonality between the integral method of fouling analysis and the ARIMA modelling of others [4].

3 Practical implementation of Integral method of fouling analysis

Demonstrating that the integral method of fouling analysis can be applied readily and accurately to give a high-quality representation of flux decline is the principal aim of this paper. The filtration data for bergamot juice [4] has been chosen so as to have a comparison with the ARIMA output. The source paper also contained data on pomegranate juice but this shows a discontinuity, possibly due to changing feed concentration, and hence this juice was not selected for further analysis. The first stage as mentioned in Sect. 2.4 is to plot volumetric flux (J) against filtration time. The flux data is available in terms of mass collected per unit area per unit time and the density of the permeate was assumed to be that of water. The data are used to generate Fig. 2. From this, a value of the flux asymptote, ${J}_{Re}$, is found for use in Stage 2.

Fig. 2

UF permeation data for bergamot juice taken from [4]. Polysulphone 100 kDa membrane of 0.16 m² operated with a TMP of 1 bar at 20 °C

With a ${J}_{Re}$value of 3 LMH, the four $fn\left(J,n\right)$ functions given in Table 1 are plotted as functions of $v-{J}_{Re}t$.; the creation of this plot is Stage 2. To make the plots a value of the initial flux, ${J}_{0}$, is required and an appropriate estimate can be obtained from the flux-time plot. A value of 20 LMH was used and the output is shown in Fig. 3.

Stage 3 is an evaluation of the plot shown in Fig. 3. If a single mode of fouling were to describe the whole data set, then one of the curves in Fig. 3 would be a straight line. This is not so. The inflection in the curves around the 5th data point in Fig. 3 indicates the need to examine the early data separately from the later data. A check on the n = 0 curve was made separately with an expanded scale on the y-axis, and this suggested that if a single mode were to be chosen to fit the data the optimal choice would be n = 0.

Stage 4 is concerned with an analysis of the data before the point of inflection. These are used to establish the most appropriate value of n for the first stage of fouling. As indicated in Fig. 4 and discussed in Sect. 4 the appropriate value is n = 2.

Fig. 3

Initial evaluation of the permeation data. Note the inflection in the curves around the 5th datum point

Due to Stage 3 having suggested two consecutive phases of fouling, Stage 5 concerns the evaluation of the rest of the data. As indicated in Fig. 5 the fit for both n = 1 and n = 0 are good. The R² value for n = 1 is marginally better but the curvature in the line for n = 1 is greater so both n = 1 and n = 0 are candidate values. Once optimal values of the parameter are established for each candidate mode, overall goodness of fit values can be used to determine the modes that best represents the data for each phase of fouling. This almost completes the description of how the integral method of fouling analysis can be readily implemented. The final stage is the conclusive finalisation of the modes of fouling and the determination of flux as a function of time. This is covered at the beginning of the next section.

Fig. 4

UF permeation of bergamot juice: analysis of the first phase of fouling

Fig. 5

UF permeation of bergamot juice: analysis of the second phase of fouling

4 Results and discussion

When as indicated in Fig. 4 the appropriate value of the fouling mode for the first phase of fouling is n = 2, then the relevant equation that requires fitting is:

$$J={J}_{0}-{K}_{1}(v-{J}_{R1}t)$$

(13)

where ${K}_{1}$ and ${J}_{R1}$have subscript ‘1’ to indicate the first phase of fouling. In addition to fitting these two parameters ${J}_{0}$ is also unknown because the first data point is for t = 5 min. As there are three adjustable parameters and only five data points for this initial phase the fit for n = 2 is excellent and therefore it prudent to check, if possible, whether ${d}^{2}{R}_{f}/d{t}^{2}$ is positive during this phase. As indicated in the Appendix there is a change in gradient in the resistance-time plot, but the 5 min time interval between data points did not give unambiguous confirmation that n > 1 because numerical differentiation was ‘noisy’. Closer inspection of Fig. 8 suggests that the first phase might be around 10–15 min rather than 25 min but without more data it is hard to be definitive. However this observation emphasises the desirability of having more data at short time intervals at the beginning of experiments.

Having determined the mode of fouling for the first phase, the remaining data point (> 65) were analysed to decide between n = 1 and n = 0. The R² value was superior for the latter mode and the overall result is shown in Fig. 6 and parameter values are given in the Appendix. The n = 0 curve will, if it is extrapolated back, give a good fit to the flux data for t = 15 and t = 20 min but will underpredict the measured values at t = 5 and t = 10 min. This observation accords with the tentative conclusion reached after inspecting Fig. 8.

Fig. 6

UF permeation of bergamot juice: comparison of flux data with modelling output from the integral method. The initial curve (green) reflects a n = 2 mode of fouling and the subsequent curve (red) reflects fouling due to cake formation

As shown in Fig. 6, the overall fit is excellent and R² value is 0.995 which is superior to the value of 0.968 obtained using the ARIMA method [4]. It is said that the ARIMA method is a means by which a “time series can be approximately modelled” [4]. The method here can be considered a means by which a “time series of permeate flux can be appropriately modelled”. ‘Appropriate’ rather than ‘approximate’ because it gives insight into the mode of fouling albeit not into precise mechanisms. Indeed, to evaluate fully the membrane performance at laboratory and industrial scale it is necessary to distinguish between any initial pore blocking (which may indicate that the membrane pores are too large) and the development of cake layers which will generally build up on the membrane surface. A strength of the integral approach is that it enables one to establish whether the initial fouling phase has a fundamentally different origin from the subsequent fouling. Often there is a paucity of data points in this region which is why a cross-checking method involving $d{R}_{f}/dt$ was introduced.

Although the classical analysis of dead-end filtration used plots of t/V vs. V to test for cake formation (n = 0) and t/V vs. t to test for standard blocking i.e. intra pore fouling, cross-flow analysis generally converts its data straight to flux-time data even though it is collected generally as mass-time data. For the optimal use of the method elucidated here, the retention of mass-time data is to be encouraged together with a bias towards have more data at early times. In the chosen example the initial 4 L/m² generates some pore blocking after which the main mode of fouling is cake build-up. This value equates to a liquid layer with a depth of 4mm, and it is the foulant in this layer which roughly doubles the overall resistance because of its interaction with the membrane.

There is confusion in the literature regarding the literature regarding the fouling mode, or modes, found in the ultrafiltration of bergamot juice. Conidi et al. [11] attributed the rapid decline in permeate flux to concentration polarisation and gel-layer formation. Interestingly (and this point has been missed by others for seek to emphasise a single mode) they added, “and it accounts for about 50% of the total decline”. In their review of ultrafiltration modelling approaches with an emphasis upon fruit juices, Quezada et al. [12] compared a number of approaches but did not distinguish between initial fouling mode and the subsequent mode. They found for their data on the UF of bergamot juice that the R-squared value for their chosen concentration polarisation model was 91.08% but a number of other models had significantly higher R-squared values. The one with the best R-squared value (99.78%) is a resistance-in-series model with the additional resistance coming from some form of pore filling. Key information as to what equation is being used to link pore filling with volume passing through the membrane is missing but they reference among others a paper by Ren et al. [13] who include a differential equation for pore shrinkage. Whether this was the particular model used or not is unclear. It is simply noted here that a pore filling model is generally associated with a n value of 1.5 [2, 6]. This is intermediate between the values deduced here which were n = 2 for the initial phase and n = 0 for the subsequent phase.

The principal aim of this paper has been the exposition of a robust methodology for fouling analysis. Nevertheless, it is appropriate to say a little more about fruit juice clarification using membranes. The clarification of fruit juices by membrane processes has been extensively studied over the last 30 years [14,15,16,17,18]. As discussed elsewhere [17, 18] these processes are excellent in producing natural fresh-tasting and additive-free products that retain, due to the absence of any heating, their nutritional and sensory properties. Whilst the worldwide market for membrane operations in the food industry has increased to €800–850 million [19] this is dominated by the dairy sector. There are few if any product quality concerns with regard to fruit and vegetable juice processed using membranes but permeate flux levels, and the level of fouling, remain as key concerns [18]. As noted above integral method can be considered a means by which a “time series of permeate flux can be appropriately modelled”. The reason for stating that it can be appropriately modelled is because the integral method of fouling analysis used in this paper not only gives insight into the mode of fouling but also can stimulate reflection upon membrane selection. For food, beverage and other applications, the integral method of fouling analysis should enable better membrane selection to be made, and where market size allows, guide in the development of tailored membranes.

5 Concluding remarks

The primary aim of this paper has been the exposition of a robust methodology for the quantitative determination of the modes of fouling and the associated J(t) relationships. Herein a clear method for determining a change in fouling mode from a time series of volumetric flux J(t) is given and illustrated using previously published filtration data of bergamot juice. As information on the osmotic difference across the membrane is an unknown (and will be small if the rejection coefficients of the sugars etc. are small) it has not been included and therefore the methodology is best viewed as being semi-empirical; there is a theoretically inspired basis with the final relationships being empirically determined from the data. For the chosen example, the mode of fouling changes from pore blocking (n = 2) to cake formation (n = 0) at around 15 min. The robust methodology also yielded characteristic J(t) equations for each mode and these are an excellent fit to the data.

For the first time the ARIMA method was compared with the integral method of fouling analysis and the latter was found to be superior. As it enables one to establish whether the initial fouling is different in character from the subsequent fouling, and the point of the switch from one mode to the other, the integral method of fouling analysis has the potential to become the cornerstone of a robust empirical process which determines the switch point from one mode of fouling to another together with the characteristic equation for each phase. Herein the stages of this straightforward process have been set out and illustrated with respect to the ultrafiltration of bergamot juice. The variation of overall resistance with time is informative and was used as a check. The overall finding for the chosen example was that during the initial passage of permeate there is some pore blocking. However, after the passage of 4 L/m² the main mode of fouling is cake build-up with the transitioning starting around 15 min.

For some feed-membrane pairs (such as the one examined in this paper) the initial phase of fouling has a relatively short duration but during this period the flux may be roughly halved. An undoubted strength of the integral approach set out in this paper is that it enables one to decide whether or not the initial phase of fouling is of a different character from the fouling that occurs subsequently. Having this key information can improve membrane selection, process strategy and hence the overall performance of the membrane filtration system.

Appendix

1.1 Evaluation of the rate of change of resistance

In Sect. 2.3 it was noted that if n > 1, then the term ${d}^{2}{R}_{f}/d{t}^{2}$ can be positive. It was shown that for ‘complete’ pore blocking (n = 2) the rate of change of $d{R}_{f}/dt$ with respect to time is given by:

$$\frac{{d}^{2}{R}_{f}}{d{t}^{2}}=\frac{\varDelta P{K}_{n}}{\mu {J}^{3}}\left[2{J}_{R}-J\right]\frac{dJ}{dt}$$

(11)

However full use of this expression is not required; one simply evaluates $d{R}_{f}/dt$ and plots this data versus time. Resistance-time data for the bergamot juice is given in Fig. 7 and derived from this the $d{R}_{f}/dt$ vs. time plot for bergamot is given in Fig. 8.

Fig. 7

Evolution of the overall resistance (10¹² m⁻¹) during the UF of bergamot juice

Fig. 8

Evolution of $d{R}_{f}/dt$ during the UF of bergamot juice

As note in Sect. 4 this data is ‘noisy’. The cause is the 5 min interval between data points. Even with a 2 min interval (Fig. 9) the data is still noisy but the positive initial gradient was clear [8].

Fig. 9

Evolution of $d{R}_{f}/dt$ during microfiltration of 2% dry weight yeast suspension using a nominal 0.2 μm Ceramesh membrane unit operated at 0.5 bar with Re = 470 [8]

1.2 Details for first phase of fouling

The expression with n = 2 was found to be superior and the relevant values of the parameters in Eq. (12) are:

${J}_{0}$ (LMH)	${J}_{R1}$ (LMH)	${K}_{1}$ (h−1)
20.13	7.02	4.59

Equation (12) can be converted to an equation giving flux as a function of time:

$$J=\left({J}_{0}-{J}_{R1}\right)\text{e}\text{x}\text{p}(-{K}_{1}t)$$

1.3 Details for second phase of fouling

The expression with n = 0 was superior and the relevant values of the parameters are:

${J}_{0}$ (LMH)	${J}_{R2}$ (LMH)	${K}_{2}$ (h−1)
18.23	1.18	0.0101

From Table 1, the flux equation is:$1/J=1/{J}_{0}+{K}_{2}(v-{J}_{R2}t)$