1 Introduction

The smart grid is the latest trend in the development of power systems in the world today and is considered to be a major technological innovation and development trend in the twenty-first century power system. Different countries in the world have proposed different design plans and ideas in the construction of intelligent substations. In China, the State Grid Corporation plans to build a unified and strong smart grid in 2009–2020. There is no uniform definition of the smart grid so far. It refers to a fully automated power supply network where each user and node is monitored in real time and guarantees a bidirectional flow of current and information at every point from the power plant to the customer premises. Through the widespread integration of distributed intelligence and broadband communication and automatic control systems, it ensures real-time market transactions and seamless connectivity and real-time interaction between members of the grid. Simply put, sensors are used to connect various devices and assets together to form a customer service bus, which integrates and analyzes information to reduce costs, improves efficiency and reliability of the entire grid, and optimizes operation and management [1].

At the beginning of the twentieth century, the International Regional Energy Association was established. Along with this century of industrialization, the United States has established a large number of industrial or community regional energy systems of 100 MW. In the middle and late nineteenth century, when the second industrial revolution was carried out in Japan, many industrial parks with comprehensive optimization of terminals were built, which greatly improved energy efficiency. In some European countries, such as Denmark, before the 1870s, about 93% of energy consumption needed to be imported [2]. However, since 1980, after two energy revolutions, Denmark has placed the development of a low-carbon economy at the national strategic level and formulated an energy development strategy suited to its national conditions. Regional energy strategies have been adopted in Sønderborg and even throughout Denmark and have been successful. Through its own success stories, Denmark presents the world with the superiority of regional integrated energy systems [3]. China’s economy has only begun to take off in the past 30 years, and the industrialization and urbanization marked by the first industrial revolution are still in progress. Therefore, it is difficult to get rid of the dependence on fossil fuels at present, which is also the historical reason for China's late development of regional energy. However, with the improvement of clean energy utilization technology and the advancement of energy structure reform, the construction of multi-energy complementary energy-related technology research and engineering demonstration projects is increasing year by year in China and has achieved fruitful results [4].

In 2003, the United States proposed the Grid 2030 program for the Integrated Energy System Development Program. The plan points out that distributed intelligent systems include nuclear energy, renewable energy, and combined energy equipment such as heat and power, which will improve the functionality and efficiency of existing systems, safety and operational quality, and change the structure of the grid structure. In the end, not only will the efficiency of the transmission be improved, but the efficiency of the market operation will also improve, so that a high-quality and safe US power network will be formed. Because of its small land area, Japan is seriously under-resourced, and its energy is mainly dependent on the imported national conditions, making it one of the first countries to conduct comprehensive energy system research in Asia. Moreover, Japan hoped to use the technological innovation in this field, combined with the construction of actual projects, to ease the pressure on domestic energy supply. Driven by the government, Japan has carried out extensive research on integrated energy systems from different aspects (such as smart community and intelligent micro-network research conducted by NEDO, and comprehensive energy network research by Tokyo Gas [5].

In China, the research on integrated energy systems is still in the development stage, but there are also some parts of the research in this direction. At the same time, with the various national policies on energy structure adjustment and comprehensive energy utilization, and the funding of various engineering projects, comprehensive energy utilization will present a research boom and a good practical vision in China. In China's "National Medium- and Long-Term Science and Technology Development Plan (2006–2020)", in-depth study of micro-scale gas turbines based on fossil energy supply and energy conversion technologies, energy storage technologies, combined heat and power systems, etc., and forming a hybrid distributed terminal energy supply system based on micro-compact gas turbines, energy storage equipment and cold and heat load supply equipment based on complementary renewable energy and fossil energy sources is emphasized [6]. On January 25, 2017, the National Energy Administration announced the first batch of 23 multi-energy complementary integrated optimization demonstration projects, including 17 terminal integrated energy supply system and 6 landscape water and fire storage multi-energy complementary systems, such as Beijing Lize Financial Business District multi-energy complementary integration optimization demonstration project, Zhangjiakou-Olympic scenery city multi-energy complementary integration optimization demonstration project, Weinan Fuping multi-energy complementary integration optimization demonstration project. With the advancement of the 13th Five-Year Plan, China has intensified its research on multi-energy complementary integrated energy systems [7]. In 2016, the National Energy Administration's Implementation Opinions on Promoting the Construction of Multi-energy Complementary Integrated Optimization Demonstration Project pointed out that building a multi-energy complementary integrated optimization demonstration project is one of the important tasks of building an “Internet + Smart Energy System”. It is conducive to improving the energy supply and demand coordination capacity, promoting energy clean production and nearby consumption, reducing wind, light, water and electricity, and promoting renewable energy consumption. and. It is an important starting point for improving the comprehensive efficiency of energy systems and has important practical significance and far-reaching strategic significance for building a clean, low-carbon, safe and efficient modern energy system [8]. The construction objectives proposed in the implementation opinion are: In 2016, on the basis of existing related projects, the project will be upgraded and integrated, and the first batch of demonstration projects will be started. During the 13th Five-Year Plan period, project indicators such as the establishment of more than 20 national-level integrated energy supply demonstration projects were also clearly proposed. Moreover, the provinces (autonomous regions and municipalities) also need to respond to the government's call to build new industrial parks and implement energy cascade utilization. The establishment of a national-level scenery, water and fire storage multi-energy complementary demonstration project effectively controls the abandonment of wind, the rate of light rejection, and the efficiency of energy use [9].

In order to achieve coordination and integration optimization of the power system itself, the energy system is established to establish an integrated energy system in a certain area. The interaction behavior and coupling relationship between different energy grids in integrated energy systems, the coordinated scheduling of multi-energy flows, and the solution of regional integrated energy optimization scheduling have become problems that need to be solved in comprehensive energy research. In this paper, the above problems are studied, the mathematical model of the hybrid power system is constructed, and the multi-objective optimization problem of the heating system is solved by the optimized particle swarm optimization algorithm, so as to optimize the overall performance of the heating system in terms of energy consumption, economic cost and environmental benefits.

2 Research method

2.1 Particle swarm optimization

The particle swarm optimization algorithm was proposed by Kennedy and Eberhart in the early 1990s. The core idea of the algorithm is to use the way of particle collaboration and information sharing to find the target location. In the algorithm, individuals in a group are considered to be particles with a volume and mass of approximately zero, which flies at a certain speed in a multidimensional space. In the process of finding the target position, each particle will feedback its own spatial position, and think that the current position is the best position found by itself. This cognition is defined as individual cognition. After each particle feedbacks its position, it is determined that the entire flock is currently finding the best position. This cognition is defined as social cognition. All the particles are constantly adjusting their current direction of movement and moving speed according to the two current best positions, and gradually approaching the optimal position. The particle search process can be illustrated as Fig. 1 [10]:

Fig. 1
figure 1

Schematic diagram of the particle search process

Full size image

As shown in Fig. 1: The current particle optimal position is represented by \(P_{itself}\); the current position of the particle is represented by \(P_{curren}\); the optimal position is represented by \(P_{globa}\); the particle speed after particle adjustment is represented by \(V_{updat}\); the current velocity of the particle is represented by \(V_{curren}\); and \(P_{updat}\) is the position after the particle is moved. If the particle combines the two optimal positions \(P_{itself}\) and \(P_{globa}\), it will adjust the flight speed to \(V_{updat}\) and quickly fly to the \(P_{updat}\) position. This process becomes a complete search and reaches the current optimal position. Through multiple searches, the optimal position of the group was found [11].

In PSO, the position of the particle corresponds to the solution to the problem. The fitness function value and the velocity and direction of particle flight determine the particle performance [12].

Assuming that the solution of the problem is distributed in the D-dimensional space, then the position of each particle in the PSO corresponds to a candidate solution to the problem. In the particle group composed of m particles, the position of the i-th particle is represented by \(z_{i} = \left( {z_{i1} ,z_{i2} , \cdots ,z_{iD} } \right)\). According to the fitness function, the fitness value of \(z_{i}\) is obtained. The quality of \(z_{i}\) can be reflected by the size of the fitness value. The larger the fitness value, the better the \(z_{i}\). The speed of the i-th particle is represented by \(v_{i} = \left( {v_{i1} ,v_{i2} , \cdots ,v_{id} \cdots ,v_{iD} } \right)\). The optimal position that the i-th particle is currently experiencing, that is, the individual extremum is represented by \(p_{i} = \left( {p_{i1} ,p_{i2} , \cdots ,p_{id} \cdots ,p_{iD} } \right)\). The best position that a particle swarm currently experiences is represented by \(p_{g} = \left( {p_{g1} ,p_{g2} , \cdots ,p_{gd} \cdots ,p_{gD} } \right)\), also known as the global extremum [13].

In the particle swarm iteration, the speed and position of the \(k + 1\)-th iteration are updated as follows [14]:

$$\left\{ {\begin{array}{*{20}c} {v_{id}^{k + 1} = wv_{id}^{k} + c_{1} r_{1} \left( {p_{id}^{k} - z_{id}^{k} } \right) + c_{2} r_{2} \left( {p_{gd}^{k} - z_{id}^{k} } \right)} \\ {if_{{}} v_{id}^{k + 1} > v_{\max } ,v_{id}^{k + 1} = v_{\max } } \\ {if_{{}} v_{id}^{k + 1} < v_{\min } ,v_{id}^{k + 1} = v_{\min } } \\ \end{array} } \right..$$
(1)
$$z_{id}^{k + 1} = z_{id}^{k} + v_{id}^{k + 1} .$$
(2)

In Eqs. (1, 2), \(i = 1,2, \cdots ,D\), w represents the inertia factor; k represents the number of iterations, \(r_{1} ,\;r_{2}\) is a random number, and its size is within the interval \(\left[ {0,1} \right]\).Moreover, \(c_{1} ,\;c_{2}\) denotes a learning factor and is also called an acceleration factor, the maximum speed threshold is \(v_{\max }\), and the minimum speed threshold is \(v_{\min }\) [15].

2.2 Binary discrete particle swarm optimization

In the binary discrete particle swarm optimization method, the binary encoding method is used to represent the position of each particle, that is, each dimension component of \(z_{i}\) can only be 1 or 0. At this time, each dimension component of the velocity \(v_{i}\) of the particle indicates the probability that the dimension component takes 1 or 0, and \(v_{i}\) represents the probability of the particle's position change [16].

In the \(k + 1\)-th iteration of the search, the speed update rule of particle i is still Eq. (1), and the update rule of position becomes the following formula [17]:

$$z_{id}^{k + 1} = \left\{ {\begin{array}{*{20}c} {1,r < Sigmoid\left( {v_{id}^{k + 1} } \right)} \\ {0,\;others} \\ \end{array} } \right..$$
(3)
$$Sigmoid\left( {v_{id}^{k + 1} } \right) = \frac{1}{{1{\text{ + exp}}\left( { - v_{id}^{k + 1} } \right)}}.$$
(4)

In Eqs. (3, 4), r is a random number in interval \(\left[ {0,1} \right]\), and the remaining parameters are the same as those in the basic particle swarm optimization algorithm.

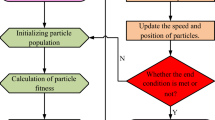
The basic process of PSO is as follows:

  1. 1.

    Initialization. Including: m particles are generated, the velocity \(v_{i}\) of the particles and the position \(z_{i}\) of the particles are initially initialized, the initial values of parameters such as w, \(c_{1} ,\;c_{2}\),\(v_{\max }\), \(v_{\min }\), and so on are set, and the fitness values of all the particles are calculated. Moreover, the initial individual extremum \(p_{i}\) of the particle is set to \(z_{i}\), and the initial value of the global extremum \(p_{g}\) is set to the optimal \(p_{i}\) of the adaptive value [18].

  2. 2.

    Update the particle swarm. The velocity and position of each particle are updated according to Eqs. (1, 2), and the binary discrete particle swarm is updated according to Eqs. (1, 4, and 5).

  3. 3.

    Evaluation of particle swarms. The fitness value of each particle is calculated based on the fitness function

  4. 4.

    Check the termination conditions. If the termination condition is met, the optimization ends, otherwise, the next step is entered.

  5. 5.

    Update the individual extreme value \(p_{i}\). If the fitness value \(p_{i}\) of the particle \(i\left( {i = 1,2, \cdots ,m} \right)\) is better than its current fitness value, the individual extremum is replaced by the current position of the particle i.

  6. 6.

    Update the global extremum \(p_{g}\). The current global extreme fitness value is compared with the optimal fitness value of each particle. If the former is better, the particle position from which the fitness value is obtained is taken as the global extreme value. Next, the algorithm returns to the second step and proceeds to the next loop.

In the actual calculation process, it is generally expected that the algorithm can converge globally within a certain solution interval, and then it performs a more detailed local search in the solution interval. Therefore, a larger inertia weight can be used at the beginning of the algorithm operation, and a smaller weight can be used later. The specific calculation formula of inertia weight is shown in formula (5) [19]:

$$w = w_{\max } - \frac{{w_{\max } - w_{\min } }}{{Iter_{\max } }} \times Iter .$$
(5)

In the above formula: the minimum and maximum values of w are usually expressed as \(w_{\min }\) and \(w_{\max }\), which are usually 0.4 and 0.9. The current number of iterations is represented by \(Iter\), and the maximum number of iterations is represented by \(Iter_{\max }\).

Through the algorithm, it is possible to achieve the goal of increasing the number of iterations and reducing the number of iterations, realizing the global fast search in the previous stage, determining the solution interval, and the requirement of more detailed search in the latter stage [20].

  1. 7.

    Acceleration factor \(c_{1} ,\;c_{2}\).\(c_{1}\) Reflects the “individual cognition” ability of the particle, and \(c_{2}\) reflects the “social learning” ability of the particle. If the value of \(c_{1}\) is small, the algorithm's individual ability in cognitive knowledge is relatively poor, and even if the convergence speed is accelerated, the optimal solution is easy to localize. If the \(c_{2}\) value is relatively small, the algorithm's ability in social cognitive ability is relatively poor, which leads to insufficient information sharing ability between particles and thus leads to a smaller probability of searching for a global optimal solution. If the values of \(c_{1}\) and \(c_{2}\) are small, the particles are not easily accessible to the target area for searching. If the values of \(c_{1}\) and \(c_{2}\) are both large, the particles may fly out of the target area. In short, if the values of the acceleration factors \(c_{1}\) and \(c_{2}\) are too large or too small, the ideal optimization effect cannot be obtained. Through research, it is found that \(c_{1} = c_{2} = 2\) is generally set in domestic and foreign periodicals.

  2. 8.

    Maximum speed \(v_{\max }\). Setting the maximum speed \(v_{\max }\) is equivalent to selecting the maximum value of the particle velocity step and is equivalent to determining the accuracy of the current interval and the optimal position interval. If \(v_{\max }\) is too large, the particle will cross the optimal solution position, and if \(v_{\max }\) is too small, the particle will easily fall into the local region and cannot explore in the global optimal region to obtain the optimal solution. Setting the flight speed of the particles by \(v_{\max }\) can effectively control the flight range of the particles. For example, if the particle \(\left( {x_{1} ,x_{2} , \cdots x_{n} } \right),x_{1} \in \left[ { - \;8,8} \right]\), the maximum velocity \(v_{\max }\) of the particle is 8.

3 Results

When a serious out-of-step or cascading failure occurs in the system, the elimination of out-of-step oscillation depends on a safe and rapid disaggregation operation, which prevents the malicious spread of the accident in the power grid and avoids a large-scale blackout. The core of out-of-step decoupling control is the out-of-step disjunction criterion. In this section, through in-depth analysis of the characteristics of each of the dissolving criteria and the adaptation occasions, combined with the application of the grid-connected composite device, this paper improves the disassembly criteria for the grid-connected composite device.

When the interconnected power grid is seriously out of step, the stability of the system is destroyed. It usually shows that the relative power angle difference δ on both sides of the system shows a periodic change of 0º–360º, and the electrical quantities such as voltage and current will oscillate strongly. Normally, the probability of out-of-step oscillation appearing on the contact line is relatively large.

Based on the synchronous grid-connected composite system, this paper integrates the out-of-step decoupling criterion into the VSC-HVDC synchronous grid-connected system. In this way, the system has the function of quickly disassembling after losing the step. After the solution, the network is re-connected by adjusting the strategy to achieve the purpose of integration of control functions and reduce the losses caused by system failure. The VSC-HVDC composite system adopts grid-connected operation when the two systems are not connected to the network. At this time, the UCosφ out-of-step disassociation criterion will judge that the system is in an asynchronous state by detecting the corresponding electric quantity, and UCosφ appears to periodically oscillate, and there is a zero crossing. According to the out-of-step disengagement criterion, the circuit breaker on the contact line always receives the disengagement signal, and the grid connected cannot continue. This means that the grid connected operation and the disjunction criteria are contradictory. If the out-of-step decoupling control function is not activated during the grid-connected operation, when the system is running in the grid, there will be no chaos on the line or the closing is not timely.

When the system is connected to the grid, the circuit breaker QF on the tie line is always off, and the line current is 0 from start to finish. In the process of completing the grid-connected function and the grid-connected mode to the UPFC, the QF is always in a closed state, and the current value on the tie line is stabilized at a value greater than zero.In the whole process of successful grid connection and the conversion of the grid-connected mode to UPFC and UPFC for tie-line power flow control, it is always necessary to detect the electrical quantities of the two sides of the system and the contact line in real time. Therefore, the state of the circuit breaker QF on the tie line is used as the starting criterion for the disjunction criterion. When the circuit breaker QF on the tie line is disconnected, the disengagement criterion is not involved, and the disengagement criterion is started when the circuit breaker QF is closed.

After the grid connection is successful, a single-phase short-circuit ground fault with a duration of 5 s is added to the line at t = 130 s. The waveform shown in the image below shows the UMosφ and the phase angle difference on both sides of the system and the action of the circuit breaker on the tie line when a short circuit fault occurs. Figure 2 shows that the system is in the grid-connected operation phase before 100 s, and the UCosφ waveform periodically crosses zero. At this time, the circuit breaker QF on the contact line is disconnected, and the out-of-step disengagement criterion is not activated. When t = 100 s, the grid connection is successful, and the UCosφ value is stable at 33.37 kV after fluctuating. At this time, the circuit breaker QF is closed, and the out-of-step disengagement criterion is started. When t = 130 s, Uxos will have a significant fluctuation but the value does not pass the zero point and the fault disappears quickly and then returns to the stable value. Therefore, the out-of-step dissolving criterion does not work. Figure 3 reflects the phase angle difference between the two sides of the system when a short-circuit fault occurs after successful grid connection. Figure 4 shows the operation of the circuit breaker QF on the tie line. It can be seen from the figure that after t = 100 s and being successfully connected to the Internet, QF is closed. From the simulation results, it can be concluded that the UCosφ-based out-of-step decoupling criterion can effectively distinguish the system short-circuit fault.

Fig. 2
figure 2

UCosφ waveform change

Full size image
Fig. 3
figure 3

Waveform image of the phase angle difference between the two ends of the contact line \({\mathrm{l}}_{12}\)

Full size image
Fig. 4
figure 4

QF breaking signal of the circuit breaker of tie line \({\mathrm{l}}_{12}\)

Full size image

In order to verify the out-of-step decoupling control function, the phase angle of the system S2 is programmed to mutate to 180° at t = 130 s (Human changes, simulating serious failures), which causes the entire system to oscillate, thereby determining whether the system is out of step by the disjunction criterion action. The simulation results in the figure below show the change of UCosφ in the whole process, the change of the phase angle difference on both sides of the system and the action of the circuit breaker on the tie line. Figure 5 reflects the current change of the tie line \({\mathrm{l}}_{12}\) when the system is out of step. It can be seen from the waveform diagram that when t = 130 s, the current of the tie line \({\mathrm{l}}_{12}\) is suddenly changed to about 4kA. Figure 6 shows a partial enlarged view of the current on the contact line after the grid connection to the fault. The waveform of UCosφ in Fig. 7 shows that the periodic oscillation occurs after UCos suddenly drops to zero at t = 130 s, which satisfies the condition of the out-of-step dissolving criterion of UCosφ, and the system issues a dissociation signal. When close to t = 133 s, the tie line \({\mathrm{l}}_{12}\) breaker is disconnected, and the system is unpacked. Figure 8 is a partial enlarged view of UCosφ at the time of grid connection. Figure 9 is a graph showing the phase angle difference waveform of the systems on both sides. Starting from t = 130 s, the phase angle difference starts to gradually increase until it is about 180°, then falls back, and finally becomes continuous periodic fluctuation. Figure 10 reflects the switching state of the circuit breaker throughout the simulation.

Fig. 5
figure 5

Current change waveform of tie line \({\mathrm{l}}_{12}\)

Full size image
Fig. 6
figure 6

Partial enlargement image of the current of the tie line \({\mathrm{l}}_{12}\) at the time of grid connection

Full size image
Fig. 7
figure 7

UCosφ waveform change diagram

Full size image
Fig. 8
figure 8

Partial enlargement of the UCosφ waveform of the UPFC mode to the UPFC

Full size image
Fig. 9
figure 9

Waveform image of the phase angle difference between the two ends of the contact line \({\mathrm{l}}_{12}\)

Full size image
Fig. 10
figure 10

QF breaking signal of tie line \({\mathrm{l}}_{12}\) breaker

Full size image

A multi-channel selection switch is connected in the composite system, and the control strategies in different operation modes are selected according to the values of \({\mathrm{K}}_{i}\left(i=\mathrm{1,2},\mathrm{3,4}\right)\) to realize the functions in different operation modes. According to the switching state, circuit structure and starting criterion of the three operating modes of the de-listing, parallel and tie-line power flow control, a closed-loop continuous control strategy flow can be formed. The running state of the composite system is determined according to the scheduling instruction. If the grid-connecting command is issued, at this time, since the systems to be paralleled are not connected and independent of each other, the composite criterion detects that the system has been in an out-of-synchronization state, so that the de-serial signal is issued and the QF is always connected to the disconnection command. Therefore, the system cannot complete the grid connected operation. In order to avoid this contradiction, the out-of-step de-column monitoring is turned off before the grid connection, that is, the out-of-step disassociation control function does not work. The composite device is converted into a back-to-back VSC-HVDC circuit structure by corresponding electrical operation, and the power transmission principle is applied to make the relevant electrical quantity reach the set value range of the grid connection requirement, the circuit breaker is closed, the synchronous grid-connected operation is completed, and the back-to-back VSC is taken out of operation. Then, the disassociation control is started to monitor the related electric quantity of the system on the contact line and the two sides. At this time, if the scheduling command compound system realizes the UPFC function, the composite device is converted into the UPFC device through the related electrical conversion operation. Under the UPFC control strategy, the power of the tie line is adjusted. When the system is subjected to large disturbances and out-of-step oscillation occurs, the disassociation criterion issues a disassociation command, the system is unpacked, and the QF is disconnected. At this time, the VSC-HVDC grid-connected device provides power support to the de-serial subsystem in an asynchronous networking manner and minimizes the impact of the cutter-loading operation on the system, so that the two systems can be in a stable state to the maximum extent. After the fault is eliminated, the grid-connected is restored.

The simulation results show that the system can be quickly decomposed under the action of the composite criterion when the step is lost, and the fault spread is avoided. After the fault is eliminated, the system can quickly restore the grid-connected and regain the steady state after the grid-connected control strategy.During the transition from the grid-connected operation mode to the UPFC operation mode, the active power, reactive power, voltage on the two sides of the system and the current change waveform on the tie line will have a significant fluctuation, but the fluctuation time is very short, and the system can quickly restore the steady state. Under the UPFC control strategy, the tie line current is controlled. Moreover, the validity and correctness of the three-in-one comprehensive control strategy proposed in the paper are fully verified.

4 Analysis and discussion

This paper preformed a comparative analysis of the existing out-of-step dissociation criteria and pointed out the limitations of the proposed out-of-step dissociation criteria for grid-connected composite devices. Aiming at the contradiction between the grid-connected process and the out-of-step disengagement criterion, combined with the characteristics of grid-connected process and out-of-synchronization, this paper proposed improvement measures for the out-of-step disengagement criterion of the grid-connected composite device, and verified the decoupling control function. Secondly, the correlation between the three operation modes of grid connection, disconnection and tie line power flow control is analyzed. In addition, on the basis of the proposed switch matrix of the grid-connected composite device, the out-of-step disengagement part was added, and the out-of-step disassociation and grid-connected, tie-line power flow control were switched through a control strategy multi-way selection switch to control the three-way operation control strategy, and the three-in-one integrated control strategy was studied and simulation.

Based on the back-to-back VSC-HVDC synchronous grid-connected composite system, this paper studied the integrated control strategy of the same set of back-to-back voltage source converters to achieve simultaneous grid-connected and tie-line power flow. Moreover, the proposed demarcation criterion for the grid-connected composite device has been improved to some extent. In addition, on this basis, the simulation control of the three sets of functions of de-listing, juxtaposition and tie line power adjustment of the same set of devices was carried out. Through the simulation results, the summary is as follows:

  1. 1.

    This paper introduces the principle of back-to-back VSC-HVDC applied to synchronous grid-connected and UPFC power flow control, and analyzes the mathematical model of voltage source converter. Moreover, this paper deeply compares the same input and output, different input and output, and control amount of the grid-connected control strategy and the UPFC control strategy selected in this paper. In addition, this paper integrates two sets of control strategies and proposes a joint control strategy to realize the simultaneous juxtaposition and tie line power adjustment between power grids.

  2. 2.

    Considering the impact that the switching action will cause on the system during the transient process of the grid-connected composite device to switch to the UPFC, the method of switching the UPFC device to the UPFC is proposed. Moreover, this paper verifies the feasibility of the grid-connected model to UPFC through simulation. At the same time, considering the impact caused by the series transformer bypass switch action in the scheme, the "zero current control" method is adopted to reduce the impact caused by the access of the UPFC series transformer to the system. Finally, the simulation verification of the power flow control function after the grid-connected device is converted to UPFC is carried out.

  3. 3.

    For the out-of-step disjunction criterion of the proposed grid-connected composite device, there is a contradiction between the grid-connected runtime and the out-of-step solution. In this paper, the previous tie line current setting start criterion is changed to the switch state of the circuit breaker QF on the tie line as the start criterion, and the UCosφ out-of-step disengagement criterion is formed. The switch state of the circuit breaker QF on the tie line is the composite criterion of the start criterion, which effectively solves the problem of the conflict between the grid connection operation and the disjunction criterion in the integrated control and simulates the validity of the composite criterion.

  4. 4.

    In this paper, some simulation studies on the integrated control of the de-column, parallel and tie-line currents are carried out. The simulation verifies the effectiveness of the three-integrated integrated control strategy.

5 Conclusion

In summary, in order to prevent the large-area fault caused by the chain reaction of the grid accident, it is necessary to effectively validate the out-of-step disengagement criterion, and also need to solve the subsystems quickly and accurately reconnected to the grid and control the tie line currents in time after the system is juxtaposed. Therefore, the comprehensive control of de-listing, juxtaposition and tie line tidal function has important theoretical and practical significance for improving the self-healing ability and automation degree of power system and the rational use of resources. Based on the back-to-back VSC-HVDC grid-connected composite system, this paper studied the integrated control strategy of the device to realize the simultaneous parallel and tie line currents. Moreover, this paper simplified and improved the proposed disassembly criteria for the grid-connected composite device and integrates it into the grid-connected composite device. In addition, on this basis, the integrated control of the three functions of de-listing, juxtaposition and tie line power adjustment of the same device was further studied. Finally, this paper taken PSCAD/EMTDC as the research tool and adopted the simulation verification for the function of the composite device to be converted into UPFC operation and the integrated control flow of the parallel and tie line power adjustment.