Abstract
Unmanned Aerial Vehicles (UAVs) have quickly become one of the promising Internet-of-Things (IoT) devices for smart cities. Thanks to their mobility, agility, and onboard sensors’ customizability, UAVs have already demonstrated immense potential for numerous commercial applications. The UAVs expansion will come at the price of a dense, high-speed and dynamic traffic prone to UAVs going rogue or deployed with malicious intent. Counter UAV systems (C-UAS) are thus required to ensure their operations are safe. Existing C-UAS, which for the majority come from the military domain, lack scalability or induce collateral damages. This paper proposes a C-UAS able to intercept and escort intruders. It relies on an autonomous defense UAV swarm, capable of self-organizing their defense formation and to intercept the malicious UAV. This fully localized and GPS-free approach follows a modular design regarding the defense phases and it uses a newly developed balanced clustering to realize the intercept- and capture-formation. The resulting networked defense UAV swarm is resilient to communication losses. Finally, a prototype UAV simulator has been implemented. Through extensive simulations, we demonstrate the feasibility and performance of our approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Unmanned Aerial Vehicles (UAVs) have quickly found their way into the Internet-of-Things (IoT) ecosystem as part of smart cities thanks to their three-dimensional mobility, agility, and onboard sensors’ customizability. UAVs are nowadays used in a wide scope of commercial applications ranging from monitoring, surveillance, mapping to parcel delivery.
As governments plan using UAVs to build fresh economic potential for innovation, urban planners are moving forward to incorporate so-called UAV flight zones and UAV highways in their smart city designs [1]. This IoT-UAV infrastructure can be deployed for UAV real-time monitoring for fire detection confirmation [2] and for UAV Air Pollutants Monitoring [3].
Initiatives like NASA UTM [4] or European U-Space [5] aim at providing a framework for a regulated and safe UAV traffic management in the yet unregulated class-G airspace. However these will not prevent potential intruders, rough drones, or UAVs with malicious intent to enter the shared airspace and potentially harm other UAVs or even citizens.
It is thus necessary to develop efficient and scalable counter-UAV systems (C-UAV) to ensure safe UAV operations. C-UAV permit to detect and identify a malicious UAV and act on it using sensing and mitigation systems respectively. This work specifically focuses on mitigation techniques, which to date mainly stem from the military domain. The most prominent ones are ground-based systems such as radio frequency (RF) of Global Navigation Satellite System (GNSS) signal jamming to disrupt the UAV communication and navigation systems [6] and net or laser guns which impact the physical integrity of the malicious UAV [7]. These however induce possible collateral damages and lack scalability. On the contrary, very few C-UAS are air-based solutions. These exist mainly for reaching the close vicinity of the malicious UAV in order to maximise the efficiency of existing ground-based mitigation techniques like signal jammers or net guns [8].
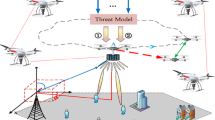
This work goes beyond the state-of-the-art by proposing an innovative air-based C-UAV system that uses a swarm of UAVs as mitigation technique. Our C-UAV system based on defense UAVs (dUAVs) which can autonomously and collaboratively act as a defense swarm. Malicious UAVs (mUAVs) can then be intercepted, captured and escorted out of the flight zone. Our swarm of dUAVs forms a three-dimensional cluster around the mUAV using both local clustering [9, 10] and local positioning in 3D-space such that the latter has a minimum number of movement possibilities. Hereby, we assume that the mUAV is trying to avoid colliding with dUAVs to maintain its functioning. The dUAVs enclose the mUAV to limite its movement possibilities (Fig. 1).
Contributions We propose a comprehensive C-UAV system, which auto-deploys a swarm of autonomous dUAVs to create intercept- and capture-formations to tackle intruders (mUAVs).
The most outstanding features and contributions of the presented approach are the balanced clustering to realize the intercept- and capture-formation. Additionally, the approach consists of a modular design containing the phases such as swarming, clustering, local formation control, and capturing. All parts of the approach are fully localized and GPS-free, with the defense UAV swarm exhibiting resilience against communication loss.
Results Simulations have been conducted to understand the influence of the parameters on the performance of the C-UAV defense system. Results show that some parameters have a greater influence over the simulation time that is needed to escort the malicious UAVs than others. More precisely, in order to minimize this time, the following measures need to be taken: The wobbling of UAVs should be as low as possible, while the collision threshold of the dUAVs should be greater than the one of the mUAVs and the dUAV communication range should be as high as possible.
The remainder of this paper is organized as follows. Section 2 presents the state-of-the-art. Section 3 gives a motivation to the problem statement, following by a listing of all used notations and the system model that will be used later on. Section 4 describes and formalizes each phase of our approach in detail. In Sect. 5, we present the prototypical implementation and discuss experimetnal results in Sect. 6. The paper concludes with Sect. 7.
2 Related work
This section describes related work to UAV defense systems and UAV defense swarms, but also to formation and positioning of UAVs in the 3D space.
2.1 UAV defense systems
UAV defense systems are used in order to protect against threats, being either intentional (e.g., hostile mission) or unintentional (e.g., trespassing in a restricted area). Such defense systems are typically described as multi-layered or multi-steps systems, designed to cope with a variety of possible attacks [11]. While the literature is replete with research on UAVs, until recently counter-UAVs systems have received little attention. Few surveys are [12,13,14,15,16], the most recent and comprehensive is by Kang et al. [17].
In this work we categorize UAV defense systems in two main classes: ground-based and air-based solutions. Both solutions rely on sensing and mitigation systems, the former allowing to detect and identify a mUAV while the latter permits to act, from simple warning to the neutralization of the mUAV.
A wide range of technologies can be used for the detection and the identification of a potential threat, such as video cameras, thermal cameras, radars, acoustics sensors, magnetic sensors or RF signal detection. These feature different levels of performance according to the type UAV to detect. Such technologies are out of the scope of this study, the interested reader can refer to [17] for detailed information.
We here focus on mitigation solutions. These can be divided into physical and non-physical systems, if they respectively impact or not on the physical integrity of the mUAV.
Existing non-physical systems have mainly focused on radio frequency (RF) and Global Navigation Satellite System (GNSS) signal jamming. These permit to disrupt the mUAV communication [6] and navigation system [18]. Even when considering sophisticated communication protocols, there are still fundamental vulnerabilities existing [19]. While mainly developed in ground-based systems, jamming mitigation is also used by some air-based systems since the closer to the target the more effective the jamming is [8]. Other non-physical solutions consider high power electromagnetic radiation (HPEM). Its purpose is to alter the electronics onboard a mUAV which will result in its crash [20]. The last non-physical systems are lasers, which permit to neutralize the sensors of a mUAV or even destroy the mUAV itself if powerful enough [21].
When it comes to physical systems, which aim at neutralizing the mUAV, solutions range from projectiles to eagles, nets and UAVs. Counter-UAS projectiles include machine guns and missiles and are usually assisted by tracking systems like electro-optical sensors which might rely on AI. These are costly and the risk of collateral damage is high. The most known physical systems are nets, which permit to block the mUAV propeller(s) and thus stop its progression. Such nets can be thrown by guns/cannons [7] as part of ground-based solutions or directly launched from one UAV [22] or carried between a couple of UAVs [23] as part of an air-based solution. Such systems are well adapted to small mUAV and cause minimum collateral damage when nets are equipped with parachutes which make them more suitable in populated environments. However their range of action is limited. A few police forces have trained eagles to catch mUAVs [24]. However this solutions remains marginal and potentially harmful for the birds For that reason, other solutions using drones as attackers (also referred to as collision UAVs) are now considered. Such UAVs are capable of flying at high speeds, are equipped with detection and tracking systems and can additionally carry explosives to increase the collision effect. Potential collateral damage is thus high.
All these solutions have considered countering a single malicious UAV. However, intruders can also be UAV swarms themselves [25]. Since such enemy swarms are difficult to target and financially not worth being taken down, the U.S. military is investing on swarm-on-swarm warfare tactics in order to attack other enemy swarms [26, 27].
Some recent works considered UAV swarms for fast area scanning, target detection and tracking [28, 29]. Such approaches use swarms in order to be more efficient and reliable in the detection and identification phases, but contrary to this work they do not use the swarm itself as a mitigation strategy.
Indeed such UAV defense swarms can be used for collapsing and trapping an enemy swarm. Collapsing is being done via communication jamming in order to disrupt the enemy swarm such that the individual drones get disintegrated and uncoordinated. The defense UAV system can also trap the enemy swarm to force it into a disadvantageous position such as an unfavorable area outside a critical zone. This strategy is similar to the approach presented in this paper.
2.2 Node positioning approaches
There exist some node positioning approaches to position UAV in the 3D-space which are related to our work. For example, Brust et al. [30] proposed VBCA, a virtual forces clustering algorithm, which imitates the VSEPR model, [31] from molecular geometry for the arrangement of UAVs in a clustered swarm. The UAV’s position is determined by the distance and role of its neighboring UAVs. VBCA assigns the role of a clusterhead to one UAV. This central UAV acts as a connector influencing the entire topology of the network geometry while individual UAVs are only affected by their direct neighbors. VBCA is maximizing the volume coverage, while maintaining advanced connectivity within the clustered UAV swarm.
Al-Turjman et al. [32] introduced a 3-D deployment strategy for relay nodes in WSNs (wireless sensor networks) for forestry applications maximizing network connectivity while maintaining a period of lifetime. The approach uses a two-layer hierarchical WSN architecture and determines the relay node positions on a 3-D grid to maximize connectivity with constraints on the available number of nodes and required lifetime.
Barnes et al. [33] addressed the problem of coordinating a swarm of Unmanned Ground Vehicles (UGV) with a UAV. The authors used a single UAV as a leader for the UGV swarm. The UGV formation is achieved by artificial potential fields. More specific swarm controlbehaving according to a set constraints, formation, and member spacing was provided by the usage of limiting functions. A small configuration of three UGVs and one UAV was used to demonstrate their approach. In addition the scalability of this approach has not been validated or discussed.
Kim et al. [34] proposed a multiple UAV platform based on artificial potential function (similar to [33]), which guarantees collision avoidance. Their approach relies on optimization techniques to generate the optimal trajectory. Although the approach is demonstrated using a single constant point, the authors claim it can be applied for multiple target points.
3 Problem description and system model
This section describes the notations and definitions as shown in Table 1 as well as the assumptions, properties, and communication model, which define the system model on which our proposed counter UAV system is based.
For this paper, we assume a malicious UAV (mUAV) has been detected in the flight zone and a number of defense UAVs (dUAVs) have been instructed to initiate the defense mission. The mUAV tends to escape when it detects the dUAVs (cf. Fig. 1).
3.1 Assumptions
-
The mUAV has already been detected by every dUAV.
-
The mUAV has a slightly lower top speed than dUAVs in order to avoid static locking.
-
Every UAV actively tries avoiding collisions with each other.
-
mUAVs have a higher collision threshold than dUAVs.
-
All UAVs have transmission, distance, relative positioning and absolute position sensing capabilities.
-
A high-quality UAV monitoring system in place that is capable to detect and identify malicious UAVs.
3.2 Properties
-
Each dUAV can have at most one parent and a child.
-
CHs have no parent and can have up to \(n_B\) children.
-
Each CH stores a \(n_B\).
-
A branch is a dUAV that has a CH as parent.
-
The length of a branch x is defined by the number of dUAVs in parent-child relations starting from x. The length of x is denoted as |x|. Example: CH\(\rightarrow a\rightarrow b \rightarrow c \rightarrow d\). Then, \(|a| = 4\).
-
Every dUAV has a clustering weight \(w_B\), which is initially set to 0.
-
A leaf is the last dUAV in a branch, has the largest \(w_B\) in the branch and has no child.
-
\(w_B\) of a dUAV is defined as its position on a branch. Example: \(CH \rightarrow a \rightarrow b \rightarrow c \rightarrow d\) with \(w_B\) assignment (CH, 0), (a, 1), (b, 2), (c, 3), (d, 4)
-
The difference of the lengths of any two branches cannot exceed 1.
3.3 Communication model
Each UAV is equipped with a network adapter to establish a communication channel between UAVs. The communication itself could be realized with infrastructure-less and self-configuring UAV Ad hoc Networks (UAANETs) [35] that are a subset of the well-known Mobile Ad hoc Network (MANET) paradigm. For the sake of simplicity, we assume that every UAV has the capability of periodically scanning the surroundings by using a circular transmission range. Furthermore, we assume a reliable communication channel.
4 Counter UAV defense system: approach
Our approach consists of a swarm of dUAVs that forms a 3-dimensional cluster around the mUAV in such a way that the mUAV has a minimal set of movement possibilities. Hereby, we assume that the mUAV is trying to avoid collisions with dUAVs to maintain its functioning. By enclosing the mUAV, the the dUAVs are then able to escort the mUAV outside the flight zone. The proposed approach follows a modular design, implementing four phases to realize the escort maneuver (task, problem), which are patrolling, detection, interception, and counter-attack.
The patrolling phase is simply explained by the defense UAVs surveying the flight zones rather passively until a detection of an anomaly triggers the next phase. The clustering and formation algorithms for detection and interception phases are executed simultaneously during the entire mission, whereas the transition between the interception and counter-attack phases are decided by the CH depending on the following conditions:
-
1.
Chase phase to escort phase: The distance between the CH and the mUAV is lower than \(r_F\).
-
2.
Escort phase to chase phase: The distance between the CH and the mUAV is higher than two times \(r_F\).
Details about the individual phases will be explained in further detail in the upcoming sections.
4.1 Detection
The clustering procedure is inspired by the design principles of the KHOPCA clustering algorithm [9, 10] (cf. Sect. 2) with the key difference that the structure of the cluster remains balanced. We use KHOPCA for three main reasons. Firstly, it provides a leader election algorithm that creates cluster heads, which is the entry point for our clustering algorithm. Secondly, KHOPCA does not require weights for the cluster head to be unique. Implementing a simple leader election would require such an assumption. Lastly, KHOPCA has been proven to be suitable for highly dynamic networks, such as the ones encountered in our problem scenario.
The cluster structure consists of the CH being in the middle of the cluster, acting as a coordinator of the whole cluster and a set of branches that originate from the CH. The reason for maintaining a balanced structure is the formation. Our goal is to construct a clustering that is suitable for the desired formation that looks like a closed hemisphere where the CH tries to enclose its branches in order to catch the mUAV. Therefore, the branches should ideally have the same length for them to be balanced. We also introduced the notation of a branch since it simplifies the modeling of the formation by considering a sequence of inter-connected dUAVs rather than single ones. The weighting constraint is defined as follows:
The weighting constraint states that the difference of the lengths of any two branches cannot exceed 1. In Sect. 4.1.4 we illustrate how the re-balancing of the cluster works. Re-balancing is required due to unexpected connection losses. In Sect. 4.2 we elaborate on the formation.
The clustering is done fully locally at each UAV. We can distinguish between the three different states that an UAV can be in: UAV, dUAV and CH. The difference between UAVs and dUAVs is that UAVs have no parent, hence are not in a cluster and are searching for a parent while dUAVs are cluster members that are being coordinated by the CH for performing the escort mission. Every other dUAV will adapt his weight according to its parent. The dUAVs with weight \(w_{B_i}\) are exactly \(w_{B_i}\) hops away from the CH. Note that the weight of the clustering is not the same as the weight that KHOPCA provides. We differentiate between \(w_B\) and \(w_K\), where \(w_B\) is the weight of the balanced clustering algorithm and \(w_K\) is the one from the KHOPCA algorithm. We run both KHOPCA and our balanced clustering algorithm simultaneously. In the following, we elaborate on the different states of UAVs.
4.1.1 Behaviour: UAV
Initially every UAV is parent-less and scans the neighborhood for a parent. Every UAV does not accept children by default and is flying to the mean position of the neighborhood. This flocking ensures that UAVs nearby will gather, consequently, forming larger and fewer clusters. The flocking is described in the Algorithm 1 and the behavior of UAVs is described in the Algorithm 2.


The UAVs scan the neighborhood for possible parents that accept children. If there exists more than one, we should consider to apply a criterion to choose one from |parents|. Our criterion is the minimal distance from the requesting UAV to the parent. Therefore, we sort the possible parent dUAVs in ascending order of distance. This enables a short communication channel and hence fewer potential connection losses. However, other criteria could be applied as well.
4.1.2 Behaviour: cluster head (CH)
As soon a UAV is elected as CH by the KHOPCA algorithm, it starts accepting children. CHs stop accepting further children if \(n_B\) is reached. CHs then inform the children that they can now start accepting an additional child. We distinguish between the following two message types:
-
1.
Basic message
These messages are sent from the CH to its branches in order to trigger them into accepting an additional child (BM-A) or to discard (BM-D) the current child. Discarding a child at \(w_{B_r}\) of a branch r leads to the discarding of \(|r|-w_{B_r}+1\) dUAVs since the message will be passed recursively to all children.
-
2.
Control message
CMs are recursively sent from dUAVs to the CH in order to notify about a new child.
CMs, as shown in Algorithm 3, have the purpose of knowing the length of the branches of a CH which is crucial for the balancing mechanism.

The algorithm runs until \(|B| = n_B\). Then, CHs only act upon message receipt. Upon receipt of a CM, CHs send a BM-A message to all its branches that have the minimal length among all branches. Hence, the leaves can start accepting a new child. This is how the CH ensures balancing. This behavior upon message receipt is described in the Algorithm 4.

4.1.3 Behaviour: dUAV
The dUAVs have a parent and hence are in a cluster. They wait for incoming messages from the CH and are ready for chasing and formation. The dUAVs that are leaves in a cluster might still accept children. Let d be a dUAV that has accepted a UAV c as a child. Then, the following steps are executed:
-
c will join the cluster, hence become a dUAV
-
\(c.w_B \leftarrow d.w_B + 1\)
-
\(d.accept = false\)
-
d will send a CM to its parent
Let d receive a CM. d will propagate the CM to his parent. Also, let d receive a BM-A message. If d has a child, it will no longer accept children and propagate the BM-A message to its child. If d is a leaf, it will start accepting a child. Furthermore, let d receive a BM-D message. If d has a child, it will propagate the message to his child and discard the connection. In the next step, d will take the state of a UAV, thus resetting its \(w_K\), performing flocking and searching for a new parent.
4.1.4 Cluster rebalancing
Due to connection losses, the cluster can lose its balance. Therefore, we implemented a auto-balancing mechanism that keeps the cluster balanced according to the weighting constraint. The re-balancing of a cluster is depicted in Fig. 2(left). Algorithm 5 shows the procedure of cluster re-balancing. Note that only CHs run the re-balancing algorithm.

For illustrating of how the cluster rebalancing functions, consider the cluster as shown in Fig. 2(left) and suppose there is a connection loss in the red branch between the dUAVs with the weights 1 and 2 respectively. It follows that the weighting constraint is violated since the difference of the lengths between the blue and red branches is 2. The re-balancing algorithm will run and search for the minimal branch length, which is \(min = 1\) in this case. Iteratively, every branch b will be checked if \(|b| > min + 1 = 2\). The green branch fulfills this condition, hence this branch will be “cut” between the weight levels \(min + 1 = 1 + 1 = 2\) and \(min + 2 = 1 + 2 = 3\). This cutting of branches is done via BM-D messages. After the balancing of the cluster, the weighting constraint is respected again.
4.2 Interception formation
With the aim of escorting in mind, the swarm of dUAVs chasing must ensure that the movement of the mUAV is restricted while the escort phase is under operation. The cluster of dUAVs must strive to restrict the mUAV to be able to only move in one direction. To achieve the following, a formation model must be realized. This model should be resistant to any disruptions caused by the mUAV. Following from the assumption that \(\epsilon _m > \epsilon _d\) , one constraint we need to ensure is that the distance between the dUAVs within the formation is not too high which could allow the mUAV to escape.
The formation shape chosen for this particular problem is an hemisphere. It is motivated by the fact that the objective is to enclose the mUAV within the cluster in order to simplify the escort mission. The formation begins to take place while approaching the mUAV and then encloses the mUAV when the cluster reaches a certain distance.
The rest of this section focuses on how the formation calculations are being done.
4.2.1 Calculating the cluster formation radius
Our goal is to place dUAVs on a branch equidistant to each other according to \(\epsilon _d\) in order to minimize the escape directions of the mUAV. Firstly, we need to determine the maximum length of the branches to derive \(r_F\). Let \(max = max(\{b \in B : b.length\})\) be this number. Suppose we inscribe a regular polygon into a circle. Then, the branch occupies only \(\frac{1}{4}{th}\) of an imaginary circle. Every member of the branch lies on the edges of this circle. Therefore, if we were to mirror the singular branch in 2D along the y-axis and then mirror the resultant along the x-axis, we would get a regular polygon with n sides. Here, \(n = 4 \cdot max\). Any regular polygon can be inscribed within a circle. With this we can now find the \(r_F\) with the following formula
where r is the formation radius, a is the length of a side in the polygon which is equal to the \(\epsilon _d\).
4.2.2 Determining branch rotations
Now that we have \(r_F\), we know how far from the cluster head the branches are going to exceed. However to determine the positions of each branch relative to the cluster head along the z-axis as shown in Fig. 2(right). we need to rotate each point along the z-axis. To calculate the rotation positions we use the Rodrigues’ rotation formula as follows
where \(\mathbf {v}\) is the vector that needs to be rotated, \(\mathbf {k}\) is the axis of rotation and \(\theta\) is the angle by which the vector \(\mathbf {v}\) needs to be rotated. Steps for calculating this rotation are listed below:
-
1.
Calculate the angular separation theta between every branch. This is done by dividing \(2 \pi\) by the total number of branches.
-
2.
From the origin of rotation, each branch is \(\theta\) away from the previous branch. Let \(b \in B\) be the current branch and \(i_b\) the current index of b. Then, b is an angle of \(\theta _{rot} = \theta \cdot (i_b-1)\) away from the origin.
-
3.
Rotate b by \(\theta _{rot}\) along the z-axis relative to the direction between the mUAV and the CH.
-
4.
Following the Rodrigues rotation formula, the \({\mathbf {v}}\) which is the formation direction is a vector perpendicular to the direction heading from CH to the mUAV with a magnitude of \({\epsilon} _d\).
-
5.
The vector \(\mathbf {v}\), once rotated along the axis of rotation \(\mathbf {k}\), will yield the branch positions along the z-axis. Note that at this rotation step, the whole branch will not be in its correct position.
-
6.
The axis of rotation \(\mathbf {k}\) is the direction that is represented by tracing a vector from the CH to the mUAV and normalizing it so that a unit vector is obtained. The values \(\mathbf {v}\) and \(\mathbf {k}\) along with the rotation angle \(\theta _{rot}\) for the concerned specific branch is substituted in the Rodrigues rotation formula to yield the position for each branch.
-
7.
Every branch member \(b_i\) occupies an angle of their corresponding \(\theta _{rot_i}\) from the origin.
-
8.
With the fractional angle, the actual positions of each branch member can be calculated. The x component is decomposed to be in the branch parent and tracing the fractional angle over the cluster radius to derive the magnitude. The z-axis is in the direction of the mUAV [see Fig. 2(right)].
The rotation procedure run by the CHs is described in Algorithm 6. Let b be a dUAV receiving a rotation message. Let c be the child of b. Then, b will run Algorithm 7.


4.3 Interception mobility
As part of our C-UAS system, a UAV Monitoring and Interception System (UMIS) permits to detect and identify the approximate location of the mUAV in the restricted area. More precisely, if the UMIS detects a mUAV, it will trigger the UAV defense system, the dUAVs deployment and then, initiate the creation/generation of the UAV defense swarm.
We consider a UMIS running on-board each dUAV, in a distributed manner, to support autonomous decision making and to prevent a single point of failure.
One of the goals of the proposed C-UAS system of the mUAVs is to intercept the mUAV. The optimization criterion is, in context of our study, to minimize the time between detection and interception of the intruder.
A naive strategy to solve mUAV interception is to predict the future position of the mUAV, while assuming extended knowledge of the intruder’s postion. For this, two positions at different timestamps can be compared to each other, forming a movement vector which then can be multiplied by a certain factor in order to obtain the next predicted mUAV position as described in more detail in our preliminary work [36].
In practice, detecting the position of the mUAV might depend on the dUAVs sensors and the precision of the detection depends on the distance between the dUAV and mUAV.
For modeling purposes, we assume that the dUAV has several types of sensors, which are complementary in sensing different information about the location of the mUAV. The sensor reading depends on the distance between dUAV and mUAV. Incorporating the sensor configuration and information in a interception strategies model, we introduce different zones or regions surrounding the dUAV. In each regions, the dUAV can perform different motions in order to increase its performance. According to the sensing capabilities, we split the regions surrounding the dUAV to three classes which are Line of Field View (LOFV), Line of Sight (LOS), and Line of Control (LOC).
We have three assumptions upon which we mainly rely on for the response design:
-
1.
When mUAV is inside the LOFV, we assume that dUAV can deduce the distance between dUAV and mUAV, and an angle which forms a spherical sector within which the mUAV could possibly reside
-
2.
When mUAV is inside the LOS, we assume that dUAV can deduce the exact location of mUAV
-
3.
When B enters inside LOC, dUAV can catch mUAV
Line of Field View (LOFV): The LOFV distance forms a sphere around the dUAV with dLOFV as radius. This region between LOFV and LOS is called the field view region. If the distance between dUAV and mUAV is reduced below dLOFV, according to our assumptions 1, dUAV can deduce both the distance and the angle of the intruder mUAV.
Line of Sight (LOS): The dLOS is the LOS distance, and this forms a sphere around dUAV with dLOS as radius. This region between LOS and LOC is called clear sight region. If the distance between dUAV and mUAV is reduced below dLOS, it means that dUAV falls inside the LOS region. According to our assumption 2, dUAV can deduce the exact location of mUAV.
Line of Control (LOC): The dLOC is the LOC distance, and this forms a sphere around dUAV with dLOC as radius. This region of the sphere is called the control region. When the distance between dUAV and mUAV is reduced below dLOC, the dUAV is assume to have mUAV intercepted (assumption 3) and the enclosement angle of the cluster formation is enlarged, thus trapping the mUAV inside the resulting spherical structure and triggering the escort phase.
Based on the model described above, strategies for the dUAV can be proposed depending on mUAV regional location. Future work will be dedicated in testing mobility strategies for dUAVs.
4.4 Counter-attack
The counter-attack consists in the context of this paper of an escorting procedure. This phase is aims to bring the previously trapped mUAV outside the regular flight zone. According to our assumptions, the mUAV will try to avoid any collision with nearby UAVs, and thus will be forced to move with them as shown in Fig. 3. Optionally, the branches could actively perform anti-escaping maneuvers in order to avoid loosing the mUAV due to larger holes in the formation. During the process, the CH is in charge of the heading, while its branches maintain their relative positions to the CH. Usually, the shortest path to the flight zone border is taken. If needed, this can be freely adjusted depending on the end goal of the mission.
5 Prototypical implementation
As a proof of concept, we developed a tool that simulates the entire process from intruder detection to counter-attack as described in this paper. Initially, the simulator creates a set of dUAVs randomaly distributed within the flight zone and a mUAV. The dUAVs start the clustering process as soon as there is notice of an incoming intruder. Both, inital state and clustering state are shown in Fig. 4. Clustering establishes designated communication channels between the dUASs, which is essential for a successful formation building.
5.1 Wobbling
Every UAV is able to slightly deviate within a given radius from its anchor point. For this, they continuously generate random Perlin Noise values for their three movement axes. The resulting pseudo-random movement is supposed to represent the real-world floating instability of UAVs, e.g. windy weather conditions. In the case of the mUAV, the wobbling can be used in order to simulate a spontaneous and unpredictable movement, making the intercept phase less trivial and thus resulting in a more realistic scenario.
5.2 Separation
Let \(u_{1}\) and \(u_2\) be two UAVs. Let \(d = \left\| u_1.pos - u_2.pos \right\|\) be the distance between \(u_1\) and \(u_2\). Then, if \(d < \epsilon _d\), a force vector parallel to d and of amplitude \(\epsilon _d - d\) is applied to \(u_{1,2}\), resulting in a separation. When more UAVs are involved, the sum of all produced vectors is applied. If desired, a constant c can be added to each force vector in order to push the UAVs even further apart, making them less likely to stay at the exact borders of the threshold radius. Note that the defense UAVs and the malicious UAV work similarly in terms of collision avoidance principles, that is, they can only move in a given direction if there is no other UAV.
5.3 Cumulative force movement logic
Multiple forces of different origins may act on some UAV at the same time. For instance, a UAV may at the same time try to head towards a certain direction and actively try to avoid a collision with another UAV. A force can be described as a directional vector v and a weight w. At the end of an update cycle, all executed forces are added together, with respect of their weights, to form a cumulative force \(v_{sum}\). The amplitude of \(v_{sum}\) cannot exceed the maximal velocity of the UAV. The wobbling effect of a UAV is the only movement component that is not translated into force as it is not produced by the UAV itself but by its environment (e.g., wind), implying that the combination of \(v_{sum}\) and the produced wobbling movement may exceed the maximal velocity of that UAV.
5.4 Formation building
As soon as clusters are established, the formation control takes over and composes several clusters to a supercluster, that develops the balanced and well-formed branches with local 3-D positioning of each dUAV in space (Fig. 5). Local positioning in 3D space is indeed challenging. We solved this particular challenge by embedding a sequential numbering on the entities (UAVs) of the cluster and by using only local reference locations for the transformation.
The last subfigure in Fig. 5 shows a single cluster as opposed to the other subfigures. This is due to a merging mechanism between several clusters which is triggered when at least two CH are within their communication range. If n CHs are within a common communication range, then \(n-1\) CHs will be degraded to UAVs by KHOPCA’s rules [9, 10] which will lead to the destruction of the individual clusters. This enables a new construction of a supercluster.
6 Study
6.1 Simulation setup and metrics
The parameters used for the simulation are communication range, number of branches, wobbling radius, collision threshold, UAV speed, UAV size, UAV deployment (positions), flightzone design (shape and size), number of dUAVs, and the formation shape (see Table 2). For all simulations, we consider the existent of one mUAV in the center of the flight zone, whereas dUAVs are uniformly positioned within an outer flight zone side. For each experiment, 100 independent simulation runs have been conducted to ensure a statistical significance.
Escort time The performance of the experiments can be measured by the time needed to successfully escort the mUAV outside the flight zone. This time is measured starting from the very beginning of the simulation and should be minimized.
6.2 Experiments and Results
The confidence interval \(ci = 90\%\) has been used and the Anderson-Darling normality test (Fig. 6) over a sample of 100 simulations has been performed, resulting in a p-value of 0.247.
In Fig. 7, one can observe that the impact of the number of dUAVs on the simulation times is more or less negligible. Indeed, the number of simulation steps is equivalent between 10 and 100 dUAVs and the variation in this range is below 5%. However, the number of clusterless dUAVs increases proportional to the total amount of dUAVs on the flight zone. Since these UAVs are not mission-active, resources could be saved by deploying fewer dUAVs.
The performance of the simulation noticeably improves when choosing a higher communication range between dUAVs as depicted in Fig 8. More precisely, while the simulation length is equivalent with a communication range of 100 or 200, it then sees a drop of more than 5% when using a a communication range of 300 and more. As expected, the number of clusterless dUAVs decreases with the increased communication range as every UAV is able to locate its neighbors. This number drastically drops between 100 and 200 to reach zero clusterless dUAVs at 300.
From Fig. 9 it is clear that the wobbling of dUAVs has an negative impact on the simulation times and therefore should be minimized as much as possible. Indeed, an increase of the wobbling radius from 1 to 5 implies an increase of more than 60% of simulation steps and more than 50% of clusterless dUAVs.
The impact of the mUAV wobbling radius similarly impacts the simulation length as illustrated in Fig. 10. The latter increases of more than 30% between when the wobbling radius increases from 1 and 5.
Figure 11 shows that the simulation fails when choosing a dUAV collision threshold over 60. Similarly, the same also happens for the collision threshold of mUAV when below 40 (cf. Fig. 12). These results provide an important insight on the initial configuration to adopt, here the collision threshold for dUAVs and the mUAV must be chosen below 60 and above 40 respectively. In fact, as soon as the value of the dUAV surpasses the one of the mUAV, the simulation fails since the dUAVs are unable to push the mUAV outside its current position.
Finally, Fig. 12 shows that the number of branches can improve the simulation time of more than 10% , the best results being obtained with 5, 6 and 8 branches. This is correlated with the number of clusterless dUAVs which is minimal for a number of branches equal or greater than 6.
6.3 Discussion
It is important to note that while the experiments show a certain behaviour of the simulation while changing different parameters one by one, there may be dependencies between the parameters themselves, meaning that those results may vary depending on the initial configuration choice. Some additional experiments would be required in order to further understand the impact of every individual parameter.
Flocking is a great mechanism to realize a natural swarm behavior and to gather nearby clusterless UAVs in order to form a bigger cluster. At the moment the flocking is realized by moving to the center position of the nearby UAVs. This leads sometimes to unexpected behavior such as preventing the cluster from chasing the mUAV by blocking it. This is because of the UAVs that try to move to the CH which is located in the center of a cluster, while only the outer leaves of certain branches are accepting additional children. The merging of clusters is being realized only when the CHs are within a communication range. Several cluster chasing the same mUAV might slow down the escort mission due to hindering each other. One might consider merging the clusters as soon as possible. More, our approach can be tested and augmented to successfully escort multiple independent mUAVs or a swarm of mUAVs with its own behavior out of the flight zone.
Inter-cluster communication can be realized to improve the cluster merging such that an early merge can be performed to prevent a hindering between several clusters. This requires special message types that are sent from branch nodes or leaves up to the CH to inform about a nearby cluster. Thus the CHs can agree upon merging which can be realized with a cluster destruction and flocking combination.
7 Conclusions
UAVs have recently found their way into the IoT ecosystem, opening perspectives to numerous new applications such as last mile delivery or surveillance. The expected growth of UAV traffic will however bring new threats like rogue or malicious UAVs (mUAVs) endangering low-level airspace operations. As a solution, C-UAV systems are expected to detect, identify and act on such mUAVs. Unfortunately, existing C-UAV, either ground-based or air-based, typically lack scalability or induce collateral damages.
This article thus proposes a unique autonomous defense system (C-UAV) consisting of collaboratively working UAVs as a swarm. The most outstanding features and contributions of the presented approach are the balanced clustering and local formation control to realize the intercept- and capture-formation, thus avoiding requirements for additional infrastructure such as required by GPS. Additionally, the approach consists of a modular design containing the phases deployment, clustering, formation, interception, capture. Empirical evidence of the capacity of the swarm-based C-UAV to chase and escort a mUAV was provided through simulations. In addition, a sensitivity analysis of the system’s parameters, i.e., number of defense UAVs, communication range, wobbling radius and collision threshold, was proposed.
As next steps, we plan to incorporate specific network-structures [37] into the swarm formation process to obtain resilience in case a dUAV is damaged or destroyed. Furthermore, a C-UAV system with more capabilities can be developed when assuming a backbone infrastructure. For this, we will adopt efficient backbone mechanisms [38] into the next generation C-UAV system.
References
Labib NS, Danoy G, Musial J, Brust MR, Bouvry P. A multilayer low-altitude airspace model for uav traffic management. DIVANet ’19. ACM; 2019.
Sharma A, Singh PK, Kumar Y. An integrated fire detection system using iot and image processing technique for smart cities. Sustain Cities Soc. 2020;61:102332.
Hernández-Vega J, Varela ER, Romero NH, Hernández-Santos C. Internet of things (iot) for monitoring air pollutants with an unmanned aerial vehicle (uav) in a smart city. Smart technology. Berlin: Springer International Publishing; 2018. p. 108–120.
Aweiss A, Homola J, Rios J, Jung J, Johnson M, Mercer J, Modi H, Torres E, Ishihara A. Flight demonstration of unmanned aircraft system (UAS) traffic management (UTM) at technical capability level 3. In: IEEE/AIAA 38th Digital Avionics Systems Conference (DASC); 2019.
Lappas V, Zoumponos G, Kostopoulos V, Shin H, Tsourdos A, Tan-tarini M, Shmoko D, Munoz J, Amoratis N, Maragkakis A, Machairas T, Trifas A. EuroDRONE, a european UTM testbed for U-Space. In: International conference on unmanned aircraft systems (ICUAS); 2020.
Prlin K, Alam MM, Le Moullec Y. Jamming of uav remote control systems using software defined radio. In: International conference on military communications and information systems (ICMCIS); 2018.
Droptec. The Dropster Net gun. https://www.droptec.ch/product. Accessed 14 Nov 2020.
Li A, Wu Q, Zhang R. UAV-enabled cooperative jamming for improving secrecy of ground wiretap channel. IEEE Wireless Commun Lett. 2019;8(1):181–4.
Brust MR, Frey H, Rothkugel S. Dynamic multi-hop clustering for mobile hybrid wireless networks. In: Proceedings of the international conference on ubiquitous information management and communication. New York: ACM; 2008.
Brust MR, Frey H, Rothkugel S. Adaptive multi-hop clustering in mobile networks. In: Proceedings of the 4th international conference on mobile technology, applications, and systems, Mobility ’07; 2007. p. 132–8.
Birch Gabriel C, Griffin John C, Erdman Matthew K. UAS detection, classification, and neutralization: Market survey 2015. Sandia National Laboratories, USA: Technical report; 2016.
Birch GC, Woo BL. Counter unmanned aerial systems testing: evaluation of vis swir mwir and lwir passive imagers. Technical report, Sandia National Laboratory, USA; 2017.
Altawy R, Youssef AM. Security, privacy, and safety aspects of civilian drones: a survey. ACM Trans Cyber-Phys Syst. 2016;1(2):1–25.
Guvenc I, Koohifar F, Singh S, Sichitiu ML, Matolak D. Detection, tracking, and interdiction for amateur drones. IEEE Commun Mag. 2018;56(4):75–81.
Ding G, Wu Q, Zhang L, Lin Y, Tsiftsis TA, Yao Y. An amateur drone surveillance system based on the cognitive internet of things. IEEE Commun Mag. 2018;56(1):29–35.
Shi X, Yang C, Xie W, Liang C, Shi Z, Chen J. Anti-drone system with multiple surveillance technologies: architecture, implementation, and challenges. IEEE Commun Mag. 2018;56(4):68–74.
Kang H, Joung J, Kim J, Kang J, Cho YS. Protect your sky: a survey of counter unmanned aerial vehicle systems. IEEE Access. 2020;8:168671–71010.
Noh J, Kwon Y, Son Y, Shin H, Kim D, Choi J, Kim Y. Tractor beam: safe-hijacking of consumer drones with adaptive gps spoofing. ACM Trans Priv Secur. 2019;22:1–26.
Pljonkin AP. Vulnerability of the synchronization process in the quantum key distribution system. Int J Cloud Appl Comput IJCAC. 2019;9(1):50–8.
Zohuri B. High-power microwave energy as weapon. Cham: Springer International Publishing; 2019. p. 269–308.
Extance A. Military technology: laser weapons get real. Nature. 2015;521:408–10.
Delft Dynamics. Drone catcher. https://dronecatcher.nl/. Accessed 14 Nov 2020.
Rothe J, Strohmeier M, Montenegro S. A concept for catching drones with a net carried by cooperative UAVs. In: 2019 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR); 2019.
The New Indian Express. Now, eagles to take down illegal drones in Telangana. https://www.newindianexpress.com/states/telangana/2020/aug/01/now-eagles-to-take-down-illegal-drones-in-telangana-2177572.html. Accessed 14 Nov 2020.
CNBC. A swarm of armed drones attacked a Russian military base in Syria. https://www.cnbc.com/2018/01/11/swarm-of-armed-diy-drones-attacks-russian-military-base-in-syria.html. Accessed 14 Nov 2020.
Scharre P. Counter-swarm: a guide to defeating robotic swarms—war on the rocks; 2017.
Padgett NE. Defensive swarm: an agent-based modeling analysis. Master’s thesis, Naval Postgraduate School, USA; 2017.
Farid AM, Egerton S, Barca JC, Kamal MAS. Adaptive multi-objective search in a swarm vs swarm context. In: IEEE international conference on systems, man, and cybernetics (SMC); 2018.
Pozniak M, Ranganathan P. Counter UAS solutions through UAV swarm environments. In: 2019 IEEE international conference on electro information technology (EIT). 2019. p. 351–356.
Brust MR, Akbas MI, Turgut D. Vbca: a virtual forces clustering algorithm for autonomous aerial drone systems. In: IEEE SysCon; 2016.
Gillespie RJ. Fifty years of the vsepr model. Coord Chem Rev. 2008;252(12–14):1315–27.
Al-Turjman FM, Hassanein HS, Ibnkahla MA. Connectivity optimization with realistic lifetime constraints for node placement in environmental monitoring. In: IEEE LCN; 2009.
Barnes L, Garcia R, Fields M, Valavanis K. Swarm formation control utilizing ground and aerial unmanned systems. In: IEEE/RSJ international conference on intelligent robots and systems; 2008.
Kim H, Ahn H. Realization of swarm formation flying and optimal trajectory generation for multi-drone performance show. In: Symposium on system integration (SII): in IEEE/SICE international; 2016.
Maxa JA, Mahmoud MSB, Larrieu N. Survey on UAANET routing protocols and network security challenges. Ad Hoc Sens Wireless Netw; 2017.
Brust MR, Danoy G, Bouvry P, Gashi D, Pathak H, Gonçalves M. Defending against intrusion of malicious uavs with networked uav defense swarms. In: 2017 IEEE 42nd conference on local computer networks workshops (LCN Workshops). New York: IEEE; 2017. p. 103–11.
Brust MR, Turgut D, Ribeiro CHC, Kaiser M. Is the clustering coefficient a measure for fault tolerance in wireless sensor networks? In: IEEE internationa; conference on communications (ICC); 2012. p. 183–7.
Brust MR, Ribeiro CHC, Turgut D, Rothkugel S. Lswtc: a local small-world topology control algorithm for backbone-assisted mobile ad hoc networks. In: IEEE local computer network conference (LCN); 2010.
Acknowledgements
This work is partially funded by the joint research programme UL/SnT-ILNAS on Digital Trust for Smart-ICT.
Author information
Authors and Affiliations
Contributions
MB and GD conceived of the presented idea. MB developed the theory. GD verified the analytical methods. MB and GD wrote the main manuscript text and MB prepared the figures. GD elaborated state-of-the-art approaches and related work. All authors discussed the results and contributed to the final manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brust, M.R., Danoy, G., Stolfi, D.H. et al. Swarm-based counter UAV defense system. Discov Internet Things 1, 2 (2021). https://doi.org/10.1007/s43926-021-00002-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43926-021-00002-x