1 Introduction

Widening inequality significantly impacts the macroeconomic trajectory, influencing its long-term development. The disparities in regional growth, particularly when excessive, serve as an impediment to the sustainable evolution of the social economy (Dabla-Norris et al., 2015). In the context of China, the reforms and opening-up policies have catalyzed the nation's economic expansion. However, this rapid growth has come at a notable cost: the exacerbation of income inequality among the various provinces (Pedroni & Yao Apr., 2006). With the further development of China’s economy, the regional inequality gap has shrunk at the provincial level, but exhibits increased polarization at the county level (“A comparative analysis of multi-scalar regional inequality in China”, 2017). This phenomenon underlines the critical need to develop methodologies that can accurately and objectively assess these regional inequalities, especially at the county level. Such an analysis is essential for promoting a sustainable, balanced, and flourishing economic environment in China (Fan & Sun n.d.; Liao & Wei Nov., 2012). Despite these considerations, a holistic understanding of the inequality landscape at the county level across China remains elusive, primarily due to the complex interplay of various socio-economic factors and the challenge of obtaining comprehensive, granular data.

In previous studies, various methods were employed to assess regional inequality (e.g., the Gini coefficient (Liao & Wei Nov., 2012) and the Theil index (“A comparative analysis of multi-scalar regional inequality in China”, 2017)). Traditional analyses often rely on indices derived from statistical data, yet this approach is not without limitations. The precision of these assessments is heavily contingent upon the quality and availability of data, highlighting a critical bottleneck in the accuracy of these evaluations. The statistical data frequently suffer from issues like temporal discontinuity and vulnerabilities to inaccuracies induced by human factors, rendering them inadequate for continuous and comprehensive assessment of regional inequalities across diverse temporal and spatial dimensions. This gap in the data landscape necessitates the exploration of alternative, more reliable sources of data. In this context, Nighttime Light (NTL) satellite imagery has emerged as a promising solution, offering the benefits of temporal and spatial continuity, objective independence, and easy access. These attributes of NTL data have been harnessed in a range of applications. For instance, numerous studies have demonstrated the efficacy of NTL imagery as a surrogate for tracking economic activities (Zhang et al., 2019), in addition to its deployment in the identification of impervious surfaces (Ou et al., Sep. 2019; Shi et al., Apr. 2014), and in disaster assessment scenarios (Zhao, et al., 2018). In addition, NTL images also provided remarkable results in the practice of regional wealth distribution inequality (RWDI) evaluation (Ivan et al., 2020; Wu et al., Feb. 2018). These applications underscore the superiority of NTL data in providing multiscale and multi-dimensional perspectives, surpassing the capabilities of traditional statistical data (Xu et al., Sep. 2015; Zhou et al., 2015). As a result, NTL data has become an invaluable reference and supplemental resource in the quantification and analysis of economic development levels, opening new avenues for in-depth and accurate exploration of regional economic disparities.

In 2018, a significant advancement in satellite technology was marked by the launch of the Luojia 1–01 (LJ1-01) Nighttime Light (NTL) satellite by China, featuring an impressive spatial resolution of 130 m. This technological leap represented a substantial improvement over its predecessors, namely the Defense Meteorological Satellite Program-Operational Linescan System (DMSP-OLS) and the Suomi National Polar-orbiting Partnership-Visible Infrared Imaging Radiometer Suite (NPP-VIIRS) NTL satellites (Ou et al., Sep. 2019; Wang et al., Mar. 2020). The LJ1-01 NTL's enhanced capabilities in spatial resolution and wavelength spectrum enabled it to capture more detailed and nuanced spatial information (Jiang et al., Sep. 2018; Li et al., Jun. 2019), thus facilitating a more granular analysis of socioeconomic parameters at a localized scale. These advancements opened new doors in various fields of study. For instance, when it comes to the extraction of detailed urban structures (Li et al., Oct. 2018) and the assessment of housing prices within urban communities (Li Jul., 2019), the LJ1-01 satellite's data proved to be exceptionally valuable. Its ability to capture intricate details of small-scale economic activities provided a new lens through which urban development and socioeconomic dynamics could be studied. This leap in data quality and resolution allows a deeper understanding of the complex interplay between urban development, economic activity, and social parameters at a micro-level.

This paper aims to calculate the wealth Gini coefficient (WGC) to assess the capability differences of NTL data at various resolutions in evaluating regional wealth distribution inequality (RWDI) in small-scale areas, with pixels as the smallest unit of extraction. The central purpose of the study is to explore whether high-resolution NTL data exhibit a more pronounced advantage over low-resolution data in such assessment tasks. This letter's main contributions are as follows: First, we compared the distribution of two types of WGC values at the county and provincial levels, derived from LJ1-01 data and NPP-VIIRS data, respectively. The WGC value calculated by the LJ1-01 data shows sensitivity to low RWDI areas. Therefore, LJ1-01 is considered to be superior for assessing regional inequality in small-scale areas. Second, we utilized LJ-Gini to evaluate economic development in China. This result demonstrates the heterogeneity of the RWDI both between different spatial scales and areas. The economy development is negatively correlated to the inequality of wealth distribution. In addition, the RWDI in counties exhibited a more polarizing trend than that in provinces, and the assessment results of the RWDI in a large-scale area tends to mask the inequality of the small-scale area within it.

2 Data and methods

2.1 Study area and data

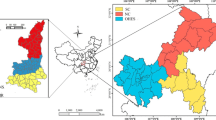
In this study, we analyzed the RWDI of 31 provinces and 2,853 counties in mainland China. Four types of data were employed in this paper: LJ1-01 data from 2018; monthly VIIRS day/night band (DNB) for the 12 months of 2018; China’s land-use remote sensing monitoring data from 2018 with a resolution of 30 m; and data on the administrative boundaries of mainland China for provinces and counties. We obtained LJ1-01 data from the High-Resolution Earth Observation System of the Hubei Data and Application Center (http://59.175.109.173:8888/) and downloaded the VIIRS DNB data from the National Oceanic and Atmospheric Administration (NOAA) National Centers for Environmental Information (NCEI) website (https://www.ngdc.noaa.gov/eog/viirs/download_dnb_composites.html). Finally, the 30-m-resolution land-use data were obtained from http://www.resdc.cn/data.aspx?DATAID=264, and these data were used to extract urban built-up areas from LJ1-01 images and NPP-VIIRS images data. Mainland China's provincial boundaries, county boundaries, and urban built-up areas are shown in Fig. 1.

Fig. 1
figure 1

Mainland China's provincial boundaries, county boundaries, and urban built-up areas (187,782.21 square kilometers)

Full size image

According to the description on the official website, the original digital number (DN) of LJ1-01 image data was preprocessed by \({DN}^\frac{3}{2}\times {10}^{-10} \left(W\bullet {m}^{-2}\bullet {sr}^{-1}\bullet {\mu m}^{-1}\right)\). In addition, we excluded the NPP image data of the summer months (May, June, July, August) because of the missing data over the high latitude region of the Northern Hemisphere resulting from the present defects of the NPP-VIIRS monthly composite material. We generated annual images by averaging the remaining monthly NPP-VIIRS composite images (Zhao et al., Nov. 2017). Therefore, 8,058,029 pixels from the LJ1-01 image data and 705,893 pixels from the NPP-VIIRS image were extracted from the study area.

2.2 Region wealthy distribution inequality analysis methods

In economics, the Gini coefficient was utilized to express a variable's dispersion among different entities. For example, this coefficient is often employed to measure the fairness of the distribution of income and the fairness of the distribution of household wealth. This paper will use NTL data to evaluate the WGC of 31 provinces and 2,853 counties in mainland China to measure the RWDI. NTL data have been shown to have a highly statistically significant correlation with the per capita gross domestic product (GDP) (Zhang et al., 2019; Zhao et al., Nov. 2017). Therefore, we applied the DN value of each pixel in an NTL image as a substitute variable for the area’s gross production value. In addition, when exploring the relationship between economic development and the WGC, we implemented Spearman’s rank correlation coefficient. It uses a monotonous equation to evaluate the correlation between two statistical variables and is an indicator to measure the dependence between two variables.

This paper mainly utilized the following five steps to calculate the WGC. First, we preprocessed LJ1-01 data and NPP-VIIRS data. Second, the urban built-up areas were extracted from the two types of nighttime light images through 30-m-resolution land-use data. Third, we applied administrative boundaries to divide urban built-up areas by province and county. Fourth, DN values within each province and county's urban built-up areas were extracted pixel by pixel. Fifth, we utilized (1) to calculate the WGC, where \({y}_{i}\) and \({y}_{j}\) represent the DN values of \({pixel}_{i}\) and \({pixel}_{j}\), respectively. \(\overline{{y }_{u}}\) represents the average of total DN values.

$$WGC=\left(\frac{1}{2\overline{{y }_{u}}}\right)\frac{1}{n\left(n-1\right)}\sum_{i}^{n}\sum_{j}^{n}|{{y}_{i}- y}_{j}|$$
(1)

3 Results and discussion

3.1 Comparison between LJ-Gini and NPP-Gini

This section delves into a comparative analysis of two datasets measuring WGC – LJ-Gini, derived from LJ1-01 satellite data, and NPP-Gini, based on NPP-VIIRS data – in their effectiveness at depicting RWDI. We commence by constructing a series of box plots (as shown in Fig. 2), which serve as a visual tool to discern the differences in the numerical distributions of LJ-Gini and NPP-Gini at both county and provincial levels. According to Fig. 2, the variation range of the two kinds of WGC values at the county level is more extensive than that at the provincial level. Data with higher volatility may be more capable of capturing subtle changes. To better compare this volatility, we conducted a Levene’s test on the two kinds of WGC values on different geographic scales. The results show that although the NPP-Gini at the county and provincial levels showed statistically significant differences in the mean, the volatility of two sets of data on different geographic scales did not show a statistically significant difference. This may imply that the NPP-Gini exhibits similar sensitivity to changes in wealth distribution across different scales. In contrast, the LJ-Gini shows significantly higher volatility at the county level than at the provincial level, with this difference being statistically significant (P-value = 0.009). This suggests that the LJ-Gini is more effective in capturing subtle variations in wealth distribution at smaller scales. In addition, the average value of LJ-Gini on different geographic scales is statistically consistent. Furthermore, compared with NPP-Gini, LJ-Gini's numerical distribution shows a significant negative skew at both the county and provincial levels, and there are some low outliers in the box plot B of Fig. 2 (county LJ-Gini). These characteristics indicate a considerable proportion of low-value WGCs in the entire data distribution, which indicates that LJ1-01 image data are very sensitive to low WGC values and can better evaluate the RWDI in areas where wealth distribution is relatively fair. In summary, the LJ-Gini dataset is considered superior in assessing RWDI due to its high volatility when evaluating small-scale areas and its heightened sensitivity to low WGC values, compared to the WGC based on NPP-VIIRS data.

Fig. 2
figure 2

Number distribution characteristics of LJ-Gini in 31 provinces and 2,853 counties. The means of A, B, C, D are 0.78, 0.77, 0.53, 0.46. The standard deviations of A, B, C, D are 0.09, 0.14, 0.13, 0.14. A Provincial LJ-Gini, B County LJ-Gini, C Provincial NPP-Gini, D county NPP-Gini

Full size image

In addition, this letter also analyzes the factors that limit the accuracy of NPP-Gini's estimation of the RWDI. According to the provincial administration division, we conducted a correlation analysis of the LJ-Gini and NPP-Gini at the county level within each province. The correlation study results for each province are shown in Fig. 3, ranging from 0.206 in Tibet to 0.945 in Tianjin. The provinces with the highest correlation are primarily found in China's central and eastern regions, with a relatively high degree of economic development (Fig. 3). To explore the effect of economic development on NPP-Gini accuracy, we divide the counties into four groups according to the economic development level (using the average DN value as a proxy variable) and conduct correlation analysis. The correlation coefficients of the four sets of data from high to low levels of economic development at the significance level of 0.01 were 0.758, 0.705, 0.665, and 0.296. This indicates that the ability of the NPP-Gini index to evaluate the RWDI is limited by economic development, and the accuracy of the NPP-VIIRS data to estimate the WGC has dropped significantly in economically underdeveloped areas.

Fig. 3
figure 3

Correlation coefficients of LJ-Gini and NPP-Gini at the county level in different provinces, as well as the economic development of each province which is replaced by average DN. (DN unit: \(W\bullet {m}^{-3}\bullet {sr}^{-1}\))

Full size image

3.2 The grading criterion of the RWDI

To more intuitively evaluate the degree of regional inequality, this paper established a grading criterion representing a correspondence between the wealth inequality degree and WGC values. Considering that the LJ-Gini index is more accurate in evaluating RWDI than the NPP-Gini index, we utilized LJ-Gini's numerical distribution law to establish the grading criterion. First, the Kolmogorov–Smirnov test was applied between the provincial and county LJ-Gini, and the results demonstrate that the provincial LJ-Gini and county LJ-Gini have the same probability distribution (p-values = 0.314). According to the normal distribution abstracted from the provincial sample data (the mean is 0.78 and the standard deviation is 0.096, Fig. 4), we set four split points (0.588, 0.684, 0.876, and 0.972) to divide the overall data into five numerical intervals. The four split points are evenly distributed on both sides of the average and are one standard deviation and two standard deviations away from the average, respectively. Based on the statistical rule 68–95–99.7 (Pukelsheim, 1994), 2.5%, 13.5%, 68%, 13.5%, and 2.5% of the data fall within 0–0.588, 0.588–0.684, 0.684–0.876, 0.876–0.972, and 0.972–1, respectively (Column A in Fig. 4). We define the above numerical intervals as RANK-ONE, RANK-TWO, RANK-THREE, RANK-FOUR, and RANK-FIVE, respectively.

Fig. 4
figure 4

Statistics of different levels of inequality in each region, and Histogram of LJ-Gini and NPP-Gini distribution at the county and provincial level. A Theoretical distribution, B 31 provinces, C 2,853 counties 1: Shanghai, 2: Tianjin, 3: Jiangsu, 4: Beijing, 5: Anhui, 6: Qinghai, 7: Ningxia, 8: Zhejiang, 9: Shandong, 10: Guangdong, 11: Shaanxi, 12: Sichuan, 13: Liaoning, 14: Fujian, 15: Henan, 16: Hunan, 17: Chongqing, 18: Hubei, 19: Hebei, 20: Yunnan, 21: Tibet, 22: Guangxi, 23: Xinjiang, 24: Gansu, 25: Jilin, 26: Jiangxi, 27: Shanxi, 28: Guizhou, 29: Inner Mongolia, 30: Heilongjiang, 31: Hainan

Full size image

This grading criterion was utilized to quantitatively grade the RWDI degree of 2,853 counties and 31 provinces in mainland China. We counted each rank's proportions in the whole, both at county and provincial level (columns B, C, in Fig. 4. No province is classified as RANK-FIVE). The relative number of counties classified as RANK-ONE to RANK-FOUR is 1.7, 1.5, 0.67, and 1.8 times that of provinces classified as RANK-ONE to RANK-FOUR, respectively. The anomaly of the ratio at the two extreme inequality ranks (RANK-ONE and RANK-FIVE) suggests that the RWDI is sensitive to spatial scales, and the RWDI of counties in mainland China exhibits a more polarizing trend than that of provinces (“A comparative analysis of multi-scalar regional inequality in China”, 2017). In addition, the WGC value on a large-scale area tends to mask the RWDI of the small-scale area within it. The statistical results classified by province are shown in columns 1 to 31 in Fig. 4. In the ranking of the percentage of RANK-ONE, Shanghai (87.5%), Tianjin (56.25%), and Jiangsu (37.5%) are the top three provinces. Qinghai (18.18%), Gansu (15.48%), and Sichuan (11.86%) are the top three provinces in the ranking of RANK-FIVE percentage.

3.3 Evaluate China’s economy based on the WGC numerical distribution

To explore the connection between the RWDI and economic development, this paper performed a Spearman correlation analysis on the LJ-Gini and the average DN values. At a 1% significance level, the LJ-Gini correlation analysis findings and the average DN values in 2,853 counties were -0.625, whereas those of 31 sets of province-level data were -0.48. This result indicates that the inequality of wealth distribution begins to decline as the economy develops. Furthermore, the stronger correlation at county-level data sets compared with provincial data sets uncovers spatial heterogeneities of RWDI across different geographic scales. In addition, we further analyzed the correlation between the LJ-Gini and the average DN value at the county level within the provincial administer division. The results demonstrate that the coefficients between the LJ-Gini and the average DN are diverse in different provinces (Table 1). This may arise from RWDI heterogeneity between different regions, including differences in policies, economic structure, and geographic location conditions.

Table 1 The results of correlation analyses between LJ-Gini and the average DN in different provinces
Full size table

In Fig. 5, the histogram depicts the average county NPP-Gini and county LJ-Gini in different provinces. The average values of WGC based on the LJ1-01 data were higher than those calculated by the NPP-VIIRS data. We calculate the ratio of the LJ-Gini and the NPP-Gini, which was defined as LN-Ratio (Fig. 5). The average and the median of the L-N-R are 1.7, and the varying range of the ratio is from 1.6 to 2.3. The line chart in Fig. 5 indicates the standard deviation of the NPP-Gini and the LJ-Gini within each province, both at the county level. The average standard deviation of the 31 sets of LJ-Gini is 0.13; and in 74% of provinces, the standard deviation is no more than 0.14. However, five provinces’ standard deviation exceeded 0.18, especially Tibet and Qinghai, which reached 0.31 and 0.22, respectively. On one hand, the rate of internal economic development in the region with a high standard deviation is uneven, and there are hidden dangers to the sustainable development of the social economy. On the other hand, regions with low standard deviation values, represented by Inner Mongolia and Shanghai, are thought to be more similar in internal economic development patterns.

Fig. 5
figure 5

The numerical distribution regulation of NPP-VIIRS data and LJ1-01 data's WGC grouped by province. \(LN-Ratio=\,\frac{Average\,LJ-Gini}{Average\,NPP-Gini}\), one decimal place was kept

Full size image

4 Conclusion

The WGC is an economic coefficient to evaluate the RWDI. The limitations in data quality and accessibility necessitate the search for effective alternative data sources for accurate calculation and assessment of WGC. In this study, we utilize NPP-VIIRS and LJ1-01 data as alternatives to conventional economic statistical data to compute the WGC for 31 provinces and 2,853 counties in mainland China. The purpose of this research is to compare NTL imagery of varying temporal and spatial accuracies, employing pixels as the basic unit of extraction, to evaluate their effectiveness in identifying RWDI in small-scale regions. The WGC values calculated by LJ1-01 data are always higher than those based on NPP-VIIRS data. Based on the comparative analysis of data distributions from the two datasets, we conclude that the LJ1-01 data demonstrates a higher sensitivity to areas with low RWDI compared to NPP-VIIRS data. Consequently, LJ1-01 data is deemed more suitable for assessing RWDI. We compared the numerical distribution of LJ-Gini at the county and province levels. Then, a grading criterion was established to express the RWDI degree more intuitively based on the normal distribution model abstracted from the LJ-Gini of 31 provinces. LJ-Gini values from low to high are divided into RANK-ONE to RANK-FIVE, respectively.

The average LJ-Gini at the county and provincial levels are statistically consistent, 0.77 and 0.78, respectively. However, the standard deviations of the two are 0.13 and 0.096, respectively, with statistically significant differences. Compared with the provincial LJ-Gini, the county LJ-Gini has greater volatility, which is more intuitively shown as more counties are divided into RANK-ONE and RANK-FIVE. The above results indicate that the RWDI assessment results of large-scale areas often mask the inequality in small-scale areas within them, proving the significance of assessing the county-level RWDI. In addition, the standard deviation of county-level LJ-Gini and the degree of negative correlation between county LJ-Gini and economic development show differences in different provinces. This shows the heterogeneity of the RWDI in different regions. For example, the standard deviation of Tibet reaches 0.31, while that of 74% of provinces was no more than 0.14.

In total, in this study, the LJ1-01 satellite remote image shows better spatial information capturing ability than its predecessor, NPP. However, the county-level area is the smallest research unit in this letter, which failed to maximize the potential of LJ1-01 satellite imagery. We speculate that the LJ1-01 data will also show remarkable evaluation capabilities for socioeconomic parameters on a small scale, such as streets.