1 Introduction

Among weather-related disasters, floods are among the most frequent events causing billions of dollars of damage every year worldwide (Xie et al., 2017). In the U.S. alone, there have been an average of 16.2 weather and climate disasters annually between 2015 to 2020 (Smith, 2021), and nearly one-third of people who live in coastal areas are exposed to elevated coastal hazard risks (United States Census Bureau, 2019). In 2021 alone, 223 flood events occurred in the U.S. (Centre for Research on the Epidemiology of Disasters (CRED), 2022) which surpassed the above-mentioned annual average, leading to a sharp increase in the severe impacts of floods on communities and the built environment. For instance, the estimated cost for Hurricane Harvey in 2017 was $198 billion, exceeding that of Hurricane Katrina at $158 billion in 2005 (or roughly $194 billion in 2017 dollars) (Hicks & Burton, 2017). In November 2021, a major rainfall event induced a series of floods in northern parts of the U.S. state of Washington and southern parts of the Canadian province of British Columbia. In British Columbia, this flood caused record-breaking insured damage of $450 million (Insurance Bureau of Canada, 2021). Floods also cause significant damage and loss in other parts of the world. In central China, the July 2021 flooding killed almost 100 people and resulted in more than $11 billion in economic losses (Wang, 2021). In the same year, deadly floods in Germany resulted in $40 billion of economic loss. In Belgium, the 2021 floods were the worst in over 100 years, resulting in an estimated damage of $3 billion (Rodriguez Castro et al., 2022). Past research has identified the key reasons behind intense and widespread floods to be climate change (Alfieri et al., 2017; Arnell & Gosling, 2016; Bjorvatn, 2000; Bowes et al., 2021; Sahin & Hall, 1996; Ward et al., 2014a, b), deforestation (Bradshaw et al., 2007; Sokolova et al., 2019), growing population (Changnon, 2000; Winsemius et al. 2016; Wing et al. 2018), and rapid urbanization (Singh & Singh, 2011; Suriya & Mudgal, 2012). A study by Forzieri et al. (2017) has shown that weather-related natural hazards could affect about two-thirds of Europe’s population annually over the next century. Huang et al. (2015) investigated the combination of different climate scenarios in the five large basins in Germany and found that most rivers in the study area could experience more 50-year floods.

The monetary damage of floods to the infrastructure and housing stock is primarily calculated using key indicators such as water depth and building characteristics (Figueiredo et al., 2018; Gerl et al., 2016; Romali & Yusop, 2021). For example, the depth-damage function, used by the U.S. Army Corps of Engineers and the Federal Insurance Administration, estimates structural damages as a percentage of structure’s value for a given water depth above or below the first occupied level of the structure (Davis & Skaggs, 1992; Wing et al., 2020). Likewise, in the aftermath of a flood event, effective response operations are highly dependent on having access to rapid and accurate flood depth data. Flood mapping systems are sought to provide flood depth data in a particular region or zone over the temporal scale. In the U.S., flood maps prepared by the Federal Emergency Management Agency (FEMA) are commonly used for estimating the extent of flood inundation. However, approximately 75% of FEMA flood maps have not been updated in the last five years, and 11% of them are significantly outdated (dating back to the 1970s and 80 s) (Eby and Ensor, 2019). While advances in urban sensing and computing technologies has led to an uptake in the use of sophisticated remote sensing methods (e.g., monostatic radars) for flood depth mapping, the communication of captured data to the public is often restricted or lagged (Chew et al., 2018). Overall, current flood mapping systems have key limitations, and existing data sources are sparse and not inclusive of many at-risk communities (resulting in data deserts) (Cutter et al., 2003; Van Zandt et al., 2012; Forati & Ghose, 2021; Arabi, 2021). This makes current flood mapping methods inefficient for delivering high-resolution, accurate, and real-time flood depth data to diverse stakeholders who live in flood-prone regions. This paper proposes a novel approach that enables the on-demand estimation of floodwater depth using deep neural networks in photos depicting submerged traffic signage. Compared to other flood mapping systems, the key advantage of this method is its simplicity (ease of use), accuracy, speed, and coverage (by significantly increasing the number of points where floodwater depth can be calculated and logged).

2 Literature review

2.1 Existing flood inundation mapping systems

Much of the information utilized for urban flood depth mapping is extracted from water level sensors and gauges (Crabit et al., 2011), remote sensing data (Feng et al., 2015; Perks et al., 2016), crowdsourcing platforms (Wang et al., 2018), and video surveillance (Liu et al., 2015). However, conventional gauge-based ground monitoring systems could result in uneven coverage of floodplains, and accrue significant sensor installation and operation costs (Dong et al., 2021; Lo et al., 2015). Also, since the estimated flood depth in each station is measured relative to the station level, further comprehensive data pooling is required for flood mapping (Lo et al., 2015). Thanks to recent advancements in remote sensing, flood maps can be generated with high-resolution spatial and temporal data. Examples include terrain data from light detection and ranging (LiDAR) (Brown et al., 2016), radar-based precipitation depths and synthetic aperture radar (SAR) fine-resolution images (Schumann et al., 2011), advanced streamflow measurement (Merwade et al., 2008), digital elevation model (DEM) with an X-band sensor (e.g., TerraSAR-X and COSMO-Skymed Constellation) (Strozzi et al., 2009; Pulvirenti et al., 2011), and short-wavelength microwaves transmitted by satellites (Frappart et al., 2005). Despite some advantages, the reliable application of these methods can be hindered by several factors. For example, data collected from satellites often suffer from restrictions such as orbital cycles and inter-track spacing of satellite movements (Stone et al., 2000). Also, while LiDAR terrain data can be used as a standalone flood inundation mapping approach, filtering LiDAR data in dense urban areas is challenging due to the complex urban landscape (Wedajo, 2017), therefore such data must be juxtaposed with cross-sectional field surveys (Klemas, 2015), which demands additional effort to combine and leverage multiple data streams to generate a complete map (Stone et al., 2000; Kamari & Ham, 2021). Another major problem with LiDAR-based flood mapping is the difficulty of matching LiDAR data with hydraulic models especially in high flood depth (Merwade et al., 2008). Near-real-time SAR flood maps (Shen et al., 2019) can be generated using a radar-based precipitation approach based on data collected from the Next Generation Weather Radar (NEXRAD) system which currently comprises 160 sites across the U.S. (National Oceanic and Atmospheric Administration, 2022). Although radar-based precipitation data uses sophisticated distributed hydrological models, a significant degree of uncertainty is associated with the outcome due to the use of variables that are averaged out over space and time (Alinezhad et al., 2020; Merwade et al., 2008; Zhou et al., 2021). In contrast to the inherent uncertainty in hydraulic and hydrologic models, probability-based predictors such as the Bayesian approach (Beck & Katafygiotis, 1998) used in conjunction with SAR imagery track changes in flood water levels, and use adjustable weights to progressively update model’s estimates and improve prediction accuracy (Hsu et al., 2009).

Another practical barrier to using conventional remote sensing is its insensitivity to data variations and noise in densely vegetated areas, adverse weather, and humid tropical regions with excessive cloud coverage (Asner 2001). Smooth impervious surfaces and shadows in urban areas can also cause over-detection in SAR imagery, thus requiring more information to describe the geometry, orientation, building materials, as well as the direction of radar illumination (Ferro et al., 2011; Shen et al., 2019). Limited access to continuous monitoring, coupled with observing flood depth in only sparsely-located fixed points are among other barriers to the effective application of most remote sensing methods (Lo et al., 2015). In general, the accuracy of existing flood mapping systems is dependent on several factors such as the method used for collecting and describing topography, estimate of the design flow, inherent model uncertainties, noise in input data, and the calibration approach (Merwade et al., 2008; Vojtek et al., 2019).

In recent years, researchers have investigated the prospect of quantifying flood depth through visual examination and detection of key objects in images using computer vision and artificial intelligence (AI). Most object detection models are one-stage or two-stage detectors (Zhan et al., 2021). Jiang et al. (2019), for example, measured the waterlogging depth in videos using single-shot object detection (Liu et al., 2016) by comparing detected ubiquitous reference objects (e.g., traffic buckets) before and after a flood event, achieving a root mean squared error (RMSE) of 2.6 cm (or 1.02 in.) with an average processing time of 0.406 s per video frame. Cohen et al. (2019) estimated the depth of flood for coastal (using a 1-m DEM) and riverine (using a 10-m DEM) locations and reported an average absolute difference of 18–31 cm (or 7–12 in.). Moy de Vitry et al. (2019) re-trained a deep convolutional neural network (CNN) on videos of flooded areas to detect floodwater in surveillance footage (Liu et al., 2015). However, the applicability of this approach was limited by the field of view of the surveillance cameras. Chaudhary et al. (2020) estimated flood depth through analyzing submerged objects in images collected from social media, and comparing them with the average human height (as a reference object). In their method, however, the distance between the location of the camera and the location of detected objects was not considered, which increased the error of projecting extracted flood depth data onto flood inundation maps. To remedy this problem, they also proposed (but did not accomplish) to use a computer vision technique called monoplotting (Golparvar & Wang, 2021) to calibrate the data based on the pixel-level correlation between DEM and the input photo (Marco et al., 2018). Park et al. (2021) estimated flood level with a precision of over 89% by analyzing images of submerged vehicles, and obtained a mean absolute error (MAE) of 6.49 cm (or 2.5 in.). Pally and Samadi (2021) used YOLOv3 (you-only-look-once version 3), Fast R–CNN (region-based CNN), Mask R–CNN, SSD MobileNet (single shot multibox detector MobileNet), and EfficientDet (efficient object detection) to detect the water surface in images of flooded areas. Hosseiny (2021) used U-Net (a CNN model) to estimate flood depth by comparing images of rivers, and achieved a maximum error of 2.7 m. Other proposed methods of flood depth estimation include taking bridges as measurement benchmarks in a study by Bhola et al. (2018), drawing a hypothetical line on walls visible in the camera footage (Sakaino, 2016), using a ruler in riverine areas (Kim et al., 2011), and comparing virtual markers determined by the operator in video frames (Lo et al., 2015). However, past research has particularly relied on in-situ measurements and site-specific calibration which require the pre-installation of target objects in the study area (Moy de Vitry et al., 2019). In our past work (Alizadeh et al., 2021; Alizadeh Kharazi & Behzadan, 2021), we proposed a method to remotely estimate flood depth by analyzing images of traffic signs as physical landmarks, considering that traffic signs are omnipresent and have standardized sizes in most parts of the world. In a nutshell, a combination of deep learning and image processing techniques was utilized to estimate flood depth by comparing crowdsourced photos of traffic signs before and after flood events, yielding an MAE of 12.62 in. for floodwater depth estimation on our in-house Blupix v.2020.1 dataset. Specifically, we utilized Mask R-CNN (which was pre-trained on the Microsoft COCO dataset (Lin et al., 2014) for detecting stop signs in photos. Consequently, image processing models (e.g., Canny Edge detection and Hough transform) were utilized to detect sign poles by searching the area underneath the traffic sign for near-vertical lines. The accuracy of the previous approach was, however, limited by factors such as image quality, noise, illumination, and excessive degree of pole tilt. In this paper, we expand our previous work by using semantic segmentation for detecting not only the traffic signs but also their poles aiming at increasing the accuracy and computational speed of the model. Specifically, this paper improves the pole detection outcome by training a neural network on 800 images with annotated stop signs and poles under various visual conditions. The performance of the new approach is presented on an in-house dataset which demonstrates a significant improvement in terms of accuracy and computational speed. To generate a high-resolution flood inundation map using the proposed approach, a large number of images should be collected and analyzed. Therefore, a crowdsourcing application (named Blupix (Blupix, 2020) was developed and launched as part of the preliminary work that led to this paper. The primary purpose of this application is to facilitate the collection of flood photos by engaging ordinary people in affected areas (particularly in underserved neighborhoods and municipalities), and create an easy-to-use interface to deliver near real-time flood depth information to various stakeholders and communities. Moreover, a mobile app was developed with a built-in computer vision model to enable real-time estimation of flood depth in urban areas (Alizadeh & Behzadan, 2022a). In the field of disaster response and mitigation, crowdsourcing is an invaluable tool where people and stakeholders can report and share needed information collected from their surroundings, thus enhancing the spatiotemporal scalability and inclusiveness of the input data (Assumpção et al., 2018; See, 2019).

2.2 Convolutional neural networks for object detection

To detect target objects in an input image, various object detection methods have been previously used. Conventionally, approaches such as deformable parts models detected objects using a sliding window and a classifier that ran over the entire image (Felzenszwalb, 2010). More recently, Girshick et al. (2014) introduced region-based CNN (R-CNN) with improved performance in object detection. R-CNN can achieve approximately 47 frames per second (FPS) detection speed by considering several regions of interest in the input image and classifying those regions for containing target objects (Gandhi, 2018). In the R-CNN architecture, independent features are extracted from each region proposal separately, resulting in a long processing time. To overcome this issue, faster variants of R-CNN were also proposed, including Fast R-CNN (Girshick, 2015) which is about 213 times faster than R-CNN, Faster R-CNN (Ren et al., 2017) which is about 250 times faster than R-CNN, and Mask R-CNN (He et al., 2017). Later, more real-time detectors were proposed such as single shot detector (SSD) (Liu et al., 2016) in which proposal generation is eliminated and anchor boxes and feature maps are predefined. Similarly, the YOLO model was proposed by Redmon et al. (2016) in which bounding boxes and class probabilities are predicted in one round of image evaluation using a single neural network. Comparing the performance and computation time of various object detection methods reveals that YOLO can perform in real-time with sufficiently high accuracy, while being less computationally expensive. Also, YOLO models can be easily converted to lighter versions, such as Tiny YOLO (Redmon et al., 2016) which is ideal for launching on mobile devices, one of the future directions of this research, i.e., large-scale crowdsourcing of floodwater depth data collection and analysis.

3 Methodology

The following sections present detailed descriptions of the flood depth estimation technique, data preparation (including augmentation), model training and validation, and performance measurement.

3.1 Flood depth estimation using street photos of traffic signs

According to the manual on Uniform and Traffic Control Devices (Federal Highway Administration, 2004), stop signs installed in U.S. roads should have a standardized width and height of 30 in. (on single-lane roads) or 36 in. (on multi-lane roads and expressways). Since our scope is residential areas, the focus of this research is stop signs in single lane streets that are 30 in. in width and height. To estimate flood depth in a particular location (described by a unique longitude and latitude), paired photos of a single stop sign before and after a flood are needed. As shown in Fig. 1a, knowing the height of the octagonal shape of the stop sign in both pixels (\(s\)) and inches (\(30''\)), a constant ratio \(r\) corresponding to the number of inches per pixel in the pre-flood photo is calculated. Using this ratio, the full length of the pole in inches is determined as the product of \(r\) and the pole length in pixels (\(p\)). Similarly, in Fig. 1b, knowing the height of the octagonal shape of the stop sign in pixels (\(s'\)) and inches (\(30''\)), the number of inches corresponding to one pixel in the post-flood photo is obtained as a constant ratio \(r'\). Using this ratio, the length of the visible parts of the pole (above the waterline) in inches is calculated by multiplying \(r'\) and the pole length in pixels (\(p'\)). It must be noted that ratios \(r\) and \(r'\) may not necessarily be equal since pre- and post-flood photos can be taken from different angles and distances from the stop sign.

Fig. 1
figure 1

Flood depth estimation in a paired a pre-flood photo and b post-flood photo (base photo in (b) is courtesy of Erich Schlegel/Getty Images)

Full size image

3.2 Object detection model for pole detection

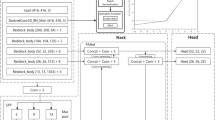
For visual recognition of stop signs and their poles, a robust and accurate object detection model is desired. Moreover, to implement the flood depth estimation technique on mobile devices, the model should be computationally light. To satisfy these two design conditions, we utilize YOLOv4 (Bochkovskiy et al., 2020) for stop sign and pole detection. YOLOv4 is fast and accurate, and features a light version (a.k.a., Tiny YOLO) for implementation on mobile devices. Other object detection models such as RetinaNet-101–500 (Lin et al., 2017a, b), R-FCN, SSD321 (Liu et al., 2016), and DSSD321 (Fu et al., 2017) achieve mean average precision (mAP) of 53.1% (at 11 FPS), 51.9% (at 12 FPS), 45.4% (at 16 FPS), and 46.1% (at 12 FPS) on the Microsoft COCO dataset (Lin et al., 2014), respectively. By comparison, YOLOv3-320, YOLOv3-416, and YOLOv3-608 models (Redmon & Farhadi, 2018) yield mAP of 51.5% (at 45 FPS), 55.3% (at 35 FPS), and 57.9% (at 20 FPS) on the same dataset, respectively. The term mAP is a metric used to evaluate the performance of object detection models, and higher mAP indicates higher accuracy of the model (Henderson & Ferrari, 2017; Robertson, 2008). YOLOv4 surpasses YOLOv3 in terms of speed and accuracy, by achieving 65.7% mAP at 65 FPS on the Microsoft COCO dataset. This superior performance is primarily the result of using a different backbone in the YOLOv4 model. Particularly, the model utilizes the cross-stage-partial-connections (CSP) network with Darknet-53 (Wang et al., 2020) as the backbone for more efficient feature extraction. As shown in Fig. 2, this backbone extracts essential features from the input image, which are then fused in the neck of the YOLO model. The neck is comprised of layers that collect feature maps from different stages. This part of the model consists of two networks, namely spatial pyramid pooling (SPP) (He et al., 2015) and path aggregation network (PANet) (Liu et al., 2018). The neck consists of several top-to-bottom paths and bottom-to-top paths that better propagate layer information. Similar to the head of YOLOv3, the head of YOLOv4 adopts the feature pyramid network (FPN) (Lin et al., 2017a, 2017b), predicts object bounding boxes, and outputs the coordinates along with the widths and heights of detected boxes (Redmon and Farhadi, 2018) through three YOLO layers.

Fig. 2
figure 2

The architecture of the YOLOv4 network adopted in this research

Full size image

3.3 Pre-trained model

The YOLOv4 model is pre-trained on the publicly available Microsoft COCO dataset to detect 80 object classes (Lin et al., 2014). To train the adopted model on the target dataset in this study, transfer learning is used, which is a validated approach for training a CNN model on a relatively small dataset (a.k.a., target dataset) by transferring pre-defined weights (that the network has learned when trained on a large dataset) to allow the model to detect relevant intermediate features (Gao & Mosalam, 2018; Han et al., 2018; Hussain et al., 2018; Tammina, 2019). The dataset used for training has images containing two classes: stop sign and pole. This reduces the output size of YOLO layers from 80 to 2 classes. Using transfer learning, all network weights except those of the last three YOLO layers are kept constant (i.e., frozen). At the beginning of the training process, the weights of the three YOLO layers are randomly selected, and then constantly optimized with the goal of maximizing the mAP for pole and stop sign detections. At these optimal values, the model is neither overfitting (i.e., unable to detect objects in new data due to overly learned features in the training set and forgetting general features) nor underfitting (i.e., unable to detect objects in training data and new data due to limited features that were learned).

3.4 Clustering the training set

YOLO models use pre-defined anchor boxes, which are a set of candidate bounding boxes with fixed width and height initially selected based on the dataset, and subsequently scaled and shifted to fit the target objects (Ju et al., 2019). The YOLOv4 model, in particular, utilizes nine anchor boxes. Therefore, all 1,262 ground-truth boxes in the training set (containing instances of both stop sign and pole classes), shown in Fig. 3a, are clustered into nine groups using k-means clustering (k = 9) (Redmon and Farhadi, 2018). The centroids of these nine clusters are used to define nine anchor boxes, as illustrated in Fig. 3b.

Fig. 3
figure 3

a Nine clusters (k = 9) corresponding to the training set, and b Recalculated anchor boxes for the in-house dataset

Full size image

3.5 Training the model

Following Bochkovskiy (2020), the adopted YOLOv4 model is trained for 4,000 iterations (2,000 iterations for each class), with a learning rate of 0.001 using Adam optimizer (Kingma & Ba, 2014), with a batch size of 1 and subdivision of 64. The Darknet-53 (backbone of this model) is built in Windows on a Lenovo ThinkPad laptop computer with 7 cores, 9750H CPU, 16 GB RAM, and Nvidia Quadro T1000 GPU with a 4 GB memory. The network resolution (i.e., image input size) is reduced to the size of \(320\times 320\times 3\) to lower computational cost and time. The total processing time for training the model is approximately 12 h, with an average loss of 0.567.

Random and real-time data augmentation is automatically applied to the training set to increase the size of training data by creating slightly modified copies of existing images. Past studies have investigated various approaches to data augmentation. In particular to the YOLO architecture, Kang et al. (2019) changed the hue, saturation and exposure of images for training a Tiny YOLO model to detect fire. Ma et al. (2020) applied color jittering and saturation, exposure, and hue change for augmenting images of thyroid nodules for training a YOLOv3 model. Koirala et al. (2019) augmented images of fruits for training a YOLO model by modifying hue, saturation, jitter and multiscale. Lastly, Niu et al. (2020) applied image mosaic, horizontal flipping, and image fusion for augmenting images of sanitary ceramics for training a Tiny YOLO model. In this study, hue, saturation, and exposure of training samples are changed within [-18… + 18], [0.66…1.5], and [0.66…1.5], respectively as recommended by Bochkovskiy et al., (2020). Also, a Jitter (random image cropping and resizing by changing the aspect ratio) of 0.3 is implemented for data augmentation. The maximum jitter allowed in data augmentation is 0.3 (Ma et al., 2020). Moreover, 50% of images are flipped horizontally but no image is flipped vertically (Hu et al., 2020). Lastly, 50% of images are augmented with a mosaic by combining four different images into one image (Hao & Zhili, 2020).

3.6 Validating the model

To prevent overfitting (i.e., a model that is exactly fitted to the training data, preventing it from correctly detecting new data), model performance is monitored on validation sets using a fivefold cross validation approach (Browne, 2000; Islam et al., 2020; Lyons et al., 2018; Seyrfar et al., 2021). Using this approach, 160 photos are randomly drawn (without replacement) from the training set (20% of the total of 800 images in the training set) for five times as validation sets, and the remaining photos are used for model training. The model is then trained on each training set for 4,000 iterations and validated on the corresponding validation set. The number of epochs is the number of iterations divided by the number of images over the batch size. With the batch size of 1, there are a total of 5 epochs in 4,000 iterations. During the training process, the highest mAPs on the validation sets along with the corresponding number of iterations are saved. Next, average performance is calculated as the average of obtained mAP values across all validation sets. The optimum number of iterations is also computed as the average of the best number of iterations (corresponding to the highest mAP) in all validation sets. In this study, the average mAP and average iteration numbers achieved in fivefold cross validation are 97.04% and ~ 3,000 (since model weights are saved at every 1,000 iterations, the optimum number of iterations is rounded to 3,000 to be exact). This means that after 3,000 iterations, the model shows a tendency to overfit to the training data. Ultimately, the model is trained on the entire training and validation sets for the obtained optimum number of iterations (i.e., 3000), and the mAP at 3000th iteration is reported. The set of network weights saved at this number of iterations is marked as optimum and used for testing the model. Table 1 shows the validation output of the trained model on each validation set.

Table 1 The highest average performance of the trained model on five validation sets using fivefold cross validation (S: Stop sign; P: sign pole; S + P: stop sign and sign pole)
Full size table

3.7 Tilt correction

Over time or as a result of floodwater flow, traffic signs can be tilted in any direction, leading to the underestimation of the submerged pole height by the YOLOv4 model (since detected bounding boxes are not tilted), and eventually erroneous floodwater depth calculation. In cases where both pre- and post-flood photos are tilted by the same angle, floodwater depth calculation is not impacted by the tilt. However, if the degrees of tilt differ between pre- and post-flood photos of the stop sign, pole length estimation should be adjusted prior to calculating the floodwater depth. In Fig. 4, pre-flood and post-flood stop signs are presented with unequal tilt degrees (α degrees for pre-flood stop sign and β degree for post-flood stop sign). For each photo, the actual pole length is the reverse projection of the height of the detected bounding box (\(P\) and \(P'\)) by the degree of tilt (α and β). Eq. 1 presents the calculation of flood depth considering unequal degrees of tilt for a given paired stop sign photo.

Fig. 4
figure 4

Adjusting flood depth estimation for pre-flood and post-flood stop signs with unequal degrees of tilt

Full size image
$$W=P\left(\frac{\cos\;\alpha}{\cos\;\beta}\right)-P'$$
(1)

To automatically detect the degree of sideways tilt, a tilt correction technique is implemented and applied before stop sign and pole detection. By visually inspecting the photos in the dataset, it is observed that the maximum tilt does not exceed 25º. Thus, we select a range of [-25º… + 25º] for tilt correction. Next, as shown in Fig. 5, the input image is rotated from 0 to -25º clockwise (in 5º intervals) and from 0 to + 25º counterclockwise (in 5º intervals). Generated images are then processed by the trained YOLO model for stop sign and pole detection. The image with the minimum width of the pole detection bounding box is ultimately selected as the one containing the most vertical pole. Consequently, the degree of tilt that was applied to the original image to generate this image is calculated as the tilt angle (β degrees for pre-flood stop sign and α degree for post-flood stop sign).

Fig. 5
figure 5

Tilt detection approach (base photo is courtesy of KjzPhotos/Shutterstock)

Full size image

3.8 Model performance

In object detection, a commonly used metric for measuring model performance is mAP (Ren et al., 2017; Turpin & Scholer, 2006). The basis of mAP calculation across all classes is the average precision (AP) for each individual class. In turn, the AP for any given class is measured using intersection over union (IoU) (Javadi et al., 2021; Kido et al., 2020; Nath & Behzadan, 2020), which is calculated for each detection based on the overlap between the predicted bounding box (\(B'\)) and the ground-truth bounding box (\(B\)) (Eq. 2). Following this, the detected object is classified as correct (if the IoU is above a predefined threshold, typically 50%), or incorrect (if the IoU is below the threshold) (Alizadeh & Behzadan, 2022b; Alizadeh et al., 2022; Nath & Behzadan, 2020; Zhu et al., 2021). Based on the correctness of the detected object, true positive (TP; correct classification to a class), false positive (FP; incorrect classification to a class), and false negative (FN; incorrect classification to other classes) cases are counted. Next, Eq. 3 and Eq. 4 are used to calculate precision (model’s ability to detect only relevant objects) and recall (model’s ability to detect all relevant classes) based on TP, FP and FN for each class (Guo et al., 2021; Mao et al., 2021; Padilla et al., 2020; Xu et al., 2021). It must be noted that true negative cases are not considered in object detection when measuring model performance, as there are countless number of objects (belonging to a large number of classes) that should not be detected in the input image (Padilla et al., 2020).

$$IoU=\frac{B'\cap B}{B'\cup B}$$
(2)
$$Precision=\frac{TP}{TP+FP}$$
(3)
$$Recall=\frac{TP}{TP+FN}$$
(4)

To calculate the AP of any object class, all detections are initially sorted based on their confidence scores in descending order, and Eq. 5 is then applied. In this Equation, \(N\) refers to the total number of detected bounding boxes, \(i\) refers the rank of a particular detection in the sorted list, \({P}_{i}\) refers to the precision of the \(i\) th detection, and \(\Delta r\) is the change in recall between two consecutive detections \(i\) th and \((i+1)\) th. Finally, mAP is calculated as the average precision over all classes, as formulated by Eq. 6 (Lyu et al., 2019; Nath & Behzadan, 2020).

$$AP={\textstyle{\displaystyle\frac1N}\sum_{i=1}^N}P_i\bigtriangleup r_i$$
(5)
$$mAP={\textstyle\sum_{i=1}^NA}P_i$$
(6)

3.9 Flood depth estimation

Flood depth is estimated using the YOLOv4 model trained on photos of stop signs taken before and after flood events. The general framework for detecting stop signs and their poles in pre- and post-flood photos and estimating flood depth is illustrated in Fig. 6. As shown in this Figure, paired pre-flood and post-flood photos of a stop sign are processed by presenting them to the model as two separate inputs. The model then detects the stop sign and its pole in each image, and measures the length of the visible part of the detected poles using geometric calculations based on the size of stop signs (Sect. 3.1). Next, the depth of floodwater at the location of the stop sign is estimated as the difference between pole lengths in pre- and post-flood photos.

Fig. 6
figure 6

Workflow for estimating flood depth in a sample paired pre- and post-flood photos (base post-flood photo is courtesy of Erich Schlegel/Getty Image)

Full size image

In addition to evaluating the model performance in stop sign and pole detection, its ability to estimate flood depth must be assessed. The literature in this field has used MAE as an informative metric to describe the discrepancy in flood depth estimation (Chaudhary et al., 2019; Cohen et al., 2019; Park et al., 2021; Alizadeh Kharazi and Behzadan, 2021; Alizadeh et al., 2021). In this study, the error of pole detection in pre-flood and post-flood photos is determined as the difference between ground-truth pole length (\({l}^{g}\)) and detected pole length (\({l}^{d}\)). The absolute error in a single image is then calculated as the cumulative error in pre-flood and post-flood photos. Since we measure the depth of flood based on the difference between pole lengths in \(M\) paired pre- and post-flood photos, the MAE for flood depth estimation can be determined as the average of absolute errors in all paired photos (Eq. 7).

$$MAE=\frac1M{\textstyle\sum_1^M}\left|\left({l^g}_{pre}-{l^d}_{pre}\right)+\left({l^g}_{post}-{l^d}_{post}\right)\right|$$
(7)

4 Data description

Table 2 shows a detailed breakdown of the image datasets used to train and test the model. The data used for training the adopted YOLO model to detect stop signs and sign poles consists of two image datasets: pre-flood photos and post-flood photos. Each dataset is described in detail in the following sections. The data used for testing the YOLO model comprises 176 pre-flood and 172 post-flood photos drawn from the Blupix v.2021.1 dataset (containing 224 pairs of pre- and post-flood photos, i.e., 448 photos in total), by filtering out photos with very low resolution or those in which entire poles are not captured. The Blupix v.2021.1 dataset is an expanded version of the Blupix v.2020.1 (Alizadeh Kharazi & Behzadan, 2021) which contained 186 pairs of pre- and post-flood photos; i.e., 372 photos in total.

Table 2 Overview of the training and test datasets
Full size table

4.1 Pre-flood training dataset

There are publicly available large-scale datasets containing images of stop signs. The pre-flood training dataset is generated by extracting a subset of photos of stop signs with the entire stop sign poles in the photo from the Microsoft COCO dataset (Lin et al., 2014). Figure 7 shows examples of stop sign photos in different countries, with different forms and pole shapes, extracted from the Microsoft COCO dataset. Although all stop sign objects were already annotated in the Microsoft COCO dataset, it was found that some annotations were not as accurate as expected. For example, shapes of masks drawn over stop signs were not always octagonal. To resolve this problem, all extracted images were re-annotated by a trained annotator. Ground-truth bounding boxes were determined by manual labeling, e.g., outlining stop signs and poles by polygons using LabelMe software (Wada, 2016). Although annotating images with rectangular bounding boxes was sufficient for implementing the YOLO model, it was ultimately decided to annotate using masks to achieve more accurate shapes (octagonal masks over stop signs and quadrilateral masks over sign poles) and to facilitate the generalizability of the annotations for future studies. At the conclusion of the annotation step, all masks were converted to bounding boxes which is the required input format of the YOLO model. Sample annotated pre- and post-flood photos are shown in Fig. 8. These photos depict a stop sign at the intersection of Tumbling Rapids Dr. and Hickory Downs Dr. in Houston, Texas. The post-flood photo was obtained via crowdsourcing after Hurricane Harvey in (2017), and the pre-flood photo was taken by the authors on January 23, 2021.

Fig. 7
figure 7

Photos of various stop signs in different forms and languages available from the Microsoft COCO dataset

Full size image
Fig. 8
figure 8

Sample annotated a pre-flood photo, and b post-flood photo (base photo in (b) is courtesy of Erich Schlegel/Getty Images)

Full size image

4.2 Post-flood training dataset

For post-flood photos, an in-house dataset is created which contains 270 web-mined photos of flooded stop signs. Web-mining is conducted using related keywords such as “flood stop sign”, “flood warning sign”, and their translations in three other languages (i.e., Spanish, French, Turkish). To increase the generalizability of the model, we also include photos taken from the back side of the sign, those depicting tilted poles or reflections in water, as well as photos taken in daylight or nighttime, photos with clear or noisy backgrounds, and photos taken in different weather conditions. Additionally, to minimize detection error, the dataset is further balanced by generating synthetic training data (Feingersh et al., 2007; Hu et al., 2021; Tremblay et al., 2018; Shaghaghian & Yan, 2019; Nazari & Yan, 2021). In particular, a new set of post-flood photos depicting flooded traffic signs (other than stop signs) is imported in a photo editing tool where the depicted traffic signs are replaced with stop signs (keeping the pole unchanged). Using this method, 64 synthetic images are added to the dataset which results in a total of 334 post-flood photos.

4.3 Non-labeled objects

Since the model is trained on stop signs in different languages (with white text on a red octagonal shape), it could learn overly detailed features that may not be generalizable, resulting in potentially false positive cases. To resolve this problem, the training set is further enriched with samples that are visually proximal to stop signs but are not stop signs, to force the model to learn distinctive characteristics specific to stop signs while avoiding false positives. In particular, 71 web-mined pre-flood photos and 61 web-mined post-flood photos of other traffic signs similar to stop signs (such as “Do Not Enter” signs) are added to the training dataset.

5 Results and analysis

5.1 Performance of the trained model

In this section, the performance of the trained YOLOv4 model is evaluated on the test dataset, and results are discussed. For the test set, we extracted 176 pre-flood and 172 post-flood photos from the Blupix v.2021.1 dataset by filtering out photos with significantly low resolution or those in which parts of poles and/or stop signs were not visible. Of these pre- and post-flood photos, 163 photos are paired. Table 3 summarizes model performance with the optimum trained weights when tested on the test set. As shown in this Table, the AP calculated for stop sign and pole detection in pre-flood photos is 100% and 99.41%, respectively. Similarly, the AP calculated for stop sign and pole detection in post-flood photos is 99.73%, and 98.73%, respectively. The mAP for pre- and post-flood photos is 99.70% and 99.23%, respectively. The relatively higher mAP for pre-flood photos can be attributed to less noise in these photos compared to post-flood photos. The average detection times for all detections in pre-flood and post-flood photos are 0.05 and 0.07 s, respectively, which is close to real-time.

Table 3 Performance of the trained model in detecting stop signs and poles in pre- and post-flood photos of the test set (S: Stop sign; P: sign pole; S + P: stop sign and sign pole)
Full size table

Without considering the uneven degrees of tilt for few paired photos, the model can calculate pole lengths in test images with an MAE of 1.856 in. and 2.882 in. for pre- and post-flood photos, respectively. The slightly higher error corresponding to post-flood photos can be primarily attributed to the presence of visual noise in post-flood scenes. To examine the tilt correction method, 37 images of stop signs in the test set with uneven pole tilt degrees in pre- and post-flood photos are identified. After implementing the tilt correction technique, the MAE of the trained YOLOv4 model on the Blupix v.2021.1 dataset is reduced to 1.723 in. and 2.846 in. for pre- and post-flood photos, respectively, showing a slight improvement in flood depth estimation outcome as a result of implementing the tilt correction technique. However, it is anticipated that with more paired photos depicting uneven degrees of tilt, the reduction in error becomes more significant. Table 4 summarizes model performance on the test set. To calculate the error of flood depth estimation, ground-truth floodwater depth (i.e., the difference between ground-truth pole lengths in paired pre- and post-flood photos) is compared with the estimated floodwater depth (i.e., the difference between detected pole lengths in paired pre- and post-flood photos). The MAE of the model for flood depth estimation on 163 paired photos were achieved as 4.737 in. and 4.710 in. before and after implementing the tilt correction technique, respectively.

Table 4 Performance of the trained model in estimating pole lengths in pre- and post-flood photos of the test before and after tilt correction
Full size table

5.2 Pole length estimation using baseline methods

In addition to assessing the performance of the trained YOLOv4 model using metrics such as MAE and RMSE, we compare model performance with two baseline approaches (a.k.a., dummy methods). The purpose of these dummy methods is to verify that the performance of the YOLOv4 model exceeds that of a simple model that returns average values given a set of pole length values. In dummy method I, for a given pre-flood (post-flood) test image, the model returns the average pole length of all pre-flood (post-flood) images in the training set. The average pole length for pre-flood and post-flood photos in the training set is 76.98 in. (n = 334) and 53.38 in. (n = 395), respectively. Using dummy method I, the MAE for the pre-flood photos and post-flood photos in the test set is thus determined as 44.628 in. (n = 176) and 49.804 in. (n = 172). In dummy method II, for a given pre-flood (post-flood) test image, the model returns the running average pole length of all previously seen pre-flood (post-flood) images in the test set. Running average is a common method for extracting an overall trend from a list of values, by continuously updating an average value considering all data points in the set until the calculation point (Crager & Reitman, 1991; Du et al., 2008; Pierce, 1971; Tan et al., 2021). To reduce the order effect and allowing for a thorough examination of the variability and accuracy of the model across a range of randomized data sets, pole length values are recorded in 100 iterations each containing a randomized order of test images. Consequently, the performance of dummy method II is calculated as the MAE of all 100 obtained running averages. The MAE achieved for dummy method II for pre-flood and post-flood photos is 13.271 in. and 20.469 in., respectively. Also, the minimum and maximum MAE achieved for pre-flood (post-flood) is found to be 0.056 in. and 42.830 in. (0.344 and 45.824), respectively. Our results show that dummy method II is able to reduce the pole length estimation error to less than 1 in. in only one randomized set. However, dummy method II outperforms dummy method I, yet is highly sensitive to the order of values. Comparing the MAE of the proposed YOLOv4 model, (i.e., 1.723 in. for pre-flood photos and 2.846 in. for post-flood photos) with the MAEs of dummy methods I and II, it is clear that our proposed model outperforms the two baseline methods. Table 5 summarizes the MAE and RSME obtained using dummy methods I and II.

Table 5 Performance of dummy methods I and II on the test set
Full size table

5.3 Impact of stop sign language on model performance

To analyze the performance of the model in different languages, MAE and RMSE values are calculated for various subsets of photos (after implementing tilt correction), with results summarized in Table 6. The analysis indicates that in pre-flood photos, the MAE for stop signs in French is 4.628 in., which is higher than the MAE of 1.585 in. for stop signs in English. On the other hand, in post-flood photos, the MAE for stop signs in French is 1.565 in., which is lower than the MAE of 2.908 in. for stop signs in English. Further investigation reveals that the MAE for pole length estimation is impacted by image quality rather than stop sign language. For example, web-mined post-flood photos of stop signs in French language are in high-resolution (taken by professional cameras), thus lowering the corresponding MAE. In contrast, the quality of one of the French pre-flood photos was significantly low which led to a higher MAE for pole length estimation in the corresponding subset.

Table 6 The performance of the flood depth estimation model based on stop sign language
Full size table

5.4 Benchmarking

As stated earlier, the model achieved an MAE of 4.710 in. on 163 paired images in the test set after implementing tilt correction. By comparison, Cohen et al. (2019) obtained an average absolute difference of 18–31 cm (approximately 7–12 in.) for flood depth estimation in coastal and riverine areas, Chaudhary et al. (2019) reported a mean absolute error of 10 cm (approximately 4 in.) in estimating flood depth based on comparing submerged objects in social media images with their predefined sizes, and Park et al. (2021) presented a mean absolute error value of 6.49 cm (approximately 2.5 in.) by comparing visible parts of submerged vehicles with their estimated size. As summarized in Table 7, a comparison of the flood depth estimation error obtained in this research to previous studies indicates the reliability and generalizability of the developed technique in measuring floodwater depth with acceptable accuracy.

Table 7 Comparison of the results of this study with the literature on floodwater depth estimation
Full size table

6 Summary and conclusion

Flooding is one of the most prevalent natural hazards that results in significant loss of life, and disrupts properties and infrastructure. Due to the constant change in water levels on the road network during a flood, reliable and real-time flood depth information at the street level is critical for decision-making in evacuation and rescue operations. Current methods of obtaining flood depth (including water gauges, DEMs, hydrological models, and SAR) often suffer from shortage of data, inherent uncertainties, high installation and maintenance costs, and the need for heavy computing power. Recent advancements in computer vision and AI have created new opportunities for remotely estimating the flood depth based on comparing submerged objects with their predefined sizes. In this paper, a deep learning approach, based on the YOLOv4 architecture, was proposed for estimating floodwater depth in crowdsourced street photos using traffic signs. Since traffic signs have standardized sizes, the difference between pole lengths in paired pre- and post-flood photos of the same sign can be computed and used as the basis for estimating the depth of floodwater at the location of the sign. An in-house training set comprising web-mined photos and photos extracted from the Microsoft COCO dataset, was used for training the YOLOv4 model. The trained model was then validated using fivefold cross validation, and subsequently tested for flood depth estimation on 163 paired photos from our in-house test set. Results indicate an MAE of 1.723 and 2.846 in. for pole length estimation in pre- and post-flood photos, respectively, and an MAE of 4.710 in. for floodwater depth estimation. Also, the performance of the proposed model surpassed that of two baseline approaches (dummy method I, which returns the average pole length of all images in the training set for each image in the test set; and dummy method II, which calculates the running average of pole lengths in all previously seen images in the test set). In addition, a tilt correction method was developed to minimize the pole length estimation error in paired photos of stop signs with uneven degrees of tilt. As a part of the future direction of this research, the authors aim to increase the generalizability of the floodwater depth estimation model by training it on various forms of traffic signs and other standardized urban landmarks. Moreover, to evaluate the real-world performance and practicality of the proposed methodology, the authors are conducting a user study of people’s perception of risk during flood events and the value of information provided by the proposed flood depth estimation method on their decisions.