1 Introduction

Complex dynamics define complex nonlinear systems as systems with high-order, multi-loop and nonlinear information feedback structures. Complex systems are often composed of a large number of interacting units. The information interaction of these units causes the system to spontaneously generate complex behaviors and present collective functional characteristics that each unit does not possess [1]. Nonlinear complex systems widely exist in nature and socioeconomic fields. For example, in nature, typical nonlinear complex systems include ecosystems, biological systems, human brains, animal digestive systems, and blood circulation systems. In socioeconomics, specific nonlinear complex systems include population systems, urban and rural systems, energy systems, transportation systems, trade systems, and financial systems are typical nonlinear complex systems [2].

Nonlinear complex systems usually have the properties of evolutionary emergence, self-organization, self-propagation, power law and critical phase transition. Among them, the critical phase transition is one of the properties most concerned by scholars. When a complex system is in critical state it will be at optimal performance or induce system-level risk [3–5]. On the hand, critical states endow complex systems with advantages such as self-adaptation, toughness, and pluripotency. For example, the nervous system tends to show better computing power if it is near the criticality [6]; the natural swarm system (birds flock, ant colony, fish swarm, flora) in the critical state can respond flexibly to change in the environment, to prevent the weak interference from destroying the entire cluster system [7].

On the other hand, a system in critical state is also prone to collapse under external disturbances due to unstable factors [8–10]. For example, the increasing number of vehicles on an urban road network can lead to localized congestion, which can lead to traffic jams when the critical point is further crossed [11, 12]; the phase transition of infectious disease incidence depends on the network topology, and propagation parameters constitute the critical value. When the transmission parameter exceeds the critical value, the epidemic scale will suddenly increase [13].

Among the critical phenomena, the amplitude death phenomenon has received attention because it is usually associated with the destructive behavior of the system. In nonlinear dynamical systems, amplitude death is a phenomenon in which the oscillatory behavior of a state variable ceases completely [14]. The main reason for amplitude death is that the system parameters drift past the critical point [15]. Since amplitude death profoundly affects the evolution and operation of complex systems, how to effectively predict amplitude death is meaningful and essential. In the real world, complex systems are characterized by high dimensionality, nonlinearity, feedback, and randomness. The system equations are most likely unknown. With the rise of machine learning methods, the research on data-driven model-free prediction has attracted the interest of many scholars [16–18].

Among the data-driven methods for predicting critical phenomena, the recurrent neural network algorithm based on reservoir computing is the mainstream. This method has high accuracy and has achieved relatively good performance in critical state prediction of complex systems such as population extinction caused by population food chains, power system collapse prediction [19], and transient spatiotemporal chaos in the Kuramoto-Sivashinsky system [20]. Jiang, et al. [21] found a “valley interval” with the slightest prediction error for the neural network’s spectral radius, which helps optimize the reservoir framework’s design and improve the prediction accuracy of critical states. Kong, et al. [15] proposed reservoir computing using additional parameter input channels to predict critical transition and critical chaos in nonlinear systems, determining whether the system has transitioned from a critical point to a transient state. Fahimeh, et al. [22] tried to modify the four critical point indicators of the autocorrelation function, variance, kurtosis and skewness to predict different critical points. Fan, et al. [23] proposed a scheme involving actual state updates for the short prediction time of reservoir computing. It demonstrated that occasional updates to a subset of state variables could significantly extend the prediction time. Zhang, et al. [24] demonstrated that reservoir computing can be used for long-term prediction of the phase of chaotic oscillators and showed that a properly designed reserve pool algorithm could reliably sense the phase synchronization between a pair of coupled chaotic oscillators.

From the above-mentioned related literature, it can be found that deep learning algorithms can be effectively applied to the study of critical phenomenon prediction, but the related algorithms are mainly based on recurrent neural networks represented by reservoir computing. Critical phenomenon prediction is usually a long-time series prediction task. When performing a long time series prediction task, reservoir computing is prone to gradient disappearance. Since recurrent neural networks deal with time series data in a tandem relationship, the output of the hidden layer further away from the current time has less influence on the output of the current hidden layer, making it difficult for the model to analyze the long-term dependencies in the long time series. Meanwhile, reservoir computing extracts the features of all nodes in the time series equally and is unable to distinguish the key information, resulting in limited accuracy when predicting long time series.

In recent years, transformer models based on the self-attention mechanism have also achieved better results in image recognition, sound classification [25] and temporal prediction [26–29] tasks. Zhou, et al. [30] proposed the informer model to address the problem of excessive computational complexity of transformer when the sequence length grows. The model is able to better capture the long-term dependencies between inputs and outputs while reducing the computational complexity and memory usage. With Self-attention Distilling, the informer is able to distinguish important information and assign higher weights to features that have a dominant role. Compared to recurrent neural networks, informer effectively improves the accuracy of time series prediction and is suitable for long time series prediction tasks [30].

In summary, this paper proposes to construct a critical phenomenon prediction model using the informer model based on the self-attention mechanism. The self-attention mechanism is used to learn the correlation and long-term dependence of elements within a complex system. However, in order to predict the amplitude death caused by parameter drift, the deep learning model needs to be parameter-aware so that it can track the changes of bifurcation parameters. Therefore, the informer model is difficult to directly apply to the amplitude death prediction task. To address this technical difficulty, this paper proposes an enhanced informer model by designing a bifurcation parameter input channel so that the model can tap the correlation between parameter drift and system variable evolution and effectively track the critical evolution of the system caused by parameter drift. The experimental results show that the enhanced informer model with bifurcated parameter channels improves the effective prediction length by 30% compared with the traditional model. Meanwhile, the enhanced informer algorithm can achieve the prediction of amplitude death.

2 Problem description

As the first chaotic attractor discovered [31], the Lorenz chaotic system is the first dissipative system that exhibits chaotic motion in numerical experiments. The state equation of the Lorenz chaotic system is:

$$ \begin{gathered} \dot{x}_{1} = a ( x_{2} - x_{1} ), \\ \dot{x}_{2} = - x_{1}x_{3} - x_{2} + bx_{1}, \\ \dot{x}_{3} = x_{1}x_{2} - cx_{3}. \end{gathered} $$
(1)

It presents a chaotic state at \(a = 10\), \(b = 28\), \(c = 8/3\), and when the initial state is set to \((1,1,1)\), the system state is shown in Fig. 1 (a).

Figure 1
figure 1

Chaotic system

Full size image

The Rössler system is a simpler chaotic system model than the Lorenz model [32], which can be expressed by ordinary differential equations as:

$$ \begin{gathered} \dot{y}_{1} = - y_{2} - y_{3}, \\ \dot{y}_{2} = y_{1} + dy_{2}, \\ \dot{y}_{3} = e + y_{3} ( y_{1} - f ). \end{gathered} $$
(2)

It presents a chaotic state at \(d = e = 0.1\), \(f = 18\), and when the initial state is set to \((1,1,1)\), the system generates a single-scroll folded chaotic attractor, as shown in Fig. 1 (b).

When isolated, the Rössler or the Lorenz chaotic system is in an oscillatory state. However, when they are coupled, amplitude death occurs. The six-dimensional system of coupled Rössler and Lorenz systems is described as follows:

$$ \begin{gathered} \dot{x}_{1} = a ( x_{2} - x_{1} ), \\ \dot{x}_{2} = - x_{1}x_{3} - x_{2} + bx_{1} + \varepsilon ( y_{2} - x_{2} ), \\ \dot{x}_{3} = x_{1}x_{2} - cx_{3}, \\ \dot{y}_{1} = - y_{2} - y_{3}, \\ \dot{y}_{2} = y_{1} + dy_{2} + \varepsilon ( x_{2} - y_{2} ), \\ \dot{y}_{3} = e + y_{3} ( y_{1} - f ). \end{gathered} $$
(3)

Where, ε is the bifurcation parameter. When the initial value of the system is \((1, 0, 0, 0, 0, 0)\), as the bifurcation parameters change, the bifurcation diagram of the six-dimensional system is shown in Fig. 2.

Figure 2
figure 2

Bifurcation diagrams of coupled Rössler and Lorenz systems

Full size image

As seen from the above figure, when the bifurcation parameter of the system exceeds the critical value \(\varepsilon _{c} = 0.40\), the system in the state of chaotic oscillation will appear the phenomenon of amplitude death. When the bifurcation parameter value is 0.3, which is lower than the critical value, the corresponding time series of each variable in the system will continue to oscillate chaotically. When the value of the bifurcation parameter is 0.5, which is higher than the critical value, the time series corresponding to each variable in the system will eventually transform into an amplitude death state after a period of chaotic oscillation. Therefore, the problem of predicting the amplitude death phenomenon of complex systems can be studied based on the coupled Rössler and Lorenz system. The amplitude death prediction problem consists of two main aspects. On the one hand, it is necessary to achieve effective prediction of the evolution of the coupled system variables for a certain length, and on the other hand, it is necessary to achieve the prediction of the system amplitude death phenomenon when the drift of the bifurcation parameter crosses the critical value.

3 Prediction model

3.1 Informer

Informer, as a self-attentive mechanism model, derives its main architecture from transformer. Transformer is the first model that entirely relies on the attention mechanism to learn the global dependencies between input and output and does not adopt the structure of CNN or RNN [25]. The model architecture of transformer is shown in Fig. 3, including an embedding layer, an encoder-decoder module and a regression layer. The primary function of the embedding layer is to expand the vector by another dimension. The method is to map the node value to a vector of length \(d_{\mathrm{model}}\). Transformer, in order to learn the location information in a sequence, needs to combine the location information encoding with the time series to form a new feature representation input. The calculation formula of the position information encoding in the vector is as follows:

$$ \begin{gathered} \mathrm{PE}_{(\mathrm{pos},2i)} = \sin \bigl(\mathrm{pos}/10{,}000^{2i/d_{\mathrm{model}}} \bigr), \\ \mathrm{PE}_{(\mathrm{pos},2i + 1)} = \cos \bigl(\mathrm{pos}/10{,}000^{2i/d_{\mathrm{model}}} \bigr). \end{gathered} $$
(4)

Where pos is the position and i is the dimension, that is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from 2π to \(10{,}000 \cdot 2\pi \).

Figure 3
figure 3

Transformer architecture

Full size image

In the encoder-decoder module, the encoder and the decoder are stacked to build N layers. Each layer structure is connected by a self-attention layer and a feedforward network layer in sequence. The decoder uses a masked self-attention layer to obtain the current node’s attention information. The self-attention mechanism is the key to transformer. For the input vector X, the self-attention mechanism first calculates three vector matrices through the Embedding vector and the random matrix \(W_{Q}\), \(W_{K}\) and \(W_{V}\), which are the Query (Q), Key (K) and Value (V) weight matrices. After that, the vector Q and K are first multiplied by the dot. Softmax gets stuck in minimal gradients for larger dimensions of V since the dot product size also gets more significant. In order to ensure the stability of the calculation, the result of the dot product needs to be divided by a constant. The obtained result is then calculated by the Softmax layer to obtain the weight vector A. Finally, the weight vector A and the V matrix are multiplied to get the attention score vector B:

$$\begin{aligned}& A = \mathrm{Softmax} \biggl(\frac{K^{T}Q}{\sqrt{d_{k}}} \biggr), \end{aligned}$$
(5)
$$\begin{aligned}& B = VA. \end{aligned}$$
(6)

Where, Q, K, and V are matrices of input vectors, \(d_{k}\) is the dimension of the input vectors.

Transformer uses Multi-headed Attention. Transformer initializes h groups of Q, K, and V matrices for the input vector and performs an attention function for each group of Q, K, and V in parallel. In order to meet the input requirements of the feedforward layer, \(W^{O}\) is defined and multiplied by h groups of weight matrices to train the model jointly. Finally, the matrix fused with all the attention header information is sent to the feedforward layer for the following calculation. The multi-head attention calculation formula is as follows:

$$\begin{aligned}& \mathrm{head}_{i} = \mathrm{Attention}\bigl(QW_{i}^{Q},KW_{i}^{K},VW_{i}^{V} \bigr), \end{aligned}$$
(7)
$$\begin{aligned}& \mathrm{MultiHead}(Q,K,V) \\& \quad = \mathrm{Concat}(\mathrm{head}_{1}, \ldots ,\mathrm{head}_{h})W^{O}. \end{aligned}$$
(8)

Where, \(W_{i}^{Q}\), \(W_{i}^{K}\), \(W_{i}^{V}\) are the parameter matrices of the Q, K, and V matrices, and \(W^{O}\) are the additional matrices.

The output of the multi-head attention layer is mapped into a higher dimensional space through a feedforward neural network. In a feedforward neural network, neurons between layers are fully connected to the input and receive signals. The core of the feedforward neural network is a 2-layer linear transformation. The first layer maps a vector of dimension \(d_{\mathrm{model}}\) to a vector of dimension \(d_{ff}\), and the second layer maps back to a vector of dimension \(d_{\mathrm{model}}\). The ReLu activation function is used in the network. The network can be expressed as:

$$ \mathrm{FFN}(x) = \max (0,xW_{1} + b_{1})W_{2} + b_{2}. $$
(9)

Where, x is the input, W is the weight of the input feature vector, and b is the coefficient.

In addition, there will be residual connections and normalization operations between each layer. After linearizing the matrix containing the global information output by the decoder, it is returned to the vector space through Softmax, and the prediction result is obtained through mapping.

Although transformer is able to learn the long-range relationships between data, it is not suitable for predicting long time series. The main reasons are: 1) The computational complexity of the self-attention mechanism operation is high; 2) The stacking of multi-layer networks leads to a bottleneck in memory usage; 3) The use of step-by-step decoding prediction results in low computational efficiency in long-term sequence prediction tasks. To address these issues, Informer proposes the following improvements:

1) ProSparse Self-attention: For the long-tailed distribution effect of the self-attention score, the relatively lazy Query matrix is eliminated by introducing the KL divergence operation to reduce the computational complexity. The formula is as follows:

$$ A = \mathrm{Softmax} \biggl(\frac{\overline{Q}K^{T}}{\sqrt{d_{k}}} \biggr). $$
(10)

The matrix Q̅ comprises top-u relatively active queries, and the sparsity of the i-th query is evaluated mainly through KL divergence. The evaluation formula is as follows:

$$ M ( q_{i},K ) = \ln \sum_{j = 1}^{L_{K}} e^{\frac{q_{i}k_{j}^{T}}{\sqrt{d}}} - \frac{1}{L_{K}}\sum_{j = 1}^{L_{K}} \frac{q_{i}K_{j}^{T}}{\sqrt{d}}. $$
(11)

Where, the first term of the above formula is the Log-sum-Exp of \(q_{i}\) for all keys, and the second term is the arithmetic mean.

2) Self-attention Distilling: Assign higher weights to dominant features with a dominant role, which reduces the number of parameters in the model network. The distillation operation from j to \(j + 1\) layers is as follows:

$$ X_{j + 1}^{t} = \operatorname{Max} \operatorname{Pool} \bigl( \operatorname{ELU} \bigl( \operatorname{Convld} \bigl( \bigl[ X_{j}^{t} \bigr]_{AB} \bigr) \bigr) \bigr). $$
(12)

Where, \([\bullet ]_{AB}\) includes the critical operations in ProSparse Self-attention. \(\mathrm{Convld}(\bullet )\) represents a one-dimensional convolution operation on time series. The activation function is ELU. \(\mathrm{MaxPool}(\bullet )\) represents max pooling operation.

3) Generative Style Decoder: Use a generative structure to generate all prediction sequences simultaneously, significantly reducing prediction decoding time. The vector provided to the decoder is as follows:

$$ X_{\mathrm{feed}\_\mathrm{de}} = \{ X_{\mathrm{token}},X_{0} \}. $$
(13)

Where, \(X_{0}\) is a placeholder for the target sequence.

3.2 Enhanced informer

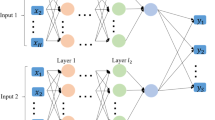
Although the informer model can assign higher weights to important features in the time series based on the attention mechanism, the model also needs to focus on the evolution of system variables caused by parameter drift when predicting critical phenomena. In order to make the model effectively exploit the correlation between parameter drift and system variable evolution, this paper enhances the informer model by designing bifurcation parameter channels. The enhanced informer model is shown in Fig. 4.

Figure 4
figure 4

Enhanced informer architecture

Full size image

As shown in Fig. 5, the enhanced informer model can be divided into three parts: 1) Input layer: the input channels of the model include parameter channels and variable channels. The input of the parameter channel is the bifurcation parameter ε of the system, and the input of the variable channel is the time series data of the system variables. The parameter channels that feed bifurcation parameters to the model can be connected to each node in the model, thus allowing the model to track changes in bifurcation parameters in the time series data. Before the data is transmitted to the Encoder-Decoder layer, the data dimension in the channel needs to be transformed to \(d_{\mathrm{model}}\). Due to the importance of the data order problem in the time series prediction problem, positional coding is used in the model to mark the local and global backward and forward temporal relationships of the variables, thus capturing the long-term dependence of the system’s six sets of variables and bifurcation parameters in time during the training process. The selection of bifurcation parameters in the parameter channel is based on empirical criteria. It is mainly selected from the bifurcation parameters when the system is oscillating, and these bifurcation parameters need to be close to the critical point of the system. The reason is that when the bifurcation parameters are near the critical point, the time series corresponding to the dynamic variables can provide more effective critical signals. In contrast, when the bifurcation parameters of the system are far from the critical point, the critical signals in the corresponding time series will be significantly lower. When selecting multi-group bifurcation parameters, the distance between bifurcation parameters needs to be reasonably spaced. The following vectors are transmitted to the Encoder and Decoder in the input layer:

$$\begin{aligned}& X_{\mathrm{feed}\_\mathrm{en}} = \bigl[ X^{p};X_{\mathrm{token}1}^{2t}; \ldots ;X_{\mathrm{token}6}^{2t} \bigr], \end{aligned}$$
(14)
$$\begin{aligned}& X_{\mathrm{feed}\_\mathrm{de}} = \bigl[ X^{p};\mathrm{Contact}\bigl(X_{\mathrm{token}1}^{t},X_{0}^{t} \bigr); \ldots ; \\& \hphantom{X_{\mathrm{feed}\_\mathrm{de}} ={}}\mathrm{Contact}\bigl(X_{\mathrm{token}6}^{t},X_{0}^{t} \bigr) \bigr], \\& \quad \mathrm{Contact}\bigl(X_{\mathrm{token}}^{t},X_{0}^{t} \bigr) \in R^{(L_{\mathrm{token}} + L_{y}) \times d_{\mathrm{model}}}. \end{aligned}$$
(15)

The input vector X consists of the values of the bifurcation parameters and the correlation measurement time series from each variable of the target system. The input of the bifurcation parameter value allows the model to focus on the effect of parameter drift on the data characteristics and fully exploit the correlation between the bifurcation parameter and the system variables. The input to the encoder is a long sequence of historical data and bifurcation parameter features, while the input of decoder consists of a short sequence and zero values, and the length of the zero value sequence is equal to the prediction length. The short sequence is the implied intermediate feature data about the system variables and bifurcation parameters output by the encoder, and the zero values in the decoder input are used as placeholders for the evolutionary values of the predictor variables.

Figure 5
figure 5

Operating states of the system under different bifurcation parameter values

Full size image

2) Encoder-Decoder layer: it consists of encoder and decoder. The encoder and decoder are stacked by Multi-head ProbSparse Self-attention module and Distilling mechanism module. The encoder can obtain the dependencies between the time series of system variables and the bifurcation parameters. Based on the multi-headed probabilistic sparse self-attentiveness mechanism, the encoder can assign greater weights to the important features that reflect the changes in the bifurcation parameters. After multiple multi-head sparse self-attention score calculations and distilling processing, the encoder outputs an intermediate feature to the decoder containing information about the drift of the bifurcation parameters and the temporal evolution of the variables. The data input to the Decoder needs to go through a masked multi-headed probabilistic sparse self-attentive operation before it can perform a multi-headed attention operation with the intermediate features output by the encoder. This process mainly prevents each location from paying attention to the system evolution information after parameter drift occurs, so as to fully exploit the association between the current bifurcation parameters and the timing information. After completing the calculation, the decoder outputs the operation result to the fully connected layer.

3) Output layer: The output layer adjusts the dimension of the data output through a fully connected neural network. After completing the loss function calculation of the predicted result, the model is continuously optimized through reverse gradient propagation.

During the training process, the enhanced informer needs to be independently trained based on multiple bifurcation parameter values. The specific process is that when the data training of a set of bifurcation parameter values is completed, the time and initial state of the system need to be reset to zero. Then, the model is repeatedly trained by inputting the data corresponding to another set of bifurcation parameter values through the parameter channel and the variable channel. After completing the model training based on all selected bifurcation parameters, multiple records of model training results can be obtained. In the training process of multi-group bifurcation parameters, the minimum MSE and MAE are used as the criterion to determine the model parameter matrix. Therefore, an essential requirement is that the enhanced informer is well-trained in each selected bifurcation parameter and thus can predict the system behavior at other parameter values that the model has not yet been exposed to. Since the training data consists of time series corresponding to the selected parameter values, the short-term prediction performance of these parameter values requires essential attention.

4 Numerical experiment and result analysis

4.1 Experiment description

In the experiment of this paper, the informer and the enhanced informer are built based on python and the deep learning framework PyTorch. In terms of experimental hardware, three Nvidia GeForce RTX 4000 GPUs are used to train and validate deep learning models. The settings of the model hyperparameters are mainly adjusted according to the model training and experimental results. The final model hyperparameter values are shown in Table 1. In order to verify the optimization effect of the enhanced informer in terms of prediction performance, the hyperparameter settings of the two models are the same.

Table 1 Hyperparameters of models. Models: Informer and Enhanced Informer
Full size table

In a single prediction task, the input data length in the Encoder and Decoder is 14.40s, and the prediction length is 7.20s. The output results of the prediction process are analyzed by inverse normalization to obtain the final prediction value of the evolution of system dynamic variables.

4.2 Data selection

When training a prediction model, it needs to be done in a state where the system does not experience amplitude death. Therefore, when generating the time series for training the model, the bifurcation parameter value of the system is required to be less than the critical value. Based on empirical criteria, when the bifurcation parameter value of the system is closer to the critical value, the corresponding time series input model can obtain a relatively better training effect. Therefore, the bifurcation parameters selected in this paper are 0.36, 0.34 and 0.32, all of which correspond to the system under oscillation. Taking \(y_{1}\) as an example, the operating states of the system under the above bifurcation parameter values are shown in Fig. 5 (a)(b)(c), respectively, and the corresponding initial values are all randomly generated.

4.3 Data preprocessing

Data preprocessing includes data normalization and dataset partitioning. There are six variables in the coupled Rössler and Lorenz system: \(x_{1}\), \(x_{2}\), \(x_{3}\), \(y_{1}\), \(y_{2}\), \(y_{3}\). These six variables and bifurcation parameters are used to construct the input of the prediction model. The total length of each set of data is 10,000s, and the sampling frequency is 0.01s. Due to the dimensional gap between variables and bifurcation parameters, it is necessary to normalize the data to improve the model’s prediction accuracy. The formula is as follows:

$$ x^{*} = \frac{x - \overline{x}}{\sigma}. $$
(16)

Where, σ is the standard deviation of the sample data, and x̅ is the mean of the sample data. The standardized data is divided into a training set, validation set and test set according to the ratio of 3/1/1.

4.4 Analysis of experimental results

The analysis of the experimental results is mainly based on comparing the effective prediction length of the two prediction models and whether they can predict the phenomenon of amplitude death.

4.4.1 Effective prediction length

First, compare the evaluation metrics MAE and MSE between the two models. The comparison results are shown in Table 2. The results in the table are the sums of MAE and MSE for the six variables of the system, averaged over the results of fifteen operations of the model.

Table 2 Evaluation of models
Full size table

Analyzing the results in the above table, it can be found that when predicting the evolution of the system variables of the coupled Rössler and Lorenz systems in the next 7.2s, the MAE and MSE of the enhanced informer are reduced by 12% and 17%, respectively, compared with the original model. According to the comparison of evaluation indicators, enhanced informer has a minor error in predicting the evolution trend of the chaotic system than the original model and can achieve better prediction accuracy.

Further, it is necessary to compare the effective length of time when the two models predict the evolution of system variables. Taking the evolution prediction of the \(x_{3}\) as an example, when the prediction target length is 7.2s, the effective prediction lengths of the informer and enhanced informer are shown in Fig. 6 (a),(b), respectively. In the comparison of results, the corresponding bifurcation parameter of the selected time series is 0.34, and the initial value is random. The result graph takes the best of the fifteen prediction results of each of the two models.

Figure 6
figure 6

Effective prediction length of models

Full size image

According to the above figure’s results, the original model’s effective prediction length is about 4.2s, and the effective prediction length of the enhanced informer is about 5.5s. Compared with the original model, the effective prediction length of the enhanced informer is increased by about 30%. It can be seen that the prediction effectiveness of both models decreases in the later stage of prediction, and the enhanced informer is still able to achieve relatively high prediction accuracy. Comparatively speaking, the predicted value of enhanced informer has a better fit to the actual value. The results show that the enhanced informer can better obtain the long-term dependencies of the time series of chaotic systems, and is more effective in the long-term forecasting process.

4.4.2 Amplitude death prediction

The amplitude death prediction experiment trains the model based on the time series when the target system bifurcation parameter value is \(\varepsilon _{0}\). Then the evolution trend of the system variables is predicted when the bifurcation parameter value is \(\varepsilon _{1} = \varepsilon _{0} + \Delta \varepsilon \). Where \(\Delta \varepsilon > 0\) is the parameter drift, \(\varepsilon _{0} < \varepsilon _{c}\), \(\varepsilon _{1} > \varepsilon _{c}\). The experimental results of the amplitude death prediction of the two models are respectively shown in Fig. 7 (a),(b). In the comparison of results, the corresponding bifurcation parameter of the selected time series is 0.5, and the initial value is random. The resulting graph includes a segment of the inputs to the predictive model. Among the fifteen prediction results of both models, there are differences as shown in Fig. 7.

Figure 7
figure 7

Prediction of amplitude death of models

Full size image

According to the experimental results, the enhanced informer model can predict the transient chaotic behavior of the system and the subsequent amplitude death phenomenon more accurately. According to the experimental results, the enhanced informer model can more accurately predict the transient chaotic behavior of the system and the subsequent amplitude death phenomenon. It shows that the enhanced model can be used to predict the characteristic changes caused by parameter drift in the behavior of chaotic systems. The experimental results prove that the ability of the enhanced informer to capture the relationship between the evolution of system variables and the drift of bifurcation parameters is optimized with the addition of parameter channels.

The above experimental results show that the enhanced informer, while introducing the self-attention mechanism, provides information on parameter drift for variable evolution by using bifurcation parameters as features of the input network model and fully explores the deep features of variable evolution in chaotic systems, thus achieving better prediction results.

5 Conclusion

Critical phenomena are research focus in all kinds of complex systems. As a classic critical phenomenon, the occurrence of amplitude death may lead to the collapse of the whole system, so the prediction method of amplitude death has attracted the attention of scholars. The rise of machine learning provides new ideas for solving this problem. However, current machine methods for predicting amplitude mortality prediction phenomena are mainly based on reservoir computing. Therefore, this paper adopts a novel deep learning method to solve the problem of amplitude death prediction. An enhanced informer model architecture is proposed based on the idea that the additional bifurcation parameter channel can improve the model’s amplitude death prediction ability. By constructing the bifurcation parameter channel of the prediction model, the model has the ability of parameter perception so that the dynamic state of the system can be more accurately predicted. This paper chooses to conduct experiments on the coupled Rössler and Lorenz systems to verify the performance of the enhanced model. The experimental results show that the enhanced informer proposed in this paper can effectively improve the adequate prediction time of the original model for predicting the evolution of chaotic system variables. When the system parameters drift to the region of amplitude death, the enhanced informer can predict whether the system will have the phenomenon of amplitude death.

Since the prediction model proposed in this paper is data-driven, future work can be expected to address the problem of complex system behavior prediction in industrial and military scenarios and provide support for critical regulation research of complex systems.